在城市交通信号控制中,城市交通系统自身复杂性是制约通行效率提升的重要因素之一.自组织可有效描述系统状态变化过程,适用于交通信号控制.自组织控制的核心要素是邻域及控制规则,其中邻域是指控制规则的规则响应半径,在控制系统内一般体现为元素空间位置的集合;邻域的重构是指关联相邻路口组合的重构, 邻域重构时控制目标对应的控制规则相关半径随即发生改变.规则邻域的重构是指邻域进行重构以后,在新邻域下重新建立的控制规则.
邻域的范围决定了系统内部的时空特性关系.对邻域的应用研究体现在各学科领域中,仅针对邻域内时间关系的研究,多以系统内元素间在时间序列上的特征演化[1-2]为主,如文献[3]利用禁止字理论等方法证明了邻域可对复杂时间特征进行表达;仅针对邻域内空间特性的研究,常采用固定半径的邻域,这类研究多集中在图像处理上[4-5],这两类方法大多无法直接应用到复杂时空特性的系统解析中.在结合邻域内时空特性的研究中,文献[6]利用自组织特征映射对汽车尾气非线性问题进行解析,利用不同的邻域半径代替固定邻域半径,证明了不同的邻域可以对不同交通状态分别进行描述;尾气解析问题具有一定的时间特征,因此邻域重构可以有效分析系统的时空特性.文献[7-8]提出了一个具有局部规则以及固定邻域半径的自组织元胞自动机模型,证明了规则邻域是自组织控制系统解析交通信号控制的一种有效方法,规则邻域在交通信号控制中可以表达路口间的空间关系以及流量间的时间关系,但无法补偿由复杂时空特性导致的通行效率难以继续提升的问题.因此,邻域的范围决定了控制规则的精度,采用固定规则邻域的控制系统随系统自身复杂性提高会带来的控制精度损失的问题,需要对控制规则邻域重构以提高系统的控制精度.本文对城市交通信号自组织控制系统中当前路口与其相邻路口集合空间实现时空量化的关系进行表达,选取关联相邻路口组合方式,并建立对应组合的规则邻域,通过规则邻域的重构解决固定邻域控制精度的问题.
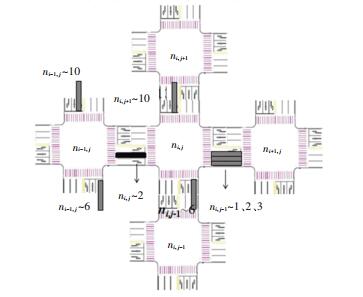
1 城市交通信号自组织系统在城市信号自组织控制系统中,每个路口独立计算信号配时且拥有各自的邻域. 图 1为本文提出的最小邻域的自组织交通控制单元,该模型由5个路口构成,中心路口(以下简称当前路口)每个方向最多连接一个路口,4个方向上相邻路口组成当前路口的最小邻域.
|
图 1 最小邻域半径的自组织交通控制单元 Fig. 1 The smallest neighborhood radius of the self-organizing traffic control unit |
定义当前路口ni, j为基点元胞,则元胞ni, j的状态集为∑ni, j=(p1, p2, …, pn), 其中pn为信号相位状态,定义共有n种有限的信号相位状态;定义最小邻域为基点元胞在二维正负方向上相邻的连接元胞,定义元胞ni, j与相邻元胞的局部连接关系为f(ni, j~l, α, cs),其中n~l为对应路口n内车道l的序号、α为路口n的上下游连接关系、cs为当前车道l交通拥挤强度.当前路口ni, j的控制参数由5个路口的实时交通信息决定.该最小邻域自组织控制单元以时间步长为单位进行时间离散,以平均速度、相对拥挤强度进行空间离散.在图 1中表示东向西直行方向下的路口n上下游连接方式,其中深色车道表示当前车道l,浅色车道表示与l在当前信号相位下的上下游连接车道,数字表示该路口内车道编号.
最小邻域在尺寸rmax×rmax城市路网中位置形式可表示为
| $ {a_n} = \left[ {\begin{array}{*{20}{c}} {{n_{0,{r_{\max }}}}}& \cdots & \cdots & \cdots & \cdots &{{n_{{r_{\max }},{r_{\max }}}}}\\ \cdots & \cdots & \cdots &{{n_{i,j + 1}}}& \cdots & \cdots \\ \cdots & \cdots &{{n_{i - 1,j}}}&{{n_{i,j}}}&{{n_{i + 1,j}}}& \cdots \\ \cdots & \cdots & \cdots &{{n_{i,j - 1}}}& \cdots & \cdots \\ {{n_{0,0}}}& \cdots & \cdots & \cdots & \cdots &{{n_{{r_{\max }},0}}} \end{array}} \right], $ |
随着状态自组织过程的演化,时刻t下,选取的基点元胞各方向关联元胞个数增加至r时,该元胞邻域扩展的形式可表示为
| $ \begin{array}{l} a_n^t = \\ \left[ {\begin{array}{*{20}{c}} {{n_{{r_{\max }},0}}}& \cdots & \cdots & \cdots & \cdots & \cdots &{{n_{{r_{\max }},{r_{\max }}}}}\\ \cdots & \cdots & \cdots &{{n_{i,j + r}}}& \cdots & \cdots & \cdots \\ \cdots & \cdots &{{n_{i - r + 1,j + r - 1}}}& \cdots &{{n_{i + r - 1,j + r - 1}}}& \cdots & \cdots \\ \cdots &{{n_{i - r,j}}}& \cdots &{{n_{i,j}}}& \cdots &{{n_{i + r,j}}}& \cdots \\ \cdots & \cdots &{{n_{i - r + 1,j - r + 1}}}& \cdots &{{n_{i + r - 1,j - r + 1}}}& \cdots & \cdots \\ \cdots & \cdots & \cdots &{{n_{i,j - r}}}& \cdots & \cdots & \cdots \\ {{n_{0,0}}}& \cdots & \cdots & \cdots & \cdots & \cdots &{{n_{{r_{\max }},0}}} \end{array}} \right], \end{array} $ |
令r在二维正负方向上都有不同取值且对角取值不对称时,该邻域模型可表示为
| $ \begin{array}{l} a_{{n_{ri}}}^t = \\ \left[ {\begin{array}{*{20}{c}} {{n_{0,{r_{\max }}}}}& \cdots & \cdots & \cdots & \cdots & \cdots &{{n_{{r_{\max }},{r_{\max }}}}}\\ \cdots & \cdots & \cdots &{{n_{i,j + {r_4}}}}& \cdots & \cdots & \cdots \\ \cdots & \cdots &{{n_{i - {r_5},j + {r_6}}}}& \cdots &{{n_{i + {r_7},j + {r_8}}}}& \cdots & \cdots \\ \cdots &{{n_{i - {r_1},j}}}& \cdots &{{n_{i,j}}}& \cdots &{{n_{i + {r_2},j}}}& \cdots \\ \cdots & \cdots &{{n_{i - {r_9},j - {r_{10}}}}}& \cdots &{{n_{i + {r_{11}},j - {r_{12}}}}}& \cdots & \cdots \\ \cdots & \cdots & \cdots &{{n_{i,j - {r_3}}}}& \cdots & \cdots & \cdots \\ {{n_{0,0}}}& \cdots & \cdots & \cdots & \cdots & \cdots &{{n_{{r_{\max }},0}}} \end{array}} \right]. \end{array} $ |
式中r定义约束为{r5≤r1, r9≤r1,r7≤r2, r11≤r2,r10≤r3, r12≤r3,r6≤r4, r7≤r4}.
在自组织过程中,时刻t将决定时刻t+1下的元胞状态,因此规则邻域下的局部规则可表示为
| $ \mathit{\boldsymbol{a}}_{{n_{ri}}}^{t + 1} = f\left( {\mathit{\boldsymbol{a}}_{i - {r_1},j}^t,\mathit{\boldsymbol{a}}_{i - {r_5},{r_6} + j}^t, \cdots ,\mathit{\boldsymbol{a}}_{i,j}^t, \cdots ,\mathit{\boldsymbol{a}}_{i + {r_{11}},j - {r_{12}}}^t,\mathit{\boldsymbol{a}}_{i + {r_2},j}^t} \right). $ | (1) |
由式(1)可知,当邻域内任意r取值发生变化时,该邻域的局部规则也随之改变.当路网结构特性比例差过大或路面交通流剧烈变化时,为提高系统控制精度,可提高r的取值.邻域每向周围扩散一个路口,则系统算法增加一步差分过程,邻域的扩大不会增加系统动力方程的阶次,因此可以保证控制系统的实时响应.
2 关联相邻路口集合的时空量化表达 2.1 当前路口相对其他任意路口的位置与连接表达路网拓扑结构决定了当前路口与其他任意路口的空间位置关系,由于路口间空间位置关系不足以表达当前路口与其相邻路口集合间因路网结构产生的交通特征变化,因此需要对当前路口与其他路口的连接关系行表达.
2.1.1 各路口位置之间的空间距离各路口之间的空间位置是一种静态的表达关系,不考虑各路口连接方式的情况下,可以通过提取路网因素构建各路口位置之间的广义空间距离[9]模型,Dnm用以路网内任意路口m相对于当前路口n的空间位置关系量化表达.
| $ \sum\limits_m {{D_{nm}}} = \sum\limits_m {\frac{1}{{{\alpha _{nm}} + 1}}} \left( {{d_{nm}} + \sum\limits_k {N_{nm}^k} L_{nm}^k} \right). $ | (2) |
式中:n为当前路口;m为区域内任意路口;Dnm为广义空间距离;αnm为上下游系数,不存在则为0;dnm为路口n、m空间最短距离;Nnm为路口n、m中间连接的不同类型路口的个数;k为每个路口的类型;定义T型与Y型路口值为3,十字型与X型路口值为4,其他类型值为5;Lnm表示连接路口n、m的实际距离,按最短路径与路口类型依次累计相邻路口的距离.
2.1.2 基于广义空间距离的路口间空间位置与连接关系的联合表达根据式(2)量化各路口间的位置参数并完成计算;通过引进因子分析法[10-11],将路口间的位置与连接关系合并为同一个因子分析项,计算得到路口空间位置与连接关系的联合特征量化值,可实现当前路口与相邻关联路口集合间空间连接关系的量化表达,为邻域构造的空间划分提供依据.其计算过程为:
1) 编制该区域内二维列联表,设路网内有东西方向路口Ai(i=1, 2...., p)、南北方向路口Bj(j=1, 2, ..., q),则可以得到p×q的广义空间距离的二维联表D,见表 1.
| 表 1 路口空间关系二位列联表D Tab. 1 Binary contingency table D of intersection spatial relations |
2) 将二维列联表D转化为自身频率矩阵F, 其中按原始数据所占的比例将任意dnpmq转化为对应因素关系的频率fnpmq,其中
| $ {F_{nm}} = \frac{{{d_{nm}}}}{{\sum\limits_n^p {\sum\limits_m^q {{d_{nm}}} } }}. $ | (3) |
3) 对频率矩阵进行标准化,得到过渡矩阵Z = [znm],其中
| $ {z_{nm}} = \frac{{{F_{nm}} - {F_n}{F_m}}}{{\sqrt {{F_n}{F_m}} }}. $ | (4) |
4) 利用协方差进行因子分析.计算可得非零特征根组λ1 < λ2 < … < λk, k∈min(p, q),设μk为相对特征根的关于Bj的各水平之间的协方差矩阵的特征向量,则Zμk为相对特征根的关于Ai的各水平之间的协方差矩阵的特征向量.可以分别得到关于Bj的q个因子矩阵Q以及关于Ai的p个因子矩阵P,可以通过分析因子矩阵计算并量化Ai、Bj之间的连接关系. P、Q表达分别为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{P}} = \left[ {\begin{array}{*{20}{c}} {{\mu _{11}}\sqrt {{\lambda _1}} }&{{\mu _{12}}\sqrt {{\lambda _2}} }& \cdots &{{\mu _{1p}}\sqrt {{\lambda _p}} }\\ {{\mu _{21}}\sqrt {{\lambda _1}} }&{{\mu _{22}}\sqrt {{\lambda _2}} }& \cdots &{{\mu _{2p}}\sqrt {{\lambda _p}} }\\ \vdots & \vdots & \vdots & \vdots \\ {{\mu _{p1}}\sqrt {{\lambda _1}} }&{{\mu _{p2}}\sqrt {{\lambda _2}} }& \cdots &{{\mu _{pp}}\sqrt {{\lambda _p}} } \end{array}} \right],}\\ {\mathit{\boldsymbol{Q}} = \left[ {\begin{array}{*{20}{c}} {Z{\mu _{11}}\sqrt {{\lambda _1}} }&{Z{\mu _{12}}\sqrt {{\lambda _2}} }& \cdots &{Z{\mu _{1q}}\sqrt {{\lambda _q}} }\\ {Z{\mu _{21}}\sqrt {{\lambda _1}} }&{Z{\mu _{22}}\sqrt {{\lambda _2}} }& \cdots &{Z{\mu _{2q}}\sqrt {{\lambda _q}} }\\ \vdots & \vdots & \vdots & \vdots \\ {Z{\mu _{q1}}\sqrt {{\lambda _1}} }&{Z{\mu _{qn2}}\sqrt {{\lambda _2}} }& \cdots &{Z{\mu _{qq}}\sqrt {{\lambda _q}} } \end{array}} \right].} \end{array} $ | (5) |
5) 计算各因子得分,得路网内各路口之间位置与连接的量化表达,见表 2.表 2中数值越小表示对应编号的路口与当前路口n在空间关系上相关性越大.需要把相邻路口按当前路口的连接方向进行分类,通过选取相对于当前路口因子得分相近的相邻路口集合进行不同邻域的划分.
| 表 2 路口空间位置与连接的量化表达 Tab. 2 Quantitative expression for spatial location and connection of intersection |
交通流间传递的相互影响程度随时间变化在空间距离上逐渐衰减,通过计算交通流间的相关系数[12],分析交通流在指定采样周期下的影响距离,通过时间序列实现所有路口的流量相对于当前路口流量的量化表达.交通流时间序列主要指路网内路段在特定时间段内统计的流量值.本文采用路口在单位时间内的交通流量作为交通流时间特征参数[7].
定义n路口内任意车道l为n~l, 将n~l的时间流量序列记为(n~l)*=(1, 2, …, G),G为该车道l内划分的路段数,将时间序列按不同的行进方向分类统计.当相关系数从路段(n~l)*1与邻域内某相邻路口m中某一路段(m~l)*G开始变化不再明显,将(n~l)*1与(m~l)*G之间的距离定义为当前路口在该时间序列下交通流的影响距离.因此,该影响距离将作为邻域重构的空间边界条件.
时间流量序列主要受采样周期影响,本文采用15 s的采样周期.采样周期的改变将直接影响各路段流量序列的采集值,在自组织控制中,在每个采样周期开始的时刻进行拥挤强度计算,需调用上一采样周期的数据.因此,时间序列相关系数只与流量大小有关,计算当前路口n与相邻路段(m~l)*的时间序列相关系数为
| $ {C_{\left( {n \sim l} \right),\left( {m \sim l} \right)}} = \frac{{{\mathop{\rm cov}} \left( {n,m} \right)}}{{\sqrt {D\left( {{{\left( {n \sim l} \right)}^ * }} \right)D\left( {{{\left( {m \sim l} \right)}^ * }} \right)} }}, $ | (6) |
式中D(·)为方差,cov(·)为协方差.其中方差是分别对(n~l)*、(m~l)*整个时间序列长度内各采样周期内的值进行方差统计计算,协方差是对(n~l)*和(m~l)*整个时间序列长度内各采样周期内的值进行协方差统计计算,时间序列长度即采样周期的个数.
式(6)计算结果仅表示不同时间序列相互影响程度的关系,其值越大,时间序列间影响关系越大.式(6)自身不体现时间因素,而(n~l)*、(m~l)*的采集值与时间因素有关,受采样周期以及整个时间序列长度影响.
将分类的流量统计数据分类比对,按时间序列相关系数即可找到交通流随时间传递的影响路段个数,相关系数越大表示两者时间关系上相互影响越大.通过设置不同的时间序列,可以对路口间交通流传递随时空特性的变化关系实现量化的表达.
3 交通信号自组织控制规则邻域的重构当前路口的关联相邻路口集合时空量化关系计算完成后,根据计算所得的时空特性系数大小选取当前路口最大的邻域边界条件,在边界条件范围中选定任意数量的关联相邻路口即构成一个邻域.在自组织控制中,当邻域发生改变,被控制个体与其相邻间个体在时空特性上的联结方式也随之改变,需要对控制规则进行修正,实现决策个体与邻域内所有个体间时空关系的描述,以完成控制规则邻域的整个重构过程.
在图 1所示的自组织最小单元中,依靠信号切换规则实现信号控制,该控制规则基于流体力学中N-S方程,通过对该方程进行数学重构后控制规则基础表达式[7]为
| $ \frac{{{\rm{d}}u}}{{{\rm{d}}t}} = {f_b} - \frac{1}{\rho }\nabla p + \mu {\nabla ^2}V. $ | (7) |
式中:
式(7)以流体力学为基础构建,将流体力学中的质量、速度、压力分别换算为交通流中的密度、车速、流量.当交通流运行状态越稳定时,越符合不可压缩流体的运动特征.将路网视为二维平面网络,利用差分方程在东西方向上对式(7)进行推导,可得到关于路口n在t+1时刻下的状态自组织控制规则为
| $ \begin{array}{l} l\left( t \right)_{{n_{i,j}},k}^{l + 1} = \left( {1 - 2{\lambda _1} - {\lambda _2}} \right)l\left( t \right)_{{n_{i,j}},k}^l + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\left( {{\lambda _1} - {\lambda _2}} \right)l\left( t \right)_{{n_{i - 1,j}},k}^t + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\left( {{\lambda _1} + {\lambda _2}} \right)l\left( t \right)_{{n_{i + 1,j}},k}^t + \frac{{{\lambda _2}}}{2}. \end{array} $ | (8) |
式中:
式(8)中,流体密度ρ对应交通量可以替代为道路上车辆数,通过检测数据获得.粘滞系数μ指流体的运动粘性系数,对应到城市交通中,由于无法直接实现该参数计算,其取值与当前时间步内车流的密度、道路形态以及驶出路口距离有关[7],通过对道路形态的取值实现路口主次干道的属性区分.在自组织城市信号控制系统中,邻域改变时需要通过对式(8)进行规则重构,以满足当前路口在该邻域下与其他路口的连接关系,表达为
| $ \left\{ \begin{array}{l} l\left( t \right)_{{n_{i,j}},k}^{l + 1} = \left( {1 - 2{\lambda _1} - {\lambda _2}} \right)l\left( t \right)_{{n_{i,j}},k}^l + \left( {{\lambda _1} - {\lambda _2}} \right)l\left( t \right)_{{n_{{n_{i - 1}},j}},k}^l + \left( {{\lambda _1} + {\lambda _2}} \right)l\left( t \right)_{{n_{i + 1,j}},k}^l + \frac{{{\lambda _2}}}{2},\\ l\left( t \right)_{{n_{i - 1,j}},k}^{l + 1} = \left( {1 - 2{\lambda _1} - {\lambda _2}} \right)l\left( t \right)_{{n_{i - 1,j}},k}^{t + 1} + \sum\limits_{r = 1}^{r1} {{C_{\left( {{n_{i - r}} - l} \right),\left( {{n_{i - r - 1}} - l} \right)}}} \left( {{\lambda _1} - {\lambda _2}} \right)l\left( t \right)_{{n_{i - r,j}},k}^{t - 1} \\+ \left( {{\lambda _1} + {\lambda _2}} \right)l\left( t \right)_{{n_{i,j}},k}^{t - 1} + \frac{{{\lambda _2}}}{2},\\ l\left( t \right)_{{n_{i + 1,j}},k}^t = \left( {1 - 2{\lambda _1} - {\lambda _2}} \right)l\left( t \right)_{{n_{i + 1,j}},k}^t + \sum\limits_{r = 1}^{r2} {{C_{\left( {{n_{i + r}} - l} \right),\left( {{n_{i + r + 1}} - l} \right)}}} \left( {{\lambda _1} + {\lambda _2}} \right)l\left( t \right)_{{n_{i + r,j}},k}^{t - 1} \\+ \left( {{\lambda _1} - {\lambda _2}} \right)l\left( t \right)_{{n_{i,j}},k}^{t - 1} + \frac{{{\lambda _2}}}{2}. \end{array} \right. $ | (9) |
式(9)表征邻域结构为anrt的沿东西方向上的规则重构方式,由于差分过程仅表示上下游关系,因此对应邻域在南北方向的规则重构与式(9)相同,只需要调整邻域的边界值即可.若邻域构型为非对称,则需要对东西或南北方向上非对称部分添加运算过程.
对应的信号相位的相对拥挤强度l(t)到达预设阈值l(t)threshold时,向系统提出信号切换请求,l(t)threshold基础值为0.7,由于自组织微观特征中单车道的拥挤相的临界值为0.75,而多车道间车辆的相互运动可以降低该值[13-14],因此选择3车道的基础值为0.7,具体数值根据路网结构可调整设计[15-19].
4 仿真验证为观察规则邻域重构对城市信号自组织控制系统在路口通行最大能力、路口整体通行能力以及应对路口拥挤程度变化的具体影响,设计一组基于实际局部城市路网的仿真试验.由于自组织控制属于变周期控制方式,更适合比较不同规则邻域的控制效果.最小规则邻域等同于固定局部规则,用于观察邻域重构能否解决固定局部规则中控制精度问题[20-22].
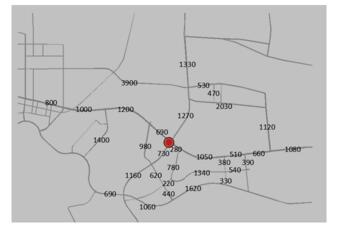
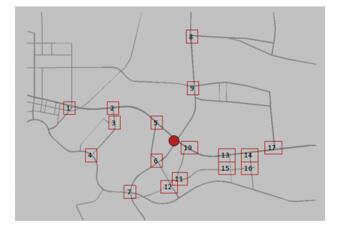
仿真采用上海市嘉定区某实际局部地图,其中路网中部分关键道路长度如图 2所示,道路长度使用卫星地图进行测距. 图 3为仿真中路口序号编序示意图,采用图 3实心圆标注路口为测试路口,取自西向东道路方向为测试数据源.设定车辆在道路中段不可再次进行换道行为;以内置检测器为时间序列路段节点;混车率取98%,最大速度为60 km/h,最小速度为10 km/h;最大周期为120 s,最小周期为60 s;输入流量分别采用600、1 000、1 800 pcu/h 3种流量;仿真总时长取3 600 s;取每一时间步长(time step)为15 s;每个道路口进口与出口都设置有检测器,用于采集路口输入输出流量;采样周期为15 s.记录并观察单位时间段内路口的最大通行能力.
|
图 2 仿真模型中关键道路长度 Fig. 2 Lengths of key sections in the simulation model |
|
图 3 仿真模型中各路口编号 Fig. 3 Numbering of the intersections in the simulation model |
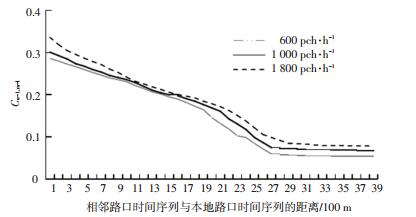
以图 3中实心圆标注路口为当前路口,相邻路口为图 3中其余标记路口.以当前路口为计算对象,在该路口4个连接方向上按100 m划分时间序列路段长度,以内置检测器为标志节点,不足100 m的部分按比例折算.系统运行一次提取记录的交通流数据后,利用式(6)计算每段内的相互关系数,若前后连接车道数不对等,则取平均值.计算所得结果为邻域重构提供范围依据,并为邻域重构后的控制规则提供路段特征参数.绘制路段距离d与交通流相关系数Cnm的关系如图 4所示,其中纵坐标为交通流相关系数Cnm,横坐标为相邻路口时间序列与本地路口时间序列的距离.
|
图 4 不同流量下距离与相关系数的关系 Fig. 4 Relationship between distance and correlation coefficient under different flow rates |
由图 4可知,不同流量下交通流沿路段间传递曲线特征有所不同.流量越大,相互作用关系越大.不同流量下流量随距离传递的衰减趋势一致,整体降幅也基本一致.流量间相互影响系数在一定距离外变化基本稳定,因此定义该距离之外的流量序列不予纳入邻域构建.
根据式(3)~(5)计算3种流量输入下各路口关于当前路口的时空特征关系,取3种流量下的因子得分的平均值记录,结果见表 3.
| 表 3 各路口对于当前路口空间特征相关性 Tab. 3 Correlation of spatial characteristics of intersections with current intersection |
按当前路口的4个方向对所有相关相邻路口分类,并按照该方向上实际路口间距离排列顺序,以每个方向上实际路口间距离最短的相邻路口为基础边界,选取4个方向上在相近因子得分对应的相邻路口为一组邻域.
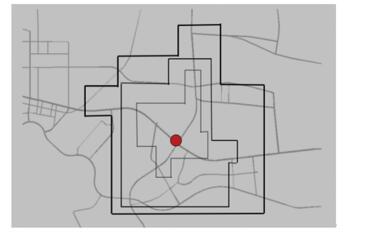
根据表 3和图 4、5的数据,本文设计了如图 5所示的3组邻域,并分别观察不同流量状态下不同规则邻域的控制效果.
|
图 5 3组不同邻域组合 Fig. 5 Three groups of different neighborhood combinations |
组合1构型:anrit=[ri|r1=r2=r3=r4=1;r5=r6=r7=r8=r9=r10=r11=r12=0].
组合2构型:anrit=[ri|r1=1, r2=r3=2, r4=1;r5=r6=r7=r8=r9=r10=0, r11=1, r12=2].
组合3构型:anrit=[ri|r1=2, r2=3,, r3=2, r4=1;r5=r6=r7=r8=r9=r10=0, r11=3, r12=2].
3种组合分别在600、1 000、1 800 pcu/h 3种边界路口输入流量的条件下进行通行能力的对比,由于仿真初始阶段,当前路口车流量不稳定,故从当前路口车流量稳定后开始记录观察.
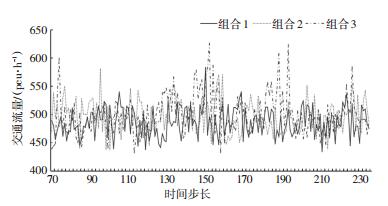
图 6为600 pcu/h各边界路口输入流量下的当前路口通行能力对比,可以明显观察到最大邻域对应的组合3整体通行能力最强,最小邻域对应的组合1整体通行能力最弱.统计可得,组合2比组合1整体通行能力提高了3.9%,组合3比组合1整体通行能力提高了5.3%.组合3可调控的通行能力范围最大,组合1可调控的通行能力范围最小.组合2与组合1最大通行能力基本接近,组合3比组合1最大通行能力提高16.7%.
|
图 6 输入流量600 pcu/h下3种组合的控制效果对比 Fig. 6 Contrast of control effects of three combinations under 600 pcu/h input flow |
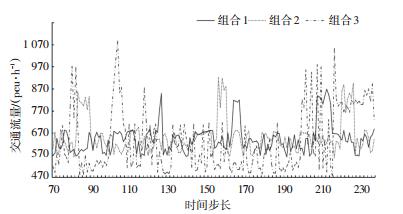
图 7为1 000 pcu/h各边界路口输入流量下的当前路口通行能力对比,可以观察到组合3数值波动次数较多.这主要由于在此流量条件输入下,交通流相变较为频繁,因此范围较大的邻域会相对范围较小的邻域提前开始调整路口通行能力以释放拥堵压力,这个过程符合自组织状态迁移的过程.统计可得,组合2比组合1整体通行能力提高了5.2%,组合3比组合1整体通行能力提高了6.1%.在可调控的最大通行能力上,组合2比组合1最大通行能力提高了12.6%,组合3比组合1最大通行能力提高26.4%.
|
图 7 输入流量1 000 pcu/h下3种组合的控制效果对比 Fig. 7 Contrast of control effects of three combinations under 1 000 pcu/h input flow |
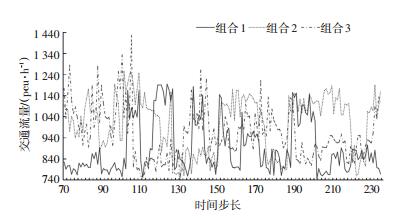
图 8为1 800 pcu/h各边界路口输入流量下的当前路口通行能力对比,组合3与组合1在频域响应变化上的相位差较图 7、8变化更大.说明邻域范围在不同负载条件下的频域特性有较大的差别,邻域越大能利用的范围内的交通信息越多,可以更好地分配各路口的使用效率,从而提高当前路口的通行能力.统计可得,组合2比组合1整体通行能力提高了7.6%,组合3比组合1整体通行能力提高了8.3%.在可调控的最大通行能力上,组合2比组合1最大通行能力提高了7.9%,组合3比组合1最大通行能力提高14.4%.
|
图 8 输入流量1 800 pcu/h下3种组合的控制效果对比 Fig. 8 Contrast of control effects of three combinations under 1 800 pcu/h input flow |
综合图 6~8数据对比可知,当邻域范围越大时,路口可调节的最大通行能力越大、路口整体通行能力越高、路口提前释放拥堵能力越强.在整体通行效率上,组合2与组合3相差不大,对比组合1都有明显提升,在保证一定的通行能力基础上,组合2的整体调节能力在3种组合中过渡最为平稳.组合1为最小规则邻域半径,最小邻域对应的局部规则固定不可变,通过对比3个组合各自的控制效果,发现邻域规则重构能有效改善固定规则半径造成的控制精度问题,随着交通拥挤程度的加剧,邻域范围越大相较于固定规则半径改善效果越好.但是由于实际交通过程中各种随机因素较多,邻域重构的选择也需要考虑流量变化的平稳性,因此邻域重构不能盲目扩大范围.综上所述,结合路网拓扑和交通负载等实时条件,为提高路网控制效率,当前路口自组织控制规则邻域的重构具有必要性.
5 结论1) 建立了城市交通信号自组织控制规则的邻域重构方法,提供了一种面向交通流相变频繁及路网拓扑结构复杂等时空条件的自组织规则构建方法,仿真试验在3种流量条件下测试结果均证明了该方法可以解决系统因固定局部规则造成的控制精度问题.同时邻域重构不能盲目使用,应根据交通状态进行选择,当路网内存在多个或者全部路口同时进行邻域重构时,对整体通行能力提升的趋势不会改变,每个路口实际的通行能力会有所区别.
2) 实现了当前路口与其相邻路口集合的时空量化表达,为邻域的组合选取提供了依据,并完成了控制规则的重构.由于邻域半径的改变只增加系统线性运算的次数,并不会提高系统计算阶次,因此不会影响系统实时控制,其核心思想在于分别简化复杂系统内部时间跟空间在控制过程中的表达方式.整个规则邻域重构的过程为复杂系统下各元素相互间因空间结构各异、时间特性影响密切而难以设计规则邻域半径提供了一种解决方法.
3) 分析仿真数据可以得知:当邻域范围越大时,路口可调节的最大通行能力越大、路口整体通行能力越高、路口提前释放拥堵能力越强;邻域范围应依据当前交通状态进行选择,随交通拥挤程度在保证系统流量平稳过度的前提下提升逐步扩大;邻域规则重构可以提高固定局部规则在交通中间相、交通拥堵相下的控制精度,在交通自由相下两种方式控制精度区别不大.目前选择邻域重构的形式还不能主动拆分系统预设的组合方案,其智能性和工程性还有待提高,训练系统对交通状态的进一步识别以自主选择规则邻域是下一步研究的重点.
| [1] |
项牧.混沌时间序列的非线性去噪方法的研究[D].大连: 大连理工大学, 2007: 11 XIANG Mu. Research on nonlinear denoising method for chaotic time series[D]. Dalian: Dalian University of Technology, 2007: 11 |
| [2] |
CHENG Anyu, JIANG Xiao, LI Yongfu, et al. Multiple sources and multiple measures based traffic flow prediction using the chaos theory and support vector regression method[J]. Physica A: Statistical Mechanics and its Applications, 2017, 466: 422. DOI:10.1016/j.physa.2016.09.041 |
| [3] |
秦大康.元胞自动机生成的时间序列的复杂性研究[D].苏州: 苏州大学, 2005: 21 QIN Dakang. The complexity of time series generated by cellular automata[D]. Suzhou: Soochow University, 2005: 21 http://d.wanfangdata.com.cn/Thesis/Y781236 |
| [4] |
NATITA W, WIBOONSAK W, DUSADEE S. Appropriate learning rate and neighborhood function of self-organizing map (SOM) for specific humidity pattern classification over southern Thailand[J]. International Journal of Modeling and Optimization, 2016, 6(1): 61. DOI:10.7763/IJMO.2016.V6.504 |
| [5] |
ROKA Z. One-way cellular automata on Cayley graphs[J]. Theoretical Computer Science, 1994, 132(1/2): 259. DOI:10.1016/0304-3975(94)90236-4 |
| [6] |
刘鸿淼, 罗德超, 李鹏华. 汽车尾气在自组织特征映射下的排放水平评估方法[J]. 汽车工程学报, 2013, 3(5): 354. LIU Hongmiao, LUO Dechao, LI Penghua. Emissions level assessment method for vehicle exhaust under self-organizing feature mapping[J]. Automotive Engineering Journal, 2013, 3(5): 354. DOI:10.3969/j.issn.2095-1469.2013.05.06 |
| [7] |
魏俊华.城市交通信号自组织控制方法的研究[D].上海: 上海交通大学, 2005: 32 WEI Junhua. Research on self-organized control method of urban traffic signals[D]. Shanghai: Shanghai Jiao Tong University, 2005: 32 http://d.wanfangdata.com.cn/Thesis/Y856784 |
| [8] |
WEI Junhua, WANG Anlin, DU Nianci. Study of self-organizing control of traffic signals in an urban network based on cellular automata[J]. Transactions on Vehicular Technology, 2005, 54(2): 744. DOI:10.1109/TVT.2004.841536 |
| [9] |
杨定华. 广义抽象距离空间的度量方程[J]. 浙江大学学报(理学版), 2003, 37(3): 263. YANG Dinghua. Metricequations of generalized abstract distance spaces[J]. Journal of Zhejiang University (Science Edition), 2003, 37(3): 263. DOI:10.3785/j.issn.10089497 |
| [10] |
陈一, 唐飞. 因子分析法在质谱成像数据分析中的应用[J]. 分析化学, 2014, 42(8): 1099. CHEN Yi, TANG Fei. Application of factor analysis in mass spectrometry imaging data analysis[J]. Analytical Chemistry, 2014, 42(8): 1099. DOI:10.11895/j.issn.0253-3820.140062 |
| [11] |
傅惠民, 林逢春, 陈建伟. 动态仿真结果相关性检验和分析方法[J]. 机械强度, 2007, 29(4): 584. FU Huimin, LIN Fengchun, CHEN Jianwei. Dynamic simulation results correlation test and analysis method[J]. Mechanical Strength, 2007, 29(4): 584. DOI:10.3321/j.issn:1001-9669.2007.04.013 |
| [12] |
高凯, 张尔扬. 空时频互相关MIMO衰落信道仿真及其性能分析[J]. 信号处理, 2007, 23(6): 861. GAO Kai, ZHANG Eryang. Space-time-frequency cross-correlation MIMO fading channel simulation and its performance analysis[J]. Signal Processing, 2007, 23(6): 861. DOI:10.3969/j.issn.1003-0530.2007.06.015 |
| [13] |
TAKASHI N. Self-organization in 2D traffic flow model with jam-avoiding drive[J]. Physical Society, 1995, 65(4): 1421. DOI:10.1143/JPSJ.64.1421 |
| [14] |
ZHANG Lele, GARONI T M, GIER J D. A comparative sudy of macroscopic fundamental diagrams of arterial road networks governed by adaptive traffic signal system[J]. Transportation Research Part B, 2013(49): 1. DOI:10.1016/j.trb.2012.12.002 |
| [15] |
NG W W, PANU U, LENNOX W C. Chaos based analytical techniques for daily extreme hydra logical observations[J]. Journal of Hydrology, 2007, 342(1/2): 17. DOI:10.1016/j.jhydrol.2007.04.023 |
| [16] |
MARR C, HUTT M T. Cellular automata on graphs: topological properties of ER graphs evolved towards low-entropy dynamics[J]. Entropy, 2012(14): 993. DOI:10.3390/e14060993 |
| [17] |
MALECKI K. The use of heterogeneous cellular automata to study the capacity of the roundabout[C]//Proceedings of International Conference on Artificial Intelligence and Soft Computing. Cham, Switzerland: Springer, 2017: 308.DOI: 10.1007/978-3-319-59060-8_28
|
| [18] |
ZHONG Fusheng, WANG Anlin. Rule optimization of self-organization control of traffic signals in urban net based on hydrodynamic[C]//Proceedings of 2018 3rd International Conference on Design, Mechanical and Material Engineering (D2ME 2018). Les Ulis, France: EDP Sciences, 2018, 237: 03004. DOI: 10.1051/matecconf/201823703004
|
| [19] |
王昊, 秦严严. 网联车混合交通流渐进稳定性解析方法[J]. 哈尔滨工业大学学报, 2019, 51(3): 88. WANG Hao, QIN Yanyan. Analytical method for the gradual stability of the mixed traffic flow[J]. Journal of Harbin Institute of Technology, 2019, 51(3): 88. |
| [20] |
莫祥伦.城市道路交通流自组织运行机理及控制研究[D].长春: 吉林大学, 2014: 23 MO Xianglun. Study on operation mechanism and control of self organization traffic flow in urban road net[D]. Changchun: Jilin University, 2014: 23 http://cdmd.cnki.com.cn/Article/CDMD-10183-1014292590.htm |
| [21] |
GERSHENSON C, ROSENBLUETH D A. Adaptive self-organization vs static optimization: a qualitative comparison in traffic light coordination[J]. Kybernetes, 2012, 41(3): 386. DOI:10.1108/03684921211229479 |
| [22] |
王安麟, 孙晓龙, 钟馥声. 一种基于通行优先度规则的城市交通信号自组织控制方法[J]. 重庆交通大学学报(自然科学版), 2018, 37(2): 96. WANG Anlin, SUN Xiaolong, ZHONG Fusheng. Self-organizing control method for urban traffic signal based on the pass-priority rules[J]. Journal of Chongqing Jiaotong University (Natural Science Edition), 2018, 37(2): 96. DOI:10.3969/j.issn.1674-0696.2018.02.15 |
 2020, Vol. 52
2020, Vol. 52


