2. 重庆能源职业学院 土木工程系, 重庆 402260
2. Department of Civil Engineering, Chongqing Energy College, Chongqing 402260, China
钢管混凝土拱桥刚度大、受力性能好、适用性和经济性较强,非常适合于多深山峡谷的中西部地区.据不完全统计,近二十年来,中国修建的跨径50 m以上的钢管混凝土拱桥超过250座,目前跨径大于400 m的有7座[1],2013年建成的波司登大桥主跨长达530 m,为当今世界最大跨度钢管混凝土拱桥.近十年来我国在钢管混凝土拱桥设计理论方面研究开展较多,并取得了较丰富的研究成果[2-3],但有关钢管混凝土拱桥施工技术及理论的研究相对匮乏.事实上要实现钢管混凝土拱桥跨径的飞跃性突破,施工问题是广大桥梁学者必须攻克的首要难题.管内混凝土灌注作为钢管混凝土拱桥施工关键工序之一[3],对结构施工受力性能、钢管同混凝土共同作用效果、拱桥承载能力、结构使用寿命等具有较大的影响.据调查,钢管混凝土拱桥由于灌注过程结构受力不合理而发生漏浆、断裂、爆管等事故的工程实例较多[4-6].文献[7]指出波司登桥大桥在首根拱肋混凝土灌注过程中,拱顶由上向下的变形变化幅度达到189.1 mm,宜对其灌注方案进行更深入的优化.
目前钢管混凝土拱肋横向灌注顺序普遍采用穷举法方案比选思路确定[8-10],计算量大、耗时长,且无统一的评价标准.对于单根拱肋可实现连续灌注的中小跨径钢管拱桥,以四肢桁架式截面为例,存在24种可选方案和64个优化计算工况[8].若拱桥跨度过大或者拱顶较高,单根拱肋纵向一次性灌注困难而必须分段时,计算工况更多.文献[4]指出不同横向灌注次序最大差异是灌注过程中外钢管的应力.本文以减小灌注过程外钢管应力为目标,基于应力影响线确定横向灌注次序,该法不涉及复杂的理论计算和施工仿真分析,工程应用简单方便.
目前,大多已建钢管混凝土拱桥单根拱肋采用拱脚-拱顶依次灌注的方式,在灌注过程中,外钢管会出现向上向下交替变形.文献[11]基于挠度影响线对劲性骨架混凝土拱桥外包混凝土浇筑方案进行研究,利用影响线叠加法寻求合理的分段点.文献[12]针对钢筋混凝土拱桥拱架现浇分段灌注进行研究,并指出合理的分段长度和加载顺序能够改善拱架施工变形.文献[13]基于拱肋挠度影响线对结构进行损伤识别,指出了控制拱肋挠度对保障结构使用寿命的重要性.事实上,对于钢管混凝土拱桥,随着跨径增大或者矢跨比加大,拱脚至拱顶依次灌注过程中,外钢管拱顶位置会发生较大的由上向下的变形变化,不利于拱桥受力.在施工中,通过局部位置预留灌注孔的方式可实现单根拱肋分段灌注.本文提出纵向自调载灌注法,基于灌注过程外钢管的挠度影响线确定合理的分段长度和灌注次序,以改善单根拱肋灌注过程中结构的力学性能.较临时扣索、水箱压重等方法,自调载灌注法不需要设置额外的辅助设施,可节约成本,降低工程造价.
混凝土刚度形成是一个缓慢的过程[14],为避免已灌混凝土在未形成合理刚度时过早受力,前一根拱肋混凝土灌注完成后需间隔一定时间方能灌注下一根拱肋.确定合理的起灌时间是钢管混凝土拱桥施工需要解决的另一关键问题,国内外有关此方面研究开展较少.本文基于有限元刚度方程[15]和力学理论公式,推导单元加权弯矩能与灌注时间间隔之间的关系,基于有限元优化理论研究合理的灌注时间间隔.
1 钢管混凝土拱肋分析方法目前钢管混凝土拱肋截面几何特性计算方法主要分为换算截面法、刚度叠加法和统一理论法3种[16],对应的计算公式分别为
| $ \left\{ {\begin{array}{*{20}{l}} {A = {A_{\rm{c}}} + n{A_{\rm{s}}},}\\ {I = {I_{\rm{c}}} + n{I_{\rm{s}}},}\\ {{I_{\rm{ \mathsf{ ρ} }}} = {I_{{\rm{ \mathsf{ ρ} c}}}} + n'{I_{{\rm{ \mathsf{ ρ} s}}}}.} \end{array}} \right. $ | (1) |
| $ \left\{ {\begin{array}{*{20}{c}} {EA = {E_{\rm{c}}}{A_{\rm{c}}} + {E_{\rm{s}}}{A_{\rm{s}}},}\\ {EI = {E_{\rm{c}}}{I_{\rm{c}}} + {E_{\rm{s}}}{I_{\rm{s}}}.} \end{array}} \right. $ | (2) |
| $ \left\{ {\begin{array}{*{20}{l}} {{E_{{\rm{sc}}}} = \frac{{{f_{{\rm{sc}}}}}}{{{\varepsilon _{{\rm{sc}}}}}},}\\ {\zeta = \frac{{{A_{\rm{s}}}{f_{\rm{y}}}}}{{{A_{\rm{c}}}{f_{{\rm{ck}}}}}}.} \end{array}} \right. $ | (3) |
式中:A、I、Iρ、E、G分别为钢管混凝土拱肋截面面积、惯性矩、扭转模量、弹性模量、剪切模量;下标c是指混凝土,下标s是指钢管;fy为钢材屈服强度;fck为混凝土强度标准值.其他符号物理意义见文献[16].
对应上述3种计算方法的有限元模拟模型分别为换算单元模型、双单元模型和整体模型.混凝土灌注期间,钢材和混凝土均处于弹性工作状态,此时混凝土泊松比较小,套箍效应不大,换算单元和双单元法的计算精度即可满足要求.为建模方便,本文算例中采用双单元法,灌注混凝土时,只激活钢管单元,混凝土以荷载形式作用于钢管,刚度形成后,再激活混凝土单元.
2 基于应力影响线的横向自调载灌注方法 2.1 定义法计算影响线影响线反映单位荷载沿拱圈移动时,结构挠度、应力、弯矩等的变化规律,其横坐标表示荷载位置,纵坐标表示荷载作用于该位置对关注截面的影响系数.
在ANSYS中,可通过建立有限元节点生成单元,单位荷载可沿着离散节点加载实现连续移动,如图 1所示.程序自带荷载步功能,可通过FADD、FDELE命令模拟单位荷载施加与删除,并运用循环法加载求解.单位荷载每施加一次,计算并提取应力结果一次,用PLNSOL命令即可绘制出应力影响线.设t时刻,拱脚混凝土拉应力为σt,有
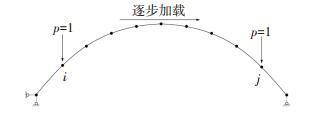
|
图 1 影响线的定义法 Fig. 1 Definition of influence line |
| $ {\sigma _{\rm{t}}} = \int_0^{{x_i}} {\frac{{\gamma {A_i}}}{{\cos {\alpha _i}}}{y_i}{\rm{d}}x} - \int_{L - {x_i}}^L {\frac{{\gamma {A_j}}}{{\cos {\alpha _j}}}{y_j}{\rm{d}}x} . $ | (4) |
式中:γ、Ai分别为钢管容重和截面面积;αi、αj分别为截面i和截面j处拱轴切线的水平倾角;yi、yj分别为截面i和截面j处的影响线竖标.
图 2为拱脚截面应力影响线,假设全桥采用等截面拱肋,且两端对称灌注,则有
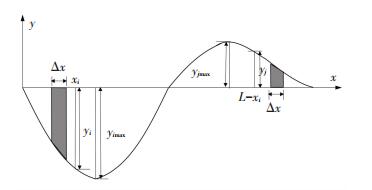
|
图 2 拱脚截面的应力影响线 Fig. 2 Stress influenceline of arch foot section |
| $ {\sigma _{\rm{t}}} = \frac{{\gamma {A_i}}}{{\cos \alpha }}\left( {\int_0^{{x_i}} {{y_i}} {\rm{d}}x - \int_{L - {x_i}}^L {{y_j}} {\rm{d}}x} \right). $ | (5) |
结合图 2和式(5),可以看出:yimax越大,应力影响线面积越大,拉应力计算结果越大.为便于分析,下文进行横向灌注次序分析时,直接选择yimax作为评价应力的指标.
2.2 横向灌注次序确定以大跨径钢管混凝土拱桥常用的四肢桁架式截面为例进行介绍,如图 3所示.遵循上下游对称施工原则,只需确定1#、2#、3#、4#拱肋的灌注次序.
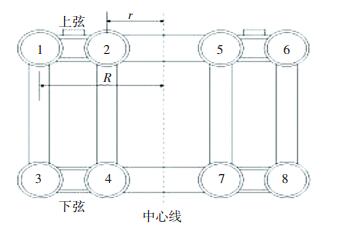
|
图 3 拱肋横截面 Fig. 3 Cross section of arch rib |
先提取单独灌注1#、2#、3#、4#拱肋时空钢管拱脚应力影响线,取峰值最小者为首先灌注的拱肋.激活已灌混凝土并计入刚度,计算灌注其余3根拱肋过程中拱脚应力影响线并确定第2根灌注拱肋,以此类推.此法思路简单,计算量小,应用方便,算法流程如图 4所示.在各根拱肋灌注完成后,要考虑整根混凝土刚度贡献,但下节计算单根拱肋纵向分段灌注过程中,时间较短,忽略已灌节段刚度的影响.
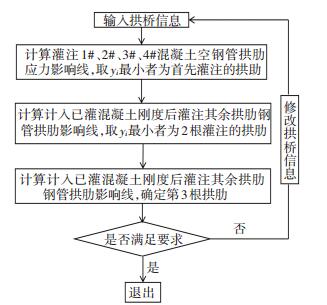
|
图 4 横向自调载灌注方法计算流程 Fig. 4 Calculation flow chart of transverseself-regulating loading pouring method |
灌注期间需对结构受力状态进行调整,结构最大应力和变形要求表达式为
| $ \left\{ {\begin{array}{*{20}{l}} {{{\left| {\sigma \left( t \right)} \right|}_{\max }} \le \left[ \sigma \right],}\\ {{{\left| {y\left( t \right)} \right|}_{\max }} \le \left[ y \right],}\\ {\Delta y{{\left( t \right)}_{\max }} \le \left[ {\Delta y} \right].} \end{array}} \right. $ | (6) |
式中:|σ(t)|max、|y(t)|max、Δy(t)max分别为灌注过程中,钢拱肋出现的最大应力、最大竖向变形和由上向下的最大变形变化幅度,[σ]、[y]、[Δy]分别为应力、竖向变形、竖向变形变化幅度的允许值.
单根拱肋灌注过程中结构挠度和应力影响线规律如图 5所示,可以看出,灌注整根混凝土在某一位置产生的变形和受力方向会发生变化.介于此,提出纵向自调载灌注法,通过合理的分段长度和灌注次序改善灌注过程结构受力变形.其原理类似数学加法交换定律,例如,1、2、-1、-2四个数按照不同顺序相加,分别有
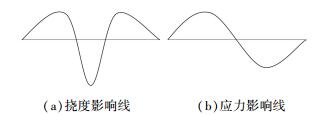
|
图 5 灌注过程中主拱影响线示意图 Fig. 5 Influence line of main arch in perfusion process |
| $ \begin{array}{*{20}{c}} {1 + 2 + \left( { - 1} \right) + \left( { - 2} \right) = 3 + \left( { - 1} \right) + \left( { - 2} \right) = }\\ {2 - 2 = 0,} \end{array} $ | (7) |
| $ 1 + \left( { - 2} \right) + 2 + \left( { - 1} \right) = \left( { - 1} \right) + 2 + \left( { - 1} \right) = 0, $ | (8) |
| $ 1 + \left( { - 1} \right) + 2 + \left( { - 2} \right) = 0 + 2 + \left( { - 2} \right) = 0. $ | (9) |
式(7)~(9)结果均为0.但式(7)最大峰值为3,式(8)最大峰值为1,式(9)最大峰值为2.单根混凝土灌注过程可看成数节段相加,自调载灌注法的主要任务是研究结构变形最合理的分段长度和灌注次序.
以5段灌注为例,取拱顶截面进行分析. 1#、2#、3#、4#钢管拱肋挠度影响线基本一致,如图 6所示.图中,x1、x2、x3、x4分别表示各分段点位置,x0表示挠度影响线零点位置,A1、A2分别表示第1段、第2段区域影响线面积,第3段分为A31和A32两部分,面积为A31+A32.
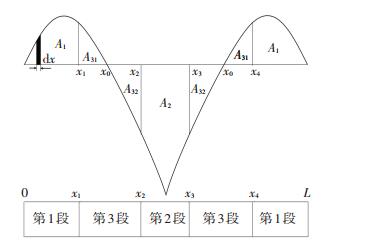
|
图 6 拱顶挠度影响线及分段灌注顺序 Fig. 6 Deflection influence line of vault andsegmental pouring order |
灌注拱脚段混凝土时,主管拱顶向上变形,灌注拱顶节段时,主管拱顶向下变形且绝对值较大.若采取拱脚-拱顶依次灌注方式,灌注至拱顶节段时,主管必然会产生较大的Δy(t)max,不利于结构受力,为减小Δy(t)max,灌注拱脚节段后,应先灌注拱顶节段. 图 6给出了合理的灌注顺序.
同时,为避免钢管拱肋出现上-下-上的交替变形,灌注第3段时,必须使得|A31| < |A32|.由影响线加载理论可知:
| $ {f_1} = 2{\eta _x}\int_0^{{x_1}} {{G_x}} = 2w\rho {\eta _x}\int_0^{{x_1}} {\frac{{{\rm{d}}x}}{{\cos \varphi }}} = 2w\rho {\eta _x}\int_0^{{x_1}} {\rm{d}} s, $ | (10) |
| $ {f_2} = {\eta _x}\int_{{x_2}}^{{x_3}} {{G_x}} = w\rho {\eta _x}\int_{{x_2}}^{{x_3}} {\frac{{{\rm{d}}x}}{{\cos \varphi }}} = w\rho {\eta _x}\int_{{x_2}}^{{x_3}} {\rm{d}} s, $ | (11) |
| $ {f_3} = 2{\eta _x}\int_{{x_1}}^{{x_2}} {{G_x}} = 2w\rho {\eta _x}\int_{{x_1}}^{{x_2}} {\frac{{{\rm{d}}x}}{{\cos \varphi }}} = 2w\rho {\eta _x}\int_{{x_1}}^{{x_2}} {\rm{d}} s, $ | (12) |
| $ {f_0} = {f_1} + {f_2} + {f_3} = w\rho {\eta _x}\int_0^L {\rm{d}} s, $ | (13) |
| $ {f_0} - {f_1} = {f_2} + {f_3}. $ | (14) |
式中:f1、f2、f3分别为灌注该段混凝土时,拱顶产生的挠度,f0为灌注整根混凝土拱肋产生的拱顶挠度,w、ρ分别为管内混凝土面积、容重,ηx为各点影响线竖标,L为拱肋跨径.
由式(10)~(13)不难看出:分段长度变化只对f1、f2、f3有影响,f0保持为一个定值.
3.2 分段点确定上述推论表明,x1越长,f1越大,f2+f3越小,则灌注过程中拱顶最大向上变形及由上向下的变形变化幅度越大,故长度分配合理情况下宜缩短第1段长度,不妨以f0为基准,引入拱顶上挠控制系数λ,有
| $ {f_1} \le \lambda {f_0},0.5 \le \lambda \le 1. $ | (15) |
式(15)λ取值越小,拱架发生的最大向上变形越小,但x1越小,A31越大,为满足|A31| < |A32|,第3段灌注长度必然较大.结合灌注长度合理原则,给出第1个分段点的控制条件为
| $ \frac{L}{5} - \frac{L}{{25}} \le {x_1} \le \frac{L}{5} + \frac{L}{{25}}. $ | (16) |
为确保节段长度合理,实际工程应用时可结合式(16)进一步综合确定λ.多座钢管混凝土拱桥的大量试算表明,λ在0.5~1之间取值是合理的.
由式(15)可知:x1一旦确定,f2+f3即为一定值. x2位置变化主要影响f2和f3的分配比例.为保证灌注第2段和第3段过程中结构变形均匀,引入变形分配系数δ.令
| $ {f_2} = \delta \left( {{f_2} + {f_3}} \right), $ | (17) |
式中δ取0.5时,变形平均分配,最合理.
由于第2段处于峰值区域,浇筑较小的长度即可产生较大的变形,故第2段长度不能过大,而为了保证|A31| < |A32|,第3段长度理应较大,考虑这一情况,扩大第2段长度分配取值范围,有
| $ \frac{L}{5} - \frac{{2L}}{{25}} \le {x_3} - {x_2} \le \frac{L}{5} + \frac{{2L}}{{25}}. $ | (18) |
δ可结合式(18),在0.5左右波动取值.管内混凝土5段灌注计算流程如图 7所示.
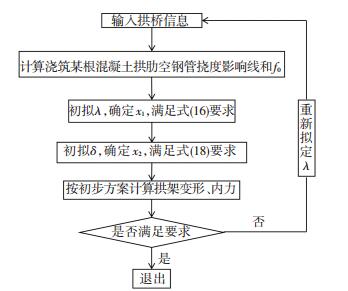
|
图 7 纵向自调载灌注方法计算流程 Fig. 7 Calculation flow of longitudinal self-regulating loading pouring method |
文献[17]指出拱桥的综合弯矩能越小,结构受力越有利,认为一次成桥设计状态的内力在理论上是合理的,则分阶段施工过程中产生的综合弯矩能与一次成桥设计状态越接近,施工过程中的受力状态越合理.同时,考虑到加权能量法[18]可通过给予每个单元弯曲变形能不同的加权系数来调整拱圈截面内力,使得主拱圈各截面内力分布更均匀,本文对单元的能量值作加权处理,推导拱圈加权弯矩能同混凝土龄期之间关系的理论公式,以分阶段施工和一次成桥的加权弯矩能差异最小为目标开展混凝土灌注时间间隔的优化分析.
4.1 混凝土龄期与工序时间间隔关系设第i根灌注的拱肋龄期为ti,灌注时间为Ti,第i根灌注完成至第i+1根开始灌注的时间间隔为Di,根据施工机械参数,可得到单位时间灌注量,不难算出各根拱肋灌注时间Ti.设灌注完成时刻为t1,各根拱肋混凝土龄期和工序间隔时间关系为
| $ \left\{ {\begin{array}{*{20}{l}} {{t_1} = {D_1} + {T_2} + {D_2} + {T_3} + {D_3} + {T_4},}\\ {{t_2} = {t_1} - {T_1} - {D_1},}\\ {{t_3} = {t_1} - {T_1} - {D_1} - {T_2} - {D_2},}\\ {{t_4} = 0.} \end{array}} \right. $ | (19) |
已知单元局部坐标系下单元节点力与节点位移关系为
| $ \mathit{\boldsymbol{p}} = \mathit{\boldsymbol{ks}}, $ | (20) |
式中:p为节点力向量,s为节点位移向量,k为单元刚度矩阵,可变换为整体刚度矩阵K,即
| $ \mathit{\boldsymbol{K}} = {\mathit{\boldsymbol{T}}^{\rm{T}}}\mathit{\boldsymbol{kT}}, $ | (21) |
| $ {\left[ {{\mathit{\boldsymbol{T}}^{\rm{T}}}} \right]^{ - 1}}\mathit{\boldsymbol{K}}{\mathit{\boldsymbol{T}}^{ - 1}} = \boldsymbol{k}. $ | (22) |
式中T为位移变换矩阵[19].
将式(22)代入式(20)得
| $ \mathit{\boldsymbol{p}} = {\left[ {{\mathit{\boldsymbol{T}}^{\rm{T}}}} \right]^{ - 1}}\mathit{\boldsymbol{K}}{\mathit{\boldsymbol{T}}^{ - 1}}\mathit{\boldsymbol{s}}, $ | (23) |
即有
| $ {\mathit{\boldsymbol{T}}^{\rm{T}}}\mathit{\boldsymbol{p}} = \mathit{\boldsymbol{K}}{\mathit{\boldsymbol{T}}^{ - 1}}\mathit{\boldsymbol{s}}, $ | (24) |
令f = TTp, δ = T-1s, 则有
| $ \mathit{\boldsymbol{f}} = \mathit{\boldsymbol{K\delta }}. $ | (25) |
式中:f为节点荷载矢量,δ为节点位移矢量,K为整体刚度矩阵.
钢管混凝土结构通常采用微膨胀高强混凝土,鉴于有关此类混凝土弹性模量时变效应的研究较少,本文在推导加权弯矩余能与灌注时间间隔之间的关系时,近似地采用文献[20]通过试验研究拟合出的普通混凝土早期弹模与龄期的关系式,即
| $ {E_{{\rm{c}},t}} = {E_{28}}\left( {1 - 0.33{{\rm{e}}^{ - 0.042{t^2}}}} \right). $ | (26) |
式中:Ec, t为t时刻的弹模,E28为28 d混凝土弹模,t为混凝土龄期.
式(26)表明,刚度可表示为与龄期有关的函数.再联合式(19),即可将刚度矩阵转化为时间间隔的函数,表达式为
| $ \mathit{\boldsymbol{K}} = w\left( {{E_{28}},D,I} \right), $ | (27) |
式中I为截面惯性矩.
将式(27)代入式(25),可得
| $ \mathit{\boldsymbol{\delta }} = {\mathit{\boldsymbol{K}}^{ - 1}}\mathit{\boldsymbol{f}} = {\left[ {w\left( {{E_{28}},D,I} \right)} \right]^{ - 1}}\mathit{\boldsymbol{f}}. $ | (28) |
令E=Ec, t=E28(1-0.33e-0.042t2), 由结构力学位移法知,不考虑温度和其他外荷载作用时,有
| $ \left\{ \begin{array}{l} {M_{ii}} = 4\frac{{EI}}{{{l_i}}}{\varphi _{ii}} + 2\frac{{EI}}{{{l_i}}}{\varphi _{ij}} - \frac{{6EI}}{{l_i^2}}\delta ,\\ {M_{ij}} = 4\frac{{EI}}{{{l_i}}}{\varphi _{ij}} + 2\frac{{EI}}{{{l_i}}}{\varphi _{ii}} - \frac{{6EI}}{{l_i^2}}\delta . \end{array} \right. $ | (29) |
将式(29)代入式(30),可得
| $ \left\{ \begin{array}{l} {M_{ii}} = 4\frac{{EI}}{{{l_i}}}{\varphi _{ii}} + 2\frac{{EI}}{{{l_i}}}{\varphi _{ij}} - \frac{{6EI}}{{l_i^2}}{\left[ {w\left( {{E_{28}},t,I} \right)} \right]^{ - 1}}\mathit{\boldsymbol{f}},\\ {M_{ij}} = 4\frac{{EI}}{{{l_i}}}{\varphi _{ij}} + 2\frac{{EI}}{{{l_i}}}{\varphi _{ii}} - \frac{{6EI}}{{l_i^2}}{\left[ {w\left( {{E_{28}},t,I} \right)} \right]^{ - 1}}\mathit{\boldsymbol{f}}. \end{array} \right. $ | (30) |
式中Mii和Mij分别为杆单元左右两端的弯矩,杆端弯矩产生的加权能量计算公式[17]为
| $ {U_i} = \frac{{{k_i}{l_i}}}{{6{E_i}{I_i}}}\left( {M_{ii}^2 + {M_{ii}}{M_{{\rm{ij}}}} + M_{ij}^2} \right), $ | (31) |
其中li和ki分别为单元长度和单元加权系数.
若主拱圈有m个单元,
| $ U = \sum {{U_i}} = \sum\limits_{i = 1}^m {\frac{{{k_i}{l_i}}}{{6{E_i}{I_i}}}} \left( {M_{ii}^2 + {M_{ii}}{M_{ij}} + M_{ij}^2} \right). $ | (32) |
将式(30)代入式(32),并令
| $ G = {\left[ {w\left( {{E_{28}},D,I} \right)} \right]^{ - 1}}\mathit{\boldsymbol{f}}, $ |
| $ H = 4\frac{{EI}}{{{l_i}}}{\varphi _{ii}} + 2\frac{{EI}}{{{l_i}}}{\varphi _{ij}} - \frac{{6EI}}{{l_i^2}}G, $ |
| $ Z = 4\frac{{EI}}{{{l_i}}}{\varphi _{ij}} + 2\frac{{EI}}{{{l_i}}}{\varphi _{ii}} - \frac{{6EI}}{{l_i^2}}G. $ |
将式(19)代人式(26), E也可表示为时间间隔Di的函数, 则有
| $ U\left( {{D_i}} \right) = \sum\limits_{i = 1}^m {\frac{{{k_i}{l_i}}}{{6{E_i}{I_i}}}} \left( {{H^2} + HZ + {Z^2}} \right). $ | (33) |
式(33)为主拱加权弯矩能与时间间隔的关系式,式中只存在Di一个自变量.
4.3 优化问题对等截面拱肋,将一次成桥设计状态下有限元分析得出的单元杆端弯矩代入式(33),不难算出一次成桥设计状态加权弯矩能为
| $ {U_0} = \frac{S}{{6EI}}\sum\limits_{i = 1}^m {{k_i}} \left( {M_{ii}^2 + {M_{ii}}{M_{ij}} + M_{ij}^2} \right). $ | (34) |
式中S、E、I分别为拱肋弧长、混凝土设计弹模、截面惯性矩.
则优化问题转化为
| $ \left\{ {\begin{array}{*{20}{l}} {\text{Min}U = \text{Min}\left| {U\left( {{D_i}} \right) - U\left( 0 \right)} \right|;}\\ {{\rm{s}}.{\rm{t}}.:{D_i} \ge 0\left( {i = 1,2,3} \right).} \end{array}} \right. $ | (35) |
综上所述,基于能量法的灌注时间间隔计算步骤如下:1)建立一次性成拱模型,计算弯矩能U0;2)建立施工仿真分析模型,计算弯矩能UD;3)定义间隔时间为设计变量,|UD-U0|为目标函数,进行优化分析,寻求最优解.
5 工程算例 5.1 工程概况巫山新龙门大桥主桥是净跨240 m的中承式悬链线钢管砼拱桥,钢管拱肋吊装就位后,高压泵灌注管内混凝土成拱,主拱圈矢跨比为1/5,设计拱轴系数为1.5,拱轴线采用悬链线.上、下弦杆由两根直径为2 016 mm,壁厚为14 mm的钢管组成,竖向设置直径为508 mm,壁厚为10 mm的空钢管腹杆连接,横向并列弦杆用12 mm缀板连接,两拱肋间用K形空钢管连接.主拱肋钢管、钢板均采用Q345B材料,管内混凝土采用C50微膨胀混凝土.拱肋横断面形式见图 3.
该桥在实际施工中,采用目前钢管混凝土拱桥灌注常用计算方法确定灌注加载程序.通过对多种方案的对比分析,横向采用1#—6#—2#—5#—3#—8#—4#—7#单侧灌注方案,纵向采取拱脚至拱顶依次对称泵送的方式.
建立的有限元模型中,主弦使用beam44梁单元模拟,相邻水平弦杆间的钢缀板采用shell63单元模拟.主拱肋材质为Q345B钢管和C50高强混凝土,钢材弹性模量为2×105 MPa,混凝土后期弹模为3.15×104 MPa.本文主要针对管内混凝土灌注过程进行研究,为节约计算时间,影响线计算时只激活裸拱.为验证全桥有限元模型的正确性,计算自重作用下,拱肋关键截面成桥阶段的应力,并和该桥施工监控报告中的实测值进行对比.为节约篇幅,只给出上游拱肋左拱脚、L/4截面和拱顶截面的对比结果,见表 1.
| 表 1 成桥状态关键截面应力对比 Tab. 1 Stress comparison of key sections in completed state |
由表 1可知:成桥状态下,关键截面应力的有限元计算值和实测值较为接近,但受实际温度、施工临时荷载、仪器误差等因素影响,两者存在一定误差.分析结果表明上述有限元模型是正确的.
5.2 横向灌注确定 5.2.1 灌注顺序计算按照第1节所述方法确定横向灌注顺序,激活空钢管模型,分别计算1#、2#、3#、4#拱肋浇筑时,钢管拱脚的应力影响线,灌注各根拱肋混凝土的影响线正峰值计算结果分别为36、40、36.1、40.2.
计算表明:灌注1#和3#拱肋,应力影响线基本一致,峰值小于灌注2#和4#时,首先浇筑1#或3#拱肋对主钢管受力较有利.大量工程实践指出:钢管混凝土拱桥中上弦杆局部受压较不利,在施工中,宜先下后上,所以选择3#为首浇拱肋.在3#拱肋已灌的基础上,再次计算,灌注1#、2#、4#拱肋混凝土的影响线峰值分别为33.2、36.4、36.7.所以第2根灌注拱肋为1#拱肋.同理,遵循先下后上原则,第3根浇筑拱肋定为4#.
为缩短工期,上下游对称灌注,横向自调载灌注方法确定最终横向灌注顺序为3#(8#)—1#(6#)—4#(7#)—2#(5#).
5.2.2 施工稳定性验算进行混凝土灌注阶段特征值屈曲分析,结果表明,该桥的前二阶失稳形式均为面外失稳.结构在自重作用下各灌注工况结构的稳定系数结果如图 8所示.
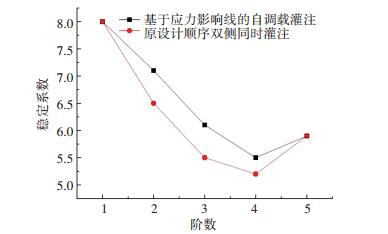
|
图 8 稳定系数对比 Fig. 8 Comparison of stability coefficients |
研究表明:巫山新龙门大桥采用横向自调载灌注方法,施工稳定性能得到提高.该桥实际施工中采取单侧灌注方式以增加结构施工稳定性能,但增加了工期.本文研究方案可实现拱肋上下游同时灌注和提高结构施工稳定性两大目的.
5.3 纵向灌注确定本节以新龙门大桥为例介绍单根拱肋纵向自调载灌注法.针对该桥,由式(13)得f0=-2.8 cm,根据式(16),不妨偏小取λ=0.5,由式(15)得f0=1.25 cm,反推出x1=39.2 cm,在给定范围内,且已接近较小值,故λ不宜继续减小.由于x1=39.2 m处无节点,取x1=40 m,此时λ为0.51,f1为-2.8 cm.
根据式(14),先按最优情况考虑,取δ为0.5,由式(18)得f2=-2.115 cm,得到x2=106.5 m,x3=136.5 m,x3-x2为30 m,满足式(18)要求.即第1段长度为40 m,第2段长度为30 m,第3段长度为65 m.
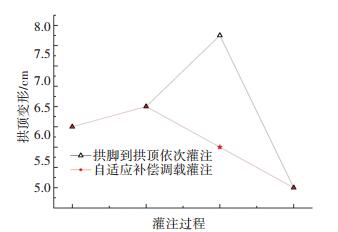
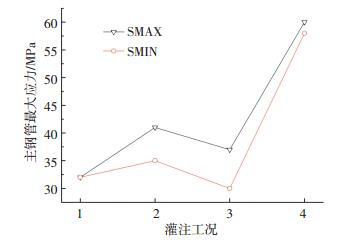
若采用设计方案(拱脚到拱顶依次灌注),灌注到图 6中x0位置处,钢管拱肋出现较大的上挠值,需要结合辅助手段进行调载.按自调载灌注法,主管施工过程变形较均匀,见图 9,各工况全桥最大SMAX、SMIN计算结果见图 10,满足材料强度要求.
|
图 9 拱顶变形 Fig. 9 Deformation of vault |
|
图 10 自调载法施工全桥应力 Fig. 10 Construction stress of the whole bridge with self-regulating loading pouring method |
该新龙门大桥核心混凝土采用C50,进行一次成桥有限元分析,以单元表方式提取各单元弯矩,代入式(34),得到U0=22 663.45.
假设每根拱肋灌注时间为10 d,此时有t1= D1+D2+D3+30、t2=t1-10-D1、t3=t1-D1- D2-20、t4=0.按3.3节研究思路进行优化.状态变量设置为各工况已浇混凝土拉应力满足抗拉强度要求,设计变量迭代范围为1~5 d,初始值定为D1=D2=D3=1 d,最优解计算结果为D1=4 d,D2=3 d,D3=3 d.目前实际工程中通常采用3~4 d,可见,加权能量优化方法用于钢管混凝土拱桥灌注时间间隔计算是合理的.
5.5 自调载灌注法与传统方法对比该桥若采用传统的方案穷举对比分析法确定横向灌注顺序,需针对24种可选方案,开展24次施工仿真分析,计算工作量大,耗时长.基于应力影响线的横向自调载灌注方法,只需计算外钢管在灌注各根拱肋过程中的应力影响线,回避了繁琐的施工仿真分析,工程应用简单方便.且从图 8可以看出,基于应力影响线的横向自调载灌注方法可满足施工安全性能要求.
从图 9可以看出,采用基于挠度影响线的纵向自调载灌注方法,拱肋灌注过程中外钢管拱顶始终保持下挠状态,采用传统灌注法,第2节段灌注完成后,拱顶出现上挠变形,会对结构后期使用性能产生不利影响.另外,采用传统灌注方法,施工过程外钢管变形变化较大,基于挠度影响线的纵向自调载灌注方法,浇筑各节段产生的变形分布更均匀,施工过程受力性能更合理.
6 结论1) 基于应力影响线的横向自调载灌注方法计算简便,实用性强,能较好地控制横向灌注过程中钢管的最大应力.
2) 基于挠度影响线的纵向自调载灌注方法可较好地控制单根拱肋灌注过程中结构变形.对钢管混凝土拱桥,拱顶上挠控制系数在0.5~1之间取值,变形分配系数在0.4~0.6之间取值是合理的.
3) 基于有限元优化原理,以分阶段成桥和一次成桥设计状态弯矩能差异最小为目标建立的灌注时间间隔优化理论应用于工程实践是合理可行的.
| [1] |
李亚东, 姚昌荣, 梁艳. 浅谈拱桥的技术进步与挑战[J]. 桥梁建设, 2012, 42(2): 13. LI Yadong, YAO Changrong, LIANG Yan. On technical advancement and challenge of arch bridges[J]. Bridge Construction, 2012, 42(2): 13. |
| [2] |
刘新华, 师少辉, 彭元诚. 总溪河大桥主桥结构设计[J]. 桥梁建设, 2016, 46(5): 95. LIU Xinhua, SHI Shaohui, PENG Yuancheng. Structural design of main bridge of Zongxi River Bridge[J]. Bridge Construction, 2016, 46(5): 95. |
| [3] |
耿悦, 丁尧, 王玉银, 等. 四肢桁式钢管混凝土拱出平面徐变稳定性能[J]. 哈尔滨工业大学学报, 2016, 48(6): 87. GENG Yue, DING Yao, WANG Yuyin, et al. Out-of-plane creep buckling behavior of quadri-trussed CFST arches[J]. Journal of Harbin Institute of Technology, 2016, 48(6): 87. |
| [4] |
徐波, 周厚斌, 王培金. 哑铃形钢管混凝土拱桥在灌注混凝土时开裂事故分析[J]. 四川建筑, 2008, 28(4): 159. XU Bo, ZHOU Houbin, WANG Peijin. Analysis of cracking accident of dumbbell-shaped CFST arch bridge during concrete pouring[J]. Sichuan Architecture, 2008, 28(4): 159. |
| [5] |
秦荣, 谢肖礼, 彭文立, 等. 钢管混凝土拱桥钢管开裂事故分析[J]. 土木工程学报, 2001, 34(3): 74. QIN Rong, XIE Xiaoli, PENG Wenli, et al. Analysis for cracking accidents of CFST arch bridge[J]. China Civil Engineering Journal, 2001, 34(3): 74. DOI:10.3321/j.issn:1000-131X.2001.03.013 |
| [6] |
夏小钢, 张玉萍, 甘进. 钢管混凝土拱桥腹板开裂事故分析[J]. 中国水运(理论版), 2006, 4(5): 65. XIA Xiaogang, ZHANG Yuping, GAN Jin. The analysis of accident for great cracking in steel belly of CFST arch bridge[J]. China Water Transport (Theory Edition), 2006, 4(5): 65. |
| [7] |
郝聂冰. 500 m级钢管混凝土拱桥施工控制研究[D].重庆: 重庆交通大学, 2017 HAO Niebing. Study on construction control of 500 m CFST arch bridge[D]. Chongqing: Chongqing Jiaotong University, 2017 http://d.wanfangdata.com.cn/Thesis/Y3225207 |
| [8] |
杨小森, 闫维明, 陈少峰, 等. 大跨度钢管混凝土拱桥拱肋混凝土灌注顺序优化[J]. 公路交通科技, 2010, 27(1): 67. YANG Xiaosen, YAN Weiming, CHEN Shaofeng, et al. Sequence optimization of concrete casting in steel tubular ribs for long-span CFST arch bridge[J]. Journal of Highway and Transportation Research and Development, 2010, 27(1): 67. DOI:10.3969/j.issn.1002-0268.2010.01.014 |
| [9] |
沈培文, 周水兴, 罗飞. 大跨度钢管混凝土拱桥施工阶段稳定性分析[J]. 重庆交通大学学报, 2010, 29(3): 340. SHEN Peiwen, ZHOU Shuixing, LUO Fei. Stability analysis on large span CFST arch bridge at construction stage[J]. Journal of Chongqing Jiaotong University, 2010, 29(3): 340. |
| [10] |
吴何.钢管混凝土拱肋混凝土灌注工序研究[D].成都: 西南交通大学, 2017 WU He. Discuss on different processes of concrete pouring in the arch rib of concrete filled steel tubular[D]. Chengdu: Southwest Jiaotong University, 2017 http://cdmd.cnki.com.cn/Article/CDMD-10613-1017138060.htm |
| [11] |
ZHOU Shuixing, ZHANG Ming, LIU Bin, et al. Determination of cast-in situ section lengths of reinforced concrete arch bridge in arch centering method[J]. Advanced Materials Research, 2011, 243(5): 1935. |
| [12] |
郝聂冰, 顾安邦. 500 m级钢管混凝土拱桥施工控制[J]. 西南交通大学学报, 2015, 50(4): 635. HAO Niebing, GU Anbang. Study on construction control of 500-meter scale CFST arch bridge[J]. Journal of Southwest Jiaotong University, 2015, 50(4): 635. DOI:10.3969/j.issn.0258-2724.2015.04.010 |
| [13] |
ZHAO Zhan, NIE Zhenhua, MA Hongwei. Damage identification of the arch bridge based on the difference of deflection with moving load[J]. Applied Mechanics & Materials, 2014, 578(7): 1096. |
| [14] |
WANG Zhibin, TAO Zhong, HAN Linhai, et al. Strength, stiffness and ductility of concrete-filled steel columns under axial compression[J]. Engineering Structures, 2017, 135(3): 209. |
| [15] |
项贻强, 郏亚坤. 基于小波总能量相对变化的拱桥吊杆损伤识别[J]. 浙江大学学报(工学版), 2017, 51(5): 870. XIANG Yiqiang, JIA Yakun. Damage detection of hangers in arch bridges based on relative variation of wavelet total energy[J]. Journal of Zhejiang University (Engineering Science), 2017, 51(5): 870. |
| [16] |
陈宝春. 钢管混凝土拱桥[M]. 2版. 北京: 人民交通出版社, 2007: 640. CHEN Baochun. Concrete filled steel tubulur arch bridges[M]. 2nd ed. Beijing: China Communication Press, 2007: 640. |
| [17] |
何雄君, 陈巧生, 朱云升. 钢管混凝土拱桥主拱混凝土浇灌方案的能量确定方法[J]. 中国公路学报, 2000, 13(2): 61. HE Xiongjun, CHEN Qiaosheng, ZHU Yunsheng. Scheme of casting concrete determined by generated energy for CFST arch bridges[J]. China Journal of Highway and Transport, 2000, 13(2): 61. DOI:10.3321/j.issn:1001-7372.2000.02.015 |
| [18] |
周倩.悬臂浇筑钢筋混凝土拱桥主拱圈构造研究[D].重庆: 重庆交通大学, 2013 ZHOU Qian. Research on main arch ring structure of cantilever cast reinforced concrete arch bridge[D]. Chongqing: Chongqing Jiaotong University, 2013 http://cdmd.cnki.com.cn/Article/CDMD-10618-1013374205.htm |
| [19] |
FUJISAWA T, SATO T, SAITOH K. Full-vector finite-element beam propagation method for helicoidal waveguides and its application to twisted photonic crystal fiber[J]. Journal of Lightwave Technology, 2017, 35(14): 2894. DOI:10.1109/JLT.2017.2703889 |
| [20] |
赵顺波, 高宇甲, 陈记豪, 等. C50泵送混凝土抗压强度和弹性模量时变性试验研究与应用[J]. 混凝土, 2015, 1(1): 98. ZHAO Shunbo, GAO Yujia, CHEN Jihao, et al. Application and study on time-dependent compressive strength and elastic modulus of C50 pumping concrete[J]. Concrete, 2015, 1(1): 98. DOI:10.3969/j.issn.1002-3550.2015.01.28 |
 2020, Vol. 52
2020, Vol. 52


