2. 广州汽车集团股份有限公司 汽车工程研究院, 广州 511434
2. Automotive Research & Development Center, Guangzhou Automobile Group Co., Ltd., Guangzhou 511434, China
目前,吸尘装置主要有纯吸式、纯扫式和吸扫结合式3种,其结构参数设计对于提升垃圾清扫效率具有重要意义[1],为此学者们研究了吸尘装置的扩展域参数和结构参数对清扫效果的影响规律.文献[1]首次提出吸嘴扩展域对仿真分析存在的影响,并指出扩展域参数对仿真的影响存在一个阈值,当参数超过阈值时,其影响可以忽略不计;文献[1-2]通过流场仿真研究还指出:吸嘴扩展域有无转角对计算精度影响并不大.上述研究对流场仿真中扩展域的参数设计有重要指导意义.对于传统吸尘装置结构参数的研究则多是针对其吸嘴结构参数,如文献[3-5]分析了吸尘装置吸嘴的各结构参数对吸尘效果的影响.文献[6]除分析吸嘴结构参数外,还以吸嘴吸尘部分的局部压力损失最小为目标,对吸嘴相关结构参数进行了优化设计.虽然上述对吸尘装置结构参数以及扩展域的研究对提高吸尘效果具有重要指导意义,但仍难以满足道路的高效清扫需求.
而自然界中龙卷风的破坏力惊人,龙卷风内部的空气稀薄,压力极低,这使得龙卷风具有强大的卷吸能力[7],因此研究者们对龙卷风作了很多研究.现阶段,关于龙卷风的研究主要是针对龙卷风本身的机理与龙卷风发生装置的设计,文献[7]在人造龙卷风形成机理的研究中提出生成龙卷风的两个必要条件:有诱导旋流和在流场中能形成一个称为漩涡生成区的流动区域,文献[7]还指出龙卷风的生成与射抽流量比有关.文献[8]通过数值模拟的方法研究了龙卷风的速度分布,分析了各种因素对龙卷风风场造成的影响,并在ward型龙卷风发生装置[9]的基础上设计制造了能成功产生龙卷风的发生装置.文献[10]则针对龙卷风发生装置进行风场模拟, 获得了风场的切向速度和径向速度,并将仿真的结果与实际速度值对比,验证了仿真的可行性.
由于龙卷风较强的卷吸能力,本文尝试将龙卷风原理应用于清扫中,探索性研究如何利用龙卷风的卷吸能力进行垃圾清扫,基于龙卷风卷吸原理设计了一个有别于现阶段吸尘装置的新型机械吸尘装置.本文研究目标是一种基于龙卷风卷吸原理的新型吸尘装置,因此无法直接采用上述研究结论.本文首先基于龙卷风原理建立机器吸尘装置的模型,然后利用近地面平均风速、压差、与吸嘴进风口平均压强为清扫效果评价指标,采用流场仿真方法,针对该新型吸尘装置的结构参数进行研究,以达到提高装置的清扫效率和增强装置的清扫效果的目的,在此基础上,对该新型装置流场的扩展域的形状及其参数阈值的规律进行研究,试图为该流场的扩展域的选定提供依据.
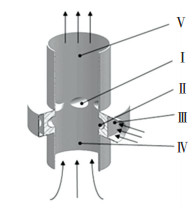
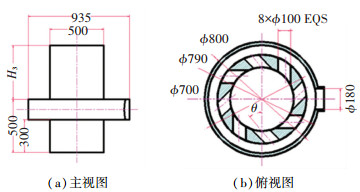
1 几何模型 1.1 基本原理与结构介绍图 1为基于龙卷风发生原理的吸尘装置的三维图.本吸尘装置包括:1个环流通道Ⅰ,8个导流孔Ⅱ,1个总进气管道Ⅲ,1个吸嘴Ⅳ和1个排尘口Ⅴ.总进气管道吹入空气,空气经过导流孔形成具有切向速度的气流,圆筒上方的负压使得这些具有切向速度的气流聚束起来并形成龙卷风.参考城市道路清扫车吸尘系统[11]的尺寸,一般的城市道路清扫吸尘系统中的吸嘴工作宽度通常在250 ~620 mm之间,本装置尺寸如图 2所示.
|
Ⅰ—环流通道;Ⅱ—导流孔;Ⅲ—总进气管道;Ⅳ—吸嘴;Ⅴ—排尘口 图 1 基于龙卷风发生原理的吸尘装置 Fig. 1 The dust collector based on the tornado generation principle |
|
图 2 基于龙卷风发生原理的吸尘装置尺寸(mm) Fig. 2 Dimensions of the dust collector based on the tornado generation principle (mm) |
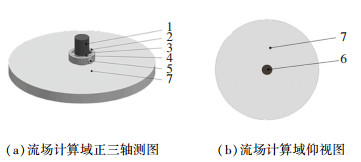
根据基于龙卷风发生原理的吸尘装置的物理模型,建立流体计算域,如图 3所示.本装置的计算域共分为7个部分,其中1、2、3、4、5、6分别为排尘口计算域、环流通道计算域、导流孔计算域、吸嘴计算域、总进气管道计算域、地面计算域;7为扩展域.
|
1—排尘口计算域;2—环流通道计算域;3—导流孔计算域;4—吸嘴计算域;5—总进气管道计算域;6—近地面计算域;7—扩展域 图 3 流场计算域 Fig. 3 Computational domain of the flow field |
抽取装置内部的流场得到流场计算域中的1、2、3、4、5部分.考虑到本装置上部出口连接排尘管道,所以增加了流场计算域的第1部分作为排尘口计算域使得出口处的气流得到充分的发展,达到了更贴近实际情况和提高计算精度的目的.流场计算域的第6部分为吸嘴进风口和地面之间的流场计算域,直接与扩展域连通.流场计算域的第7部分为流场计算域扩展域部分,是由吸嘴进风口与地面之间的区域以及吸嘴进风口以上的一部分区域组成的,由于龙卷风是旋转涡流,因此这部分设计成圆柱形.
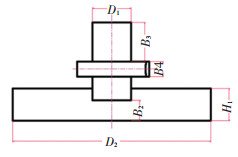
1.3 扩展域及结构参数如图 2(b)与图 4所示,θ为导流孔倾斜角度,D1为吸嘴以及排尘口管道直径,D2为扩展域直径,H1为扩展域高度,H2为近地面计算域高度,H3为排尘口高度.
|
图 4 装置参数 Fig. 4 Parameters of the dust collector |
由于吸嘴的结构参数对于吸尘装置具有重要影响,参考一般道路清扫车吸嘴的宽度,本装置的D1的初始取值为500 mm.考虑到实际流场范围比吸嘴的直径大,且高度超过吸嘴距地面的高度,所以H1的初始值不妨取200 mm.扩展域直径D2应尽可能大,其初始值不妨取6 000 mm,这样才能保证流场的充分发展;排尘口计算域1的直径是由吸嘴直径决定的,而其高度H3足够高才能不影响仿真结果的准确性,在此不妨取其初始值为1 800 mm;本吸尘装置的卷吸效应主要来源于导流孔,导流孔的倾斜角度θ可能极大地影响吸尘装置内的风场结构,由于θ受本装置设计的导流孔直径与数量的影响,其变化为-45°~45°,不妨其初始值取为45°;近地面计算域高度H2主要是由清扫对象的尺寸大小决定的,一般为10~20 mm[12],在此不妨取其初始值为20 mm;扩展域的高度和直径、排尘口的高度及近地面高度均对仿真结果有很大影响,随着这些参数的变化,近地面风速、压强和圆筒进风口的压强也发生着变化.因此,选用6个几何变量对基于龙卷风卷吸原理的吸尘装置进行流场仿真研究,计算时选其中1个参数作为变量,分别研究其余参数的变化对流场仿真结果精度的影响规律.根据图 2的装置尺寸,各参数初始值分别为H3= 1 800 mm、H2= 20 mm、θ = 45°、D2= 200 mm、H1= 6 000 mm、D1= 500 mm.
涡流比是表征装置产生的类龙卷风结构特征的一个无量纲量[13],涡流比S定义为
| $ S=\frac{{{V}_{\tau }}}{{{V}_{r}}}\frac{{{R}_{0}}}{2{{H}_{0}}}=\frac{{{V}_{\tau }}}{{{V}_{r}}}\frac{{{D}_{1}}}{4{{H}_{0}}}. $ | (1) |
式中:Vτ为切向速度;Vr为径向速度;R0为圆筒的半径,当D1= 500 mm时,R0= 250 mm;H0为气体环流通道的高度,如图 2(a)所示,H0= 200 mm.
在本装置中,可影响到涡流比的参数为导流孔倾斜角度、导流孔数量、进气速度与D1/H0,由于影响因素较多,因此在本文后续研究中,对导流孔数量、进气速度与D1/H0进行固定,即只研究导流孔倾斜角度改变时的涡流比.仿真研究的具体参数组合方案见表 1.
| 表 1 装置结构参数组合 Tab. 1 Combinations of structure parameters of the dust collector |
仿真模拟中,在计算误差允许的范围内对模型进行必要的简化并给出以下基本假定:1)假定空气为不可压缩流体;2)假定空气为粘性牛顿流体,即空气的动力粘度恒定,不随速度梯度的变化而变化;3)计算中不考虑空气重力影响.流场遵循以下动力学方程.
1) 连续性方程:
| $ \frac{\partial \rho }{\partial t}+\nabla \cdot (\rho v)=0. $ | (2) |
式中:ρ为流体密度,v为流体速度,t为时间.
2) 动量方程:
| $ \begin{array}{*{35}{l}} \rho \frac{\partial v}{\partial t}+\rho (v\cdot \nabla )v= \\ -\nabla {{p}^{\prime }}+\nabla \cdot \left( {{\mu }_{e}}\nabla v \right)+\nabla \cdot \left( {{\mu }_{e}}{{(\nabla v)}^{\text{T}}} \right). \\ \end{array} $ | (3) |
式中:
3) RNG k-ε方程[14].由于该吸尘装置内部流场雷诺数Re= 9×105~2.57×106,该流场属于湍流,且流场有旋转及旋流流动的情况,文献[15-16]在对龙卷风进行数值模拟时使用RNG k-ε模型,其计算结果精准可靠,所以本文计算模型采用RNG k-ε方程:
| $ \frac{\partial (\rho k)}{\partial t}+\frac{\partial \left( \rho k{{u}_{i}} \right)}{\partial {{x}_{i}}}=\frac{\partial }{\partial {{x}_{j}}}\left[ {{\alpha }_{k}}{{\mu }_{\text{eff}}}\frac{\partial k}{\partial {{x}_{j}}} \right]+{{G}_{k}}+\rho \varepsilon , $ | (4) |
| $ \begin{matrix} \frac{\partial (\rho \varepsilon )}{\partial t}+\frac{\partial \left( \rho \varepsilon {{u}_{i}} \right)}{\partial {{x}_{i}}}=\frac{\partial }{\partial {{x}_{j}}}\left[ {{\alpha }_{\varepsilon }}{{\mu }_{\text{eff}}}\frac{\partial \varepsilon }{\partial {{x}_{j}}} \right]+ \\ \frac{C_{1\varepsilon }^{*}\varepsilon }{k}{{G}_{k}}-{{C}_{2\varepsilon }}\rho \frac{{{\varepsilon }^{2}}}{k}. \\ \end{matrix} $ | (5) |
式中:
由于本文的清扫装置内流场比较复杂,所以,所有的研究组别均采用ANSYS MESH 16.0进行非结构化四面体网格划分.为准确捕捉吸尘装置内流场与涡结构的细微变化,对装置内导流孔区域等处的网格进行加密处理,另外,为了充分解决壁面附近的气流,捕捉气流的分离位置,运用Inflation膨胀层划分边界层网格.控制边界层第1层网格高度在5×10-4 m左右,同时保证各参数组合下装置壁面的y+值均在30~150之间.
为了确保本文采用的网格尺度达到数值仿真的要求,即继续加密网格不会对流场结果造成较大的影响,对采用初始参数值的几何模型进行了网格无关性验证,分别采用0.12、0.08、0.04 m的粗、中、细3套网格尺度划分网格,对应的网格数量为352 059、702 622、1 606 387. 图 5是根据图 2中的结构尺寸和扩展域几何变量的初始值绘制的几何模型采用中等网格尺度划分的网格模型. 图 6为不同网格对吸尘装置轴线上的速度仿真结果的影响曲线,由图 6可知,粗网格与细网格的速度仿真值之间差别较大,而中等网格与细网格的速度仿真值之间差别较小.考虑计算精度与计算资源,因此本文采用中等网格尺度进行网格划分.

|
图 5 基于龙卷风发生原理的初始吸尘装置网格模型 Fig. 5 Grid model of the dust collector based on the tornado generation principle using initial values |
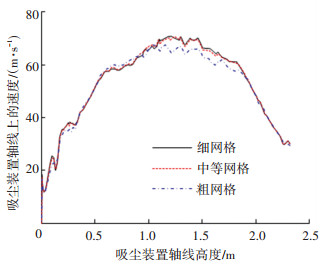
|
图 6 不同网格尺度对吸尘装置轴线上速度的影响曲线 Fig. 6 Effect curve of different grid scales on the velocity along the axis of the dust collector |
表 2给出了不同研究参数时的几何模型采用中等网格尺度划分网格得到的网格数量与网格质量指标值,由表 2可知,网格的单元最大扭曲度均小于0.9,平均扭曲度均小于0.26,最大纵横比均未大于40,平均纵横比均小于3,平均正交程度质量均在0.85左右,其网格质量均符合本文仿真要求[17].
| 表 2 不同研究变量下的网格数与网格质量范围 Tab. 2 Range of grid numbers and grids quality under different structure parameters of the dust collector |
由于总进风口吹入的空气经过环流通道和导流孔会有沿程损失和局部损失,所以为了使气流具有足够的切向速度,总进风口吹入的空气需要足够的风速.排尘口的负压也要足够大才能使得产生的具有切向速度的气流聚束起来形成龙卷风并且向上方运动. 1)总进风口定义为速度入口,风速为60 m/s;2)排尘口出口处定义为压力出口,相对压力值为-3 000 Pa;3)与大气连通的扩展域表面为压力入口,取标准大气压值;4)地面及模型的内部边界均定义为壁面;5)模型内部空气流动的地方定义为流体.
2.4 算法选择流场计算选择Fluent软件压力基求解器完成,三维定常计算,迭代步数设为10 000步,求解器的收敛精度设为1.0×10-6,各项计算量不断进行迭代,直至残差均低于收敛精度时停止计算.选用RNG k-ε湍流模型和增强壁面函数,计算方法采用压力-速度耦合SIMPLE算法.压力插值选择Standard格式,动量方程、湍动能和湍流耗散率的离散方式均采用二阶迎风离散格式,保证计算精度.
3 计算结果分析 3.1 评价指标尘粒启动理论[18]指出:当近地面气流平均速度大于尘粒启动速度时,尘粒才能被顺利吸起,吸嘴进风口处的负压大有利于尘粒吸入吸嘴中.并且随着扩展域越来越接近真实的流场情况,近地面风速以及吸嘴进风口处的负压都应该趋向于一个稳定的值.所以,本文借助吸嘴覆盖区域的近地面气流的平均速度和吸嘴进风口平均压强来判断扩展域参数变化对仿真结果的影响.由于龙卷风其内外有较大的气压差,所以具有极强的抽吸能力以及破坏力[19].本文采用圆筒中心区和壁面区的压差作为评价形成的龙卷风的好坏的指标,判别形成的龙卷风的强度.综上所述,本文选择近地面平均风速、压差和吸嘴进风口平均压强作为对扩展域与结构参数研究的评价指标.
3.2 结构参数对流场的影响 3.2.1 排尘口高度的分析图 7是根据仿真结果得到的排尘口高度H3对近地面平均风速及入口平均压强的影响曲线.由图 7可以看出,随着排尘口高度H3的逐渐增加,近地面平均风速先增后减,入口平均压强出现波动,在H3/D1增加到1.6时,此时的近地面平均风速和入口平均压强达到一个相对稳定的值,即再增加排尘口高度对人造龙卷风的生成以及清扫效果的评估几乎没有影响.
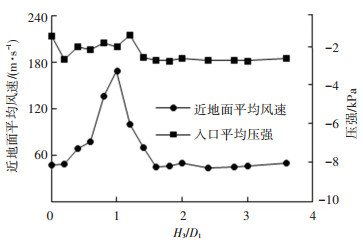
|
图 7 排尘口高度的影响曲线 Fig. 7 Effect curve of the height of the dust outlet |
产生上述现象的原因是:当排尘口高度H3的值太小时装置产生的龙卷风的上部得不到充分的发展,所以随着H3的值的增加,龙卷风在上部的发展状况也在不断改变,这就造成了近地面平均风速和入口平均压强随着H3的值改变而改变,当H3/D1达到1.6时,此时的排尘口高度已经满足了龙卷风的上部的完全发展,所以再增大H3的值时,对本装置产生的龙卷风几乎没有影响了,此时近地面平均风速和入口平均压强均达到了一个相对稳定的值.
3.2.2 近地面计算域高度的分析由于近地面计算域高度H2决定着扩展域的高度H1,所以在研究扩展域的高度之前先对近地面计算域的高度H2进行研究. 图 8是根据仿真结果得到的排尘口无量纲高度H3/D1=1.6时近地面计算域在不同高度H2下的圆筒区内部的轴向压力分布云图.图 9为近地面计算域高度变化对涡核中心位置的影响曲线,其中L/D1为涡核中心与圆筒区中心的无量纲距离.由图 8、9可以看出,随着近地面计算域高度H2的逐渐增加,本装置形成的涡的涡核逐渐靠近吸嘴的中心并且变成规则的圆形,当H2/D1=0.2时,涡核处于吸嘴的中心,当近地面计算域高度H2继续增大时涡核偏离进风口的中心且变得不规则.
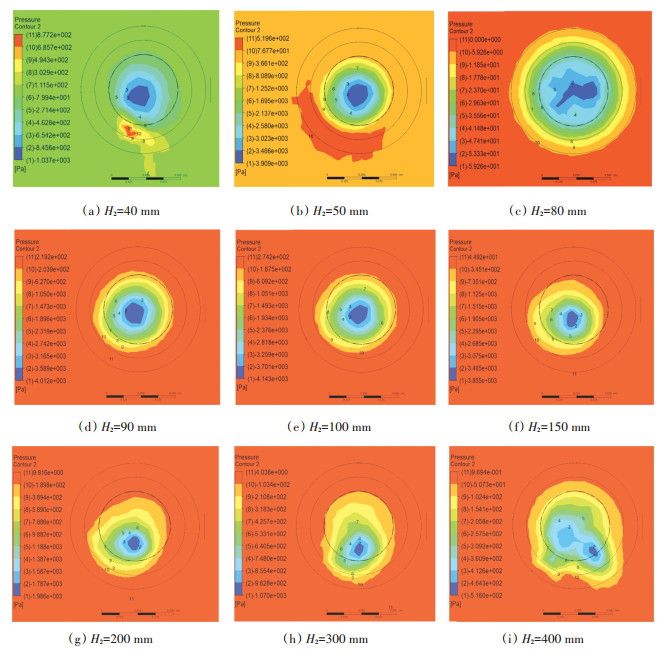
|
图 8 近地面计算域高度不同时圆筒内部压力分布云图 Fig. 8 Distribution of the internal pressure of the cylinder with varying heights of the near-ground computational domain |
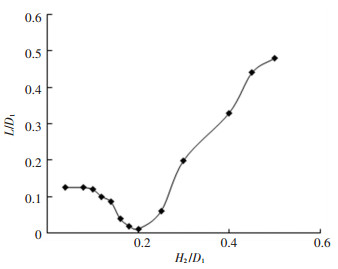
|
图 9 近地面计算域高度对涡核中心位置的影响曲线 Fig. 9 Effect curve of the height of the near-ground computational domain on the center position of the vortex core |
产生上述现象的原因是:当近地面计算域高度H2的值很小时,吸嘴内的气流与大气连通度太低,对龙卷风的生成造成了阻碍,所以生成的龙卷风的涡核不规则且偏离吸嘴的中心.当H2/D1=0.2时,此时的吸嘴内部的气流和大气的连通度刚好,有利于龙卷风的生成,所以此时的龙卷风从云图上可以看出其涡核是规则的圆形且位置在吸嘴的中心.当H2/D1>0.2时,由于吸嘴距地面太高,所以受大气的影响很大,此时大气中的气流流动对吸嘴内的龙卷风的形成造成了干扰,生成的龙卷风的涡核逐渐变得不规则且远离了吸嘴的中心.
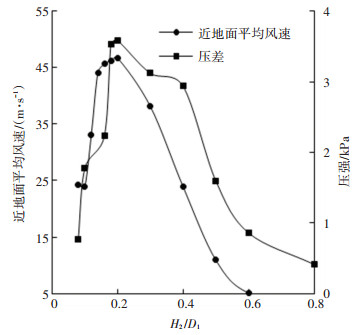
图 10是根据仿真结果得到的近地面计算域高度H2对吸嘴内压差及近地面平均风速的影响曲线.从图 10可以看出,当H2/D1 < 0.2时,吸嘴内的压差值及近地面平均风速逐渐增大;当H2/D1=0.2时,吸嘴内压差值及近地面平均风速值出现了阈值,此时在吸嘴内生成的龙卷风的强度大且稳定性好;当H2/D1>0.2时,吸嘴内的压差值及近地面平均风速逐渐减小.
|
图 10 近地面计算域高度的影响曲线 Fig. 10 Impact curve of the height of the near-ground computational domain |
产生上述现象的原因是:压差可以直观反映龙卷风的强弱和稳定性,当本装置生成的龙卷风强且稳定时其中心处和外围的压差就会相对较大,同时具有更强的卷吸能力,所以当H2/D1 < 0.2时其压差和近地面平均风速随着H2的增加而增大;当H2/D1=0.2时其压差和近地面平均风速达到阈值且值最大,因为此时装置产生的龙卷风最稳定且强度最大;当H2/D1>0.2时,装置产生的龙卷风强度渐渐减小,所以压差值和近地面平均风速也逐渐减小.
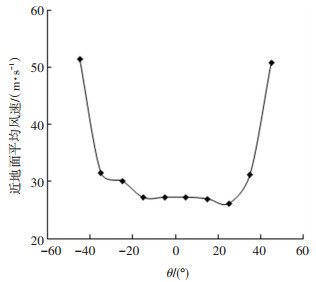
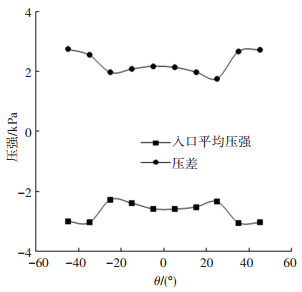
3.2.3 导流孔倾斜角度的分析图 11、12是根据仿真结果得到的导流孔倾斜角θ对近地面平均风速、入口平均压强及压差的影响曲线.由图 11、12可以看出,当θ>0°时,随着导流孔倾角θ的逐渐增大,近地面平均风速逐渐增大,入口平均压强逐渐减小,压差逐渐增大;当θ < 0°时,随着导流孔倾角θ的逐渐减小,近地面平均风速逐渐增大,入口平均压强逐渐减小,压差逐渐增大;当θ=45°或θ=-45°时装置产生的龙卷风的涡流比为0.625,此时装置产生的龙卷风最稳定且强度最大,近地面平均风速最大、入口平均压强最小且压差也最大.根据式(1)可知,当|θ|从0°到45°递增时,该吸尘装置内龙卷风的涡流比也单调递增,结合θ对流场的影响效果,说明在本装置研究的倾斜角范围内对应的涡流比,随涡流比增加,吸尘装置内的风场结构强度变大,有利于吸尘效率的提高.
|
图 11 导流孔倾斜角度对近地面平均风速的影响曲线 Fig. 11 Effect curve of inclination angle of diversion orifice on the near-ground mean velocity |
|
图 12 导流孔倾斜角度的影响曲线 Fig. 12 Effect curve of inclination angle of diversion orifice |
产生上述现象的原因是:当导流孔倾角θ靠近0°时,此时的导流孔吹进的气流的切向速度较小,不利于龙卷风的形成;当导流孔倾角θ从0°逐渐增大到45°或减小到-45°时,此时的导流孔吹进的气流为形成龙卷风提供了逐渐增大的切向速度,有利于形成结构稳定且强度大的龙卷风.
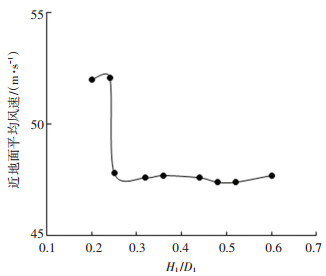
3.3 扩展域参数对流场的影响 3.3.1 扩展域高度图 13是根据仿真结果得到的近地面计算域无量纲高度H2/D1=0.2时扩展域高度H1对近地面平均风速的影响曲线.由于近地面计算域无量纲高度H2/D1=0.2,所以为了能把吸嘴进风口和地面之间的这段的气体流动情况包含进去,从扩展域高度H1与圆筒直径D1的比值为0.2即扩展域高度H1=100 mm时开始取值.由图 13可以看出随着扩展域高度的增大吸嘴进风口覆盖区域的近地面平均风速先减小,在扩展域高度与吸嘴直径的比值为0.25即扩展域高度为125 mm时保持稳定.
|
图 13 扩展域高度的影响曲线 Fig. 13 Effect curve of the extended domain height |
产生上述现象的原因是:开始时扩展域高度不足造成与大气的连通度不够,使得近地面处的气流受大气的影响相比实际情况较小,所以近地面的速度大;当扩展域的高度增大到适当的高度的时候,此时的扩展域高度达到了实际情况的连通度,再增大高度对近地面速度的影响变得十分小,所以近地面的速度基本达到了稳定.
3.3.2 扩展域直径本文在原有的装置的基础上其进行等比例缩放,并且在仿真时不改变进出口的条件,这样来确保不同大小的装置产生的龙卷风都具有相同的涡流比.本组仿真实验采用的D1= 500 mm时的涡流比为0.625. 图 14是根据仿真结果得到的吸嘴直径D1取值不同时的扩展域直径D2对吸嘴进气口覆盖区域的近地面平均风速的影响曲线,仿真时取扩展域的无量纲高度为0.3. 图 15为吸嘴直径D1对扩展域直径阈值D2/D1的影响曲线.
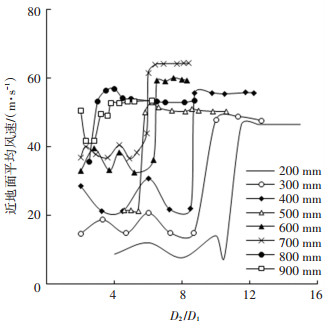
|
图 14 扩展域直径的影响曲线 Fig. 14 Effect curve of the extended domain diameter |
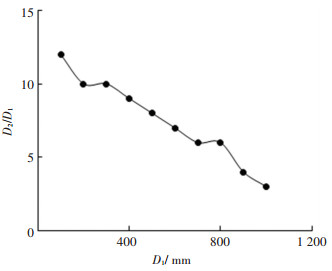
|
图 15 扩展域直径阈值的影响曲线 Fig. 15 Effect curve of diameter threshold in extended domain |
由图 14可以看出,吸嘴直径在不同水平下,均在增大扩展域直径的开始阶段近地面平均风速的数值有一段无规则的波动,当扩展域直径与圆筒直径的比值达到一定数值时,此时的近地面平均风速达到一个相对稳定的值,也就是再增大扩展域的直径对人造龙卷风的生成以及清扫效果的评估几乎没有影响.由图 15可知,扩展域的阈值随着吸嘴直径的增大而减小,即本装置所需扩展域的直径与吸嘴直径的比值随着吸嘴直径的增大而减小.
产生上述现象的原因是:当扩展域直径较小时,扩展域的尺寸小引起仿真失真,装置与大气的联通情况相比实际情况差距很大,这造成了近地面速度剧烈变动,而随着扩展域的直径的逐渐增大,扩展域所包裹的区域与装置实际情况下所扰动的大气的区域逐渐接近,所以在扩展域直径增大到5倍圆筒直径的时候近地面的风速稳定下来.
4 结论1) 根据龙卷风发生原理设计了新型吸尘装置,并基于计算流体动力学方法研究了排尘口高度、吸嘴直径、吸嘴进风口距地面高度、导流孔倾斜角度、涡流比和扩展域参数.
2) 在本装置其他结构参数不改变的情况下,排尘口高度与吸嘴直径的比值为1.6时,此时装置产生的龙卷风上部完全发展且结构稳定.
3) 在本装置其他结构参数不改变的情况下,吸嘴进风口距地面高度与吸嘴直径的比值为0.25时,此时装置产生的龙卷风具有明显的单涡结构,吸嘴覆盖区域的近地面风速最大,吸尘效果最好.
4) 在本装置其他结构参数不改变的情况下,导流孔倾斜角度θ= 45°或θ= -45°时装置产生的龙卷风最稳定且强度最大,此时装置产生的龙卷风的涡流比为0.625.当仅通过改变导流孔倾斜角度θ使涡流比改变的情况下,随着一定范围内的涡流比的增加,吸尘装置内的风场结构的强度变大,有利于吸尘效率的提高.
5) 在本装置其他结构参数不改变的情况下,扩展域的高度和直径均存在阈值.当扩展域高度与吸嘴直径的比值为0.2时扩展域高度达到阈值,扩展域直径的阈值随着吸嘴直径的增大而减小,即本装置所需扩展域的直径与吸嘴直径的比值随着吸嘴直径的增大而减小.当扩展域参数大于相应阈值时,其影响可以忽略不计.
| [1] |
ZHANG Yicheng, YANG Chunzhao, BAKER C, et al. Effects of expanding zone parameters of vacuum dust suction mouth on flow simulation results[J]. Journal of Central South University, 2014, 21(6): 2547. DOI:10.1007/s11771-014-2210-2 |
| [2] |
郗元.轻型扫路车反吹式吸嘴流动特性及吸尘效率优化研究[D].长春: 吉林大学, 2016 XI Yuan. Research on the flow characteristics and overall removal efficiency optimization of reverse blowing pickup mouth for a light sweeper[D]. Changchun: Jilin University, 2016 http://cdmd.cnki.com.cn/Article/CDMD-10183-1017011772.htm |
| [3] |
杨春朝, 章易程, 欧阳智江, 等. 基于流场模拟的真空清扫车吸尘口的参数设计[J]. 中南大学学报(自然科学版), 2012, 43(9): 385. YANG Chunzhao, ZHANG Yicheng, OUYANG Zhijiang, et al. Parametric design of dust collection port of vacuum sweeper based on flow simulation[J]. Journal of Central South University (Science and Technology), 2012, 43(9): 385. |
| [4] |
朱伏龙, 张冠哲, 陈杰. 真空吸尘车吸尘口的流场仿真和结构优化[J]. 机械设计与制造, 2008, 50(11): 50. ZHU Fulong, ZHANG Guanzhe, CHEN Jie. Flow field analysis and structure optimization of vacuum sweeper suction mouth[J]. Machinery Design & Manufacture, 2008, 50(11): 50. DOI:10.3969/j.issn.1001-3997.2008.11.020 |
| [5] |
台冰丰, 吴杰灵. 清扫车吸尘口结构优化设计[J]. 专用汽车, 2014(4): 96. TAI Bingfeng, WU Jieling. Optimized design of suction mouth of sweeper[J]. Special Purpose Vehicle, 2014(4): 96. DOI:10.3969/j.issn.1004-0226.2014.04.025 |
| [6] |
李成林.全吸式干湿两用扫路车关键技术研究[D].镇江: 江苏科技大学, 2012 LI Chenglin. Research on key technologies of full-suction dry-wet dual-purpose road sweeper[D]. Zhenjiang: Jiangsu University of Science and Technology, 2012 http://cdmd.cnki.com.cn/Article/CDMD-10289-1012043796.htm |
| [7] |
张景松. 人造龙卷风形成机理[J]. 煤炭学报, 1996(4): 403. ZHANG Jingsong. Formation mechanism of artificial tornado[J]. Journal of Coal Science, 1996(4): 403. |
| [8] |
张翼喆.龙卷风风场数值模拟及发生装置研制[D].哈尔滨: 哈尔滨工业大学, 2015 ZHANG Yizhe. Numerical simulation of tornado wind field and development of generator[D].Harbin: Harbin Institute of Technology, 2015 http://cdmd.cnki.com.cn/Article/CDMD-10213-1015979636.htm |
| [9] |
WARD N B. The exploration of certain features of tornado dynamics using a laboratory model[J]. Journal of Atmospheric Sciences, 1972, 29(6): 1194. DOI:10.1175/1520-0469(1972)029<1194:TEOCFO>2.0.CO;2 |
| [10] |
YING S J, CHANG C C. Exploratory model study of tornado-like vortex dynamics[J]. Journal of the Atmospheric Sciences, 1970, 27(1): 3. DOI:10.1175/1520-0469(1970)027<0003:EMSOTL>2.0.CO;2 |
| [11] |
陈忠基, 吴晓元, 徐广普, 等. 路面清扫车吸嘴装置的实验研究[J]. 同济大学学报(自然科学版), 2001, 29(12): 1483. CHEN Zhongji, WU Xiaoyuan, XU Guangpu, et al. Experimental study on the nozzle device of road sweeper[J]. Journal of Tongji University (Natural Science), 2001, 29(12): 1483. DOI:10.3321/j.issn:0253-374X.2001.12.023 |
| [12] |
王翔.城市道路吸扫车吸尘系统的结构设计和流场分析[D].武汉: 武汉理工大学, 2013 WANG Xiang. Structural design and flow field analysis of vacuum cleaning system of urban road sweeper[D]. Wuhan: Wuhan University of Technology, 2013 |
| [13] |
LEWELLEN W S. A solution for three-dimensional vortex flows with strong circulation[J]. Journal of Fluid Mechanics, 1962, 14(3): 420. DOI:10.1017/S0022112062001330 |
| [14] |
王福军. 计算流体动力学分析[M]. 北京: 清华大学出版社, 2004. WANG Fujun. Computational fluid dynamics analysis[M]. Beijing: Tsinghua University Press, 2004. |
| [15] |
徐枫, 肖仪清, 李波, 等. 龙卷风风场特性的CFD数值模拟[J]. 空气动力学学报, 2013, 31(3): 350. XU Feng, XIAO Yiqing, LI Bo, et al. CFD numerical simulation of tornado wind field characteristics[J]. Journal of Aerodynamics, 2013, 31(3): 350. |
| [16] |
王威, 王聪, 魏英杰. 超空泡航行体转弯运动多相流场特性[J]. 哈尔滨工业大学学报, 2018, 50(10): 130. WANG Wei, WANG Cong, WEI Yingjie. Multiphase flow field characteristics of turning motion of super-cavitating vehicle[J]. Journal of Harbin Institute of Technology, 2018, 50(10): 130. |
| [17] |
胡坤, 李振北. ANSYS ICEM CFD工程实例详解[M]. 北京: 人民邮电出版社, 2014. HU Kun, LI Zhenbei. Detailed engineering examples for ANSYS ICEM CFD[M]. Beijing: People's Posts and Telecommunications Press, 2014. |
| [18] |
李战军, 郑炳旭. 尘粒起动机理的初步研究[J]. 爆破, 2003, 20(4): 17. LI Zhanjun, ZHENG Bingxu. Mechanism of the movement of dust particles[J]. Blasting, 2003, 20(4): 17. |
| [19] |
潘玉伟.龙卷风风场与结构风荷载CFD数值模拟[D].哈尔滨: 哈尔滨工业大学, 2013 PAN Yuwei. CFD numerical simulation of tornado wind field and structural wind load[D].Harbin: Harbin Institute of Technology, 2013 http://cdmd.cnki.com.cn/article/cdmd-10213-1014081029.htm |
 2020, Vol. 52
2020, Vol. 52


