2. 桥梁工程结构动力学国家重点实验室(重庆交通科研设计院), 重庆 400067
2. State Key Laboratory of Bridge Engineering Structural Dynamic (Chongqing Communications Technology Research & Design Institute), Chongqing 400067, China
在桥梁结构中,伸缩缝是最容易发生早期损坏的部件[1],与伸缩缝相关的维修花费超过桥梁结构早期维护费用的20%[2].伸缩缝早期损坏的重要原因是载重汽车轮胎的长期冲击作用,这个冲击荷载也是伸缩缝设计的主要参数.遗憾的是,目前该冲击荷载的确定还缺乏明确的理论与实验依据,世界各国的取值差别也很大.中国伸缩缝设计指南[3]以140 kN作为车辆的标准轴重,并考虑0.45的冲击系数;美国桥梁规范[4]以145 kN作为标准轴重,并计入0.75的冲击系数;英国规范[5]和德国规范[6]取200 kN的车辆轴重,但冲击系数取值不同,分别为0.5、0.4.因此,明确伸缩缝冲击荷载,可为伸缩缝及其周边桥(路)面的设计与维护提供参考[7-9].
关于伸缩缝跳车冲击荷载的实验研究还很少,文献[10]通过测量模数式伸缩缝在车辆作用下的动应变与动位移,推测汽车轮胎荷载竖向的冲击系数为0.2~0.3,横向的冲击系数约为0.15;文献[11]则认为0.1~0.5的冲击系数与其实测结果比较符合.在上述实验研究中,由于跳车冲击荷载大,直接测试困难,因此都是通过伸缩缝结构动力响应间接获得车轮冲击荷载,且都没有计及汽车行驶的快慢、伸缩缝开口的大小等对冲击系数的影响.
在理论算法上,往往通过分析车辆通过伸缩缝时的振动来计算冲击荷载,其中轮底在伸缩缝上的局部脱空现象是分析的难点.文献[12]假设车轮通过伸缩缝时的轮底运动轨迹是长20 cm,深2~4 cm的凹台,这个假设源于对伸缩缝的外形量测,与实际的轮底轨迹存在差别.文献[13]提出了一种基于分布式弹簧-阻尼单元(distributed spring-damp element,以下简称DSD单元)的计算方法,可以模拟车轮通过伸缩缝时的局部脱空情况,并用于计算作用在伸缩缝上的车轮冲击荷载,但是该方法忽略了轮胎通过伸缩缝时接触长度的变化,并且还缺乏实验验证.
本文在上述工作基础上,对桥梁伸缩缝跳车冲击荷载问题进行了算法改进和实验研究.首先制作了桥梁与车辆的缩尺实验模型,实测缩尺模型在伸缩缝跳车时的车轮冲击力.然后改进了假设轮底运动轨迹的车轮荷载计算方法,考虑了荷载大小、轮胎和伸缩缝尺寸对轮底运动轨迹的影响.同时,也改进了基于DSD单元的车轮荷载计算方法,考虑了车轮经过伸缩缝时轮胎-路面接触长度的变化.最后,对典型三轴载重汽车经过伸缩缝时的冲击荷载进行了数值模拟,讨论了伸缩缝宽度、车辆速度对轮载冲击系数的影响.
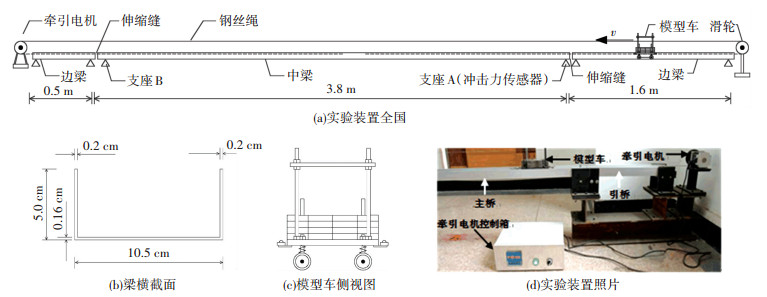
1 模型实验以图 1所示的单缝式桥梁伸缩缝为例,建立缩尺模型实验装置.实验装置的设计图和制作完成后的照片如图 2所示.桥梁采用1:30的单车道铝合金梁缩尺模型,相当于宽度为3米的桥.桥梁模型分3段:第1、3段为引桥,第2段为简支梁主桥.每两段模型连接处布置单缝式伸缩缝.车辆模型采用1:30的两轴车模型,车轮用弹性橡胶制作,受压变形后,可以反映轮胎与路面之间的接触长度.车辆动力由牵引电机通过钢丝绳提供,运动路径包含3段桥梁模型,因此可以模拟车辆通过桥梁伸缩缝时的跳车现象.
|
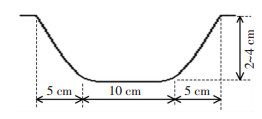
图 1 单缝式桥梁伸缩缝 Fig. 1 Bridge expansion joint with single gap |
|
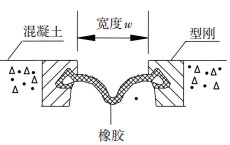
图 2 缩尺模型实验装置 Fig. 2 Reduced-scale experimental model |
测试系统主要是伸缩缝冲击力测试装置,该装置由冲击力传感器和信号处理系统组成.如图 2(a)和图 3所示,冲击力传感器有两个,为美国PCB公司的200B02型石英冲击力传感器,代替支座A支撑简支梁主桥,位于伸缩缝旁,直接实测车轮冲击力导致的支座竖向支撑力.因为作为支座A的冲击力传感器距离梁端只有0.5 cm,简支梁长度达3.8 m,所以当模型车的前轮经过伸缩缝驶上中梁时,竖向支座反力之和与两前轮冲击荷载之和差别很小,可以认为两者相等.

|
图 3 冲击力传感器(支座A) Fig. 3 Impact force sensor(bearing A) |
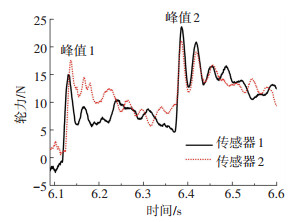
实测得到的典型冲击力曲线如图 4所示,其中两条曲线分别为模型车辆通过伸缩缝时两个冲击力传感器测得的力,图 4对应的模型车速度为0.4 m/s,伸缩缝宽度为3 mm.
|
图 4 车辆冲击力实测值 Fig. 4 Measured impactload of vehicle |
在图 4中,峰值1是图 2(c)所示模型车前轮通过伸缩缝时的冲击力峰值,峰值2是后轮通过伸缩缝时的冲击力峰值.因为压电式冲击力传感器测得的力随时间衰减,所以实测结果中的峰值1精度较高,反映了前轮的冲击荷载.实测结果中的峰值2包含了后轮冲击荷载和前轮荷载的影响,由于前轮冲击荷载测试值的衰减,所以峰值2的精度受到干扰,不宜用于分析车轮的冲击荷载.
由于实验误差,图 4中的左前轮和右前轮的冲击力略有不同,因此本文取两者的平均值作为前轮的平均冲击力,这也和下文采用二维的车辆模型计算伸缩缝冲击荷载相一致.
2 计算方法实测得到的车轮冲击力可以用来检验对应的计算方法,此时通过对车辆在伸缩缝上的动力响应进行有限元分析,得到车轮的冲击荷载.以缩尺模型实验中的小车为例,如图 2(c)所示,相应的二维有限元模型,如图 5所示,包含7个节点,6个单元.其中车体用刚性梁单元模拟,车体悬挂系统用弹簧-阻尼单元模拟[14],对应于不同的计算方法,弹性车轮分别选用弹簧-阻尼单元或分布式弹簧-阻尼单元来模拟[15].
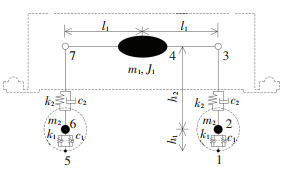
|
图 5 试验小车的有限元模型 Fig. 5 FEM model of the vehicle model in experiment |
通过对模型车辆的实测,得到图 5所示车辆有限元模型的计算参数. l1为0.05 m,h1、h2分别为0.013、0.054 m,m1、m2分别为4.35、0.125 kg,J1为0.007 9 kg·m2.由压缩试验得到轮胎刚度k1为53.4 kN/m,由自由振动衰减曲线测得轮胎阻尼c1为61.4 N·s/m.由于轮胎以上部分为钢结构,其支撑刚度远大于轮胎刚度,因此k2取为远大于k1的常数,阻尼c2则取为远小于c1的常数.
经过单元组集,获得模型车的振动方程组为
| $ {\mathit{\boldsymbol{M}}_v}{{\mathit{\boldsymbol{\ddot u}}}_v} + {\mathit{\boldsymbol{C}}_v}{{\mathit{\boldsymbol{\dot u}}}_v} + {\mathit{\boldsymbol{K}}_v}{\mathit{\boldsymbol{u}}_v} = {\mathit{\boldsymbol{F}}_v}\left( t \right). $ | (1) |
其中:uv为节点位移向量;Mv、Cv、Kv分别为质量、阻尼、刚度矩阵;Fv为车辆所受荷载向量;t为时间.
方程(1)用Newmark法在时域内积分求解,求解难点在于车轮经过伸缩缝时轮底局部脱空,导致轮底位移是未知量[13].在图 5所示的有限元模型中,1号、5号节点在车轮通过伸缩缝时的位移即为未知量.为了确定伸缩缝上的轮底脱空段位移,本文提出了以下两种方法.
2.1 假设轮底运动轨迹图 6为载重车的轮胎在路(桥)面和伸缩缝上行驶时的变形情况.由图可见,车轮在伸缩缝外的路面上时,轮胎压缩量为ΔR,轮胎-路面接触长度为a;车轮通过伸缩缝时,轮底局部脱空,最大脱空长度即为伸缩缝宽度w,此时轮胎压缩量为ΔR′,轮胎-路面接触长度为a′.文献[12]假设车轮通过伸缩缝时的轮底运动轨迹如图 7所示,该轨迹来自对特定伸缩缝、在特定时间的测量,适用面不广.
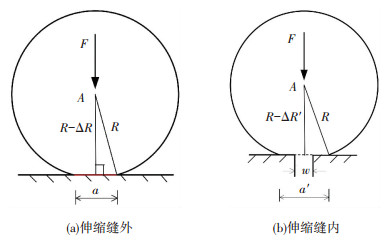
|
图 6 载重车轮胎变形 Fig. 6 Deformation of the tire of heavy vehicle |
本文对上述假设轮底轨迹方法进行了改进,考虑了轮载大小、轮胎和伸缩缝尺寸对轮底运动轨迹的影响.如图 6(a)所示,当轮胎在普通路面上时,轮轴荷载F作用下的竖向压缩量为
| $ \Delta R = F/K, $ |
其中K为轮胎的刚度.
当车轮位于伸缩缝中心时,如图 6(b)所示,由于轮底局部脱空,脱空部分不受路面的支持,所以车轮的竖向压缩量为
| $ \Delta R' = F/\left( {K\frac{{a' - w}}{{a'}}} \right) = \Delta R\frac{{a' - w}}{{a'}}. $ | (2) |
假定轮胎在变形前后的半径R不变,那么图 6(b)中轮胎与地面的接触长度为
| $ a' = 2\sqrt {{R^2} - {{\left( {R - \Delta R'} \right)}^2}} . $ | (3) |
由式(2)、(3)可得关于a′的方程为
| $ \frac{{{{\left( {a'} \right)}^2}}}{4} = {R^2} - {\left[ {R - \Delta R\frac{{a'}}{{\left( {a' - w} \right)}}} \right]^2}. $ | (4) |
由式(4)求得a′,再由式(3)可得轮胎在伸缩缝内的压缩量ΔR′.
轮胎在伸缩缝内和普通路面上的压缩量之间的差别为ΔR′-ΔR.考虑到伸缩缝中的车轮底部局部脱空,因此车轮的实际支撑刚度减小.但是在有限元计算模型中,轮胎单元的刚度K大小不变,因此在有限元计算中,需要将轮胎在伸缩缝内、外的压缩量之差作折减,即
| $ h = \left( {\Delta R' - \Delta R} \right)\frac{{\left( {a' - w} \right)}}{{a'}}, $ | (5) |
其中h为折减后的轮胎压缩量之差.
假设式(5)所示的压缩量之差为车轮跨越伸缩缝过程中的轮底最大位移,整个跨越过程中轮底的运动轨迹如图 8所示.过伸缩缝前、后的轮底位移为零;在上、下伸缩缝的w长度段内,轮底位移为余弦函数;中间a-w长度段内,轮底位移保持为h.
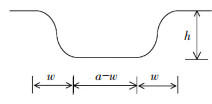
|
图 8 车轮底部的运动轨迹 Fig. 8 Trajectory of the tire bottom |
上述假设轮底位移是对文献[12]假设轮底位移的改进,考虑了轮胎-路面接触长度、伸缩缝宽度的影响,使之可以用于各种类型的车轮通过桥梁伸缩缝的情况,包括缩尺模型车辆的车轮.
2.2 改进的分布式弹簧-阻尼单元文献[13]曾用一种分布式弹簧-阻尼单元(DSD单元)代表汽车轮胎的力学特性,进一步分析汽车轮胎对伸缩缝的冲击力,但是该工作假定车轮经过伸缩缝时,与路面的接触长度保持为常数a.由于轮胎在伸缩缝上的脱空情况,该假定会带来一定的计算误差.为此,本文改进了上述分布式弹簧-阻尼单元,其结构如图 9所示.该单元中轮胎经过伸缩缝时与路面接触长度为a′,a′由式(3)计算.因为伸缩缝中的车轮压缩量ΔR′与车轮所在位置和振动位移有关,所以a′不再保持为常数.

|
图 9 改进的分布式弹簧-阻尼单元 Fig. 9 Improved distributed spring-damper (DSD) element |
如图 10所示,当用改进的DSD单元所代表的汽车轮胎通过伸缩缝时,仍然分为3阶段:下缝段、跨缝段、上缝段,单元底部B点的等效位移为
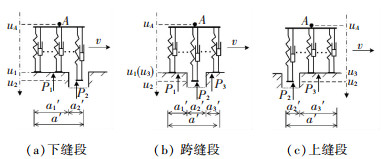
|
图 10 车轮DSD单元通过伸缩缝 Fig. 10 DSD element of thewheel passing through the expansion joint |
| $ {u_B} = {u_1}\frac{{a_1^\prime }}{{{a^\prime }}} + {u_2}\frac{{a_2^\prime }}{{{a^\prime }}} + {u_3}\frac{{a_3^\prime }}{{{a^\prime }}}. $ |
其中u1、u2、u3分别为轮底在a1′、a2′、a3′段的竖向位移.
分布式弹簧-阻尼单元的平衡方程依旧和普通的弹簧-阻尼单元一样[15].有限元分析获得节点位移和速度后,进一步可求得轮压荷载为
| $ P = k\left( {{u_B} - {u_A}} \right) + c\left( {{{\dot u}_B} - {{\dot u}_A}} \right). $ | (6) |
也可得到轮胎作用于伸缩缝结构a1′、a2′、a3′段的压力分别为
| $ {P_1} = k\frac{{a_1^\prime }}{{{a^\prime }}}\left( {{u_1} - {u_A}} \right) + c\frac{{a_1^\prime }}{{{a^\prime }}}\left( {{{\dot u}_1} - {{\dot u}_A}} \right), $ | (7) |
| $ \begin{array}{l} {P_2} = k\frac{{a_2^\prime }}{{{a^\prime }}}\left( {{u_2} - {u_A}} \right) + c\frac{{a_2^\prime }}{{{a^\prime }}}\left( {{{\dot u}_2} - {{\dot u}_A}} \right) + \\ \;\;\;\;\;\;\;\frac{c}{{{a^\prime }}}\left( {\dot a_1^\prime {u_1} + \dot a_{2,{\rm{ in}}}^\prime {u_2}} \right), \end{array} $ | (8) |
| $ \begin{array}{l} {P_3} = k\frac{{a_3^\prime }}{{{a^\prime }}}\left( {{u_3} - {u_A}} \right) + c\frac{{a_3^\prime }}{{{a^\prime }}}\left( {{{\dot u}_3} - {{\dot u}_A}} \right) + \\ \;\;\;\;\;\;\;\frac{c}{{{a^\prime }}}\left( {\dot a_{2,{\rm{ out}}}^\prime {u_2} + \dot a_3^\prime {u_3}} \right), \end{array} $ | (9) |
其中:
前述各段的长度变化率与轮胎所处的位置有关,当轮胎位于下缝段时,
用改进的DSD单元模拟轮胎,建立汽车有限元模型,如图 5所示,进一步建立式(1)所示的振动方程组.该方程组求解时,由于车轮经过伸缩缝时a2′段脱空,u2是未知量,导致轮底等效位移uB也是未知量.因此,汽车过伸缩缝时,求方程组(1)的解还要增加a2′段的脱空条件方程,并由迭代方法获得轮底位移.迭代方法如图 11所示,增加的方程组为
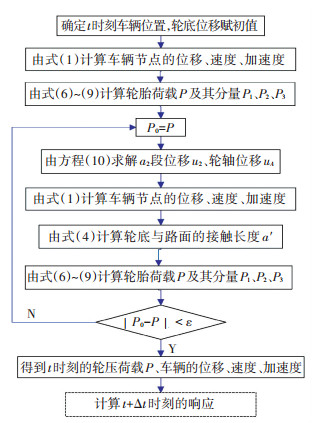
|
图 11 分析汽车通过伸缩缝的迭代算法 Fig. 11 Iteration algorithm in the analysis of vehicle bumping at expansion joint |
| $ \left\{ {\begin{array}{*{20}{l}} {{P_2} = 0,}\\ {{P_1} + {P_3} = P.} \end{array}} \right. $ | (10) |
需要说明的是,本文模型实验和数值计算研究的都是竖向的轮压荷载,而不是横向(顺桥向)的轮压荷载,对顺桥向冲击荷载的研究还有待开展.
3 模型实验与理论计算结果 3.1 轮胎对伸缩缝的动力荷载以图 5所示模型车以0.4 m/s的速度通过3 mm缝宽的伸缩缝为例,用第2节方法计算车轮动力荷载.以前轮为例,结果如图 12所示.
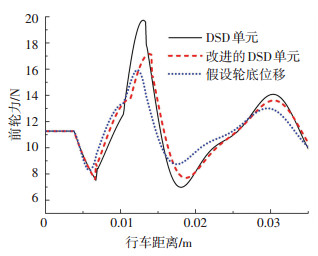
|
图 12 轮胎对伸缩缝的动荷载 Fig. 12 Dynamic load ofvehicle tire on expansion joint |
由图 12可知,DSD单元[13]、改进的DSD单元、假设轮底位移这3种算法得到的车轮冲击荷载变化趋势一致;DSD单元得到的冲击力偏大,原因是DSD单元没有考虑车轮通过伸缩缝时轮底接触长度的增大,高估了此时轮胎对车体的支撑刚度.
用冲击系数度量轮胎荷载的动力效应,有
| $ \mu = \left( {{P_{\max }} - {P_{\rm{s}}}} \right)/{P_{\rm{s}}}. $ | (11) |
其中Pmax为最大动荷载,Ps为静力荷载.根据图 4、12和式(11),计算模型车轮对伸缩缝的荷载冲击系数.由DSD单元、改进的DSD单元、假设轮底位移方法得到的前轮荷载冲击系数分别为0.75、0.52、0.41,而实验平均值为0.44,由此可知,用改进的DSD单元和假设轮底位移算法得到的冲击系数更接近实测值.
3.2 轮载冲击系数的影响因素以伸缩缝开口宽度、汽车行驶速度作为影响轮胎荷载冲击系数的主要参数,进一步进行缩尺模型实验和相应的理论计算.
首先维持模型车的速度不变,为0.4 m/s,测试和计算伸缩缝开口宽度变化时的车轮荷载冲击系数,所得结果参见图 13.由此可知:1)轮胎荷载的冲击系数与伸缩缝的开口宽度近似成正比;2)改进的DSD单元和假设轮底位移方法得到的冲击系数比DSD单元方法更接近实测值,在伸缩缝开口宽度较大时,以往的DSD单元误差较大.
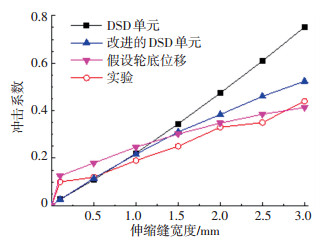
|
图 13 伸缩缝开口宽度对车轮荷载的影响 Fig. 13 Effect of opening width of expansion joint on impact load |
如保持伸缩缝宽度为1.5 mm不变,测试和计算不同速度时模型车的跳车冲击荷载,获得的冲击系数如图 14所示,图 14表明:1)当模型车的速度小于0.5 m/s时,轮胎荷载冲击系数的实验与计算值都随着车速的增加而增大;当车速大于0.5 m/s后,冲击系数计算值不再增加,保持稳定,实测值则继续增加,但是实验中发现,当模型车的速度大于0.5 m/s后,车身左右摇晃运行不稳,车桥系统运行振动较大,影响了实验的可靠性. 2)用改进的DSD单元或假设轮底位移计算方法得到的冲击系数比以往的DSD单元计算方法所得结果更接近实测值.

|
图 14 不同车速下的冲击系数 Fig. 14 Impact factor at different velocities |
对比模型实验与理论计算的结果,基于改进的DSD单元的计算方法所得结果与实测接近;相比假设轮底位移的计算方法,其假定也较少,因此更适合用于分析车辆轮胎对桥梁伸缩缝的冲击荷载.
4 载重汽车对伸缩缝的冲击荷载分析与控制为了研究实际载重汽车对于桥梁伸缩缝及其周边桥(路)面的冲击荷载,本节采用基于改进的DSD单元的方法,对典型的三轴载重汽车对伸缩缝的冲击荷载进行了计算.二维的车辆有限元模型如图 15所示,车辆的计算参数见文献[16],其所通过的伸缩缝为图 1所示的单缝式伸缩缝.
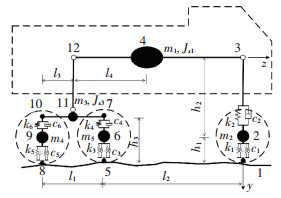
|
图 15 典型的三轴载重汽车模型 Fig. 15 Model of typical three-axle heavy vehicle |
采用式(11)定义的轮胎荷载冲击系数来度量载重汽车对伸缩缝的冲击力.针对实际桥梁上常见的单缝式伸缩缝,为了涵盖一般工况下的伸缩缝冲击荷载,综合考虑伸缩缝的开口宽度w、载重汽车的速度v的变化,其中开口宽度为1~9 cm,汽车速度为10~80 km/h,求解各种工况(参数组合)下轮胎对伸缩缝的冲击荷载.分析结果用车轮荷载冲击系数的三维云图来表示,如图 16~18所示.
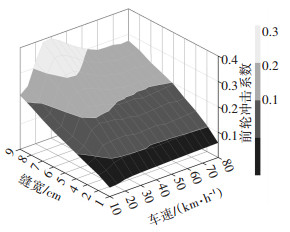
|
图 16 由改进的DSD单元得到的前轮荷载冲击系数 Fig. 16 Impact factor of front tire obtained by improved DSD element |
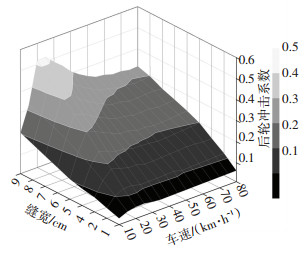
|
图 17 改进的DSD单元得到的中轮荷载冲击系数 Fig. 17 Impact factor of middle tire obtained by improved DSD element |
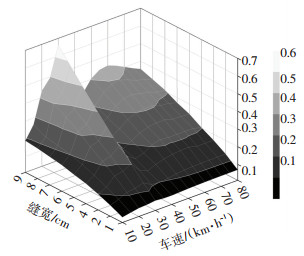
|
图 18 改进的DSD单元得到的后轮荷载冲击系数 Fig. 18 Impact factor of rear tire obtained by improved DSD element |
由图 16~18汇总得到三轴载重汽车轮胎荷载的最大冲击系数.由改进的DSD单元得到的前轮荷载冲击系数最大值为0.39,该值比中国伸缩缝设计指南[3]的给定值0.45、美国AASHTO规范[4]的给定值0.75小,但是大于中国桥梁规范[17]和欧洲桥梁规范[18]的设计值0.3.中轮和后轮的冲击系数仍然小于美国AASHTO规范的给定值,但是大于其他规范或者设计指南的推荐值.由此可知,当前中国伸缩缝设计指南和桥梁设计规范对伸缩缝跳车轮载冲击系数的估计略有不足,可能会导致桥梁伸缩缝及其前后桥面的设计强度不足.
由图 16~18还可得到轮载冲击系数的变化规律:1)在伸缩缝的开口宽度不变情况下,随着汽车速度的增加,车轮对伸缩缝结构的冲击力上下波动,最大的冲击系数在车速为25~30 km/h时出现,因此减小汽车速度不一定能降低车轮对伸缩缝的冲击力,除非是车辆速度很小时;2)车轮对伸缩缝的荷载冲击系数与伸缩缝的开口宽度近似成正比例,可以通过减少伸缩缝开口宽度来降低车轮冲击力.根据图 16~18,为了控制车轮对伸缩缝的冲击系数小于中国设计指南的给定值0.45,载重车前轮、中轮、后轮要求的伸缩缝最大开口宽度分别为9.0、7.7、6.4 cm,取三者中的最小值,即要求伸缩缝开口宽度应小于6.4 cm.因此,该方法也可用来确定保证伸缩缝结构强度安全所容许的开口宽度.
5 结论1) 设计并制作车辆通过桥梁伸缩缝的缩尺实验模型,实现了对作用于桥梁伸缩缝上的车轮冲击力的实测.
2) 提出了汽车轮胎对伸缩缝冲击荷载的两种改进算法,即假设轮底位移的方法和改进的DSD单元方法,通过与缩尺模型实验的比较,证明改进算法提高了轮胎冲击荷载的计算精度.
3) 用改进的DSD单元方法,计算了三轴载重汽车的轮胎对桥梁伸缩缝的冲击荷载,结果表明,最大荷载冲击系数超过现行伸缩缝结构设计取值.
4) 车轮对伸缩缝的荷载冲击系数与伸缩缝的开口宽度近似成正比,通过减少伸缩缝开口宽度能降低车轮冲击力,由此可以确定保证伸缩缝结构强度安全所容许的开口宽度.
| [1] |
YANEV B. Joints: the weak link in bridge structures and lifecycles[J]. Smart Structures & Systems, 2015, 15(3): 543. DOI:10.12989/sss.2015.15.3.543 |
| [2] |
LIMA J M, DE BRITO J. Management system for expansion joints of road bridges[J]. Structure and Infrastructure Engineering, 2010, 6(6): 703. DOI:10.1080/15732470802087823 |
| [3] |
中国交通企业管理协会.公路桥梁伸缩装置设计指南: JTQX-2011-12-1[S].北京: 中国交通企业管理协会, 2011 China Transportation Enterprise Management Association. Design guide of highway bridge expansion joint: JTQX-2011-12-1[S]. Beijing: China Transportation Enterprise Management Association, 2011 |
| [4] |
AASHTO. LRFD bridge design specifications[S]. 8th ed. Washington DC: American Association of State Highway and Transportation Officials, 2017
|
| [5] |
UK Highways Agency. Expansionjoints for use in highway bridge decks: BD 33/94[S]. Birmingham: UK Highways Agency, 1994
|
| [6] |
Deutschland Bundesministerium für Verkehr.Technische liefer-und prüfvorschriften für wasserundurchlässige fahrbahnübergänge von straẞen-und wegbrücken: TL-TP-FV 92[S]. Berlin: Deutschland Bundesministerium für Verkehr, 1993 Germany Federal Ministry of Transport. Technical delivery and test specifications for waterproof expansion joints of road and root bridges: TL-TP FV 92[S]. Berlin: Germany Federal Ministry of Transport, 1993
|
| [7] |
SUN Z, ZHANG Y. Failure mechanism of expansion joints in a suspension bridge[J]. Journal of Bridge Engineering, 2016, 21(10): 05016005-1. DOI:10.1061/(ASCE)BE.1943-5592.0000942 |
| [8] |
邓露, 闫王晨, 朱全军. 路桥过渡段容许台阶高度的确定[J]. 湖南大学学报(自然科学版), 2015, 42(3): 101. DENG Lu, YAN Wangchen, ZHU Quanjun. Determination of allowable differential settlement between the bridge and the approach embankment[J]. Journal of Hunan University (Natural Science), 2015, 42(3): 101. |
| [9] |
韩万水, 李彦伟, 乔磊, 等. 基于车-桥耦合振动理论的移动荷载识别[J]. 中国公路学报, 2013, 26(1): 74. HAN Wanshui, LI Yanwei, QIAO Lei, et al. Moving load identification based on vehicle-bridge coupling vibration theory[J]. China Journal of Highway and Transport, 2013, 26(1): 74. DOI:10.3969/j.issn.1001-7372.2013.01.011 |
| [10] |
ROEDER C W. Fatigue and dynamic load measurements on modular expansion joints[J]. Construction and Building Materials, 1998, 12(2/3): 143. DOI:10.1016/S0950-0618(97)00016-0 |
| [11] |
STEENBERGEN M J M M. Dynamic response of expansion joints to traffic loading[J]. Engineering Structures, 2004, 26(12): 1677. DOI:10.1016/j.engstruct.2004.05.020 |
| [12] |
GONZALEZ A, CANTERO D, O'BRIEN E J. Dynamic increment for shear force due to heavy vehicles crossing a highway bridge[J]. Computers and Structures, 2011, 89(23/24): 2261. DOI:10.1016/j.compstruc.2011.08.009 |
| [13] |
丁勇, 黄奇, 谢旭, 等. 载重汽车桥梁伸缩缝跳车动力荷载计算方法与影响因素分析[J]. 土木工程学报, 2013, 46(7): 98. DING Yong, HUANG Qi, XIE Xu, et al. Computational method for dynamic load in heavy-vehicle bumping at the bridge expansion joint and analysis of the influencing factors[J]. China Civil Engineering Journal, 2013, 46(7): 98. |
| [14] |
JU S H, LIN H T, HSUEH C C, et al. A simple finite element model for vibration analyses induced by moving vehicles[J]. International Journal for Numerical Methods in Engineering, 2006, 68(12): 1232. DOI:10.1002/nme.1748 |
| [15] |
DING Y, ZHANG W, AU F T K. Effect of dynamic impact at modular bridge expansion joints on bridge design[J]. Engineering Structures, 2016, 127: 645. DOI:10.1016/j.engstruct.2016.09.007 |
| [16] |
谢旭, 吴冬雁, 王建峰, 等. 伸缩缝车辆冲击引起的钢箱梁桥振动特性[J]. 浙江大学学报(工学版), 2009, 43(10): 1923. XIE Xu, WU Dongyan, WANG Jianfeng, et al. Dynamical behavior of steel box girder bridges due to vehicle-induced[J]. Journal of Zhejiang University (Engineering Science), 2009, 43(10): 1923. DOI:10.3785/j.issn.1008-973X.2009.10.030 |
| [17] |
中华人民共和国交通部.公路桥涵设计通用规范: JTJ D60—2015[S].北京: 人民交通出版社, 2015 Ministry of Transport of the People's Republic of China. General code for design of highway bridges and culverts: JTJ D60—2015[S]. Beijing: China Communications Press, 2015 |
| [18] |
BSI. Eurocode 1-actions on structures-part 2-traffic loads on bridges: BS EN 1991-2[S]. London: British Standards Institution, 2003
|
 2020, Vol. 52
2020, Vol. 52