2. 成都济通路桥科技有限公司, 成都 610031;
3. 中南大学 土木工程学院, 长沙 410083
2. Chengdu Xetong Technology Co. Ltd., Chengdu 610031, China;
3. School of Civil Engineering, Central South University, Changsha 410083, China
近年来,随着西南山区铁路网的快速崛起,西南山区涌现出大量的铁路线,如成贵高铁、西成高铁、成兰铁路、郑万高铁、渝昆高铁、川藏铁路、大瑞铁路、玉磨铁路等等,由于西南山区特殊复杂的地理环境,使得上述铁路线需要跨越地质构造复杂、高山峡谷、沟壑纵横且板块活动强烈的地区.而中承式钢管混凝土拱桥具有刚度大、承载能力强、跨越能力大以及与地形协调等诸多优势,故这类桥型已成为西南山区铁路桥梁主要结构形式之一.对于大跨度中承式铁路拱桥,若采用半漂浮体系,则列车荷载作用下将导致梁端位移过大,直接影响行车安全,且地震作用下主梁位移难以控制,通常采用粘滞阻尼器对拱桥进行减震耗能,文献[1-2]针对中承式拱桥研究了粘滞阻尼器对大桥抗震性能的影响,但阻尼器往往造价高.如采用完全约束体系,则整个结构将产生很大的温度次内力,且完全约束体系对桥梁的抗震性能也极为不利[3].因此为控制大桥在列车牵引、制动力作用下发生过大位移,保证行车安全,同时减少大桥温度次内力影响、提高桥梁结构减震耗能能力,迫切需要研究一种经济适用的新型限位减震金属阻尼器装置.
在文献[4-5]提出金属阻尼器后,金属阻尼器作为耗能元件或者限位装置,能较好地为结构提供附加阻尼和刚度,而因其构造简单、耗能性能优越、更换方便,近年来在土木工程中得到广泛应用,各国学者也研发了多种形式的金属阻尼装置.文献[6]研究开发了X形加劲钢阻尼器,并通过试验研究表明其具有良好的耗能效果;文献[7]通过拟静力试验比较研究了X形、三角形加劲钢板阻尼器的力学性能和疲劳性能,并建立了合理的理论计算模型;文献[8]等设计研发了蜂窝形钢板阻尼器,文献[9]等设计了槽形钢板阻尼器,这两种阻尼器仅开孔形式不同,工作性能与耗能原理相似;文献[10]提出了E型钢阻尼器,并通过振动台试验验证了其具有良好的滞回性能.中国于2008年在南京江心洲大桥上应用了多套E型钢阻尼器,这也是国内首次在桥梁中应用金属阻尼器[11].随后文献[12]研发了一种双圆锥金属阻尼器,文献[13]研究了单悬臂减震榫的合理结构形式;文献[14]推导了减震榫的力学性能理论计算公式,并通过试验验证了减震榫可有效提供结构刚度和阻尼.文献[15]提出了一种缓冲型防落梁钢圈限位耗能装置,并对装置构造参数进行了敏感性分析.然而,上述学者研究的金属阻尼装置往往尺寸小,且主要是应用在房屋建筑结构及常规简支梁桥上,而对西部常见大跨铁路中承式拱桥这类大跨桥梁的减震限位金属阻尼装置研究较少.
因此,为了研究适用于大跨铁路桥梁的金属限位减震装置,本文以郑万高铁某372 m中承式拱桥为工程背景,建立了大跨度桥梁金属限位减震装置设计方法,研发了大桥金属限位减震装置设计软件,给出了工程背景桥限位减震装置的具体设计参数,建立了3种连接构造形式的装置实体分析模型,对装置自身的力学性能进行了综合评估,而后对比分析了各种连接构造方案的应力分布情况,比选出最优方案,通过有限元计算结果验证了本文所提设计方法的正确性.最后开展了全桥模型的时程分析,验证了金属限位减震装置对大桥的减震效果,以期为该类大跨铁路桥梁的抗震设计提供依据.
1 金属限位减震耗能装置设计理论经综合比选拟采用金属高延性软钢阻尼器作为大跨度铁路桥梁限位减震装置(以下简称限位减震装置),其结构形式采用典型的悬臂梁结构形式,下面将结合弹塑性力学、材料力学、结构力学等理论建立该限位减震装置的计算分析理论.
1.1 装置结构形状参数计算方法为满足设计需求,使限位减震装置在各方向上限位和减震性能相同,结合文献[14, 16]研究成果,选取圆形作为大跨度铁路桥梁限位减震装置的截面形式.
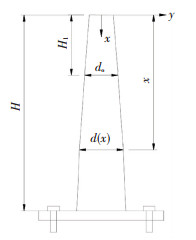
为了使装置在地震作用下具有良好的延性变形能力,滞回曲线饱满,耗能能力更强,本文采用了等强度梁设计原则设计装置截面尺寸参数,采用该原则设计的装置可使大部分截面同时进入屈服状态,最大程度增加延性变形能力.但采用等强度梁设计时,存在装置顶端截面直径为零的问题,因此为解决该问题,在装置顶端区域截面直径按线性变换设计,称该区域为过渡段.装置主体杆件构造如图 1所示.图中H1为渡段长度,H为装置高度;do为过渡和等强段交接截面直径.
|
图 1 限位减震装置主体结构形式 Fig. 1 Main structure of the bridge limit damping device |
按照等强度梁设计原则可知,装置各截面同时发生屈服,则装置顶端在水平荷载F作用下,各截面外侧同时达到最大应力,各截面最大弯曲应力为
| $ {\sigma _{\max }}\left( x \right) = \frac{{32Fx}}{{{\rm{ \mathsf{ π} }}{d^3}\left( x \right)}}. $ | (1) |
式中σmax(x)为边缘最大应力,d(x)为直径.
按等强度梁设计原则,则装置各截面直径变化函数可由式(1)求解得到,即
| $ d\left( x \right) = \left\{ {\begin{array}{*{20}{l}} {2{d_{\rm{o}}}/3 + {d_{\rm{o}}}x/3/{H_1},}&{0 \le x \le {H_1};}\\ {{d_{\rm{o}}}{x^{1/3}}/H_1^{1/3},}&{{H_1} \le x \le H.} \end{array}} \right. $ | (2) |
运用式(2)可求解限位减震装置的构造参数.
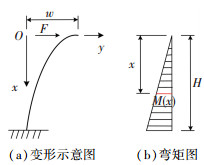
1.2 装置弹性力学性能参数计算方法本文设计的桥梁金属限位减震装置为悬臂梁受力模式,装置在顶部水平力F作用下,其变形及内力分布如图 2所示,图中w为装置顶部水平位移,M为装置截面弯矩.
|
图 2 装置力学性能计算模式 Fig. 2 Mechanical property computing mode of the device |
当装置处于弹性状态时,由结构力学计算理论,可求解出装置在F作用下顶端水平位移为
| $ w = \sum {\int {\frac{{{M_{\rm{o}}}\left( x \right)M\left( x \right)}}{{EI\left( x \right)}}{\rm{d}}x} } . $ | (3) |
式中:Mo(x)、M(x)分别为单位荷载、水平力F作用下,距装置顶端x处截面承受的弯矩值,即Mo(x)=x、M(x)=Fx;E为弹性模量;I(x)为截面惯性矩,因采用圆形截面,故I(x)=πd(x)4/64.将1.1节得到的装置结构形状参数即式(2)代入式(3),求解积分函数可得
| $ \begin{array}{l} w = \frac{1}{{E{\rm{ \mathsf{ π} }}}}\left( {\int_0^{{H_1}} {\frac{{F{x^2}}}{{{{\left( {2{d_{\rm{o}}}/3 + {d_{\rm{o}}}x/3/{H_1}} \right)}^4}/64}}{\rm{d}}x} + } \right.\\ \;\;\;\;\;\;\;\left. {\int_{{H_1}}^H {\frac{{F{x^2}}}{{{{\left( {{d_{\rm{o}}}{x^{1/3}}/H_1^{1/3}} \right)}^4}/64}}{\rm{d}}x} } \right) = \\ \;\;\;\;\;\;\;\;\frac{{64F}}{{E{\rm{ \mathsf{ π} }}d_{\rm{o}}^4}}\left( {{3^4}\int_0^{H1} {\frac{{{x^2}}}{{{{\left( {2 + x/{H_1}} \right)}^4}}}{\rm{d}}x} + H_1^{4/3}\int_{{H_1}}^H {{x^{2/3}}} {\rm{d}}x} \right) = \\ \;\;\;\;\;\;\;\;\frac{{64F \times 81}}{{E{\rm{ \mathsf{ π} }}d_{\rm{o}}^4}} \times \frac{{H_1^3}}{{162}} + \frac{{64FH_1^{4/3}}}{{E{\rm{ \mathsf{ π} }}d_{\rm{o}}^4}} \times \frac{3}{5}\left( {{H^{5/3}} - H_1^{5/3}} \right) = \\ \;\;\;\;\;\;\;\;\frac{{192FH_1^{4/3}{H^{5/3}} - 32FH_1^3}}{{5E{\rm{ \mathsf{ π} }}d_{\rm{o}}^4}}. \end{array} $ | (4) |
故金属限位减震装置的弹性刚度为
| $ {k_{\rm{e}}} = \frac{F}{w} = \frac{{5E{\rm{ \mathsf{ π} }}d_{\rm{o}}^4}}{{192H_1^{4/3}{H^{5/3}} - 32H_1^3}}. $ | (5) |
假设钢材屈服应力为σs,装置所能承受的极限弹性水平力为Fe.当装置处于弹性状态时,各截面外侧应力相等,取x=H1处截面为研究对象,将σs、do代入式(1)便可反算弹性极限水平力Fe,即
(1)便可反算弹性极限水平力Fe,即
| $ {\sigma _{\rm{s}}} = \frac{{{F_{\rm{e}}}{H_1}{d_{\rm{o}}}/2}}{{{\rm{ \mathsf{ π} }}d_{\rm{o}}^4/64}} = \frac{{32{F_{\rm{e}}}{H_1}}}{{{\rm{ \mathsf{ π} }}d_{\rm{o}}^3}} \Rightarrow {F_{\rm{e}}} = \frac{{{\sigma _{\rm{s}}}{\rm{ \mathsf{ π} }}d_{\rm{o}}^3}}{{32{H_1}}}. $ | (6) |
则装置的弹性极限位移为
| $ \begin{array}{l} {w_{\rm{e}}} = \frac{{{F_{\rm{e}}}}}{{{k_{\rm{e}}}}} = \frac{{{\rm{ \mathsf{ π} }}d_{\rm{o}}^3{\sigma _{\rm{s}}}}}{{32{H_1}}} \times \frac{{192H_1^{43}{{\rm{H}}^{5/3}} - 32H_1^3}}{{5E{\rm{ \mathsf{ π} }}d_{\rm{o}}^4}} = \\ \;\;\;\;\;\;\;\;{\sigma _{\rm{s}}}\frac{{6H_1^{1/3}{H^{5/3}} - H_1^2}}{{5E{d_{\rm{o}}}}}. \end{array} $ | (7) |
为计算金属限位减震装置力-位移本构骨架曲线.根据结构力学、材料力学、弹塑性力学计算理论,结合装置的实际情况,对装置的力学计算模式作如下假设:1)各截面服从平截面假定;2)仅考虑纯弯状态;3)材料各向同性.
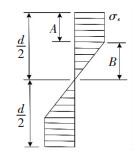
当水平力F超过Fe时,装置截面部分范围会进入弹塑性状态,此时截面应力分布情况如图 3所示.图中截面高度为d,塑性段高度为A,弹性段高度为B,由弹塑性理论可知,装置的水平变形w的计算公式[17]为
|
图 3 截面应力分布图 Fig. 3 Diagram of section stress distribution |
| $ EI\frac{{{{\rm{d}}^2}w}}{{{\rm{d}}{x^2}}} = \left\{ {\begin{array}{*{20}{l}} { - M(x),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;弹性段;}\\ { - {M_{\rm{u}}}/B\left( {I(x)/2{S_{\rm{o}}}} \right)sgnM,\;\;\;弹塑性段.} \end{array}} \right. $ | (8) |
式中:M(x)为x位置处的截面弯矩;I(x)为x位置处的截面惯性矩;E为弹性模量;Mu为极限弯矩,So为半截面对中性轴的静矩.
运用数值分析法求解上述微分方程组,即可计算得到任意水平力F对应的装置弹塑性变形.
上述方法计算过程繁琐,不便于工程应用,考虑到实际应用中更关注整个装置的力-顶部位移的本构关系曲线.故本文提出一种简化计算方法,过程如下.
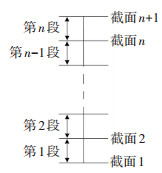
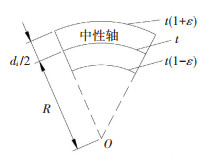
1) 已知金属限位装置高H,将装置在高度方向上划分n个小节段(见图 4),单个节段长度为t,单个节段纯弯变形如图 5所示.
|
图 4 装置力学性能计算模式 Fig. 4 Mechanical property computing mode of the device |
|
图 5 单个节段变形图 Fig. 5 Deformation diagram of segment |
2) 假设第i个节段中所有截面直径、曲率相同,第i个节段截面直径为di,在金属限位装置顶部施加水平力F,可得到第i个节段截面弯矩Mi,以及截面边缘应变εi,则根据平截面假定,可得到第i个节段截面曲率ϕi,即
| $ \frac{{t(1 + \varepsilon )}}{{t(1 - \varepsilon )}} = \frac{{R + {d_i}/2}}{{R - {d_i}/2}} \Rightarrow 4\varepsilon = 2{d_i}/R \Rightarrow {\varphi _i} = 2{\varepsilon _i}/{d_i}. $ | (9) |
3) 利用高等数学中对面积的曲面积分计算方法近似求解积分方程
| $ \begin{array}{l} w = {\varphi _1}{t^2} + \left( {{\varphi _1} + {\varphi _2}} \right){t^2} + \left( {{\varphi _1} + {\varphi _2} + {\varphi _3}} \right){t^2} + \cdots + \\ \left( {{\varphi _1} + {\varphi _2} + \cdots + {\varphi _i}} \right){t^2} = \sum\limits_{i = 1}^n {(n + 1 - i)} {\varphi _i}{t^2}. \end{array} $ | (10) |
由式(10)分析可知,求解w的关键就是求解各截面的应变εi,由材料力学可知,截面弹性应变为
| $ \varepsilon = Md/\left( {2EI} \right), $ | (11) |
截面塑性应变为
| $ \varepsilon = d{\varepsilon _{\rm{s}}}/\left( {d - 2A} \right). $ | (12) |
式中εs为屈服应变,d为直径.
利用上述简化算法,便可计算出任意等截面、变截面的金属限位装置的弹塑性位移.
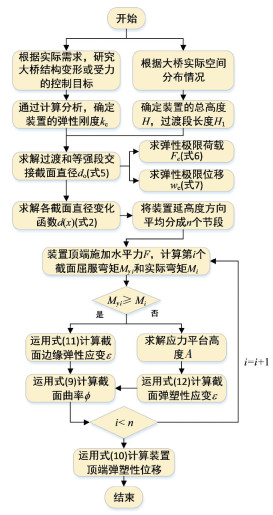
1.4 建立大跨桥梁金属限位减震装置设计方法基于1.1~1.3节的计算理论,本文提出了大跨度桥梁限位减震耗能装置设计方法,方法基本分析步骤如图 6所示.
|
图 6 限位减震装置简化设计方法流程 Fig. 6 Simplified design method flow of bridge limit damping device |
运用上述设计方法,可设计出适用于不同类型大跨铁路桥梁的金属限位减震装置,但在设计过程中需考虑不同类型大跨桥梁自身特点和实际应用需求(如正常运营阶段对桥梁位移或力控制需求、地震作用下的减震耗能需求等),有针对性地设计该装置,并按本文所提设计流程便可得到装置合理的力学、构造参数.
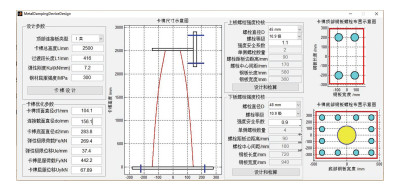
基于第1节装置的力学计算理论和图 6的设计方法流程,并结合文献[18-20],应用MATLAB软件GUI技术,编制大跨度桥梁金属限位减震装置的设计软件,软件界面示意图如图 7所示.通过输入“设计参数”栏中相关参数便可计算出装置的相关力学参数,同时该软件还可根据规范自动对装置上、下连接钢板尺寸、螺栓数量进行设计.
|
图 7 软件操作界面 Fig. 7 Software operation interface |
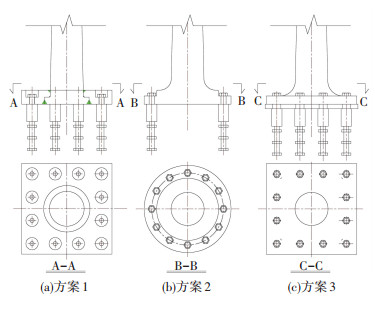
在水平荷载作用下,限位减震装置底部锚固螺栓需要承受较大的抗拔力和水平剪力,因此除了对装置主体杆件进行设计验算,还需要重点对装置底部的连接构造进行设计验算.一般将其与桥墩顶面(或者拱肋横梁、桥塔横梁顶面)的预埋件进行刚性连接,故本文提出了3种连接构造方案,如图 8所示.方案1采用阶梯形矩形钢板形式焊接连接,方案2采用整体锻造圆形钢板连接形式,方案3采用整体锻造矩形钢板连接形式.下文将采用有限元法对3种方案进行计算分析,研究3种方案的可行性.
|
图 8 装置底部连接构造方案示意图 Fig. 8 Schematic diagram of connection structural schemes at the bottom of the device |
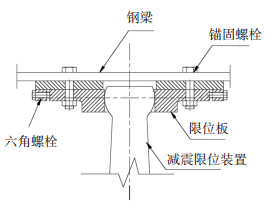
对于限位减震装置顶部连接构造,其将锚固在钢主梁底面,主要功能是实现装置与钢主梁的连接,保证钢主梁只传递水平力到限位装置顶部,因限位减震装置自身高度较高,施工误差极有可能导致上、下部连接构造中心线不能完全对中,因此本文提出了一种可调式顶板连接组件,如图 9所示,通过设计的可调式顶板连接组件,可以实现桥上所有金属限位减震装置同步工作,解决上、下连接构造安装对中问题.
|
图 9 装置顶部连接构造方案示意图 Fig. 9 Schematic diagram of connection structural scheme at the top of the device |
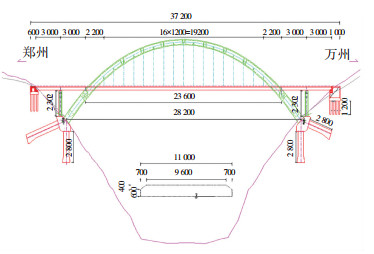
本文以郑万高铁某典型大跨度中承式混凝土平行拱桥为工程背景,主桥桥跨为30 m+296 m+30 m,采用半漂浮体系,桥上线路为双线,全桥共计16对吊杆,主拱基础采用竖桩+斜桩,采用ZK荷载形式,温度荷载整体升降温按照30 ℃计算;主梁采用钢混结合梁,箱型断面形式,梁高2.5m;横梁与纵梁等高,支座处横梁为箱型断面,主梁钢梁采用Q345qD、Q345qE钢材,主梁桥面板采用C50混凝土,桥址处地震烈度为8度0.2g,全桥布置如图 10所示.
|
图 10 全桥布置示意图(cm) Fig. 10 Schematic diagram of full-bridge layout (cm) |
利用Midas/Civil建立全桥模型,采用梁单元模拟主梁、拱肋钢管,采用板单元模拟混凝土桥面,拱肋外包混凝土采用板单元模拟,考虑自重、二期恒载及列车荷载等,桩基础采用6个弹簧单元进行等效模拟[21],全桥模型如图 11所示.

|
图 11 全桥模型示意图 Fig. 11 Finite element model of the bridge |
本文工程背景为大跨度铁路中承式钢管混凝土拱桥,全桥采用半漂浮体系,纵向约束较弱,为保证高速列车行车的舒适性与安全性,拟设计限位减震耗能装置.在综合考虑轨道变形、行车平顺性、桥梁结构受力合理性等因素前提下,明确了限位减震装置的设计目标:1)装置能够保在证列车牵引力或制动力作用下,大桥梁端位移不超过5 mm;2)装置水平刚度设计合理,因装置约束作用产生的温度次内力和温度变形不影响结构安全和行车安全;3)在正常运营荷载作用下,装置保持弹性状态,不出现塑性,装置具有良好的减震耗能能力.
通过大桥的列车型号为CRH380AL,列车编组长度403 m,最大牵引力520 kN,最大制动力为455 kN.
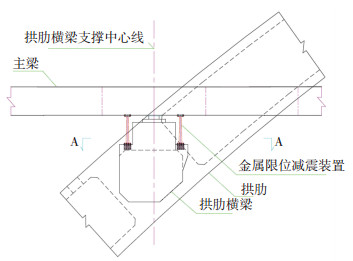
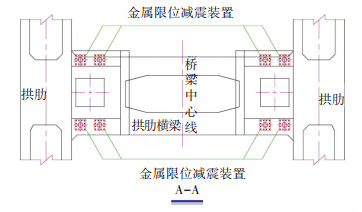
3.3 确定金属限位减震装置基本设计参数由3.2节车辆信息可知,高速列车过桥时在桥上引起的最大牵引力、制动力为460 kN,按5 mm控制梁端位移,则限位减震装置的水平总的弹性刚度需要92 kN/mm,考虑装置制造误差、施工偏差、材料特性误差等因素,预留25%的富余量来设计装置的水平弹性刚度为110.4 kN/mm,根据大桥拱肋横梁空间分布情况,在大桥每个拱肋横梁上设计布置了8个限位减震装置,全桥共布置16个,单个装置水平弹性刚度为7.2 kN/mm,金属限位减震装置在单个拱肋横梁上立面和平面布置形式分别如图 12、13所示.将该弹性刚度模拟到全桥模型中,利用Midas软件分析各运营工况下装置的内力和变形情况,计算结果见表 1.各运营工况下大桥主体结构的受力和变形验算结果均满足规范要求,由于篇幅有限,这里不再详细给出.
|
图 12 单个拱肋横梁上金属限位减震装置立面布置 Fig. 12 Elevation distribution of metal limit damping device in the arch rib beam |
|
图 13 单个拱肋横梁上金属限位减震装置平面布置 Fig. 13 Plane distribution of metal limit damping device in the arch rib beam |
| 表 1 各种最不利工况下装置内力、变形计算结果 Tab. 1 Calculation results of internal force and deformation for device under various most unfavorable operating conditions |
由表 1分析可知:1)列车牵引制动力作用下,大桥梁端位移为4.7 mm,这说明限位装置刚度按7.2 kN/mm设计可以控制梁端位移,满足设计要求. 2)大桥正常运营状态各种最不利工况下装置最大水平力为240 kN,为保证装置在运营期间处于弹性状态,故将装置的弹性极限荷载设计为240 kN,即Fe=240 kN.
此外,根据设计图纸可知拱肋横梁顶面与主梁底面净空为3 m,经综合考虑后,本桥装置总高度设计为H=2.5 m,过渡段长度取H1=416 mm.
3.4 金属限位减震装置形状参数与力学性能参数计算根据3.3节确定的装置基本设计参数(弹性刚度ke=7.2 kN/mm、设计弹性极限荷载Fe=240 kN,高度H=2.5 m,过渡段高度H1=0.416 m),运用第1节提出的设计方法与研发的设计软件,可依次计算出装置交接截面直径、弹性极限位移、装置截面直径变化函数以及力-位移本构曲线,装置各截面直径变化函数为
| $ d(x) = \left\{ {\begin{array}{*{20}{l}} {104 + 0.125x,9{\rm{mm}} \le x \le 416{\rm{mm;}}}\\ {20.897{x^{1/3}},416{\rm{mm}} \le x \le 2500{\rm{mm}}{\rm{.}}} \end{array}} \right. $ |
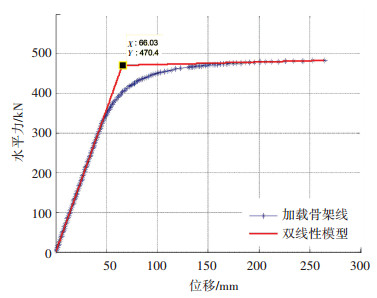
单个金属限位减震装置的力学参数计算结果为弹性极限荷载为287.4 kN,弹性极限位移为39.9 mm,屈服荷载为470.4 kN,屈服位移为66.03 mm,弹性刚度为7.17 kN·mm-1,屈服后刚度为0.062 kN·mm-1,极限荷载为482.8 kN,极限位移为264.1 mm.装置的力-位移曲线如图 14所示.
|
图 14 装置的力-位移曲线 Fig. 14 Force-displacement curve of the device |
为分析本文设计的金属限位减震装置的力学性能,同时验证本文所提设计计算方法的正确性,采用有限元法对其进行力学性能分析.具体设计参数如下:装置总高H=2 500 mm,过渡段高度H1=416 mm,装置底部直径d=284 mm,装置过渡段交界面直径do=156 mm,装置底部矩形钢板尺寸为780 mm×780 mm,装置底部圆形钢板直径为780 mm,底部钢板采用M42高强螺栓,强度等级为8.8级,装置主体杆件钢材选用Q345b,但需经过特殊处理以增大延性变形能力.
采用弹塑性有限元分析软件Abaqus建立金属限位减震装置的有限元模型,装置采用C3D8R实体单元模拟,钢材屈服强度根据拉伸试验结果取为320 MPa,材料弹性模量为2.06×105 MPa,泊松比为0.3.分析时考虑材料非线性和几何非线性[22],有限元模型网格划分具体如图 15所示.在分析装置力学性能时,装置顶部最大水平力按照理论计算的极限水平力480 kN进行施加,并以此荷载作为连接构造的检算荷载.

|
图 15 3种连接方案下的装置实体有限元模型 Fig. 15 Solid finite element model of metal limit damping device under three connection structural schemes |
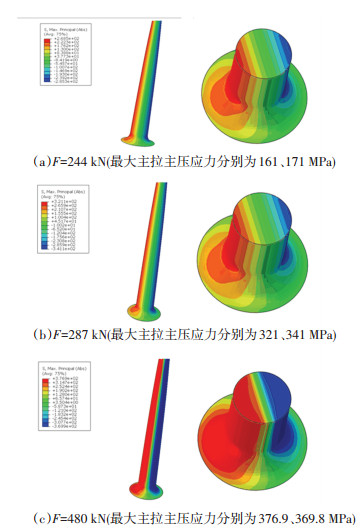
以方案3作为研究对象,分析主体杆件的应力分布情况,图 16分别给出了方案3中金属限位减震装置主体杆件在240、287、480 kN时对应的主应力分布.由图 16分析可知:当F=240 kN时,主体杆件的最大主应力小于320 MPa,钢材未屈服,处于弹性状态,这表明在运营荷载工况下装置满足设计要求;当F=287 kN时(理论计算弹性极限荷载),主体杆件的最大主拉应力321 MPa,最大主压应力341 MPa,略大于钢材屈服强度320 MPa,此时装置处于刚刚进入弹塑性状态,这与本文所提方法计算的弹性极限荷载吻合;当F=480 kN,装置的最大主拉应力为367.9 MPa,最大主压应力为369.9 MPa,此时装置已经进入弹塑性状态,材料屈服,发生延性变形.
|
图 16 主体杆件主拉主压应力分布 Fig. 16 Distribution of main tensile and compressive stress of tenon |
此外,由截面应力分布图可知,装置延高度方向各截面几乎同时进入屈服状态,这说明大桥装置的设计已达到了等强度设计原则的要求.其他两种方案与方案3计算结果类似.
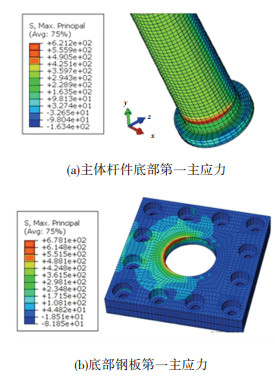
3.5.2 连接构造应力分析图 17给出了方案1对应的连接构造应力云图,由图分析可知:方案1焊缝处应力较大,当水平力达到极限荷载F=480 kN时,主体杆件焊缝处的最大主拉应力达到了621 MPa,钢板焊缝最大主拉应力达到了678 MPa,其远大于焊缝容许应力,这表明方案1的连接构造不能满足正常使用的要求.
|
图 17 方案1连接构造应力云图(MPa) Fig. 17 Stress cloud chart of connection structural scheme 1 (MPa) |
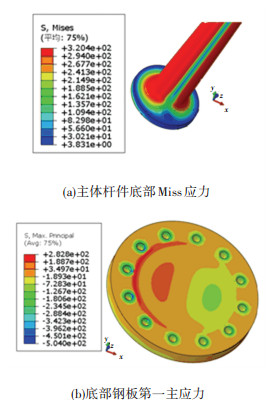
图 18给出了方案2对应的连接构造应力云图.由主体杆件底部Miss应力图分析可知,主体杆件应力分布比较均匀,在最大水平荷载F=480 kN作用下,最大Miss应力320 MPa,主要集中在杆件上,底部过渡段应力分布变化均匀.由底部钢板第一主应力分析可知,最大主拉应力为282 MPa,小于钢板材料的屈服应力,最大主压应力为504 MPa,但主要集中在螺栓孔附件小范围内,属于应力集中现象.此外在对螺栓进行抗拉检算时,结果表明需采用M52的螺栓型号才能满足检算要求.综上所述,方案2连接构造形式满足设计要求,但螺栓直径需采用M52以上.
|
图 18 方案2连接构造应力云图(MPa) Fig. 18 Stress cloud chart of connection structural scheme 2 (MPa) |
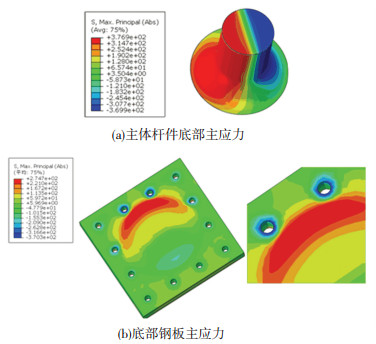
图 19给出了方案3对应的连接构造应力云图.由图 19(a)分析可知,主体杆件底部应力分布均匀,无应力集中现象,最大水平荷载F=480 kN,最大主拉应力为376 MPa,最大主压应力为369 MPa,主体杆件进入弹塑性状态;由图 19(b)分析可知,底部钢板最大主拉应力为274 MPa,最大主压应力370 MPa,但主要集中在螺栓孔附件小范围内,属于应力集中现象.此外对螺栓进行强度检算结果表明,采用M42的螺栓可满足规范设计要求.
|
图 19 方案3连接构造应力云图(MPa) Fig. 19 Stress cloud chart of connection structural scheme 3 (MPa) |
综合分析表明:连接构造方案3各构件应力满足设计要求,本文推荐采用方案3作为大跨度中承式拱桥限位减震装置的连接构造方案,限位减震装置的加工制造实物照片如图 20所示.

|
图 20 金属限位减震装置加工制造实物照片 Fig. 20 Photo of the metal limit damping device |
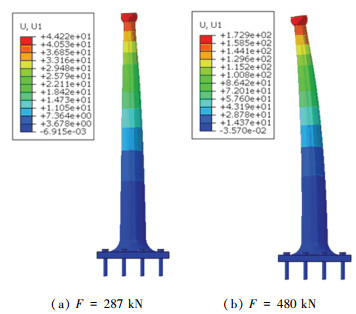
图 21给出了水平荷载作用下装置的变形云图.当水平荷载F=480 kN时,装置的顶部最大位移达到172.9 mm.
|
图 21 装置变形图(mm) Fig. 21 Deformation diagram of the device (mm) |
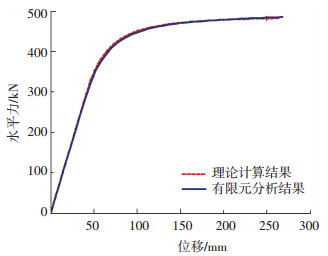
为了验证本文所提力-位移本构关系骨架曲线计算方法的正确性,将有限元模型计算结果与理论计算结果绘制于同一幅图中,如图 22所示.
|
图 22 理论计算与有限元模型结果对比分析图 Fig. 22 Comparison and analysis diagram of theoretical calculation and finite element model result |
由图 22分析可知,两种方法计算结果误差较小,计算结果较为吻合,这也验证了本文所提方法的正确性,可满足工程应用的精度要求.
3.6 金属限位减震装置对大桥抗震性能影响分析地震波输入按照地震安评报告提供的9条地震动进行时程分析(多遇、设计、罕遇地震各3条),考虑纵向地震动输入,本文将重点研究设计、罕遇地震作用下限位减震装置对大桥抗震性能的影响.
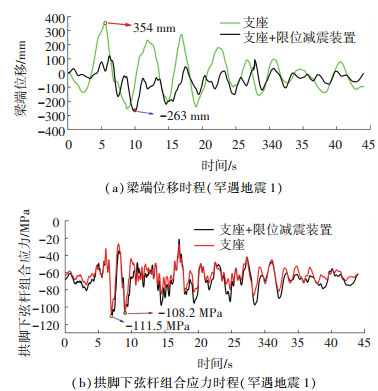
图 23给出了罕遇地震动作用下采用支座、支座+限位减震金属阻尼器工况下梁端位移、拱脚下弦杆应力时程曲线.由图分析可知,相较于无限位减震装置的桥梁,限位减震装置可显著降低拱桥的梁端位移,以罕遇地震为例,无限位减震装置工况下桥梁梁端位移为354 mm,采用设计的限位减震装置后,梁端位移下降到263 mm,位移减小了25.7%.此外由应力时程曲线可知,两种工况下,拱肋下弦杆应力差异较小,有限位减震装置下应力为111.5 MPa,无装置工况下应力为108.2 MPa,这表明限位减震装置在不增加主拱圈应力前提下,可有效限制主梁位移.
|
图 23 有无金属阻尼器工况下的时程对比曲线 Fig. 23 Time history comparison curves under two cases (with or without device) |
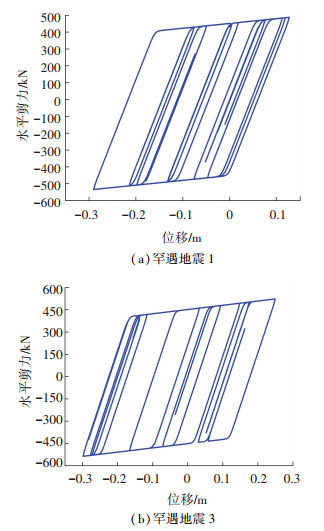
表 2给出了设计、罕遇地震作用下梁端位移、拱圈弦杆应力、拱肋横梁弯矩及其减震率结果. 图 24给出了两条罕遇地震波作用下限位减震装置的滞回耗能曲线.分析可知,本文设计的限位减震装置,可使主梁梁端位移在设计、罕遇地震下减震率达20%左右,而主拱圈弦杆应力与横梁内力均无明显增加.这充分表明限位减震装置较好地耗散了地震能量,可以有效地降低大桥主梁位移,起到了限位作用,对大跨度铁路桥梁适应性良好.
|
图 24 限位减震装置滞回曲线 Fig. 24 Hysteretic curves of the limit damping device |
| 表 2 有、无限位减震耗能装置对应大桥变形内力结果 Tab. 2 Calculation results of internal force and deformation for bridge under various seismic conditions |
1) 详细推导了大跨铁路桥梁金属限位减震装置弹性、弹塑性力学计算公式,建立了大跨度桥梁金属限位减震装置的简化设计方法,并采用有限元法对本文方法进行了验证,结果表明:本文设计方法正确,算法计算精度高、速度快,适应工程实际应用的要求.
2) 运用本文提出的设计方法,设计了郑万高铁某大跨度中承式拱桥的金属限位减震装置,利用有限元法对该装置力学性能及其对大桥的抗震性能进行了分析,结果表明:装置能很好地限制梁端位移,满足高铁对行车舒适性和安全性的要求,在地震下装置可有效耗散地震能量,降低大跨桥梁梁端位移约20%,减震效果明显.该装置也可应用于其他大跨桥梁结构.
3) 提出了3种金属限位减震装置连接构造措施,通过有限元实体模型计算,对比分析了3种构造措施的适应性,分析结果表明:方案3应力分布均匀,整体性能较好,可作为装置连接构造的最优设计方案.
| [1] |
胡伟岸.钢管混凝土下承式刚架系杆拱桥抗震性能和分析方法研究[D].南京: 东南大学, 2006 HU Weian. Research on seismic behavior of frame tied concrete-filled steel tubular arch bridge and the analysis methods[D]. Nanjing: Southeast University, 2006 http://cdmd.cnki.com.cn/article/cdmd-10286-2007030209.htm |
| [2] |
谢祥兵.半中承式连续系杆拱桥抗震性能关键参数分析[D].西安: 西安建筑科技大学, 2014 XIE Xiangbing. The analysis of key parameters of seismic performance of half through continuous tied-arch bridge[D]. Xi'an: Xi'an University of Architecture and Technology, 2014 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D560606 |
| [3] |
董俊, 曾永平, 单德山. 高墩大跨铁路桥梁构件三维地震易损性分析[J]. 哈尔滨工业大学学报, 2019, 51(3): 141. DONG Jun, ZENG Yongping, SHAN Deshan. Three-dimensional seismic vulnerability analysis of long-span railway bridge components with high pier[J]. Journal of Harbin Institute of Technology, 2019, 51(3): 141. |
| [4] |
KELLY J M, SKINNER R I, HEINE A J. Mechanisms of energy absorption in special devices for use in earthquake resistant structures[J]. Bulletin of New Zealand Society for Earthquake Engineering, 1972, 5(3): 63. |
| [5] |
SKINNER R I, KELLY J M, HEINE A J. Hysteretic dampers for earthquake-resistant structures[J]. Earthquake Engineering & Structural Dynamics, 1975, 3(3): 287. |
| [6] |
WHITTAKER A S, BERTERO V V, THOMPSON C L, et al. Seismic testing of steel plate energy dissipation devices[J]. Earthquake Spectra, 1991, 7(4): 563. DOI:10.1193/1.1585644 |
| [7] |
欧进萍, 吴斌. 摩擦型与软钢屈服型耗能器的性能与减振效果的试验比较[J]. 地震工程与工程振动, 1995, 15(3): 73. OU Jinping, WU Bin. Experimental comparison of the properties of friction and mild steel yielding energy dissipaters and their effects on reducing vibration of structure under earthquakes[J]. Earthquake Engineering and Engineering Vibration, 1995, 15(3): 73. |
| [8] |
YASUSHI K, MITSUO S, TOSHIKAZU Y, et al. Structural design of a tall building with elastic-plastic steel dampers for the attenuation of torsional and lateral motion[J]. Structure Design Tall Building, 1988, 7(1): 21. |
| [9] |
WADA A, HUANG Y, IWATA M. Passive damping technology for buildings in Japan[J]. Progress in Structural Engineering & Materials, 2000, 2(3): 335. |
| [10] |
ARCANGELI M, CIAMPI V, PAOLACCI F, et al. Shaking table tests of a two story frame equipped with dissipative bracings[C]//The 11th World Conference on Earthquake Engineering. Acapulco: Copyright Elsevier Science Ltd., 1996
|
| [11] |
李爱丽.分离式减震榫-活动支座简支梁桥的抗震性能研究[D].北京: 北京交通大学, 2018 LI Aili. Research on seismic performance of the simply supported girder bridge with separated shock absorber-movable support[D]. Beijing: Beijing Jiaotong University, 2018 http://cdmd.cnki.com.cn/Article/CDMD-10004-1018316349.htm |
| [12] |
周云, 黄慧敏, 朱勇. 组合式双圆锥耗能器的设计与性能模拟分析[J]. 振动与冲击, 2012, 31(1): 131. ZHOU Yun, HUANG Huimin, ZHU Yong. Design and FE analysis for assembled biconical energy dissipator (BED)[J]. Journal of Vibration and Shock, 2012, 31(1): 131. DOI:10.3969/j.issn.1000-3835.2012.01.028 |
| [13] |
李承根, 高日. 高速铁路桥梁减震技术研究[J]. 铁道建筑技术, 2009, 11(2): 81. LI Chenggen, GAO Ri. Study on the shock absorbing technique of high speed railway bridges[J]. Railway Construction Technology, 2009, 11(2): 81. |
| [14] |
孟兮.减震榫的减震性能及其在铁路桥梁中的应用[D].北京: 北京交通大学, 2015 MENG Xi. Damping performance of shock absorber and its application research on railway bridge[D]. Beijing: Beijing Jiaotong University, 2015 http://cdmd.cnki.com.cn/Article/CDMD-10004-1016074108.htm |
| [15] |
王占飞, 孙巨搏, 程浩波, 等. 缓冲型防落梁钢圈限位装置力学性能研究[J]. 桥梁建设, 2018, 48(6): 18. WANG Zhanfei, SUN Jubo, CHENG Haobo, et al. Study on mechanical properties of a steel ring anti-fall restrainer with buffer capacity[J]. Bridge Construction, 2018, 48(6): 18. DOI:10.3969/j.issn.1003-4722.2018.06.004 |
| [16] |
董俊, 曾永平, 单德山. 核密度估计的桥梁结构地震易损性分析[J]. 哈尔滨工业大学学报, 2018, 50(3): 109. DONG Jun, ZENG Yongping, SHAN Deshan. Seismic fragility analysis of railway bridge using kernel density estimation[J]. Journal of Harbin Institute of Technology, 2018, 50(3): 109. |
| [17] |
潘晋, 吴成亮, 仝强, 等. E型钢阻尼器数值仿真及试验研究[J]. 振动与冲击, 2009, 28(7): 192. PAN Jin, WU Chengliang, TONG Qiang, et al. Simulation and experimental study on an E-shape steel damper[J]. Journal of Vibration and Shock, 2009, 28(7): 192. DOI:10.3969/j.issn.1000-3835.2009.07.042 |
| [18] |
中铁大桥勘测设计院有限公司.铁路桥梁钢结构设计规范: TB 10091—2017[S].北京: 中国铁道出版社, 2017 China Railway Bridge Survey and Design Institute Group Corporation. Code for design on steel structure of railway bridge: TB 10091—2017[S]. Beijing: China Railway Press, 2017 |
| [19] |
中华人民共和国建设部.钢结构设计规范: GB 50017—2003[S].北京: 中国计划出版社, 2003 Ministry of Construction of the People's Republic of China. Code for design of steel structures: GB 50017—2003[S]. Beijing: China Planning Press, 2003 |
| [20] |
中铁工程设计咨询集团有限责任公司.铁路桥涵混凝土结构设计规范: TB 10092-2017[S].北京: 中国铁道出版社, 2017 China Railway Engineering Design Consulting Institute Group Corporation. Code for design of concrete structures of railway bridge and culvert: TB 10092—2017[S]. Beijing: China Railway Press, 2017 |
| [21] |
董俊, 单德山, 张二华, 等. 非规则桥梁近、远场地震易损性对比分析[J]. 哈尔滨工业大学学报, 2016, 48(3): 159. DONG Jun, SHAN Deshan, ZHANG Erhua, et al. Near and far-field seismic fragility comparative analysis of irregular bridge[J]. Journal of Harbin Institute of Technology, 2016, 48(3): 159. |
| [22] |
JIA L J, KUWAMURA H. Ductile fracture simulation of structural steels under monotonic tension[J]. Journal of Structural Engineering, 2014, 140(5): 1. |
 2020, Vol. 52
2020, Vol. 52


