故障诊断,就是对故障进行检测,分离和识别[1-2],进入21世纪之后,出现了故障预测与健康管理技术,传统的故障诊断已经发展到诊断与预测并重的阶段[3].随着时代的发展,故障诊断技术的分类也变得更加复杂,总体来说可以分为两类:基于模型和基于数据[4].模型是最近研究的重要方向,但是对于一个复杂的工业系统,不可能将其完全重现.以污水处理系统举例,其处理过程复杂、变量多、回路多、反应时间长,并且具有非线性、大滞后、易受干扰等特点,某些情况下还会造成在线监测参数的仪器出现滞后和误差,尤其是在污水处理故障诊断系统尚不完善的情况下,故障诊断依靠的是经验判断法,具有一定的主观性,结果可靠性低.依靠完善的模型分析污水处理系统的故障非常困难,由于污水处理系统会在各环节产生大量的过程数据,其中包含设备运行和工艺变动等重要信息,所以能够高效准确地处理这些数据使其不至于浪费的统计分析法成为了一个比较好的选择[5].
多元统计在不直接对大量数据进行处理的前提下,找到一组简明的数据来描述过程特征,相对于单元统计而言,多元统计鲁棒性更强,可靠性更高,抗干扰能力也得以提升.单元统计对单一变量进行监控,简单而易于实现,但是随着系统复杂性的提升,变量间的耦合性增强,导致“牵一发而动全身”的形象时常出现,即一个故障多个报警.多元统计是研究多个随机变量之间相互依赖关系以及内在统计规律性的学科,基于多元统计分析的故障诊断方法就是利用多个过程变量之间的相关性对过程进行故障诊断,主要有主元分析法(PCA),偏最小二乘法(PLS)和独立成分分析法(ICA)[6].传统的PCA方法是在假设数据遵循高斯分布,不考虑数据序列相关性的条件下对数据进行分解降维,属于静态方法,在工业应用中适用于采样时间较长(2~12 h)的过程. PLS方法对于故障预测作用较弱. ICA监控方法则存在独立元数目不确定及排序等缺点[7].
除了经典的PCA,PLS,ICA和扩展算法[8],还有一种已经发展的比较成熟的降维技术,FDA(费舍尔判别分析),这种技术可以避免数据在投影到低维空间时发生严重的重叠现象,可以实现故障类数据之间最大程度的分离,但是这种技术尚未被成熟地运用到污水处理系统中[9].
一般污水处理厂需要处理大量污水,而污水具有很多表示其状态的“指标”,从最简单的颜色、气味、反射率到比较复杂的碱度、化学需氧量,这些指标反映着水体的状态.为了有效地进行故障诊断,需要选择最能反映污水处理效果的数据来进行处理,所以引入“关键性能指标”来对数据的选择进行规范.关键性能指标(KPI),用于反映系统的运行情况. KPI的理论基础是二八法则:80%的工作是由20%的关键行为完成.关注这些代表着关键行为的指标,可以最有效地得知系统工作的整体情况[10-11].在液体样本的多种指标中,有接近20种指标可以反映出污水处理系统的工作情况,这些指标即是关键性能指标,虽然只占据了可测量指标中的小部分,却可以表现出污水处理的效率.
利用关键性能指标结合多元统计分析,将有效避免分析无用数据导致故障诊断系统的误报和延迟,有利于得出准确性高,可靠性好,稳定性强的故障诊断结果.
1 偏最小二乘法的故障诊断技术 1.1 偏最小二乘算法偏最小二乘法与主元分析法一样都是数据驱动的基础方法,其主旨是通过对在线过程变量的观测来预测输出变量,在过程控制中,这种方法可以检测与输出变量最相关的输入变量中的错误,其输出的结果经常是在工业过程中不可实时测量的与产品质量相关的信息[12],通过这种信息,产品的状态便可见一斑.
一个数据驱动的故障诊断问题,可以将其分为离线状态和在线状态两部分.离线状态用于得到数据模型参数并设计故障检测方案;在线状态通过获得在线样本,根据离线状态时得到的参数检测故障发生与否.对于一个故障检测问题,比较常用的方法是基于T2统计量和基于SPE统计量的故障检测.
本文选取的离线测量数据为m个过程变量的观测样本和l个输出变量观测样本.这些样本满足正态分布,需要对其进行归一化处理,首先求取变量的均值和方差,利用所求取的均值和方差,即可实现归一化.
归一化后的过程变量观测样本U和输出变量观测样本Y可以分别表示为N×l和N×m的矩阵形式.同样,在线测量的l个过程变量的观测样本Unew也需要进行归一化处理.
由于输出变量无法进行在线测量,所以只能通过归一化后的在线样本的T2统计量获取故障信息.然而当在线样本与输出变量之间的关系未建立起来时,其T2统计量也无法反映当前故障是否为输出变量相关故障,因此输出变量相关的故障检测也可以表示为
| $ \mathit{\boldsymbol{u}} = \mathit{\boldsymbol{C}}_1^{{\rm{kpi}}}{\mathit{\boldsymbol{u}}_{{\rm{new}}}} + \cdots + \mathit{\boldsymbol{C}}_v^{{\rm{kpi}}}{\mathit{\boldsymbol{u}}_{{\rm{new}}}} + \mathit{\boldsymbol{C}}_1^{{\rm{no}}}{\mathit{\boldsymbol{u}}_{{\rm{new}}}} + \cdots + \mathit{\boldsymbol{C}}_\xi ^{{\rm{no}}}{\mathit{\boldsymbol{u}}_{{\rm{new}}}}. $ | (1) |
式中:C1kpi代表将Unew向着输出变量相关的子空间投影的投影,而Cjno所代表的是将Unew向着输出变量无关的子空间投影的投影矩阵,其中i=1, 2, …, v;j=1, 2, …, ξ.
将它们全部相加,将会得到一个l×l的单位阵.即归一化后的在线样本将可以表示为
| $ {\mathit{\boldsymbol{u}}_{{\rm{new }}}} = \sum\limits_{i = 1}^v {{{\mathit{\boldsymbol{\hat u}}}_{i,{\rm{new}}}}} + \sum\limits_{j = 1}^\xi {{{\mathit{\boldsymbol{\tilde u}}}_{j,{\rm{new}}}}} . $ | (2) |
| $ {{\mathit{\boldsymbol{\hat u}}}_{i,{\rm{new}}}} = {\bf{C}}_i^{{\rm{kpi}}}{\mathit{\boldsymbol{u}}_{{\rm{new}}}} \in \mathit{\boldsymbol{S}}_i^{{\rm{kpi}}},i = 1,2, \cdots ,v; $ | (3) |
| $ {{\mathit{\boldsymbol{\tilde u}}}_{j,{\rm{new}}}} = \mathit{\boldsymbol{C}}_j^{{\rm{no}}}{\mathit{\boldsymbol{u}}_{{\rm{new}}}} \in \mathit{\boldsymbol{S}}_j^{{\rm{no}}},j = 1,2, \cdots ,\xi . $ | (4) |
这两个子空间组成了过程变量空间,分别代表“和输出变量完全有关”(主元子空间)与“和输出变量完全无关”(残差子空间),输出变量相关和无关的故障检测就可以在这两个子空间中分别进行.有关输出变量故障检测的核心思路就是根据离线数据U和Y求解满足过程变量空间按输出变量分解的投影矩阵.
偏最小二乘法的步骤可以总结为4步:第1步收集过程变量与输出变量矩阵并且进行归一化处理.第2步通过运算律来获得用于表示它们之间关系的状态矩阵并且生成阈值.根据这些状态矩阵,可以预测输出变量的值,并且产生测量值.第3步就是应用在实际系统中,收集在线测量得到的过程变量矩阵并生成输出变量预测值和用于故障诊断的测量值,需要注意的是当系统的“正常工作条件”变化的时候,相应的状态矩阵和阈值也需要重新计算.第4步就是根据判断逻辑来判断故障的产生,当测量值高于阈值的时候就是故障发生.
偏最小二乘法有两个测量值,Hotelling T2与SPE,分别用于检测主元子空间的故障和残差子空间的故障.偏最小二乘法实现了输出变量预测、故障诊断和故障分离3个功能,但是其故障分离功能受到因斜投影而分离不彻底的影响,在判断故障是否与输出变量相关时的表现不好.偏最小二乘法的应用需要先验知识,在本文中不介绍先验知识的具体来源,仅探讨其在偏最小二乘法的故障诊断中所起到的影响.以下将把偏最小二乘法故障诊断的4个步骤用公式表示出来.
第1步 获得了过程变量U和关键性能指标Y之后,要先进行归一化,其目的是让运算更加简便.计算公式为
| $ {{\mathit{\boldsymbol{\bar u}}}_{{\rm{obs}},i}} = \frac{1}{N}\sum\limits_{j = 1}^N {{\mathit{\boldsymbol{u}}_{{\rm{obs}},i}}} \left( j \right); $ | (5) |
| $ \mathit{\boldsymbol{\sigma }}_{u,{\rm{obs}},i}^2 = \frac{1}{{N - 1}}\sum\limits_{j = 1}^N {{{\left( {{\mathit{\boldsymbol{u}}_{{\rm{obs}},i}}\left( j \right) - {{\mathit{\boldsymbol{\bar u}}}_{{\rm{obs}},i}}} \right)}^2}} ,i = 1,2, \cdots ,l; $ | (6) |
| $ \mathit{\boldsymbol{u}}(k) = \left[ {\begin{array}{*{20}{c}} {\frac{{{\mathit{\boldsymbol{u}}_{{\rm{obs}},1}}(k) - {{\mathit{\boldsymbol{\bar u}}}_{{\rm{obs}},1}}}}{{{\mathit{\boldsymbol{\sigma }}_{u,{\rm{obs}},1}}}}}\\ \vdots \\ {\frac{{{\mathit{\boldsymbol{u}}_{{\rm{obs}},l}}(k) - {{\mathit{\boldsymbol{\bar u}}}_{{\rm{obs}},l}}}}{{{\mathit{\boldsymbol{\sigma }}_{u,{\rm{obs}},l}}}}} \end{array}} \right]; $ | (7) |
| $ \mathit{\boldsymbol{U}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{u}}{{(1)}^{\rm{T}}}}\\ \vdots \\ {\mathit{\boldsymbol{u}}{{(N)}^{\rm{T}}}} \end{array}} \right] \in {\mathit{\boldsymbol{R}}^{N \times l}}. $ | (8) |
通过已经获得的U, Y和γ得到P, T, Q, R等数据模型矩阵. U为N×l的一个矩阵,代表着l个过程变量的N个样本. Y为N×m的一个矩阵,代表着m个输出的N个样本,在本项目面向KPI的想法下,即是m个KPI的N个样本.
| $ \mathit{\boldsymbol{U}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{u}}_1^{\rm{T}}}\\ {\mathit{\boldsymbol{u}}_2^{\rm{T}}}\\ \vdots \\ {\mathit{\boldsymbol{u}}_N^{\rm{T}}} \end{array}} \right] \in {\mathit{\boldsymbol{R}}^{N \times l}}, $ | (9) |
| $ \mathit{\boldsymbol{Y}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{y}}_1^{\rm{T}}}\\ {\mathit{\boldsymbol{y}}_2^{\rm{T}}}\\ \vdots \\ {\mathit{\boldsymbol{y}}_N^{\rm{T}}} \end{array}} \right] \in {\mathit{\boldsymbol{R}}^{N \times m}}. $ | (10) |
| $ {\mathit{\boldsymbol{u}}_i} \in {\mathit{\boldsymbol{R}}^l},{\mathit{\boldsymbol{y}}_i} \in {\mathit{\boldsymbol{R}}^m}. $ |
其中
| $ \mathit{\boldsymbol{U}} = \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{P}}^{\rm{T}}} + \mathit{\boldsymbol{\tilde U}} = \mathit{\boldsymbol{\hat U}} + \mathit{\boldsymbol{\tilde U}}, $ | (11) |
| $ \mathit{\boldsymbol{Y}} = \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{Q}}^{\rm{T}}} + {\mathit{\boldsymbol{E}}_y} = \mathit{\boldsymbol{UM}} + {\mathit{\boldsymbol{E}}_y}. $ | (12) |
引入的T为得分矩阵,是一个N×γ的矩阵,其中γ可以通过采用一个已知的标准来确定,在本文中取值为3.
而P∈Rl×m, Q ∈ Rm×γ分别是U和Y的负载矩阵,M ∈ Rl×m被称为系数矩阵.通过上面的式子可以得出T = UR, M = RQT,而其中的R可以通过PTR = RTP = Iγ×γ得出,所以可以总结出被称为“非线性最小二乘法迭代运算律”(NIPALS)的运算律.具体方式:首先获得U和Y,并且决定γ,然后开始运算迭代.
| $ \left( {\mathit{\boldsymbol{\omega }}_i^ * ,\mathit{\boldsymbol{q}}_i^ * } \right) = \arg \mathop {\max }\limits_{\begin{array}{*{20}{c}} {\left\| {{\mathit{\boldsymbol{\omega }}_1}} \right\| = 1}\\ {\left\| {{\mathit{\boldsymbol{q}}_1}} \right\| = 1} \end{array}} \mathit{\boldsymbol{\omega }}_i^{\rm{T}}\mathit{\boldsymbol{U}}_i^{\rm{T}}\mathit{\boldsymbol{Y}}{\mathit{\boldsymbol{q}}_i}. $ | (13) |
| $ {\mathit{\boldsymbol{U}}_1} = \mathit{\boldsymbol{U}}, $ | (14) |
| $ {\mathit{\boldsymbol{t}}_i} = {\mathit{\boldsymbol{U}}_i}\mathit{\boldsymbol{\omega }}_i^ * , $ | (15) |
| $ {\mathit{\boldsymbol{p}}_i} = \frac{{\mathit{\boldsymbol{U}}_{\rm{i}}^{\rm{T}}{\mathit{\boldsymbol{t}}_i}}}{{{{\left\| {{\mathit{\boldsymbol{t}}_i}} \right\|}^2}}}, $ | (16) |
| $ {\mathit{\boldsymbol{U}}_{i + 1}} = {\mathit{\boldsymbol{U}}_i} - {\mathit{\boldsymbol{t}}_i}\mathit{\boldsymbol{p}}_i^{\rm{T}}, $ | (17) |
| $ {\mathit{\boldsymbol{r}}_i} = \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\omega }}_1^*,i = 1;}\\ {\prod\limits_{j = 1}^{i - 1} {\left( {{\mathit{\boldsymbol{I}}_{n \times n}} - \mathit{\boldsymbol{\omega }}_j^*\mathit{\boldsymbol{p}}_j^{\rm{T}}} \right)\mathit{\boldsymbol{\omega }}_i^*} ,i > 1.} \end{array}} \right. $ | (18) |
其中γ便是迭代的次数,i=1, 2, …,γ.
运算率可以得出P, T, Q, R四个矩阵,并且利用这4个矩阵,可以获得M, E, F三个额外的矩阵.获得的矩阵大小:T ∈ RN×γ, P ∈ Rl×γ, Q ∈ Rm×γ, R ∈ Rl×γ.
而M通过M = RQT得到,用于表示过程变量与关键性能指标之间的线性关系,即
第2步 在得到这几个矩阵之后,已知PLS就是把原来的过程变量空间分解为主元子空间
| $ \mathit{\boldsymbol{\hat U}} = \mathit{\boldsymbol{P}}{\mathit{\boldsymbol{R}}^{\rm{T}}}\mathit{\boldsymbol{U}}, $ | (19) |
| $ \mathit{\boldsymbol{\tilde U}} = \mathit{\boldsymbol{U}} - \mathit{\boldsymbol{\hat U}} = \left( {{\mathit{\boldsymbol{I}}_l} - \mathit{\boldsymbol{P}}{\mathit{\boldsymbol{R}}^{\rm{T}}}} \right)\mathit{\boldsymbol{U}}, $ | (20) |
| $ \mathit{\boldsymbol{U}} = \mathit{\boldsymbol{P}}{\mathit{\boldsymbol{R}}^{\rm{T}}}\mathit{\boldsymbol{U}} + \left( {{\mathit{\boldsymbol{I}}_l} - \mathit{\boldsymbol{P}}{\mathit{\boldsymbol{R}}^{\rm{T}}}} \right)\mathit{\boldsymbol{U}}, $ | (21) |
| $ {\mathit{\boldsymbol{u}}_{{\rm{new}}}} = {{\mathit{\boldsymbol{\hat u}}}_{{\rm{new}}}} + {{\mathit{\boldsymbol{\tilde u}}}_{{\rm{new}}}} = \mathit{\boldsymbol{P}}{\mathit{\boldsymbol{R}}^{\rm{T}}}{\mathit{\boldsymbol{u}}_{{\rm{new}}}} + \left( {{\mathit{\boldsymbol{I}}_l} - \mathit{\boldsymbol{P}}{\mathit{\boldsymbol{R}}^{\rm{T}}}} \right){\mathit{\boldsymbol{u}}_{{\rm{new}}}}. $ | (22) |
在公式中,
T2统计量可以用来对主元子空间进行监控,SPE可以对存在高度相关性的残差子空间进行监控,SPE的监控一般很不精确,所以更常用T2统计量.在给定置信区间α(一般是0.99)之后,可以算出阈值,这里的置信区间是第二个先验知识.
| $ {J_{{\rm{th}},{T^2}}} = \frac{{\gamma \left( {{N^2} - 1} \right)}}{{N(N - \gamma )}}{F_\alpha }(\gamma ,N - \gamma ), $ | (23) |
| $ {J_{{\rm{th}},{\rm{SPE}}}} = gX_\alpha ^2(h). $ | (24) |
其中:
| $ {\rm{SPE}} = {\left\| {\left( {{\mathit{\boldsymbol{I}}_l} - \mathit{\boldsymbol{P}}{\mathit{\boldsymbol{R}}^{\rm{T}}}} \right)\mathit{\boldsymbol{u}}} \right\|^2}. $ | (25) |
第3步 根据得到的在线过程变量Unew得到测量值.
在线测量的过程变量Unew首先要根据已经获得的均值和方差进行归一化:
| $ {\mathit{\boldsymbol{u}}_i} = \frac{{{\mathit{\boldsymbol{u}}_{{\rm{new}},i}} - {{\mathit{\boldsymbol{\bar u}}}_{{\rm{obs}},i}}}}{{{\sigma _{u,{\rm{obs}},i}}}},i = 1,2, \cdots ,l. $ | (26) |
然后根据归一化的Unew计算测量值:
| $ {T^2} = {\mathit{\boldsymbol{u}}^{\rm{T}}}\mathit{\boldsymbol{R}}{\left( {\frac{{{\mathit{\boldsymbol{T}}^{\rm{T}}}\mathit{\boldsymbol{T}}}}{{N - 1}}} \right)^{ - 1}}{\mathit{\boldsymbol{R}}^{\rm{T}}}\mathit{\boldsymbol{u}}, $ | (27) |
| $ {\rm{SPE}} = {\left\| {\mathit{\boldsymbol{\tilde u}}} \right\|^2} = {\left\| {\left( {{\mathit{\boldsymbol{I}}_{l \times l}} - \mathit{\boldsymbol{P}}{\mathit{\boldsymbol{R}}^{\rm{T}}}} \right)\mathit{\boldsymbol{u}}} \right\|^2}, $ | (28) |
同时,可以根据获得的Unew得到不能直接在线上获得的Y,在仿真中,可以通过对比预测的Ypre与真实的Y的差值来确定状态矩阵的正确性.在实际运用中,可以通过预测的值来获得关键性能指标的信息. Ypre的运算公式为
| $ {\mathit{\boldsymbol{Y}}_{{\rm{pre}}}} = {\left( {\mathit{\boldsymbol{Q}}{\mathit{\boldsymbol{R}}^{\rm{T}}}\mathit{\boldsymbol{U}}_{{\rm{new}}}^{\rm{T}}} \right)^{\rm{T}}}. $ | (29) |
第4步 如果测量值与阈值的关系符合事先定好的运算率,一般是测量值高于阈值,则代表出现了故障,此时可以通过代码实现故障提醒和计数,以测量误报率和漏报率.
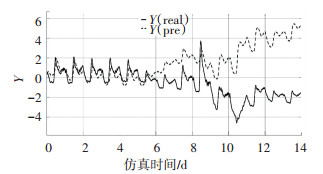
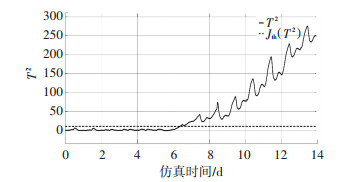
偏最小二乘法是利用获得的过程变量矩阵来预测关键性能指标,图 1所示是引入故障后对于关键性能指标的预测值和此时关键性能指标真实值的对比.从图 2中可以看到在发生了故障后关键性能指标的预测值明显地发生了变化,在这种情况发生时,测量值将会超出阈值(Jth),产生故障的检测信号,提醒使用者此时的预测值已经不可以当作真实值的近似来使用.
|
图 1 引入故障后对关键性能指标的预测值和真实值的对比 Fig. 1 Comparison between predicted value and true value of key performance indicators (KPI) after the introduction of a fault |
|
图 2 引入故障后产生的测量值高于阈值代表检测到故障 Fig. 2 A measured value higher than a threshold value after the introduction of a fault indicates a fault is detected |
通过算法过程可知,这其中有两个属于先验知识的变量,不通过数据收集或者计算,而是在计算之初就默认已经确定:潜变量个数γ和置信区间α,这其中置信区间一般取0.99是没有问题的,潜变量个数一般默认为3,在接下来的仿真验证中,会验证如果取的是5会产生什么影响.
1.2 使用的仿真模型活性污泥数学模型是国际水协会为了研究污水处理系统的特性而发布的模型,其主要包含了5个反应池和一个沉淀池,前两个反应池为缺氧池,后3个反应池为曝气池.在仿真模型中,沉淀池的数据是立即可得的,但是在实际过程中,沉淀池里经过处理的水的数据需要经过测量才能得到.
仿真模型中的过程变量是根据活性污泥法的化学过程来制定的[13],过程变量有13个,分别为可溶性惰性有机物Sl,易生物降解有机底物SS,颗粒性惰性有机物Xl,慢速可生物降解有机底物XS,活性异养菌生物量XB, H,活性自养菌生物量XB, A,微生物衰减产生的颗粒性产物XP,溶解氧SO, 硝态氨SNO, 氨氮SNH,溶解性可生物降解有机氮SND,颗粒性可生物降解有机氮XND,碱度SALK.
这13个过程变量的测量难度和精确度都存在不同,但是这其中的每一个过程变量都影响着某一个关键性能指标, 尽管关键性能指标是随意选取的, 但是最能反映污水处理系统工作效率的是其中5个,而在本文中选择这5个指标中的化学需氧量.因为化学需氧量相关的故障更容易控制,避免看不清故障引入前后的对比.而且,随着测量技术和仪器的发展,COD的测量越来越智能化和迅速化,由朗伯比尔定律所启发的紫外COD测量技术已经发展出来,对比以前时期使用高锰酸钾、硫酸银等会对环境产生二次污染,化学过程冗长的方法,已经有了极大的进步.
该模型有两层设计准则[13],第1层设计准则是绝对误差积分准则(IAE)和平方误差积分准则(ISE),这一层在设计时已经被合理地考虑了,而第2层设计准则则是故障诊断系统所关注的.
第2层设计准则又被分为4个部分.在这里只关注第1个部分:流出的水的质量,也被称为effluent quality index(EQI),其运算中各指标的重要因素以权重参数的形式来表达[13].其中TSS对应权重为2,COD对应权重为1,NKJ对应权重为30,NO对应权重为0,BOD5对应权重为2.而根据化学需氧量的计算公式为
| $ \begin{array}{l} {\rm{CO}}{{\rm{D}}_\varepsilon } = {S_{{\rm{S}},\varepsilon }} + {S_{{\rm{I}},\varepsilon }} + {X_{{\rm{S}},\varepsilon }} + {X_{{\rm{I}},\varepsilon }} + {X_{{\rm{B}},{\rm{H}},\varepsilon }} + \\ \;\;\;\;\;\;\;\;\;\;\;{X_{{\rm{B}},{\rm{A}},\varepsilon }} + {X_{{\rm{P}},\varepsilon }}. \end{array} $ | (30) |
COD指标容易计算,方便控制.因为如果权重过大, 会导致故障信号很高,从而无法看到前后的清楚对比,所以选择了权重系数较小的化学需氧量作为关键性能指标.
从上面的公式可以看出与化学需氧量相关的有7个过程变量,而这些过程变量也就是要收集的U矩阵,而化学需氧量则是需要收集的Y矩阵,并且根据实际情况,Y在故障诊断运行的过程中将是不可测量的.这里的U并不需要严格限制为这7个过程变量,而是可以再多选取一些,从而可以验证与关键性能指标有关与无关的过程变量发生故障时,对于故障检测系统的影响.
图 3是设计完成的故障诊断系统的主体子系统. 图 4是活性污泥数学模型的整体架构(包含已设计完成的故障诊断系统).

|
图 3 设计完成的故障诊断系统的主体子系统架构 Fig. 3 Inside of the main subsystem of the designed fault diagnosis system |

|
图 4 活性污泥数学模型整体架构 Fig. 4 Overall architecture of mathematical model of activated sludge (BSM1) |
模拟时间14 d,产生算例1 345个,每天产生96个算例,基本可以等同于每天产生100个.模拟故障无(即没有故障产生),天气为干燥,选取的U为所有的过程变量. “所有的过程变量”,也就是既包括了与关键性能指标有关的7个过程变量,也包含了另外6个与关键性能指标无关的过程变量.这个仿真是为了验证选取的过程变量矩阵U和关键性能指标矩阵Y的关系对于故障诊断的影响.
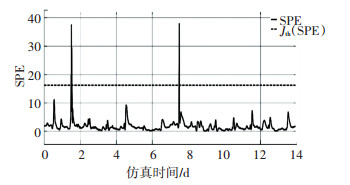
从图 5、6中可以看到,选取所有的过程变量离线训练并线上验证的时候,有比较高的误报率,为了起到对比作用,选择6个完全与关键性能指标无关的过程变量进行离线训练和在线检测,并且在第4天的时候引入一个1%的阻塞误差.

|
图 5 无故障时T2测量值与阈值的关系(干燥) Fig. 5 Relationship between T2 measured value and threshold value when there is no fault (dry weather) |
|
图 6 无故障时SPE测量值与阈值的关系(干燥) Fig. 6 Relationship between SPE measured value and threshold value when there is no fault (dry weather) |
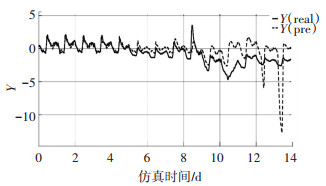
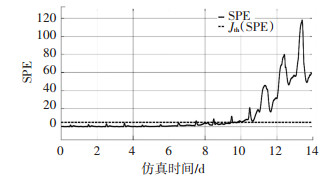
如图 7所示,在第4天引入故障之后,预测值和真实值在第6天就出现了较大的偏差,而根据图 8和图 9,两个测量值在仿真时间第10天才开始高于阈值,明显其反应过于滞后,故障诊断功能也受到影响,所以需要选择与关键性能指标相关的过程变量.
|
图 7 使用完全无关过程变量并引入故障时KPI预测值与真实值的关系 Fig. 7 Relationship between predicted value and true value of KPI when using completely unrelated process variables and introducing faults |

|
图 8 使用完全无关过程变量并引入故障时T2测量值与阈值的关系 Fig. 8 Relationship between T2 measured value and threshold value when using completely unrelated process variables and introducing faults |
|
图 9 使用完全无关过程变量并引入故障时SPE测量值与阈值的关系 Fig. 9 Relationship between SPE measured value and threshold value when using completely unrelated process variables and introducing faults |
而其他运行条件不变,将过程变量的选择数降低为8个,其中7个与关键性能指标有关,一个与关键性能指标无关,仿真结果如下.
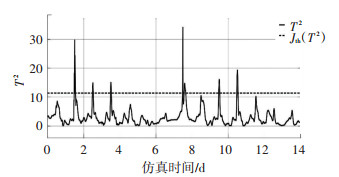
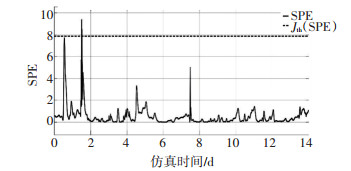
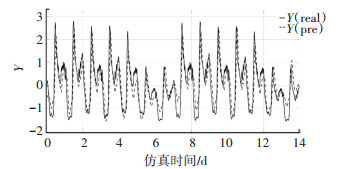
如图 10~12所示,系统的误报率很明显降低了,而且误报时恰好是预测值与真实值出现偏差的时候,这也说明了偏最小二乘法可以用于预测关键性能指标.在实际工业过程中,正确选择过程变量对于降低故障诊断的误报率,准确预测输出具有很大帮助,同时也可以避免无关变量发生的故障对于故障检测系统的干扰.
|
图 10 减少过程变量的选择数量后T2测量值与阈值的关系(干燥) Fig. 10 Relationship between T2 measured value and threshold value after reducing the selection number of process variables (dry weather) |
|
图 11 减少过程变量的选择数量后SPE测量值与阈值的关系(干燥) Fig. 11 Relationship between SPE measured value and threshold value after reducing the selection number of process variables (dry weather) |
|
图 12 减少过程变量的选择数量后关键性能指标的预测值与真值的关系(干燥) Fig. 12 Relationship between predicted value and true value of KPI after reducing the selection number of process variables (dry weather) |
把天气改换为下雨天气,过程变量为全部可选的过程变量,再一次在没有故障的情况下运行故障诊断系统.此次仿真是为了验证天气对于误报率的影响.
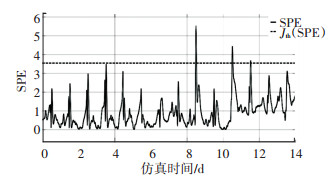
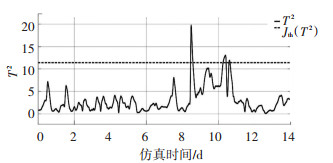
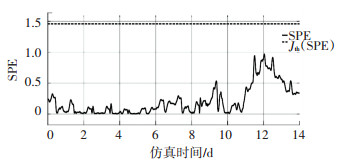
如图 13~16所示,相同的过程变量选择下,雨天的误报率更小.在不同的天气下,减少与关键性能指标不相关的过程变量可以降低误报率,接下来的仿真将继续使用8个过程变量的设定.

|
图 13 无故障时T2测量值与阈值的关系(下雨) Fig. 13 Relationship between T2 measured value and threshold value when there is no fault (rainy weather) |
|
图 14 无故障时SPE测量值与阈值的关系(下雨) Fig. 14 Relationship between SPE measured value and threshold value when there is no fault (rainy weather) |
|
图 15 减少过程变量的选择数量后T2测量值与阈值的关系(下雨) Fig. 15 Relationship between T2 measured value and threshold value after reducing the selection number of process variables (rainy weather) |
|
图 16 减少过程变量的选择数量后SPE测量值与阈值的关系(下雨) Fig. 16 Relationship between SPE measured value and threshold value after reducing the selection number of process variables (rainy weather) |
由图 13~16可以发现,发生误报的位置正是预测值与真值出现了较大差异的位置,所以在实际应用中,测量值低于阈值的时候,可以把预测值近似地当作真值,因为当预测值与真值出现了偏差的时候,测量值将会高于阈值产生故障信号(尽管真值在实际中是不可测的).
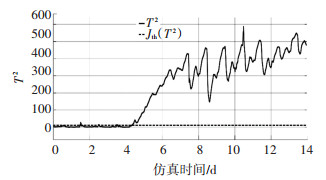
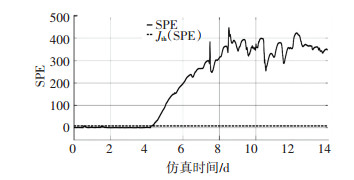
2.2 天气和故障发生位置对于故障诊断的影响模拟时间14 d,天气为干燥天气,过程变量选择8个,对一个与关键性能指标相关的过程变量XP施加一个10%的减小故障,因为在干燥天气时系统对故障太过敏感,1%的阻塞故障会导致测量值在1024数量级上无法看清楚检测值与阈值的变化关系,所以施加较为轻微的单一参数减小故障.故障在第4天加入,如图 17、18所示,干燥天气下故障检测系统非常灵敏,检测速度极快.
|
图 17 T2测量值与阈值的关系(干燥) Fig. 17 Relationship between T2 measured value and threshold value (dry weather) |
|
图 18 SPE测量值与阈值的关系(干燥) Fig. 18 Relationship between SPE measured value and threshold value (dry weather) |
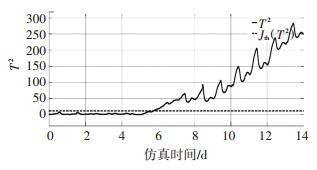
把环境天气改变为下雨,在第4天的时候引入一个从反应池2到反应池3的1%的阻塞误差.重新进行离线训练和在线测量对比,如图 19、20所示.此次仿真是为了验证天气对于故障诊断的影响.
|
图 19 T2测量值与阈值的关系(下雨) Fig. 19 Relationship between T2 measured value and threshold value (rainy weather) |
|
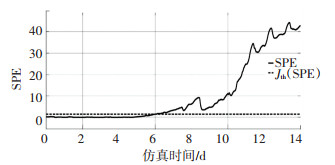
图 20 SPE测量值与阈值的关系(下雨) Fig. 20 Relationship between SPE measured value and threshold value (rainy weather) |
由图 19、20可以发现,下雨导致故障检测存在一定延迟.这也可能是因为下雨导致阻塞故障影响不明显,从而未引起较大影响.
将天气切换为下雨时,选择过程变量XND对其加入10%的阻塞故障,该变量不会影响关键性能指标,故障第4天引入,观察测量值的反应.同时验证潜变量个数γ对测量结果的影响.首先需要确定的是该过程变量对关键性能指标的影响.
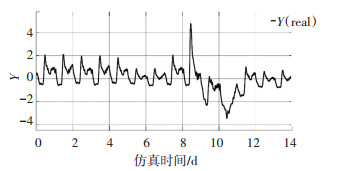
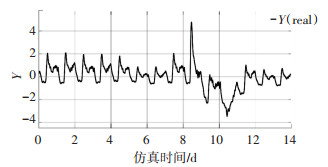
从图 21、22的对比中可以看出,引入XND故障后,Y的真值与没有发生故障时的情况是基本吻合的.在实际过程中,这代表尽管某一变量出现异常情况,但是使用者所关心的性能指标并没有受到影响,在使用中视需求而定可以认为并未产生故障.
|
图 21 引入XND故障后Y的真值 Fig. 21 True value of Y after introducing XND fault |
|
图 22 无故障时Y的真值 Fig. 22 True value of Y when there is no fault |
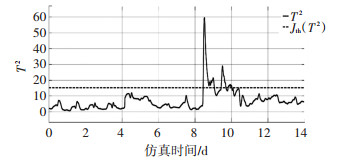
当潜变量个数为5时,SPE测量值始终高于阈值,而T2测量值出现了时而高于阈值时而低于阈值的现象,此时T2的表现和SPE的表现是不一样的. T2本意是检测主元子空间,只有当影响KPI的故障发生时,T2测量值才会大于阈值,而在实验验证中仍然有故障信息被检测出来,说明偏最小二乘法对于主元子空间和残差子空间分离不彻底,导致主元子空间中还残留与KPI无关的信息,所以故障发生时T2测量值会大于阈值.也有可能属于正常范畴内的误报.
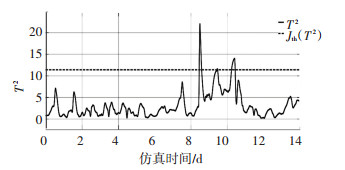
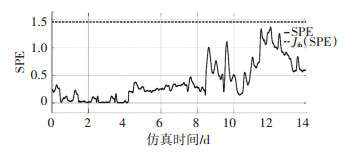
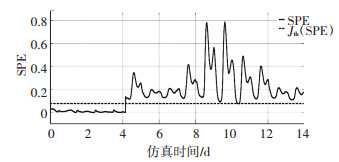
根据图 23~26所示,潜变量增加的时候,故障分离效果变好了,说明潜变量的变化会导致故障诊断系统性能的变化.以及,如果潜变量个数选择为3可以发现SPE测量值和T2测量值几乎一直小于阈值,意味着此时故障几乎没有被检测出来.
|
图 23 XND故障下T2测量值与阈值的关系(γ=3, 下雨) Fig. 23 Relationship between T2 measured value and threshold value under XND fault (γ=3, rainy weather) |
|
图 24 XND故障下T2测量值与阈值的关系(γ=5, 下雨) Fig. 24 Relationship between T2 measured value and threshold value under XND fault (γ= 5, rainy weather) |
|
图 25 XND故障下SPE测量值与阈值的关系γ=3, 下雨) Fig. 25 Relationship between SPE measured value and threshold value under XND fault (γ=3, rainy weather) |
|
图 26 XND故障下SPE测量值与阈值的关系(γ =5, 下雨) Fig. 26 Relationship between SPE measured value and threshold value under XND fault (γ= 5, rainy weather) |
从运行结果可以得到基础偏最小二乘法应用于故障诊断系统时,该故障诊断系统在模拟污水处理系统中的表现情况.
首先是故障检测的及时性,从图中可以得知在引入故障后测量值都有显著上升,但是在有雨天气时,对于阻塞故障略微不敏感,超过阈值时间延迟了大约2 d,考虑到故障非常细微,延迟的时间处于可接受的范围内.
其次是早期检测的灵敏度,根据运行条件和结果可以得知,故障诊断系统对会影响到关键性能指标的极微小的1%阻塞故障也有很好的反应,所以偏最小二乘法的故障诊断灵敏度很好.
然后是故障的误报率和漏报率,根据结果,误报是不可避免地存在的,误报率受到选择的过程变量数量的影响,越多与关键性能指标无关的过程变量被选取,误报率就越高.
接下来是故障分离能力,T2与SEP是分别监测两个子空间的测量值,当T2测量值大于阈值的时候,意味着与关键性能指标相关的部分发生了故障,T2测量值大于阈值的时候,意味着与关键性能指标无关的部分发生了故障.只要观察这两种测量值与阈值的关系存在的区别,就可以大致判断故障是否影响到了选定的关键性能指标.但是这种理论上的区分方法在仿真验证中存在问题.首先故障诊断系统判断故障是否与KPI相关会受到天气和所选变量的影响;其次故障本身的严重程度和造成的影响也是一个因素,需要根据实际系统的稳定性进行专门的验证,不能对所有的系统都一概而论.
综上所述,面向关键性能指标的偏最小二乘法的故障诊断便于实现,计算方便,但是仍然存在一些问题,例如对不同的运行条件需要重复收集数据和进行训练,在目前数据量急剧增大的情况下,有可能造成处理缓慢的情况.
4 结论1) 偏最小二乘法可有效应用于系统故障诊断.过程变量的选择验证表明,与关键性能指标无关的过程变量选择的越多,误报率就越高.
2) 天气会对故障诊断的误报率和及时性产生影响,如果追求更高的准确度,将有必要针对不同天气修改算法.
3) 验证了故障发生的位置对于故障诊断的影响,当发生的故障位于与关键性能指标无关的过程变量时,可以发现两种测量值与阈值的关系不一样,这种区别可以用来判断故障发生的位置与严重程度,辨识该区别的能力受到潜变量个数影响,所以选择潜变量个数将是研究偏最小二乘法的故障诊断方法中的一个重点.
| [1] |
黄道平, 邱禹, 刘乙奇, 等. 面向污水处理的数据驱动故障诊断及预测方法综述[J]. 华南理工大学学报, 2015, 43(3): 111. HUANG Daoping, QIU Yu, LIU Yiqi, et al. Summary of data-driven fault diagnosis and prediction methods for sewage treatment[J]. Journal of South China University of Technology, 2015, 43(3): 111. DOI:10.3969/j.issn.1000-565X.2015.03.017 |
| [2] |
DING S X. Model-based fault diagnosis techniques[M]. 2nd ed. Berlin, Heidelberg: Springer-Verlag, 2013.
|
| [3] |
张金玉, 张炜. 装备智能故障诊断与预测[M]. 北京: 国防工业出版社, 2013. ZHANG Jinyu, ZHANG Wei. Intelligent fault diagnosis and prediction of equipment[M]. Beijing: National Defense Industry Press, 2013. |
| [4] |
周东华, 王桂增. 故障诊断技术综述[J]. 化工自动化及仪表, 1998, 25(1): 58. ZHOU Donghua, WANG Guizeng. Summary of fault diagnosis technology[J]. Chemical Automation and Instrumentation, 1998, 25(1): 58. |
| [5] |
王道平, 冯振声, 何海燕. 故障诊断专家系统中不确定性问题[J]. 计算机工程与应用, 1998, 34(12): 33. WANG Daoping, FENG Zhensheng, HE Haiyan. Uncertainty in fault diagnosis expert system[J]. Computer Engineering and Applications, 1998, 34(12): 33. |
| [6] |
DING S X. Data-drivendesign of fault diagnosis and fault-tolerant control systems[M]. London: Springer-Verlag, 2014.
|
| [7] |
蒋浩天.工业系统的故障检测与诊断[M].段建民, 译.北京: 机械工业出版社, 2003: 48 JIANG Haotian. Fault detection and diagnosis of industrial systems[M]. DUAN Jianmin, translate. Beijing: Mechanical Industry Press, 2003: 48 |
| [8] |
ZHANG Yingwei. Fault detection and diagnosis of nonlinear processes using improved kernel independent component analysis (KICA) and support vector machine (SVM)[J]. Industrial and Engineering Chemistry Research, 2008, 47(18): 6961. DOI:10.1021/ie071496x |
| [9] |
RONG Gang, LIU Suyu, SHAO Jidong. Fault diagnosis by Locality Preserving Discriminant Analysis and its kernel variation[J]. Computers and Chemical Engineering, 2013, 49: 105. DOI:10.1016/j.compchemeng.2012.10.008 |
| [10] |
DING S X, YIN S, PENG K, et al. A novel scheme for key performance indicator prediction and diagnosis with application to an industrial hot strip mill[J]. IEEE Transactions on Industrial Informa-tics, 2013, 9: 2239. DOI:10.1109/TII.2012.2214394 |
| [11] |
KRUEGER M, LUO H, DING S X, et al. Data-driven approach of KPI monitoring and prediction with application to wastewater treatment process[J]. IFAC-PapersOnLine, 2015, 48(21): 627. DOI:10.1016/j.ifacol.2015.09.596 |
| [12] |
YIN S, DING S X, ZHANG P, et al. Study on modifications of PLS approach for process monitoring[J]. IFAC Proceedings Volumes, 2011, 44(1): 12389. DOI:10.3182/20110828-6-IT-1002.02876 |
| [13] |
GERNAEY K V, JEPPSSON U, VANROLLEGHEM P A, et al. Benchmarking of control strategies for wastewater treatment plants[M]. London: IWA Publishing, 2014.
|
 2020, Vol. 52
2020, Vol. 52


