2. 武汉大学 遥感信息工程学院, 武汉 430079;
3. 国网山东省电力公司 菏泽供电公司, 山东 菏泽 274000
2. School of Remote Sensing and Information Engineering, Wuhan University, Wuhan 430079, China;
3. Heze Power Supply Company, State Grid Shandong Electric Power Company, Heze 274000, Shandong, China
星载合成孔径雷达(SAR)不受云雾、雨雪、太阳光照等条件的限制,可对大面积区域内的电力设施进行全天候、全天时监测,非常适合应用于冰雪、地震、洪水等大范围自然灾害条件下输电杆塔和输电导线等电力设施的安全状态(比如毁损、覆冰等)评估.随着星载SAR分辨率的不断提高,基于其影像监测输电杆塔和输电导线正受到越来越多的关注.文献[1-3]已经建立了从TerraSAR-X卫星1 m分辨率影像中提取特高压铁塔目标和检测铁塔形变的方法,验证了基于高分SAR卫星监测覆冰铁塔及其形变的可行性.此外,还分析了特高压输电导线在不同分辨率和不同极化模式SAR卫星影像中呈现出的散射特征[4],发现极化方式、卫星地面运动轨迹与输电线路走向之间的夹角会对特高压输电导线在卫星影像上形成的散射亮斑造成显著影响.侯爱羚等[5]在此基础之上详细分析了特高压输电线路的夹角、跨度和垂曲率对散射亮斑形成及其雷达像空间位置的影响.李沙和陈志国等[6-7]分别基于时序TerraSAR-X卫星影像分别分析了散射亮斑亮度、面积、位置和相位的变化特征.但上述研究只分析了特高压输电导线在高分SAR卫星影像上呈现出的散射特征,并没有深入阐述其形成机理,因此无法合理解译某些散射特征,同时也限制了基于高分SAR卫星影像进一步提取特高压输电导线的状态参数.由此可见,分析特高压输电导线对SAR卫星信号的电磁散射特性,并进一步阐明高分SAR卫星影像上特高压输电导线散射亮斑的形成机理,对利用这类卫星监测特高压输电导线有非常重要的意义,但目前尚未见到相关研究报道.另一方面,国内外针对机载毫米波防撞雷达,详细分析了输电导线对毫米波信号的电磁散射特性[8-10],但现有SAR卫星的信号波长、极化方式、成像几何结构明显不同于机载毫米波雷达,导致输电导线的电磁散射特性也会存在明显差异.
针对监测特高压输电线路常用的TerraSAR-X卫星,本文基于增量长度绕射系数(ILDC)方法分析了特高压输电导线对工作在X波段上的TerraSAR-X卫星信号的电磁散射特性,在此基础之上推导了求解特高压输电导线三维雷达横截面积(RCS)的公式,并将导线RCS的理论计算结果与微波暗室测量结果进行了对比分析,为后续阐明高分辨率TerraSAR-X卫星影像上特高压输电线路散射亮斑的形成机理奠定理论基础.
1 特高压输电导线的X波段电磁散射特性分析 1.1 特高压输电导线物理模型的建立高分辨率TerraSAR-X卫星工作在X波段(关于该卫星的详细工作参数可参见文献[11]),发射信号载波的中心频率fc为9.6 GHz,因此可得信号波长为
| $ \lambda = c/{f_c} \approx 0.031{\rm{m,}} $ | (1) |
式中c为光速.
依据弗兰霍夫判据[12],当利用TerraSAR-X卫星监测目标时,如果目标表面高度标准偏离差小于1.88 mm,那么可认为目标表面光滑.特高压输电导线中单根铝芯线的直径为2.4 mm,绞合之后的导线表面起伏差小于1.2 mm[5],因此可认为特高压输电导线的表面是光滑的.此外,针对式(1)给出的信号波长,还可以认为导线表面的绝缘层是透明的,而且绝缘层下面的材料是完美电导体.
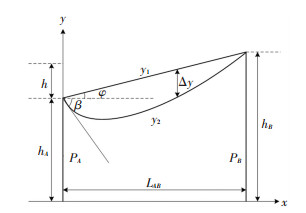
由于输电导线不是完全刚性的,在自身重力和相邻两基输电杆塔高度差的影响下,具有一定跨度的特高压输电导线的实际形状如图 1所示的一条悬链线.
|
图 1 具有一定跨度的特高压输电导线的实际形状 Fig. 1 Actual geometry of ultra-high-voltage power transmission line with a certain amount of span length |
图 1中PA和PB为输电导线相邻两基输电杆塔,hA和hB为两基输电杆塔对应的高度,h和LAB分别为两基输电杆塔之间的高程差和档距,y2为输电导线,y1为悬挂点之间的直线线段,φ为y1与水平面之间的夹角,β为输电导线在杆塔PA悬挂点处的对地倾斜角,Δy为输电导线上任意一点的弧垂.因此,可利用无摆动情况下输电导线的悬链线方程构建实际特高压输电导线的物理模型[13],即
| $ y = a \cdot \cosh \frac{{x - b}}{a} + d. $ | (2) |
式中:a为悬链系数,cosh(·)为双曲余弦函数,系数b、d的求解见文献[13].
1.2 特高压输电导线三维RCS的求解由于特高压输电导线的直径大约为30 mm,与式(1)给出的TerraSAR-X卫星信号波长非常接近,因此绕射场在特高压输电导线对卫星信号的电磁散射中占主导地位[14],明显不同于其他类型输电导线的X波段电磁散射特性和各类输电导线在毫米波段上的电磁散射特性.另一方面,由于SAR卫星与输电线路相距非常远,因此可认为卫星信号以平面波的方式照射输电导线.
基于上述近似,首先将式(2)所示的整条输电导线划分为多个有限长完美电导光滑圆柱体,然后分析单个圆柱体对TerraSAR-X卫星信号的电磁散射特性,最后通过对所有圆柱体的电磁散射场强度进行相干累加,获得整条输电导线对卫星信号的电磁散射特性以及输电导线的三维RCS.具体分析过程如下.
麦克斯韦波动方程组为
| $ \left\{ {\begin{array}{*{20}{c}} {{\Delta ^2}\mathit{\boldsymbol{E}} - \frac{1}{{{c^2}}}\frac{{{\partial ^2}\mathit{\boldsymbol{E}}}}{{\partial {t^2}}} = \frac{1}{{{\varepsilon _0}}}\Delta \rho + {\mu _0}\frac{{\partial \mathit{\boldsymbol{M}}}}{{\partial t}},}\\ {{\Delta ^2}\mathit{\boldsymbol{B}} - \frac{1}{{{c^2}}}\frac{{{\partial ^2}\mathit{\boldsymbol{B}}}}{{\partial {t^2}}} = {\mu _0}\Delta \times \mathit{\boldsymbol{M}}.} \end{array}} \right. $ | (3) |
式中:E为电场强度,B为磁感应强度,M为传导电流密度,ρ为自由电荷体密度,Δ为拉普拉斯算符,ε0为介电常数,μ0为介质磁导率.
在没有自由电荷和电流的情况下ρ= M =0,式(3)可以转变为如下所示的矢量Helmholtz方程:
| $ \left\{ {\begin{array}{*{20}{l}} {{\Delta ^2}\mathit{\boldsymbol{E}} + k_0^2\mathit{\boldsymbol{E}} = 0,}\\ {{\Delta ^2}\mathit{\boldsymbol{B}} + k_0^2\mathit{\boldsymbol{B}} = 0.} \end{array}} \right. $ | (4) |
式中k0为载波波数,k0=2πfc/c.
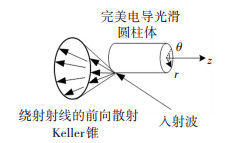
在特定坐标系下,将电磁强度E和磁感应强度B用它们的矢量分量表示,并求解所产生的标量Helmholtz方程,即可求解式(4)给出的方程组.对于图 2所示的圆柱坐标系,标量Helmholtz方程可表示为
| $ \begin{array}{l} \left[ {{\Delta ^2} + k_0^2} \right]f\left( {r,\theta ,z} \right) = \\ \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial f}}{{\partial r}}} \right) + \frac{1}{{{r^2}}}\frac{{{\partial ^2}f}}{{\partial {\theta ^2}}} + \frac{{{\partial ^2}f}}{{\partial {\theta ^2}}} + k_0^2f = 0. \end{array} $ | (5) |
|
图 2 完美电导光滑圆柱体对斜入射信号的电磁散射示意图 Fig. 2 Electromagnetic scattering from a perfectly conducting smooth cylinder in the case of oblique-incidence illumination |
由于SAR卫星与输电线路相距非常远,即观测点位于远场,因此对完美电导圆柱体施加边界条件,可得到斜入射情况下标量Helmholtz方程的特殊解[15]为
| $ \begin{array}{l} {E_{\rm{s}}} = \sqrt {\frac{2}{{{\rm{ \mathsf{ π} }}{k_0}R}}} {E_{{\rm{in}}}}\sqrt {\cos \vartheta } \times \\ \;\;\;\;\;\;\;\exp \left[ {{\rm{j}}\left( {{k_0}{z_0}\sin \vartheta + {k_0}R\cos \vartheta - \frac{{\rm{ \mathsf{ π} }}}{4}} \right)} \right] \times \\ \;\;\;\;\;\;\;\sum\limits_{n = - \infty }^\infty {{{\left( { - 1} \right)}^n}{C_n}} . \end{array} $ | (6) |
式中:Es、Ein分别为散射电场和入射电场的强度,R为圆柱体与观测点之间的距离,ϑ为倾角,zo为沿着圆柱体到选定基准点的距离,Cn为取决于极化、圆柱体尺寸和辐射波长的一个量.对于完美电导圆柱体,交叉极化项为0,因此Cn仅由辐射波长和圆柱体的直径a0决定,即
| $ C_n^{{\rm{TM}}} = - \frac{{{J_n}\left( {{k_0}{a_0}\cos \vartheta } \right)}}{{H_n^{\left( 1 \right)}\left( {{k_0}{a_0}\cos \vartheta } \right)}}, $ | (7) |
| $ C_n^{{\rm{TE}}} = - \frac{{{{J'}_n}\left( {{k_0}{a_0}\cos \vartheta } \right)}}{{H_n^{{{\left( 1 \right)}^\prime }}\left( {{k_0}{a_0}\cos \vartheta } \right)}}, $ | (8) |
| $ C_n^{{\rm{TM}}} = C_{ - n}^{{\rm{TM}}},C_n^{{\rm{TE}}} = C_{ - n}^{{\rm{TE}}}. $ | (9) |
式中:TM为横磁波,TE为横电波,Jn(·)为第1类的n阶Bessel函数,Hn(1)(·)为第1类的n阶Hankel函数,(′)为求导数符号.
不失一般性,假设zo=0,依据式(6)可得到Keller锥中前向散射场强的二维解.基于该二维解,并利用方程:
| $ {\sigma _{2{\rm{D}}}} = \mathop {\lim }\limits_{R \to \infty } 2{\rm{ \mathsf{ π} }}R\frac{{{{\left| {{E_{\rm{s}}}} \right|}^2}}}{{{{\left| {{E_{{\rm{in}}}}} \right|}^2}}}, $ | (10) |
可得到圆柱体的二维RCS.这里引入矢量:二维绕射系数d,而且在圆柱坐标系下该参量通过方程:
| $ {E_{\rm{s}}} = {E_{{\rm{in}}}}\frac{{{{\rm{e}}^{{\rm{j}}\left( {{k_0}R - \frac{{\rm{ \mathsf{ π} }}}{4}} \right)}}}}{{\sqrt {2{\rm{ \mathsf{ π} }}} R}}\mathit{\boldsymbol{\bar d}} \cdot \mathit{\boldsymbol{p}}, $ | (11) |
将散射场与入射场进行关联[16].式中p为沿入射电场极化方向的一个单元矢量.结合式(6),可推得斜入射情况下反映完美电导光滑圆柱体电磁散射特性的二维绕射系数,即
| $ \mathit{\boldsymbol{\bar d}} = 2\sqrt {\frac{2}{{\rm{ \mathsf{ π} }}}} \exp \left( { - {\rm{j}}\frac{{\rm{ \mathsf{ π} }}}{4}} \right)\sum\limits_{n = 0}^\infty {{{\left( { - 1} \right)}^{n + 1}}} {{\bar C}_n}. $ | (12) |
从图 2中可以看出,式(12)给出的二维绕射系数只描述了Keller锥中的散射场.为获得比较准确的电磁散射强度,还需要考虑Keller锥之外的散射场,进而获得三维绕射系数. Mitzner提出的ILDC方法综合考虑了Keller锥内外的散射场[17],进而可求得比较准确的三维绕射系数.具体求解过程如下.
与二维绕射系数的定义相似,三维绕射系数的定义[17]为
| $ \mathit{\boldsymbol{\bar D}} = \frac{1}{{2{\rm{ \mathsf{ π} }}}}\exp \left[ { - {\rm{j}}(2\mathit{\boldsymbol{k}} \cdot \mathit{\boldsymbol{l}}) + \frac{{\rm{ \mathsf{ π} }}}{4}} \right]{k_0}{T_{{\rm{cy}}}}\sin c\left( {{X_{{\rm{in}}}}} \right){{\mathit{\boldsymbol{\bar d}}}_{3{\rm{D}}}}. $ | (13) |
式中:Tcy为圆柱体的长度,Xin定义成
在文献[17]中,Mitzner指出完美电导光滑圆柱体后向散射的同极化d3D正好等于前向散射Keller锥中的二维绕射系数d,因此将式(12)代入到式(13),即可求得三维绕射系数D.此外,由于三维RCS的表达式为
| $ {\sigma _{3{\rm{D}}}} = 4{\rm{ \mathsf{ π} }}\mathop {\lim }\limits_{R \to \infty } {R^2}\frac{{\left( {{\mathit{\boldsymbol{E}}_{\rm{s}}} \cdot \mathit{\boldsymbol{E}}_{\rm{s}}^*} \right)}}{{\left( {{\mathit{\boldsymbol{E}}_{{\rm{in}}}} \cdot \mathit{\boldsymbol{E}}_{{\rm{in}}}^*} \right)}}, $ | (14) |
结合式(11)~(14),可推得三维绕射系数与三维RCS之间的关系式为
| $ {\sigma _{3{\rm{D}}}} = {\lambda ^2}{\left| {\sum\limits_{q = 1}^m {{{\mathit{\boldsymbol{\bar D}}}_q}} {{\left( {{\mathit{\boldsymbol{\beta }}_{{\rm{in}}}}} \right)}_q}} \right|^2}. $ | (15) |
式中m为将输电导线分割之后得到的圆柱体的总个数.
综上所述,针对所建立的特高压输电导线物理模型,首先通过求解圆柱坐标系下的Helmholtz方程,获得输电导线的二维绕射系数.然后利用ILDC方法获得输电导线的三维绕射系数.最后利用三维RCS与三维绕射系数之间的关系,推得特高压输电导线的三维RCS.
2 试验结果及分析为验证上述特高压输电导线X波段电磁散射特性分析方法的正确性,下面将特高压输电导线RCS的理论计算结果与微波暗室测量结果进行比较分析.理论计算和实验测试中所用到的参数包括:1)特高压输电导线的长度为0.5 m,直径分别为30.1、35.2 mm,材质为钢芯铝绞线;2)观测角度为-10°~80°,步进为1°;3)输电导线与观测点之间的距离为20 m;4)测试天线的极化方式为双极化,天线3 dB波束宽度为10°;5)测试信号采用线性调频信号,中心频率为9.6 GHz;6)将输电导线分割成1 000个小圆柱体,每个小圆柱体的长度为0.5 mm.
此外,理论计算中需要用到的其他角度值和距离值可依据观测角度和导线分割之后每个小圆柱体中心的位置计算得到,并且依据式(15)获得特高压输电导线在X波段上的RCS理论计算值.
微波暗室和部分测量装置的实物如图 3所示.测试中使用一套动态范围为100 dB而且具备全极化性能的矢量网络分析仪测量来自特高压输电导线的后向散射回波.天线系统由一套直接式收发转换器和一套交叉极化隔离度为20 dB的双极化方形喇叭天线组成.目标被放置在垫有泡沫并且可灵活调节方位角和仰角的旋转台上.测试目标直径分别为30.1、35.2 mm的两根0.5 m长钢芯铝绞线.在测量之前,先进行校正以获得校正因子,校正步骤包括:1)在10个不同的视角上对校准用的小球的复数幅值进行10次测量;2)撤掉小球,再次在10个视角上对安装平台的复数幅值进行10次测量;3)将步骤1中测量结果的平均复数幅值减去步骤2中测量结果的平均复数幅值;4)将步骤3得到的结果的幅度平方除以小球的RCS得到校正因子.

|
图 3 微波暗室测量装置实物图 Fig. 3 Pictures of some measuring devices in the anechoic chamber |
实际测量中,在相对于垂直入射角-10°~80°之间以1°的步进测量输电导线的平均复数幅值,然后减去校正步骤2中测得的安装平台的平均复数幅值,最后取幅度平方,并除以校正因子,即可测得输电导线的RCS.此外,依据瑞利远场准则,对于0.5 m长特高压输电导线和TerraSAR卫星信号波长,满足远场条件的最小测量距离为
| $ {d_{\min }} = \frac{{2{L^2}}}{\lambda } \approx 16{\rm{m ,}} $ | (16) |
式中L为特高压输电导线的长度.在实验中,设置测量距离为20 m,因此可认为观测点位于远场.
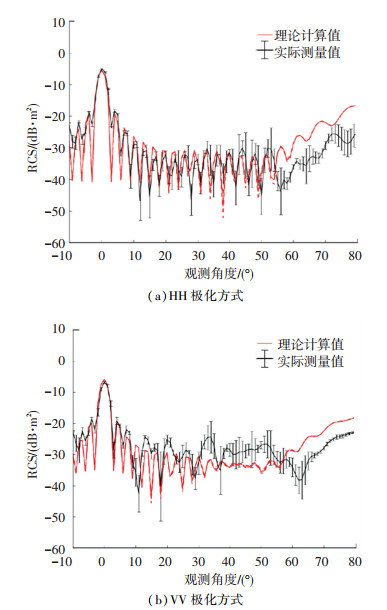
由于TerraSAR卫星只有水平-水平(horizontal-horizontal, HH)和垂直-垂直(vertical-vertical, VV)两种极化工作方式,因此这两种极化方式下直径为30.1 mm、长度为0.5 m的钢芯铝绞材质型特高压输电导线RCS的理论计算结果与微波暗室测量结果的对比分析如图 4所示.
|
图 4 直径为30.1 mm的特高压输电导线的RCS结果 Fig. 4 RCS results for ultra-high-voltage power transmission lines with a diameter of 30.1 mm |
从该图中可以看出,在HH极化和VV极化方式下,特高压输电导线RCS的理论计算值和实际测量值在靠近垂直入射方向上吻合得比较好.随着观测方向偏离垂直入射方向的角度越大,理论计算值与实际测量值之间的偏离也越大.这是由于在微波暗室中测试的特高压输电导线的长度有限,当偏离垂直入射方向的观测角度很大时,需要考虑输电导线两端部分的电磁散射场.另外,依据图 4可以测得HH极化方式下特高压输电导线RCS的理论计算值与实际测量值之间的平均误差为3.5%,VV极化方式下两者之间的平均误差为6.5%.由此可见,VV极化方式下的平均误差明显大于HH极化方式下的平均误差,这可能是由于分析中将表面有凹槽的螺旋缠绕输电导线近似为表面光滑圆柱体.
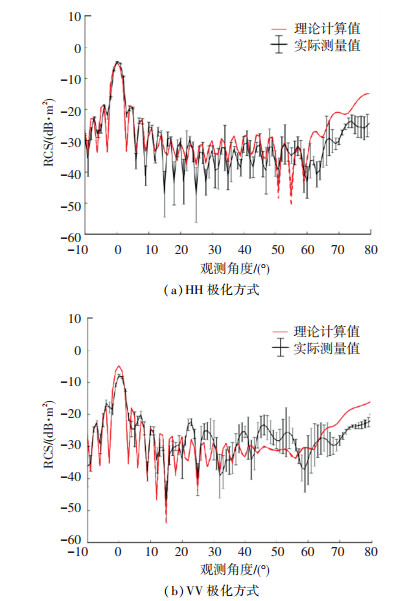
HH极化和VV极化方式下,直径为35.2 mm、长度为0.5 m的钢芯铝绞线材质型特高压输电导线RCS的理论计算结果与微波暗室测量结果的对比分析如图 5所示.
|
图 5 直径为35.2 mm的特高压输电导线的RCS结果 Fig. 5 RCS results for ultra-high-voltage power transmission lines with a diameter of 35.2 mm |
从图 5中可以看出,在HH极化和VV极化方式下,特高压输电导线RCS的理论计算值和实际测量值在靠近垂直入射方向上同样吻合得比较好.但随着观测方向偏离垂直入射方向的角度越大,理论计算值与实际测量值之间的偏离也同样会变得越大.另外,依据图 5可以测得HH极化方式下特高压输电导线RCS的理论计算值与实际测量值之间的平均误差为3.2%,VV极化方式下两者之间的平均误差为8.1%.由此可见,当特高压输电导线的直径发生变化时,VV极化方式下的平均误差还是明显大于HH极化方式下的平均误差.通过对比图 4和图 5,还可以发现不同直径的特高压输电导线在相同极化方式下具有不同的RCS值.这是因为波数与导线直径的乘积会影响特高压输电导线在X波段上的电磁散射特性.
3 结论1) 分析了特高压输电导线在高分TerraSAR-X卫星工作波段上的电磁散射特性,推导了输电导线的三维RCS表达式,并将其理论计算结果与微波暗室测量结果进行了对比分析.
2) 当输电导线的直径为30.1 mm时,HH极化方式下理论计算结果与实际测量结果之间的平均误差为3.5%,VV极化方式下该平均误差为6.5%.
3) 当输电导线的直径为35.2 mm时,HH极化方式下理论计算结果与实际测量结果之间的平均误差为3.2%,VV极化方式下该平均误差为8.1%.
4) 分析结果初步验证了所提出的特高压输电导线X波段电磁散射特性分析方法的正确性.接下来,一方面将在计算二维绕射系数中,综合考虑输电导线两端部分引起的电磁散射场以及输电导线的螺旋缠绕结构,进一步提高计算三维RCS的精度.另一方面,还需将所得到的三维RCS值结合到SAR回波信号相位历史构建中,以模拟TerraSAR-X卫星对特高压输电导线进行成像的回波信号,并利用对应的成像算法获得模拟SAR影像.
| [1] |
刘艳, 胡毅, 王力农, 等. 高分辨率SAR卫星监测特高压输电铁塔形变[J]. 高电压技术, 2009, 35(9): 2076. LIU Yan, HU Yi, WANG Linong, et al. Surveillance for 1000 kV transmission tower deformation using high-resolution SAR satellite[J]. High Voltage Engineering, 2009, 35(9): 2076. |
| [2] |
刘艳, 刘经南, 李陶, 等. 利用高分辨率SAR卫星监测灾害条件下电网铁塔形变[J]. 武汉大学学报(信息科学版), 2009, 34(11): 1354. LIU Yan, LIU Jingnan, LI Tao, et al. Monitoring damage of state grid transmission tower in bad weather by high-resolution SAR satellites[J]. Geomatics and Information Science of Wuhan University, 2009, 34(11): 1354. |
| [3] |
胡毅, 王力农, 刘凯, 等. 高分辨率SAR图像中特高压铁塔覆冰特性分析[J]. 高电压技术, 2010, 36(7): 1589. HU Yi, WANG Linong, LIU Kai, et al. Characteristics of icing UHV transmission tower in high-resolution SAR images[J]. High Voltage Engineering, 2010, 36(7): 1589. |
| [4] |
LIU Yan, HOU Ailing, LI Sha, et al. High voltage power line scattering feature analysis in multi SAR sensors and dual polarization[C]//Proceedings of the Second International Workshop on Earth Observation and Remote Sensing Applications. Piscataway, NJ: IEEE Press, 2012: 225
|
| [5] |
侯爱羚, 李陶, 李沙, 等. 高压输电线散射斑雷达像空间位置形成条件分析[J]. 测绘工程, 2015, 24(4): 53. HOU Ailing, LI Tao, LI Sha, et al. A study of high voltage power line scattering spot forming condition and spatial position[J]. Engineering of Surveying and Mapping, 2015, 24(4): 53. DOI:10.3969/j.issn.1006-7949.2015.04.012 |
| [6] |
李沙, 李陶, 王明洲, 等. 针对超高压输电导线的散射亮斑时间序列分析[J]. 测绘科学, 2015, 40(4): 126. LI Sha, LI Tao, WANG Mingzhou, et al. Analysis on scatterers time series of extra-high voltage power line[J]. Science of Surveying and Mapping, 2015, 40(4): 126. |
| [7] |
陈志国, 李陶, 张校志, 等. 雷达卫星影像中输电导线散射斑的相位时间序列稳定性分析[J]. 测绘工程, 2017, 26(4): 22. CHEN Zhiguo, LI Tao, ZHANG Xiaozhi, et al. Analysis on time series phase stability of power line scatterers in SAR images[J]. Engineering of Surveying and Mapping, 2017, 26(4): 22. |
| [8] |
ESSEN H, BOEHMSDORFF S, BIEGEL G, et al. On the scattering mechanism of power lines at millimeter-waves[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(9): 1895. DOI:10.1109/TGRS.2002.805144 |
| [9] |
SARABANDI K, PARK M. A radar cross-section model for power lines at millimeter-wave frequencies[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 51(9): 2353. |
| [10] |
HUANG Wei, YANG Xiaoliang, WEI Qingchun. The detection model analysis for power lines at millimeter-waves[C]//Proceedings of the 5th Global Symposium on Millimeter Waves. Piscataway, NJ: IEEE Press, 2012: 541
|
| [11] |
German Aerospace Center. TerraSAR-X—Germany's radar eye in space[EB/OL]. (2014-03-21)[2018-07-11]. http://www.dlr.de/dlr/en/desktopdefault.aspx/tabid-10377/
|
| [12] |
杨钰琦.粗糙面散射的BRDF方法研究[D].西安: 西安电子科技大学, 2012 YANG Yuqi. Study on electromagnetic scattering from rough surface based on BRDF[D]. Xi'an: Xidian University, 2012 http://cdmd.cnki.com.cn/Article/CDMD-10701-1013112740.htm |
| [13] |
张江华.高压输电线路弧垂在线监测研究[D].武汉: 华中科技大学, 2012 ZHANG Jianghua. Research on online monitoring of sag of HV power lines[D]. Wuhan: Huazhong University of Science and Technology, 2012 http://cdmd.cnki.com.cn/Article/CDMD-10487-1013013529.htm |
| [14] |
UFIMTSEV P Y. Fundamentals of the physical theory of diffraction[M]. Hoboken, NJ: Wiley, 2007.
|
| [15] |
RUCK G T, BARRICK D E, STUART W D, et al. Radar cross section handbook[M]. New York: Plenum Publishing Corporation, 1970.
|
| [16] |
BLUME S, KREBS V. Numerical evaluation of dynamic diffraction coefficients and bistatic radar cross sections for a perfectly conducting semi-infinite elliptic cone[J]. IEEE Transactions on Antennas and Propagation, 1998, 46(3): 414. DOI:10.1109/8.662661 |
| [17] |
MITZNER K M.Incremental length diffraction coefficients: No.AFAL-TR-73-296[R]. Falls Church, Virgina: Northrop Corporation Aircraft Division, 1974
|
 2020, Vol. 52
2020, Vol. 52


