由于永磁同步电机具有体积小、重量轻、高效率、高可靠性等优点,广泛应用于航空航天、风力发电、军事、轨道交通、电动汽车等重要领域[1-2].偏心故障是永磁同步电机的一种常见故障.这种故障通常是由不平衡负载、联轴器不对中、装配不当、转轴弯曲等因素引起的[3].偏心可以分为3类:静态偏心、动态偏心、混合偏心.早期的偏心故障对电机的性能影响不明显,但随着时间的推移,故障很可能会不断加重,发展成轴承故障、短路故障等更严重的故障[4-5],最终导致整个驱动系统失效,造成远大于电机本身价值的经济损失,甚至人员伤亡.
故障诊断是侦测偏心故障、识别故障参数的主要手段.多年来的事故统计表明,故障处理不及时是电机恶性事故的主要原因[6-7].实时性和可靠性是及时侦测出故障、避免电机事故的重要前提,对于故障诊断尤为重要.发现故障后,简单地让电机停机检修也会带来不小的损失.由于不同严重程度的故障对电机的影响有很大差异,因此针对不同严重程度的故障应该采取不同的应对措施.准确的故障诊断可以有效识别故障严重程度等参数,是根据故障具体情况合理安排运行策略和检修计划的重要基础.总的来说,实时、可靠、准确的偏心故障诊断方法对于减小偏心故障造成的损失,提高电机及驱动系统的可靠性意义重大.
近年来,研究者们针对偏心故障的诊断进行了大量的研究.文献[8-9]提出在停止的开关磁阻电机中注入信号,并利用绕组电流差值诊断偏心故障.该方法实现了对偏心类型、方向的诊断.文献[10-11]发现d轴电感会随偏心程度的增大而减小.在此基础上,他们提出了一种基于d轴电感监测的偏心故障离线诊断方法,并且实现了对偏心故障程度的诊断.
为了弥补离线诊断方法在实时性上的不足,科研人员对偏心故障在线诊断方法进行了研究.偏心故障会导致电机气隙不均匀,进而在电机电流、转矩、振动中产生特定的边频谐波[12].文献[13-16]提出利用这些边频谐波对偏心故障进行诊断;同时,还利用模糊支持向量机来进行分类[17].类似地,连续小波变换[18-19]、角域阶次跟踪法[20]等方法也被用于分析定子电流,并诊断偏心故障.然而,由于部分失磁故障往往也会产生类似的边频谐波,这些方法无法有效地区分这两种故障,难以可靠地诊断偏心故障[21].文献[22]提出了一种基于探测线圈的偏心故障诊断方法,由于探测线圈可以反映电机磁场的分布情况,该方法可以轻易地区分偏心故障和部分失磁故障,从而实现可靠的偏心故障诊断.然而,该方法没有深入研究偏心故障参数和故障特征之间的内在联系,不能识别偏心的方向、程度等参数.
针对现有方法难以实时诊断偏心故障参数问题,本文提出了一种实时、准确的新型偏心故障在线诊断方法.通过建立偏心故障下定子齿磁通的数学模型,分析了偏心故障及其各种参数和定子齿磁通时间、空间分布之间的定量关系.提出了基于定子齿磁通的偏心故障及其类型、方向、程度诊断方法.建立了场路结合的联合仿真模型,对诊断方法的性能进行了分析.还搭建了偏心故障实验平台,对诊断方法的有效性进行了验证.本文提出的方法是建立在文献[23]所述基于探测线圈的定子齿磁通实时测量装置的基础上的,文献[23]在该装置的基础上已经实现了灵敏、准确的匝间短路故障诊断,本文所述方法可以有效地扩展该装置的诊断范围,为最终实现基于该装置的永磁同步电机多故障综合诊断奠定了重要基础.
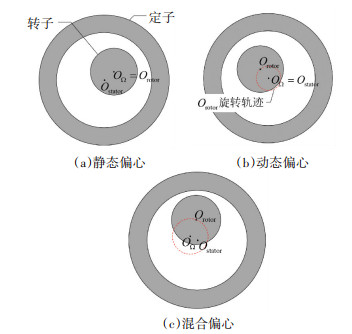
1 诊断原理如果电机的定子几何中心(Ostator)、转子几何中心(Orotor)、转子旋转中心(OΩ)不在同一位置,那么电机就发生了偏心故障.偏心故障可以分为3类:1)如果Orotor和OΩ同时偏离Ostator至同一位置,那么故障为静态偏心,此时气隙分布不随时间变化;2)如果Orotor偏离Ostator,而OΩ仍然和Ostator重合,那么故障为动态偏心,此时气隙分布的形状不变,但整体随转子同步旋转;3)如果Orotor和OΩ都偏离Ostator,但处于不同位置,那么故障为混合偏心,此时偏心的程度和方向都随时间变化.各类偏心故障示意图如图 1所示.偏心率的计算公式[22]为
| $ \mathit{\boldsymbol{E}} = \frac{\varepsilon }{{{l_{{\rm{g}}0}}}} = \frac{{{\varepsilon _{\rm{s}}} + \left| {{\varepsilon _{\rm{d}}}} \right|\angle \mathit{\Omega }t}}{{{l_{{\rm{g}}0}}}}, $ | (1) |
|
图 1 偏心故障示意图 Fig. 1 Diagram of eccentricity fault |
式中:ε为从Ostator到Orotor的矢量,lg0为正常情况下气隙长度,Ω为转子旋转的机械角速度,εs、εd分别为静、动态偏心对应的ε,εs、|εd|都是常数.
如果偏心类型是静态偏心,那么εs≠0, εd=0;如果偏心类型是动态偏心,那么εs=0, εd≠0;如果偏心类型是混合偏心,那么εs≠0, εd≠0.混合偏心可以分解为一个静态偏心和一个动态偏心.无论发生何种偏心,气隙分布的计算公式[16]为
| $ \begin{array}{l} {l_{{\rm{ge}}}}\left( \theta \right) = {r_{\rm{s}}} - {l_{{\rm{g0}}}}\left| \mathit{\boldsymbol{E}} \right|\cos \left( {\theta - \varphi } \right) - \\ \;\;\;\;\;\;\;\;\;\;\;\sqrt {r_{\rm{r}}^2 - {{\left| \mathit{\boldsymbol{E}} \right|}^2}l_{{\rm{g}}0}^2{{\sin }^2}\left( {\theta - \varphi } \right)} , \end{array} $ | (2) |
式中:θ为气隙对应的空间位置角,rs为定子内径,rr为转子外径,φ为E的方向角.
对于永磁同步电机而言,通常定子内径和转子外径远大于气隙长度,因此式(2)可以近似为
| $ \begin{array}{l} {l_{{\rm{ge}}}}\left( \theta \right) \approx {r_{\rm{s}}} - {l_{{\rm{g}}0}}\left| \mathit{\boldsymbol{E}} \right|\cos \left( {\theta - \varphi } \right) - {r_{\rm{r}}} = \\ \;\;\;\;\;\;\;\;\;\;\;{l_{{\rm{g}}0}} \cdot \left[ {1 - \left| \mathit{\boldsymbol{E}} \right|\cos \left( {\theta - \varphi } \right)} \right]. \end{array} $ | (3) |
对于定子齿磁通,其等效磁路由气隙和铁心组成,根据磁路的欧姆定律,其计算公式[22]为
| $ {\phi _{i{\rm{e}}}} = \frac{{{F_i}}}{{{R_{\rm{c}}} + \frac{{{l_{{\rm{g}}0}} \cdot \left[ {1 - \left| \mathit{\boldsymbol{E}} \right|\cos \left( {\frac{{2{\rm{ \mathsf{ π} }} \cdot (i - 1)}}{N} - \varphi } \right)} \right]}}{{{\mu _0} \cdot {A_{\rm{g}}}}}}}, $ | (4) |
式中:下标i为定子齿编号,i=1, 2, …, N (N为电机定子槽数),Fi为第i号齿对应的等效磁动势,Rc为第i号齿等效磁路对应的定转子铁心(包括永磁体)磁阻,μ0为真空磁导率,Ag为截面积,lg为气隙长度,θi为第i号齿的空间位置角(以1号齿位置为参考位置,即θ1=0).
显然,偏心故障会对定子齿磁通产生影响,并且这一影响和定子齿的位置(编号)和偏心率的大小、方向有关.定义各齿对应的故障特征量为
| $ \alpha \left( i \right) = \frac{{{\phi _{i{\rm{h}}}} - {\phi _{i{\rm{e}}}}}}{{{\phi _{i{\rm{e}}}}}}. $ | (5) |
电机正常时,ϕie=ϕih,fi(i)=0;偏心时故障特征α满足:
| $ \alpha \left( {i,t} \right) = \frac{{ - \left| {{\mathit{\boldsymbol{E}}_{\rm{d}}}\left( t \right)} \right|\cos \left( {\frac{{2{\rm{ \mathsf{ π} }} \cdot (i - 1)}}{N} - \mathit{\Omega }t} \right) - \left| {{\mathit{\boldsymbol{E}}_{\rm{s}}}} \right|\cos \left( {\frac{{2{\rm{ \mathsf{ π} }} \cdot (i - 1)}}{N} - {\varphi _{\rm{s}}}} \right)}}{{\beta + 1}}, $ | (6) |
式中β满足:
| $ \beta = \frac{{{R_{\rm{c}}}}}{{{{\left. {{R_\text{g}}} \right|}_{{l_\text{g}} = {l_{{\rm{g0}}}}}}}} = \frac{{{R_{\rm{c}}} \cdot {\mu _0} \cdot {A_\text{g}}}}{{{l_{\text{g}0}}}}. $ | (7) |
一方面,正常情况下的气隙磁阻(Rg|lg=lg0)是一个常数;另一方面,Rc主要由永磁体和隔磁桥的磁阻构成,也可以认为是一个常数.因此对于一个特定的电机而言,可以认为β是一个常数.
式(6)明,静态、动态、混合偏心时,α在空间上均呈正弦分布.静态偏心时,α不随时间变化,其幅值和偏心率的大小成正比,相位和偏心率方向(φs)有关;动态偏心时,α的分布以同步速度反向旋转,其幅值不随时间变化且和偏心率的大小成正比;混合偏心是静态偏心和动态偏心的叠加,α分布也是一个静止的正弦波和一个旋转的正弦波的叠加,其幅值和相位都随时间变化.
本节介绍了用于诊断偏心故障的故障特征量,其定义见式(5).理论分析表明该故障特征量可以反映偏心故障和偏心率.为了在实际应用中实现诊断,还需要对故障特征量的算法以及偏心故障的具体判定方法进行进一步的分析.
2 诊断的实施方法 2.1 定子齿磁通测量方法本节用一台16极18槽集中绕组永磁同步电机为例,详细介绍了偏心故障诊断的实施方法.本文提出故障特征量是由定子齿磁通计算得到,因此定子齿磁通的实时测量是诊断的前提.本文采用和文献[23]相同的装置测量定子齿磁通,该装置主要由安装在每个定子齿上的探测线圈、电压数据采集卡以及负责数据处理的PC机组成.数据采集卡采集得到的探测线圈感应电势通常都是有限时间长度内的离散信号,并且通常定子齿磁通中没有直流分量,因此定子齿磁通计算公式为
| $ \begin{array}{l} {\phi _i}(n) = \sum\limits_{m = 1}^n {\frac{{{u_{{\rm{c}}i}}\left( m \right)}}{{{N_{\rm{s}}}}}} \cdot \Delta t - \\ \;\;\;\;\;\;\;\;\;\frac{1}{{{n_T}}} \cdot \sum\limits_{n = 1}^{n = {n_T}} {\left[ {\sum\limits_{m = 1}^n {\frac{{{u_{{\rm{c}}i}}(m)}}{{{N_{\rm{s}}}}}} \cdot \Delta t} \right]} , \end{array} $ | (8) |
式中Δt为采样时间间隔,nT为一个周期内的采样次数.
利用FFT,可以求得一个周期内ϕi的基波相量
为了避免谐波和逆变器的干扰,只采用磁通基波分量进行计算.根据故障特征量的定义,被诊断电机对应的故障特征量计算公式为
| $ \alpha \left( i \right) = \frac{{{{\dot \phi }_{i{\rm{h}}}} - {{\dot \phi }_i}}}{{{{\dot \phi }_i}}}, $ | (9) |
式中:
根据样机本身具有的对称性,正常情况下,有
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot \phi }_i} = {{\dot \phi }_{i + 9}},}\\ {{{\dot F}_i} = {{\dot F}_{i + 9}}.} \end{array}} \right. $ | (10) |
如果电机发生偏心故障, 那么,第(i+9)号齿磁通可以表示为
| $ \begin{array}{l} {{\dot \phi }_{i + 9{\rm{e}}}} = \frac{{{{\dot F}_{i + 9}}}}{{{R_\text{c}} + \frac{{{l_{{\rm{g}}0}} \cdot \left[ {1 - \left| \mathit{\boldsymbol{E}} \right|\angle \left( {\frac{{2{\rm{ \mathsf{ π} }} \cdot \left( {i + 9 - 1} \right)}}{{18}} - \varphi } \right)} \right]}}{{{\mu _0} \cdot {A_{\rm{g}}}}}}} = \\ \;\;\;\;\;\;\;\;\;\;\frac{{{{\dot F}_{i + 9}}}}{{{R_{\rm{c}}} + \frac{{{l_{{\rm{g}}0}} \cdot \left[ {1 - \left| \mathit{\boldsymbol{E}} \right|\angle \left( {\frac{{2{\rm{ \mathsf{ π} }} \cdot \left( {i - 1} \right)}}{{18}} - \varphi } \right)} \right]}}{{{\mu _0} \cdot {A_{\rm{g}}}}}}}. \end{array} $ | (11) |
根据式(9)~(11),偏心故障下
| $ {{\dot \phi }_{i{\rm{h}}}} = \frac{2}{{\frac{1}{{{{\dot \phi }_i}}} + \frac{1}{{{{\dot \phi }_{i + 9}}}}}} = \frac{{2 \cdot {{\dot \phi }_i} \cdot {{\dot \phi }_{i + 9}}}}{{{{\dot \phi }_i} + {{\dot \phi }_{i + 9}}}}. $ | (12) |
显然,对于正常电机而言,上式仍然成立.将式(12)代入式(9),α可以按照下式计算:
| $ \alpha \left( i \right) = \frac{{\frac{{2{{\dot \phi }_i} \cdot {{\dot \phi }_{i + 9}}}}{{{{\dot \phi }_i} + {{\dot \phi }_{i + 9}}}} - {{\dot \phi }_i}}}{{{{\dot \phi }_i}}} = \frac{{{{\dot \phi }_{i + 9}} - {{\dot \phi }_i}}}{{{{\dot \phi }_i} + {{\dot \phi }_{i + 9}}}}. $ | (13) |
式中所有参数都可以通过测量得到,因此该算法可以用于实际诊断.
2.3 故障及其类型的诊断方法根据第1节的分析,α的分布情况可以反映偏心故障.对于正常电机而言,α=0;偏心故障时,α呈空间正弦分布;部分失磁故障会影响永磁体产生的磁动势,使式(10)不再成立,进而影响α的分布,不过部分失磁故障只会对失磁永磁体附近的定子齿磁通产生影响,α不呈正弦分布.综上,可以根据α的分布形状侦测偏心故障,并排除部分失磁故障对诊断的影响.
为了便于准确地诊断,采用离散傅里叶变换对α的空间分布特征进行量化,αk为α的第k次空间谐波.根据偏心故障时α的空间分布特征,如果故障特征量满足下式,那么可以判断电机存在偏心故障.
| $ \left\{ \begin{array}{l} \left| {{\alpha _1}} \right| > {T_1},\\ \gamma = \frac{{\sum\limits_{n = 2}^N {\alpha _n^2} }}{{\sum\limits_{n = 1}^N {\alpha _n^2} }} < {T_2}. \end{array} \right. $ | (14) |
式中:γ为除基波外其他谐波能量在αk中的占比; T1、T2为阈值,T1表示最小程度的偏心故障对α1的影响,T2表示偏心故障可能引起的γ的最大值,一般来说,两个阈值的取值为0 < T1 < 0.02,0 < T2 < 0.2,本文两个阈值的取值为T1=0.01,T2=0.1.
如果诊断出偏心故障,α1可以用于进一步的诊断.通过改变计算
根据对式(6)的分析,静态偏心时故障特征量静止不动;动态偏心时故障特征量的形状保持不变,但以同步速度反向旋转;混合偏心是静态、动态偏心的叠加.因此,偏心故障类型的判定方法可以总结为:1)如果α1(t)基本上不随时间变化,那么故障是静态偏心;2)如果α1(t)的幅值近似为一个常数,相位随时间以同步速度减小,那么故障是动态偏心;3)如果α1(t)的幅值随时间变化,那么故障是混合偏心.
2.4 故障程度和方向诊断方法偏心率的大小表示转子几何中心偏离定子几何中心的程度,可以用来表征故障严重程度;偏心率的方向表示转子几何中心偏离定子中心的方向,可以用来表征偏心方向.对于动态偏心(及混合偏心的动态部分),转子偏移方向是旋转的,识别这一参数的意义不大,在本文中不作诊断.
式(5)表明,β是计算偏心率的一个必要参数,可以通过有限元仿真获取,对于本文采用的样机, β=3.6.根据式(6),静态偏心时故障特征量的幅值和相位可以用来计算故障程度和方向.为了减小误差带来的影响,取一个周期内的平均值用来计算故障程度FS和故障方向FO,即
| $ {F_{\rm{S}}} = \frac{{\left( {1 + \beta } \right) \cdot \sum\limits_{n = 1}^{n = p \cdot {n_T}} {\left| {{\alpha _1}\left( n \right)} \right|} }}{{p \cdot {n_T}}}, $ | (15) |
| $ {F_{\rm{O}}} = {\rm{ \mathsf{ π} }} - \frac{{\sum\limits_{n = 1}^{n = p \cdot {n_T}} \angle {\alpha _1}\left( n \right)}}{{p \cdot {n_T}}}. $ | (16) |
动态偏心时对应的故障程度仍然可以按照式(15)计算,动态偏心的方向不作诊断.混合偏心是静态、动态偏心的结合.如果故障是混合偏心,可以按照下式将其分解为静态和动态部分,并分别按静态、动态偏心进行诊断.
| $ \left\{ {\begin{array}{*{20}{c}} {{\alpha _{1{\rm{s}}}}\left( t \right) = \sum\limits_{n = 1}^{n = p \cdot {n_T}} {{\alpha _1}} (n),}\\ {{\alpha _{1{\rm{r}}}}\left( t \right) = {\alpha _1}\left( t \right) - {\alpha _{1{\rm{s}}}}\left( t \right).} \end{array}} \right. $ | (17) |
式中α1s为α1的静态部分,α1r为α1的动态部分.
本节详细描述了实际应用时定子齿磁通的测量、故障特征量的计算、偏心故障及其类型、程度方向诊断的具体实施方法.除了常数β需要通过有限元仿真或实验计算,诊断所需的信号均由探测线圈实时测量得到.
3 仿真分析和性能评估为了对诊断方法的性能进行分析和评估,建立了电机及控制器的联合仿真模型[23].仿真中设置了和样机相同的探测线圈,本节利用仿真得出的感应电势信号对电机进行诊断,并对诊断结果进行详细的分析.
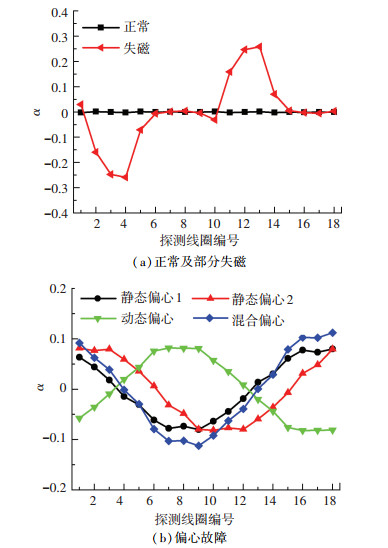
3.1 故障及其类型诊断分析不同状态下故障特征量α的空间分布如图 2所示,图中静态偏心1的偏心率为0.35∠150°,静态偏心2的偏心率为0.4∠150°,动态偏心的偏心率为0.4∠Ωt,混合偏心的偏心率为0.4∠180°+0.2∠Ωt.
|
图 2 故障特征量仿真结果 Fig. 2 Simulation results of the fault indicator |
图 2(a)展示了正常和部分失磁故障下的故障特征量α.根据α的定义,α反映的是和正常状态相比,各定子齿对应磁阻的相对变化情况;电机正常运行时,α应该等于0.从图 2(a)可以看出,电机正常时,所有定子齿对应的α都非常小,最大值仅为0.002左右,仿真结果和理论分析相符.部分失磁故障会影响永磁体产生的磁动势,进而影响α.图中失磁永磁体所在区域(2~5号齿)对应的α明显增大,最大值增至0.26左右.根据式(13),α(i)不仅和第i号齿有关,还和与其相隔180°的定子齿有关,因此和失磁永磁体相隔180°的区域(11~14号齿)对应的α也有所增大.部分失磁故障对α影响是局部性的,α不呈正弦分布.
图 2(b)展示了不同类型偏心故障下的故障特征量α,和正常情况相比,偏心时α明显增大,并且其空间分布近似为正弦.根据偏心率的设定值以及诊断时刻,根据式(6),理论上α的基波幅值的相位为:0.076∠30°(静态偏心1),0.087∠-20°(静态偏心2),0.087∠-140°(动态偏心),0.110∠25°(混合偏心).从图中可以直观看出,仿真结果和式(6)所得理论结果基本一致,说明式(13)所示α的算法是合理的.
总的来说,图 2所示仿真结果和理论分析相符,提出的故障特征量可以正确地反映偏心故障及其偏心率.对比图 2(a)和图 2(b)可以看出,偏心故障时α具有明显的特征,显著区别于正常、部分失磁故障下的α.
根据式(14),图 2所示各状态是否存在偏心故障的诊断结果见表 1.从表 1可以看出,所有诊断结果都和仿真设置一致,说明提出的偏心故障存在性诊断方法可以正确侦测出偏心故障.
| 表 1 故障存在性诊断结果 Tab. 1 Diagnosed results of fault existence |
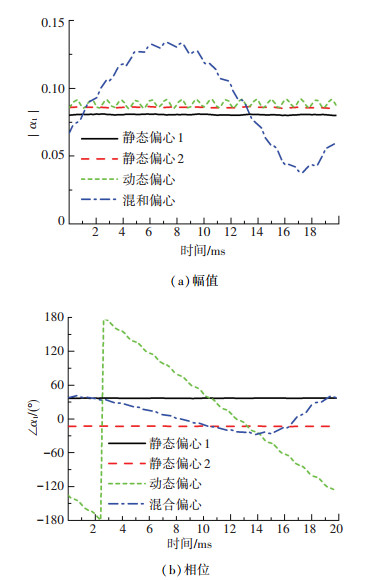
如果电机存在偏心故障,那么提出的方法将根据故障特征量基波随时间的变化情况来判断故障类型.对于图 2(b)中,不同类型的偏心故障,一个机械周期内故障特征量基波的幅值和相位如图 3所示.所有状态对应的转速都是3 000 r/min,机械周期为20 ms.
|
图 3 故障特征量基波随时间变化 Fig. 3 Variation of the fundament component of the fault indicator with time |
从图 3可以看出,静态偏心时,α1的幅值和相位都基本上是常数,它们的波动范围分别在0.002、1°以内,这是由于静态偏心时,气隙分布不随时间变化.动态偏心时,α1的幅值有一定的高频波动,波动的范围约为0.007以内,频率是机械频率的18倍,这一波动是由齿槽效应引起的.由于动态偏心时,偏心率的大小不随时间变化,偏心率的方向随转子同步旋转,因此α1的幅值总体趋势仍然不随时间变化,而α1的相位在一个机械周期内均速减小了360°.混合偏心时,α1的幅值除了有和动态偏心类似的高频波动外,还随时间以机械频率近似正弦波动,这是由于混合偏心时不同时刻的偏心率大小不同.类似地,混合偏心时α1的相位也出现明显的波动.
上述规律符合第2.3节中的分析,不同类型的偏心故障对应的α1有明显的区别,根据α1随时间的而变化情况,可以识别偏心故障的类型.
3.2 故障程度和方向诊断分析利用式(15)~(17)可以得到不同偏心故障对应的FS和FO见表 2,其中rS为FS的相对误差,rO为FO的误差.从表中可以看出,FS和FO都能正确地反映偏心率的大小和方向,所有FS的相对误差都在8%以内,所有FO的误差都在10°以内.此外,所有的FO都比∠E小7°左右,这是由于电机负载运行时定子齿磁通实际通过的气隙位置和定子齿中线位置有一定差异.总的来说,FS和FO的精度都能满足工程应用的需要,可以比较准确地反映偏心率,提出的方法可以正确诊断出偏心故障的程度和方向.
| 表 2 故障程度及方向诊断结果 Tab. 2 Diagnosed results of fault severity and orientation |
电机的工况会显著影响定子齿磁通,由于本文提出的方法是基于定子齿磁通的,因此有必要分析电机工况对诊断结果的影响.电机工况可以由两个参数表示:转速和定子电流.偏心故障是否存在以及偏心类型的诊断都是定性的,不易受电机工况影响,因此主要分析电机工况对故障程度和方向诊断影响.电机转速和定子电流变化对FS和FO的影响如图 4所示,图中所示故障参数为:E=0.4∠180°(静态偏心),|E|=0.4(动态偏心).

|
图 4 电机工况对诊断结果的影响 Fig. 4 Influence of operation conditions on diagnosis results |
从图 4(a)可以看出,FS基本上不受定子电流变化的影响,定子电流从0 A到280 A的过程中,FS的变化小于5%.定子电流对FO有一定的影响,当定子电流从50 A增大到280 A时,FO的误差从2.3°增大到了8.8°.这是因为定子电流会扭曲电机内部的磁场,使定子齿磁通不沿定子齿中线位置垂直通过气隙,电流越大磁场扭曲的程度越大,FO的误差也相应地越大.虽然如此,FO的误差始终保持在10°以内.从图 4(b)可以看出,转速对诊断结果没有明显的影响.转速从1 500 r/min增大到3 000 r/min的过程中,FS和FO的变化量都小于1%.
总的来说,本文提出的方法可以在不同电机工况下准确地诊断出偏心故障的程度和方向.
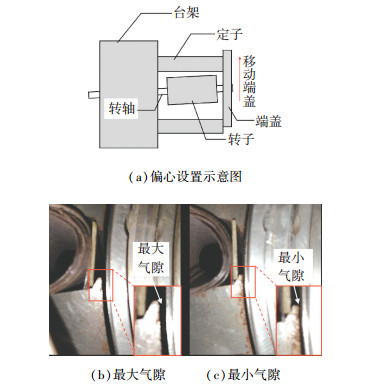
4 实验验证为了验证诊断方法的有效性,建立了一个电机故障实验平台[23],偏心故障是通过故意将电机后端盖偏移一定的位置得到的,如图 5(a)所示.设置偏心后电机最长和最短的气隙对比如图 5(b)、5(c)所示.由于无法弯曲实验电机的转轴,无法设置动态偏心和混和偏心,因此仅对静态偏心的诊断进行验证.设置好故障以后,使用铜制塞尺对各定子齿下的气隙长度进行测量,并根据测得的气隙长度确定偏心率E.
|
图 5 偏心实验设置 Fig. 5 Eccentricity experiment setting |
通过上述方法,分别设置了两个不同的静态偏心故障:0.35∠150°(偏心1)和0.4∠200°(偏心2),这两个故障的参数和图 2(b)中所示的两个静态偏心参数一致;此外,还设置了一组部分失磁故障以验证诊断方法区分部分失磁故障的能力,部分失磁故障的参数和图 2(a)一致.实验和仿真所得故障特征量对比如图 6所示.

|
图 6 故障特征量的实验和仿真结果对比 Fig. 6 Comparison of experimental and simulation results of the fault indicator |
从图 6可以看出,无论是正常,失磁还是偏心状态,故障特征量α的实验结果和仿真结果都基本一致,说明仿真分析是合理的,本文提出的方法可以正确诊断偏心故障,并有效区别部分失磁故障.
确认存在偏心故障以后,需要进一步识别偏心故障的类型及偏心率的大小和方向,这需要根据α1随时间的变化情况来判断.对于实验的两个故障,α1的幅值和相位随时间的变化如图 7所示.
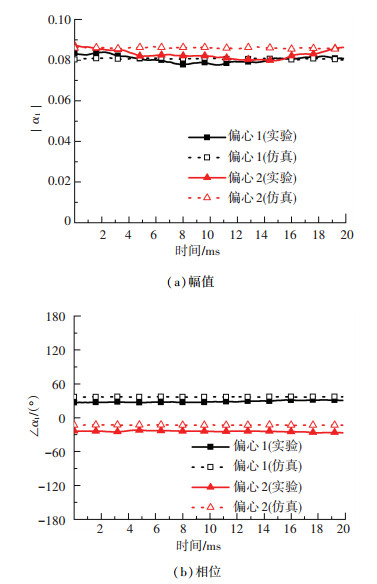
|
图 7 故障特征量基波实验结果 Fig. 7 Experimental results of the fundamental component of the fault indicator |
从图 7可以看出,实验时,α1的相位基本上不随时间变化,但幅值有一定的波动.出现这一现象的原因是实验时电机运行没有仿真时平稳.不过实验结果中α1的波动仍远小于其本身的大小,α1大体上仍不随时间变化.实验时α1的相位略小于仿真时的结果,这是由于实验和仿真时定子电流差异较大,电机内部磁场分布不同造成的.定子电流对诊断结果的影响已经在3.2中讨论,在此不再赘述.总的来说实验结果和仿真结果比较接近,它们都是合理的.
实验时,α1幅值和相位大体上都不随时间变化,由此可以诊断偏心类型为静态偏心.根据偏心故障程度、方向的诊断方法,可得不同工况下的诊断结果见表 3.
| 表 3 不同工况下偏心故障程度和方向的实验结果 Tab. 3 Experimental results of eccentricity fault severity and orientation under different operation conditions |
从表 3可以看出,在不同的转速、定子电流下,诊断结果FS、FO都和偏心率设定值非常接近. FS的相对误差始终保持在10%以内,FO的误差保持在4°以内,所有误差均在合理范围内.说明在不同工况下,诊断结果都可以比较准确地反映偏心故障的实际程度和方向.
上述实验结果和仿真结果基本吻合,说明仿真分析是正确的,本文提出的方法可以有效诊断偏心故障及其类型、方向、程度.
5 结论1) 提出了一种基于定子齿磁通的永磁同步电机偏心故障在线诊断方法,可以在电机运行过程中有效侦测偏心故障,并识别其类型、程度、方向,仿真和实验结果表明,偏心程度诊断结果的相对误差在10%以内,偏心方向的诊断结果误差在10°以内.
2) 该方法基本不受电机工况变化的影响,仿真和实验结果表明,不同工况下诊断结果均能保持在结论1)所述误差范围内.
3) 提出的诊断方法可以提供全面、准确的故障信息,这对于降低偏心故障带来的损失,提高电机维护的效率,提高电机及驱动系统的可靠性具有重要意义.提出的方法为最终实现以同一定子齿磁通实时测量装置为基础,实时、可靠、准确的永磁同步电机多故障综合诊断奠定了重要基础.目前,也在对基于该装置的永磁同步电机失磁故障诊断方法进行研究.由于齿磁通实时测量装置成本相对较高,主要适用于高价值、大功率、高可靠性要求的电机(如:风力发电、航空航天、军事领域的电机).
| [1] |
郝振洋, 胡育文. 电力作动器用高可靠性永磁容错电机控制系统的设计及其试验分析[J]. 航空学报, 2013, 34(1): 141. HAO Zhenyang, HU Yuwen. Design and experimental analysis on the control system of high reliability fault tolerant permanent magnet motor used in electric actuator[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(1): 141. |
| [2] |
郭磊磊.大功率永磁直驱风力发电系统驱动技术研究[D].合肥: 合肥工业大学, 2016 GUO Leilei. Research on drive control technologies of high-power permanent magnet direct-drive wind generation system[D]. Hefei: Hefei University of Technology, 2016 http://cdmd.cnki.com.cn/Article/CDMD-10359-1016270341.htm |
| [3] |
HUR J, REU J W, KIM B W, et al. Vibration reduction of IPM-type BLDC motor using negative third harmonic elimination method of air-gap flux density[J]. IEEE Transactions on Industry Applications, 2011, 47(3): 1300. DOI:10.1109/TIA.2011.2128850 |
| [4] |
GANDHI A, CORRIGAN T, PARSA L. Recent advances in modeling and online detection of stator interturn faults in electrical motors[J]. IEEE Transactions on Industrial Electronics, 2011, 58(5): 1564. DOI:10.1109/TIE.2010.2089937 |
| [5] |
PARK J K, HUR J. Detection of inter-turn and dynamic eccentricity faults using stator current frequency pattern in IPM-type BLDC motors[J]. IEEE Transactions on Industrial Electronics, 2016, 63(3): 1771. DOI:10.1109/TIE.2015.2499162 |
| [6] |
刘英斌. 电动机故障及处理方法[J]. 当代化工, 2010, 39(3): 329. LIU Yingbin. Motor faults and processing methods[J]. Contemporary Chemical Industry, 2010, 39(3): 329. DOI:10.3969/j.issn.1671-0460.2010.03.032 |
| [7] |
李辉. 电机故障在线诊断与预防性保护浅谈[J]. 电气传动自动化, 2010, 32(3): 58. LI Hui. Discussion for online diagnosis and preventive protection of motor faults[J]. Electric Drive Automation, 2010, 32(3): 58. DOI:10.3969/j.issn.1005-7277.2010.03.015 |
| [8] |
肖丽, 范书瑞, 刘卫朋, 等. 基于电流分析的四相开关磁阻电机气隙偏心故障综合检测方法[J]. 电工技术学报, 2015, 30(6): 122. XIAO Li, FAN Shurui, LIU Weipeng, et al. Fault detection method of air gap eccentricity for switched reluctance motors based on analysis of current[J]. Transactions of China Electrotechnical society, 2015, 30(6): 122. DOI:10.3969/j.issn.1000-6753.2015.06.016 |
| [9] |
肖丽, 范书瑞, 李洁, 等. 开关磁阻电机气隙偏心故障综合检测方法[J]. 电机与控制学报, 2015, 19(2): 66. XIAO Li, FAN Shurui, LI Jie, et al. Fault detection method of air gap eccentricity for switched reluctance motor based on analysis of current[J]. Electri c Machines and Control, 2015, 19(2): 66. |
| [10] |
HONG J, LEE S B, KRAL C, et al. Detection of airgap eccentricity for permanent magnet synchronous motors based on the d-Axis inductance[J]. IEEE Transactions on Power Electronics, 2012, 27(5): 2605. DOI:10.1109/TPEL.2011.2176145 |
| [11] |
HONG J, PARK S, HYUN D, et al. Detection and classification of rotor demagnetization and eccentricity faults for PM synchronous motors[J]. IEEE Transactions on Industry Applications, 2012, 48(3): 923. DOI:10.1109/TIA.2012.2191253 |
| [12] |
BRUZZESE C. Diagnosis of eccentric rotor in synchronous machines by analysis of split-phase currents: part Ⅱ experimental analysis[J]. IEEE Transactions on Industrial Electronics, 2014, 61(8): 4206. DOI:10.1109/TIE.2013.2284554 |
| [13] |
EBRAHIMI B M, FAIZ J. Magnetic field and vibration monitoring in permanent magnet synchronous motors under eccentricity fault[J]. IET Electric Power Applications, 2012, 6(1): 35. DOI:10.1049/iet-epa.2010.0159 |
| [14] |
EBRAHIMI B M, FAIZ J. Diagnosis and performance analysis of three-phase permanent magnet synchronous motors with static, dynamic and mixed eccentricity[J]. IET Electric Power Applications, 2010, 4(1): 53. DOI:10.1049/iet-epa.2008.0308 |
| [15] |
EBRAHIMI B M, FAIZ J, ARAABI B N. Pattern identification for eccentricity fault diagnosis in permanent magnet synchronous motors using stator current monitoring[J]. IET Electric Power Applications, 2010, 4(6): 418. DOI:10.1049/iet-epa.2009.0149 |
| [16] |
EBRAHIMI B M, FAIZ J, ROSHTKHARI M J. Static-, dynamic-, and mixed-eccentricity fault diagnoses in permanent-magnet synchronous motors[J]. IEEE Transactions on Industrial Electronics, 2009, 56(11): 4727. DOI:10.1109/TIE.2009.2029577 |
| [17] |
EBRAHIMI B M, ROSHTKHARI M J, FAIZ J, et al. Advanced eccentricity fault recognition in permanent magnet synchronous motors using stator current signature analysis[J]. IEEE Transactions on Industrial Electronics, 2014, 61(4): 2041. DOI:10.1109/TIE.2013.2263777 |
| [18] |
ROSERO J, ORTRGA J A, GACIA A, et al. On-line condition monitoring technique for PMSM operated with eccentricity[C]//IEEE International Symposium on Diagnostics for Electric Machines, Power Electronics and Drives. Cracow: IEEE Press, 2007: 95
|
| [19] |
ROSERO J, ROMERAL L, ROSERO E, et al. Fault detection in dynamic conditions by means of discrete wavelet decomposition for PMSM running under bearing damage[C]//24th Annual IEEE Applied Power Electronics Conference and Exposition. Washington DC: IEEE Press, 2009: 951
|
| [20] |
EKER M, AKAR M. Eccentricity fault diagnosis in a permanent magnet synchronous motor under nonstationary speed conditions[J]. Turkish Journal of Electrical Engineering and Computer Sciences, 2017, 25(3): 1881. |
| [21] |
GOKTAS T, ZAFARANI M, AKIN B. Discernment of broken magnet and static eccentricity faults in permanent magnet synchronous motors[J]. IEEE Transactions on Energy Conversion, 2016, 31(2): 585. |
| [22] |
DA Yao, SHI Xiaodong, KRISHNAMURTHY M. A new approach to fault diagnostics for permanent magnet synchronous machines using electromagnetic signature analysis[J]. IEEE Transactions on Power Electronics, 2013, 28(8): 4104. DOI:10.1109/TPEL.2012.2227808 |
| [23] |
ZENG Chong, HUANG Song, YANG Yongming, et al. Inter-turn fault diagnosis of permanent magnet synchronous machine based on tooth magnetic flux analysis[J]. IET Electric Power Applications, 2018, 12(6): 837. DOI:10.1049/iet-epa.2017.0865 |
 2020, Vol. 52
2020, Vol. 52


