陀螺飞轮是一种适用于微小航天器的新型姿态控制与测量装置,它迎合了微小航天器轻质、低功耗、高功能密度的需求[1].为了同时实现姿态测量与控制,陀螺飞轮的转子需要进行较大范围的倾侧(±4°)和调速(调谐转速的±15%),相比于结构类似的动力调谐陀螺仪,它的姿态测量原理更为复杂[2].为了保证陀螺飞轮的姿态测量精度,需要通过标定实验对系统机械参数和确定性漂移进行辨识[3].然而,由于存在不可避免的加工装配误差,陀螺飞轮的特殊工作状态使得系统中产生多种频率成分的高频振荡力矩[1],同时,机械和电路部分的非稳定性会引入随机噪声.标定实验中所需要的有用信号淹没在这些噪声中,因此必须对采集信号进行有效的去噪处理.
当信号是平稳的且其频谱与噪声不重叠时,基于傅里叶变换的传统去噪方法是有效的.然而,陀螺仪的输出信号通常是弱非平稳的,并且受多种不确定因素的影响,信号与噪声频谱往往重叠,传统方法难以获得所需的去噪效果[4].维纳滤波是现代滤波理论的代表,但它本质上是一种线性方法,仅适用于平稳信号,且需要信号和噪声的先验知识[5],也不适用于陀螺飞轮系统.小波变换作为一种非平稳信号分析与处理工具,在信号去噪方面得到广泛应用[6].但小波去噪的效果严重依赖于小波基、分解尺度的选取,缺乏自适应性,如果选取不当,会出现去噪效果不理想或信号失真的现象[7].经验模态分解(EMD)是一种适用于非平稳信号处理的新方法,它是一种完全数据驱动的算法,能够自适应地将信号分解为一组本征模态函数(IMF)[8],它克服了小波变换基函数固定的缺点,因此被广泛应用于信号去噪领域.
EMD去噪的基本思想是选择部分IMF对信号有用成分进行重构.文献[9]针对白噪声研究了其统计特性,并给出了基于能量密度的模态判定方法.文献[10-11]分别根据相关系数和连续均方误差对相关模态进行了判定,但在信噪比较低的情况下效果不理想.文献[12-13]通过比较信号和各IMF的概率密度函数对模态进行判定,但对原理的解释不够充分.上述方法将噪声相关模态完全舍弃,是强制去噪方法,容易导致信号的变形.受到小波阈值方法的启发,文献[14]研究了基于EMD的阈值去噪方法,文献[15-16]分别将阈值方法应用于激光陀螺和光纤陀螺并得到了满意的降噪效果.
由于陀螺飞轮信号中除随机噪声外还含有大量高频周期噪声,使得上述针对白噪声或有色噪声的研究成果不再适用,EMD去噪方法无法直接应用于陀螺飞轮系统.因此本文针对信号特性,提出了一种混合去噪方法.该方法在不影响信号低频特性的前提下对高频周期噪声进行抑制,然后针对预处理后的信号特性,给出了有效的模态判定准则,并对噪声主导模态进行了阈值处理,以获得满意的去噪效果.
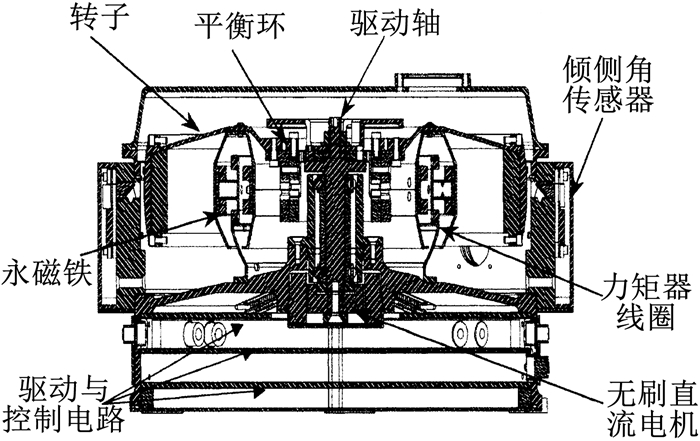
1 陀螺飞轮信号特性分析 1.1 陀螺飞轮系统概述陀螺飞轮的机械结构与动力调谐陀螺仪类似,因此具有两轴姿态测量功能,其基本结构如图 1所示[1].与动调陀螺不同的是,为了同时输出三轴姿态控制力矩,陀螺飞轮需要长期工作于转子倾侧和非调谐状态.陀螺飞轮系统工作于闭环状态,通过测量力矩器线圈中的反馈电流,可以间接获得载体运动角速度的大小.
|
图 1 陀螺飞轮系统结构示意 Fig. 1 Cross-sectional view of the gyrowheel system |
为了保证陀螺飞轮的姿态测量精度,需要进行标定实验,以实现对系统机械参数、误差系数的辨识.参数辨识精度依赖于采集的力矩器电流信号的精度,因此需要针对电流信号特性,研究有效的信号去噪方法.
1.2 信号噪声特性分析为了兼顾姿态测量和控制力矩输出,陀螺飞轮需要长期工作于转子倾侧和非调谐状态.当转子自转轴与驱动轴不重合时,平衡环一边随驱动轴高速旋转,一边相对驱动轴作扭摆运动,这种复合运动会引起2倍于陀螺转子旋转频率的周期振荡力矩,称为二次谐波力矩[1].由于受到加工制造工艺水平的制约,实际的陀螺飞轮样机中不可避免地存在加工装配误差,如转子质心偏移、支撑结构不垂直、不共面等.这些机械不理想因素会引起作用于转子的干扰力矩,其直流成分会引起漂移误差,需要通过标定实验对误差系数进行辨识与补偿.此外,干扰力矩中还包含多种谐波成分,如一次谐波力矩、三次谐波力矩、五次谐波力矩等.驱动电机磁钢的分布特性会引起十一次谐波力矩.这些谐波力矩作用于转子上,从而力矩器的反馈电流中也包含相同的谐波成分,它们可视为高频噪声.
另外,陀螺飞轮机械部分和电路部分的非稳定性,如轴承的随机跳动、电路热噪声,以及量化噪声等因素使得测量信号中包含随机噪声,与高频噪声相比,随机噪声虽然相对较小,但其影响也不容忽视.
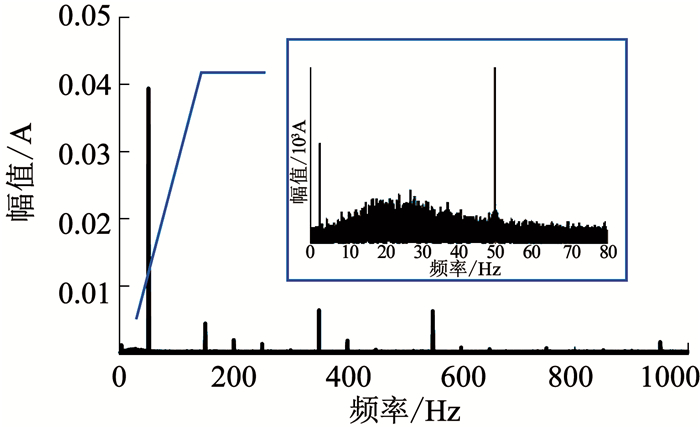
图 2给出了实测力矩器电流信号的频谱分析结果,数据采集过程中,陀螺飞轮样机固定于水平地面上,转子保持倾侧0.5°,转子旋转频率为50 Hz,采样频率2 000 Hz.与上述分析一致,实测信号中包含多次谐波噪声和随机噪声,信号的有用成分淹没在噪声中.
|
图 2 电流信号频谱分析结果 Fig. 2 Frequency spectrum of current signals |
对于任意给定信号,经验模态分解(EMD)通过筛选过程可自适应地将其分解为一系列本征模态函数(IMF)[8].
2.1 本征模态函数IMF必须满足如下两个条件[8]:
1) 零点数和极值点数相等或至多相差一个;
2) 函数由局部极大值点确定的包络线和由局部极小值点确定的包络线的均值为零.
2.2 筛选过程对于给定信号x(t),筛选过程可总结如下[8].
步骤1 初始化.设定筛选门限ε,i=1,j=0,令ri-1(t)=x(t).
步骤2 循环筛选获得第i个IMF,具体过程如下:
1) 初始化,令hi, j(t)=ri-1(t);
2) 利用三次样条插值分别对hi, j(t)的极大值点和极小值点进行拟合,构造上、下包络线Ui, j(t)和Li, j(t);
3) 计算包络均值
4) 更新hi, j+1(t)=hi, j(t)-mi, j(t);
5) 根据下式计算停止条件:
| $ \mathrm{SD}_{i, j+1}=\sum\limits_{t=0}^{(N-1) t_{\mathrm{s}}} \frac{\left|h_{i, j+1}(t)-h_{i, j}(t)\right|^{2}}{h_{i, j}^{2}(t)}. $ |
式中:N为信号长度,ts为采样周期;判断SDi, j+1是否不大于给定的门限ε,通常ε的取值为0.2~0.3,若不大于ε,则得到第i个IMF,记为ci(t)=hi, j+1(t);否则,令j=j+1,转到2).
步骤3 计算余量ri(t)=ri-1(t)-ci(t),如果余量是单调函数或常量,则整个分解过程结束;否则令i=i+1,转到步骤2.
经过上述步骤后,EMD将信号x(t)分解为n个模态和1个余量之和,即
| $x(t)=\sum\limits_{i=1}^{n} c_{i}(t)+r_{n}(t), $ |
式中c1(t), …, cn(t)分别包含了信号从高到低不同频段的成分,并且任一阶IMF的平均周期大约为前一阶IMF平均周期的2倍.因此,可以根据信号特性,合理地利用部分IMF分量重构信号,以达到信号去噪的目的.
3 EMD/LPF混合去噪方法考虑到陀螺飞轮的姿态测量带宽[1],在辨识标定实验中,力矩器电流信号的有用成分集中在低频段,通常不超过0.5 Hz.信号噪声特性分析中的分析结果表明,电流信号中包含高频的谐波噪声和分布于整个频段内的随机噪声.
3.1 基于低通滤波的信号预处理与信号的有用低频成分和随机噪声相比,信号中的高频谐波噪声十分明显.陀螺飞轮系统的转子旋转频率在50~65 Hz范围内,因此,信号的有用成分与高频谐波噪声分布在不同的频段.在不影响信号低频特性的前提下,对信号进行预处理以减小高频谐波噪声的影响,能够提高EMD的有效性和效率.
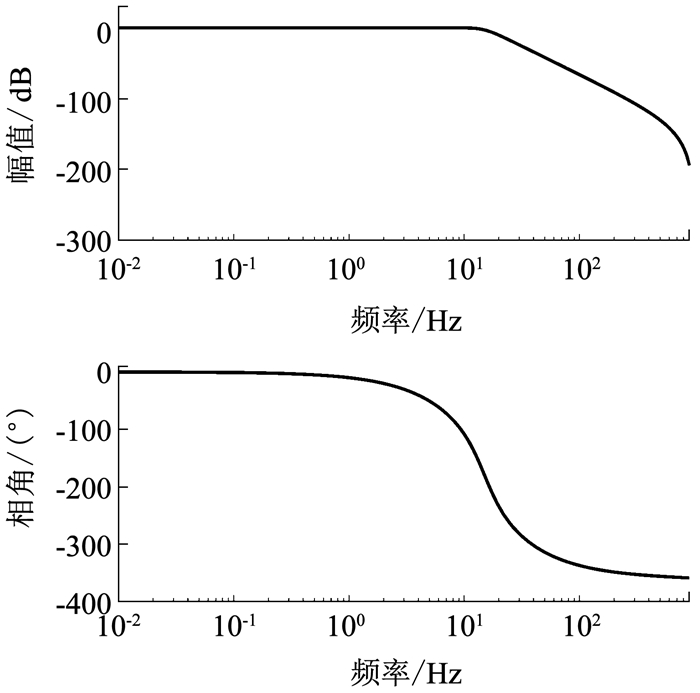
考虑到巴特沃斯滤波器具有通频带内频率响应曲线最大限度平坦的特点,设计四阶低通巴特沃斯数字滤波器对电流信号进行预处理,截止频率为15 Hz,其频率响应如图 3所示.显然,该低通滤波器(LPF)几乎不会影响信号的有用低频成分.
|
图 3 低通滤波器的频率响应 Fig. 3 Frequency response of the LPF |
利用低通滤波器对原始信号x(t)进行处理后,信号中的高频谐波成分得到了有效地抑制,滤波后的信号
定义ns为噪声主导模态与有用信号模态的分界,所有IMF可以分为:只包含噪声的第1阶IMFc1(t),噪声主导的模态分量c2(t), …, cns-1(t)和信号模态分量cns(t), …, cn(t).直接利用信号IMF分量重构原信号可达到去噪的目的,但这种强制去噪方法会损失存在于噪声主导IMF分量中的有用信息.为了保证信号去噪效果,本文对这些IMF分量进行阈值处理,以保留其中的有用信息,其中阈值函数的具体形式可参照文献[14].
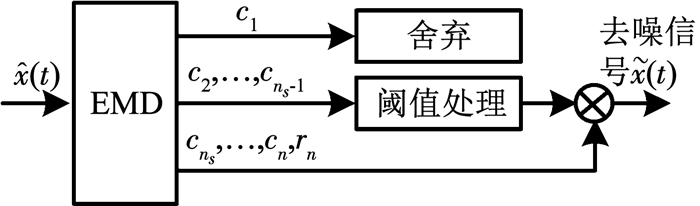
基于EMD的信号去噪原理如图 4所示.
|
图 4 基于EMD的信号去噪原理 Fig. 4 Schematic of the EMD-based denoising method |
利用图 4所示方法进行信号重构,可得到去噪之后的信号为
| $ \tilde{x}(t)=\sum\limits_{i=2}^{n_{s}-1} \bar{c}_{i}(t)+\sum\limits_{i=n_{s}}^{n} c_{i}(t)+r_{n}, $ | (1) |
式中ci(t)为经过阈值处理后的第i阶IMFci(t).
3.3 基于PDF-BD的模态分界点判定准则应用上述方法实现信号去噪的关键在于确定噪声主导模态与信号模态的分界点ns.
对于含噪信号来说,进行EMD分解后,前ns-1阶IMF为噪声主导模态,各阶IMF包含的噪声信息越来越少,直至第ns阶IMF可认为几乎不包含噪声信息,成为信号模态分量.因此,比较含噪信号及其各阶IMF的概率密度函数(PDF),噪声主导模态与原信号PDF的差异会随着阶数的增加而变大,而在第1个信号模态处(即第ns阶IMF处),这一差异会显著变小,从而在第ns-1阶处出现局部极大值.基于这一特性,本文通过对含噪信号和各阶IMF的PDF进行相似性度量,来确定模态分界点ns.基于核密度估计方法可以获得信号和各阶IMF的PDF,该方法是一种非参数检验方法,它无需有关数据分布的先验知识,对数据分布不附加任何假定[17].
在统计学中,巴氏距离(Bhattacharyya distance,BD)可以用于度量两个概率分布的相似性[18].对于两个概率分布p1, p2,它们之间的巴氏距离定义为[18]
| $ D_{\mathrm{B}}\left(p_{1}, p_{2}\right)=-\ln \left(c_{\mathrm{B}}\left(p_{1}, p_{2}\right)\right), $ | (2) |
其中cB(p1, p2)为Bhattacharyya系数,定义为
| $ c_{\mathrm{B}}\left(p_{1}, p_{2}\right)=\int\limits_{x \in X} \sqrt{p_{1}(x) p_{2}(x)} \mathrm{d} x. $ | (3) |
对于两个高斯分布,pi=N(μi, σi2),i=1, 2,巴氏距离可表示为[18]
| $D_{\mathrm{B}}\left(p_{1}, p_{2}\right)=\frac{1}{8}\frac{{{{\left( {{\mu _1} - {\mu _2}} \right)}^2}}}{\sigma } + \frac{1}{2} \ln \left(\frac{\sigma^{2}}{\sigma_{1} \sigma_{2}}\right), $ | (4) |
其中
| $ \sigma^{2}=\frac{\sigma_{1}^{2}+\sigma_{2}^{2}}{2}. $ | (5) |
计算含噪信号与其各阶IMF的PDF的巴氏距离,并绘制巴氏距离关于IMF阶数的折线图,找到第1个局部极大值点对应的阶数nlm1,则模态分界点可表示为
| $n_{s}=n_{\mathrm{lm1}}+1. $ | (6) |
本文提出的基于EMD/LPF的混合去噪方法的具体步骤可以描述如下.
步骤1 设计截止频率为15 Hz的四阶巴特沃斯低通滤波器,对采集的原始电流信号x(t)进行低通滤波,以抑制高频谐波噪声的影响,得到预处理后的信号
步骤2 对含噪信号
步骤3 采用核密度估计方法估计信号
步骤4 根据式(2)~式(5)计算信号PDF和各阶IMF的PDF的巴氏距离,绘制巴氏距离关于IMF阶数的折线图,根据式(6)确定模态分界点ns.
步骤5 舍弃噪声模态分量c1(t),对分量c2(t), …, cns-1(t)进行阈值处理,利用式(1)重构信号,实现对陀螺飞轮原始电流信号的去噪.
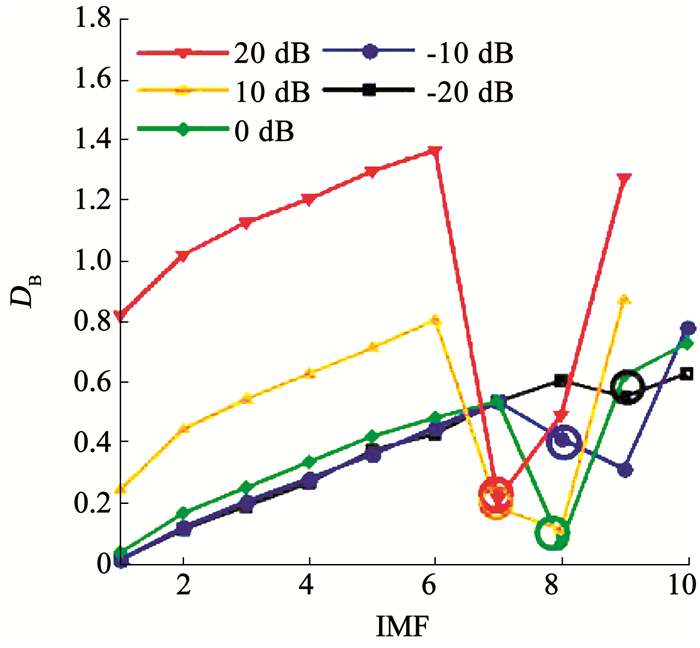
4 实验验证及结果分析 4.1 仿真实验及结果分析 4.1.1 模态分界点判定方法验证以简单的正弦信号作为真实信号,添加不同强度的高斯白噪声作为含噪信号进行仿真实验,将PDF-BD方法确定的分界点结果与真实值进行对比,以验证该方法在不同信噪比(SNR)条件下的有效性,结果见表 1和图 5.
| 表 1 不同信噪比下的分界点判定结果 Tab. 1 Results under different SNR conditions |
|
图 5 巴氏距离与IMF阶数的关系曲线 Fig. 5 Bhattacharyya distance versus IMF index |
表 1和图 5的结果表明,即使在低信噪比情况下,有用信号的能量很低,本文所提出的PDF-BD方法仍然能够实现模态分界点的准确判定.
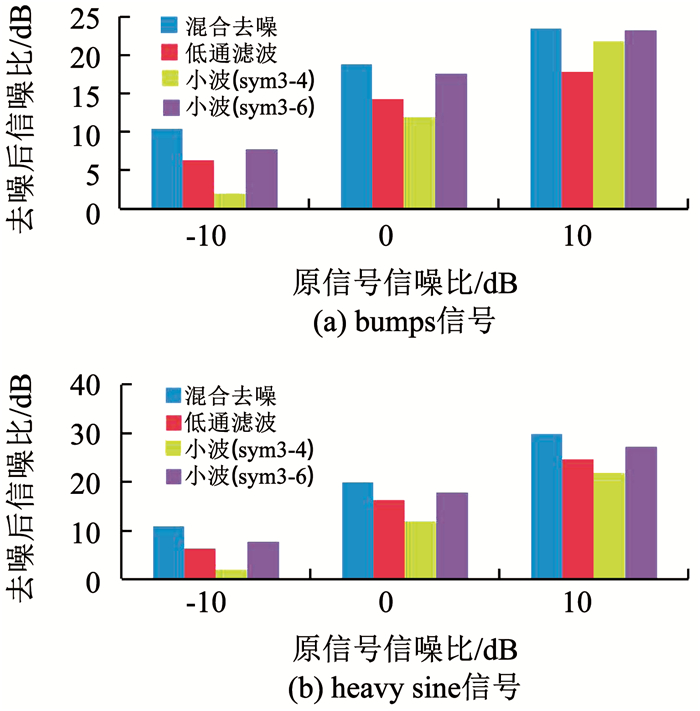
4.1.2 EMD/LPF混合去噪方法验证采用标准测试信号bumps、heavy sine作为真实信号[11, 14],添加不同强度的高斯白噪声,并叠加频率为60 Hz和120 Hz的高频周期噪声,形成含噪信号.分别利用传统低通滤波方法(截止频率2 Hz),小波去噪方法(小波基选择sym3,分解层次4层和6层),EMD/LPF混合去噪方法对含噪信号进行处理.不同方法的去噪效果对比由图 6给出,图 7给出输入信噪比0 dB条件下的信号曲线,其中输入信噪比计算时,噪声能量只考虑白噪声.为了更清晰地展示去噪结果,图 7中未绘制效果较差的sym3-4小波去噪结果.
|
图 6 去噪效果对比 Fig. 6 Performance comparison of different methods |
|
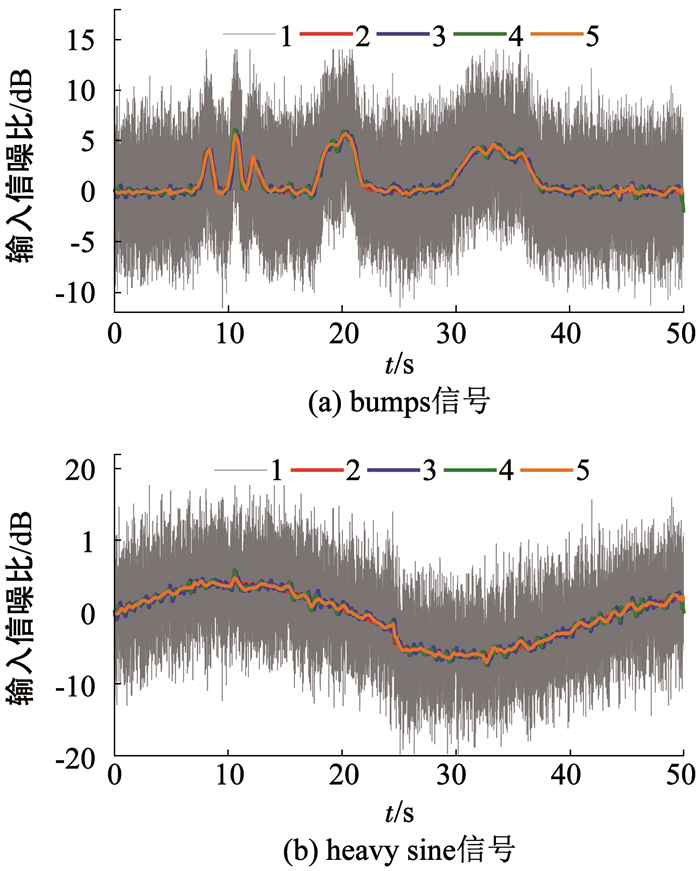
1.原始含噪信号; 2.真实信号; 3.低通滤波结果; 4.sym3-6小波去噪结果; 5.EMD/LPF混合去噪结果 图 7 bumps和heavy sine信号的去噪结果 Fig. 7 Denoising results for bumps and heavy sine |
由图 6、7可见,传统低通滤波方法可以实现对高频周期噪声的滤除,但无法抑制频谱与有用信号重叠的随机噪声,而且,传统滤波方法不可避免会带来相位延迟问题,无法满足陀螺飞轮系统的标定实验要求.而小波去噪效果受到选择的小波基和分解层次的影响,不具有自适应性,如果选择不合理,去噪效果很不理想(如-10 dB条件下采用sym3小波基,4层分解).相比于其他方法,基于EMD/LPF的混合去噪方法在不同信噪比条件下对不同信号都有更为理想的去噪效果.
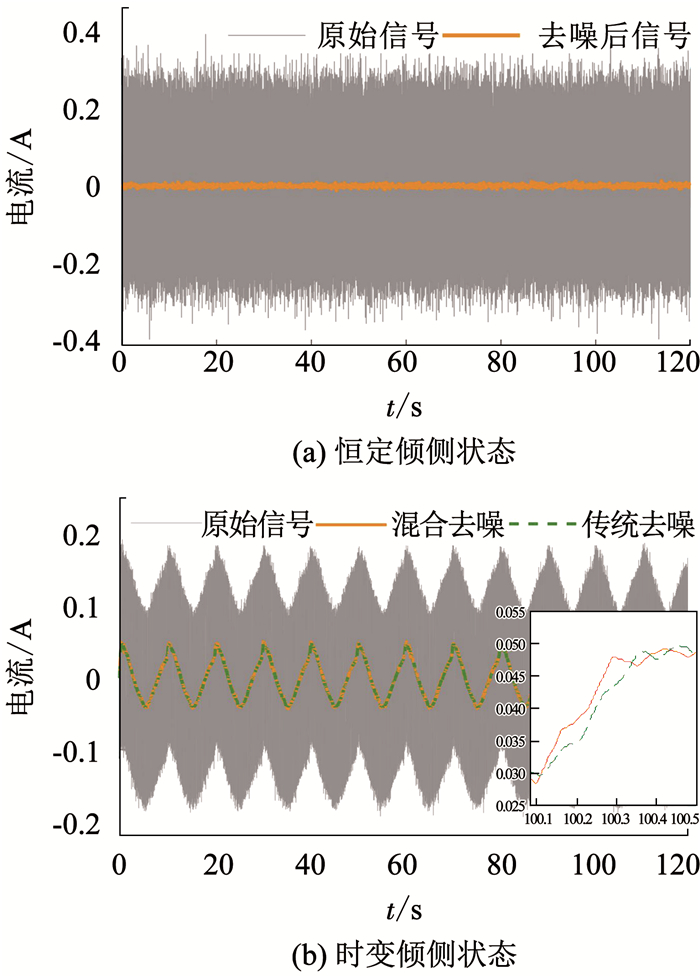
4.2 样机实验及结果分析陀螺飞轮样机如图 8所示,采用本文提出的EMD/LPF混合去噪方法,对采集的力矩器电流数据进行处理.以两种实验条件为例:1)系统工作于恒定倾侧状态下,转子旋转频率为62.5 Hz;2)系统工作于时变倾侧状态下,转子旋转频率为58.3 Hz;图 9给出这两种实验条件下的信号去噪结果.

|
图 8 陀螺飞轮实验样机 Fig. 8 Gyrowheel prototype |
|
图 9 电流信号去噪结果 Fig. 9 Denoising results for current signals |
去噪前后,恒定倾侧状态下的电流信号标准差由0.112 A降为0.003 A,降低了数十倍.为了更好地体现混合去噪方法的优越性,在时变倾侧状态下,将传统低通滤波结果与混合去噪结果一同绘制于图 9(b)中,并对曲线进行部分放大,可以看出,传统方法具有明显的相位延迟问题.实验结果表明混合去噪方法能够有效地抑制陀螺飞轮采集信号的噪声,这对陀螺飞轮系统实现参数辨识具有重要意义.
5 结论1) 根据EMD分解后各阶IMF中包含信号/噪声信息的特点,提出了一种基于PDF-BD的模态分界点判定准则,即使在低信噪比条件下,该方法仍然能够实现分界点的准确判定.
2) 针对陀螺飞轮采集信号的噪声特性,将EMD与LPF进行有效地结合来充分发挥二者的优点,提出了EMD/LPF混合去噪方法,实现了对高频周期噪声和随机噪声的有效抑制.
3) 混合去噪方法在高信噪比和低信噪比条件下都具有稳定的去噪效果,比小波去噪方法更具有自适应性.该方法不仅适用于陀螺飞轮系统,也可以应用于其他高速旋转机械系统的信号去噪中.
| [1] |
OWER J C. Analysis and control system design of an innovative tuned-rotor instrument[D]. Ottawa, Ontario: Carleton University, 2000
|
| [2] |
ZHAO Yuyu, ZHAO Hui, HUO Xin, et al. Angular rate sensing with Gyrowheel using genetic algorithm optimized neural networks[J]. Sensors, 2017, 17(7): 1692. DOI:10.3390/s17071692 |
| [3] |
ZHAO Yuyu, ZHAO Hui, HUO Xin. A new multi-position calibration method for the gyrowheel using multiple objective particle swarm optimization algorithm[C]//Proceedings of the AIAA Guidance, Navigation, and Control Conference. Grapevine: AIAA, 2017. DOI: 10.2514/6.2017-1906
|
| [4] |
LI Qian, XU Guoping, TIAN Weifeng, et al. A novel hybrid EMD-based drift denoising method for a dynamically tuned gyroscope[J]. Measurement, 2009, 42(6): 927. DOI:10.1016/j.measurement.2009.01.017 |
| [5] |
王婷. EMD算法研究及其在信号去噪中的应用[D].哈尔滨: 哈尔滨工程大学, 2010 WANG Ting. Research on EMD algorithm and its application in signal denoising[D]. Harbin: Harbin Engineering University, 2010 |
| [6] |
DONOHO D L, JOHNSTONE I M. Threshold selection for wavelet shrinkage of noisy data[C]//Proceedings of 16th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Baltimore, MD: IEEE, 2002. DOI: 10.1109/iembs.1994.412133
|
| [7] |
于金涛, 赵树延, 王祁. 基于经验模态分解和小波变换声发射信号去噪[J]. 哈尔滨工业大学学报, 2011, 43(10): 88. YU Jintao, ZHAO Shuyan, WANG Qi. De-noising of acoustic emission signals based on empirical mode decomposition and wavelet transform[J]. Journal of Harbin Institute of Technology, 2011, 43(10): 88. |
| [8] |
HUANG N E, SHEN Zheng, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London A, 1998, 454(1971): 903. DOI:10.1098/rspa.1998.0193 |
| [9] |
WU Zhaohua, HUANG N E. A study of the characteristics of white noise using the empirical mode decomposition method[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2004, 460(2046): 1597. DOI:10.1098/rspa.2003.1221 |
| [10] |
AYENU-PRAH A, ATTOH-OKINE N. A criterion for selecting relevant intrinsic mode functions in empirical mode decomposition[J]. Advances in Adaptive Data Analysis, 2010, 2(1): 1. DOI:10.1142/s1793536910000367 |
| [11] |
BOUDRAA A O, CEXUS J C. EMD-based signal filtering[J]. IEEE Transactions on Instrumentation and Measurement, 2007, 56(6): 2196. DOI:10.1109/tim.2007.907967 |
| [12] |
KOMATY A, BOUDRAA A O, AUGIER B, et al. EMD-based filtering using similarity measure between probability density functions of IMFs[J]. IEEE Transactions on Instrumentation and Measurement, 2014, 63(1): 27. DOI:10.1109/tim.2013.2275243 |
| [13] |
李宇寰, 杨功流, 刘元元. 基于l2范数的EMD滤波方法在光纤陀螺信号中的应用[J]. 中国惯性技术学报, 2017, 25(2): 244. LI Yuhuan, YANG Gongliu, LIU Yuanyuan. Application of EMD filtering based on l2-norm in denoising FOG signal[J]. Journal of Chinese Inertial Technology, 2017, 25(2): 244. DOI:10.13695/j.cnki.12-1222/o3.2017.02.020 |
| [14] |
KOPSINIS Y, MCLAUGHLIN S. Development of EMD-based denoising methods inspired by wavelet thresholding[J]. IEEE Transactions on Signal Processing, 2009, 57(4): 1351. DOI:10.1109/tsp.2009.2013885 |
| [15] |
曲从善, 于鸿, 许化龙, 等. 基于经验模态分解的激光陀螺随机信号消噪[J]. 红外与激光工程, 2009, 38(5): 859. QU Congshan, YU Hong, XU Hualong, et al. Random signal de-noising based on empirical mode decomposition for laser gyro[J]. Infrared and Laser Engineering, 2009, 38(5): 859. DOI:10.3969/j.issn.1007-2276.2009.05.022 |
| [16] |
崔冰波, 陈熙源, 宋锐. EMD阈值滤波在光纤陀螺漂移信号去噪中的应用[J]. 光学学报, 2015, 35(2): 0207001. CUI Bingbo, CHEN Xiyuan, SONG Rui. Application of EMD threshold filtering for fiber optical gyro drift signal de-noising[J]. Acta Optica Sinica, 2015, 35(2): 0207001. DOI:10.3788/AOS201535.0207001 |
| [17] |
ROSENBLATT M. Remarks on some nonparametric estimates of a density function[J]. Annals of Mathematical Statistics, 1956, 27(3): 832. DOI:10.1214/aoms/1177728190 |
| [18] |
KAILATH T. The divergence and bhattacharyya distance measures in signal selection[J]. IEEE Transactions on Communication Technology, 1967, 15(1): 52. DOI:10.1109/TCOM.1967.1089532 |
 2020, Vol. 52
2020, Vol. 52


