2. 哈尔滨工业大学 航天学院, 哈尔滨 150001
2. School of Astronautics, Harbin Institute of Technology, Harbin 150001, China
近年来,考虑避免碰撞的编队飞行航天器系统协同控制受到了广泛的研究和关注[1-7].与鲁棒性较差的单个航天器系统相比较[8],多航天器编队飞行系统具有通信成本低、鲁棒性强、效率高等优点[9],可以突破单个航天器编队系统的局限,对探测所需要的控制目标有更广阔的前景和更有意义的研究价值.
在航天器编队飞行系统协同控制的实际应用中,要求航天器能获得相互信息以实现对期望状态的跟踪.然而在信息获取的过程中由于距离和传输设备的约束,通常存在通信延迟[10]、信息无法实时准确获取[11]、航天器之间存在碰撞等情况.在编队飞行过程中,由于存在燃料损耗,航天器质量等信息无法精确实时获取,且在信息传递时会受到各种外部扰动的影响.根据上述分析的问题,为了提高编队航天器间协同控制的性能和精度,设计相应的自适应协同避碰控制算法具有重要的研究意义.文献[12]中对航天器编队协同控制进行分析,同时考虑避免碰撞提出了3种不同的编队跟踪控制方法.在文献[13]中基于编队卫星姿态动力学模型方程,通过引入速度滤波器设计了能够保证速度误差渐近收敛的自适应协同控制器.文献[14]进一步考虑推力校正和系统增益存在不确定性的情况下,提出了自适应跟踪控制算法.在上述分析的协同控制律中均为全状态反馈,而在实际的航天器编队飞行任务应用中,为节约燃料消耗、防止航天器之间的相对速度测量装置发生故障导致整个系统不稳定,需要保证编队系统在无速度测量情况下的有效协同作用.文献[15]提出了一种仅利用领航-跟踪航天器编队中的相对姿态反馈跟踪相对转动的控制器.文献[16]考虑输入受限的情况下,针对多Euler-Lagrange系统提出了一种无速度测量的分布式有限时间跟踪控制算法.
在编队飞行过程中,航天器之间避免碰撞是实现多航天器编队跟踪控制目标的重要保证.近年来,在多无人机协同控制、机械系统同步控制、多无人车协同控制等方面引起了国内外广泛的研究和关注.碰撞规避的主要研究方法可以分为:博弈论、碰撞概率分析、数学规划、半定规划[17]和势函数法[18].而势函数因其简单直观的物理意义成为解决避免碰撞的一种重要方法[19-20].文献[21]基于势函数的方法对模型不确定的编队飞行卫星系统设计了避免碰撞的自适应协同控制器,同时考虑了参考轨迹作用的问题.文献[22]设计了能保证Lagrange系统协同避碰的控制律,并考虑输入扰动的影响.在此基础上,文献[23]分析了Lagrange系统同时存在外部干扰和参数不确定的情况下的稳定性,并利用势函数的方法设计相应的鲁棒自适应控制算法.
受上述文献的启发,本文针对航天器质量未知和存在通信时延的情况,考虑反馈状态对航天器编队飞行系统的影响,分别对于全状态反馈和无速度测量设计两种自适应协同避碰控制律.首先,本文考虑了存在通信时延的航天器编队飞行系统的自适应协同避碰控制问题,在设计相应控制律时,选取合理满足系统的势函数,实现避免碰撞的控制目标;其次,考虑航天器编队反馈状态的角度,分别提出了全状态反馈和无速度测量的自适应协同避碰控制律,并同时考虑了航天器质量不确定性和通信时延,对于参数不确定有较好的自适应性; 最后通过仿真分析证明了所设计控制律的有效性.
1 基础理论 1.1 相对运动非线性模型在本文中每个航天器均假设为刚体结构,则n个航天器绕参考航天器编队飞行情况示意图,如图 1所示.其中FI
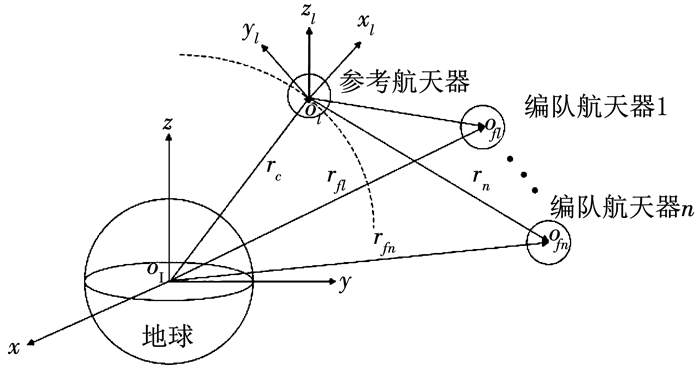
|
图 1 编队航天器飞行系统坐标系 Fig. 1 Coordinate frame for the formation spacecraft flying system |
在不考虑参考航天器所受主动力控制的作用下,假设参考航天器在椭圆轨道上运行.ri、vi分别为第i个航天器相对与参考航天器的在编队飞行系统中的位置和速度,则第i个航天器非线性动力学模型的相对运动方程为:
| $ {{\mathit{\boldsymbol{\dot r}}}_i} = {\mathit{\boldsymbol{v}}_i}, $ | (1) |
| $ \begin{array}{l} {m_{{f_i}}}{{\mathit{\boldsymbol{\dot v}}}_i} = {\mathit{\boldsymbol{C}}_i}\left( {{{\dot \theta }_{\rm{c}}}} \right){\mathit{\boldsymbol{v}}_i} + {\mathit{\boldsymbol{D}}_i}\left( {{{\ddot \theta }_c},{{\dot \theta }_c},{r_{{f_i}}}} \right){\mathit{\boldsymbol{r}}_i} + \\ {\mathit{\boldsymbol{n}}_i}\left( {{\mathit{\boldsymbol{r}}_{{f_i}}},{\mathit{\boldsymbol{r}}_l}} \right) + {\mathit{\boldsymbol{d}}_i} + {\mathit{\boldsymbol{f}}_i}, \end{array} $ | (2) |
其中:
| $ {\mathit{\boldsymbol{C}}_i}\left( {{{\dot \theta }_{\rm{c}}}} \right) = 2{m_{{f_i}}}{{\dot \theta }_{\rm{c}}}\left[ {\begin{array}{*{20}{c}} 0&1&0\\ { - 1}&0&0\\ 0&0&0 \end{array}} \right], $ | (3) |
| $ \begin{array}{l} {\mathit{\boldsymbol{D}}_i}\left( {{{\ddot \theta }_c},{{\dot \theta }_c},{r_{{f_i}}}} \right) = - {m_{{f_i}}}\frac{\mu }{{\mathit{\boldsymbol{r}}_{{f_i}}^3}}{\mathit{\boldsymbol{I}}_{3 \times 3}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{m_{{f_i}}}\left[ {\begin{array}{*{20}{c}} {\dot \theta _c^2}&{{{\ddot \theta }_c}}&0\\ {{{\ddot \theta }_c}}&{\dot \theta _c^2}&0\\ 0&0&0 \end{array}} \right], \end{array} $ | (4) |
| $ {\mathit{\boldsymbol{n}}_i}\left( {{r_{{f_i}}},{r_i}} \right) = \mu {m_{{f_i}}}{\left[ { - \frac{{{r_l}}}{{r_{{f_i}}^3}} + \frac{1}{{r_l^2}}\quad 0\quad 0} \right]^{\rm{T}}}, $ | (5) |
| $ {\mathit{\boldsymbol{d}}_i} = {\mathit{\boldsymbol{d}}_{{f_i}}} - \frac{{{m_{{f_i}}}}}{{{m_l}}}{\mathit{\boldsymbol{d}}_l}, $ | (6) |
式中:dl、dfi分别为参考航天器和第i个航天器所受到的外部干扰总和; θc为参考航天器的真近点角; rl、rfi分别为参考航天器和第i个航天器到地球中心的距离; I3×3为适当维数的单位矩阵,μ为地球引力常数.
为能够更好地设计本文所提出的自适应协同避碰控制律,利用Euler-Lagrange方程来描述编队飞行航天器系统的相对运动[25]:
| $ {m_{{f_i}}}{{\mathit{\boldsymbol{\ddot r}}}_i} + \mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{\dot r}}}_i} + \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{r}}_i} + \mathit{\boldsymbol{C}} = {\mathit{\boldsymbol{d}}_i} + {\mathit{\boldsymbol{f}}_i}, $ | (7) |
式中:
| $ \mathit{\boldsymbol{A}} = - {\mathit{\boldsymbol{C}}_i}\left( {{{\dot \theta }_c}} \right),\mathit{\boldsymbol{B}} = - {\mathit{\boldsymbol{D}}_i}\left( {{\theta _c},{\theta _c},{r_{{f_i}}}} \right),\mathit{\boldsymbol{C}} = - {\mathit{\boldsymbol{n}}_i}\left( {{r_{{f_i}}},{r_l}} \right). $ |
本文中用加权无向图G=(V, E, A)来描述编队航天器之间的信息传递[26]:V={v1, …, vn}为节点集,E⊆V×V为连接节点的边集,A=[aij]∈ Rn×n为加权邻接矩阵.若(j, i)∈E,且(i, j)∈E,则称G为无向图.如果第j个节点有指向第i个节点的路径且存在信息传递,则第j个节点就有一条边指向第i个节点,记为(j, i)∈E.在无向图中,如果任意两点之间存在路径连接,则无向图具有连通性[26].
1.3 势函数设计与控制目标设定 1.3.1 势函数设计本文利用势函数的方法来完成多航天器编队飞行避免碰撞的控制目标,使系统达到期望的控制状态.势函数的主要优点在于:在期望的状态下具有全局最小值,且具有较高势函数值的区域代表障碍碰撞等限制情况.受文献[27]启发,设计势函数的主要思想如下:首先,定义一个反映系统约束条件的标量势函数.其次,利用势函数的梯度值表示施加在航天器编队上避免碰撞的控制力.最后,设计适当的控制律使系统势函数的值具有减小的趋势,并且应用Lyapunov稳定性理论,保证编队系统的位置和速度均同时收敛于期望状态,满足避免碰撞的控制目标.
Rij、rij分别为编队系统通信和最小安全区域的距离,选取如下的避免碰撞势函数:
| $ {\mathit{\boldsymbol{V}}_{ij}}\left( {{r_i},{r_j}} \right) = {\left( {\min \left\{ {0,\frac{{{{\left\| {{\mathit{\boldsymbol{r}}_i} - {\mathit{\boldsymbol{r}}_j}} \right\|}^2} - R_{ij}^2}}{{{{\left\| {{\mathit{\boldsymbol{r}}_i} - {\mathit{\boldsymbol{r}}_j}} \right\|}^2} - r_{ij}^2}}} \right\}} \right)^2},i \ne j $ |
式中, Vij(ri, rj)为一个非负连续的可微函数.
Vij沿向量ri的梯度表示为
| $ \nabla {r_i}{\mathit{\boldsymbol{V}}_{ij}} = \left\{ {\begin{array}{*{20}{l}} {4\frac{{\left( {R_{ij}^2 - r_{ij}^2} \right)\left( {{{\left\| {{\mathit{\boldsymbol{r}}_i} - {\mathit{\boldsymbol{r}}_j}} \right\|}^2} - R_{ij}^2} \right)}}{{{{\left( {{{\left\| {{\mathit{\boldsymbol{r}}_i} - {\mathit{\boldsymbol{r}}_j}} \right\|}^2} - r_{ij}^2} \right)}^3}}}{{\left( {{\mathit{\boldsymbol{r}}_i} - {\mathit{\boldsymbol{r}}_j}} \right)}^{\rm{T}}},}\\ {{\rm{if}}:{r_{ij}} < \left\| {{\mathit{\boldsymbol{r}}_i} - {\mathit{\boldsymbol{r}}_j}} \right\| < {R_{ij}};}\\ 0\\ {{\rm{if}}:\left\| {{\mathit{\boldsymbol{r}}_i} - {\mathit{\boldsymbol{r}}_j}} \right\| \ge {R_{ij}},\left\| {{\mathit{\boldsymbol{r}}_i} - {\mathit{\boldsymbol{r}}_j}} \right\| \le {r_{ij}}.} \end{array}} \right. $ |
在航天器编队飞行控制系统中,假设编队中各航天器均能获取到期望位置rid和期望速度
| $ {{\mathit{\boldsymbol{\tilde r}}}_i} = {\mathit{\boldsymbol{r}}_i} - \mathit{\boldsymbol{r}}_i^d, $ |
| $ {{\mathit{\boldsymbol{\dot {\tilde r}}}}_i} = {{\mathit{\boldsymbol{\dot r}}}_i} - \mathit{\boldsymbol{\dot r}}_i^d. $ |
在航天器质量参数不确定性、通信拓扑结构存在时延的情况下,将避免碰撞势函数与自适应协同控制相互结合,实现航天器在编队飞行过程中保持编队稳定不发生碰撞并保证系统的拓扑连通性,最终实现对期望位置和期望速度的跟踪, 即当t→∞时,对于
在本文中,为实现编队航天器飞行系统的自适应协同避免碰撞控制,分别对于全状态反馈和无速度测量情况,设计相应的控制律.在设计控制律时,为实现编队系统的稳定性应考虑:1)编队航天器对期望位置和期望速度的跟踪;2)编队航天器的协同控制作用使其状态趋于稳定;3)保证编队航天器之间不发生碰撞.
2.1 全状态反馈自适应协同控制律将辅助变量定义如下:
| $ \mathit{\boldsymbol{\dot z}}_i^r = \mathit{\boldsymbol{\dot r}}_i^d - \eta \left( {{\mathit{\boldsymbol{r}}_i} - {\mathit{\boldsymbol{r}}_d}} \right) = \mathit{\boldsymbol{\dot r}}_i^d - \eta {{\mathit{\boldsymbol{\tilde r}}}_i}. $ |
通过利用滑模变结构理论,第i个航天器可以表示为
| $ {\mathit{\boldsymbol{\varpi}} _i} = {{\mathit{\boldsymbol{\dot r}}}_i} - \mathit{\boldsymbol{\dot z}}_i^r = {{\mathit{\boldsymbol{\dot {\tilde r}}}}_i} + \mathit{\boldsymbol{\eta }}{{\mathit{\boldsymbol{\tilde r}}}_i}, $ |
式中η为正常数.
定理1 考虑航天器编队相对运动模型(1)~(6),如果通信拓扑结构为无向图,假设第i个航天器所受到的外部扰动di=0,在存在航天器质量参数不确定性、通信时延的情况下,同时考虑避免碰撞的控制目标,将航天器编队飞行系统控制律设计如下:
| $ \begin{array}{l} {\mathit{\boldsymbol{f}}_i} = {{\hat m}_{{f_i}}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_i} - {\delta _i}{\mathit{\boldsymbol{\varpi}} _i} - \\ \;\;\;\;\;\;\beta \sum\limits_{j = 1}^n {{a_{ij}}} \left[ {{\mathit{\boldsymbol{\varpi}} _i} - {\mathit{\boldsymbol{\varpi}} _j}\left( {t - {T_{ij}}} \right)} \right] - \sum\limits_{j = 1}^n \nabla {r_i}{\mathit{\boldsymbol{V}}_{ij}}, \end{array} $ | (8) |
| $ {{\dot {\hat m}}_{{f_i}}} = - {\psi _i}\mathit{\boldsymbol{\varpi}} _i^{\rm{T}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_i}, $ | (9) |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_i} = - \frac{1}{{{m_{{f_i}}}}}{\mathit{\boldsymbol{D}}_i}\left( {{{\ddot \theta }_c},{{\dot \theta }_c},{r_{{f_i}}}} \right){\mathit{\boldsymbol{r}}_i} - \frac{1}{{{m_{{f_i}}}}}{\mathit{\boldsymbol{n}}_i}\left( {{r_i},{r_c}} \right). $ | (10) |
式中:δi、ψi为正常数;aij为加权邻接矩阵元素;Tij为第i个航天器获取第j个航天器相对信息的定常时延,其中包括位置时延
定义第i个航天器的质量估计误差为
| $ {{\tilde m}_{{f_i}}} = {m_{{f_i}}} - {{\hat m}_{{f_i}}}, $ |
式中,
根据势函数设计与控制目标设定提出的势函数方法和文献[27]所提出的相关内容,本文对势函数作如下假设.
假设1 若拓扑结构为无向图且Vij(‖ri-rj‖)对称,则可以得到▽riVij(‖ri-rj‖)=-▽rjVij(‖ri-rj‖).
假设2
在本文中,假设航天器所受到外部扰动di=0,将控制律(8)~(10)代入式(2), 则闭环系统可以写为
| $ \begin{array}{l} {m_{{f_i}}}{{\mathit{\boldsymbol{\dot v}}}_i} = {\mathit{\boldsymbol{C}}_i}\left( {{{\dot \theta }_c}} \right){\mathit{\boldsymbol{v}}_i} + \beta \sum\limits_{j = 1}^n {{a_{ij}}} \left[ {{\mathit{\boldsymbol{\varpi}} _i} - {\mathit{\boldsymbol{\varpi}} _j}\left( {t - {T_{ij}}} \right)} \right] - \\ \;\;\;\;\;\;\;\;\;\;\;\sum\limits_{j = 1,j \ne i}^n {{\nabla _{{r_i}}}} {\mathit{\boldsymbol{V}}_{ij}} - {{\tilde m}_{{f_i}}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_i} - {\delta _i}{\mathit{\boldsymbol{\varpi}} _i}. \end{array} $ |
证明1 定义如下Lyapunov函数:
| $ \begin{array}{l} V(t) = \frac{1}{2}\sum\limits_{i = 1}^n {\mathit{\boldsymbol{\varpi}} _i^{\rm{T}}} {m_{{f_i}}}{\mathit{\boldsymbol{\varpi}} _i} + \frac{1}{2}\sum\limits_{i = 1}^n {\frac{1}{{{\psi _i}}}\tilde m_{{f_i}}^2} + \\ \;\;\;\;\;\;\;\;\;\frac{\beta }{2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{a_{ij}}} } \int_{t - {T_{ij}}}^t {\mathit{\boldsymbol{\varpi}} _j^{\rm{T}}} (\rho ){\mathit{\boldsymbol{\varpi}} _j}(\rho )d\rho + \\ \;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^n {\sum\limits_{j > i} {{\mathit{\boldsymbol{V}}_{ij}}} } \left( {\left\| {{\mathit{\boldsymbol{r}}_i} - {\mathit{\boldsymbol{r}}_j}} \right\|} \right). \end{array} $ | (11) |
将式(11)对时间求导,可以得到:
| $ \begin{array}{l} \dot V\left( t \right) = \sum\limits_{i = 1}^n {\mathit{\boldsymbol{\varpi}} _i^{\rm{T}}} {m_{{f_i}}}{{\dot {\mathit{\boldsymbol{\varpi}}} }_i}\sum\limits_{i = 1}^n {\frac{1}{{{\psi _i}}}} {{\tilde m}_{{f_i}}}\tilde m_{{f_i}}^2 + \\ \;\;\;\;\;\;\;\;\;\;\;\frac{\beta }{2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{a_{ij}}} } \left[ {\mathit{\boldsymbol{\varpi}} _j^{\rm{T}}{\mathit{\boldsymbol{\varpi}} _j} - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {\mathit{\boldsymbol{\varpi}} _j^{\rm{T}}\left( {t - {T_{ij}}} \right){\mathit{\boldsymbol{\varpi}} _j}\left( {t - {T_{ij}}} \right)} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^n {\sum\limits_{j > i} {{{\left( {{\nabla _{{r_i}}}{\mathit{\boldsymbol{V}}_{ij}}} \right)}^{\rm{T}}}} } {{\mathit{\boldsymbol{\dot r}}}_i} + {\left( {{\nabla _{ij}}{\mathit{\boldsymbol{V}}_{ij}}} \right)^{\rm{T}}}{{\mathit{\boldsymbol{\dot r}}}_j}. \end{array} $ | (12) |
在对式(12)推导过程中,需要分析如下几点:
1) 由于
2) 若航天器编队系统的通信拓扑结构为无向图,则aij=aji,进一步可以得到如下等式成立:
| $ \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{a_{ij}}} } \mathit{\boldsymbol{\varpi}} _i^{\rm{T}}{\mathit{\boldsymbol{\varpi}} _i} = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{a_{ij}}} } \mathit{\boldsymbol{\varpi}} _j^{\rm{T}}{\mathit{\boldsymbol{\varpi}} _i}. $ |
3) 若通信拓扑结构为无向图且▽riVij=-▽rjVij,则
| $ \begin{array}{*{20}{c}} {\left. {\sum\limits_{i = 1}^n {\left[ {{{\left( {{\nabla _{{r_i}}}{\mathit{\boldsymbol{V}}_{ij}}} \right)}^{\rm{T}}}{{\mathit{\boldsymbol{\dot r}}}_i}} \right]} + {{\left( {{\nabla _{{r_i}}}{\mathit{\boldsymbol{V}}_{ij}}} \right)}^{\rm{T}}}{{\mathit{\boldsymbol{\dot r}}}_j}} \right] - }\\ {\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\mathit{\boldsymbol{r}}_i^{\rm{T}}} } {\nabla _{{r_i}}}{\mathit{\boldsymbol{V}}_{ij}} = 0.} \end{array} $ |
4) 时间延迟满足如下不等式:
| $ \begin{array}{l} - \frac{\beta }{2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{a_{ij}}} } \mathit{\boldsymbol{\varpi}} _i^{\rm{T}}{\mathit{\boldsymbol{\varpi}} _i} + \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{a_{ij}}} } \mathit{\boldsymbol{\varpi}} _i^{\rm{T}}{\mathit{\boldsymbol{\varpi}} _j}\left( {t - {T_{ij}}} \right) - \\ \;\;\;\frac{\beta }{2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{a_{ij}}} } \mathit{\boldsymbol{\varpi}} _j^{\rm{T}}\left( {t - {T_{ij}}} \right){\mathit{\boldsymbol{\varpi}} _j}\left( {t - {T_{ij}}} \right) \le 0. \end{array} $ |
根据上述分析,式(12)可以写为
| $ \dot V(t) \le - \sum\limits_{i = 1}^n {\mathit{\boldsymbol{\varpi}} _i^{\rm{T}}} {\delta _i}{\mathit{\boldsymbol{\varpi}} _i} \le 0. $ |
因此
在航天器编队飞行的实际任务中,航天器的相关信息需要先进的通信设备进行实时测量,为降低航天器之间的通信消耗成本,应考虑设计无速度测量的相应控制律.因此在本文中,针对无速度测量中
受文献[29]启发,考虑到通信时延的情况,设计一种无源滤波器:
| $ {{\mathit{\boldsymbol{\dot {\hat g}}}}_i} = \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}{\mathit{\boldsymbol{{\hat g}}}_i} + \sum\limits_{j = 1}^n {{a_{ij}}} \left[ {{\mathit{\boldsymbol{r}}_i} - {\mathit{\boldsymbol{r}}_j}\left( {\mathit{\boldsymbol{t}} - {T_{ij}}} \right)} \right], $ | (13) |
| $ {\mathit{\boldsymbol{h}}_i} = \mathit{\Lambda }\left\{ {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}{{\mathit{\boldsymbol{\hat g}}}_i} + \sum\limits_{j = 1}^n {{a_{ij}}} \left[ {{\mathit{\boldsymbol{r}}_i} - {\mathit{\boldsymbol{r}}_j}\left( {t - {T_{ij}}} \right)} \right]} \right\}. $ | (14) |
式中:i=1, …, n,Θ ∈ R3是Hurwitz矩阵.Λ=ΛT∈R3×3为正定矩阵满足如下Lyapunov等式:
| $ {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varLambda} }} + \mathit{\boldsymbol{ \boldsymbol{\varLambda} \boldsymbol{\varTheta} }} = - \mathit{\boldsymbol{Q}}, $ |
式中,Λ、Q均为对称正定阵.
定理2 考虑航天器编队相对运动模型(7),如果通信拓扑结构为无向图,假设第i个航天器所受到的外部扰动di=0,在存在航天器质量参数不确定性、通信时延及速度无法测量的情况下,同时考虑避免碰撞的控制目标,将航天器编队飞行系统控制律设计如下:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{f}}_i} = - \beta \sum\limits_{j = 1}^{n} {{a_{ij}}} \left[ {{\mathit{\boldsymbol{r}}_i} - {\mathit{\boldsymbol{r}}_j}\left( {t - {T_{ij}}} \right)} \right] - }\\ {{\mathit{\boldsymbol{h}}_i} + {{\hat m}_{{f_i}}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_i} + \sum\limits_{j = 1,j \ne i}^n {{\nabla _{{r_i}}}} {\mathit{\boldsymbol{V}}_{ij}},} \end{array} $ | (15) |
| $ {{\dot {\hat m}}_{{f_i}}} = - {\xi _i}\mathit{\boldsymbol{r}}_i^{\rm{T}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_i}, $ | (16) |
式中, ξi为自适应更新律的正常数量.则有
| $ {{\dot {\hat m}}_{{f_i}}} = {m_{{f_i}}}(0) - {\xi _i}\int_{r_i^{(0)}}^{r_i^{(t)}} {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_i^{\rm{T}}} {\rm{d}}{r_i}. $ |
引理1 文献[30]假设M∈Qp×p,N∈Qq×q,则下式成立:
1)(M⊗N)(A⊗B)= MA⊗NB.
2) 假设M和N为可逆矩阵,则满足(M⊗N)-1= M-1⊗N-1.
3) 如果M和N是对称正定的,则M⊗N同样也为对阵矩阵.
与设计全状态反馈控制律相似,假设航天器编队受到的外部干扰为零,则闭环系统方程可写为
| $ \begin{array}{*{20}{c}} {{m_{{f_i}}}{{\mathit{\boldsymbol{\ddot {\tilde r}}}}_i} + A{{\mathit{\boldsymbol{\dot {\tilde r}}}}_i} + B{{\mathit{\boldsymbol{\tilde r}}}_i} + \mathit{\boldsymbol{C}} + \beta \left( {\mathit{\boldsymbol{ \boldsymbol{\varXi} }} \otimes {\mathit{\boldsymbol{I}}_3}} \right){{\mathit{\boldsymbol{\tilde r}}}_i}\left( {t - {T_{ij}}} \right) + }\\ {{s_i} + {{\tilde m}_{{f_i}}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_i} - \sum\limits_{j = 1,j \ne i}^n {{\nabla _{{r_i}}}} {\mathit{\boldsymbol{V}}_{ij}} = 0.} \end{array} $ |
证明 定义如下Lyapunov函数:
| $ \begin{array}{l} V(t) = \frac{1}{2}\mathit{\boldsymbol{\dot {\hat g}}}_i^{\rm{T}}{\left( {\mathit{\boldsymbol{ \boldsymbol{\varXi} }} \otimes {\mathit{\boldsymbol{I}}_3}} \right)^{ - 1}}\left( {{\mathit{\boldsymbol{I}}_n} \otimes \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}} \right){{\mathit{\boldsymbol{\dot {\hat g}}}}_i} + \frac{1}{2}\sum\limits_{i = 1}^n {\mathit{\boldsymbol{\tilde r}}_i^{\rm{T}}} {m_{{f_i}}}{{\mathit{\boldsymbol{\tilde r}}}_i} + \\ \;\;\;\;\;\;\;\;\;\;\frac{1}{2}\sum\limits_{i = 1}^n {\frac{1}{{{\xi _i}}}} \tilde m_{{f_i}}^2 + \frac{\beta }{2}\int_{t - {T_{ij}}}^t {\mathit{\boldsymbol{\tilde r}}_i^{\rm{T}}} (\rho )(\mathit{\boldsymbol{ \boldsymbol{\varXi} }} \otimes \\ \;\;\;\;\;\;\;\;\;\;\left. {{\mathit{\boldsymbol{I}}_3}} \right){{\mathit{\boldsymbol{\tilde r}}}_i}(\rho ){\rm{d}}\rho + \sum\limits_{i = 1}^n {\sum\limits_{j > i} {{\mathit{\boldsymbol{V}}_{ij}}} } \left( {\left\| {{\mathit{\boldsymbol{r}}_i} - {\mathit{\boldsymbol{r}}_j}} \right\|} \right). \end{array} $ | (17) |
将式(17)对时间求导,可以得到:
| $ \begin{array}{l} \dot V(t) = \frac{1}{2}\mathit{\boldsymbol{\dot {\hat g}}}_i^{\rm{T}}{\left( {\mathit{\boldsymbol{ \boldsymbol{\varXi} }} \otimes {\mathit{\boldsymbol{I}}_3}} \right)^{ - 1}}\left( {{\mathit{\boldsymbol{I}}_n} \otimes \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}} \right){{\mathit{\boldsymbol{\ddot {\hat g}}}}_i} + \\ \;\;\;\;\;\;\;\;\;\;\frac{1}{2}\mathit{\boldsymbol{\ddot {\hat g}}}_i^{\rm{T}}{\left( {\mathit{\boldsymbol{ \boldsymbol{\varXi} }} \otimes {\mathit{\boldsymbol{I}}_3}} \right)^{ - 1}}\left( {{\mathit{\boldsymbol{I}}_n} \otimes \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}} \right){{\mathit{\boldsymbol{\dot {\hat g}}}}_i} + \\ \;\;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^n {\mathit{\boldsymbol{\dot {\tilde r}}}_i^{\rm{T}}} {m_{{f_i}}}{{\mathit{\boldsymbol{\ddot {\tilde r}}}}_i} + \sum\limits_{i = 1}^n {\frac{1}{{{\xi _i}}}} {{\tilde m}_{{f_i}}}{{\dot {\tilde m}}_{{f_i}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\beta \left( {\mathit{\boldsymbol{ \boldsymbol{\varXi} }} \otimes {\mathit{\boldsymbol{I}}_3}} \right)\left[ {\mathit{\boldsymbol{\tilde r}}_i^{\rm{T}}{{\mathit{\boldsymbol{\dot {\tilde r}}}}_i} - \mathit{\boldsymbol{\tilde r}}_i^{\rm{T}}\left( {t - {T_{ij}}} \right){{\mathit{\boldsymbol{\dot {\tilde r}}}}_i}\left( {t - {T_{ij}}} \right)} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^n {\sum\limits_{j > i} {{{\left( {{\nabla _{{r_i}}}{\mathit{\boldsymbol{V}}_{ij}}} \right)}^{\rm{T}}}} } {{\mathit{\boldsymbol{\dot r}}}_i} + {\left( {{\nabla _{{r_j}}}{\mathit{\boldsymbol{V}}_{ij}}} \right)^{\rm{T}}}{{\mathit{\boldsymbol{\dot r}}}_j}. \end{array} $ | (18) |
在对式(18)推导过程中,需要分析如下几点:
1) 根据式(13)可以得到如下:
| $ \mathit{\boldsymbol{\ddot {\hat g}}} = \left( {{\mathit{\boldsymbol{I}}_n} \otimes \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}} \right){{\mathit{\boldsymbol{\dot {\hat g}}}}_i} + \left( {\mathit{\boldsymbol{ \boldsymbol{\varXi} }} \otimes {\mathit{\boldsymbol{I}}_3}} \right){{\mathit{\boldsymbol{\dot {\tilde r}}}}_i}. $ | (19) |
2) 如果编队航天器之间相互作用的通信拓扑结构是无向的,且拓扑图的边指向航天器,则矩阵Ξ =LA+diag(a10, …, an0)是对阵正定的.
3) 根据引理1可知,等式(Ξ⊗I3)-1(In⊗Λ)= Ξ-1⊗Λ是对称正定的.
根据上述分析,式(18)可以重新写为
| $ \begin{array}{l} \dot V(t) = - \sum\limits_{i = 1}^n {\mathit{\boldsymbol{\dot {\tilde r}}}_i^{\rm{T}}} {m_{{f_i}}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_i} + \mathit{\boldsymbol{\dot r}}_i^{\rm{T}}{\mathit{\boldsymbol{h}}_i} - \sum\limits_{i = 1}^n {\mathit{\boldsymbol{\tilde r}}_i^{\rm{T}}} {m_{{f_i}}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_i} + \\ \;\;\;\;\;\;\;\;\;\;\frac{1}{2}\mathit{\boldsymbol{\dot {\hat g}}}_i^{\rm{T}}\left( {\mathit{\boldsymbol{ \boldsymbol{\varXi} }} \otimes {\mathit{\boldsymbol{I}}_3}} \right)\left( {{\mathit{\boldsymbol{I}}_n} \otimes \mathit{\boldsymbol{ \boldsymbol{\varLambda} \boldsymbol{\varTheta} }}} \right){{\mathit{\boldsymbol{\dot {\hat g}}}}_i} + \\ \;\;\;\;\;\;\;\;\;\;\frac{1}{2}\mathit{\boldsymbol{\dot {\hat g}}}_i^{\rm{T}}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varXi} }}^{ - 1}} \otimes {\mathit{\boldsymbol{I}}_3}} \right)\left( {{\mathit{\boldsymbol{I}}_n} \otimes {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}} \right){{\mathit{\boldsymbol{\dot {\hat g}}}}_i} + \\ \;\;\;\;\;\;\;\;\;\;{{\mathit{\boldsymbol{\dot {\hat g}}}}_i}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varXi} }}^{ - 1}} \otimes {\mathit{\boldsymbol{I}}_3}} \right)\left( {{\mathit{\boldsymbol{I}}_n} \otimes \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}} \right)\left( {\mathit{\boldsymbol{ \boldsymbol{\varXi} }} \otimes {\mathit{\boldsymbol{I}}_r}} \right){{\mathit{\boldsymbol{\dot {\tilde r}}}}_i} + \\ \;\;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^n {\sum\limits_{j > i} {{{\left( {{\nabla _{{r_j}}}{\mathit{\boldsymbol{V}}_{ij}}} \right)}^{\rm{T}}}} } {{\mathit{\boldsymbol{\dot r}}}_i} + {\left( {{\nabla _{{r_j}}}{\mathit{\boldsymbol{V}}_{ij}}} \right)^{\rm{T}}}{{\mathit{\boldsymbol{\dot r}}}_j} - \\ \;\;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^n {\sum\limits_{j = i}^n {\mathit{\boldsymbol{r}}_i^{\rm{T}}} } {\nabla _{{r_i}}}{\mathit{\boldsymbol{V}}_{ij}} = \mathit{\boldsymbol{\dot {\tilde r}}}_i^{\rm{T}}\left( {{\mathit{\boldsymbol{I}}_n} \otimes \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}} \right){{\mathit{\boldsymbol{\dot {\hat g}}}}_i} + \\ \;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{\dot {\hat g}}}_i^{\rm{T}}\left( {{\mathit{\boldsymbol{I}}_n} \otimes \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}} \right){{\mathit{\boldsymbol{\dot {\tilde r}}}}_i} + \\ \;\;\;\;\;\;\;\;\;\;\frac{1}{2}\mathit{\boldsymbol{\dot {\hat g}}}_i^{\rm{T}}\left[ {{\mathit{\boldsymbol{ \boldsymbol{\varXi} }}^{ - 1}} \otimes \left( {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varLambda} }} + \mathit{\boldsymbol{ \boldsymbol{\varLambda} \boldsymbol{\varTheta} }}} \right)} \right]{{\mathit{\boldsymbol{\dot {\hat g}}}}_i} = \\ \;\;\;\;\;\;\;\;\;\; - \frac{1}{2}\mathit{\boldsymbol{\dot {\hat g}}}_i^{\rm{T}}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varXi} }}^{ - 1}} \otimes \mathit{\boldsymbol{Q}}} \right){{\mathit{\boldsymbol{\dot {\hat g}}}}_i} \le 0. \end{array} $ |
由于Ξ-1∈R3×3和Q∈R3×3均为对称正定矩阵,通过引理1可知Ξ-1⊗Q也为对称正定矩阵.由于V(t)>0,
为了验证本文所设计控制律的有效性,以3个航天器编队飞行系统为例,分别对全状态反馈和无速度测量自适应协同控制进行相应的仿真.
编队航天器在仿真初始设定的轨道参数分别如下:半长轴a=125 km,轨道偏心率e=0.07,轨道倾角i=30°,升交点赤经Ω=45°,近地点幅角ω=30°,真近点角为-2.5×10-4、-5.0×10-4、2.5×10-4;仿真初始时刻参数设定如下,参考航天器真近点角0°,航天器质量分别为:110、115、105 kg,航天器质量估计初始值
将避免碰撞的最小安全距离设置为cij=10 m,选取势函数为
| $ {\mathit{\boldsymbol{V}}_{ij}}\left( {{\mathit{\boldsymbol{r}}_i},{\mathit{\boldsymbol{r}}_j}} \right) = \sum\limits_{i = 1}^3 {\frac{{211000}}{{{{\left( {{{\left\| {{\mathit{\boldsymbol{r}}_i} - {\mathit{\boldsymbol{r}}_j}} \right\|}^2} - {{20}^2}} \right)}^2}}}} . $ |
首先,设置全状态反馈自适应协同控制律(14)~(16)中的参数如下:λi=50, γi=50, α=1,通信拓扑图为无向图,则aij=0.5,反之aij=0.
在全状态反馈自适应协同避碰控制律(8)~(10)的作用下,图 2、3分别为航天器编队相对位置误差曲线和相对速度误差曲线.由图 2、3可以看出,在跟踪到期望位置的过程中,编队航天器相对于参考航天器速度收敛于零附近,同时编队航天器相对距离在100 s后基本保持不变,在任意时刻相对距离均不小于c=10 m,避免碰撞的发生.
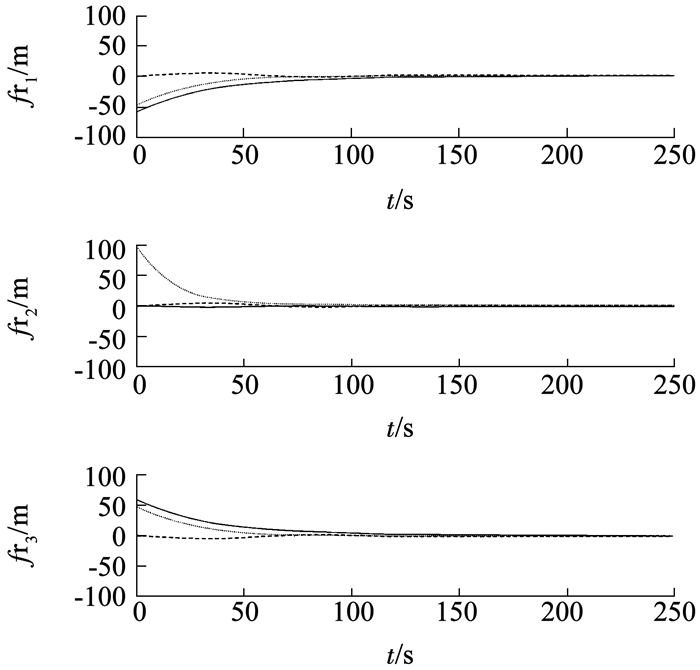
|
图 2 全状态反馈相对位置误差曲线 Fig. 2 Error curves of relative position with full state feedback |
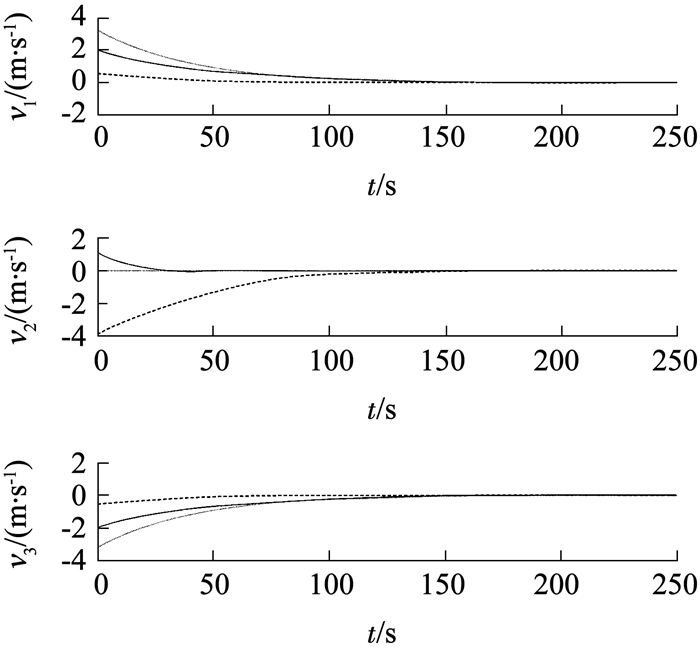
|
图 3 全状态反馈相对速度误差曲线 Fig. 3 Error curves of relative velocity with full state feedback |
其次,设置无速度测量自适应协同避碰控制律(15)~(16)中的参数如下:β=1, ξi=0.1通信拓扑图为无向图,则aij=0.3,反之aij=0.
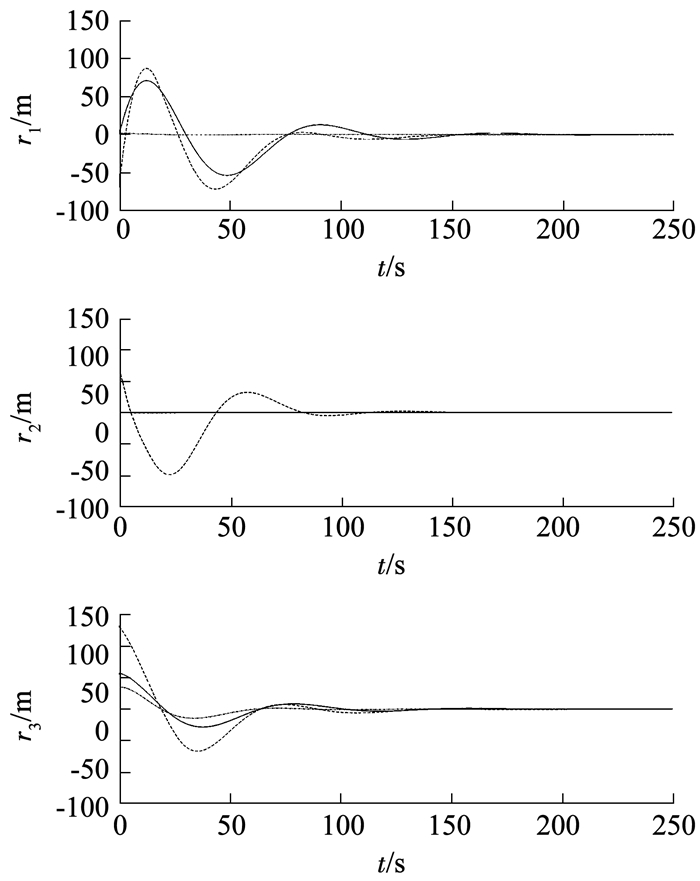
在无速度测量自适应协同避碰控制律(15)~(16)的作用下,图 4、5分别为航天器编队相对位置误差曲线和相对速度误差曲线.由图 4、5可以看出,位置跟踪误差曲线和速度跟踪误差曲线均能收敛到零附近,且收敛时间具有同步性并保持编队飞行系统稳定,在图 4中,相对位置跟踪误差以稳态误差约为10-3 m,而在图 5中相对速度跟踪的稳态误差约为10-5 m/s.
|
图 4 无速度测量相对位置误差曲线 Fig. 4 Error curves of relative position without velocity measurements |
|
图 5 无速度测量相对速度误差曲线 Fig. 5 Error curves of relative velocity without velocity measurements |
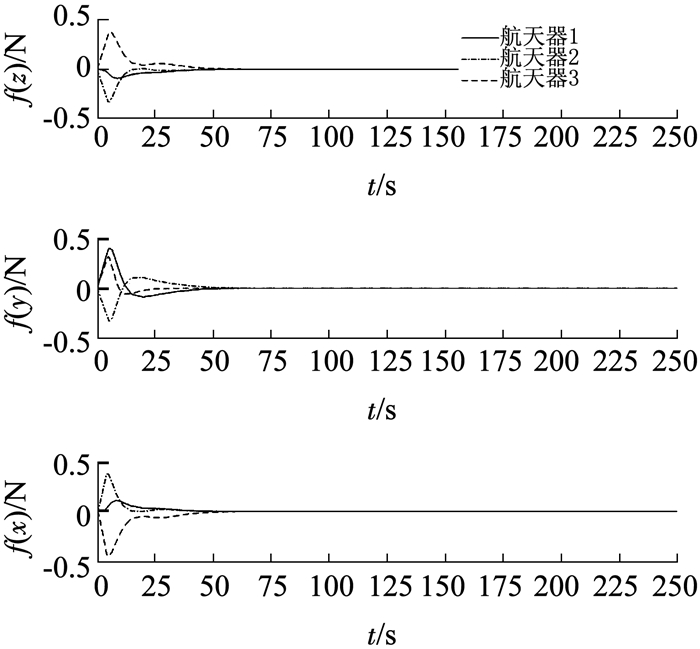
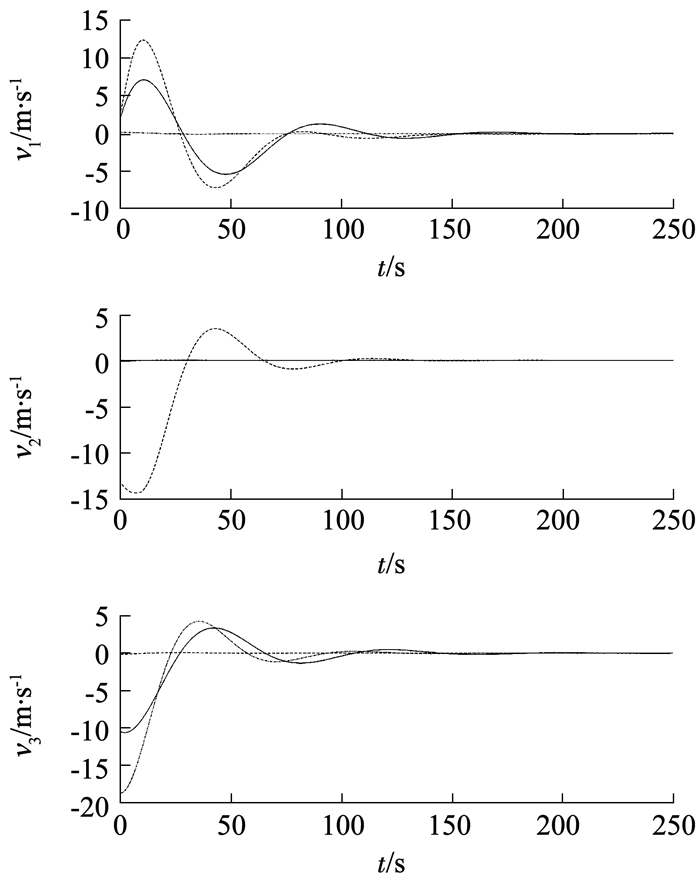
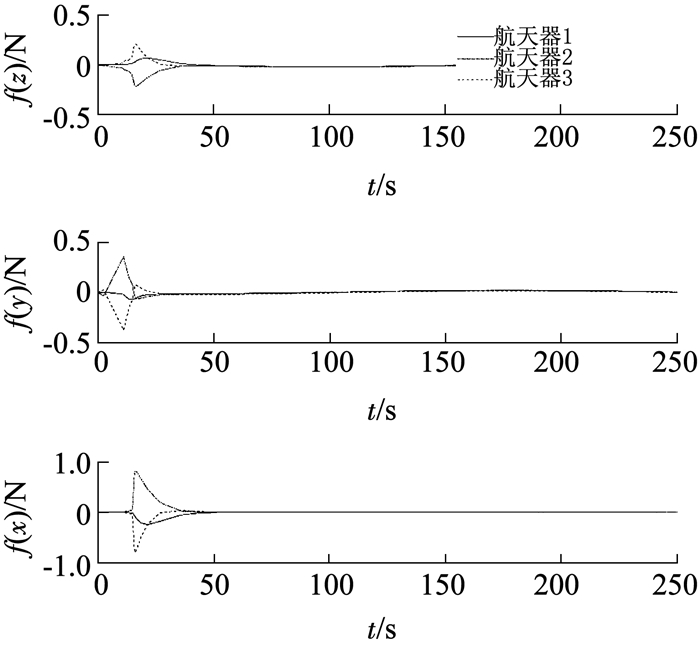
图 6、图 7分别给出了全状态反馈和无速度测量控制力曲线图.在图 6、图 7中可以看出,在仿真的初始阶段由于存在通信延迟会产生较大的抖振,但随着时间的变化曲线均达到收敛.与全状态反馈自适应协同避碰控制律相比,编队航天器在无速度测量自适应协同避碰控制律作用下,相对振幅较大,是由于航天器质量估计值在自适应更新律中稳态控制不能为零.因此,根据设计的控制律(8)~(10)、(15)~(16)可以看出,当辅助变量收敛到零附近时,控制变量不能达到零.
|
图 6 全状态反馈控制力曲线 Fig. 6 Curves of control force with full state feedback |
|
图 7 无速度测量控制力曲线 Fig. 7 Curves of control force without velocity measurements |
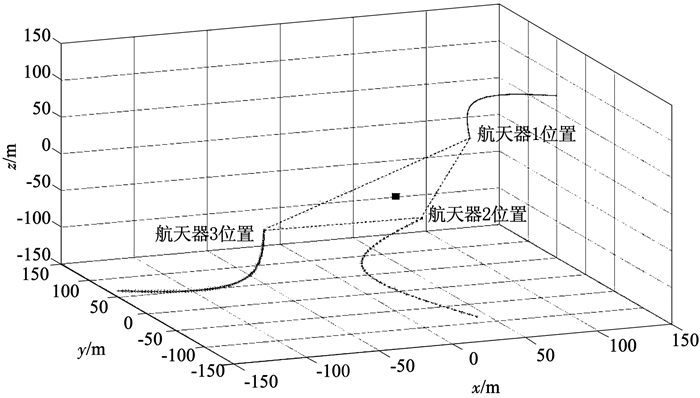
编队航天器避免碰撞的相对位置变化轨迹如图 8所示,在航天器编队飞行时假设各航天器为刚体结构,但是在实际应用运行过程中会受到姿态展开等因素的影响,这些干扰因素仍然是无法忽略的.由图 8可以看出,各航天器均能到达期望轨迹且不发生碰撞.根据上述分析可知,航天器编队飞行闭环系统稳定性,并完成编队跟踪、避免碰撞、自适应协同控制的控制目标.
|
图 8 编队航天器避免碰撞相对运动轨迹 Fig. 8 Relative motion trajectories of formation spacecraft for collision avoidance |
1) 在航天器编队飞行控制系统存在通信时延、质量参数不确定的情况下,考虑反馈状态信息的不同状态,提出了两种具有较强鲁棒性的自适应协同避碰控制律.
2) 选取合理的势函数包含在自适应协同避碰控制律中,实现编队飞行系统避免碰撞的发生,具有较高的控制精度.
3) 利用Lyapunov稳定性理论对所设计的两种控制律进行理论分析证明,证明航天器编队飞行闭环系统的渐近稳定性.仿真结果进一步验证了所设计控制律的有效性.
| [1] |
SLATER G L, BYRAM S M, WILLIAMS T W. Collision avoidance for satellites in formation flight[J]. Journal of Guidance Control & Dynamics, 2006, 29(5): 1140. DOI:10.2514/1.16812 |
| [2] |
XIA Yuanqing, NA Xitai, SUN Zhongqi, et al. Formation control and collision avoidance for multi-agent systems based on position estimation[J]. ISA Transactions, 2016, 61: 287. DOI:10.1016/j.isa.2015.12.010 |
| [3] |
HUANG Xu, YAN Ye, ZHOU Yang. Underactuated spacecraft formation reconfiguration with collision avoidance[J]. Acta Astronautica, 2017, 131: 166. DOI:10.1016/j.actaastro.2016.11.037 |
| [4] |
WEN Guoxing, CHEN C L P, LIU Yanjun. Formation control with obstacle avoidance for a class of stochastic multi-agent systems[J]. IEEE Transactions on Industrial Electronics, 2018, 65(7): 5847. DOI:10.1109/TIE.2017.2782229 |
| [5] |
NI Qing, HUANG Yiyong, CHEN Xiaoqian. Nonlinear control of spacecraft formation flying with disturbance rejection and collision avoidance[J]. Chinese Physics B, 2017, 26(1): 250. DOI:10.1088/1674-1056/26/1/014502 |
| [6] |
LI Chuanjiang, CHEN Lianming, GUO Yanning, et al. Cooperative surrounding control with collision avoidance for networked Lagrangian systems[J]. Journal of the Franklin Institute, 2018, 355(12): 5182. DOI:10.1016/j.jfranklin.2018.04.017 |
| [7] |
GHAPANI S, MEI Jie, REN Wei, et al. Fully distributed flocking with a moving leader for Lagrange networks with parametric uncertainties[J]. Automatica, 2016, 67(3): 67. DOI:10.1016/j.automatica.2016.01.004 |
| [8] |
CHEN Ti, WEN Hao, HU Haiyan, et al. Distributed finite-time tracking for a team of planar flexible spacecraft[J]. ISA Transactions, 2017, 69: 214. DOI:10.1016/j.isatra.2017.04.019 |
| [9] |
HE Xiaoyan, WANG Qingyun, YU Wenwu. Finite-time distributed cooperative attitude tracking control for multiple rigid spacecraft[J]. Applied Mathematics and Computation, 2015, 256(4): 724. DOI:10.1016/j.amc.2015.01.061 |
| [10] |
ZOU Anmin, KUMAR K D, DE RUITER A H J. Robust attitude tracking control of spacecraft under control input magnitude and rate saturations[J]. International Journal of Robust and Nonlinear Control, 2016, 26: 799. DOI:10.1002/rnc.3338 |
| [11] |
ZHOU Ning, CHEN Riqing, XIA Yuanqing, et al. Finite-time formation reconfiguration of multiple spacecraft with collision avoidance problems[C]//Proceedings of the 35th Chinese Control Conference. Chengdu: IEEE, 2016: 3200. DOI: 10.1109/ChiCC.2016.7553852
|
| [12] |
RUNE S, KRISTIANSEN R, NICKLASSON P J. Brief paper: Spacecraft formation reconfiguration with collision avoidance[J]. Automatica, 2011, 47(7): 1443. DOI:10.1016/j.automatica.2011.02.014 |
| [13] |
WONG H, DE QUEIROZ M S, KAPILA V. Adaptive tracking control using synthesized velocity from attitude measurements[J]. Automatica, 2001, 37(6): 947. DOI:10.1016/S0005-1098(01)00038-3 |
| [14] |
YOON H, EUN Y, PARK C. Adaptive tracking control of spacecraft relative motion with mass and thruster uncertainties[J]. Aerospace Scienceand Technology, 2014, 34(4): 75. DOI:10.1016/j.ast.2014.02.002 |
| [15] |
RAYMOND K, ANTONIO L, ANTOINE C, et al. Spacecraft relative rotation tracking without angular velocity measurements[J]. Automatica, 2009, 45(3): 750. DOI:10.1016/j.automatica.2008.10.012 |
| [16] |
ZHAO Yu, DUAN Zhisheng, WEN Guanghui. Distributed finite-time tracking of multiple Euler-Lagrange systems without velocity measurements[J]. International Journal of Robust and Nonlinear Control, 2015, 25(11): 1688. DOI:10.1002/rnc.3170 |
| [17] |
FRAZZOLI E, MAO Z H, OH J H, et al. Resolution of conflicts involving many aircraft via semidefinite programming[J]. Journal of Guidance, Control and Dynamics, 2001, 24(1): 79. DOI:10.2514/2.4678 |
| [18] |
CAO Lu, QIAO Dong, XU Jingwen. Suboptimal artificial potential function sliding mode control for spacecraft rendezvous with obstacle avoidance[J]. Acta Astronautica, 2018, 143(2): 133. DOI:10.1016/j.actaastro.2017.11.022 |
| [19] |
HAN Zhimin, LIN Zhiyun, CHEN Zhiyong, et al. Formation maneuvering with collision avoidance and connectivity maintenance[C]//Proceedings of International Symposium on Intelligent Control. Sydney, NSW: IEEE, 2015: 652. DOI: 10.1109/ISIC.2015.7307284
|
| [20] |
LI Xuehui, ZHU Zhibin, SONG Shenmin. Non-cooperative autonomous rendezvous and docking using artificial potentials and sliding mode control[J]. Proceedings of the Institution of Mechanical Engineers Part G Journal of Aerospace Engineering, 2018, 233(4): 1. DOI:10.1177/0954410017748988 |
| [21] |
郑重, 宋申民. 考虑避免碰撞的编队卫星自适应协同控制[J]. 航空学报, 2013, 34(8): 1934. ZHENG Zhong, SONG Shenmin. Adaptive coordination control of satellites within formation considering collision avoidance[J]. Acta Aeronautics et Astronautica Sinica, 2013, 34(8): 1934. DOI:10.7527/S1000-6893.2013.0174 |
| [22] |
HOKAYEM P F, STIPANOVIC D M, SPONG M W. Coordination and collision avoidance for Lagrangian systems with disturbances[J]. Applied Mathematics and Computation, 2010, 217(3): 1085. DOI:10.1016/j.amc.2010.03.074 |
| [23] |
PEREIRA A, LIU H, ORTEGA R. Globally stable adaptive formation control of Euler-Lagrange agents via potential functions[C]//Proceedings of American Control Conference. St. Louis, MO: IEEE, 2009: 2606. DOI: 10.1109/ACC.2009.5160707
|
| [24] |
黄涣, 杨乐平, 朱彦伟, 等. 双星电磁编队的动力学平衡态稳定性与控制[J]. 国防科技大学学报, 2013, 35(3): 12. HUANG Huan, YANG Leping, ZHU Yanwei, et al. Stability and control of dynamics equilibrium for two-spacecraft electromagnetic formation[J]. Journal of National University of Defense Technology, 2013, 35(3): 12. DOI:10.3969/j.issn.1001-2486.2013.03.003 |
| [25] |
郭永, 宋申民, 李学辉. 非合作交会对接的姿态和轨道耦合控制[J]. 控制理论与应用, 2016, 33(5): 638. GUO Yong, SONG Shenmin, LI Xuehui. Attitude and orbit coupled control for non-cooperative rendezvous and docking[J]. Control Theory & Applications, 2016, 33(5): 638. DOI:10.7641/CAT.2016.50709 |
| [26] |
张保群, 宋申民, 陈兴林. 带时延和拓扑切换的编队卫星鲁棒协同控制[J]. 宇航学报, 2012, 33(7): 910. ZHANG Baoqun, SONG Shenmin, CHEN Xinglin. Robust coordinated control for formation flying satellites with time delays and switching topologies[J]. Journal of Astronautics, 2012, 33(7): 910. DOI:10.3873/j.issn.1000-1328.2012.07.009 |
| [27] |
YAO Jingyi, ORDÓNEZ R, GAZI V. Swarm tracking using artificial potentials and sliding mode control[J]. Journal of Dynamic System, Measurement and Control, 2007, 129(5): 749. DOI:10.1115/1.2764511 |
| [28] |
SLOTINE J E, LI Weiping. Applied nonlinear control[M]. Englewood Cliffs, NJ: Prentice Hall, 1990.
|
| [29] |
REN Wei. Distributed leaderless consensus algorithms for networked Euler-Lagrange systems[J]. International Journal of Control, 2009, 82(11): 2137. DOI:10.1080/00207170902948027 |
| [30] |
GRAHAM A. Kronecker products and matrix calculus with applications[M]. New York: Halsted Press, 1981.
|
 2020, Vol. 52
2020, Vol. 52


