2. 上海宇航系统工程研究所,上海 201109
2. Aerospace System Engineering Shanghai, Shanghai 201109, China
垂直起降(vertical takeoff vertical landing,VTVL)可重复使用运载器(reusable launch vehicle,RLV)相较于其他起降方案具有仅需对传统火箭进行小幅改动,着陆场地需求弱、技术跨度小、研发成本相对较低等优点[1-2].随着SpaceX等多次成功实现垂直起降可重复使用火箭(VTVL-RLV)的子级垂直回收并复用,VTVL-RLV逐渐显现其在商业航天发射市场的竞争力[2].
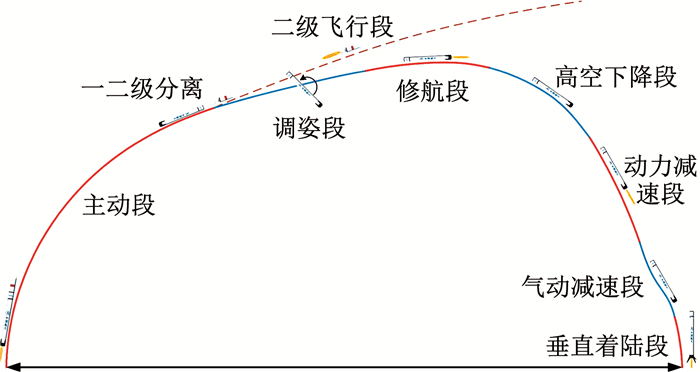
典型的VTVL-RLV在火箭一二级分离后,一子级经过6个飞行段后垂直软着陆于预定着陆场(如图 1所示),返回飞行空域广、速域大,发动机多次开关机、不同飞行段执行机构切换工作,结构、气动、风干扰等不确定性和内外扰动强[2].在返回飞行时其姿态控制呈现出强非线性和高动态的特点.
|
图 1 典型垂直起降火箭飞行剖面 Fig. 1 Flight profile of typical VTVL launch vehicle |
对于复杂干扰和大不确定性下的非线性控制问题,滑模控制(sliding mode control,SMC)由于具有对匹配扰动和不确定性的不变性而被广泛应用[3].但由于实际应用中系统惯性和采样频率有限等原因,滑模控制中的不连续控制项将会引起系统的抖振(chattering).对于滑模抖振问题,一种可行的解决途径为自适应滑模控制方法[4-9],即通过增益的自适应调整以匹配扰动变化,但自适应滑模方法的收敛速度将受限于增益的自适应调整过程.另一种可行的解决途径为基于观测器的控制方法(disturbance-observer-based control,DOBC),即利用扰动观测器估计扰动进而补偿其影响[10],其关键过程为对扰动观测器的合理设计.Zhang等[11]针对RLV返回的姿态控制问题,设计了基于四元数的自抗扰控制器(ADRC),通过扩张状态观测器(ESO)来实现扰动观测.Hall等[12-13]基于有限时间收敛滑模观测器估计扰动进而补偿.Su等[14]设计了RLV非奇异终端滑模(non-singular terminal sliding mode control,NTSMC)姿态控制器,模型不确定性和外部扰动采用有限时间收敛扰动观测器进行估计.针对VTVL-RLV,钱默抒等[15]设计了自适应滑模观测器用于估计扰动和不确定性,进而设计了基于观测器的滑模动态面控制方法.在观测器的设计中需要权衡收敛速度、精度和鲁棒性,上述有限时间收敛观测器能够在有限时间内收敛,但其收敛时间取决于初始偏差并随着初始偏差范数趋近于无穷而趋于无穷[16],而观测器的调节过程过长将对控制系统性能造成不利影响.为降低观测器的调节过程对系统的影响,可以采用收敛时间有常值上界且与初始偏差无关的固定时间收敛观测器[17-18].
考虑到VTVL-RLV返回飞行姿态跟踪控制的强非线性和高动态特性,以及气动减速段的制导机动需求,在控制器的设计中要求能够快速高精度跟踪制导指令姿态角,以避免控制动态过程和控制误差对制导系统造成影响.传统的有限时间收敛滑模控制方法由于其收敛时间随着初始偏差范数趋近于无穷而趋于无穷[16],因此本文将进一步研究对初始偏差具有不变性的固定时间收敛方法设计滑模控制器.
本文针对复杂扰动影响下的VTVL-RLV返回飞行快速姿态跟踪控制问题进行研究,首先建立垂直起降火箭返回飞行的动力学模型,并考虑扰动和不确定性构建气动减速段姿态跟踪控制状态方程;进而设计基于固定时间收敛扰动观测器(fixed-time convergence disturbance observer,FxTDO)的快速姿态跟踪控制器,其中控制指令通过双幂次固定时间收敛滑模方法(double-order power fixed-time convergence sliding mode control,DPFxTSMC)生成,并采用FxTDO快速高精度的估计扰动以补偿扰动影响,从而去除不连续控制项以抑制抖振影响;最后通过气动减速段的仿真对固定时间收敛扰动观测器和基于观测器的双幂次固定时间收敛滑模控制器的性能进行了分析和讨论.
1 垂直起降可重复使用火箭动力学模型VTVL-RLV一子级的返回全程可采用的执行机构为变推力可摇摆火箭发动机、栅格舵(grid fin)和反推力控制系统(RCS),各段执行机构见表 1.
| 表 1 返回全程各段执行机构 Tab. 1 Actuators of return flight phases |
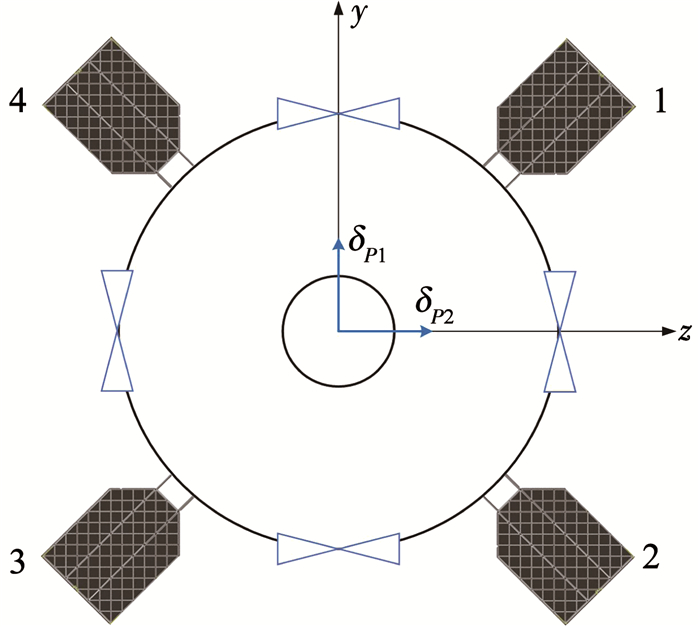
返回飞行中的火箭一子级的执行机构具体如图 2所示.本文研究的火箭一子级在返回过程中仅中间一台发动机点火工作,为双向“十”字形摆动;4个栅格舵为“×”字布局,安装在一子级头部,发射时收起紧贴箭体,在进入大气前栅格舵展开工作;8个RCS安装在一子级头部,分别负责俯仰、偏航和滚转通道.定义发动机的俯仰等效摆角为δφ、偏航等效摆角为δψ,则发动机等效摆角与实际摆角的关系可写为:
| $ {\delta _\varphi } = - {\delta _{p1}},{\delta _\psi } = {\delta _{p2}}. $ |
|
图 2 一子级返回飞行执行机构示意图(后视图) Fig. 2 Diagram of first stage actuator of VTVL (back view) |
一子级进入大气后自尾部来流,定义δz, δy, δx分别为栅格舵的等效俯仰舵偏角、等效偏航舵偏角、等效滚转舵偏角,δz, δy, δx可表示为:
| $ {\delta _z} = \left( {{\delta _3} + {\delta _4} - {\delta _1} - {\delta _2}} \right)/4, $ |
| $ {\delta _y} = \left( {{\delta _3} + {\delta _2} - {\delta _1} - {\delta _4}} \right)/4, $ |
| $ {\delta _x} = \left( {{\delta _1} + {\delta _2} + {\delta _3} + {\delta _4}} \right)/4. $ |
因此建立VTVL-RLV一子级返回飞行动力学模型,其中式(1)为发射坐标系下质心动力学方程,式(2)为箭体坐标系下绕质心动力学方程,各坐标系和坐标系转换关系详见文献[19].
| $ \begin{array}{l} m\frac{{\rm{d}}}{{{\rm{d}}t}}\left[ {\begin{array}{*{20}{c}} {{V_x}}\\ {{V_y}}\\ {{V_z}} \end{array}} \right] = \mathit{\boldsymbol{C}}_B^G\left[ {\begin{array}{*{20}{c}} P\\ {P{\delta _\varphi }}\\ { - P{\delta _\psi }} \end{array}} \right] + \mathit{\boldsymbol{C}}_V^G\left[ {\begin{array}{*{20}{c}} { - {R_x}}\\ {{R_y}}\\ {{R_z}} \end{array}} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;m\left[ {\begin{array}{*{20}{l}} {{g_x}}\\ {{g_y}}\\ {{g_z}} \end{array}} \right] + {\mathit{\boldsymbol{F}}_e} + {\mathit{\boldsymbol{F}}_k} + {{\mathit{\boldsymbol{F'}}}_k}, \end{array} $ | (1) |
| $ \begin{array}{l} \frac{{{\rm{d}}\mathit{\boldsymbol{H}}}}{{{\rm{d}}t}} + \mathit{\boldsymbol{\omega }} \times \mathit{\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}} 0\\ { - P\left( {{x_R} - {x_r}} \right){\delta _\psi }}\\ { - P\left( {{x_R} - {x_T}} \right){\delta _\varphi }} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0\\ {{M_{{{\ddot \delta }_\psi }}}}\\ {{M_{{{\ddot \delta }_\varphi }}}} \end{array}} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {{M_{{\rm{RCS}}x}}}\\ {{M_{{\rm{RCS}}y}}}\\ {{M_{{\rm{RCS}}z}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{M_{\delta x}}}\\ {{M_{\delta y}}}\\ {{M_{\delta z}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0\\ {{M_\beta }}\\ {{M_\alpha }} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{M_{\omega x}}}\\ {{M_{\omega y}}}\\ {{M_{\omega z}}} \end{array}} \right] + {{\mathit{\boldsymbol{M'}}}_k}. \end{array} $ | (2) |
式(1)中:m为火箭一子级的质量; 定义V为发射系下火箭一子级的速度矢量;[Vx Vy Vz]T为V在发射系各轴的分量;ωe为地球自转角速度;CBG=L(γ, ψ, φ)为箭体系到发射系的转换矩阵;(γ, ψ, φ)分别为滚转角、偏航角和俯仰角,而[P Pδφ-Pδψ]T为箭体系下发动机推力的分量;CVG=L(v, σ, θ)为速度系到发射系的转换矩阵,(v, δ, θ)分别为倾侧角、弹道偏角和弹道倾角,而[-Rx Ry Rz]T为速度系下气动力的分量;[mgx mgy mgz]T分别为发射系下引力的分量;Fe为离心惯性力,Fk为哥式惯性力,F′k为附加哥氏力.式(2)中:[0-P(xR-xT)δψ-P(xR-xT)δφ]T为推力产生的控制力矩的分量;xR为中心摇摆发动机铰链的纵轴位置;xT为火箭质心的纵轴位置;
| $ \mathit{\boldsymbol{J}} = \left[ {\begin{array}{*{20}{c}} {{J_{xx}}}&{{J_{xy}}}&{{J_{xz}}}\\ {{J_{yx}}}&{{J_{yy}}}&{{J_{yz}}}\\ {{J_{zx}}}&{{J_{zy}}}&{{J_{zz}}} \end{array}} \right],\mathit{\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}} {{H_x}}\\ {{H_y}}\\ {{H_z}} \end{array}} \right] = \mathit{\boldsymbol{J}} \times \mathit{\boldsymbol{\omega }}. $ |
对于轴对称的VTVL-RLV一子级,一般认为箭体坐标系为惯性主轴系,可认为火箭一子级对箭体坐标系各轴的惯量积为零.因此转动惯量矩阵可简化为
| $ \mathit{\boldsymbol{J}} = \left[ {\begin{array}{*{20}{c}} {{J_x}}&0&0\\ 0&{{J_y}}&0\\ 0&0&{{J_z}} \end{array}} \right]. $ |
VTVL-RLV一子级在进入大气后的气动减速段采用栅格舵进行气动力控制,且该段面临的扰动特性在返回全程中较为突出,因此本文将主要建立气动减速段控制系统模型并以气动减速段为基础开展VTVL-RLV姿态跟踪控制方法研究.
基于火箭一子级绕质心动力学模型(2)建立如下的非线性系统模型:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{ \boldsymbol{\dot \varOmega} }} = \mathit{\boldsymbol{R\omega }} + \Delta \mathit{\boldsymbol{f}},}\\ {\mathit{\boldsymbol{\dot \omega }} = - {\mathit{\boldsymbol{J}}^{ - 1}}{\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{J\omega }} + {\mathit{\boldsymbol{J}}^{ - 1}}{\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{U}} + {\mathit{\boldsymbol{J}}^{ - 1}}\Delta \mathit{\boldsymbol{d}}.} \end{array}} \right. $ |
式中:ω=[ωx ωy ωz]T为箭体转动角速度矢量;Ω=[φ ψ γ]T为姿态角向量;Δf、Δd分别为系统各阶未建模的不确定性及内外干扰;其中,ω×和R分别为:
| $ {\mathit{\boldsymbol{\omega }}^ \times } = \left[ {\begin{array}{*{20}{c}} 0&{ - {\omega _z}}&{{\omega _y}}\\ {{\omega _z}}&0&{ - {\omega _x}}\\ { - {\omega _y}}&{{\omega _x}}&0 \end{array}} \right], $ |
| $ \mathit{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} 0&{\sin \gamma /cos\psi }&{\cos \gamma /\cos \psi }\\ 0&{cos\gamma }&{ - \sin \gamma }\\ 1&{\tan \psi \sin \gamma }&{\tan \psi \cos \gamma } \end{array}} \right]. $ |
在气动减速段,控制矩阵B1和控制向量U分别为:
| $ {\mathit{\boldsymbol{B}}_1} = \left[ {\begin{array}{*{20}{c}} {m_x^{{\delta _x}}qSL}&0&0\\ 0&{m_y^{{\delta _y}}qSL}&0\\ 0&0&{m_z^{{\delta _z}}qSL} \end{array}} \right], $ |
| $ \mathit{\boldsymbol{U}} = {\left[ {\begin{array}{*{20}{c}} {{\delta _x}}&{{\delta _y}}&{{\delta _z}} \end{array}} \right]^{\rm{T}}}. $ |
式中:mxδx、myδy、mzδz分别为栅格舵的滚转、偏航、俯仰的操纵力矩系数;q为来流的动压;L为火箭箭体的特征长度.
由火箭姿态动力学方程式可得:
| $ \mathit{\boldsymbol{ \boldsymbol{\ddot \varOmega} }} = \frac{{\rm{d}}}{{{\rm{d}}t}}(\mathit{\boldsymbol{R}}\omega + \Delta \mathit{\boldsymbol{f}}) = \mathit{\boldsymbol{\dot R\omega }} + \mathit{\boldsymbol{R\dot \omega }} + \Delta \mathit{\boldsymbol{\dot f}} = \mathit{\boldsymbol{F}} + \mathit{\boldsymbol{BU}} + \Delta \mathit{\boldsymbol{D}}. $ | (3) |
式中,F=(
| $ \mathit{\boldsymbol{ \boldsymbol{\ddot \varOmega} }} = \mathit{\boldsymbol{\bar H}} + \mathit{\boldsymbol{BU}}, $ |
式中H=F+ΔD,视为火箭姿态系统的总扰动.总扰动H包含已建模量、未建模动态、未知扰动及其微分量.
若VTVL-RLV一子级返回飞行的制导指令为ΩC=[φc ψc γc]T,那么控制系统的目标是使火箭一子级的实际姿态快速稳定的跟踪制导指令,即:
| $ \mathop {\lim }\limits_{t > {t_F}} \left\| {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} - {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_c}} \right\| = 0,\mathop {\lim }\limits_{t \to {t_F}} \left\| {\mathit{\boldsymbol{ \boldsymbol{\dot \varOmega} }} - {{\mathit{\boldsymbol{ \boldsymbol{\dot \varOmega} }}}_c}} \right\| = 0, $ |
式中, tF为有限的时间小量.
定义
| $ {{\mathit{\boldsymbol{\dot x}}}_1} = {\mathit{\boldsymbol{x}}_2},{{\mathit{\boldsymbol{\dot x}}}_2} = \mathit{\boldsymbol{H}} + \mathit{\boldsymbol{BU}}, $ | (4) |
式中,
假设1 扰动H和H均连续可微,其本身及其导数未知但一致有界.
2 基于FxTDO的双幂次固定时间收敛滑模控制针对式(4)所示的姿态控制系统,本文将三通道进行解耦设计各通道独立的单输入单输出(single input single output,SISO)控制器,各通道之间耦合量视作各通道总扰动的一部分,显然各通道的扰动均满足假设1,各通道(俯仰/偏航/滚转)的状态方程均可写为:
| $ y = {x_1},{{\dot x}_1} = {x_2},{{\dot x}_2} = bu + h, $ | (5) |
由假设1可知h满足|h|≤h0,
针对式(5)所示的二阶SISO系统,经典的滑模控制设计的滑模面为
| $ s = k{x_1} + {x_2}, $ | (6) |
式中,滑模面增益k>0.对应的滑模控制律为
| $ u\left( t \right) = - {b^{ - 1}}\left( {k{x_2} + \lambda \text{sign}\left( s \right)} \right), $ | (7) |
式中,λsign (s)是用于补偿未知匹配扰动的不连续控制项,增益λ为设计参数.在工程中,由于扰动边界值未知增益λ的取值较为保守,进而导致抖振.
2.1 非线性控制预备知识考虑如下非线性动态系统:
| $ \mathit{\boldsymbol{\dot x}}\left( t \right) = \mathit{\boldsymbol{f}}\left( {\mathit{\boldsymbol{x}}\left( t \right),\mathit{\boldsymbol{u}}\left( t \right)} \right),\mathit{\boldsymbol{x}}\left( 0 \right) = {\mathit{\boldsymbol{x}}_0}. $ | (8) |
式中,x=[x1, x2, …, xn]T∈
引理1[20] 假设系统(8)存在连续可微正定函数V(x):
| $ \mathit{\boldsymbol{\dot V}}(\mathit{\boldsymbol{x}}) + c{V^a}(\mathit{\boldsymbol{x}}) \le 0,\mathit{\boldsymbol{x}} \in {\mathscr N}\backslash \left\{ {\bf{0}} \right\}, $ |
则系统(8)在原点处有限时间收敛,且系统从初始状态x0收敛到原点的收敛时间T(x0)满足:
| $ T\left( {{\mathit{\boldsymbol{x}}_0}} \right) \le \frac{1}{{c\left( {1 - \alpha } \right)}}{V^{1 - \alpha }}\left( {{\mathit{\boldsymbol{x}}_0}} \right),{\mathit{\boldsymbol{x}}_0} \in {\mathscr N}\backslash \left\{ {\bf{0}} \right\}, $ |
此外,若
针对式(5)所示的二阶SISO系统,由假设1可知h满足|h|≤h0,
| $ \begin{array}{*{20}{c}} {{{\dot z}_1} = {z_2} + {k_1}\varepsilon {\phi _1}\left( {\frac{{y - {z_1}}}{{{\varepsilon ^2}}}} \right),}\\ {{{\dot z}_2} = {z_3} + {k_2}{\phi _2}\left( {\frac{{y - {z_1}}}{{{\varepsilon ^2}}}} \right) + bu\left( t \right),}\\ {{{\dot z}_3} = {k_3}{\varepsilon ^{ - 1}}{\phi _3}\left( {\frac{{y - {z_1}}}{{{\varepsilon ^2}}}} \right).} \end{array} $ | (9) |
式中:z=[z1, z2, z3]T∈
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} { - {k_1}}&1&0\\ { - {k_2}}&0&1\\ { - {k_3}}&0&0 \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{A}}_r} = \left[ {\begin{array}{*{20}{c}} { - {k_1}\left( {1 + \tau } \right)}&1&0\\ { - {k_2}\left( {1 + {\tau ^2}} \right)}&0&1\\ { - {k_3}\left( {1 + {\tau ^3}} \right)}&0&0 \end{array}} \right]. $ |
式中:τ∈(0, 1];ϕi(·)(i=1, 2, 3)为设计的修正项,具体形式为:
| $ {\phi _i}\left( x \right) = {⎾ x ⏌^{{\alpha _i}}} + {⎾ x ⏌^{{\beta _i}}},i = 1,2,3 $ |
| $ {\alpha _i} = i\alpha - \left( {i - 1} \right),\alpha \in \left( {0.5,1.0} \right) $ |
| $ {\beta _i} = i\beta - \left( {i - 1} \right),\beta \in \left( {1.0,1.5} \right). $ |
式中,函数「·」m=|·|msign(·), 其中sign(·)为符号函数.观测器输出的估计误差变量为:
| $ {e_i}\left( t \right) = {x_i}\left( t \right) - {z_i}\left( t \right),i = 1,2 $ |
| $ {e_3}\left( t \right) = {x_3}\left( t \right) - {z_3}\left( t \right) = h\left( t \right) - {z_3}\left( t \right). $ |
定理1[21-22] 针对式(5)所示的二阶SISO系统,假设系统输出y(t)和控制输入bu(t)均为已知量,且系统不确定干扰h(t)满足|h|≤h0,
注1[21-22] 定理1所示FxTDO在确定ki,α和β后,主要可通过调节ε得到满意的估计值.
2.3 双幂次固定时间收敛滑模面针对式(5)所示的二阶SISO系统,为补偿系统扰动影响并消除抖振,考虑双幂次修正项的特性,本文给出了一种双幂次固定时间收敛滑模面(double-order power fixed-time convergence sliding mode surface)[23]为:
| $ \begin{array}{*{20}{c}} {s\left( t \right) = {x_2}\left( t \right) - \int w \left( t \right){\rm{d}}t,}\\ {w(t) = - {\kappa _1}{{{⎾ {{x_1}} ⏌}^{{\gamma _1}}}} - {\kappa _2}{{{⎾ {{x_2}} ⏌}^{{\gamma _2}}}} - {K_1}{{⎾ {{x_1}} ⏌}^{{\chi _1}}} - {K_2}{{⎾ {{x_2}} ⏌}^{{\chi _2}}},} \end{array} $ | (10) |
其中,指数γi(i=1, 2)和χi(i=1, 2)均满足:
| $ \begin{array}{l} 0 < {\gamma _i} < 1,i = 1,2\\ \gamma \in \left( {1 - {\varepsilon _1},1} \right),{\gamma _3} = 1,{\gamma _2} = \gamma ,{\gamma _1} = {\gamma _2}{\gamma _3}/\left( {2{\gamma _3} - {\gamma _2}} \right), \end{array} $ |
| $ \begin{array}{l} {\chi _i} > 1,i = 1,2\\ \chi \in \left( {1,1 + {\varepsilon _2}} \right),{\chi _3} = 1,{\chi _2} = \chi ,{\chi _1} = {\chi _2}{\chi _3}/\left( {2{\chi _3} - {\chi _2}} \right). \end{array} $ |
式中, ε1>0,ε2>0,均为充分小的正数.由增益κi(i=1, 2)可定义矩阵A1,增益Ki(i=1, 2)可定义矩阵A2,均满足Hurwitz条件,具体表示为:
| $ {\mathit{\boldsymbol{A}}_1} = \left[ {\begin{array}{*{20}{c}} 0&1\\ { - {\kappa _1}}&{ - {\kappa _2}} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{A}}_2} = \left[ {\begin{array}{*{20}{c}} 0&1\\ { - {K_1}}&{ - {K_2}} \end{array}} \right]. $ |
定理2[23] 如果系统(5)达到式(10)所示的双幂次滑模面即s=0,则系统将沿着滑模面固定时间内收敛到原点.参考文献[23]给出如下证明.
证明 令s=0,由式(10)可得:
| $ {x_2}\left( t \right) = \int w \left( t \right){\rm{d}}t, $ | (11) |
将式(11)代入式(5),有:
| $ \begin{array}{*{20}{c}} {{{\dot x}_1} = {x_2}\left( t \right),}\\ {{{\dot x}_2}\left( t \right) = w\left( t \right) = - {\kappa _1}{{{⎾ {{x_1}} ⏌}^{{\gamma _1}}}} - {\kappa _2}{{{⎾ {{x_2}} ⏌}^{{\gamma _2}}}} - }\\ {{K_1}{{⎾ {{x_1}} ⏌}^{{\chi _1}}} - {K_2}{{⎾ {{x_2}} ⏌}^{{\chi _2}}}.} \end{array} $ | (12) |
这里将式(12)所示系统的低阶幂次和高阶幂次两部分进行分别讨论.
Step 1 考虑如下低阶幂次系统:
| $ \begin{array}{*{20}{c}} {{{\dot x}_1} = {x_2}\left( t \right),}\\ {{{\dot x}_2}\left( t \right) = - {\kappa _1}{{{⎾ {{x_1}} ⏌}^{{\gamma _1}}}} - {\kappa _2}{{{⎾ {{x_2}} ⏌}^{{\gamma _2}}}},} \end{array} $ | (13) |
其向量场形式可写成
由于矩阵A1满足Hurwitz条件,因此满足如下Lyapunov方程:
| $ {\mathit{\boldsymbol{P}}_1}{\mathit{\boldsymbol{A}}_1} + \mathit{\boldsymbol{A}}_1^{\rm{T}}{\mathit{\boldsymbol{P}}_1} = - {\mathit{\boldsymbol{Q}}_1}. $ |
式中: P1为正定对称矩阵,Q1为正定矩阵.
构造关于系统(13)的Lyapunov函数:
| $ {V_1}\left( {\gamma ,\mathit{\boldsymbol{x}}} \right) = {V_1}\left( \zeta \right) = {\zeta ^T}{\mathit{\boldsymbol{P}}_1}\zeta , $ | (14) |
式中,ζ=[x1γ1, x2γ2]T.显然,当且仅当x=0时V1=0.
若γ=1,系统(13)可表示为线性系统
| $ {V_1}\left( {1,\mathit{\boldsymbol{x}}} \right) = {\mathit{\boldsymbol{x}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_1}\mathit{\boldsymbol{x}}, $ |
求V1(1, x)的全导数为
| $ {{\dot V}_1}\left( {1,\mathit{\boldsymbol{x}}} \right) = {{\dot x}^{\rm{T}}}{\mathit{\boldsymbol{P}}_1}\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{x}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_1}\mathit{\boldsymbol{\dot x}} = - {\mathit{\boldsymbol{x}}^{\rm{T}}}{\mathit{\boldsymbol{Q}}_1}\mathit{\boldsymbol{x}} < 0. $ |
考虑到f1(x)关于γ连续,因此必然存在一个充分小的正数ε1>0,使得当γ∈(1-ε1)时,全导数
根据加权齐次性(weighted homogeneity)[24]定义,f1(x)、V1(γ, x)和
| $ {{\dot V}_1}\left( {\gamma ,x} \right) \le - {c_1}V_1^{1 + {d_1}}\left( {\gamma ,x} \right), $ |
成立,式中0<(1+d1)<1.
Step 2 考虑如下高阶幂次系统:
| $ \begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right) = {x_2}\left( t \right),}\\ {{{\dot x}_2}\left( t \right) = - {\kappa _1}{{⎾ {{x_1}} ⏌}^{{\chi _1}}} - {\kappa _2}{{⎾ {{x_2}} ⏌}^{{\chi _2}}},} \end{array} $ | (15) |
其向量场形式可写成
由于矩阵A2满足Hurwitz条件,因此满足如下Lyapunov方程:
| $ {\mathit{\boldsymbol{P}}_2}{\mathit{\boldsymbol{A}}_2} + \mathit{\boldsymbol{A}}_2^{\rm{T}}{\mathit{\boldsymbol{P}}_2} = - {\mathit{\boldsymbol{Q}}_2}. $ |
式中:P2为正定对称矩阵,Q2为正定矩阵.
构造关于系统(15)的Lyapunov函数:
| $ {V_2}\left( {\chi ,\mathit{\boldsymbol{x}}} \right) = {V_2}\left( \mathit{\boldsymbol{\psi }} \right) = {\mathit{\boldsymbol{\psi }}^T}{\mathit{\boldsymbol{P}}_2}\mathit{\boldsymbol{\psi }}, $ |
式中,ψ=[x1χ1, x2χ2]T.显然,当且仅当x=0时V2=0.
同理,必然存在一个充分小的正数ε2>0,使得当χ∈(1, 1+ε2)时,全导数
| $ {{\dot V}_2}\left( {\chi ,x} \right) \le - {c_2}V_2^{1 + {d_2}}\left( {\chi ,x} \right), $ |
成立,式中d2=(χ-1)/χ>0, (1+d2)>1.
由于P2和P1为正定对称矩阵,根据关于二次型的Rayleigh不等式可得:
| $ {\lambda _{\min }}\left( {{\mathit{\boldsymbol{P}}_2}} \right){\left\| \psi \right\|^2} \le {V_2} \le {\lambda _{\max }}\left( {{\mathit{\boldsymbol{P}}_2}} \right){\left\| \psi \right\|^2}, $ | (16) |
| $ {\lambda _{\min }}\left( {{\mathit{\boldsymbol{P}}_1}} \right){\left\| \zeta \right\|^2} \le {V_1} \le {\lambda _{\max }}\left( {{\mathit{\boldsymbol{P}}_1}} \right){\left\| \psi \right\|^2}. $ | (17) |
将全导数
| $ \begin{array}{l} {{\dot V}_2} \le {{\dot V}_2}\left( \psi \right) + \frac{{\partial {V_2}}}{{\partial {x_2}}}\left( { - {\kappa _1}{{⎾ {{x_1}} ⏌}^{{\gamma _1}}} - {\kappa _2}{{⎾ {{x_2}} ⏌}^{{\gamma _2}}}} \right) \le \\ \;\;\;\;\;\;{{\dot V}_2}\left( \psi \right) \le - {c_2}V_2^{1 + {d_2}}. \end{array} $ | (18) |
考虑到存在常数Θ满足0<Θ≤λmin(P2),由式(18)可知,当初值V2|t=t0>Θ时,V2将从初始状态固定时间Ts2内收敛到Θ,收敛时间Ts2满足:
| $ {T_{s2}} \le 1/{c_2}{d_2}{\mathit{\Theta }^{{d_2}}}, $ |
由于Θ≤λmin(P2),根据式(16), 可知当t>Ts2时:
| $ {\left\| \psi \right\|^2} \le {V_2}/{\lambda _{\min }}\left( {{\mathit{\boldsymbol{P}}_2}} \right) \le \mathit{\Theta }/{\lambda _{\min }}\left( {{\mathit{\boldsymbol{P}}_2}} \right) \le 1. $ |
考虑到χi>1和0<γi<1,i=1, 2,根据ψ和ζ的定义可知,当系统状态x满足‖ψ‖2≤1时,‖x‖一致有界, 则对应的‖ψ‖2≤Ξ(常数Ξ≥1).根据式(17)可得:
| $ {V_1} \le {\lambda _{\max }}\left( {{\mathit{\boldsymbol{P}}_1}} \right){\left\| \zeta \right\|^2} \le {\lambda _{\max }}\left( {{\mathit{\boldsymbol{P}}_1}} \right), $ |
同理, 将全导数
| $ \begin{array}{l} {{\dot V}_1} \le {{\dot V}_1}\left( \xi \right) + \frac{{\partial {V_1}}}{{\partial {x_2}}}\left( { - {K_1}{{⎾ {{x_1}} ⏌}^{{\chi _1}}} - {K_2}{{⎾ {{x_2}} ⏌}^{{\chi _2}}}} \right) \le \\ \;\;\;\;\;\;{{\dot V}_1}\left( \xi \right) \le - {c_1}V_1^{1 + {d_1}}, \end{array} $ | (19) |
由式(19)可知,V1将从V1=Ξ·λmax(P1)固定时间Ts1内收敛到原点,收敛时间Ts1满足:
| $ {T_{s1}} \le {\left| {{\lambda _{\max }}\left( {{\mathit{\boldsymbol{P}}_1}} \right)} \right|^{\left| {{d_1}} \right|}}/{c_1}\left| {{d_1}} \right|, $ |
综上所述,式(12)所示系统状态x将固定时间Tf内收敛到原点,收敛时间Tf满足:
| $ {T_f} \le {T_{s1}} + {T_{s2}} \le \frac{{{{\left[ {\mathit{\Xi } \cdot {\lambda _{\max }}\left( {{\mathit{\boldsymbol{P}}_1}} \right)} \right]}^{\left| {{d_1}} \right|}}}}{{{c_1}\left| {{d_1}} \right|}} + \frac{1}{{{c_2}{d_2}{\mathit{\Theta }^{{d_2}}}}}, $ |
即系统(5)达到式(10)所示的双幂次滑模面后,系统将沿着滑模面固定时间内收敛到原点.
2.4 双幂次固定时间收敛滑模控制律针对二阶SISO系统(5),结合式(9)所示固定时间收敛扰动观测器(FxTDO)和式(10)所示双幂次固定时间收敛滑模面,设计的基于FxTDO的双幂次固定时间收敛滑模控制律(FxTDO-based double-order power fixed-time convergence sliding mode control,FxTDOB-DPFxTSMC)为
| $ u\left( t \right) = {b^{ - 1}}\left[ {w\left( t \right) - \left( {\eta s + \zeta {{⎾ s ⏌}^{{v_1}}} + \zeta {{⎾ s ⏌}^{{v_2}}} + \tilde h} \right)} \right]. $ | (20) |
式中:参数满足η>0,ζ>0,0<υ1<1,υ2>1;
定理3 对于式(5)所示系统,设计式(9)所示固定时间收敛扰动观测器、式(10)所示固定时间收敛双幂次滑模面以及相应的控制器(20),系统(5)将固定时间内收敛到原点的邻域内.
证明 对滑模面(10)求时间导数并沿系统(5)展开后将式(20)代入,有
| $ \begin{array}{l} \dot s = {{\dot x}_2} - w = bu + h - w = \\ \;\;\;\; - \eta s - \zeta {⎾ s ⏌^{{v_1}}} - \zeta {⎾ s ⏌^{{v_2}}} - \left( {\tilde h - h} \right). \end{array} $ | (21) |
定义如下Lyapunov函数:
| $ V\left( s \right) = \frac{1}{2}{s^2}, $ |
当前仅当s=0时V=0;当s→∞时V→∞.
对V求时间导数并将式(21)代入,有
| $ \begin{array}{l} \dot V = - \eta {\left| s \right|^2} - \zeta {\left| s \right|^{{v_1} + 1}} - \zeta {\left| s \right|^{{v_2} + 1}} - \left( {\tilde h - h} \right)s \le \\ \;\;\;\;\;\; - \zeta {\left| s \right|^{{v_1} + 1}} - \zeta {\left| s \right|^{{v_2} + 1}} + \left| {h - \tilde h} \right|\left| s \right|. \end{array} $ | (22) |
根据定理1,观测器估计误差
| $ \left| {h - \tilde h} \right| \le N,{\rm{if}}\;t > {t_f}, $ | (23) |
结合式(22)、(23),当t>tf时,有
| $ \begin{array}{l} \dot V \le - \zeta {\left| s \right|^{{v_1} + 1}} - \zeta {\left| s \right|^{{v_2} + 1}} + N\left| s \right| \le \\ \;\;\;\;\;\; - {2^{\frac{{{v_1} + 1}}{2}}}\zeta {V^{\frac{{{v_1} + 1}}{2}}} - {2^{\frac{{{\nu _2} + 1}}{2}}}\zeta {V^{\frac{{{\nu _2} + 1}}{2}}} + {2^{\frac{1}{2}}}N{V^{\frac{1}{2}}}. \end{array} $ | (24) |
式(24)可分别表示为:
| $ \dot V \le - {2^{\frac{{{v_2} + 1}}{2}}}\zeta {V^{\frac{{{v_2} + 1}}{2}}} - \left( {{2^{\frac{{{v_1} + 1}}{2}}}{\xi ^{\frac{{{v_1} + 1}}{2}}} - {2^{\frac{1}{2}}}N{V^{\frac{1}{2}}}} \right), $ | (25) |
| $ \dot V \le - {2^{\frac{{{v_1} + 1}}{2}}}{\zeta ^{\frac{{{v_1} + 1}}{2}}} - \left( {{2^{\frac{{{v_2} + 1}}{2}}}{\xi ^{\frac{{{v_2} + 1}}{2}}} - {2^{\frac{1}{2}}}N{V^{\frac{1}{2}}}} \right), $ | (26) |
令:
| $ {2^{\frac{{{v_1} + 1}}{2}}}\zeta {V^{\frac{{{v_1} + 1}}{2}}} - {2^{\frac{1}{2}}}N{V^{\frac{1}{2}}} \ge 0, $ |
| $ {2^{\frac{{{v_2} + 1}}{2}}}\zeta {V^{\frac{{{v_2} + 1}}{2}}} - {2^{\frac{1}{2}}}N{V^{\frac{1}{2}}} \ge 0, $ |
则有:
| $ V \ge {2^{ - 1}}{\left( {N/\zeta } \right)^{2/{v_1}}} \buildrel \Delta \over = {V_1}, $ | (27) |
| $ V \ge {2^{ - 1}}{\left( {N/\zeta } \right)^{2/{v_2}}} \buildrel \Delta \over = {V_2}. $ | (28) |
Step 1 假设N/ζ≥1时,这种情况下V1≥V2,根据式(25)有:
| $ \dot V \le - {2^{\frac{{{v_2} + 1}}{2}}}\zeta {V^{\frac{{{v_2} + 1}}{2}}},V \ge {V_1} $ |
由引理1可得,V从初值V0收敛到V1的收敛时间T1满足:
| $ \begin{array}{l} {T_1} \le \frac{{{2^{\frac{{1 - {v_2}}}{2}}}}}{{\zeta \left( {{v_2} - 1} \right)}}\left( {V_1^{\left( {1 - {v_2}} \right)/2} - V_0^{\left( {1 - {v_2}} \right)/2}} \right) \le \\ \;\;\;\;\;\;\frac{{{2^{\frac{{1 - {v_2}}}{2}}}}}{{\zeta \left( {{v_2} - 1} \right)}}V_1^{\left( {1 - {v_2}} \right)/2} = {T_{{\rm{max}},1}}. \end{array} $ |
Step 2 假设N/ζ≤1时,这种情况下V1≤V2≤1,有
| $ \dot V \le \left\{ {\begin{array}{*{20}{l}} { - {2^{\frac{{{v_2} + 1}}{2}}}\zeta {V^{\frac{{{v_2} + 1}}{2}}},V \ge 1;}\\ { - {2^{\frac{{{v_1} + 1}}{2}}}\zeta {V^{\frac{{{v_1} + 1}}{2}}},1 \ge V \ge {V_2},} \end{array}} \right. $ |
由引理1可得,V从初值V0收敛到V2的收敛时间T2满足:
| $ \begin{array}{l} {T_2} \le \frac{{{2^{\frac{{1 - {v_2}}}{2}}}}}{{\zeta \left( {{v_2} - 1} \right)}} + \frac{{{2^{\frac{{1 - {v_1}}}{2}}}}}{{\zeta \left( {1 - {v_1}} \right)}}\left( {1 - V_2^{\left( {1 - {v_1}} \right)/2}} \right) \le \\ \;\;\;\;\;\;\frac{{{2^{\frac{{1 - {v_2}}}{2}}}}}{{\zeta \left( {{v_2} - 1} \right)}} + \frac{{{2^{\frac{{1 - {v_1}}}{2}}}}}{{\zeta \left( {1 - {v_1}} \right)}} = {T_{\max ,2}}. \end{array} $ |
因此,系统将在时间Ts内收敛到滑模面s=0的邻域Es内,具体可表示为:
| $ {\mathit{\boldsymbol{E}}_s} = \left\{ {s \in \mathbb{R}|V\left( s \right) \leqslant {V_f}} \right\}, $ |
| $ {V_f} = \left\{ {\begin{array}{*{20}{l}} {{V_1},}&{{V_1} \ge {V_2};}\\ {{V_2},}&{{V_1} \le {V_2},} \end{array}} \right. $ |
| $ {T_s} \le \left\{ {\begin{array}{*{20}{l}} {{T_{\max ,1}},{V_1} \ge {V_2};}\\ {{T_{\max ,2}},{V_1} \le {V_2}.} \end{array}} \right. $ |
进一步结合定理2及文献[22, 26]可以认为,当系统到达滑模面s=0的邻域内后,系统将在固定时间内收敛到原点的邻域内.
注2 由式(27)、(28)可知无不连续控制项的控制器的收敛域边界主要取决于观测器估计精度上界N,因此采用高精度观测器能够提高控制精度.
2.5 控制器结构考虑到针对火箭一子级返回过程中飞行段及制导律切换等因素造成的姿态角指令突变,本文引入了如下跟踪微分器(tracking differentiator,TD)对参考输入(姿态角指令)安排过渡过程[27],具体为:
| $ {{\dot {\hat x}}_1}\left( t \right) = {{\hat x}_2}\left( t \right), $ |
| $ {{\dot {\hat x}}_2}(t) = {{\hat x}_3}(t), $ |
| $ \begin{array}{l} {{\dot {\hat x}}_3}(t) = - {\beta _1}{R^3}\left( {{{\hat x}_1}(t) - v(t)} \right) - {\beta _2}{R^2}{{\hat x}_2}(t) - \\ \;\;\;\;\;\;\;\;{\beta _3}R{{\hat x}_3}(t). \end{array} $ |
式中:v(t)为系统的期望输入值;
| $ {\mathit{\boldsymbol{K}}_\beta } = \left[ {\begin{array}{*{20}{c}} 0&1&0\\ 0&0&1\\ { - {\beta _1}}&{ - {\beta _2}}&{ - {\beta _3}} \end{array}} \right]. $ |
对于本文研究的VTVL-RLV姿态控制系统,系统期望输入v(t)为火箭制导系统输出的姿态角指令,跟踪微分器输出的
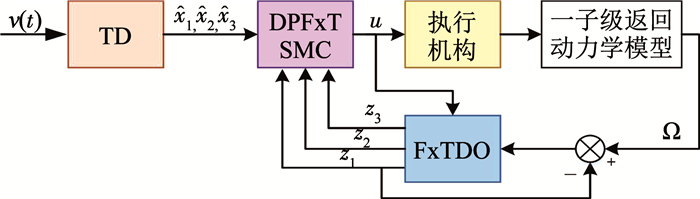
在实际应用中,由于制导律并不输出指令加速度,因此控制律中滑模面和控制律中
|
图 3 FxTDOB-DPFxTSMC的框图 Fig. 3 Structure ofFxTDOB-DPFxTSMC |
考虑轴向气动力系数偏差15%,法力/侧向力系数偏差-15%,大气密度偏差15%,质量偏差800 kg,质心纵向偏差50 mm,转动惯量偏差10%,存在风干扰,姿态角(γ, ψ, φ)初始偏差(1°,3°,-3°),考虑栅格舵的实际物理特性和偏差,且等效舵偏角限幅20°,仿真步长为0.001 s, 仿真5 s的参数见表 2.
| 表 2 气动减速段仿真参数设定 Tab. 2 Settings of simulation parameters of aerodynamic deceleration flight phase |
为了验证本文给出的固定时间收敛扰动观测器(FxTDO),引入基于跟踪微分器拓展的经典扩张状态观测器(ESO)[27]进行比较,具体为:
| $ {e_1} = {z_1} - y, $ |
| $ {{\dot z}_1} = {z_2}, $ |
| $ {{\dot z}_2} = {z_3} + bu\left( t \right), $ |
| $ {{\dot z}_3} = - {\beta _{01}}{\rho ^3}{e_1} - {\beta _{02}}{\rho ^2}{z_2} - {\beta _{03}}\rho {z_3}. $ |
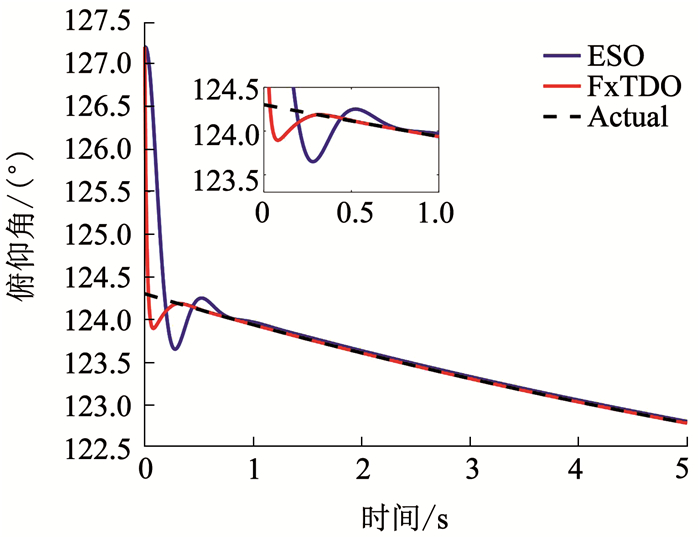
仿真中,各通道ESO的各参数均为ρ=25,β01=1,β02=2,β03=4;观测器FxTDO的各通道增益均为k1=3,k2=3,k3=1,α=0.8,β=1.2,ε=0.1.通过进行零控(控制量为零)仿真对比观测器的一阶输出(以俯仰角为例),结果如图 4和表 3所示.
|
图 4 观测器估计值 Fig. 4 Estimation results of observers |
| 表 3 观测器估计俯仰角偏差的统计特征(3-4 s) Tab. 3 Statistic characteristics of pitch angle deviations estimated by observers (3-4 s) |
由图 4可得,在初始偏差条件下,固定时间收敛扰动观测器(FxTDO)相较于扩张状态观测器(ESO)具有更快的收敛速度和更小的超调;如表 3所示,在稳态条件下FxTDO具有更高的收敛精度.因而,在有限的1 000 Hz采样频率下,FxTDO能够实现对状态和扰动的高精度估计.
3.2 控制器对比为了验证本文给出的FxTDOB-DPFxTSMC,本文引入如式(6)、(7)不带观测器的经典滑模控制方法(SMC)和基于类super-twisting方法的双幂次固定时间收敛滑模控制方法(super-twisting based DPFxTSMC,STB-DPFxTSMC),STB-DPFxTSMC采用的滑模面与本文给出的FxTDOB-DPFxTSMC相同,采用类高阶滑模super-twisting方法替换观测器输出,对应的控制律[28]为:
| $ u\left( t \right) = {b^{ - 1}}\left[ {w\left( t \right) - \eta s - {\lambda _1}{{⎾ s ⏌}^{1/2}} - {\lambda _2}{{⎾ s ⏌}^p} - u'\left( t \right)} \right], $ |
| $ \dot u'\left( t \right) = \alpha\ \text{sign}\left( {s\left( t \right)} \right). $ |
式中:η>0,λ1, λ2>0,p>1,增益α>0需要大于对应系统扰动的Lipschitz常数,即α>h1.
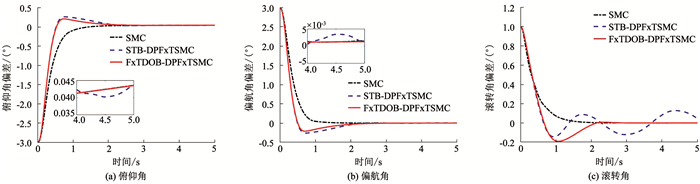
仿真中的参数选取具体为:SMC的三通道滑模面增益均为k=2.8,三通道不连续控制增益均为λ=0.05;STB-DPFxTSMC和FxTDOB-DPFxTSMC的滑模面参数中俯仰/偏航通道均为κ1=1, κ2=2.2, K1=K2=1, γ=0.6, χ=1.1,滚转通道为к1=0.3, к2=0.55, K1=K2=0.1, γ=0.6, χ=1.1;STB-DPFxTSMC的控制律参数中俯仰/偏航通道均为η=λ1=λ2=0.5, p=1.2, α=0.05,滚转通道为η=0.1, λ1=λ2=0.1, p=1.2, α=0.05;FxTDOB-DPFxTSMC的控制律参数中俯仰/偏航通道均为η=0.5, ζ=0.5, υ1=0.5, υ2=1.2,滚转通道为η=0.1, ζ=0.1, υ1=0.5, υ2=1.2;观测器FxTDO的各通道增益同观测器对比一致;各通道TD的参数均为R=25, β1=1, β2=2, β3=4.通过跟踪标称轨迹程序角仿真对比上述各控制器,结果如图 5、6所示.
|
图 5 姿态角偏差响应曲线 Fig. 5 Attitude deviation response of control |
|
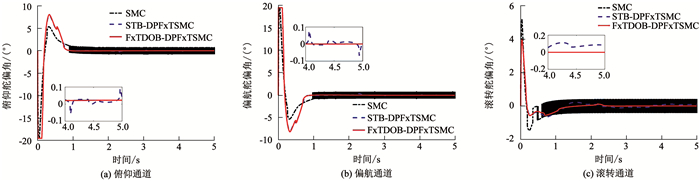
图 6 舵偏角响应曲线 Fig. 6 Rudderdeflection angle response of control |
如图 5、6所示,SMC、STB-DPFxTSMC和本文设计的FxTDOB-DPFxTSMC均能实现对程序制导指令的快速高精度跟踪,其中无观测器的经典SMC采用了保守不连续控制项以保证系统收敛,但一旦系统到达滑模面,控制量抖振就不可避免;由高阶滑模控制理论和仿真结果可知,STB-DPFxTSMC方法中的不连续控制项仅显式存在于控制量的导数
由图 5、6可知,FxTDOB-DPFxTSMC的控制指令较为光滑,分析可知该方法虽然无不连续控制项,但通过FxTDO估计扰动以补偿扰动影响,降低了观测器动态过程对控制系统的影响并有效抑制了抖振.如图 5的局部放大图,FxTDOB-DPFxTSMC的系统状态量并不能保证完全收敛于零,这正是由于通过去除不连续控制项抑制抖振造成的控制精度损失.理论分析可知去除了不连续控制项后的控制精度主要取决于观测器估计精度,由于FxTDO对扰动的高精度估计,系统的收敛精度仍能得到保证.通过权衡系统的收敛速度、精度和鲁棒性可以判断,为消除抖振损失一定的精度是可以容许的,并且通过合理设计观测器能够有效降低控制精度的损失.
4 结论1) 本文针对垂直起降火箭(VTVL-RLV)返回飞行的姿态跟踪控制问题设计了基于固定时间收敛扰动观测器(FxTDO)的双幂次固定时间收敛滑模控制方法(FxTDOB-DPFxTSMC).在有限的采样频率下,引入的FxTDO能够实现对扰动的快速高精度估计,进而在无不连续控制项的情况下利用双幂次修正项实现了固定时间收敛并有效抑制滑模抖振;同时,通过合理设计观测器参数,能够有效降低去除不连续控制项后的控制精度损失.
2) 本文设计的FxTDOB-DPFxTSMC方法的设计参数较多,控制器参数整定难度较大;此外,固定时间收敛方法在保证快速收敛性时不可避免的带来的控制饱和问题,因此后续可进一步研究便于参数整定或参数自适应的控制方法和开展固定时间收敛方法的抗饱和控制研究.
| [1] |
王振国, 罗世彬, 吴建军. 可重复使用运载器研究进展[M]. 长沙: 国防科技大学出版社, 2004. WANG Zhenguo, LUO Shibin, WU Jianjun. Development of reusable launch vehicle[M]. Changsha: NUDT Publish House, 2004. |
| [2] |
崔乃刚, 吴荣, 韦常柱, 等. 垂直起降可重复使用运载器发展现状与关键技术分析[J]. 宇航总体技术, 2018, 2(2): 27. CUI Naigang, WU Rong, WEI Changzhu, et al. Development and key technologies of vertical takeoff vertical landing reusable launch vehicle[J]. Astronautical Systems Engineering Technology, 2018, 2(2): 27. |
| [3] |
LEVANT A. Higher-order sliding modes, differentiation and output-feedback control[J]. International Journal of Control, 2003, 76(9/10): 924. DOI:10.1080/0020717031000099029 |
| [4] |
WANG Zhao, WANG Qing, ZHANG Xinjuan. An adaptive fuzzy sliding-mode technique for attitude control of launch vehicle[C]//Proceedings of the 2007 IEEE International Conference on Mechatronics and Automation. Harbin, China: IEEE, 2007: 1587. DOI: 10.1109/ICMA.2007.4303786
|
| [5] |
孙慧杰.火箭起飞段姿态系统的滑模变结构控制[D].哈尔滨: 哈尔滨工业大学, 2013 SUN Huijie. Sliding mode variable structure control for the attitude system of rockets during ascending stage[D]. Harbin: Harbin Institute of Technology, 2013 |
| [6] |
SONG Xiaojuan, YUE Baozeng, WU Wenjun. Investigation on attitude disturbance control and vibration suppression for fuel-filled flexible spacecraft[J]. Acta Mechanica Sinica, 2015, 31(4): 581. DOI:10.1007/s10409-015-0431-8 |
| [7] |
邢健, 齐瑞云. 考虑燃料晃动效应的航天器自适应滑模姿态控制[J]. 空间控制技术与应用, 2013, 39(2): 42. XING Jian, QI Ruiyun. Adaptive sliding-mode attitude control of spacecraft with fuel sloshing[J]. Aerospace Control and Application, 2013, 39(2): 42. DOI:10.3969/j.issn.1674-1579.2013.02.008 |
| [8] |
宋晓娟.液体多模态晃动柔性航天器姿态机动复合控制研究[D].北京; 北京理工大学, 2015 SONG Xiaojuan. Study on the hybrid control method for the attitude maneuver of flexible spacecraft with multiple mode liquid sloshing[D]. Beijing: Beijing Institute of Technology, 2015 |
| [9] |
岳宝增, 于嘉瑞, 吴文军. 多储液腔航天器刚液耦合动力学与复合控制[J]. 力学学报, 2017, 49(2): 390. YUE Baozeng, YU Jiarui, WU Wenjun. Rigid and liquid coupling dynamics and hybrid control of spacecraft with multiple propellant tanks[J]. Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(2): 390. DOI:10.6052/0459-1879-16-342 |
| [10] |
CHEN Wenhua, YANG Jun, GUO Lei, et al. Disturbance-observer-based control and related methods—an overview[J]. IEEE Transactions on Industrial Electronics, 2016, 63(2): 1083. DOI:10.1109/TIE.2015.2478397 |
| [11] |
ZHANG L, WU R, WEI C Z, et al. Quaternion-based reusable launch vehicle composite attitude control via active disturbance rejection control and sliding mode approach[C]//Proceedings of the 21st AIAA International Space Planes and Hypersonics Technologies Conference. Xiamen, China: IEEE, 2017. DOI: 10.2514/6.2017-2320
|
| [12] |
HALL C E, SHTESSEL Y B. Sliding mode disturbance observer-based control for a reusable launch vehicle[J]. Journal of Guidance Control and Dynamics, 2006, 29(6): 1315. DOI:10.2514/1.20151 |
| [13] |
SHTESSEL Y B, HALL C, BAEV S, et al. Flexible modes control using sliding mode observers: application to Ares I[C]//AIAA Guidance, Navigation, and Control Conference. Toronto, Ontario, Canada: AIAA, 2010. DOI: 10.2514/6.2010-7565
|
| [14] |
SU Rui, ZONG Qun, TIAN Bailing, et al. Comprehensive design of disturbance observer and non-singular terminal sliding mode control for reusable launch vehicles[J]. IET Control Theory and Applications, 2015, 9(12): 1821. DOI:10.1049/iet-cta.2014.0846 |
| [15] |
钱默抒, 熊克, 王海洋. 重复使用运载火箭精确回收滑模动态面控制[J]. 宇航学报, 2018, 39(8): 879. QIAN Moshu, XIONG Ke, WANG Haiyang. Sliding mode dynamic surface control in precise recovery phase for reusable launch vehicle[J]. Journal of Astronautics, 2018, 39(8): 879. DOI:10.3873/j.issn.1000-1328.2018.08.007 |
| [16] |
SHTESSEL Y, EDWARDS C, FRIDMAN L, et al. Sliding mode control and observation[M]. New York: Springer, 2014.
|
| [17] |
LOPEZ-RAMIREZ F, POLYAKOV A, EFIMOV D, et al. Finite-time and fixed-time observer design via implicit Lyapunov function[C]//Proceedings of the 2016 European Control Conference (ECC). Aalborg, Denmark: IEEE, 2016. DOI: 10.1109/ECC.2016.7810300
|
| [18] |
ZHANG Liang, WEI Changzhu, WU Rong, et al. Fixed-time extended state observer based non-singular fast terminal sliding mode control for a VTVL reusable launch vehicle[J]. Aerospace Science and Technology, 2018, 82(1): 70. DOI:10.1016/j.ast.2018.08.028 |
| [19] |
陈克俊, 刘鲁华, 孟云鹤. 远程火箭飞行动力学与制导[M]. 长沙: 国防科技大学出版社, 2014. CHEN Kejun, LIU Luhua, MENG Yunhe. Launch vehicle flight dynamics and guidance[M]. Changsha: NUDT Publish House, 2014. |
| [20] |
POLYAKOV A, FRIDMAN L. Stability notions and Lyapunov functions for sliding mode control systems[J]. Journal of the Franklin Institute, 2014, 351(4): 1831. DOI:10.1016/j.jfranklin.2014.01.002 |
| [21] |
WU Rong, WEI Changzhu, YANG Feng, et al. FxTDO-based non-singular terminal sliding mode control for second-order uncertain systems[J]. IET Control Theory and Applications, 2018, 12(18): 2459. DOI:10.1049/iet-cta.2018.5455 |
| [22] |
YANG Feng, WEI Changzhu, WU Rong, et al. Non-recursive fixed-time convergence observer and extended state observer[J]. IEEE Access, 2018, 6: 62339. DOI:10.1109/Access.2018.2875894 |
| [23] |
BASIN M, SHTESSEL Y, ALDUKALI F. Continuous finite and fixed-time high-order regulators[J]. Journal of the Franklin Institute, 2016, 353(18): 5001. DOI:10.1016/j.ifranklin.2016.09.026 |
| [24] |
BERNUAU E, EFIMOV D, PERRUQUETTI W, et al. On homogeneity and its application in sliding mode control[J]. Journal of the Franklin Institute, 2014, 351(4): 1866. DOI:10.1016/j.jfranklin.2014.01.007 |
| [25] |
BHAT S P, BERNSTEIN D S. Geometric homogeneity with applications to finite-time stability[J]. Mathematics of Control Signals and Systems, 2005, 17(2): 101. DOI:10.1007/s00498-005-0151-x |
| [26] |
BASIN M, YU P, SHTESSEL Y. Finite-and fixed-time differentiators utilising HOSM techniques[J]. IET Control Theory and Applications, 2017, 11(8): 1144. DOI:10.1049/iet-cta.2016.1256 |
| [27] |
GUO Baozhu, ZHAO Zhiliang. Active disturbance rejection control for nonlinear systems: an introduction[M]. Singapore: John Wiley & Sons (Asia) Pte. Ltd., 2016.
|
| [28] |
BASIN M, RODRIGUEZ-RAMIREZ P, DING S X, et al. Continuous fixed-time convergent regulator for dynamic systems with unbounded disturbances[J]. Journal of the Franklin Institute, 2018, 355(5): 2762. DOI:10.1016/j.ifranklin.2018.01.010 |
 2020, Vol. 52
2020, Vol. 52


