2. 中国航天科技集团 宇航部,北京 100048;
3. 哈尔滨工业大学 航天学院,哈尔滨 150001
2. Aerospace Department, China Aerospace Science and Technology Corporation, Beijing 100048, China;
3. School of Astronautics, Harbin Institute of Technology, Harbin 150001, China
绳系卫星系统(tethered satellite system,TSS)是由太空系绳和通过太空系绳连接到一起的太空设备构成,如卫星、空间站或太空操纵手等[1].TSS适用于许多空间任务,如轨道转移[2]、碎片清除[3]、深空探索[4]等.执行任何一个TSS任务的首要条件就是能够将系绳连接的设备释放到指定的位置,即,释放是绳系卫星系统的基本操作之一.但是,由于柔软的系绳只能提供张力而不能提供支撑力,且被释放子设备上的推进器功率较小,实现稳定和快速释放是相当具有挑战性的[5].因此,深入研究绳系卫星系统的释放过程是具有重要意义.
为了获得更好的释放性能,许多控制方法在绳系卫星系统中得到了应用,例如滑模控制[6]、鲁棒控制[7]、反馈线性化等[8].反步法(backstepping)控制形成于上世纪90年代,是一种相对新型的控制方法[9].Backstepping控制方法的优点是有较高的自适应性和稳定性,但缺点是其设计过程需要逐步迭代,只能应用于严格反馈系统[10].这一缺点极大地限制了Backstepping方法的应用范围.因为绳系卫星系统不是严格反馈系统,故Backstepping在TSS中的应用较少.例如钟睿等[11]研究了退步控制的张力控制方法,彭鹏[12]利用微分同胚变换将绳系卫星系统动力学模型转换为严格反馈系统,然后设计了Backstepping控制器.但是该文中采用了微分同胚变换使得控制器设计过程非常繁琐且控制器变量含义不明确.本文致力于在吸收Backstepping控制方法思想的基础上,提出一种可以应用于绳系卫星系统释放过程且设计简单明确的控制方法.
另一个在绳系卫星系统研究中存在的问题是大部分研究都假设TSS运行轨道为圆轨道[13-15].但是在实际系统中,绝大部分空间飞行器的飞行轨道都是椭圆轨道.在椭圆轨道上运行时,由于地球引力随着TSS位置的变化会存在周期性摄动,而摄动的存在会导致基于圆轨道设计的控制器失效,无法在实际系统中应用[16].因此本文主要着力于椭圆轨道上绳系卫星系统释放过程的建模和控制方法研究.
本文针对上述问题,提出了一种基于椭圆轨道非线性模型的类反步非线性控制方案.其中,利用Euler-Lagrange力学方程,建立了椭圆轨道TSS释放的动力学模型;构造了一种基于坐标转换的量纲为1的变换用于简化动力学方程;基于动力学模型设计了类反步非线性控制器并进行了仿真实验.
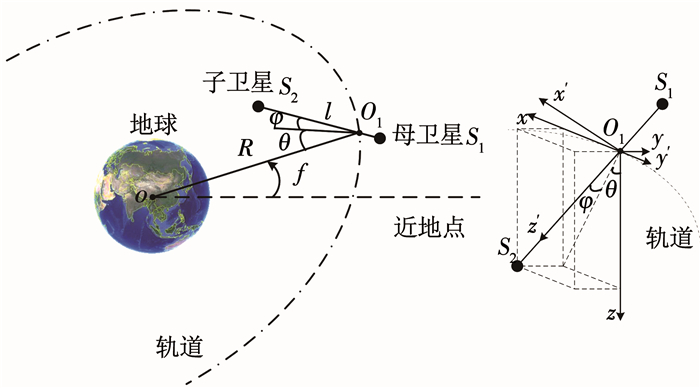
1 TSS动力学建模如图 1所示,本文考虑一类实际太空实验中广泛采用的双星系统,且运行在椭圆轨道上;该系统一般由母卫星、子卫星和系绳组成[17].为了获得子卫星释放过程的动力学模型,本文建立了两个坐标系O1xyz和O1x′y′z′,分别是轨道坐标系和机体坐标系.轨道坐标系O1xyz原点为TSS的质心,O1x轴指向TSS在轨道平面内的前进方向,O1z轴指向地心向下,O1y轴的指向由右手定则确定.机体坐标系O1x′y′z′的O1z′轴沿着系绳指向子卫星,且可通过旋转与坐标系O1xyz重合,即O1x′可以通过O1x绕着O1y轴旋转角θ得到,O1y′可以通过O1y绕着O1x轴旋转角φ得到.
|
图 1 TSS几何模型 Fig. 1 TSS geometric representation |
为便于分析系统模型及简化控制器的设计步骤,文中做出如下合理假设.
假设1 在TSS子卫星释放过程中,系绳长度尺度远大于卫星尺度,故在释放过程中将两个卫星视为质点.并把地球当作一个完美的球体,从而地球质心与它的几何中心重合.
假设2 母卫星的质量远大于子卫星的质量.此时,在子卫星释放过程中,母卫星能够保持名义轨道.
假设3 系绳是无弹性且无质量的.
考虑系绳是极其柔软的,因此当绳变形或弯曲时,母卫星无法对子卫星施加控制力.所以在子卫星释放过程中,系绳必须始终处于拉紧状态,即系绳张力始终大于0.且在释放过程中,系绳张力必须小于系绳最大可承受张力.根据这一特点,系绳在展开期间可视为刚性杆,称为哑铃模型[18].
在推导动力学模型之前,首先介绍一些必要的符号.O为地球地心,R为距离OO1.μe、f分别为地球重力场系数和真近点角.母卫星质量和子卫星质量分别为m1和m2,而系统总质量为m=m1+m2.用于描述TSS系统状态变量有3个,分别为l、θ和φ.其中,l为两个卫星之间系绳的长度,θ为面内角,φ为面外角.基于上述假设及符号,可得到TSS系统在子卫星释放过程的动能和势能如下[19]:
| $ \begin{array}{l} T = \frac{1}{2}m\left( {{{\dot R}^2} + {R^2}{{\dot f}^2}} \right) + \\ \;\;\;\;\;\;\frac{1}{2}\bar m{l^2}\left[ {{{\dot \varphi }^2} + {{\left( {\dot \theta + \dot f} \right)}^2}{{\cos }^2}\varphi } \right] + \frac{1}{2}\bar m{{\dot l}^2},\\ V = - \frac{{{\mu _{\rm{e}}}m}}{R} + \frac{{{\mu _{\rm{e}}}\bar m{l^2}}}{{2{R^3}}}\left( {1 - 3{{\cos }^2}\theta {{\cos }^2}\varphi } \right). \end{array} $ | (1) |
其中,m =m1m2/m.应用拉格朗日力学原理,可以得到下式:
| $ \begin{array}{l} \bar m\ddot l - \frac{{2e\sin f}}{{{k_f}}}\dot lf - \bar ml\left[ {{{\dot \varphi }^2} + {{\left( {\dot \theta + \dot f} \right)}^2}{{\cos }^2}\varphi } \right] + \\ \frac{{\bar ml{\ddot f^2}}}{{{k_f}}}\left( {1 - 3{{\cos }^2}\varphi {{\cos }^2}\theta } \right) = - {\tau _t},\\ \bar m{l^2}{\cos ^2}\varphi \ddot \theta - \frac{{2e\sin f}}{{{k_f}}}\dot \theta f{l^2}{\cos ^2}\varphi - \frac{{2e\sin f}}{{{k_f}}}\dot \theta {f^2}{l^2}{\cos ^2}\varphi + \\ 2\bar m\left( {\dot \theta + \dot f} \right){l^2}{\cos ^2}\varphi \left( {\frac{{\dot l}}{l} - \dot \varphi \tan \varphi } \right) + \\ \frac{3}{{{k_f}}}\bar m{{\dot f}^2}{l^2}\sin \theta \cos \theta {\cos ^2}\varphi = {\tau _\theta },\\ \bar m{l^2}\ddot \varphi - \frac{{2e\sin f}}{{{k_f}}}\dot \varphi f{l^2} + 2\bar m\dot \varphi \dot ll + \\ \bar m{l^2}\sin \varphi \cos \varphi \left[ {{{\left( {\dot \theta + \dot f} \right)}^2} + 3\bar m\dot f{{\cos }^2}\theta } \right] = {\tau _\varphi }. \end{array} $ | (2) |
式中:kf=1+ecos f.其中,e为开普勒轨道的偏心率;τt为系绳的张力;τθ、τφ分别为控制面内角和面外角力矩.根据分析可知,τt始终为正,τθ和τφ可正可负.这3种广义力矩的取值类型并不相同使得控制器的设计难度加大.此外,式(2)中存在质量、长度以及弧度等多种量纲,不利于仿真验证,因此有必要进行进一步化简.
2 类反步非线性控制器设计 2.1 问题描述为了解决如上所述问题并简化仿真过程,设计量纲为1的变换如下[20]:
| $ \begin{array}{*{20}{c}} {\lambda = l/L,}\\ {d(\;)/dt = \dot fd(\;)/df,}\\ {{{\hat \tau }_t} = - {\tau _t}/\left( {\bar m{{\dot f}^2}L} \right) + \rho ,}\\ {{{\hat \tau }_\theta } = {\tau _\theta }/\left( {\bar m{{\dot f}^2}{L^2}} \right),}\\ {{{\hat \tau }_\varphi } = {\tau _\varphi }/\left( {\bar m{{\dot f}^2}{L^2}} \right).} \end{array} $ | (3) |
式中,ρ为一个正常数.利用式(3)的变换,可以得到量纲为1的规范型Euler-Lagrange动力学模型为
| $ H\left( q \right)\ddot q + C\left( {q,\dot q} \right)\dot q + {B_0}\dot q + G\left( q \right) = \tau , $ |
其中各矩阵如式(4)所示,根据动力学方程,显然下式成立:
| $ {q^{\rm{T}}}\left( {\dot H\left( q \right) - 2C\left( {q,\dot q} \right)} \right)q = 0. $ |
至此,本文得到了椭圆轨道绳系卫星系统释放过程的动力学模型.该模型中参数均为量纲为1的参数,为后续仿真实验开展奠定基础.
2.2 控制器设计从本文关于椭圆轨道上绳系卫星系统动力学方程的推导可以看出,该系统是非严格反馈系统,各个状态之间存在着很强的耦合关系,传统的Backsteping方法无法直接应用[11].因此,需要提出一种新型的非线性控制方法,具体表述为定理1.
定理1 设计子卫星释放类反步非线性控制器为
| $ \tau = H\left( q \right)\mathit{\boldsymbol{E}} + C\left( {q,\dot q} \right)\dot q + {B_0}\dot q + G\left( q \right). $ |
式中,矩阵E表示为式(5),式中k1到k6均为正常数.则在该控制器作用下,绳系卫星系统的状态参数λ、θ和φ是渐进稳定的.
| $ q = {\left( {\begin{array}{*{20}{l}} \lambda &\theta &\varphi \end{array}} \right)^{\rm{T}}}, $ |
| $ \tau = {\left( {\begin{array}{*{20}{l}} {{{\hat \tau }_t}}&{{{\hat \tau }_\theta }}&{{{\hat \tau }_\varphi }} \end{array}} \right)^{\rm{T}}}, $ |
| $ H\left( q \right) = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&{{\lambda ^2}{{\cos }^2}\varphi }&0\\ 0&0&{{\lambda ^2}} \end{array}} \right], $ |
| $ C\left( {q,\dot q} \right) = \left[ {\begin{array}{*{20}{l}} {{C_1}}&{{C_2}}&{{C_3}} \end{array}} \right], $ |
| $ {C_1} = \left[ {\begin{array}{*{20}{c}} 0\\ {\left( {2\lambda + \lambda \dot \theta } \right){{\cos }^2}\varphi }\\ {\lambda \dot \varphi } \end{array}} \right], $ |
| $ {C_2} = \left[ {\begin{array}{*{20}{c}} { - \left( {\lambda \dot \theta + 2\lambda } \right){{\cos }^2}\varphi }\\ {\lambda \dot \lambda {{\cos }^2}\varphi - {\lambda ^2}\dot \varphi \sin \varphi \cos \varphi }\\ {{\lambda ^2}\left( {\dot \theta + 2} \right)\sin \varphi \cos \varphi } \end{array}} \right], $ |
| $ {C_3} = \left[ {\begin{array}{*{20}{c}} { - \lambda \dot \varphi }\\ { - \left( {\dot \theta + 2} \right){\lambda ^2}\sin \varphi \cos \varphi }\\ {\lambda \dot \lambda } \end{array}} \right], $ |
| $ {B_0} = \left[ {\begin{array}{*{20}{c}} { - \frac{{2e\sin f}}{{{k_f}}}}&0&0\\ 0&{ - \frac{{2e\sin f}}{{{k_f}}}}&0\\ 0&0&{ - \frac{{2e\sin f}}{{{k_f}}}} \end{array}} \right], $ |
| $ G\left( q \right) = \left[ {\begin{array}{*{20}{c}} { - \lambda {{\cos }^2}\varphi + \frac{\lambda }{{{k_f}}}\left( {1 - 3{{\cos }^2}\theta {{\cos }^2}\varphi } \right) + \rho }\\ {\frac{3}{{{k_f}}}{\lambda ^2}\cos \theta \sin \theta {{\cos }^2}\varphi - \frac{{2e\sin f}}{{{k_f}}}}\\ {\left( {{\lambda ^2} + \frac{3}{{{k_f}}}{\lambda ^2}{{\cos }^2}\theta } \right)\sin \varphi \cos \varphi } \end{array}} \right]. $ | (4) |
| $ \mathit{\boldsymbol{E}} = \left[ {\begin{array}{*{20}{c}} {\left( {k_1^2 - 1} \right){e_1} - \left( {{k_1} + {k_2}} \right){e_2}}\\ {\left( {k_3^2 - 1} \right){e_3} - \left( {{k_3} + {k_4}} \right){e_4}}\\ {\left( {k_5^2 - 1} \right){e_5} - \left( {{k_5} + {k_6}} \right){e_6}} \end{array}} \right]. $ | (5) |
式(5)中的各项误差定义如下:
| $ {e_1} = \lambda - {\lambda _d}, $ |
| $ {e_2} = \dot \lambda - {{\dot \lambda }_d} + {k_1}{e_1}, $ |
| $ {e_3} = \theta - {\theta _d}, $ |
| $ {e_4} = \dot \theta - {{\dot \theta }_d} + {k_3}{e_3}, $ |
| $ {e_5} = \varphi - {\varphi _d}, $ |
| $ {e_6} = \dot \varphi - {{\dot \varphi }_d} + {k_5}{e_5}. $ |
证明 构造系统的Lyapunov函数如下:
| $ V = \frac{1}{2}\left( {e_1^2 + e_2^2 + e_3^2 + e_4^2 + e_5^2 + e_6^2} \right), $ |
则,V正定.对时间求导可得其导数
| $ \begin{array}{l} \dot V = {e_1}{{\dot e}_1} + {e_2}{{\dot e}_2} + {e_3}{{\dot e}_3} + {e_4}{{\dot e}_4} + {e_5}{{\dot e}_5} + {e_6}{{\dot e}_6} = \\ \;\;\;\;\;\;{e_1}\left( {{e_2} - {k_1}{e_1}} \right) + {e_2}\left( {\ddot \lambda - {{\ddot \lambda }_d} + {k_1}{{\dot e}_1}} \right) + \\ \;\;\;\;\;\;{e_3}\left( {{e_4} - {k_3}{e_3}} \right) + {e_4}\left( {\ddot \theta - {{\ddot \theta }_d} + {k_3}{{\dot e}_3}} \right) + \\ \;\;\;\;\;\;{e_5}\left( {{e_6} - {k_5}{e_5}} \right) + {e_6}\left( {\ddot \varphi - {{\ddot \varphi }_d} + {k_5}{{\dot e}_5}} \right). \end{array} $ |
设计目标是将子卫星释放到指定的位置,故可知
| $ \begin{array}{l} \dot V = {e_1}{{\dot e}_1} + {e_2}{{\dot e}_2} + {e_3}{{\dot e}_3} + {e_4}{{\dot e}_4} + {e_5}{{\dot e}_5} + {e_6}{{\dot e}_6} = \\ \;\;\;\;\;\;{e_1}\left( {{e_2} - {k_1}{e_1}} \right) + {e_2}\left( {\ddot \lambda + {k_1}{{\dot e}_1}} \right) + {e_3}\left( {{e_4} - {k_3}{e_3}} \right) + \\ \;\;\;\;\;\;{e_4}\left( {\ddot \theta + {k_3}{{\dot e}_3}} \right) + {e_5}\left( {{e_6} - {k_5}{e_5}} \right) + {e_6}\left( {\ddot \varphi + {k_5}{{\dot e}_5}} \right). \end{array} $ |
代入定理1中的控制输入,可得:
| $ \dot V = - {k_1}e_1^2 - {k_2}e_2^2 - {k_3}e_3^2 - {k_4}e_4^2 - {k_5}e_5^2 - {k_6}e_6^2, $ |
式中,k1~k6均为正常数,故Lyapunov函数的导数始终小于等于0.即
| $ \dot V \le 0, $ |
因此,在类反步非线性控制器作用下,子卫星释放过程是渐进稳定的.
3 仿真分析为了分析类反步非线性控制方法的有效性,本文将基于椭圆轨道绳系卫星系统的动力学实施两种控制方法的仿真和对比.这两种控制方法分别是类反步非线性控制和PID控制,为了便于表示,分别称这两种方法为BLN和PID.首先给出本次仿真中双星TSS系统的相关参数,见表 1.
| 表 1 TSS系统参数 Tab. 1 System parameters of TSS |
本文仿真在CPU为Intel i7-8750H、操作系统Windows10 64位、内存8 G的电脑上,应用MATLAB2016b模拟椭圆轨道绳系卫星系统的释放过程.仿真初始时刻选择为TSS在近地点的时刻,定义初始真近点角为0 rad.根据TSS系统的轨道参数以及卫星的相关信息,本文可计算求得初始时刻量纲为1的状态的数值为q0=[0.000 9, 0.1, 0.1]T,量纲为1的状态的导数为
在仿真实验中,本文选取BLN控制器的设计参数如下:
| $ {k_1} = 0.1,{k_2} = 2,{k_3} = 1,{k_4} = 2,{k_5} = 2,{k_6} = 1. $ |
选取PID控制器的设计参数如下:
| $ k{p_\lambda } = 8,k{d_\lambda } = 15,k{i_\lambda } = 0.01, $ |
| $ k{p_\theta } = 10,k{d_\theta } = 15,k{i_\theta } = 0.05, $ |
| $ k{p_\varphi } = 5,k{d_\varphi } = 1,k{i_\varphi } = 0. $ |
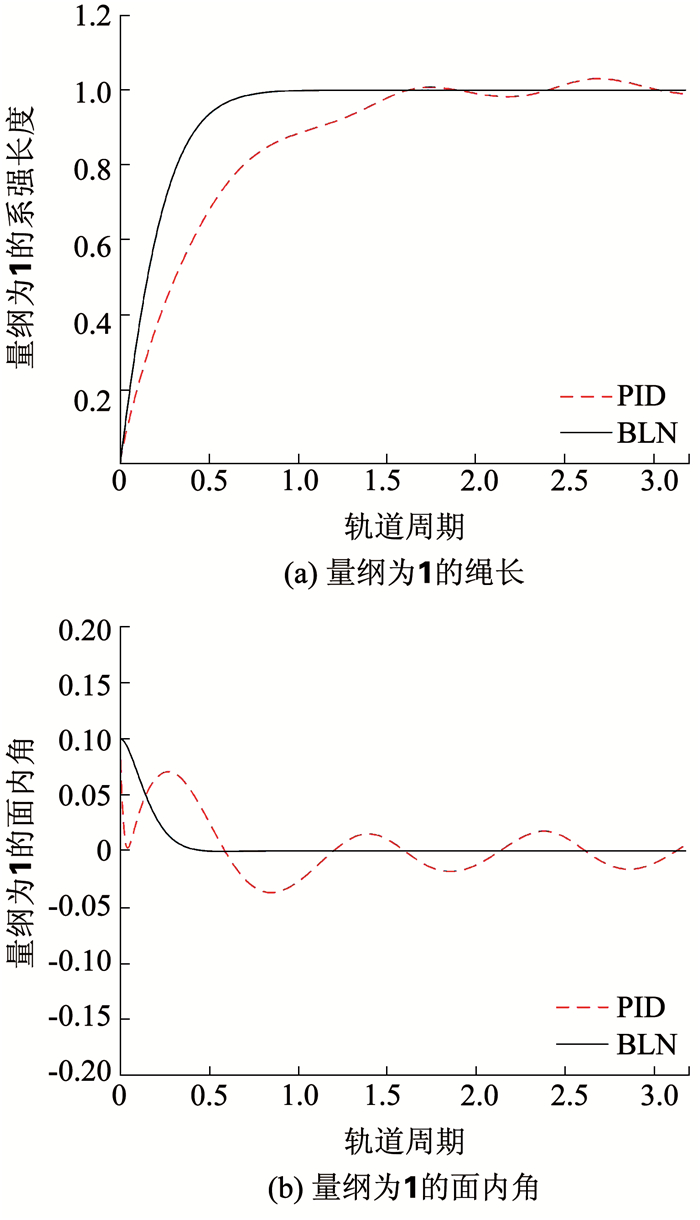
由此,本文可以给出在两种控制器作用下绳系卫星系统的释放曲线如图 2~图 3.图 2(a)显示了量纲为1的系绳长度的变化,而图 2(b)展示了释放过程面内角的动态特性.面外角和系绳量纲为1的张力曲线如图 3(a)和图 3(b)所示.
|
图 2 量纲为1的系绳长度和量纲为1的面内角变化曲线 Fig. 2 Variation curves of dimensionless tether length and dimensionless in-plane angle |
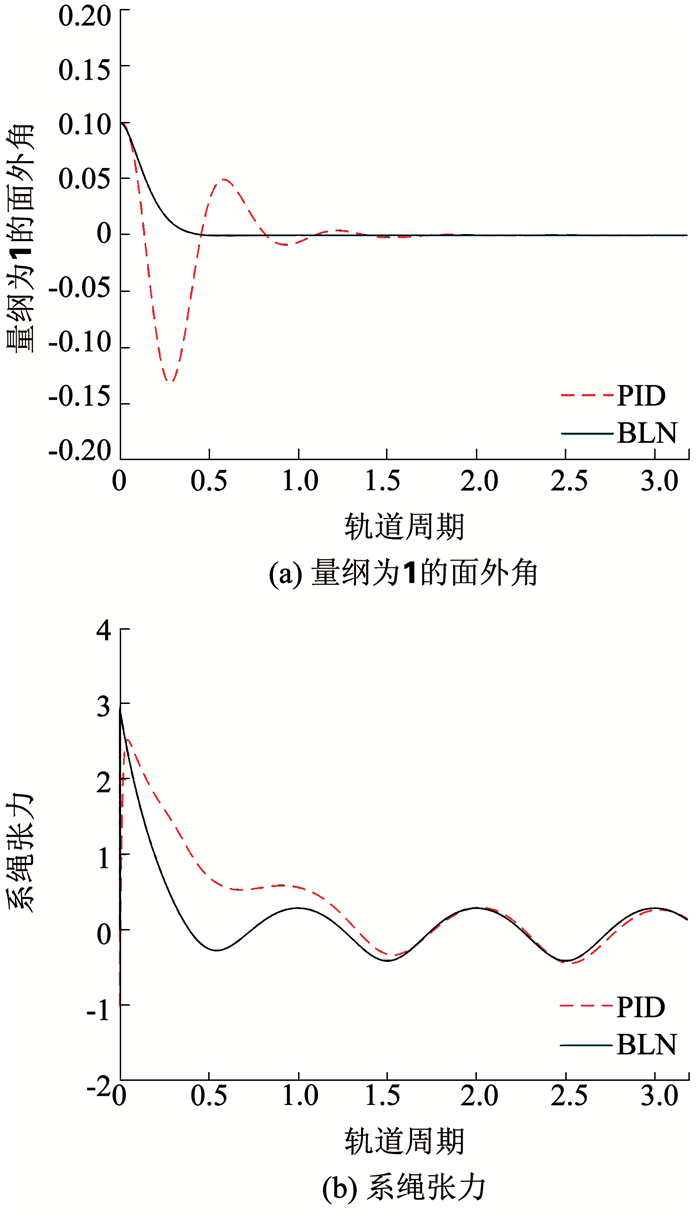
|
图 3 量纲为1的面外角和系绳张力变化曲线 Fig. 3 Variation curves of dimensionless out-of-plane angle and tether tension |
图 2(a)所示为在两种控制器作用下,绳系卫星系统绳长曲线.总体上来看,两种控制器都能稳定地释放子卫星,使之达到期望值.但对比来看,PID虽然能够到达期望值,但是无法稳定在该数值,而是在该数值附近小幅度波动.相反,BLN可以稳定在期望位置.产生该现象的原因是,与理论上的圆轨道相比,椭圆轨道存在时变的参数项,PID控制无法消除椭圆轨道时变参数对绳系卫星系统产生的影响.而BLN在控制器设计过程中引入了名义模型,从而抑制了周期性摄动的影响.从时间上来看,在BLN控制和PID作用下,绳系卫星系统的绳长度分别在0.8和1.6个轨道周期后稳定在期望值.图 2(b)所示为在两种控制器作用下,绳系卫星系统面内角的变化过程.总体上来看,两种控制器都能稳定地控制子卫星的面内角.但是无论是从精度还是速度的角度来看,BLN方法的控制效果均优于PID控制.
绳系卫星系统面外角的动态过程如图 3(a)所示.通过观察两种控制下面外角的变化过程,本文可以得到相同的结论,即BLN和PID都能稳定地控制面外角,但是前者的控制效果更好.如图 3(b)展示了两种控制下系绳张力的变化.可以看出,两种情况下,系绳的张力均在合理范围之内.而BLN方法下系绳张力变化更加迅速,可以更快地响应控制输入.子卫星到达指定位置后,两种控制器输出的系绳张力趋于一致.
从仿真结果和分析中可以看出,总体上BLN和PID方法都能够稳定地控制TSS系统释放子卫星的绳长、面内角和面外角.进一步地,BLN方法控制子卫星的释放效果要明显优于PID方法.
4 结论1) 为了解决椭圆轨道上绳系卫星系统的子卫星稳定释放的问题,本文首先建立了椭圆轨道上双星绳系卫星系统释放的动力学模型,并设计了一种全新的量纲为1的变换对动力学模型进行了化简,方便了后续控制器的设计和仿真.并且,实际系统中绝大部分卫星轨道都是椭圆轨道,本文建立的椭圆轨道模型较理想的圆轨道模型具有更大的实用价值.
2) 针对普通反步法无法应用于非严格反馈系统的问题,本文提出了类反步非线性控制方法来控制TSS系统子卫星的释放.该方法利用椭圆轨道上绳系卫星系统的动力学方程来设计控制器.一方面解决了在严格反馈系统上无法应用Backstepping控制的问题,另一方面通过引入动力学模型到控制器中能够改善其控制效果.
3) 在椭圆轨道双星绳系卫星模型上对类反步非线性控制方法进行了仿真验证,仿真结果表明类反步非线性控制可以稳定高效地控制子卫星释放的过程.并且相对于PID控制,类反步非线性控制可以取得更优异的控制效果.
| [1] |
COLOMBO G, GAPOSCHKIN E M, GROSSI M D, et al. Shuttle-borne skyhook: A new tool for low-orbital-altitude research[J]. Smithsonian Astrophysical Observatory, Reports in Geoastronomy, 1975, 10(1): 3. DOI:10.1007/BF02148280 |
| [2] |
BEKEY I, PENZO P A. Tetherpropulsion[J]. Aerospace America, 1986, 24: 40. |
| [3] |
ANZ-MEADOR P D. Tether-debris interactions in low Earthorbit[J]. AIP Conference Proceedings, 2001, 552(1): 525. DOI:10.1063/1.1357972 |
| [4] |
李俊峰, 宝音贺西. 深空探测中的动力学与控制[J]. 力学与实践, 2007, 29(4): 1. LI Junfeng, BAOYIN Hexi. Dynamics and control in deep space exploration[J]. Mechanics in Engineering, 2007, 29(4): 1. DOI:10.3969/j.issn.1000-0879.2007.04.001 |
| [5] |
WEN Hao, JIN Dongping, HU Haiyan. Advances in dynamics and control of tethered satellite systems[J]. Acta Mechanica Sinica, 2008, 24(3): 229. DOI:10.1007/s10409-008-0159-9 |
| [6] |
KESHTKAR S, POZNYAK A. Tethered space orientation via adaptive sliding mode[J]. International Journal of Robust and Nonlinear Control, 2016, 26(8): 1632. DOI:10.1002/rnc.3371 |
| [7] |
YU Miao, HUANG Deqing, HE Wei. Robust adaptive iterative learning control for discrete-time nonlinear systems with both parametric and nonparametric uncertainties[J]. International Journal of Adaptive Control and Signal Processing, 2016, 30(7): 972. DOI:10.1002/acs.2648 |
| [8] |
MANKALA K K, AGRAWAL S K. Equilibrium to equilibrium maneuvers of flexible electrodynamic tethers in equatorial orbits[J]. Journal of Spacecraft and Rockets, 2006, 43(3): 651. DOI:10.2514/1.13956 |
| [9] |
KRSTIC M, KANELLAKOPOULOS I, KOKOTOVIC P V. Nonlinear and adaptive control design[M]. New York: Wiley, 1995. DOI:10.1007/3-540-45802-6
|
| [10] |
EBRAHIM A, MURPHY G V. Adaptive backstepping controller design of an inverted pendulum[C]//Proceedings of the 37th Southeastern Symposium on System Theory. Tuskegee, AL: IEEE, 2005: 172. DOI: 10.1109/SSST.2005.1460900
|
| [11] |
钟睿, 徐世杰. 基于退步控制方法的绳系卫星回收张力控制[J]. 北京航空航天大学学报, 2010, 36(1): 26. ZHONG Rui, XU Shijie. Tension control strategy for TSS retrieval process based on backstepping control method[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(1): 26. DOI:10.13700/j.bh.1001-5965.2010.01.015 |
| [12] |
彭鹏.空间绳系卫星系统的动力学与张力控制[D].哈尔滨: 哈尔滨工业大学, 2015 PENG Peng. Dynamics and tension control of space tethered satellite system[D]. Harbin: Harbin Institute of Technology, 2015 |
| [13] |
KUMAR K D. Review on dynamics and control of nonelectrodynamic tethered satellite systems[J]. Journal of Spacecraft and Rockets, 2006, 43(4): 705. DOI:10.2514/1.5479 |
| [14] |
LEAMY M J, NOOR A K, WASFY T M. Dynamic simulation of a tethered satellite system using finite elements and fuzzy sets[J]. Computer Methods in Applied Mechanics and Engineering, 2001, 190(37/38): 4847. DOI:10.1016/s0045-7825(00)00352-2 |
| [15] |
XU Shidong, SUN Guanghui, MA Zhiqiang, et al. Fractional-order fuzzy sliding mode control for the deployment of tethered satellite system under input saturation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 55(2): 747. DOI:10.1109/TAES.2018.2864767 |
| [16] |
WILLIAMS P. Libration control of tethered satellites in ellipticalorbits[J]. Journal of Spacecraft and Rockets, 2006, 43(2): 476. DOI:10.2514/1.17499 |
| [17] |
ZHONG Xiaoqing, SHAO Xiangyu, LI Xiaolei, et al. Fractional order adaptive sliding mode control for the deployment of space tethered system with input limitation[J]. IEEE Access, 2018, 6: 48958. DOI:10.1109/ACCESS.2018.2867627 |
| [18] |
PERKINS TT, SMITH D E, LARSON R G, et al. Stretching of a single tethered polymer in a uniform flow[J]. Science, 1995, 268(5207): 83. DOI:10.1126/science.7701345 |
| [19] |
WEN Hao, ZHU Zhenghong, JIN Dongping, et al. Exponentially convergent velocity observer for an electrodynamic tether in an elliptical orbit[J]. Journal of Guidance, Control, and Dynamics, 2016, 39(5): 1112. DOI:10.2514/1.G001532 |
| [20] |
MA Zhiqiang, SUN Guanghui. Adaptive sliding modecontrol of tethered satellite deployment with input limitation[J]. Acta Astronautica, 2016, 127: 67. DOI:10.1016/j.actaastro.2016.05.022 |
 2020, Vol. 52
2020, Vol. 52


