2. 哈尔滨工业大学 电子与信息工程学院,哈尔滨 150001
2. School of Electronic and Information Engineering, Harbin Institute of Technology, Harbin 150001, China
卷积神经网络近年来在目标检测[1]、图像修复[2]、自然语言处理、机器视觉等应用领域获得了巨大突破.面对这些复杂任务,神经网络系统需要强大的数据存储以及数据处理能力.高速定制化的硬件处理器为处理能力的提高提供了一个可行的途径[3-6].相比于其他硬件处理器,FPGA拥有良好的性能、较短的开发周期、更高的能源利用率及重配置功能,因此越来越多的开发者选择基于FPGA设计卷积神经网络硬件加速器[3, 7-8].
目前,基于FPGA的卷积神经网络硬件加速器仍面临诸多挑战. 1)卷积硬件加速器具有较高的并行计算特性,因此数据传输速度往往成为性能继续提升的瓶颈,例如Qiu等[9]设计提出的采用多个卷积处理单元并行计算的方法,其较低的片上数据传输速度就限制了整体系统的计算性能;2)硬件设计空间巨大,不同的硬件并行设计方法将影响加速器性能与资源使用率,例如端到端的设计[10-11]的方法把所有卷积层的计算引擎都放置到片上.这种方法对片上资源和带宽要求较高,并且只适用于较小网络模型.如何设计加速器的高度并行传输与计算架构以及如何在有限的硬件资源下选择出最佳并行方案以实现加速器的高性能是目前亟需解决的问题.
针对上述问题,本文首先提出了数据对齐并行处理的方法以实现数据层面的高速并行传输与计算,采用多卷积核并行处理的方法实现同一卷积层的多个卷积核并行计算,并通过建立性能与资源评估模型,生成性能与资源协同优化的并行方案.最终在Xilinx Zynq XC7Z045上的SSD网络模型测试结果表明,该加速器在175 MHz时钟下可以达到44.59 FPS与306.6 GOP·s-1.
1 卷积神经网络卷积神经网络是一种具有共享权重结构、平移不变性特征的人工神经网络,其主要由卷积层、下采样层和全连接层组成.卷积层的作用是通过权值共享来提取特征,下采样层则主要是为了降低数据维度与防止图像过拟合,全连接层的作用是把最后一层卷积的输出图像由高维变成低维,并且把输入的信息进行提取整合,再经过激活函数的映射,以实现特征到标签的映射.
卷积层从上层局部邻域特征图中提取特征,然后施加一个加性偏差,其结果如下:
| $ \begin{array}{*{20}{c}} {{Q_i}\left( {x,y} \right) = {b_i} + \sum\limits_{j = 0}^{{M_i} - 1} {\sum\limits_{p = 0}^{{P_i} - 1} {\sum\limits_{q = 0}^{{Q_i} - 1} {{W_{ij}}} } } \left( {p,q} \right) \times }\\ {{g_j}\left( {x + p,y + q} \right).} \end{array} $ | (1) |
式中:Qi(x, y)为第i张输出图像上的(x, y)处的输出特征;bi为第i张输出特征的偏差;gj(x+p, y+q)为第j张输入图像在(x+p, y+q)处特征值;Wij(p, q)为卷积核(p, q)处的权重值;Mi为输入图像的通道数;Pi、Qi分别为卷积核长宽.
除此之外,卷积层的输出还要经过激活函数和批量归一化处理.激活函数可以把特征保留并映射出来,以增强卷积神经网络系统的非线性,常用的激活函数有tanh,sigmoid,ReLU,PReLU等.本文选择下式所示ReLU函数[12]作为非线性激活函数.
| $ \text{ReLU}\left( x \right) = \text{Max}\left( {x,0} \right), $ |
式中x为输入像素.
经过卷积层权值共享和局部连接后,图像权值参数已经大大减少,但是对于全连接层来说仍有着计算量方面的挑战,并且还会出现过拟合现象.为了解决这些问题,可按着一定的方法对特征图进行下采样操作,提升整个网络模型的性能.
全连接层是将特征图进行整合和分类的高层,以得到整个图像的信息.该层的每一个神经元都与上一层的所有神经元相连,简单来说全连接层就是矩阵向量乘法过程,输入向量与权重矩阵相乘,以实现特征的分类.
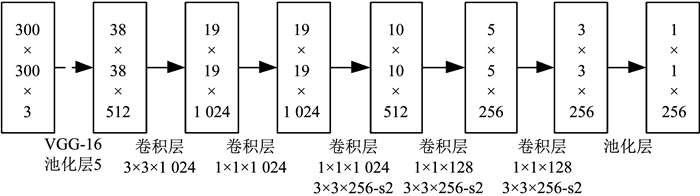
为了兼顾目标检测的时效性和不变性,SSD算法在2016年被Liu等[13]提出.SSD算法的网络模型是一个基于VGG16结构的卷积神经网络,其核心是利用小型卷积滤波器来预测目标类别与边界框,并达到速度与精确度的平衡.如图 1所示为一个基本的SSD网络架构.
|
图 1 基本SSD网络模型 Fig. 1 Basic SSD network model |
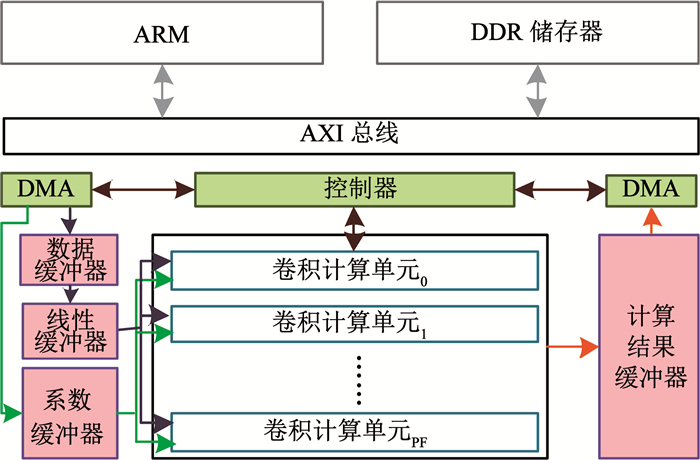
本文所提出的系统整体架构如图 2所示,主要包含:片外双倍速率同步动态随机存储器(double data rate synchronous dynamic random access memory, DDR SDRAM)、ARM(advanced risc machine)处理器、直接内存存取单元(direct memory access, DMA)、片上缓冲器、控制器以及卷积计算单元.片外DDR将储存外设获取的输入图像数据以及网络的权值系数;ARM处理器对整体系统进行控制;卷积计算单元主要完成卷积神经网络的卷积计算,还包括池化、激活等操作;片上缓冲器用于缓存计算所需图像数据,权值系数以及计算结果;DMA用于片外储存器与片上缓冲器之间的数据传输;控制器从外部获取指令并对其进行解码,以控制可编程逻辑端的所有模块.
|
图 2 系统整体硬件架构图 Fig. 2 An overview of the accelerator architecture |
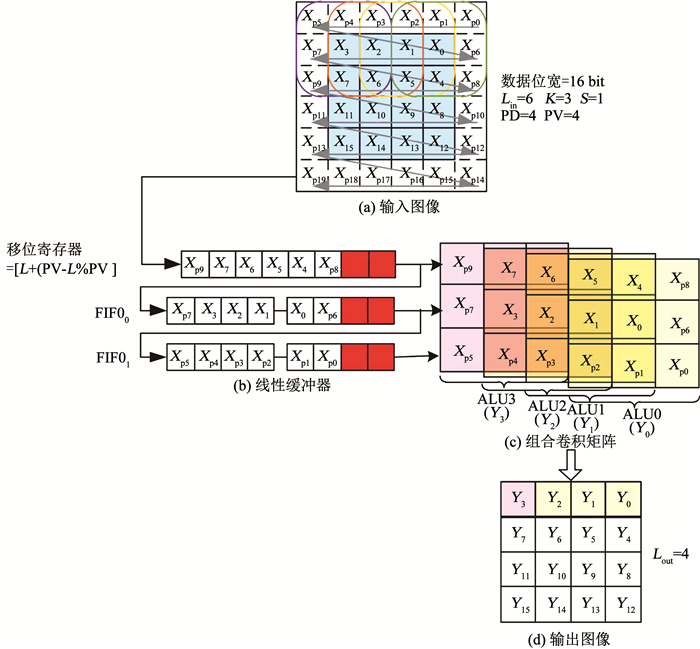
本文首先提出了一种数据对齐并行预处理的方法实现数据层面的高度并行传输与计算,以提高数据传输、并行计算速度和硬件设计的通用性.文中用PD表示数据传输的并行度,即一个时钟周期内并行传输的数据个数.PV表示数据计算的并行度,为一个卷积核在图像上可同时计算的结果个数,K为卷积核大小.预处理单元由两部分组成:移位寄存器与先进先出(first input first output, FIFO)线性缓冲器.根据式(1),卷积运算要求数据按照行对齐输出,所以首先要对图像数据进行行缓存.由于一个时钟内数据传输的个数为PD,当图像边长不能被数据传输并行度PD整除,需要对输入图像添加无效数据以使边长为PD的整数倍,保证图像的每行像素以每个时钟周期传输PD个数据的方式经过N个时钟周期传输完毕.这样,图像数据就可以以行对齐的方式存储在线性FIFO中,不会产生行错位.其次,行对齐输出要求对线性缓冲器FIFO进行同时读取,使不同行的相同位置的数据一起输出(如图 3中的Xp0, Xp6, Xp8同时输出).最后将读取到的图像数据组合成卷积矩阵,输入到计算模块中与系数进行卷积运算.
|
图 3 输入数据对齐并行处理 Fig. 3 Data alignment parallel processing |
图 3所示为一个3×3大小的卷积核在6×6输入图像上滑动的过程.其中蓝色表示原始图像大小为4×4.由于应用需要,原始图像进行了像素填充,因此实际输入图像变成6×6(这里填充像素层数设置为1).输入图像数据将按行依次读取.数据并行传输个数PD设置为4,数据计算并行度PV为4,卷积核尺寸K为3,滑动步长为1.由于此时图像边长6不为数据传输并行度4的整数倍,需要在每行的左侧添加2个无效数据(图中的红色像素)存入寄存器中补充成8个数据,以保证每行数据正好可以经过2个时钟周期传完.该例中实现的3×3的卷积核计算需要对3行的数据进行行对齐读取以组成卷积矩阵.因此使用2个FIFO缓存前两行输入数据,在第3个周期时便可与移位寄存器中的第3行数据实现行对齐输出,其结构如图 3(b)所示.由于数据传输并行度为PD,一个时钟周期便可得到3×PD个数据.根据式(1)可知当卷积核滑动步长为1时,每个卷积操作的输入矩阵之间有重叠,按照图 3(c)中的方式进行组合可得到PV个卷积矩阵.然后将这PV个矩阵按所标顺序分别输入到PV个K×K卷积核计算单元的中与系数进行卷积运算,这样一个周期内就可以得到PV个卷积结果.边长为6的图像,经过卷积操作后输出图像边长为4.如图 3(d)所示,输出图像的一行像素可经过一次数据并行计算同时得到.
综上所述,PD、PV的选择主要受到输出图像尺寸的限制.本文要实现一个完整的网络模型,因此硬件加速器的PD与PV的大小最终将需要考虑网络的所有卷积层的尺寸来确定.
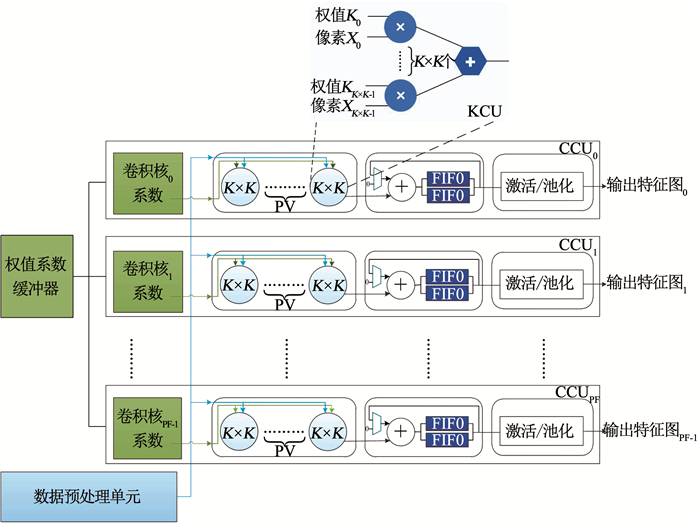
2.2 多卷积核并行计算经过对卷积层的分析发现,网络的每层卷积层都是用不同数量的卷积核在同一个输入图像上不断滑动进行卷积.因此,可以在硬件上实现PF个卷积核运算单元,使PF个不同的卷积核同时与图像数据进行卷积运算.图 4是一个多卷积核并行计算的硬件结构.其中数据预处理单元表示数据对齐并行处理的移位寄存器与FIFO线性缓冲器组成的预处理单元.权值系数缓冲器缓存计算所需的权值系数.KCU为一个K×K卷积核计算单元.这里假设卷积核的并行度PF为3,即可同时进行3个不同卷积核的卷积运算.依上文所述,每一层卷积层的所有卷积核处理的为同一张图像,所以其输入图像数据是同时读取的,只是被映射到不同的卷积核的卷积单元.假设输入图像为RGB三通道图像,图像将依照通道顺序依次进入预处理单元.一个通道的图像经过数据预处理单元处理后得到的PV个卷积矩阵将会被同时输送到每个卷积核的CCU卷积单元,然后再对应输入到CCU的PV个K×K卷积核计算单元当中与卷积系数进行乘累加操作.由于有PF个卷积核,每个卷积核的CCU单元可同时进行一个卷积核的PV个卷积结果的计算,因此一个周期内可以得到PF×PV个卷积运算结果.每个卷积核的卷积单元计算完输入图像的一个通道后,把结果暂时存放在FIFO当中,等待下一个通道计算结果的到来再进行累加.最终,输入图像的所有通道计算完后,存放在FIFO中的结果依次输出.多卷积核并行计算单元的计算速度快于暂存结果的FIFO的数据输出速度.为了减少计算等待时间,使上一周期的PF个卷积核的结果计算完后,无需等待FIFO中的数据全部取出,即可开始下一周期PF个卷积计算,在最后的通道累加单元中,使用了乒乓结构,使两个FIFO交替存取并行计算单元的卷积结果.
|
图 4 多卷积核并行计算单元 Fig. 4 Parallel computation unit with multiple filters |
根据多卷积核并行计算,加速器的PV大小将由输出图像确定,而卷积核并行度PF则主要受到片上资源的限制.卷积模块中的乘法全部利用FPGA的数字信号处理资源(digital signal processing, DSP)实现.采用图 4所示多卷积核并行策略后,所用的乘法器总数应该小于总的DSP资源为
| $ {\rm{PV}} \times {\rm{PF}} \times {\rm{Kerne}}{{\rm{l}}_k} \le {\rm{DS}}{{\rm{P}}_{{\rm{sum}}}}. $ | (2) |
式中:Kernelk为计算一个K×K大小卷积所需乘法器个数;DSPsum为FPGA片上DSP资源总数.
除此之外,还需要使用随机存取存储器块(block random access memory, BRAM)存储卷积计算所需的临时数据,因此需要考虑片上的存储资源.片上存储主要包括:输入缓冲区、线性缓冲区以及临时计算结果存储区.每层卷积层的输出图像大小公式如下:
| $ H_{{\rm{out}}}^i = \frac{{H_{{\rm{in}}}^i - K}}{s} + 1, $ | (3) |
| $ W_{{\rm{out}}}^i = \frac{{W_{{\rm{in }}}^i - K}}{s} + 1. $ | (4) |
式中:Hini、Wini分别为第i层输入图像的长和宽;K为卷积核大小;s为卷积滑动步长小;Houti、Wouti分别为第i层输出图像的长宽.
输入缓冲区需要存放下网络的最大输入图像与系数,所以大小为max[(Hini×Wini+K×K×PF)×Cini].由于输出缓冲区也需要储存最大输出图像并且采用了乒乓结构,所以总共大小为max(Houti×Wouti)×PF×2.线性缓冲区大小为max(Wini)×(K-1).所以,总的存储资源需要满足:
| $ \begin{array}{l} \max \left[ {\left( {H_{{\rm{in}}}^i \times W_{{\rm{in}}}^i + K \times K \times {\rm{PF}}} \right) \times C_{{\rm{in}}}^i} \right] + \\ \max \left( {W_{{\rm{in}}}^i} \right) \times \left( {K - 1} \right) + \max \left( {H_{{\rm{out}}}^i \times W_{{\rm{out}}}^i} \right) \times \\ {\rm{PF}} \times 2 \le {\rm{BRA}}{{\rm{M}}_{{\rm{sum}}}}. \end{array} $ | (5) |
式中:BRAMsum为总的片上RAM资源;K为卷积核大小;Cini为第i层输入图像的通道个数.
除资源限制之外,为了保证数据并行传输速度与计算速度匹配,PD应尽量大于等于PV;同时为了减少再对输出结果的处理,PV应尽量能被输出图像边长整除,即:
| $ W_{{\rm{out}}}^i\bmod {\rm{PV}} = 0, $ | (6) |
| $ {\rm{PD}} \ge {\rm{PV,}} $ | (7) |
式中,Wouti为第i层的输出图像边长.
图 5为卷积层执行时间示意图,可以看到一次的硬件执行时间Ttotal主要由计算所需图像的输入时间Tdata,PF个卷积核的权值系数输入时间TcoefPF,计算时间Tcomputetotal以及最终PF个计算结果输出时间ToutputPF组成.其中:
| $ T_{{\rm{coef}}}^{{\rm{PF}}} = K \times K \times {\rm{PF}} \times {C_{{\rm{in}}}} \times {t_{{\rm{clk}}}}, $ | (8) |
| $ {T_{{\rm{data}}}} = {H_{{\rm{in}}}} \times {W_{{\rm{in}}}} \times {C_{{\rm{in}}}} \times \delta \times {t_{{\rm{clk}}}}, $ | (9) |
| $ T_{{\rm{output}}}^{{\rm{PF}}} = \frac{{{H_{{\rm{out}}}} \times {W_{{\rm{out}}}} \times {\rm{PF}}}}{{{\rm{PV}}}} \times {t_{{\rm{clk}}}}, $ | (10) |
| $ T_{{\rm{compute}}}^{{\rm{total }}} = \frac{{{H_{{\rm{out}}}} \times {W_{{\rm{out}}}} \times {C_{{\rm{in}}}} \times {F_{{\rm{out}}}}}}{{{\rm{PV}} \times {\rm{PF}}}} \times \theta \times {t_{{\rm{clk}}}}, $ | (11) |
| $ {T_{{\rm{total}}}} = {T_{{\rm{data}}}} + T_{{\rm{coef}}}^{{\rm{PF}}} + T_{{\rm{compute}}}^{{\rm{total }}} + T_{{\rm{output}}}^{{\rm{PF}}}. $ | (12) |

|
图 5 卷积层硬件执行时间 Fig. 5 Execution time of each convolution layer |
式中:K为卷积核大小;Win、Hin分别为该次卷积计算的输入图像尺寸;Wout、Hout分别为输出图像尺寸;Cin为输入图像通道数;Fout为卷积核个数;δ、θ分别为架构所决定的传输与计算效率;tclk为时钟周期.
网络硬件执行时间为所有卷积层的执行时间总和.每层卷积层的执行时间则为该层所有的分割块的执行时间总和,即
| $ {\rm{Tim}}{{\rm{e}}_{{\rm{all}}}} = \sum\limits_{i = 1}^M {\left( {T_{{\rm{total}}}^i \times N_{{\rm{block}}}^i} \right)} . $ | (13) |
式中:Timeall为网络的总共硬件执行时间;Ttotali为式(12)所表示的第i层的一个分割块的硬件运算时间; Nblocki为第i层的分割块数.
3 结果本文将根据上述硬件架构分析对设计架构进行评估,以确定出最佳的并行方案.
表 1为本文所实现的SSD网络模型所包含的卷积层,加速器需要将每层卷积层的图像数据与权值系数从片外DDR读取到片上进行临时储存.当图像数据和系数的数量较为庞大时,由于片上资源有限,无法将完整一层的数据和参数全部储存到片上存储器中.这时,需要对图像进行分割,以分块的方式进行处理.表 1中列出了对于较大的卷积层所需进行的分割尺寸.这里相同输入图像大小的卷积层只列举了一个.为了降低加速器的资源与功耗,本文采用16位定点实现SSD网络模型,相比于单浮点数,其mAP仅下降了0.8%.
| 表 1 SSD网络模型卷积层 Tab. 1 Convolutional layer of SSD network model |
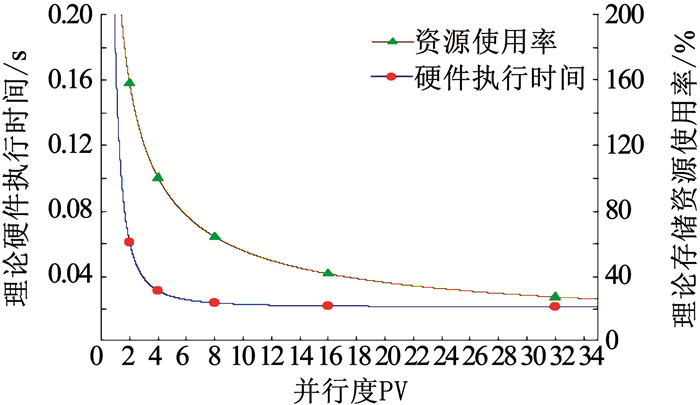
图 6是根据硬件架构分析式(2)~(13)所绘制的资源与性能评估模型图.在充分利用实验所用Xilinx Zynq XC7Z045片上DSP资源的情况下,理论执行时间与存储资源都与PV成反比.由于PV需满足式(6)的限制,因此根据表 1中的输出尺寸分别对PV=2、4、8、16、32这5种可选方案进行取点.可以看出当PV小于8时,硬件执行时间明显增加,并且需要的存储资源大于实际片上存储资源.网络中最小的输出图像大小边长为8,因此最终根据式(2)~(7)选择PD=8、PV=8、PF=12的并行方案.对该方案进行实际综合,DSP、BRAM、查找表单元(look-up-table, LUT)以及触发器(flip-flop, FF)的使用率见表 2.
|
图 6 性能与资源评估 Fig. 6 Evaluation of performance and resource |
| 表 2 硬件实现资源使用情况 Tab. 2 Resource utilization |
表 3列出了将同一SSD网络分别在CPU、GPU、FPGA32和FPGA16上实现的结果对比.从表 3中可以看出,本文基于16位定点数实现的SSD网络模型在175 MHz的时钟频率下,可以达到44.59帧/s,比基于32位定点数的硬件设计快4.99倍,分别是CPU与GPU的1.39倍与0.41倍.动态功耗为3.72 W,相比CPU与GPU分别降低85.1%与93.9%,是FPGA32的1.04倍.综上所述,本文所提出的16位卷积神经网络加速器与CPU、GPU相比,具有较低的功耗,与32位的加速器相比,具有较高性能的优势,因此更适用于移动设备上.
| 表 3 SSD网络硬件实验结果比较 Tab. 3 Comparison of SSD implementations |
表 4列出了3种基于Xilinx Zynq XC7Z045实现的卷积神经网络加速器[9, 14-15].可以看出,相比于其他设计,本设计采用数据对齐并行处理、多卷积核并行计算等方法能够充分利用片上资源,实现高度并行计算,使加速器的能效达到31.54 GOP/(s·W),比文献[9, 14-15]有较大性能提升.
| 表 4 与已有文献实验结果比较 Tab. 4 Comparison between several existing implementations and the proposed design |
1) 本文所提出的卷积神经网络加速器采用数据对齐并行处理与多卷积核并行计算的方法,实现了数据的高速并行传输,与多个层面的并行计算,并根据该设计方法建立了资源与性能模型,找出最佳并行方案,实现了加速器整体硬件架构的高能效.
2) 实验结果表明,加速器在175 MHz时钟频率下实现的SSD网络模型,其速度可以达到44.59 FPS,功耗为9.72 W,整体能效达到31.54 GOP/(s·W).
| [1] |
岳颀, 马彩文. 指数弹性动量卷积神经网络及其在行人检测中的应用[J]. 哈尔滨工业大学学报, 2017, 49(5): 159. YUE Qi, MA Caiwen. A deep convolution neural network for object detection based[J]. Journal of Harbin Institute of Technology, 2017, 49(5): 159. DOI:10.11918/j.issn.0367-6234.201603145 |
| [2] |
郭继昌, 郭昊, 郭春乐. 多尺度卷积神经网络的单幅图像去雨方法[J]. 哈尔滨工业大学学报, 2018, 50(3): 185. GUO Jichang, GUO Hao, GUO Chunle. Single image rain removal based on multi-scale convolutional neural network[J]. Journal of Harbin Institute of Technology, 2018, 50(3): 185. DOI:10.11918/j.issn.0367-6234.20170407 |
| [3] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. Imagenet classification with deep convolutional neural networks[C]//Proceedings of the 25th International Conference on Neural Information Processing Systems. Lake Tahoe, USA: ACM, 2012: 1097. DOI: 10.1145/3065386
|
| [4] |
CHAKRADHAR S, SANKARADAS M, JAKKULA V, et al. A dynamically configurable coprocessor for convolutional neural networks[C]//Proceedings of the 37th Annual International Symposium on Computer Architecture, ser. ISCA'10. New York, NY: ACM, 2010: 247. DOI: 10.1145/1815961.1815993
|
| [5] |
DU Zidong, FASTHUBER R, CHEN Tianshi, et al. ShiDianNao: Shifting vision processing closer to the sensor[C]//Proceedings of the 42nd Annual International Symposium on Computer Architecture. Portland, OR, USA: IEEE, 2015, 43(3): 92. DOI: 10.1145/2749469.2750389
|
| [6] |
CHEN Tianshi, DU Zidong, SUN Ninghui, et al. Diannao: A small-footprint high-throughput accelerator for ubiquitous machine-learning[C]//Proceedings of the 19th International Conference on Architectural Support for Programming Languages and Operating Systems. Salt Lake City, USA: ACM, 2014, 49(4): 269. DOI: 10.1145/2541940.2541967
|
| [7] |
SANKARADAS M, JAKKULA V, CADAMBI S, et al. A massively parallel coprocessor for convolutional neural networks[C]//Proceedings of the 20th IEEE International Conference on Application-Specific Systems, Architectures and Processors. Boston, USA: IEEE, 2009: 53. DOI: 10.1109/ASAP.2009.25
|
| [8] |
SUNG Wonyong, PARK J. Architecture exploration of a programmable neural network processor for embedded systems[C]//Proceedings of International Conference on Embedded Computer Systems: Architectures, Modeling and Simulation (SAMOS). Agios Konstantinos, Greece: IEEE, 2016: 124. DOI: 0.1109/SAMOS.2016.7818339
|
| [9] |
QIU Jiantao, WANG Jie, YAO Song, et al. Going deeper with embedded FPGA platform for convolutional neural network[C]//Proceedings of 2016 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays. Monterey, California: ACM, 2016: 26. DOI: 10.1145/2847263.2847265
|
| [10] |
LI Himin, FAN Xitian, JIAO Li, et al. A high performance FPGA-based accelerator for large-scale convolutional neural networks[C]//Proceedings of the 26th International Conference on Field Programmable Logic and Applications. Lausanne, Switzerland: IEEE, 2016: 1. DOI: 10.1109/FPL.2016.7577308
|
| [11] |
HUANG Chao, NI Siyu, CHEN Gengsheng. A layer-based structured design of CNN on FPGA[C]//Proceedings of the 12th International Conference on ASIC. Guiyang, China: IEEE, 2017: 1037. DOI: 10.1109/ASICON.2017.8252656
|
| [12] |
GLOROT X, BORDES A, BENGIO Y. Deep sparse rectifier neural networks[C]//Proceedings of the 14th International Conference on Artificial Intelligence and Statistics. Fort Lauderdale, FL, USA: IEEE, 2011: 315
|
| [13] |
LIU Wei, ANGUELOV D, ERHAN D, et al. SSD: Single shot multibox detector[C]//Proceedings of Computer Vision-European Conference on Computer Vision. Cham: Springer, 2016: 21. DOI: 10.1007/978-3-319-46448-0_2
|
| [14] |
GUO Kaiyuan, SUI Lingzhi, QIU Jiantao, et al. Angel-eye: A complete design flow for mapping CNN onto embedded FPGA[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2018, 37(1): 35. DOI:10.1109/TCAD.2017.2705069 |
| [15] |
XIAO Qingchen, LIANG Yun, LU Liqiang, et al. Exploring heterogeneous algorithms for accelerating deep convolutional neural networks on FPGAs[C]//Proceedings of the 54th Annual Design Automation Conference. Austin, TX: IEEE, 2017: 1. DOI: 10.1145/3061639.3062244
|
 2020, Vol. 52
2020, Vol. 52


