自19世纪80年代Pearl^[1]首次提出信度传播算法以来，越来越多的学者逐渐将其作为解决雷达多目标跟踪问题的一种新思路^[2]，其中Meyer等^[3-4]将迭代信度传播算法应用在多传感器多目标跟踪环境中，并提出粒子数值实现方式.但现阶段的研究内容只针对于低杂波背景环境，在实际的战场环境中，一方面存在大量低信噪比、运动形式复杂的目标，加大了检测难度；另一方面雷达信号处理器的检测输出存在虚警或漏检，产生大量的剩余杂波和干扰等，易发生误跟、失跟等现象^[5].因此需要对密集杂波环境下信度传播多目标跟踪算法的性能进行深入研究.

随着雷达和多传感器技术的逐渐成熟，不仅可以得到目标在空间中的位置、速度和加速度等运动信息，还可以获得幅度信息、回波宽度信息和多普勒速度信息等，因此有学者提出知识辅助的多目标跟踪方法.其中幅度信息最早在1990年由Lerro等^[6]指出，将幅度信息与PDA算法结合，证明了该方法的有效性.为了更准确的体现在复杂跟踪环境中杂波长拖尾情况，2009年Brekke等^[7]在K分布幅度模型下将幅度信息应用到JPDA算法中，通过计算具体的幅度似然比提高数据关联效率，得到了更好的杂波抑制效果.在国内, 文献[8-9]也将幅度信息分别引入PDA和JPDA算法中，改善了多目标跟踪性能.除此之外也有学者以类似的方法将幅度信息分别引入多假设跟踪算法^[10]、多伯努利滤波器^[11]和概率假设密度滤波器^[12]等，在不同的数据关联算法中均得到了较好的跟踪效果.

在此基础上，国内外学者也对信噪比进行了深入研究.一般情况下均假设目标信噪比已知，且保持不变，或者假设目标信噪比在规定区间内服从均匀分布.为了更加充分体现目标信噪比的波动情况，Bae等^[13]提出一种基于序贯蒙特卡洛方法的新型SNR估计算法，证明了该方法的有效性和高精度性，随后又提出了一种基于最大后验估计的SNR估计算法^[14]，并与极大似然估计方法对比发现该方法的估计效果更强.

本文提出基于幅度杂波抑制的高斯混合信度传播多目标跟踪算法.首先基于瑞利分布幅度模型和极大似然估计法，依据先验信息构造截断正态分布信噪比模型；然后结合幅度信息，一方面引入幅度似然比，提高信度传播过程中目标与量测的关联效率，另一方面设置量测信息录取率，提高目标起始效率；最后通过仿真实验对比，验证本文算法在密集杂波环境下的高效性.

1 幅度信息

幅度信息(amplitude information，AI)即回波的强度信息，由于杂波与目标的幅度概率密度函数有显著的不同，因此基于该特性可区分杂波和目标.令量测的幅度信息为l，当只有杂波时幅度信息的概率密度函数为p_c(l)，目标信噪比为d_t，当目标存在时幅度信息的概率密度函数为p_t(l|d_t)，幅度检测门限为τ，检测概率为P_D^τ(d_t)，虚警概率为P_FA^τ，本文依据文献[6]中的瑞利分布描述杂波和目标的幅度变化，相关公式详见文献[6].

由于在实际情况中目标信噪比具有一定程度的不确定性，需要对目标信噪比进行深入研究.本文首先产生n个样本的幅度信息，其中令n足够大，随后依据该样本对目标的初始信噪比进行极大似然估计为

$ {{\hat d}_{\rm{t}}} = \mathop {\text{ argmax}}\limits_d \sum\limits_{i = 1}^n {\ln } \left[ {{p_{\rm{t}}}\left( {{l_i}|d} \right)} \right] = \frac{1}{{2n}}\left( {\sum\limits_{i = 1}^n {l_i^2} } \right) - 1, $

得到目标初始信噪比的估计值$\hat{d}_{\mathrm{t}}$之后，在区间[d_low, d_high]内构造均值为$\hat{d}_{\mathrm{t}}$，方差为σ_t²的截断正态分布模型为

$ p\left( d \right) = \left\{ {\begin{array}{*{20}{l}} {C\frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} {\sigma _{\rm{t}}}}}\exp \left( { - \frac{{{{\left( {d - {\hat d_{\rm{t}}}} \right)}^2}}}{{2\sigma _{\rm{t}}^2}}} \right),d \in \left[ {{d_{{\rm{low}}}},{d_{{\rm{high}}}}} \right];}\\ {0,{\rm{ otherwise}}{\rm{. }}} \end{array}} \right. $

参数C保证p(d)在区间[d_low, d_high]内的累计概率为1，根据标准正态分布的累计分布函数Φ(·)计算可得到C为

$ C = {\left[ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {\frac{{{d_{{\rm{high}}}} - {{\hat d}_{\rm{t}}}}}{{{\sigma _{\rm{t}}}}}} \right) - \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {\frac{{{d_{{\rm{low}}}} - {{\hat d}_{\rm{t}}}}}{{{\sigma _{\rm{t}}}}}} \right)} \right]^{ - 1}}. $

由于检测概率P_D^τ(d_t)和有效幅度概率密度函数p_t^τ(l|d_t)均与信噪比有关，则依据目标信噪比模型进行边缘化处理，得到不以目标信噪比为参数的检测概率P_D^τ和有效幅度概率密度函数p_t^τ(l)为：

$ \begin{array}{l} P_{\rm{D}}^\tau = \int_{{d_{{\rm{low}}}}}^{{d_{{\rm{high}}}}} p \left( \delta \right)P_{\rm{D}}^\tau \left( \delta \right){\rm{d}}\delta = \\ \;\;\;\;\;\;\;\frac{C}{{\sqrt {2{\rm{ \mathsf{ π} }}} {\sigma _{\rm{t}}}}}\int_{{d_{{\rm{low}}}}}^{{d_{{\rm{high}}}}} {\exp } \left[ {\frac{{ - {{\left( {\delta - {{\hat d}_{\rm{t}}}} \right)}^2}}}{{2\sigma _{\rm{t}}^2}} - \frac{{{\tau ^2}}}{{2\left( {1 + \delta } \right)}}} \right]{\rm{d}}\delta , \end{array} $

(1)

$ \begin{array}{l} p_{\rm{t}}^\tau \left( l \right) = \int_{{d_{{\rm{low}}}}}^{{d_{{\rm{high}}}}} p (\delta )p_{\rm{t}}^\tau (l|\delta ){\rm{d}}\delta = \\ \;\;\;\;\;\;\;\;\;\frac{C}{{\sqrt {2{\rm{ \mathsf{ π} }}} {\sigma _{\rm{t}}}}}\int_{{d_{{\rm{low}}}}}^{{d_{{\rm{high}}}}} {\frac{l}{{1 + \delta }}} \exp \left[ {\frac{{\left( {{\tau ^2} - {l^2}} \right)}}{{2(1 + \delta )}} - \frac{{{{\left( {\delta - {{\hat d}_{\rm{t}}}} \right)}^2}}}{{2\sigma _{\rm{t}}^2}}} \right]{\rm{d}}\delta . \end{array} $

(2)

最终得到截断正态分布信噪比模型下的幅度似然比为

$ \begin{array}{l} \rho \left( {l,\tau } \right) = \frac{C}{{\sqrt {2{\rm{ \mathsf{ π} }}} {\sigma _{\rm{t}}}}}\exp \left( {\frac{{{l^2} - {\tau ^2}}}{2}} \right) \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\int_{{d_{{\rm{low}}}}}^{{d_{{\rm{bigh}}}}} {\frac{1}{{1 + \delta }}} \exp \left[ {\frac{{\left( {{\tau ^2} - {l^2}} \right)}}{{2\left( {1 + \delta } \right)}} - \frac{{{{\left( {\delta - {{\hat d}_{\rm{t}}}} \right)}^2}}}{{2\sigma _{\rm{t}}^2}}} \right]{\rm{d}}\delta ,l \ge \tau . \end{array} $

(3)

2 信度传播多目标跟踪算法

基于信度传播的多目标跟踪算法主要是将马尔科夫随机场理论与多目标跟踪问题结合，构造信度传播因子图模型，得到目标増广状态的信度函数，在此基础上判断目标的存在性，并对目标的状态进行估计，本文主要依据文献[3]建立多目标跟踪的马尔科夫随机场模型及相关方程.

假设目标个数为K，引入目标序号下标k∈{1, …, K}，定义第n时刻第k个目标的増广状态向量为y_n.k$ \buildrel \Delta \over = $[x_{n, k}^T, r_{n, k}]^T，其中x_{n, k}为状态向量，r_{n, k}为目标的存在状态，当目标存在时r_{n, k}=1，否则r_{n, k}=0.

假设传感器个数为S，引入传感器序号下标s∈{1, …, S}，定义第n时刻第s个传感器的量测个数为Mn(s)，引入量测信息序号下标m∈{1, …, Mn(s)}，第n时刻第s个传感器的第m个量测信息为zn, m(s)，第n时刻第s个传感器的Mn(s)个量测形成了联合量测向量zn(s)$ \buildrel \Delta \over = $[zn, 1(s)T; …; zn, Mn(s)(s)T]T.

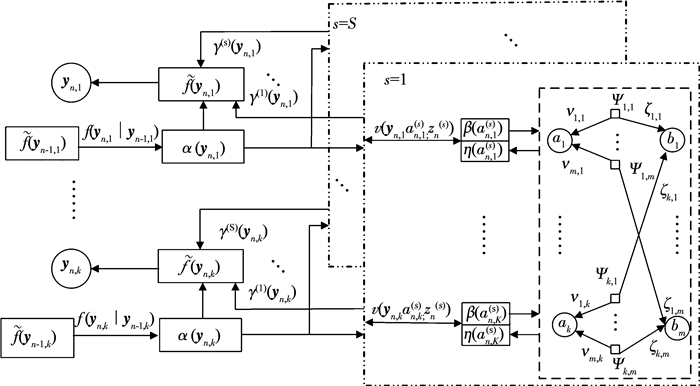
令第n时刻在第s个传感器中第k个目标的分配变量为a_{n, k}^(s)∈{0, 1, …, M_n^(s)}，若第k个目标未产生量测即漏检a_{n, k}^(s)=0，若第k个目标产生了序号为m的量测则a_{n, k}^(s)=m.为了与分配变量对应，引入冗余分配变量b_{n, m}^(s)∈{0, 1, …, K}，若第n时刻在第s个传感器中第m个量测是虚警则b_{n, m}^(s)=0，若第m个量测来源于序号为k的目标则b_{n, m}^(s)=k，信度传播多目标跟踪算法的因子图模型如图 1所示.

图 1中：$ \tilde{f}\left(\boldsymbol{y}_{n-1, k}\right) $为第n－1时刻第k个目标的信度函数；f(y_{n, k}|y_{n－1, k})为增广目标状态转移函数；α(y_{n, k})为预测后的信度函数；υ(y_{n, k}, a_{n, k}^(s); z_n^(s))为第n时刻第s个传感器的量测信息函数；β(a_{n, k}^(s))为量测估计函数；a_k=a_{n, k}^(s)为分配变量；b_m=b_{n, m}^(s)为冗余分配变量；v_{m, k}=v_m→k^(p)(a_{n, k}^(s))为第m个冗余分配变量向第k个分配变量传播的信息；ζ_{k, m}=ζ_k→m^(p)(b_{n, m}^(s))为第k个分配变量向第m个冗余分配变量传播的信息；η(a_{n, k}^(s))为迭代信度传播返回的函数；γ^(s)(y_{n, k})为量测更新后的函数；y_{n, k}为最终更新得到的目标状态.

3 基于幅度杂波抑制的高斯混合信度传播多目标跟踪算法

本文首先对系统模型扩维，令第n时刻第k个目标增广状态为y_{n, k}$ \buildrel \Delta \over = $[x_{n, k}^T, r_{n, k}]^T，其中x_{n, k}包括位置信息[x_{n, k}, y_{n, k}, z_{n, k}]和速度信息$ \left[\dot{\boldsymbol{x}}_{n, k}, \dot{\boldsymbol{y}}_{n, k}, \dot{\boldsymbol{z}}_{n, k}\right] $，r_{n, k}为目标的存在状态.第n时刻第s个传感器的第m个增广量测为$\mathit{\boldsymbol{\tilde z}}_{n, m}^{(s)} \buildrel \Delta \over = {\left[ {\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over z} }}_{n, m}^{(s){\rm{T}}}, l_{n, m}^{(s)}} \right]^{\rm{T}}}, \mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over z} }}_{n, m}^{(s)}$为量测的位置信息[x_{n, m}^(s), y_{n, m}^(s), z_{n, m}^(s)]^T，l_{n, m}^(s)为量测的幅度信息.

依据信度传播多目标跟踪算法的粒子数值实现方式^[4]，给出并完善高斯混合数值实现方式，令第n－1时刻第k个目标状态用高斯三元组集合表示，即{(w_{n－1, k}⁽ⁱ⁾, m_{n－1, k}⁽ⁱ⁾, P_{n－1, k}⁽ⁱ⁾)}_i=1^{J_{n－1, k}}，则第n－1时刻第k个目标信度函数的高斯和形式为:

$ \tilde f\left( {{\mathit{\boldsymbol{x}}_{n - 1,k}},1} \right) = \sum\limits_{i = 1}^{{J_{n - 1,k}}} {w_{n - 1,k}^{\left( i \right)}} N\left( {{\mathit{\boldsymbol{x}}_{n,k}};\mathit{\boldsymbol{m}}_{n - 1,k}^{\left( i \right)},\mathit{\boldsymbol{P}}_{n - 1,k}^{\left( i \right)}} \right), $

$ \tilde f\left( {{\mathit{\boldsymbol{x}}_{n - 1,k}},0} \right) = \left( {1 - \sum\limits_{i = 1}^{{J_{n - 1,k}}} {w_{n - 1,k}^{(i)}} } \right){f_{\rm{D}}}\left( {{\mathit{\boldsymbol{x}}_{n - 1,k}}} \right). $

式中f_D(x_{n－1, k})为虚拟函数.

3.1 预测步

令第n－1时刻得到的存活目标集合为К_{n－1, s}，新生目标集合为К_{n－1, b}，存活概率为p_s，分别对存活目标和新生目标进行一步预测.

当x_{n－1, ks}∈ К_{n－1, s}时，可得:

$ {\alpha _{\rm{s}}}\left( {{\mathit{\boldsymbol{x}}_{n,{k_{\rm{s}}}}},1} \right) = \sum\limits_{i = 1}^{{J_{n - 1}},{k_{\rm{s}}}} {w_{n|n - 1,{k_{\rm{s}}}}^{(i)}} N\left( {{\mathit{\boldsymbol{x}}_{n,{k_{\rm{s}}}}};\mathit{\boldsymbol{m}}_{n|n - 1,{k_{\rm{s}}}}^{(i)},\mathit{\boldsymbol{P}}_{n|n - 1,{k_{\rm{s}}}}^{(i)}} \right), $

$ {\alpha _{\rm{s}}}\left( {{\mathit{\boldsymbol{x}}_{n,{k_s}}},0} \right) = \left( {1 - \sum\limits_{i = 1}^{{J_{n - 1,{k_{\rm{s}}}}}} {w_{n - 1,{k_{\rm{s}}}}^{(i)}} } \right){f_{\rm{D}}}\left( {{\mathit{\boldsymbol{x}}_{n,{k_{\rm{s}}}}}} \right), $

其中，存活目标三元组分别为:

$ w_{n\left| {n - 1} \right.,{k_{\rm{s}}}}^{\left( i \right)} = {p_{\rm{s}}}w_{n - 1,{k_{\rm{s}}}}^{\left( i \right)}, $

$ \mathit{\boldsymbol{m}}_{n|n - 1,{k_{\rm{s}}}}^{\left( i \right)} = {\mathit{\boldsymbol{F}}_{n - 1}}\mathit{\boldsymbol{m}}_{n - 1,{k_s}}^{\left( i \right)}, $

$ \mathit{\boldsymbol{P}}_{n|n - 1,{k_{\rm{s}}}}^{(i)} = {\mathit{\boldsymbol{Q}}_{n - 1}} + {\mathit{\boldsymbol{F}}_{n - 1}}\mathit{\boldsymbol{P}}_{n - 1,{k_{\rm{s}}}}^{(i)}\mathit{\boldsymbol{F}}_{n - 1}^{\rm{T}}, $

则存活目标最终所有的高斯分量个数为J_{n, ks}=J_{n－1, ks}，最终信度函数可表示为{(w_{n, ks}⁽ⁱ⁾, m_{n, ks}⁽ⁱ⁾, P_{n, ks}⁽ⁱ⁾)}_i=1^{J_{n, ks}}~α(y_{n, ks}).

当x_{n－1, kb}∈К_{n－1, b}时，可得:

$ {\alpha _{\rm{b}}}\left( {{\mathit{\boldsymbol{x}}_{n,{k_{\rm{b}}}}},1} \right) = \sum\limits_{j = 1}^{{J_{\beta ,n - 1}},{k_{\rm{b}}}} {w_{\beta ,n|n - 1,{k_{\rm{b}}}}^{(j)}} N\left( {{\mathit{\boldsymbol{x}}_{n,{k_{\rm{b}}}}};\mathit{\boldsymbol{m}}_{n|n - 1,{k_{\rm{b}}}}^{(j)},\mathit{\boldsymbol{P}}_{n|n - 1,{k_{\rm{b}}}}^{(j)}} \right), $

$ {\alpha _{\rm{b}}}\left( {{\mathit{\boldsymbol{x}}_{n,{k_{\rm{b}}}}},0} \right) = \left( {1 - \sum\limits_{j = 1}^{{J_{\beta ,n - 1}},{k_{\rm{b}}}} {w_{\beta ,n|n - 1,,{k_{\rm{b}}}}^{(j)}} } \right){f_{\rm{D}}}\left( {{\mathit{\boldsymbol{x}}_{n,{k_b}}}} \right). $

其中，新生目标三元组分别为

$ w_{\beta ,n|n - 1,{k_{\rm{b}}}}^{(j)} = {p_{\rm{s}}}w_{\beta ,n - 1,{k_{\rm{b}}}}^{(j)}, $

$ \mathit{\boldsymbol{m}}_{n|n - 1,{k_{\rm{b}}}}^{(j)} = {\mathit{\boldsymbol{F}}_{n - 1}}\mathit{\boldsymbol{m}}_{n - 1,{k_{\rm{b}}}}^{(j)}, $

$ \mathit{\boldsymbol{P}}_{n|n - 1,{k_{\rm{b}}}}^{(j)} = {\mathit{\boldsymbol{Q}}_{n - 1}} + {\mathit{\boldsymbol{F}}_{n - 1}}\mathit{\boldsymbol{P}}_{n - 1,{k_{\rm{b}}}}^{(j)}\mathit{\boldsymbol{F}}_{n - 1}^{\rm{T}}, $

则新生目标最终所有的高斯分量个数为J_{n, kb}=J_{β, n－1, kb}，最终信度函数可表示为

$ \left\{ {\left( {w_{n,{k_{\rm{b}}}}^{(j)},\mathit{\boldsymbol{m}}_{n,{k_{\rm{b}}}}^{(j)},\mathit{\boldsymbol{P}}_{n,{k_{\rm{b}}}}^{(j)}} \right)} \right\}_{j = 1}^{{J_n},{k_{\rm{b}}}} \sim \alpha \left( {{\mathit{\boldsymbol{y}}_{n,{k_{\rm{b}}}}}} \right). $

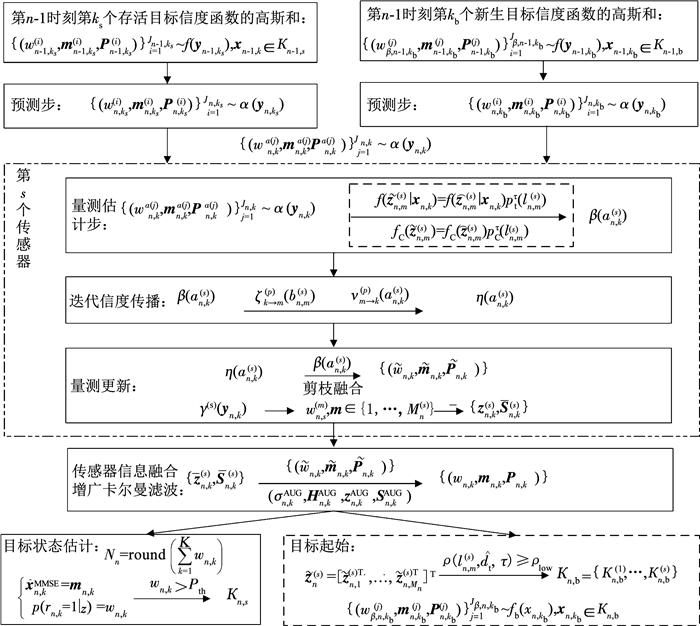
当得到存活目标与新生目标的一步预测后，各目标其余的步骤同基于信度传播的多目标跟踪算法基本保持一致，因此在本文所提算法在剩下的步骤中不再区分新生目标与存活目标，统一令第n时刻第k个目标通过预测步后最终的高斯分量个数为J_{n, k}，且最终经预测步后得到的信度函数为{(w_{n, k}^α(j), m_{n, k}^α(j), P_{n, k}^α(j))}_j=1^{J_{n, k}}~α(y_{n, k}), 基于幅度杂波抑制的高斯混合信度传播多目标跟踪的具体流程如图 2所示.

3.2 量测估计步

在该步骤中传感器量测信息函数主要由量测似然函数和杂波分布函数构成，计算各幅度信息的幅度似然比并引入该信息函数，较准确地得到与目标对应的量测信息.第n时刻对第k个目标预测的信度函数分别进入各传感器中，其中对于第s个传感器中的第k个目标，其先验分配向量信息为

$ \begin{array}{l} \beta \left( {a_{n,k}^{(s)}} \right) = \sum\limits_{j = 1}^{{J_{n,k}}} v \left( {{\mathit{\boldsymbol{x}}_{n,k}},1,a_{n,k}^{(s)};\mathit{\boldsymbol{\tilde z}}_n^{(s)}} \right)w_{n,k}^{\alpha (j)} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;v\left( {{\mathit{\boldsymbol{x}}_{n,k}},0,a_{n,k}^{(s)};\mathit{\boldsymbol{\tilde z}}_n^{(s)}} \right)\left( {1 - \sum\limits_{j = 1}^{{J_{n,k}}} {w_{n,k}^{\alpha (j)}} } \right). \end{array} $

在各传感器中，将与目标状态有关的检测概率首先转化为与目标信噪比相关，再依据式(1)选择将目标信噪比边缘化后的检测概率为

$ P_{\rm{D}}^{(s)}\left( {{\mathit{\boldsymbol{x}}_{n,k}}} \right) = P_{\rm{D}}^\tau \left( {{d_{\rm{t}}}} \right) = P_{\rm{D}}^\tau . $

令各传感器的虚警概率保持一致均为P_FA^τ，杂波数目服从参数为μ^(s)的泊松分布，结合文献[6]可知杂波的空间分布函数为

$ {f_{\rm{C}}}\left( {\mathit{\boldsymbol{\tilde z}}_{n,m}^{\left( s \right)}} \right) = {f_{\rm{C}}}\left( {\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over z} }}_{n,m}^{\left( s \right)}} \right){p_{\rm{c}}}\left( {l_{n,m}^{\left( s \right)}} \right), $

结合式(2)量测似然函数为:

$ f\left( {\mathit{\boldsymbol{\tilde z}}_{n,m}^{\left( s \right)}|{\mathit{\boldsymbol{x}}_{n,k}}} \right) = f\left( {\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over z} }}_{n,m}^{(s)}|{\mathit{\boldsymbol{x}}_{n,k}}} \right)p_t^\tau \left( {l_{n,m}^{(s)}} \right), $

$ f\left( {\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over z} }}_{n,m}^{(s)}|{\mathit{\boldsymbol{x}}_{n,k}}} \right) = N\left( {\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over z} }}_{n,m}^{(s)};{\mathit{\boldsymbol{\sigma }}_{n,k}},{\mathit{\boldsymbol{S}}_{n,k}}} \right), $

结合式(3)，代入幅度似然比，得到第s个传感内的量测信息函数为:

$ v\left( {{\mathit{\boldsymbol{x}}_{n,k}},1,a_{n,k}^{(s)};\mathit{\boldsymbol{\tilde z}}_n^{(s)}} \right) =\\ \left\{ \begin{array}{l} \frac{{P_{\rm{D}}^{(s)}\left( {{\mathit{\boldsymbol{x}}_{n,k}}} \right)\sum\limits_{j = 1}^{{J_{n,k}}} {w_{n,k}^{\alpha (j)}} N\left( {\mathit{\boldsymbol{\tilde z}}_{n,m}^{(s)}|\mathit{\boldsymbol{\sigma }}_{n,k}^{(j)},\mathit{\boldsymbol{S}}_{n,k}^{(j)}} \right)}}{{P_{{\rm{FA}}}^\tau {\mu ^{(S)}}{f_{\rm{C}}}\left( {\mathit{\boldsymbol{\tilde z}}_{n,m}^{(s)}} \right)}} = \frac{{P_{\rm{D}}^\tau \sum\limits_{j = 1}^{{J_{n,k}}} {w_{n,k}^{\alpha (j)}} N\left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over z} _{n,m}^{(s)}|\mathit{\boldsymbol{\sigma }}_{n,k}^{(j)},\mathit{\boldsymbol{S}}_{n,k}^{(j)}} \right)p_{\rm{t}}^\tau \left( {l_{n,m}^{(s)}} \right)}}{{P_{{\rm{FA}}}^\tau {\mu ^{(S)}}{f_{\rm{C}}}\left( {\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over z} }}_{n,m}^{(s)}} \right)p_{\rm{c}}^\tau \left( {l_{n,m}^{\left( s \right)}} \right)}} = \\ \frac{{P_{\rm{D}}^\tau \sum\limits_{j = 1}^{{J_{n,k}}} {w_{n,k}^{\alpha (j)}} N\left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over z} _{n,m}^{(s)}|\mathit{\boldsymbol{\sigma }}_{n,k}^{(j)},\mathit{\boldsymbol{S}}_{n,k}^{(j)}} \right)}}{{P_{{\rm{FA}}}^\tau {\mu ^{(S)}}{f_{\rm{C}}}\left( {\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over z} }}_{n,m}^{(s)}} \right)}}\rho \left( {l_{n,m}^{(s)},\tau } \right),a_{n,k}^{(s)} = m \in \left\{ {1, \cdots ,M_n^{(s)}} \right\},{r_{n,k}} = 1;\\ 1 - P_{\rm{D}}^{(s)}\left( {{x_{n,k}}} \right) = 1 - P_{\rm{D}}^\tau ,a_{n,k}^{(s)} = 0. \end{array} \right. $

$ v\left( {{\mathit{\boldsymbol{x}}_{n,k}},0,a_{n,k}^{(s)};\mathit{\boldsymbol{\tilde z}}_n^{(s)}} \right) = 1\left( {a_{n,k}^{(s)}} \right) = 1,a_{n,k}^{(s)} = 0. $

其中相关量测信息为:

$ \mathit{\boldsymbol{\sigma }}_{n,k}^{(j)} = {\mathit{\boldsymbol{H}}_n}\mathit{\boldsymbol{m}}_{n,k}^{\alpha (j)}, $

$ \mathit{\boldsymbol{S}}_{n,k}^{(j)} = {\mathit{\boldsymbol{R}}_n} + {\mathit{\boldsymbol{H}}_n}\mathit{\boldsymbol{P}}_{n,k}^{\alpha (j)}\mathit{\boldsymbol{H}}_n^{\rm{T}}. $

3.3 迭代信度传播

在量测估计步基础上对β(a_{n, k}^(s))进行迭代信度传播，其中令迭代步数为P_max，由M_n^(s)个冗余分配分量节点向K个分配分量节点传播的信息为v_m→k^(p)(a_{n, k}^(s))^[3]，由K个分配分量节点向M_n^(s)个冗余分配分量节点传播的信息为ζ_k→m^(p)(b_{n, m}^(s))^[3]，完成第n时刻完成P_max步迭代后，返回第s个传感器第k个目标的分配向量信息为

$ \eta \left( {a_{n,k}^{(s)}} \right) = \prod\limits_{m = 1}^{M_n^{\left( s \right)}} {v_{m \to k}^{\left( {{P_{\max }}} \right)}} \left( {a_{n,k}^{(s)}} \right). $

3.4 量测更新

完成迭代信度传播后，得到返回各传感器第k个目标的分配向量信息η(a_{n, k}^(s))，对先验分配向量信息β(a_{n, k}^(s))进行更新，即：

$ w_{n,k}^{A(j)} = w_{n,k}^{\alpha (j)}\prod\limits_{s = 1}^S {\sum\limits_{a_{n,k}^{(s)} = 0}^{M_n^{\left( s \right)}} v } \left( {{\mathit{\boldsymbol{x}}_{n,k}},1,a_{n,k}^{(s)};\mathit{\boldsymbol{\tilde z}}_n^{(s)}} \right)\eta \left( {a_{n,k}^{(s)}} \right),j \in {J_{n,k}}, $

$ w_{n,k}^B = \left( {1 - \sum\limits_{j = 1}^{{J_{n,k}}} {w_{n,k}^{\alpha \left( j \right)}} } \right)\prod\limits_{s = 1}^S \eta \left( {a_{n,k}^{(s)} = 0} \right),j \in {J_{n,k}}, $

则归一化后的高斯分量权重为

$ w_{n,k}^{(j)} = \frac{{w_{n,k}^{A(j)}}}{{\sum\limits_{{j^\prime } = 1}^{{J_{n,k}}} {w_{n,k}^{A\left( {{j^\prime }} \right)}} + w_{n,k}^B}}. $

考虑到高斯分量的特殊性，需要对所有的高斯分量进行剪枝融合操作，设置权重阈值w_th，只保留w_{n, k}^(j)≥w_th的高斯分量，令最大的高斯分量权重w_max=max(w_{n, k}^(j))_j=1^{J_{n, k}}，以w_max为基准将距离小于门限L的高斯分量进行融合，最终对于第k个目标只需保留一个高斯分量即$\left\{\left(\tilde{w}_{n, k}, \tilde{\boldsymbol{m}}_{n, k}, \tilde{\boldsymbol{P}}_{n, k}\right)\right\}$，且其相关量测信息为：

$ {\mathit{\boldsymbol{\sigma }}_{n,k}} = {\mathit{\boldsymbol{H}}_n}{{\mathit{\boldsymbol{\tilde m}}}_{n,k}}, $

$ {\mathit{\boldsymbol{S}}_{n,k}} = {\mathit{\boldsymbol{R}}_n} + {\mathit{\boldsymbol{H}}_n}{{\mathit{\boldsymbol{\tilde P}}}_{n,k}}\mathit{\boldsymbol{H}}_n^{\rm{T}}. $

随后分别在各传感器内，得到迭代信度传播后的分配向量为：

$ {\gamma ^{\left( s \right)}}\left( {{x_{n,k}},1} \right) = \sum\limits_{a_{n,k}^{\left( s \right)}} v \left( {{\mathit{\boldsymbol{x}}_{n,k}},1,a_{n,k}^{(s)};\mathit{\boldsymbol{\tilde z}}_n^{(s)}} \right)\eta \left( {a_{n,k}^{(s)}} \right), $

$ {\gamma ^{(s)}}\left( {{\mathit{\boldsymbol{x}}_{n,k}},0} \right) = \eta \left( {a_{n,k}^{(s)} = 0} \right). $

依据γ^(s)(x_{n, k}, 1)得到第s个传感器中所有量测信息分别对第k个目标的贡献权重w_{n, s}^(m), m∈{1, …, M_n^(s)}，则第k个目标的关联量测信息为：

$ \mathit{\boldsymbol{\bar z}}_{n,k}^{(s)} = \sum\limits_{m = 1}^{M_n^{(s)}} {w_{n,s}^{(m)}} \mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over z} }}_{n,m}^{(s)}, $

$ \mathit{\boldsymbol{\bar S}}_{n,k}^{(s)} = \sum\limits_{m = 1}^{M_n^{(s)}} {w_{n,s}^{(m)}} \left[ {{\mathit{\boldsymbol{S}}_{n,k}} + \left( {\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over z} }}_{n,m}^{(s)} - {\mathit{\boldsymbol{\sigma }}_{n,k}}} \right){{\left( {\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over z} }}_{n,m}^{(s)} - {\mathit{\boldsymbol{\sigma }}_{n,k}}} \right)}^{\rm{T}}}} \right]. $

式中: $ {\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over z} }}_{n, m}^{(s)}} $为第n时刻第s个传感器中第m个量测的位置信息；z_{n, k}^(s)为第n时刻第s个传感器通过迭代信度传播后对第k个目标的加权关联量测；S_{n, k}^(s)为加权关联量测协方差信息.

3.5 目标状态估计

首先将第n时刻所有传感器对第k个目标关联的量测信息进行融合，令：σ_{n, k}^AUG为第n时刻第k个目标的増广预测量测信息矩阵；H_{n, k}^AUG为増广量测矩阵；z_{n, k}^AUG是増广量测信息矩阵；S_{n, k}^AUG为増广量测协方差矩阵，即：

$ \mathit{\boldsymbol{\sigma }}_{n,k}^{{\rm{AUG}}} = \left[ {{\mathit{\boldsymbol{\sigma }}_{n,k}}; \cdots ;{\mathit{\boldsymbol{\sigma }}_{n,k}}} \right], $

$ \mathit{\boldsymbol{H}}_{n,k}^{{\rm{AUG}}} = \left[ {{\mathit{\boldsymbol{H}}_n}; \cdots ;{\mathit{\boldsymbol{H}}_n}} \right], $

$ \mathit{\boldsymbol{z}}_{n,k}^{{\rm{AUG}}} = \left[ {\mathit{\boldsymbol{\bar z}}_{n,k}^{(1)}; \cdots ;\mathit{\boldsymbol{\bar z}}_{n,k}^{(S)}} \right], $

$ \begin{array}{l} \mathit{\boldsymbol{S}}_{n,k}^{{\rm{AUG}}} = \text{rep}\left( {{\mathit{\boldsymbol{S}}_{n,k}},S,S} \right) + \text{diag}\left( {\mathit{\boldsymbol{\bar S}}_{n,k}^{(1)}, \cdots ,\mathit{\boldsymbol{\bar S}}_{n,k}^{(S)}} \right) - \\ \;\;\;\;\;\;\;\;\;\;\;{\rm{diag}}\left( {{\mathit{\boldsymbol{S}}_{n,k}}, \cdots ,{\mathit{\boldsymbol{S}}_{n,k}}} \right). \end{array} $

式中：diag为分块对角矩阵函数，即构造以参数矩阵为对角线的分块对角矩阵；rep为重复矩阵函数，即构造S×S个分块的分块矩阵，每一个分块皆为参数矩阵.其中S是传感器数量.

然后对目标进行增广卡尔曼滤波为：

$ {\mathit{\boldsymbol{K}}_{n,k}} = {{\mathit{\boldsymbol{\tilde P}}}_{n,k}}{\left( {\mathit{\boldsymbol{H}}_{n,k}^{{\rm{AUG}}}} \right)^{\rm{T}}}{\left[ {\mathit{\boldsymbol{S}}_{n,k}^{{\rm{AUG}}}} \right]^{ - 1}}, $

$ {\mathit{\boldsymbol{P}}_{n,k}} = \left[ {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_{n,k}}\mathit{\boldsymbol{H}}_{n,k}^{{\rm{AUG}}}} \right]{{\mathit{\boldsymbol{\tilde P}}}_{n,k}}, $

$ {\mathit{\boldsymbol{m}}_{n,k}} = {{\mathit{\boldsymbol{\tilde m}}}_{n,k}} + {\mathit{\boldsymbol{K}}_{n,k}}\left( {z_{n,k}^{{\rm{AUG}}} - \mathit{\boldsymbol{\sigma }}_{n,k}^{{\rm{AUG}}}} \right), $

$ {w_{n,k}} = {{\tilde w}_{n,k}}. $

设置概率阈值P_th，当w_{n, k}>P_th时认为目标存在，且将该目标加入到该时刻的存活目标集合К_{n, s}中，该目标对应的三元组{(w_{n, k}, m_{n, k}, P_{n, k})}将会在下一步的高斯混合信度传播中使用.

则第n时刻第k个目标的状态估计为

$ \mathit{\boldsymbol{\hat x}}_{n,k}^{{\rm{MMSE}}} = {\mathit{\boldsymbol{m}}_{n,k}}, $

第n时刻第k个目标存活概率为

$ p\left( {{r_{n,k}} = 1|z} \right) = {w_{n,k}}, $

第n时刻所有目标的数目估计为

$ {N_n} = \text{round}\left( {\sum\limits_{k = 1}^K {{w_{n,k}}} } \right). $

(4)

3.6 目标起始

传感器的量测信息主要包括目标的真实量测和杂波的量测，这些量测信息均是通过幅度检测门限τ筛选得到的，认为这些量测信息录取率为1.但是通过筛选得到的量测信息仍然包含一些剩余杂波量测信息，这样在每个时间步长内需要为大量无用的量测信息独立添加新生目标，造成新生目标数量庞大，在密集的杂波干扰中进一步加大信度传播中数据关联的错误率.

本文定义一个量测信息录取率P_low，为简化算法运算量，依据极大似然估计得到的目标初始信噪比$ \hat{d}_{\mathrm{t}} $和对应信噪比下有效目标幅度概率密度函数p_t^τ(l|$\hat{d}_{\mathrm{t}}$)进行计算为

$ {P_{{\rm{low}}}} \buildrel \Delta \over = \int_{{l_{{\rm{low}}}}}^\infty {p_{\rm{t}}^\tau } \left( {l|{{\hat d}_{\rm{t}}}} \right){\rm{d}}l \buildrel \Delta \over = \exp \left[ {\frac{{{\tau ^2} - l_{{\rm{low}}}^2}}{{2\left( {1 + {{\hat d}_{\rm{t}}}} \right)}}} \right]. $

从而得到幅度下限l_low和幅度似然比下限ρ_low，若量测的幅度似然比超过该下限值则直接录取进入目标起始过程，否则舍弃，即：

$ {l_{{\rm{low}}}} \buildrel \Delta \over = \sqrt {{\tau ^2} - 2\ln \left( {{P_{{\rm{low}}}}} \right)\left( {1 + {{\hat d}_{\rm{t}}}} \right)} , $

$ {\left. {{\rho _{{\rm{low}}}} \buildrel \Delta \over = \rho \left( {l,d,\tau } \right)} \right|_{{l_{{\rm{low}}}},{{\hat d}_{\rm{t}}},\tau }} \buildrel \Delta \over = \frac{1}{{1 + {{\hat d}_{\rm{t}}}}}\exp \left[ { - {{\hat d}_{\rm{t}}}\ln \left( {{P_{{\rm{low}}}}} \right)} \right]. $

在第n时刻第s个传感器得到M_n^(s)个量测信息中，若第m个量测的幅度信息l_{n, m}^(s)满足ρ(l_{n, m}^(s), $ \hat{d}_{\mathrm{t}}$, τ)≥ ρ_low，则将其加入新生目标集合К_{n, b}^(s)，最终得到第n时刻所有传感器新生目标集合为К_{n, b}={ К_{n, b}⁽¹⁾, …, К_{n, b}^(S)}，其中第k_b个新生目标的信度函数为：

$ \tilde f\left( {{\mathit{\boldsymbol{x}}_{n,{k_{\rm{b}}}}},1} \right) = {f_{\rm{b}}}\left( {{\mathit{\boldsymbol{x}}_{n,{k_{\rm{b}}}}}} \right) = \sum\limits_{j = 1}^{{J_{\beta ,n,{k_{\rm{b}}}}}} {w_{\beta ,n,{k_{\rm{b}}}}^{(j)}} N\left( {{\mathit{\boldsymbol{x}}_{n,{k_{\rm{b}}}}};\mathit{\boldsymbol{m}}_{n,{k_{\rm{b}}}}^{\left( j \right)},\mathit{\boldsymbol{P}}_{n,{k_{\rm{b}}}}^{\left( j \right)}} \right), $

$ \tilde f\left( {{\mathit{\boldsymbol{x}}_{n,{k_{\rm{b}}}}},0} \right) = \left( {1 - \sum\limits_{j = 1}^{{J_{\beta ,n,{k_{\rm{b}}}}}} {w_{\beta ,n,{k_{\rm{b}}}}^{\left( j \right)}} } \right){f_{\rm{D}}}\left( {{\mathit{\boldsymbol{x}}_{n,{k_{\rm{b}}}}}} \right). $

式中：$ \sum\limits_{j=1}^{J_{\beta, n, k_{\mathrm{b}}}} w_{\beta, n, k_{\mathrm{b}}}^{(j)}=p_{\mathrm{b}} $为目标新生概率；f_b(x_{n, kb})为新生目标信度函数；f_D(x_{n, kb})为虚拟函数，在下一时刻重复算法步骤预测步、量测估计步、迭代信度传播、量测更新、目标状态估计、目标起始.

4 仿真实验

本文在不同的杂波密度和不同信噪比情况下进行50次蒙特卡洛仿真，对比分析高斯混合概率假设密度(Gaussian mixture probability hypothesis density, GMPHD)、高斯混合信度传播(Gaussian mixture belief propagation, GMBP)、基于幅度信息且信噪比已知的高斯混合信度传播(amplitude information and known SNR-based Gaussian mixture belief propagation, GMBP-AK)和基于幅度杂波抑制的高斯混合信度传播(amplitude clutter suppression-based Gaussian mixture belief propagation，GMBP-AC)多目标跟踪算法的目标数目估计误差、跟踪精度和仿真时间等，进一步验证本文所提GMBP-AC算法的高性能.

4.1 场景设置

设定实验的三维背景仿真区域为[－3, 3] km× [－3, 3] km×[－3, 3] km，跟踪时间为100 s，时间步长Δt=1 s，目标存活概率p_s=1，目标新生概率p_b=0.01，量测更新过程中权重阈值w_th=0.01，距离门限L=5，概率阈值P_th=0.1，目标起始过程中的量测信息录取率P_low=0.9.传感器个数为3，且3个传感器类型保持一致，杂波数目服从泊松分布，均值分别为10、15和20，杂波在空间中服从均匀分布，虚警概率P_FA^τ=0.1，幅度检测门限τ=2.146，目标个数为5，各目标初始运动状态见表 1.

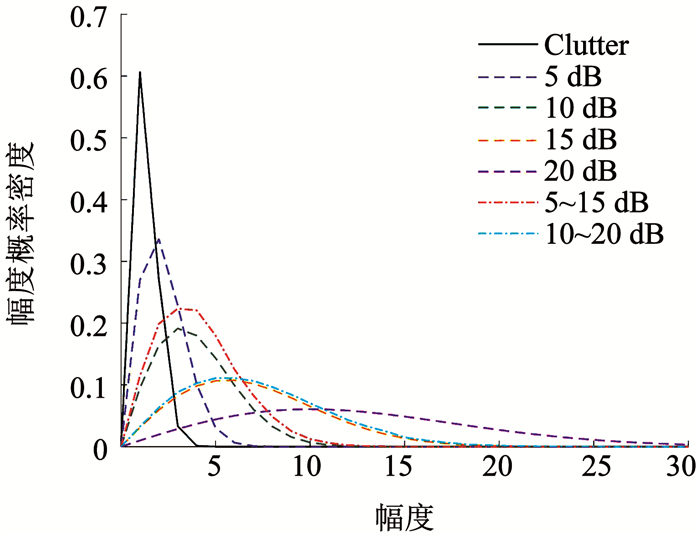
令背景杂波信噪比保持归一化即SNR_c=1 dB，当目标信噪比为SNR_t1=10 dB即d_t1=10时，通过随机数产生500个幅度信息样本，依据极大似然估计得到目标初始信噪比$\hat{d}_{\mathrm{t1}}$=9.176，在给定信噪比区间[SNR_low1, SNR_high1]=[5 dB, 15 dB]构造10 dB情况下的截断正态分布目标信噪比模型，其中信噪比方差σ_t1²=4，[d_low1, d_high1]=[3.162, 31.623].当目标信噪比为SNR_t2=15 dB即d_t2=31.623时，对目标初始信噪比进行极大似然估计得到$ \hat{d}_{\mathrm{t2}} $=30.585，在区间[SNR_low2, SNR_high2]=[10 dB, 20 dB]中构造15 dB情况下的截断正态分布目标信噪比模型，且信噪比方差σ_t2²=20，[d_low2, d_high2]=[10, 100].如图 3所示，分别给出了不同信噪比和截断正态分布信噪比模型下的幅度概率密度函数变化曲线，可以发现截断正态模型下的幅度概率密度函数曲线介于区间边界对应的幅度概率密度函数曲线之间，在一定程度上与10 dB和15 dB对应的幅度特性接近.

不同信噪比下的检测概率见表 2，可以发现当目标信噪比已知时，信噪比值越高，对应的检测概率越大，且在[5 dB, 15 dB]和[10 dB, 20 dB]区间内截断正态分布信噪比模型下的检测概率能够保持一个较高的值.

为避免目标的机动对算法产生干扰采用常速度模型，离散形式的状态转移方程和观测方程分别为：

$ {\mathit{\boldsymbol{x}}_n} = \mathit{\boldsymbol{F}}{\mathit{\boldsymbol{x}}_{n - 1}} + \mathit{\boldsymbol{G}}{\mathit{\boldsymbol{w}}_{n - 1}}, $

$ {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over z} }_n} = \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{x}}_n} + {\mathit{\boldsymbol{u}}_n}. $

式中：状态转移矩阵$\mathit{\boldsymbol{F}} = \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{I}}_3}}&{\Delta t{\mathit{\boldsymbol{I}}_3}}\\ {{\mathit{\boldsymbol{0}}_3}}&{{\mathit{\boldsymbol{I}}_3}} \end{array}} \right]$; 过程噪声矩阵$\boldsymbol{G}=\left[\begin{array}{c} 0.5 \Delta t^{2} \boldsymbol{I}_{3} \\ \Delta t \boldsymbol{I}_{3} \end{array}\right]$；量测矩阵H=[I₃, 0₃]；w_n－1为第n－1时刻的过程噪声，满足w_n－1~N(0, Q_n－1)，且$\boldsymbol{Q}_{n-1}=\sigma_{f}^{2}\left[\begin{array}{lll} 0.25 \boldsymbol{I}_{3} & 0.5 \boldsymbol{I}_{3} \\ 0.5 \boldsymbol{I}_{3} & I_{3} \end{array}\right]$, 过程噪声标准差σ_f=0.1；u_n为第n时刻的观测噪声，且满足u_n~N(0, R_n)，其中R_n=σ_h²I₃，量测噪声标准差σ_h=15，其中I₃表示3×3的单位矩阵，0₃表示3×3的零矩阵.

依据极大似然估计得到的目标初始信噪比$\hat{d}_{\mathrm{t}}$、有效幅度概率密度函数p_t^τ(l|$\hat{d}_{\mathrm{t}}$)和p_c^τ(l)得到量测幅度值，其中假设ε是0~1之间的均匀分布随机数.令$ \int_{{l_{\rm{t}}}}^\infty {p_{\rm{t}}^\tau } \left( {l|{{\hat d}_{\rm{t}}}} \right){\rm{d}}l = 1 - \varepsilon $，得到目标的有效量测幅度信息为${l_{\rm{t}}} = \sqrt {{\tau ^2} - 2\left( {1 + {{\hat d}_{\rm{t}}}} \right)\ln (1 - \varepsilon )} $，令$ \int_{{l_{\rm{c}}}}^\infty {p_{\rm{c}}^\tau } (l){\rm{d}}l = 1 - \varepsilon $，则杂波的有效量测幅度信息为${l_{\rm{c}}} = \sqrt {{\tau ^2} - 2\ln (1 - \varepsilon )} $.

4.2 仿真结果与分析 4.2.1 目标航迹

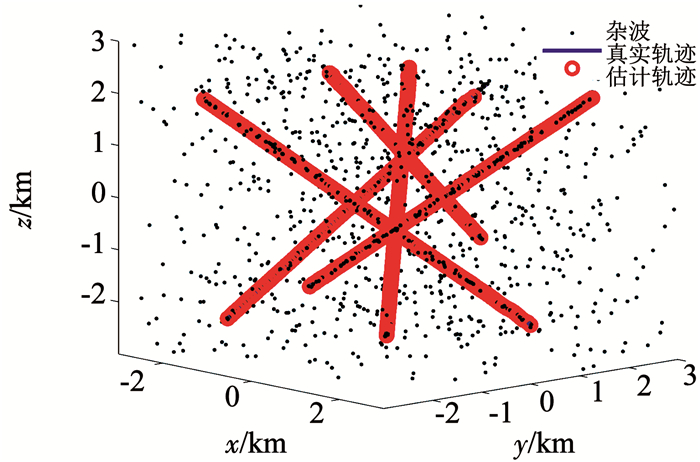
在不同信噪比下采用GMBP-AC算法得到的目标跟踪轨迹如图 4所示，可以看出在三维密集杂波环境中可以得到较为准确的目标航迹，且在邻近目标交汇处基本不会发生误跟、失跟等情况.

4.2.2 运行时间

为避免积分环节对算法运行时间的影响，采用蒙特卡洛方法进行积分计算.由图 5可知，当杂波密度较小时，各算法的运行时间相差不大，此时杂波对算法的干扰作用较小.随着杂波密度的增大，由于多次的迭代信度传播过程和大量的杂波干扰，GMBP算法的计算复杂度较大，且运行时间大于GMPHD算法，引入幅度信息后的GMBP-AK和GMBP-AC算法的运行时间明显缩短，均得到不同幅度的下降，能够较理想地应用在实际情况中.

4.2.3 目标数目估计

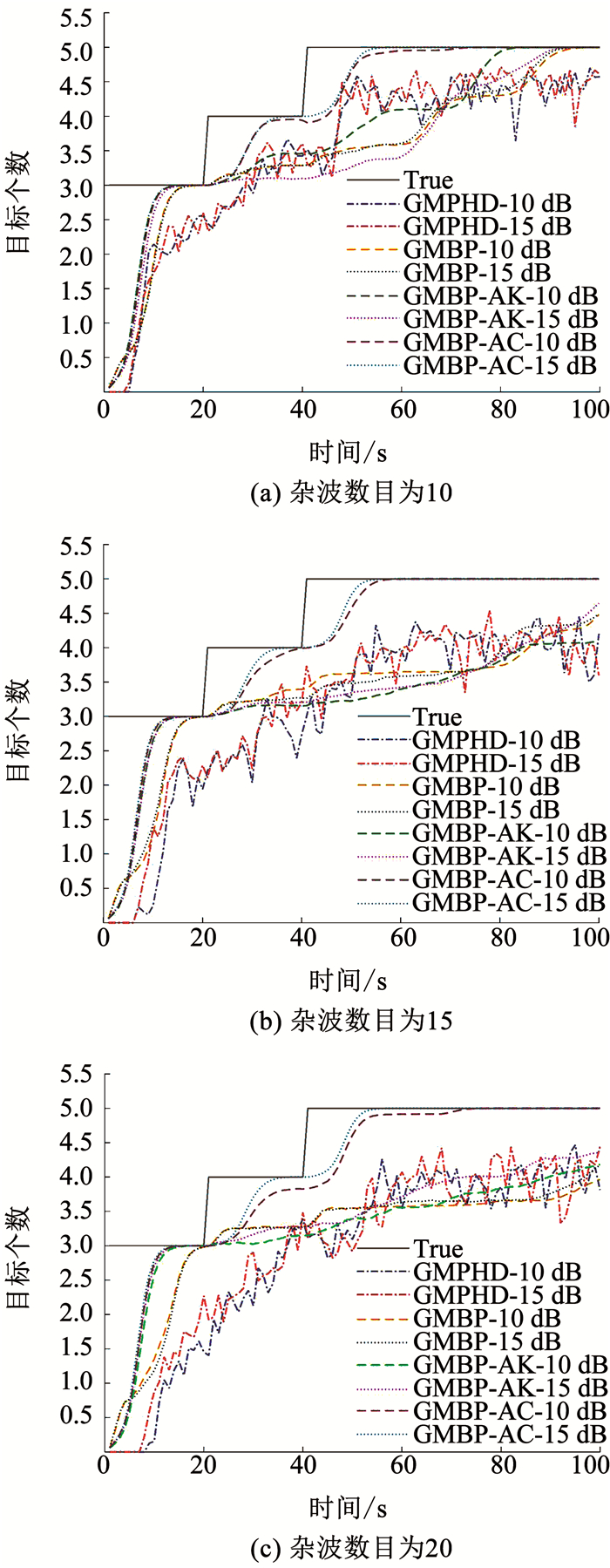
为了反映估计目标个数随时间的渐变情况，在仿真实验中对式(4)将不进行取整操作.由图 6可知，在相同杂波密度和相同信噪比情况下，各算法均能以相对较短的时间完成对前3个目标的数目估计，但GMPHD的估计误差大.当第4个目标出现时，GMPHD算法的估计误差消除，而GMBP和GMBP-AK算法的估计时间均较长，估计误差增大.当第5个目标出现时，GMPHD、GMBP和GMBP-AK算法的估计性能变差，而本文所提GMBP-AC算法在各时间段内均能够较准确地估计目标数目.

在不同杂波密度相同信噪比情况下，当杂波密度较小时，各算法的估计性能较理想.随着杂波密度的增大，在跟踪前期GMPHD算法的估计误差逐渐大于GMBP算法，且GMPHD算法对目标数目的估计曲线上、下波动幅度大，估计不稳定.与GMBP算法相比，GMBP-AK算法对目标数目的估计性能改善情况不明显，而本文所提的GMBP-AC算法能够在各时间段内快速响应目标数目的变化，对目标数目估计误差平均减小65%左右.在相同杂波密度不同信噪比情况下，当信噪比较高时，各算法的估计性能相对变高，即在高信噪比情况下更有利于算法对目标数目的估计.

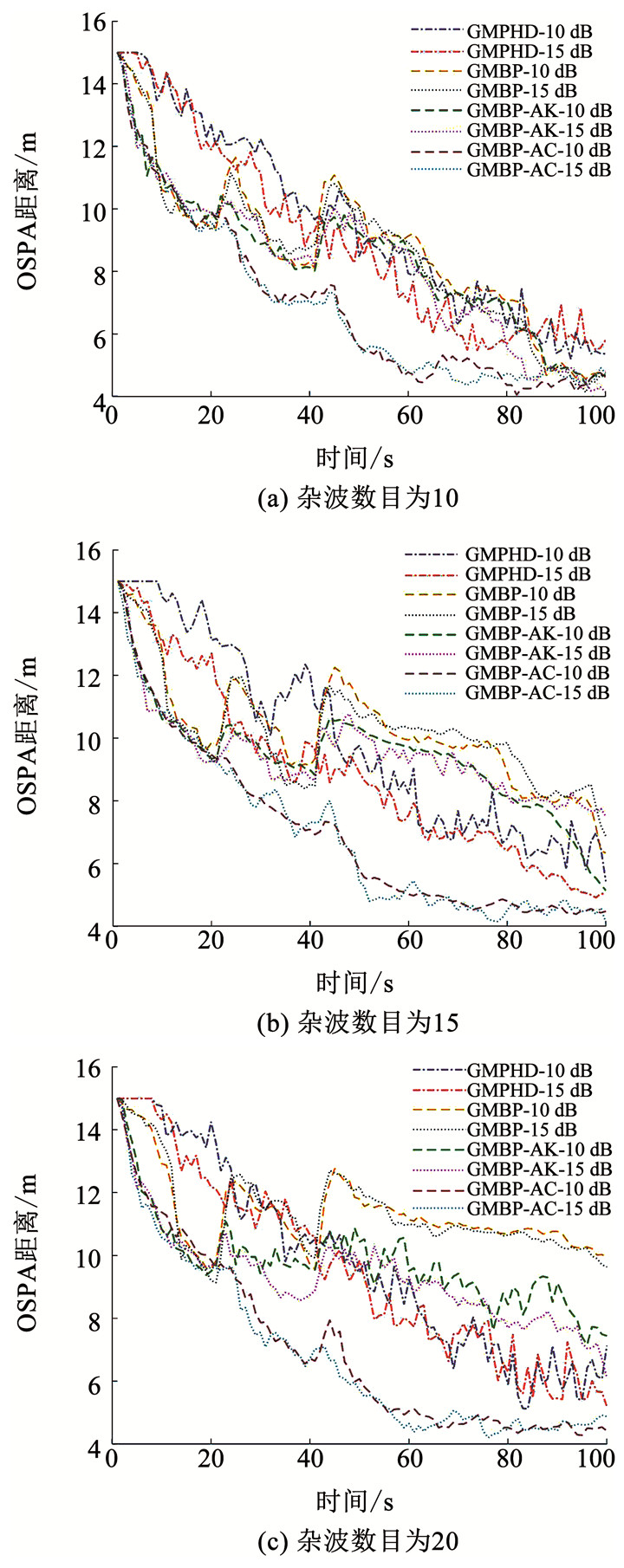
4.2.4 跟踪精度

为了对比各算法的跟踪精度，采用最优次模式分配(optimal subpattern assignment，OSPA)距离作为评价指标^[15](取1阶距，误差调节因子c=15).由图 7可知，在相同杂波密度和相同信噪比情况下，在跟踪前期GMPHD的跟踪精度不如GMBP算法，由于幅度似然比的作用，与GMBP算法相比GMBP-AK和GMBP-AC算法的跟踪精度均得到提高，且这两种算法的跟踪精度基本保持一致，说明本文所提的截断正态分布目标信噪比模型能够较好地应用在目标信噪比未知的情况中.在跟踪后期与GMPHD算法相比，GMBP和GMBP-AK算法的跟踪精度变差，说明受目标起始过程的影响较大，本文所提GMBP-AC算法添加了以幅度信息为条件的目标起始过程，较好地剔除剩余杂波干扰，能够保持较高的跟踪精度.

在不同杂波密度相同信噪比情况下，低杂波密度干扰下各算法的平均OSPA距离相差不大，跟踪精度较理想.随着杂波密度的增大，GMPHD与GMBP算法的跟踪性能均下降，而与GMBP算法相比，GMBP-AK算法的跟踪精度平均提升8%左右，GMBP-AC算法平均提升25%左右，较好地弥补了GMBP-AK算法跟踪精度不高的问题.在相同杂波密度不同信噪比情况下，当信噪比较高时，各算法的OSPA距离相对较小，即在高信噪比情况下更有利于算法跟踪精度的提高.

5 结论

1) 本文基于瑞利分布幅度模型和极大似然估计法，依据先验信息构造截断正态分布信噪比模型，通过边缘化得到不以目标信噪比为参数的检测概率和有效幅度概率密度函数.

2) 提出了基于幅度杂波抑制的高斯混合信度传播多目标跟踪算法，将幅度似然比引入信度传播的量测信息函数中，提高目标与量测的关联正确率，同时设置量测信息录取率，提高目标起始效率.

3) 仿真结果表明，在不同杂波密度和信噪比情况下，相比于标准GMPHD和GMBP算法，GMBP-AK和GMBP-AC算法的目标数目估计性能和跟踪精度均得到了提高，其中本文所提GMBP-AC算法的杂波抑制效果更强.