多输入多输出(Multiple-Input Multiple-Output, MIMO)系统可以利用自适应调制, 预编码, 功率注水等预处理技术实现更好的性能, 这些技术都需要提前知道当前时刻的信道状态信息(Channel State Information, CSI).频分双工(Frequency Division Duplex, FDD)系统将接收端估计的CSI反馈到发送端, 但信道时变使反馈的CSI迅速过时, 引起容量的损失.在时分双工(Time Division Duplex, TDD)系统中, 通常利用上下行信道的互易性来获得CSI, 再对发送信号进行预处理, 但由于获得的CSI与真实CSI存在误差, 降低了信道容量^[1].文献[2]表明信道预测可以有效地弥补这种损失.

现有的信道预测算法可以大致分为基于正弦和SOS(Sum of Sinusoidal)模型的算法, 基于自动回归(Autoregressive, AR)模型的算法和其他扩展算法.SOS算法^[3-6]用谱估计的方法来确定与各个正弦波相关的参数, 例如幅度、多普勒频移、相位, 并将其外推到将来时刻叠加预测出可靠的CSI.基于AR模型的算法通常是指线性预测器, 慢时变AR模型系数可以通过最小化均方误差(Minimum Mean Square Error, MMSE)准则^[7]计算, 对于快变系统, 其预测性能急剧下降.为了更好地追踪快变系统信道系数的变化, 学者们提出了各种有效的自适应技术^[8-10].对于其他的扩展算法, 主要有基于回声状态网络^[11]、长短期记忆网络^[12]等信道预测算法.

MIMO信道具有多维结构, 但上述算法大多是基于二维模型, 直接在信道上进行预测, 忽略了其内在结构, 文献[13]将基于张量的预测框架与简单的线性滤波器相结合, 提出基于张量的维纳滤波预测算法.为了降低算法的复杂度并改善其通用性, 文献[14]提出了基于高阶奇异值分解(High Order Singular Value Decomposition, HOSVD)降噪的信道预测算法, 即在利用传统算法预测CSI前, 先使用HOSVD降噪.该算法的局限性是, 对多普勒频移及天线数较少比较敏感, 导致其预测性能急剧恶化.

对此, 本文提出了一种改进的信道预测算法.该算法首先对估计的信道进行数据平滑处理, 随后利用HOSVD对平滑后的信道矩阵降噪, 最后使用递归最小二乘(Recursive Least Squares, RLS)滤波器进行信道预测.数据处理部分可以平滑噪声并解决因天线数较少而引起的秩不足的问题, 从而改善文献[14]中算法的不足.在载波频率为2 GHz、最大多普勒频移为50 Hz(移动速度为27 km/h)的市区拥堵场景下对所提算法的性能进行了仿真验证.

1 信道模型

在TDD系统中, 考虑一个时变MIMO瑞利平坦衰落信道, t时刻采样的信道脉冲响应可以表示为一个复矩阵h(t)∈$\mathbb{C}$^M_T×M_R, 其中M_T和M_R分别是基站发送和用户接收天线数.实际中, 由于估计误差和噪声的影响, 得到的CSI并不理想.因而, 可以将估计的CSI建模为

$ \mathit{\boldsymbol{\tilde h}}\left( t \right) = \mathit{\boldsymbol{h}}\left( t \right) + \mathit{\boldsymbol{n}}\left( t \right), $

式中n(t)是噪声, 服从复高斯分布.对于采样间隔为T_S, N个采样的CSI可以表示为

$ \mathit{\boldsymbol{\tilde h}}\left( u \right) = \mathit{\boldsymbol{h}}\left( u \right) + \mathit{\boldsymbol{n}}\left( u \right). $

式中$0 < \left( {u = \frac{t}{{{T_{\rm{S}}}}}} \right) < N + 1$.

2 信道预测算法 2.1 数据处理

为了降低多普勒频移以及天线数对预测算法性能的影响, 该文提出在基于HOSVD降噪前, 利用空时相关性, 对估计的CSI进行平滑.

首先估计的信道可以转化为$\mathit{\boldsymbol{\widetilde h}}(\mathit{u})$∈$\mathbb{C}$^M₂×M₁, 其中M₁=max{M_T, M_R}, M₂=min{M_T, M_R}, 之后将各个时刻采样估计的信道矩阵$\mathit{\boldsymbol{\widetilde h}}(\mathit{u})$组合为

$ \mathit{\boldsymbol{\tilde H}} = {\left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\tilde h}}(1)}&{\mathit{\boldsymbol{\tilde h}}(2)}&{ \cdots \mathit{\boldsymbol{\tilde h}}(N)} \end{array}} \right]^{\text{T}}} \in {\mathbb{C}^{{M_1}N \times {M_2}}}. $

本文使用空时平滑来重构数据结构, N个采样点分为P个过采样子阵, 每个子阵包括L=N－P+1个采样点.定义第P个子阵的选择矩阵为

$ {\mathit{\boldsymbol{f}}_p} = \left[ {\begin{array}{*{20}{c}} {{{\bf{0}}_{{M_1}L \times {M_1}\left( {p - 1} \right)}}}&{{\mathit{\boldsymbol{I}}_{{M_1}L}}}&{{{\bf{0}}_{{M_1}L \times {M_1}\left( {P - p} \right)}}} \end{array}} \right]. $

空时平滑后的信道矩阵${\mathit{\boldsymbol{\tilde H}}_{{\rm{sm}}}}$可表示为

$ {{\mathit{\boldsymbol{\tilde H}}}_{{\rm{sm}}}} = {\left[ {\begin{array}{*{20}{c}} {{f_1}\mathit{\boldsymbol{\tilde H}}}&{{f_2}\mathit{\boldsymbol{\tilde H}}}& \cdots &{{f_P}\mathit{\boldsymbol{\tilde H}}} \end{array}} \right]^{\rm{T}}}, $

式中${\mathit{\boldsymbol{\tilde H}}_{{\rm{sm}}}}$∈$\mathbb{C}$^M₁L×M₂P, 可看作是通过减少采样数N来虚拟增加天线数, 解决因天线数少而引起的秩不足的问题, 充分利用空时相关性来重构信道矩阵, 从而平滑噪声提高预测性能.

2.2 HOSVD降噪

平滑后的信道矩阵${\mathit{\boldsymbol{\tilde H}}_{{\rm{sm}}}}$可以表示为一个三维复张量^[13]${\mathit{\boldsymbol{\tilde H}}_{{\rm{sm}}}}$∈$\mathbb{C}$^{M₁×L×M₂P}, 其中M₁和L代表空域和时域的采样数, M₂P看作是空时混合域的采样数.在描述HOSVD之前, 需要介绍张量χ∈$\mathbb{C}$^{I₁×I₂×…×I_N}和矩阵U∈$\mathbb{C}$^T_n×I_n的n-mode乘积：

$ \mathit{\boldsymbol{Y}} = \mathit{\boldsymbol{X}} \times {}_n\mathit{\boldsymbol{U}} \in {\mathbb{C}^{{I_1} \times {I_2} \times \cdots \times {I_{n - 1}} \times {T_n} \times {I_{n + 1}} \times \cdots \times {I_N}}}, $

$ {y_{{i_1} \times {i_2} \times \cdots \times {i_{n - 1}} \times {t_n} \times {i_{n + 1}} \times \cdots \times {i_N}}} = \sum\limits_{{i_n} = 1}^{{I_n}} {{x_{{i_1} \times {i_2} \times \cdots \times {i_n}}}} \cdot {u_{{t_n} \times {i_n}}}. $

根据文献[13]可知, 张量${\mathit{\boldsymbol{\tilde H}}_{{\rm{sm}}}}$可以分解为

$ {{\mathit{\boldsymbol{\tilde H}}}_{{\rm{sm}}}} = \mathit{\boldsymbol{S}} \times {}_1{\mathit{\boldsymbol{U}}_1} \times {}_2{\mathit{\boldsymbol{U}}_2} \times {}_3{\mathit{\boldsymbol{U}}_3}. $

式中：酉矩阵U₁∈$\mathbb{C}$^M₁×M₂PL, U₂∈$\mathbb{C}$^L×M₁M₂P和U₃∈$\mathbb{C}$^M₂P×M₁L分别是1-mode, 2-mode和3-mode奇异向量, S是大小为M₁×L×M₂P的核心张量.

在噪声存在时, 酉矩阵U_n是由信号子空间和噪声子空间组成, 若n-秩等于r_n, 则${\mathit{\boldsymbol{\tilde H}}_{{\rm{sm}}}}$的低秩约等式可以表示为^[14]

$ {{\mathit{\boldsymbol{\hat H}}}_{{\rm{sm}}}} = {\mathit{\boldsymbol{S}}^{\left[ {{r_1},{r_2},{r_3}} \right]}} \times {}_1\mathit{\boldsymbol{U}}_1^{\left[ {{r_1}} \right]} \times {}_2\mathit{\boldsymbol{U}}_2^{\left[ {{r_2}} \right]} \times {}_3\mathit{\boldsymbol{U}}_3^{\left[ {{r_3}} \right]}, $

(1)

式中U_n^[r_n]由r_n个n-mode奇异向量组成.降噪后的信道矩阵${\mathit{\boldsymbol{\hat H}}_{{\rm{sm}}}}$可以看作是截断的核心张量S^{[r₁, r₂, r₃]}和信号子空间U_n^[r_n]计算得到.截断的核心张量可以通过如下的等式获得:

$ {\mathit{\boldsymbol{S}}^{\left[ {{r_1},{r_2},{r_3}} \right]}} = {{\mathit{\boldsymbol{\hat H}}}_{{\rm{sm}}}} \times {}_1{\left[ {\mathit{\boldsymbol{U}}_1^{\left[ {{r_1}} \right]}} \right]^{\rm{H}}} \times {}_2{\left[ {\mathit{\boldsymbol{U}}_2^{\left[ {{r_2}} \right]}} \right]^{\rm{H}}} \times {}_3{\left[ {\mathit{\boldsymbol{U}}_3^{\left[ {{r_3}} \right]}} \right]^{\rm{H}}}, $

(2)

式中[·]^H表示共轭转置.

根据式(1)和(2)可以计算降噪的信道${\mathit{\boldsymbol{\hat H}}_{{\rm{sm}}}}$, 随后使用相同的逆过程去平滑得到信道矩阵$\mathit{\boldsymbol{\hat H}}(\mathit{u})$∈$\mathbb{C}$^M₁×M₂, 最后再预测未来的CSI.

可以看出如果直接使用HOSVD降噪, 当M₂＜r₂时, 矩阵U₃∈$\mathbb{C}$^M₂×M₁N会出现缺秩的问题.上节中的数据处理可以选择P, 使其满足M₂P≥r₂, 从而解决秩不足的问题, 更准确地估计信道, 降低预测误差, 进而提高信道容量.

2.3 信道预测

RLS滤波器是根据最小均方自适应滤波器(Least Mean Squares, LMS)^[15]扩展的一种自适应算法, 其使用指数加权的误差平方和作为代价函数, 对于快变信道有更好的性能和更快的收敛速度^[16].因此, 得到降噪的信道$\mathit{\boldsymbol{\hat H}}(\mathit{u})$后, 本文使用RLS算法预测未来的CSI.

设滤波器的记忆长度为K, 抽头权重向量w(n)=[w₀(n) w₁(n) … w_K－1(n)]^T, 期望输出d(u)和滤波器实际输出y(u)的误差为

$ e\left( u \right) = d\left( u \right) - y\left( u \right) = d\left( u \right) - {\mathit{\boldsymbol{w}}^{\rm{H}}}\left( n \right){{\mathit{\boldsymbol{\hat h}}}_{i,j}}\left( u \right). $

式中：i=1, 2, …, M₁, j=1, 2, …, M₂, 期望响应$d\left( u \right) = {\hat H_{i, j}}\left( {u + 1} \right)$, 输入向量${\mathit{\boldsymbol{\hat h}}_{i, j}}\left( u \right)$可以表示为

$ {{\mathit{\boldsymbol{\hat h}}}_{i,j}}\left( u \right) = \left[ \begin{array}{l} {{\hat H}_{i,j}}\left( u \right)\\ {{\hat H}_{i,j}}\left( {u - 1} \right)\\ \;\; \vdots \\ {{\hat H}_{i,j}}\left( {u - K + 1} \right) \end{array} \right]. $

RLS算法通过最小化下面的代价函数来更新抽头系数

$ \varepsilon \left( n \right) = \sum\limits_{u = 1}^n {{\lambda ^{n - u}}} {\left| {e\left( u \right)} \right|^2} + \sigma {\lambda ^{n - u}}{\left\| {w\left( n \right)} \right\|^2}. $

式中：n和u分别为当前和过去的时刻, σ是正则化参数, λ是遗忘因子, 其取值范围为0≤λ≤1.当λ=1时, 表示每个时刻的误差权重一样, 等同于一般的最小二乘算法; λ=0代表只有当前时刻的误差起作用, 其他时刻的误差被遗忘.抽头权重可以通过梯度下降法最小化上面的代价函数递归得到.

整个改进算法的流程见图 1.

3 仿真结果

本文通过仿真实验对提出的算法, 文献[14]中的算法(图中数据是对文献[14]算法进行复现得出, 使用相同的假设, 不一样的场景)以及直接信道预测算法(简称为RLS)进行比较.使用归一化均方误差(Normalized Mean Aquare Error, NMSE)来衡量预测误差, 定义为

$ {\rm{NMSE}} = \frac{{E\left[ {\left\| {\mathit{\boldsymbol{\hat h}} - \mathit{\boldsymbol{h}}} \right\|_F^2} \right]}}{{E\left[ {\left\| \mathit{\boldsymbol{h}} \right\|_F^2} \right]}}, $

式中$\mathit{\boldsymbol{\hat h}}$是预测的CSI, h是无噪的CSI.

3.1 复杂度分析

对于3种算法的复杂度, 因最后都需使用RLS进行信道预测, 只需对比降噪的复杂度即可.表 1给出了两种算法降噪的复杂度, 仿真中P=10, L=61, 提出算法降噪的复杂度约为文献[14]的8.7倍.

3.2 仿真分析

实验均采用瑞利衰落的统计信道模型, 参数设置为：采样时间T_s=1 ms, CSI采样数N=70, 预测未来30个采样点的信道信息.

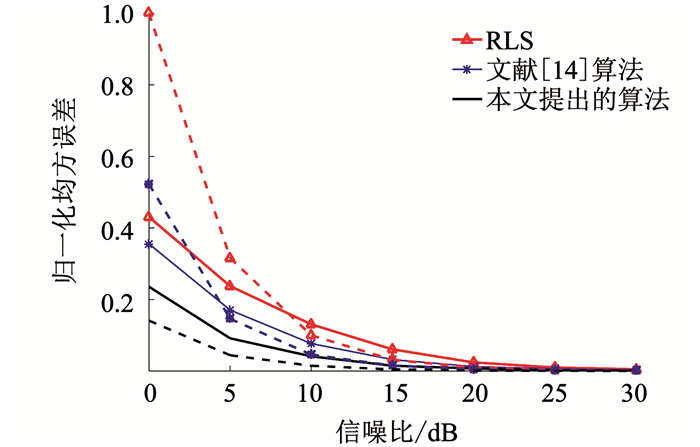
图 2画出了在收发天线对为6×6, 最大多普勒频移为50 Hz时不同方法所获得的信噪比(Signal to Noise Ratio, SNR)与NMSE的关系曲线.虚线表示降噪后得到的CSI, 即$\mathit{\boldsymbol{\hat H}}\left( u \right)$的NMSE, 实线表示预测的CSI误差.显而易见, 3种算法降噪后的误差和预测误差均随信噪比的增加而降低; 同时, 可以看出该文所提算法降噪后的误差明显低于对比算法的误差, 从而降低预测误差.可对比出, 虽然本文提出的算法复杂度相对较高, 但相比算法对性能的提升来看, 是可以接受的.

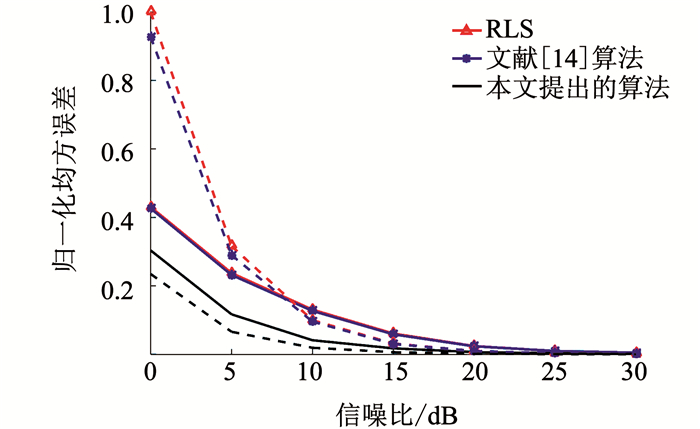
图 3是收发天线对为6×2, 最大多普勒频移为50 Hz时不同方法所获得的信噪比与NMSE的关系曲线.可以看出, 该文所提算法降噪后的误差和预测误差都明显低于对比算法的误差.对比图 2、图 3可以得出, 文献[14]算法和提出算法的估计误差和预测误差均随天线数减少而上升.这是因为天线数减少会引起秩不足, 使张量在空域上的秩等于天线数, 难以区分开噪声子空间和信号子空间, 减弱了降噪效果, 进而降低预测性能; 同时, 因为提出算法使用矩阵重排和空时平滑来解决秩不足问题, 使其估计误差低于对比算法, 进而提高预测性能.

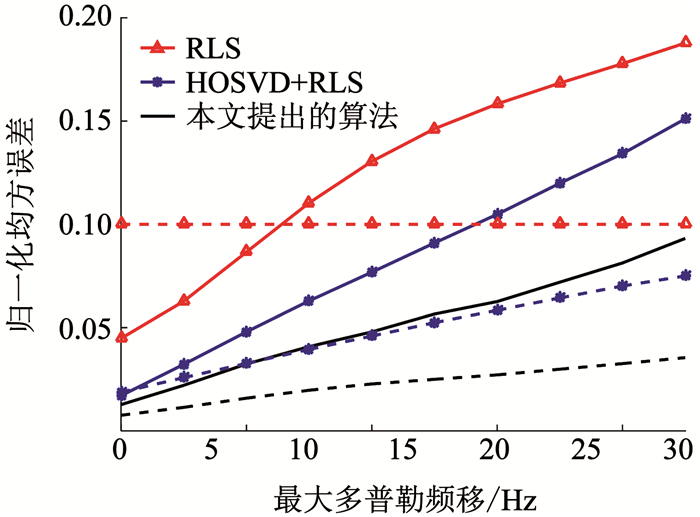
图 4是在收发天线对为6×6, 信噪比为10 dB时NMSE随最大多普勒频移的变化曲线.从图 4中可以看出, NMSE随最大多普勒频移增加而增加; 无论是降噪后的误差还是预测误差, 提出算法的性能均明显优于对比算法, 这是由于提出的算法在HOSVD降噪前, 对噪声进行平滑, 从而导致更低的误差.

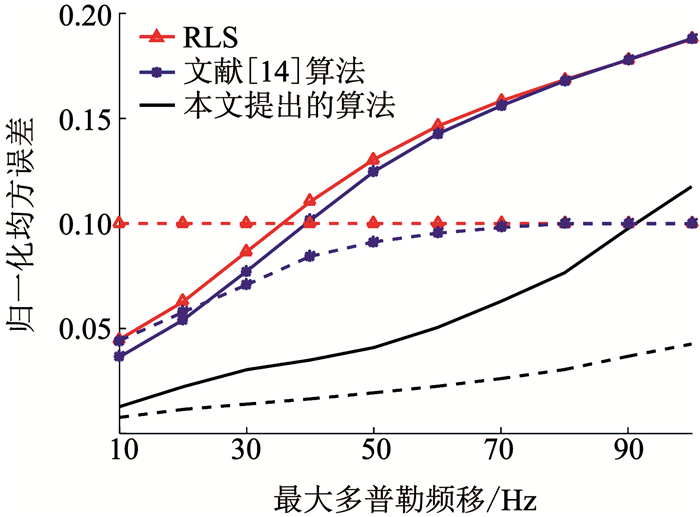
图 5画出了收发天线对为6×2, 信噪比为10 dB时NMSE随最大多普勒频移的变化曲线.文献[14]算法和提出的算法均优于RLS, 但对于最大多普勒频移大于70 Hz时, 文献[14]算法的性能几乎与RLS性能一致, 而提出的算法预测误差低于对比算法, 因此, 提出的算法可以更好地减小多普勒频移的影响.

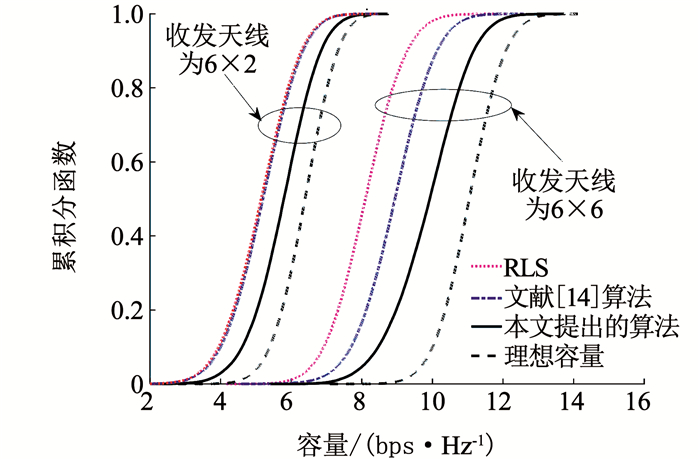
图 6是不同信道预测算法下, 基于SVD传输的注水容量的累积分布函数.其信噪比为5 dB, 最大多普勒频移为50 Hz.可以看出, 由于预测信道与实际信道存在误差, 使信道容量低于理想容量.结合图 2、图 3的预测误差和图 6中收发天线对为6×2、6×6时的信道容量, 可对比出, 提出算法能有效降低天线数少引起的秩不足问题对预测误差的影响, 从而减小了容量的损失.

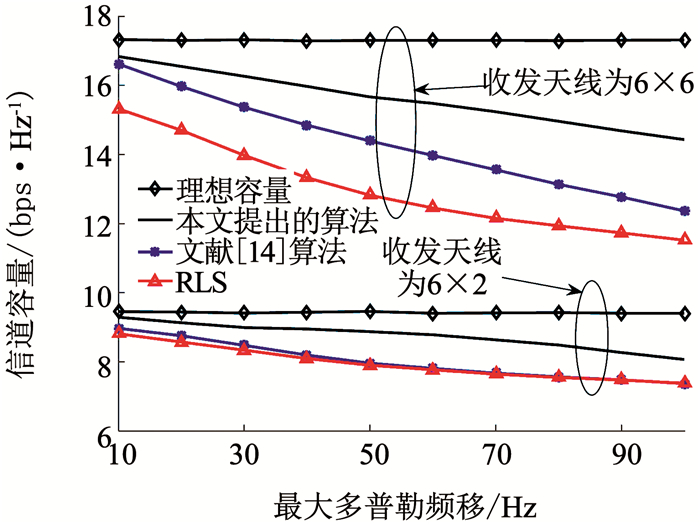
图 7仿真了信噪比为10 dB, 收发天线对分别为6×6和6×2时, 最大多普勒频移对信道容量的影响.可以看出, 3种预测算法的信道容量随多普勒频移增加而降低, 这是由于多普勒频移的增加会提高预测误差, 进而影响信道容量.同样地可对比出, 提出算法可以最大程度地补偿信道容量的损失.

4 结论

本文提出了一种改进的信道预测算法, 先对采样的CSI使用平滑重构信道矩阵, 随后对重构的信道矩阵在张量域降噪, 最后使用RLS算法进行信道预测.该算法充分利用了MIMO信道的多维结构特性, 将张量域降噪和预测分离开, 可以降低传统的张量框架下预测算法的复杂度.同时, 平滑使算法可以有效地降低多普勒频移以及天线数较少引起的秩缺失问题对预测误差的影响, 从而提高信道容量.仿真结果验证了所提算法的性能.