2. 哈尔滨工业大学 仪器科学与工程学院, 哈尔滨 150001
2. School of Instrumentation Science and Engineering, Harbin Institute of Technology, Harbin 150001, China
在控制系统中, 系统的内部状态矢量是根据系统一段时间内的外部量测信息, 通过系统的状态方程以及量测方程计算得到的.可观测性即是描述系统在一段时间内能否根据量测输入准确估计出系统内部状态的能力.对于线性定常系统而言, 可直接通过可观测性矩阵来判断系统的可观测性.但对于线性时变系统, 可观测性矩阵的计算复杂, 因此可通过Goshen-Meskin等[1-2]提出分段式线性定常系统(PWCS)可观测性分析理论, 以提取可观测性矩阵(SOM)替代总可观测性矩阵(TOM)对系统进行可观测性分析, 以简化计算.
通过系统可观测性仅能定性的判断系统状态是否可估计, 但却无法具体描述各状态的估计效果, 而状态估计效果与其状态特性分析密切相关.例如, 惯导系统中初始对准精度很大程度取决于对平台失准角的估计精度, 而在不同情况下, 即使可观测性矩阵的秩相同, 各状态的估计速度及精度也可能不同.因此为提高对准精度, 则需对平台失准角在不同情况下估计效果的变化进行分析; 在进行反馈校正时, 若将估计精度低的状态直接对内部参数校正, 则会导致系统误差发散, 根据各状态的估计效果, 采用自适应反馈校正可有效解决该问题.因此对状态的估计效果进行定量分析具有重要意义.
Ham等[3]提出了一种基于Kalman滤波均方误差矩阵的特征值来描述与其特征向量相对应的状态向量的线性组合的可观测度.但这种方法需要经过Kalman滤波后得到均方误差阵, 不能直接依据状态方程以及量测方程进行分析.冯绍军等[4]提出一种基于可观测性矩阵特征值分解的方法, 以系统可观测性矩阵的特征值大小来描述其特征向量对应的状态线性组合的可观测度.但该方法只能描述状态组合的可观测度, 而不是独立状态的可观测度.程向红等[5]提出根据线性时变系统可观测性矩阵奇异值来定性分析系统的可观测度大小, 而后这种基于奇异值分解(SVD)的可观测度分析方法近年来得到广泛的应用[6-7].
本文由已有的基于PWCS系统可观测性矩阵SVD的可观测度分析方法入手, 分析其存在的不足之处并对该方法进行改进, 利用该方法对SINS/DVL构建Kalman滤波器, 进行可观测度分析, 然后通过不同机动状态下各状态量的估计误差均方差曲线进行仿真验证.
1 PWCS可观测性分析理论由于研究系统可观测性不涉及外部输入激励, 故对齐次系统状态方程及量测方程进行讨论即可, 线性时变系统模型如下:
| $ \mathit{\boldsymbol{\dot X}}\left( t \right) = \mathit{\boldsymbol{A}}\left( t \right)\mathit{\boldsymbol{X}}\left( t \right), $ |
| $ \mathit{\boldsymbol{Z}}\left( t \right) = \mathit{\boldsymbol{H}}\left( t \right)\mathit{\boldsymbol{X}}\left( t \right). $ |
式中:A(t)∈Rn×n; H(t)∈Rm×n; X(t)∈Rn.若直接通过求算可观测性矩阵以对该线性时变系统进行可观测性分析, 则需要进行Grammian矩阵运算, 计算量巨大.因此为简化计算, 将系统整个运行时间按适当时间间隔进行分段, 若在每个时间段内A(t)和H(t)变化缓慢, 可分别近似为常量, 则在该时间段内可视为线性定常系统, 在整个时域内该线性时变系统则可近似为分段式线性定常系统(PWCS).该近似对于系统精度以及系统特性分析的影响很小, 并且能很大程度的简化分析过程, 因此可用PWCS替代原线性时变系统进行可观测性分析.
上述线性时变系统近似的PWCS从第1个时间段到第r个时间段内的总可观测性矩阵(TOM)为
| $ \mathit{\boldsymbol{Q}}\left( r \right) = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Q}}_1}}\\ {{\mathit{\boldsymbol{Q}}_2}{{\rm{e}}^{{A_1}{\Delta _{{t_1}}}}}}\\ \vdots \\ {{\mathit{\boldsymbol{Q}}_r}{{\rm{e}}^{{A_{r - 1}}{\Delta _{{t_{{\rm{r}} - 1}}}}}} \cdots {{\rm{e}}^{{A_1}{\Delta _{{t_1}}}}}} \end{array}} \right]. $ |
式中:Ai为第i个时间段内系统的状态矩阵常值; Δti为第i个时间段的时长; Qi为第i个时间段内已视为线性定常系统的可观测性矩阵, 计算如下:
| $ {\mathit{\boldsymbol{Q}}_i} = {\left[ {\mathit{\boldsymbol{H}}_i^{\rm{T}}{{\left( {{\mathit{\boldsymbol{H}}_i}{\mathit{\boldsymbol{A}}_i}} \right)}^{\rm{T}}}{{\left( {{\mathit{\boldsymbol{H}}_i}\mathit{\boldsymbol{A}}_i^2} \right)}^{\rm{T}}} \cdots {{\left( {{\mathit{\boldsymbol{H}}_i}\mathit{\boldsymbol{A}}_i^{n - 1}} \right)}^{\rm{T}}}} \right]^{\rm{T}}}. $ |
但是由于Q(r)中含有指数函数矩阵项, 计算极为复杂, 因此引入Goshen-Meskin和Bar-Itzhack提出分段式线性定常系统可观测性分析定理.
若null(Qi)⊂null(Ai), 1≤i≤r, 则有
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{null}}\left( {\mathit{\boldsymbol{Q}}\left( r \right)} \right) = {\rm{null}}\left( {{\mathit{\boldsymbol{Q}}_s}\left( r \right)} \right),}\\ {{\rm{rank}}\left( {\mathit{\boldsymbol{Q}}\left( r \right)} \right) = {\rm{rank}}\left( {{\mathit{\boldsymbol{Q}}_s}\left( r \right)} \right).} \end{array}} \right.. $ |
式中:null()为矩阵的零空间; rank()为矩阵的秩; Qs(r)为系统的提取可观测性矩阵(SOM), 计算如下:
| $ {\mathit{\boldsymbol{Q}}_s}\left( r \right) = {\left[ {\mathit{\boldsymbol{Q}}_1^{\rm{T}}\mathit{\boldsymbol{Q}}_2^{\rm{T}}\mathit{\boldsymbol{Q}}_3^{\rm{T}} \cdots \mathit{\boldsymbol{Q}}_{\rm{r}}^{\rm{T}}} \right]^{\rm{T}}}. $ |
若PWCS满足该定理, 则可使用提取可观测性矩阵Qs(r)代替总可观测性矩阵Q(r)对系统进行可观测性分析, 进一步简化分析过程.捷联惯导系统一般都符合该定理的条件[8-11].当使用Qs(r)对Q(r)进行替换时, 系统观测方程为
| $ \mathit{\boldsymbol{Y}} = {\mathit{\boldsymbol{Q}}_s}\left( r \right)\mathit{\boldsymbol{X}}, $ | (1) |
式中, Y=[Y1T Y2T … YrT]T, 其中Yi=[ZiT (Z′i)T … (Zi(n-1))T]T.当Qs(r)的秩等于系统阶数n时, 可由系统各时间段的外部量测量以及其各阶导数唯一确定系统内部状态, 即系统状态完全可观测; 当Qs(r)的秩小于系统阶数n时, 只能确定部分状态量或者状态量组合, 系统状态不完全可观测.
2 基于可观测性矩阵SVD的可观测度分析 2.1 SVD可观测度分析方法对式(1)中的Qs(r)进行奇异值分解可得:
| $ \mathit{\boldsymbol{Y}} = \left( {\mathit{\boldsymbol{U \boldsymbol{\varSigma} }}{\mathit{\boldsymbol{V}}^{\rm{T}}}} \right)\mathit{\boldsymbol{X}} = \left( {\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{u}}_i}{\mathit{\sigma }_i}\mathit{\boldsymbol{v}}_i^{\rm{T}}} } \right)\mathit{\boldsymbol{X}}. $ | (2) |
式中:U=[u1 u2…urmn]、V=[v1 v2…vn]分别为rmn×rmn维和n×n维的酉矩阵;
根据式(2)变换可得:
| $ \mathit{\boldsymbol{X}} = \sum\limits_{i = 1}^m {\left( {\mathit{\boldsymbol{u}}_i^{\rm{T}}\mathit{\boldsymbol{Y}}/{\sigma _i}} \right){\mathit{\boldsymbol{v}}_i}} , $ | (3) |
定义状态矢量X的任一元素Xk对应的奇异值σk为使{(uiTY/σi)vi}k, (i=1, 2, …, m)取得最大值的奇异值σi, 获得Xk应奇异值σk后, 定义该状态可观测度为
| $ {\eta _k} = {\sigma _k}/{\sigma _o}, $ | (4) |
式中σo为可直接由外部量测信息得到的状态分量对应的奇异值.
2.2 SVD可观测度方法合理性分析将式(2)中等式两边同时乘以酉矩阵UT, 则有
| $ {\mathit{\boldsymbol{U}}^{\rm{T}}}\mathit{\boldsymbol{Y}} = {\mathit{\boldsymbol{U}}^{\rm{T}}}\mathit{\boldsymbol{U \boldsymbol{\varSigma} }}{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{X}} = \mathit{\boldsymbol{ \boldsymbol{\varSigma} }}{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} {{\sigma _1}\mathit{\boldsymbol{v}}_1^{\rm{T}}\mathit{\boldsymbol{X}}}\\ {{\sigma _2}\mathit{\boldsymbol{v}}_2^{\rm{T}}\mathit{\boldsymbol{X}}}\\ \vdots \\ {{\sigma _n}\mathit{\boldsymbol{v}}_n^{\rm{T}}\mathit{\boldsymbol{X}}} \end{array}} \right], $ |
式中奇异值σi为状态量组合viTX系数, 表示了viTX在UTY中所占的权重.σi越大, 依靠外量测信息Y越能准确反映出viTX.而方向向量vi中绝对值最大的元素所对应的状态分量在该方向的投影最大, 视为该方向上的观测状态.因此σi的大小在一定程度上反映了该观测状态的可观测程度.而可直接由外部量测得到的状态量完全可观测, 故将其对应的奇异值作为其他状态量的衡量基准, 通过与其比较得到各状态量的可观测程度.
2.3 已有SVD可观测度方法存在的问题1) 系统状态的可观测度属于系统自身性质, 应与外部量测输入无关, 但由式(3)可知, 对于状态量所对应的奇异值的判断需要外部量测信息.
2) 系统内部各个状态的量纲不同导致其对应的奇异值也不具有可比性[12], 不能以此计算状态的可观测度.
3) 当外部量测信息反映的状态在数量级上差异较大时, 会导致它们各自对应的奇异值也相差较大, 在式(4)中无法选取唯一的σo作为其他观测度的衡量基准.
3 基于SVD可观测度分析方法的改进及应用对式(2)进行变换可得:
| $ \mathit{\boldsymbol{Y}} = {\sigma _1}{Y_1} + {\sigma _2}{Y_2} + \cdots + {\sigma _n}{Y_n}, $ | (5) |
式中, Yi=uiviTX, (i=1, 2, …, n).使得Hi=uivTi, 则系统状态矢量X通过矩阵Hi投影得到Yi.使Hi=[Hi1 Hi2 … Hin], 则列向量Hij的元素代表了状态分量Xj经投影后在Yi中的系数, 因此可通过Hij大小反映Xj在Yi中所占权重的大小.根据上述分析定义:
| $ {\theta _{ij}} = \mathit{\boldsymbol{H}}_{ij}^{\rm{T}}{\mathit{\boldsymbol{H}}_{ij}},\left( {j = 1,2, \cdots ,n} \right) $ |
为得到HijTHij, 令Hi转置与自身相乘, 则有
| $ \mathit{\boldsymbol{H}}_i^{\rm{T}}{\mathit{\boldsymbol{H}}_i} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{H}}_{i1}^{\rm{T}}{\mathit{\boldsymbol{H}}_{i1}}}&{\mathit{\boldsymbol{H}}_{i1}^{\rm{T}}{\mathit{\boldsymbol{H}}_{i2}}}& \cdots &{\mathit{\boldsymbol{H}}_{i1}^{\rm{T}}{\mathit{\boldsymbol{H}}_{in}}}\\ {\mathit{\boldsymbol{H}}_{i2}^{\rm{T}}{\mathit{\boldsymbol{H}}_{i1}}}&{\mathit{\boldsymbol{H}}_{i2}^{\rm{T}}{\mathit{\boldsymbol{H}}_{i2}}}& \cdots &{\mathit{\boldsymbol{H}}_{i2}^{\rm{T}}{\mathit{\boldsymbol{H}}_{in}}}\\ \vdots & \vdots & \cdots & \vdots \\ {\mathit{\boldsymbol{H}}_{in}^{\rm{T}}{\mathit{\boldsymbol{H}}_{i1}}}&{\mathit{\boldsymbol{H}}_{in}^{\rm{T}}{\mathit{\boldsymbol{H}}_{i2}}}& \cdots &{\mathit{\boldsymbol{H}}_{in}^{\rm{T}}{\mathit{\boldsymbol{H}}_{in}}} \end{array}} \right], $ | (6) |
又由ui为酉阵U的单位列向量, 故有
| $ \mathit{\boldsymbol{H}}_i^{\rm{T}}{\mathit{\boldsymbol{H}}_i} = {\left( {{\mathit{\boldsymbol{u}}_i}\mathit{\boldsymbol{v}}_i^{\rm{T}}} \right)^{\rm{T}}}\left( {{\mathit{\boldsymbol{u}}_i}\mathit{\boldsymbol{v}}_i^{\rm{T}}} \right) = {\mathit{\boldsymbol{v}}_i}\mathit{\boldsymbol{u}}_i^{\rm{T}}{\mathit{\boldsymbol{u}}_i}\mathit{\boldsymbol{v}}_i^{\rm{T}} = {\mathit{\boldsymbol{v}}_i}\mathit{\boldsymbol{v}}_i^{\rm{T}}, $ |
由vi=[vi1 vi2… vin]T将上式展开可得:
| $ \mathit{\boldsymbol{H}}_i^{\rm{T}}{\mathit{\boldsymbol{H}}_i} = \left[ {\begin{array}{*{20}{c}} {v_{i1}^2}&{{v_{i1}}{v_{i2}}}& \cdots &{{v_{i1}}{v_{in}}}\\ {{v_{i2}}{v_{i1}}}&{v_{i2}^2}& \cdots &{{v_{i2}}{v_{in}}}\\ \vdots & \vdots & \cdots & \vdots \\ {{v_{in}}{v_{i1}}}&{{v_{in}}{v_{i2}}}& \cdots &{v_{in}^2} \end{array}} \right]. $ | (7) |
通过将式(6)、(7)进行对比, 则有
| $ {\theta _{ij}} = \mathit{\boldsymbol{H}}_{ij}^{\rm{T}}{\mathit{\boldsymbol{H}}_{ij}} = v_{ij}^2,\;\;\;\left( {j = 1,2, \cdots ,n} \right) $ |
θij反映了Xj在Yi中的权值大小, 当θij越大, 根据Yi越容易估计出Xj; θij趋于零时, Xj在Yi中几乎不可见.因此, θij大小可用来描述Xj在不同情况下可观测度变化趋势.又由式(5)知, Yi在经过σi的加权求和后得到Y, 故状态量Xj在Y中所占权值大小由θij与σi共同决定, 因此定义:
| $ {O_j} = \sum\limits_{i = 1}^n {{\sigma _i}{\theta _{ij}}} = \sum\limits_{i = 1}^n {{\sigma _i}v_{ij}^2} , $ |
Oj的大小仅描述了系统在不同状态下Xj的可观测程度的变化, 为了得到Xj的可观测度, 则需要知道Xj完全可观测时在Y中所占权值的大小, 并将其作为基准值进行比较.
文献[13-14]研究分析了载体的各种运动对系统状态可观测性的影响.结论表明, 当载体做S形机动时, 捷联惯性导航系统的各状态均可得到较好的估计.因此定义Xj的可观测度为
| $ {\eta _j} = {O_j}/{O_{sj}},\;\;\;\;\left( {j = 1,2, \cdots ,n} \right) $ |
式中Osj为载体在做S形机动状态时Xj在Y中所占的权值大小的.
通过上述方法计算状态量可观测度, 不需外部量测信息, 计算简单(通过奇异值和酉阵V各列元素的平方的乘积之和, 可得到全部状态的可观测度矢量), 并且将状态在不同情况下纵向比较, 解决了量纲不同及基准不唯一的问题.
由于Kalman滤波器为线性滤波器, 故一般惯性组合导航系统均采用间接滤波方式对导航参数误差进行估计, 在以估计误差对惯导导航参数进行校正.当滤波器对误差估计准确时, 导航参数可以得到准确校正, 但当误差估计较差时, 进行校正则可能导致导航参数误差发散.因此为了得到更精准的导航参数, 则需要知道滤波器对误差估计的准确程度, 然后根据其决定是否对误差进行反馈及反馈程度大小.间接滤波中的状态可观测度即是定量描述误差估计效果的, 可用来作为误差的反馈因子, 得到更精准的参数估计, 即
| $ \mathit{\boldsymbol{\hat X}} = {\mathit{\boldsymbol{X}}_I} - \eta \Delta \mathit{\boldsymbol{X}}. $ | (8) |
式中:
本文将SINS与DVL的速度之差作为外部量测信息, 构建Kalman滤波器, 选取东北天地理坐标系为导航坐标系, 选取系统状态变量为
| $ \mathit{\boldsymbol{X}} = {\left[ {\delta {v_e}\delta {v_n}\delta {v_u}{\varphi _e}{\varphi _n}{\varphi _u}{\nabla _x}{\nabla _y}{\nabla _z}{\varepsilon _x}{\varepsilon _y}{\varepsilon _z}} \right]^{\rm{T}}}. $ |
式中:δve、δvn、δvu分别为速度误差; φe、φn、φu分别为平台失准角;
表 1表示在一定时间段内针对一些常见机动动作(机体初始位置纬度45°, 经度126°; 匀速100 m/s; 加速运动a=0.1 g; 转弯角速度3°/s), 根据上述方法计算得到的状态分量的可观测度.
| 表 1 常见机动状态下状态可观测度 Tab. 1 Observable degree of the body under typical maneuver conditions |
根据表 1可知, δve、δvn、δvu在各种状况下的可观测度均为1, 这是由于速度误差在任何情况下均可由Kalman滤波器外量测信息得到, 故保持可观测状态; φe、φn在各种机动情况下均能保持较高的观测度, 通过对比还可发现, 机体的线加速方向对于水平失准角观测度也会产生影响.图 1、2为水平失准角估计误差均方差曲线, 根据该图, 机体的北向、东向加速运动会影响同方向水平失准角的估计效果, 并且加速度越大, 估计效果越差.机体线加速、转弯运动均可提高φu的可观测度, 如图 3所示, 同时转弯运动也明显提高

|
图 1 φe估计误差均方差曲线 Fig. 1 Estimated error curve of φe |

|
图 2 φn估计误差均方差曲线 Fig. 2 Estimated error curve of φn |

|
图 3 φu估计误差均方差曲线 Fig. 3 Estimated error curve of φu |

|
图 4
|

|
图 5 εy估计误差均方差曲线 Fig. 5 Estimated error curve of εy |
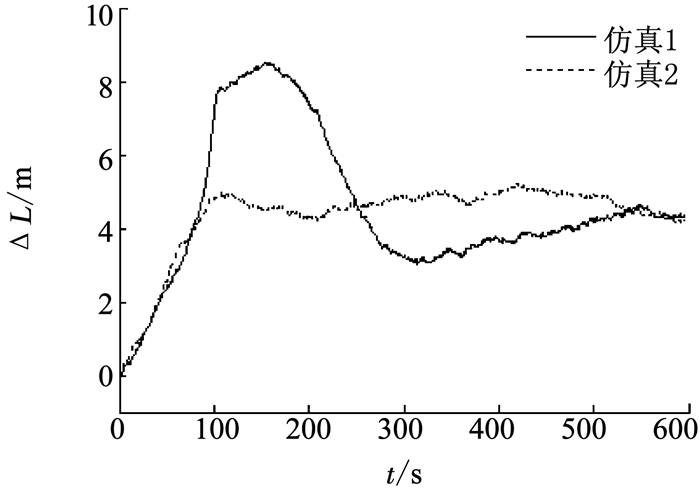
由上述状态可观测度分析结果, 根据式(8)中的反馈校正方法进行仿真.载体运动仿真条件设为:先进行120 s加速度为0.1 g的北向加速运动, 然后以3°/s的角速度经过30 s转弯使航向向东, 以匀速直线运动继续行驶450 s.仿真1为速度、平台失准角完全反馈时的位置误差, 仿真2为将状态可观测度作为估计误差的反馈因子时的校正, 即在匀速直线时, φu不反馈; 北向加速运动时, φu与可观测度0.332 0相乘在对系统进行校正; 转弯运动时φu完全反馈.其他状态反馈校正方式相同.如图 6~图 8所示, 采用依据可观测度的自适应反馈校正方式, 可在一定程度上提高到导航参数精度.
|
图 6 纬度误差 Fig. 6 Latitude error |
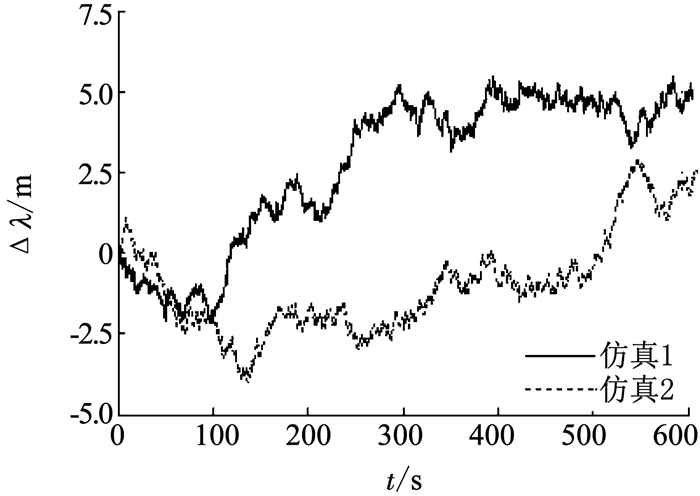
|
图 7 经度误差 Fig. 7 Longitude error |

|
图 8 航向角误差 Fig. 8 Heading angle error |
1) 已有的基于PWCS可观测性矩阵SVD的可观测度分析方法计算过程中存在着状态量纲不同、奇异值基准不唯一等问题, 针对这些问题提出一种改进的基于PWCS可观测性矩阵SVD的可观测度分析方法.
2) 该方法根据PWCS系统可观测性矩阵的奇异值以及对应的右奇异值向量来计算各状态量的可观测度.通过SINS/DVL组合导航系统仿真, 该方法计算得到的观测度与系统各状态经过Kalman滤波的误差估计特性具有相符, 且根据Kalman间接滤波校正原理, 可将状态可观测度应用于系统自适应反馈校正.
3) 仿真结果表明, 通过该改进的SVD可观测度方法计算得到的各状态可观测度, 可以较为准确的预见及定量描述系统对各状态的估计效果.将可观测度作为反馈因子对状态校正时, 可在一定程度上提高导航参数精度, 故在惯导系统的初始对准及自适应反馈校正等方面具有实用意义.
| [1] |
GOSHEN-MESKIN D, BAR-ITZHACK I Y. Observability analysis of piece-wise constant systems-Part I: Theory[J]. IEEE Transactions on Aerospace and Electronic Systems, 1992, 28(4): 1056. DOI:10.1109/7.165367 |
| [2] |
GOSHEN-MESKIN D, BAR-ITZHACK I Y. Observability analysis of piece-wise constant systems-Part Ⅱ: Application to inertial navigation in-flight alignment (military applications)[J]. IEEE Transactions on Aerospace and Electronic Systems, 1992, 28(4): 1068. DOI:10.1109/7.165368 |
| [3] |
HAM F M, BROWN R G. Observability, eigenvalues, and Kalman filtering[J]. IEEE Transactions on Aerospace and Electronic Systems, 1983, AES-19(2): 269. DOI:10.1109/TAES.1983.309446 |
| [4] |
冯绍军, 袁信. 观测度及其在卡尔曼滤波器设计中的应用[J]. 中国惯性技术学报, 1999, 7(2): 18. FENG Shaojun, YUAN Xin. Observation and its application in Kalman filter design[J]. Journal of Chinese Inertial Technology, 1999, 7(2): 18. DOI:10.13695/j.cnki.12-1222/o3.1999.02.005 |
| [5] |
程向红, 万德钧, 仲巡. 捷联惯导系统的可观测性和可观测度研究[J]. 东南大学学报, 1997, 27(6): 6. CHENG Xianghong, WAN Dejun, ZHONG Xun. Study on observability and its degree of strapdown inertial navigation system[J]. Journal of Southeast University, 1997, 27(6): 6. |
| [6] |
吴海仙, 俞文伯, 房建成. 高空长航时无人机SINS/CNS组合导航系统仿真研究[J]. 航空学报, 2006, 27(2): 299. WU Haixian, YU Wenbo, FANG Jiancheng. Simulation of SINS/CNS integrated navigation system used on high altitude and long-flight-time unpiloted aircraft[J]. Acta Aeronautica Sinica, 2006, 27(2): 299. DOI:10.3321/j.issn:1000-6893.2006.02.027 |
| [7] |
吴俊伟, 孙国伟, 张如, 等. 基于SVD方法的INS传递对准的可观测性能分析[J]. 中国惯性技术学报, 2005, 13(6): 26. WU Junwei, SUN Guowei, ZHANG Ru, et al. Analysis on observability of INS transfer alignment based on SVD method[J]. Journal of Chinese Inertial Technology, 2005, 13(6): 26. DOI:10.3969/j.issn.1005-6734.2005.06.007 |
| [8] |
胡小毛, 刘飞, 翁海娜. MSINS/GPS全组合系统可观测性分析[J]. 中国惯性技术学报, 2011, 19(1): 38. HU Xiaomao, LIU Fei, WENG Haina. Observability analysis of MSINS/GPS complete integrated system[J]. Journal of Chinese Inertial Technology, 2011, 19(1): 38. DOI:10.13695/j.cnki.12-1222/o3.2011.01.024 |
| [9] |
弓川锦. SINS/GPS组合导航系统可观测度分析及精度评估方法研究[D].哈尔滨: 哈尔滨工业大学, 2007 GONG Chuanjin. Method research on degree of observability analysis and precision assessment of SINS/GPS integrated navigation system[D]. Harbin: Harbin Institute of Technology, 2007 |
| [10] |
赵琳, 李亮, 孙明, 等. 基于SVD的SINS多位置对准可观测性分析[J]. 中国惯性技术学报, 2008, 16(5): 523. ZHAO Lin, LI Liang, SUN Ming, et al. Analysis on observability of SINS multi-position alignment based on singular value decomposition[J]. Journal of Chinese Inertial Technology, 2008, 16(5): 523. DOI:10.13695/j.cnki.12-1222/o3.2008.05.009 |
| [11] |
朱兰伟, 张燕, 蔡春龙. 基于可观测性分析的光纤陀螺SINS/测速仪组合系统技术[J]. 中国惯性技术学报, 2011, 19(1): 50. ZHU Lanwei, ZHANG Yan, CAI Chunlong. FOG SINS/Speedometer integrated system technique based on observability analysis[J]. Journal of Chinese Inertial Technology, 2011, 19(1): 50. |
| [12] |
马艳红, 胡军. 基于SVD理论的可观测度分析方法的几个反例[J]. 中国惯性技术学报, 2008, 16(4): 448. MA Yanhong, HU Jun. Counterexamples for degree of observability analysis method based on SVD theory[J]. Journal of Chinese Inertial Technology, 2008, 16(4): 448. |
| [13] |
房建成, 周锐, 祝世平. 捷联惯导系统动基座对准的可观测性分析[J]. 北京航空航天大学学报, 1999, 25(6): 714. FANG Jiancheng, ZHOU Rui, ZHU Shiping. Observability analysis of strapdown inertial navigation system on moving base[J]. Journal of Beijing University of Aeronautics and Astronautics, 1999, 25(6): 714. DOI:10.13700/j.bh.1001-5965.1999.06.023 |
| [14] |
万德钧, 房建成. 惯性导航初始对准[M]. 南京: 东南大学出版社, 1998. WAN Dejun, FANG Jiancheng. Initial alignment of inertial navigation[M]. Nanjing: Southeast University Press, 1998. |
| [15] |
黄曦, 程向红. 机动对SINS对准中惯性仪表误差估计的影响[J]. 船舶电子工程, 2007, 27(1): 63. HUANG Xi, CHENG Xianghong. Effect of inertial instrument error estimations with maneuvers during sins initial alignment[J]. Ship Electronic Engineering, 2007, 27(1): 63. DOI:10.3969/j.issn.1627-9730.2007.01.019 |
 2020, Vol. 52
2020, Vol. 52


