具备极区导航能力是现代船舶在极区航行时的重要性能指标[1].惯性导航系统因其自主性、导航信息的连续性与完备性成为船舶在极区航行的首选[2-3].由于高纬度地区经线快速收敛,常用的指北方位惯导力学编排在极区存在定位与定向的困难[4-6].以格网坐标系为导航坐标系的格网惯性导航力学编排可以作为船舶在极区航行时的理想力学编排[7].
由于惯性器件测量误差等误差源的存在,同常规指北方位惯导系统,格网惯导系统同样存在导航误差随时间积累的问题,文献[8-9]分析得出格网惯导系统同样存在3类周期性振荡误差:84.4 min舒勒振荡、傅科振荡以及24 h地球振荡,这种随时间积累的周期性振荡误差对于在海上长时间工作的船舶来说是极为不利的[10].
为抑制格网惯导系统随时间积累的误差,可采取常用的组合导航方式如卫星导航系统/惯性导航系统的方式通过卡尔曼滤波器对系统误差进行准确估计并进行实时补偿[11-12].然而,船舶在实际航行中为确保自身的隐蔽性及自主性,通常不会获取连续的卫星导航信息[13].综合校正技术通过定期地对陀螺漂移进行测定补偿,并对惯导系统的航向和位置进行重调来提高系统的导航精度.针对非连续性的外部参考信息,文献[14-16]对适用于指北方位惯导系统的两点校、三点校以及点点校等综合校正方式进行了详细的推导.然而目前并没有相关文献对适用于极区的格网惯导力学编排综合校正算法进行叙述.
本文在格网惯导力学编排的基础上,首先通过外水平阻尼技术对格网惯导系统舒勒振荡进行抑制.为进一步提高格网惯导系统的导航精度,在外水平阻尼的基础上,针对有间断的外部位置及航向信息辅助的情况,基于格网坐标系推导了P方程以及ψ方程,设计了适用于船用格网惯导力学编排的两点校综合校正算法,其中P方程建立起位置误差、格网航向误差与平台漂移角ψ的关系,ψ方程建立起平台漂移角与陀螺常值漂移的关系.该算法利用两次间断的外部位置和航向信息对陀螺常值漂移进行估计,即在第1次外部导航信息辅助下完成系统重调,在第2次外部导航信息辅助下同时完成陀螺常值漂移的估计和系统重调,从而通过陀螺漂移补偿抑制船用格网惯导系统随时间积累的导航误差,以保证船舶在极区航行时的自主性.
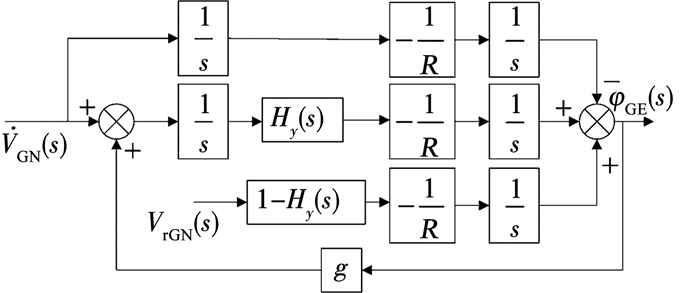
1 格网惯导外水平阻尼算法本文所设计的两点校综合校正算法在外水平阻尼条件下进行,外水平阻尼条件下进行综合校正的原因有两点:一方面当外部测速设备如多普勒计程仪提供的参考速度可用时,外水平阻尼状态是船舶常用的工作状态; 另一方面由于水平阻尼可有效减小水平姿态误差,这有助于在校正过程中提高系统重调的性能.在船用格网惯性导航力学编排的基础上,参考指北方位惯导力学编排外水平阻尼舒勒振荡抑制方法,可以设计出适用于格网惯导系统力学编排的外水平阻尼算法,格网惯导力学编排详见文献[8].格网惯性导航系统外水平阻尼算法系统方块图如图 1所示,算法实现过程中所涉及的控制方程详见文献[9].
|
图 1 外水平阻尼系统方块图 Fig. 1 Block diagram of external level damping |
图 1中,VGN为格网北向速度,VrGN为外部参考速度在格网北向的速度分量,φGE为格网东向姿态误差角,R为地球半径,g为重力加速度常量,s为拉普拉斯变量,Hy(s)为水平阻尼网络.本文用到的水平阻尼网络为
| $ {H_y}\left( s \right) = \frac{{\left( {s + 8.5 \times {{10}^{ - 4}}} \right)\left( {s + 9.412 \times {{10}^{ - 2}}} \right)}}{{\left( {s + 8.0 \times {{10}^{ - 3}}} \right)\left( {s + 1.0 \times {{10}^{ - 2}}} \right)}}. $ |
本文用到的坐标系及其定义如下.
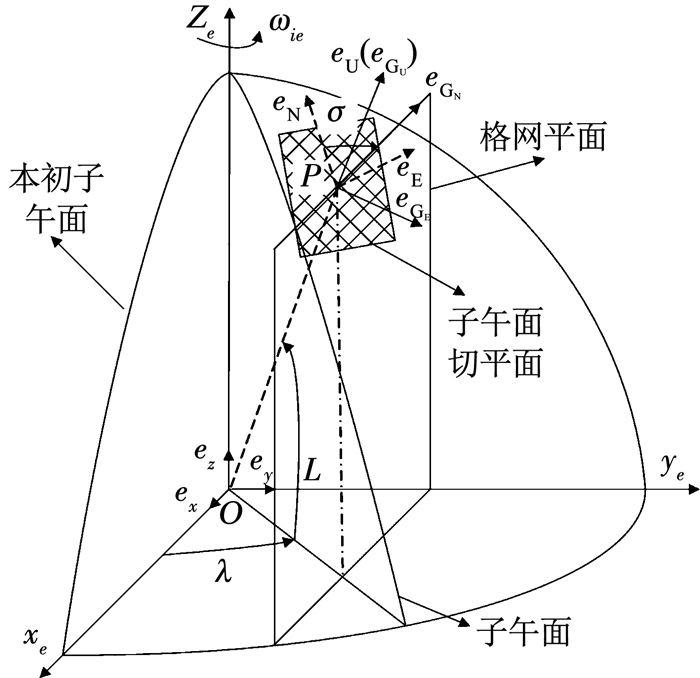
1) 格网坐标系G.格网坐标系如图 2所示.过P点分别作本初子午面的平行平面和当地水平面,以两平面的交线作为格网坐标系的GN轴,P点处的天向作为格网坐标系的GU轴,GE轴与GN轴和GU轴构成右手坐标系.
|
图 2 格网坐标系 Fig. 2 Grid frame |
2) OEPQ坐标系.原点位于载体质心,E轴与纬度圈相切指向东,P轴平行于地球极轴,Q轴与另外两轴构成右手坐标系.
3) 计算机坐标系c.原点位于导航计算机计算出来的位置,坐标轴指向同格网坐标系.计算机坐标系相对于格网坐标系的夹角为θ.
4) 数学平台坐标系p.原点位于载体质心,模拟格网坐标系.数学平台坐标系相对于格网坐标系的夹角为φ,数学平台坐标系相对于计算机坐标系的夹角为ψ.
φ、θ和ψ之间的关系为
| $ \varphi = \theta + \mathit{\boldsymbol{\psi }}. $ | (1) |
其他用到的坐标系还包括:载体坐标系b、地理坐标系g、惯性系i以及地心地固坐标系e(ECEF).
2.2 P方程P方程即为建立位置误差、格网航向误差与平台漂移角ψ之间关系的方程.设船舶所在点P的经、纬度以及格网方位角分别为λ、L和σ (σ为格网北向为地理北向夹角),计算机坐标系所对应的经、纬度以及格网方位角的计算值分别为λc、Lc和σc.考虑格网坐标系与计算机坐标系由于位置差异造成的格网方位角误差,则计算机坐标系相对于格网坐标系的夹角θ在地理坐标系g下的投影为
| $ {\theta ^g} = \left[ {\begin{array}{*{20}{c}} { - \delta L}\\ {\delta \lambda \cos L}\\ {\delta \lambda \sin L - \delta \sigma } \end{array}} \right]. $ |
式中:δλ为经度误差; δL为纬度误差; δσ为格网方位角误差.
计算机坐标系相对于格网坐标系的夹角θ在格网坐标系下的投影为
| $ \theta = \mathit{\boldsymbol{C}}_g^G{\theta ^g} = \left[ {\begin{array}{*{20}{c}} {\cos \sigma }&{ - \sin \sigma }&0\\ {\sin \sigma }&{\cos \sigma }&0\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} { - \delta L}\\ {\delta \lambda \cos L}\\ {\delta \lambda \sin L - \delta \sigma } \end{array}} \right]. $ | (2) |
展开式(2)可以得到:
| $ \left\{ {\begin{array}{*{20}{l}} {{\theta _x} = - \delta L\cos \sigma - \delta \lambda \cos L\sin \sigma ,}\\ {{\theta _y} = - \delta L\sin \sigma + \delta \lambda \cos L\cos \sigma ,}\\ {{\theta _z} = \delta \lambda \sin L - \delta \sigma .} \end{array}} \right. $ |
水平阻尼条件下,当系统达到稳态时,格网水平姿态误差主要受加速度计零偏影响,而现代惯性导航系统所用的加速度计零偏较小,其所引起的φx、φy均很小,即有φx≈0和φy≈0成立.结合式(1)则有:
| $ \left\{ {\begin{array}{*{20}{l}} {{\psi _x} = - {\theta _x} = \delta L\cos \sigma + \delta \lambda \cos L\sin \sigma ,}\\ {{\psi _y} = - {\theta _y} = \delta L\sin \sigma - \delta \lambda \cos L\cos \sigma ,}\\ {{\varphi _z} = {\psi _z} + \delta \lambda \sin L - \delta \sigma .} \end{array}} \right. $ | (3) |
为简化推导过程,假设地球模型为圆球模型.P点处ECEF坐标系下的位置为(x y z)T.忽略高度通道的影响,因为x=Rcos Lcos λ,y=Rcos Lsin λ,对两式两边取一阶全增量有
| $ \left\{ {\begin{array}{*{20}{l}} { - R\sin L\cos \lambda \delta L - R\cos L\sin \lambda \delta \lambda = \delta x,}\\ { - R\sin L\sin \lambda \delta L + R\cos L\cos \lambda \delta \lambda = \delta y,} \end{array}} \right. $ | (4) |
由式(4)可以分别解出δλ、δL为
| $ \left\{ {\begin{array}{*{20}{l}} {\delta \lambda = \frac{{\delta y\cos \lambda - \delta x\sin \lambda }}{{R\cos L}},}\\ {\delta L = - \frac{{\delta x\cos \lambda + \delta y\sin \lambda }}{{R\sin L}}.} \end{array}} \right. $ | (5) |
又根据(λ L)T与(x y z)T的转换关系, 即
| $ \left\{ {\begin{array}{*{20}{l}} {\sin \lambda = \frac{y}{{\sqrt {{x^2} + {y^2}} }},\cos \lambda = \frac{x}{{\sqrt {{x^2} + {y^2}} }},}\\ {\sin L = \frac{z}{R},\cos L = \frac{{\sqrt {{x^2} + {y^2}} }}{R},} \end{array}} \right. $ | (6) |
将式(6)代入式(5)可得:
| $ \left\{ {\begin{array}{*{20}{l}} {\delta \lambda = \frac{{x\delta y - y\delta x}}{{{x^2} + {y^2}}},}\\ {\delta L = - \frac{{x\delta x + y\delta y}}{{z\sqrt {{x^2} + {y^2}} }}.} \end{array}} \right. $ | (7) |
格网方位角σ与(λ L)T的转换关系为
| $ \left\{ {\begin{array}{*{20}{l}} {\sin \sigma = \frac{{\sin L\sin \lambda }}{{\sqrt {1 - {{\cos }^2}L{{\sin }^2}\lambda } }},}\\ {\cos \sigma = \frac{{\cos \lambda }}{{\sqrt {1 - {{\cos }^2}L{{\sin }^2}\lambda } }}.} \end{array}} \right. $ | (8) |
将式(6)代入式(8)可得:
| $ \left\{ {\begin{array}{*{20}{l}} {\sin \sigma = \frac{{yz}}{{\sqrt {{x^2} + {y^2}} \sqrt {{x^2} + {z^2}} }},}\\ {\cos \sigma = \frac{{Rx}}{{\sqrt {{x^2} + {y^2}} \sqrt {{x^2} + {z^2}} }}.} \end{array}} \right. $ | (9) |
将式(6)、(7)和式(9)代入式(3)可得:
| $ \left\{ \begin{array}{l} {\psi _x} = - \frac{{\sqrt {{x^2} + {z^2}} }}{{Rz}}\delta x - \frac{{xy}}{{Rz\sqrt {{x^2} + {z^2}} }}\delta y,\\ {\psi _y} = - \frac{1}{{\sqrt {{x^2} + {z^2}} }}\delta y,\\ {\varphi _z} = {\psi _z} + \frac{{x\delta y - y\delta x}}{{{x^2} + {y^2}}}\frac{z}{R} - \delta \sigma , \end{array} \right. $ | (10) |
由式(10)前两式可以解得:
| $ \left\{ {\begin{array}{*{20}{l}} {\delta x = \frac{{xy}}{{\sqrt {{x^2} + {z^2}} }}{\psi _y} - \frac{{Rz}}{{\sqrt {{x^2} + {z^2}} }}{\psi _x},}\\ {\delta y = - \sqrt {{x^2} + {z^2}} {\psi _y}.} \end{array}} \right. $ | (11) |
由式(8)对cos σ两边求一阶全增量可得:
| $ \delta \sigma = \frac{{\delta \lambda \sin L}}{{1 - {{\cos }^2}L{{\sin }^2}\lambda }} + \frac{{\delta L\sin \lambda \cos \lambda \cos L}}{{1 - {{\cos }^2}L{{\sin }^2}\lambda }}. $ | (12) |
将式(6)、(7)代入式(12)并结合式(11)可以得到:
| $ \delta \sigma = \frac{{{R^2}y{\psi _x}}}{{\left( {{x^2} + {y^2}} \right)\sqrt {{x^2} + {z^2}} }} - \frac{{Rxz{\psi _y}}}{{\left( {{x^2} + {y^2}} \right)\sqrt {{x^2} + {z^2}} }}. $ | (13) |
由式(10)、式(13)可以进一步得到:
| $ {\varphi _z} = {\psi _z} - \frac{y}{{\sqrt {{x^2} + {z^2}} }}{\psi _x}. $ | (14) |
联立式(11)、式(14)可以得到:
| $ \left[ {\begin{array}{*{20}{c}} {\delta x}\\ {\delta y}\\ {{\varphi _z}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - \frac{{Rz}}{{\sqrt {{x^2} + {z^2}} }}}&{\frac{{xy}}{{\sqrt {{x^2} + {z^2}} }}}&0\\ 0&{ - \sqrt {{x^2} + {z^2}} }&0\\ { - \frac{y}{{\sqrt {{x^2} + {z^2}} }}}&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\psi _x}}\\ {{\psi _y}}\\ {{\psi _z}} \end{array}} \right]. $ |
令
| $ \mathit{\boldsymbol{N}} = \left[ {\begin{array}{*{20}{c}} { - \frac{{Rz}}{{\sqrt {{x^2} + {z^2}} }}}&{\frac{{xy}}{{\sqrt {{x^2} + {z^2}} }}}&0\\ 0&{ - \sqrt {{x^2} + {z^2}} }&0\\ { - \frac{y}{{\sqrt {{x^2} + {z^2}} }}}&0&1 \end{array}} \right]. $ | (15) |
为了便于分析和计算,引入OEPQ坐标系,OEPQ坐标系与格网坐标系的转换关系为
| $ \mathit{\boldsymbol{C}}_{OEPQ}^G = \left[ {\begin{array}{*{20}{c}} {\cos \sigma }&{ - \sin \sigma }&0\\ {\sin \sigma }&{\cos \sigma }&0\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&{\cos L}&{ - \sin L}\\ 0&{\sin L}&{\cos L} \end{array}} \right], $ | (16) |
则可求得格网坐标系下位置误差、航向误差与OEPQ坐标系下的平台漂移角的关系为
| $ \mathit{\boldsymbol{P}}(t) = \left[ {\begin{array}{*{20}{l}} {\delta x}\\ {\delta y}\\ {{\varphi _z}} \end{array}} \right] = \mathit{\boldsymbol{NC}}_{OEPQ}^G\left[ {\begin{array}{*{20}{c}} {{\psi _E}(t)}\\ {{\psi _p}(t)}\\ {{\psi _Q}(t)} \end{array}} \right] = \mathit{\boldsymbol{M\psi }}(t). $ | (17) |
将式(6)与式(9)代入式(16)结合式(15)可进一步得到M为
| $ \begin{array}{l} \mathit{\boldsymbol{M}} = \\ \left[ {\begin{array}{*{20}{c}} {\frac{{ - xz}}{{\sqrt {{x^2} + {y^2}} }}}&y&{\frac{{ - yz}}{{\sqrt {{x^2} + {y^2}} }}}\\ {\frac{{ - yz}}{{\sqrt {{x^2} + {y^2}} }}}&{ - x}&{\frac{{xz}}{{\sqrt {{x^2} + {y^2}} }}}\\ {\frac{{ - Rxy}}{{\sqrt {{x^2} + {y^2}} \left( {{x^2} + {z^2}} \right)}}}&{\frac{{Rz}}{{{x^2} + {z^2}}}}&{\frac{{R{x^2}}}{{\sqrt {{x^2} + {y^2}} \left( {{x^2} + {z^2}} \right)}}} \end{array}} \right]. \end{array} $ |
式(17)建立起了适用于格网惯性导航力学编排的P方程,如果能从外界得到准确的位置和航向信息计算出P(t),就可以利用式(17)计算出OEPQ坐标系下的平台漂移角ψ(t).由于P方程的推导是基于格网坐标系,因而该方是适用于极区的.
2.3 ψ方程为了使数学平台跟踪格网坐标系的旋转角速度,计算机根据载体的位置及速度计算出平台的指令角速度,理想情况下系统不存在定位误差,陀螺也没有漂移,这时格网、计算机和数学平台坐标系完全重合.但由于数学平台坐标系与计算机坐标系之间存在ψ角,同时又由于陀螺漂移ε的存在,平台的指令角速度为
| $ {\mathit{\boldsymbol{\omega }}_{ip}} = {\mathit{\boldsymbol{\omega }}_{ic}} + \mathit{\boldsymbol{\psi }} \times {\mathit{\boldsymbol{\omega }}_{ic}} + \varepsilon . $ | (18) |
由矢量角ψ的定义可知,数学平台坐标系相对计算机坐标系的角速度为
| $ {\left. {\frac{{{\rm{d}}\mathit{\boldsymbol{\psi }}}}{{{\rm{d}}\mathit{\boldsymbol{t}}}}} \right|_{\rm{c}}} = \mathit{\boldsymbol{\dot \psi }}. $ | (19) |
根据角速度合成定理有
| $ {\mathit{\boldsymbol{\omega }}_{ip}} = {\mathit{\boldsymbol{\omega }}_{ic}} + {\left. {\frac{{{\rm{d}}\mathit{\boldsymbol{\psi }}}}{{{\rm{d}}\mathit{\boldsymbol{t}}}}} \right|_c}. $ | (20) |
由式(18)和式(20)可以得到:
| $ {\left. {\frac{{{\rm{d}}\mathit{\boldsymbol{\psi }}}}{{{\rm{d}}\mathit{\boldsymbol{t}}}}} \right|_c} + {\mathit{\boldsymbol{\omega }}_{ic}} \times \mathit{\boldsymbol{\psi }} = \mathit{\boldsymbol{\varepsilon }}. $ | (21) |
根据矢量相对微商原理,式(21)相对格网坐标系的微分方程为
| $ {\left. {\frac{{{\rm{d}}\mathit{\boldsymbol{\psi }}}}{{{\rm{d}}\mathit{\boldsymbol{t}}}}} \right|_G} + {\mathit{\boldsymbol{\omega }}_{iG}} \times \mathit{\boldsymbol{\psi }} = {\mathit{\boldsymbol{\varepsilon }}_G}. $ | (22) |
由于船舶的航行速度很低,地球自转角速度Ω≫ωeG,结合式(19),式(22)可以简化为
| $ {{\mathit{\boldsymbol{\dot \psi }}}_G} + \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \times \mathit{\boldsymbol{\psi }} = {\mathit{\boldsymbol{\varepsilon }}_G}. $ | (23) |
地球自转角速度Ω仅在OEPQ坐标系OP轴存在分量,只考虑陀螺常值漂移,将式(23)投影到OEPQ坐标系可得:
| $ \left\{ \begin{array}{l} {{\dot \psi }_{\rm{E}}} + \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}{\psi _{\rm{Q}}} = {\varepsilon _{\rm{E}}},\\ {{\dot \psi }_{\rm{P}}} = {\varepsilon _{\rm{P}}},\\ {{\dot \psi }_{\rm{Q}}} - \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}{\psi _{\rm{E}}} = {\varepsilon _{\rm{Q}}}, \end{array} \right. $ | (24) |
式(24)即为ψ方程,该方程建立起了陀螺常值漂移与平台漂移角的关系.
2.4 系统综合校正方案由式(24)参考文献[14]的推导方式, 可以得到载体系下的陀螺漂移为
| $ \begin{array}{l} {\mathit{\boldsymbol{\varepsilon }}_b} = \mathit{\boldsymbol{C}}_G^b\mathit{\boldsymbol{B \boldsymbol{\varOmega} }}{\mathit{\boldsymbol{U}}^{ - 1}}\left( {{t_{n + 1}},{t_n}} \right) \cdot \\ \;\;\;\;\;\;\;\left[ {\mathit{\boldsymbol{\psi }}\left( {{t_{n + 1}}} \right) - \mathit{\boldsymbol{T}}\left( {{t_{n + 1}},{t_n}} \right)\mathit{\boldsymbol{\psi }}\left( {{t_n}} \right)} \right]. \end{array} $ | (25) |
式中:CGb为格网坐标系与载体坐标系之间的转换矩阵; tn、tn+1分别为两次获得外部参考信息的时刻.令an=Ω(tn+1-tn),则:
| $ \mathit{\boldsymbol{U}}\left( {{t_{n + 1}},{t_n}} \right) = \left[ {\begin{array}{*{20}{c}} {\sin {a_n}}&0&{\cos {a_n} - 1}\\ 0&{{a_n}}&0\\ {1 - \cos {a_n}}&0&{\sin {a_n}} \end{array}} \right], $ |
| $ \mathit{\boldsymbol{T}}\left( {{t_{n + 1}},{t_n}} \right) = \left[ {\begin{array}{*{20}{c}} {\cos {a_n}}&0&{ - \sin {a_n}}\\ 0&1&0\\ {\sin {a_n}}&0&{\cos {a_n}} \end{array}} \right]. $ |
式(25)表示了平台漂移角ψ与陀螺漂移ε的关系.在两次观测点上,测出惯导系统的误差P(tn)、P(tn+1),结合式(17)将式(25)改写为
| $ \begin{array}{l} {\mathit{\boldsymbol{\varepsilon }}_b} = \mathit{\boldsymbol{C}}_G^b\mathit{\boldsymbol{B \boldsymbol{\varOmega} }}{\mathit{\boldsymbol{U}}^{ - 1}}\left( {{t_{n + 1}},{t_n}} \right) \cdot \\ \;\;\;\;\;\;\;\left[ {{\mathit{\boldsymbol{M}}^{ - 1}}\mathit{\boldsymbol{P}}\left( {{t_{n + 1}}} \right) - \mathit{\boldsymbol{T}}\left( {{t_{n + 1}},{t_n}} \right){\mathit{\boldsymbol{M}}^{ - 1}}\mathit{\boldsymbol{P}}\left( {{t_n}} \right)} \right]. \end{array} $ | (26) |
在第1个观测点取得外部位置及航向角信息后,利用外部位置及航向角信息对格网惯导系统进行重调,即将外部位置及航向信息分别赋值给惯导系统对应导航参数,重调后t=tn+时,δx=0,δy=0,δz=0,φ=0,此时P(tn+)=0,式(26)简化为
| $ {\mathit{\boldsymbol{\varepsilon }}_b} = \mathit{\boldsymbol{C}}_G^b\mathit{\boldsymbol{B \boldsymbol{\varOmega} }}{\mathit{\boldsymbol{U}}^{ - 1}}\left( {{t_{n + 1}},{t_n}} \right){\mathit{\boldsymbol{M}}^{ - 1}}\mathit{\boldsymbol{P}}\left( {{t_{n + 1}}} \right). $ | (27) |
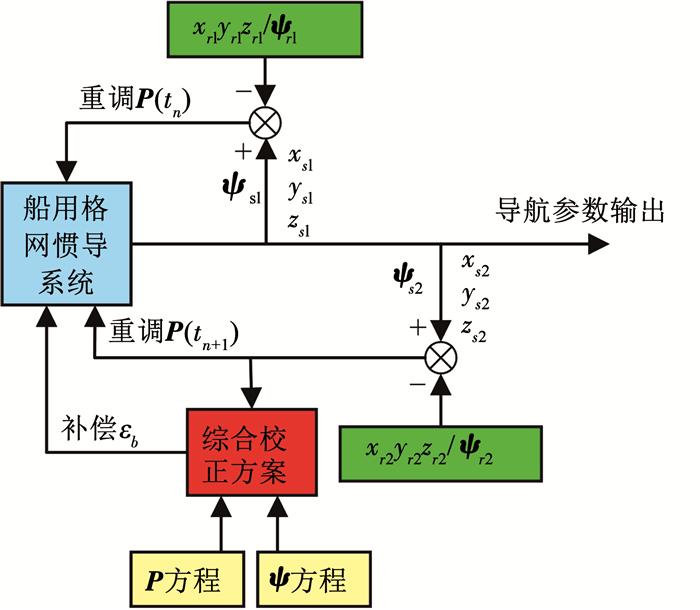
通过式(27)即可估计出陀螺常值漂移,利用第2个观测点取得的位置及航向信息对系统进行重调,同时补偿陀螺常值漂移,即完成两点校综合校正过程.通过OEPQ坐标系设计综合校正策略的好处在于简化了综合校正算法的复杂程度,在两次系统重调后,通过简单的矩阵运算即可准确地估计出陀螺常值漂移.两点校综合校正方案原理图如图 3所示.图 3中,[xr1 yr1 zr1]T、[xr2 yr2 zr2]T分别为tn、tn+1时刻外部参考位置; ψr1、ψr2分别为tn、tn+1时刻外部参考航向; [xs1 ys1 zs1]T、[xs2 ys2 zs2]T分别为tn、tn+1时刻惯导输出的位置; ψs1、ψs2分别为tn、tn+1时刻惯导输出的航向.
|
图 3 综合校正方案原理图 Fig. 3 Schematic diagram of comprehensive calibration scheme |
为验证所设计的基于格网坐标系的两点校综合校正算法的可行性,对算法进行仿真分析,在外水平阻尼条件下实现两点校综合校正算法.采用数值解法给出陀螺和加速度计输出信息,仿真条件设置为:仿真时长10 h,采样频率100 Hz; t=2 h与t=3.5 h时刻引入外部位置和航向角信息,ECEF坐标系下外部位置沿3个轴的误差均为5 m,外部航向角误差为6″; 陀螺常值漂移为1×10-2(°)/h,加速度计常值零偏为10-4 g,陀螺随机漂移以及加速度计随机零偏设置为白噪声; 初始位置中纬度(85°N),经度(18°E); 初始姿态误差角中格网横摇角误差(6″),格网纵摇角误差(6″),格网航向角误差(6′); 船舶沿着纬度圈向东以10 m/s的速度匀速运动; 船舶摇摆以正弦规律变化,如下式所示:
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{pitch}} = {P_{\rm{m}}}\sin \left( {\frac{{2{\rm{ \mathsf{ π} }}}}{{{T_{\rm{p}}}}}t + {\varphi _{\rm{p}}}} \right),}\\ {{\rm{roll}} = {R_{\rm{m}}}\sin \left( {\frac{{2{\rm{ \mathsf{ π} }}}}{{{T_{\rm{r}}}}}t + {\varphi _{\rm{r}}}} \right),}\\ {{\rm{yaw}} = {{90}° } + {Y_{\rm{m}}}\sin \left( {\frac{{2{\rm{ \mathsf{ π} }}}}{{{T_y}}}t + {\varphi _y}} \right).} \end{array}} \right. $ | (28) |
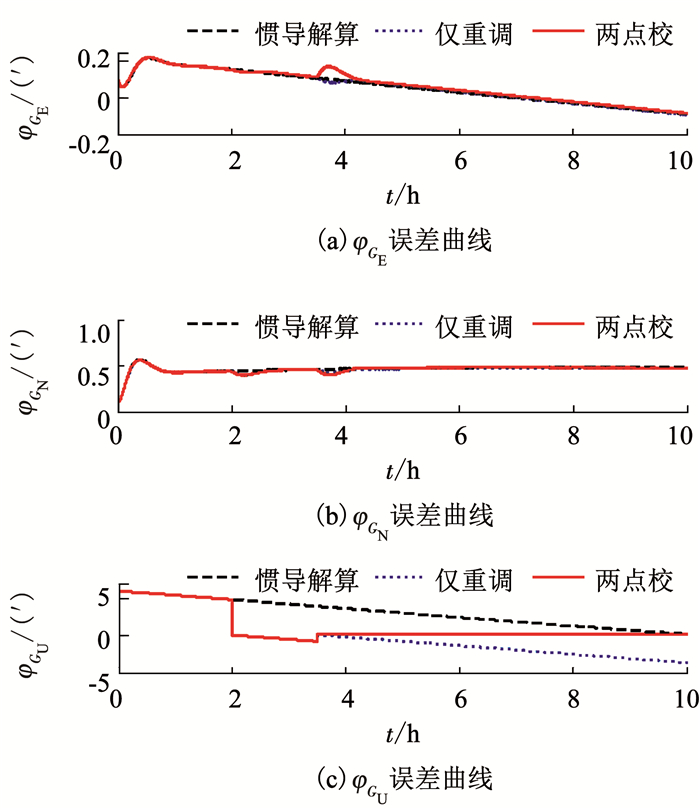
式中:摇摆幅值Pm=3°, Rm=5°, Ym=4°,摇摆周期Tp=7 s,Tr=9 s,Ty=12 s,摇摆初始相位设置为随机值.仿真结果如图 4~6所示.
|
图 4 格网姿态误差角仿真曲线 Fig. 4 Simulation curves of grid attitude angle errors |
|
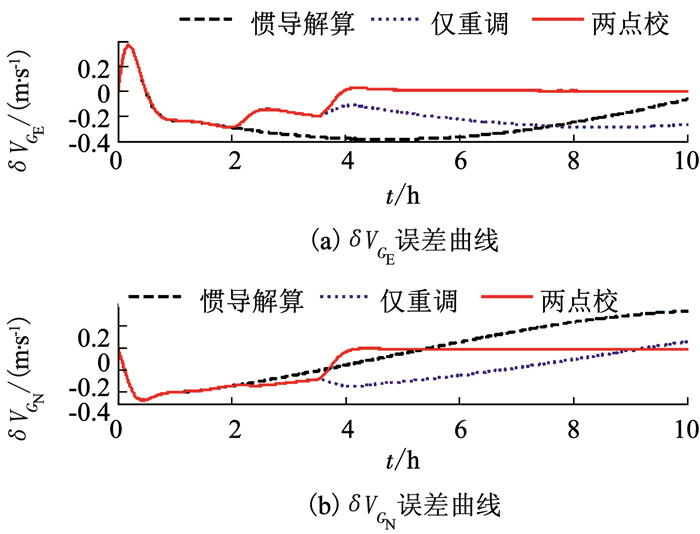
图 5 格网水平速度误差仿真曲线 Fig. 5 Simulation curves of grid level velocity errors |
|
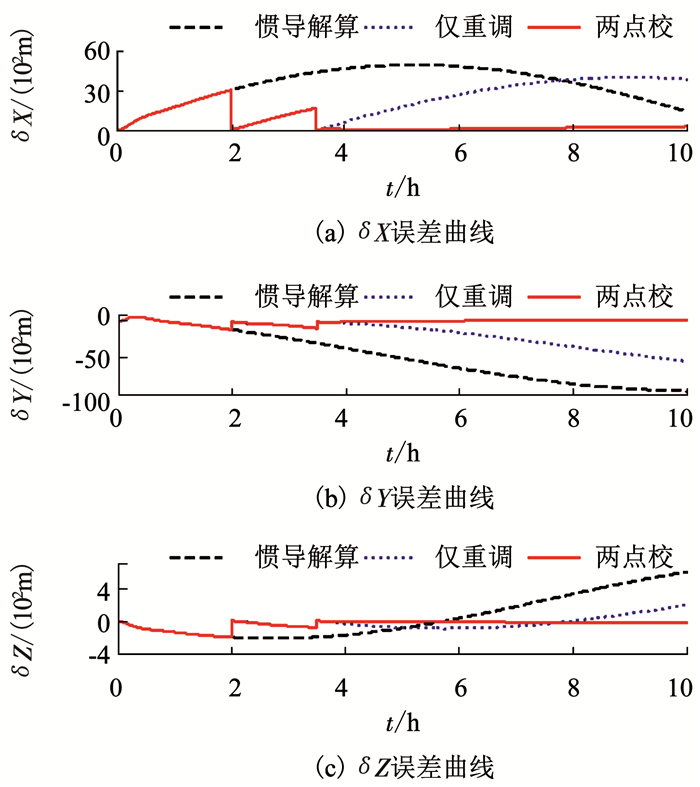
图 6 ECEF坐标系下位置误差仿真曲线 Fig. 6 Simulation curves of position errors within ECEF frame |
由图 4~6可知,外水平阻尼状态下系统舒勒振荡误差得到了有效抑制,但格网航向误差、格网水平速度误差和位置误差将仍随时间积累.对于格网航向角、格网水平速度以及位置而言,与仅利用外部位置及航向信息进行重调(图中蓝色虚线)相比,两点校综合校正算法由于准确地估计并补偿了陀螺常值漂移,在第2次观测点后系统导航误差得到了有效抑制; 对格网水平姿态而言,由于稳态条件下格网水平姿态误差主要受加速度计零偏的影响,因而两点校综合校正算法对格网水平姿态误差抑制能力有限.需要补充的一点是:校正点后由于航向和位置重调破坏了系统平衡条件,因而格网水平姿态误差以及位置误差在校正点后将出现短时间的超调误差[17],这与格网水平速度误差在校正点后不能立刻得到抑制,而需要经过一段调整时间才能减小是一致的.
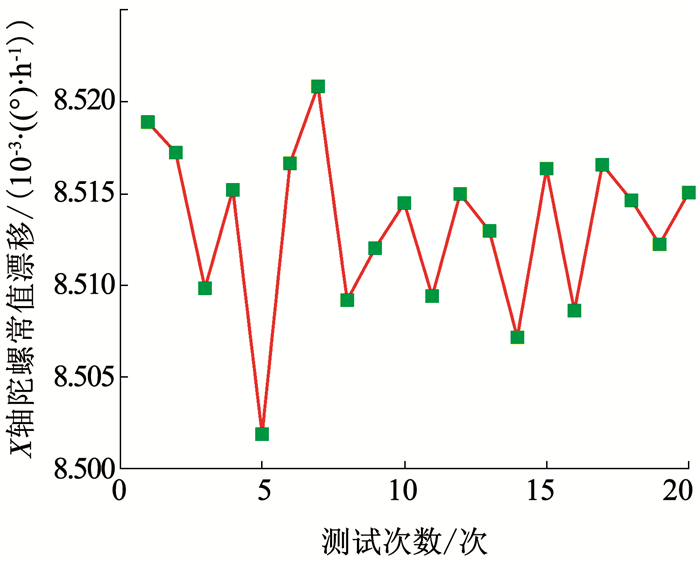
对该仿真条件下的综合校正算法进行20次测试,得到X轴陀螺常值漂移估计情况如图 7所示,3轴陀螺常值漂移估计平均值及标准差见表 1.
|
图 7 20次X轴陀螺常值漂移估计值 Fig. 7 Estimation of X-axis gyroscope constant drift for 20 times |
| 表 1 估计的陀螺常值漂移平均值及标准差 Tab. 1 Mean and standard deviation of estimated three-axis gyro constant drift |
由表 1可知,所设计的两点校综合校正算法可以准确地估计出载体坐标系下3轴陀螺常值漂移,所估计的陀螺常值漂移可用于陀螺测量误差的补偿.
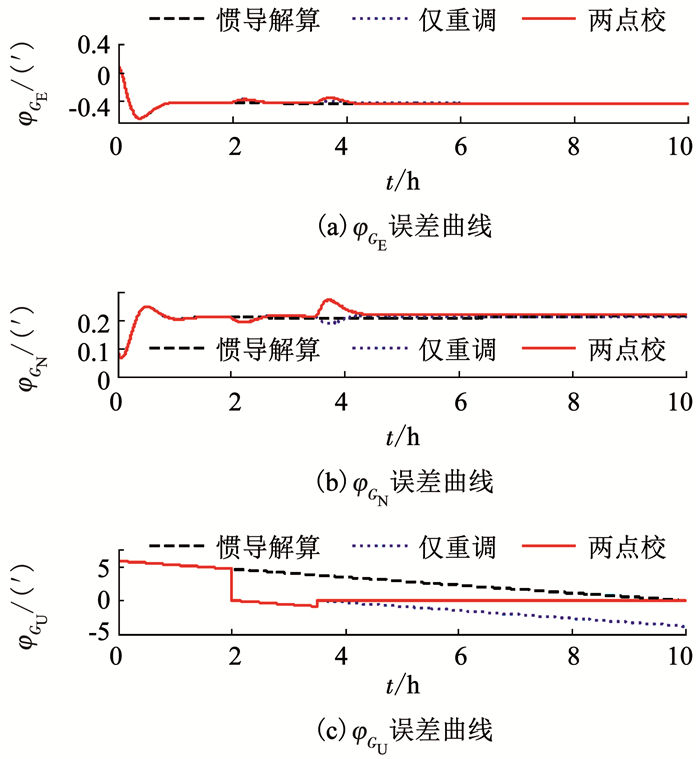
OEPQ在极点附近其E轴指向将发生较快变化,这种情况下综合校正将受到一定影响,因而有必要对第2次观测点在极点附近这种情况下的综合校正算法进行仿真测试,进而确定由于E轴指向变化速率加快所产生的影响.仿真条件设置如下:初始位置中纬度(88.868 168°N),经度(18°E); 航向角常值为0°,其余姿态变化如式(28)所示; 船舶沿着经线圈向北以10 m/s的速度匀速运动; 其他仿真条件与上述仿真条件设置相同.仿真结果如图 8~10所示.
|
图 8 格网姿态误差角仿真曲线 Fig. 8 Simulation curves of grid attitude angle error |
|
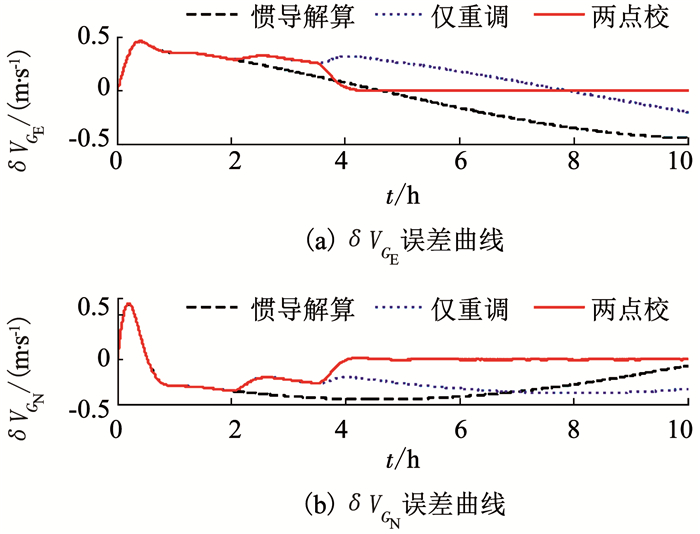
图 9 格网水平速度误差仿真曲线 Fig. 9 Simulation curves of grid level velocity errors |
|
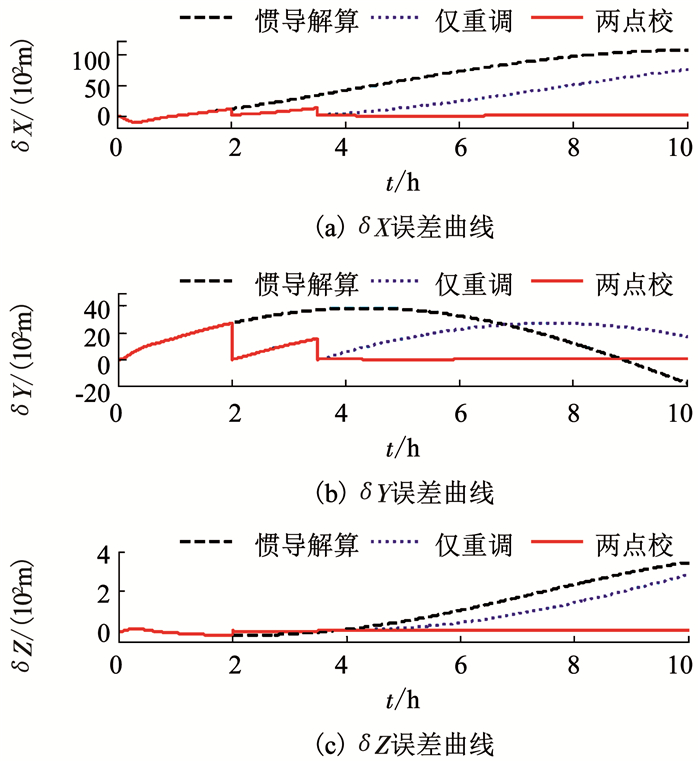
图 10 ECEF坐标系下位置误差仿真曲线 Fig. 10 Simulation curves of position errors within ECEF frame |
对该仿真条件下的综合校正算法进行20次测试,3轴陀螺常值漂移估计平均值及标准差见表 2.
| 表 2 估计的陀螺常值漂移平均值及标准差 Tab. 2 Mean and standard deviation of estimated three-axis gyro constant drift |
t=3.5 h,船舶航行至纬度为89.999 999 8°处,按圆球模型计算,距离极点不足2 cm.由图 8~10可知,所设计的综合校正算法在进行穿过极点仿真测试后仍能取得较好的校正效果,所得到的结论与上述仿真结果一致.同时结合表 2可知,所设计的综合校正算法对3轴陀螺常值漂移的估计仍能取得较好的估计性能.因而,可以认为OEPQ坐标系在极点附近处E轴指向变化速率加快所影响的范围很小,所设计的两点校综合校正算法在实际应用中具备一定的可行性,可有效保证船舶在极区航行时的导航精度.由于格网东向姿态误差微分包含格网方位误差与航向正弦值乘积项,格网方位误差在阻尼条件下其值有正负变化,因而两次仿真结果中格网东向姿态误差变化趋势不同.
文献[18]指出在目前的外部信息测量精度和惯导系统输出的水平姿态精度下,为了得到较好的陀螺常值漂移估计效果,当使用两点校作为综合校正方案时,陀螺精度应处于1×10-2(°)/h量级.若要进一步提高本文所提出的基于格网坐标系的两点校综合校正算法的性能,需要从提高外测信息精度以及补偿格网水平姿态误差这两个方面入手.
4 结论1) 外水平阻尼条件下,船用格网惯性导航系统的舒勒振荡得到了有效抑制.然而外水平阻尼技术并不能抑制船用格网惯导系统随时间积累的导航误差.
2) 所推导的P方程建立起了位置误差、格网航向误差与平台漂移角之间的关系; 所推导的ψ方程建立起了陀螺常值漂移与平台漂移角之间的关系.基于以上两方程所设计的综合校正方案准确地建立起了载体坐标系下陀螺常值漂移与外部观测量误差之间的关系,进而完成对陀螺常值漂移的估计.
3) 所提出的两点校综合校正算法可以准确地估计出载体坐标系下的陀螺常值漂移,对系统进行陀螺常值漂移补偿以及系统重调后可有效抑制船用格网惯导系统随时间积累的导航误差.
| [1] |
CHENG Jianhua, WANG Tongda, GUAN Dongxue, et al. Polar transfer alignment of shipborne SINS with a large misalignment angle[J]. Measurement Science and Technology, 2016, 27(3): 035101. DOI:10.1088/0957-0233/27/3/035101 |
| [2] |
YAN Zheping, WANG Lu, ZHANG Wei, et al. Polar grid navigation algorithm for unmanned underwater vehicles[J]. Sensors, 2017, 17(7): 1599. DOI:10.3390/s17071599 |
| [3] |
周琪, 秦永元, 付强文, 等. 极区飞行格网惯性导航算法原理[J]. 西北工业大学学报, 2013, 31(2): 210. ZHOU Qi, QIN Yongyuan, FU Qiangwen, et al. Grid mechanization in inertial navigation systems for transpolar aircraft[J]. Journal of Northwestern Polytechnical University, 2013, 31(2): 210. DOI:10.3969/j.issn.1000-2758.2013.02.010 |
| [4] |
YAO Yiqing, XU Xiaosu, LI Yao, et al. Transverse navigation under the ellipsoidal earth model and its performance in both polar and non-polar areas[J]. Journal of Navigation, 2016, 69(2): 335. DOI:10.1017/S0373463315000715 |
| [5] |
周琪, 岳亚洲, 张晓冬, 等. 极区飞行间接格网惯性导航算法[J]. 中国惯性技术学报, 2014, 22(1): 18. ZHOU Qi, YUE Yazhou, ZHANG Xiaodong, et al. Indirect grid inertial navigation mechanization for transpolar aircraft[J]. Journal of Chinese Inertial Technology, 2014, 22(1): 18. DOI:10.13695/j.cnki.12-1222/o3.2014.01.005 |
| [6] |
张海峰, 张礼伟, 王兴岭, 等. 捷联惯导系统极区导航算法优化设计及误差特性分析[J]. 中国惯性技术学报, 2015, 23(6): 701. ZHANG Haifeng, ZHANG Liwei, WANG Xingling, et al. Optimization design and error analysis of strapdown inertial navigation system mechanization in polar region[J]. Journal of Chinese Inertial Technology, 2015, 23(6): 701. DOI:10.13695/j.cnki.12-1222/o3.2015.06.001 |
| [7] |
KANG Yingyao, ZHAO Lin, CHENG Jianhua, et al. A novel grid sins/dvl integrated navigation algorithm for marine application[J]. Sensors, 2018, 18(2): 364. DOI:10.3390/s18020364 |
| [8] |
HUANG Weiquan, FANG Tao, LUO Li, et al. A damping grid strapdown inertial navigation system based on a kalman filter for ships in polar regions[J]. Sensors, 2017, 17(7): 1551. DOI:10.3390/s17071551 |
| [9] |
杨槊, 李群, 姜述明, 等. 极区格网阻尼导航方法[J]. 导航定位与授时, 2016, 3(5): 27. YANG Shuo, LI Qun, JIANG Shuming, et al. A damping method for polar navigation based on grid mechanization[J]. Navigation Positioning and Timing, 2016, 3(5): 27. DOI:10.19306/j.cnki.2095-8110.2016.05.006 |
| [10] |
赵琳, 李久顺, 程建华. 双滤波器捷联惯导外阻尼导航算法[J]. 哈尔滨工业大学学报, 2018, 50(3): 178. ZHAO Lin, LI Jiushun, CHENG Jianhua. Double-filters external damping strapdown inertial navigation algorithm[J]. Journal of Harbin Institute of Technology, 2018, 50(3): 178. DOI:10.11918/j.issn.0367-6234.201612054 |
| [11] |
CHANG Lubin, LI Kailong, HU Baiqing. Huber's M-estimation-based process uncertainty robust filter for integrated INS/GPS[J]. IEEE Sensors Journal, 2015, 15(6): 3367. DOI:10.1109/JSEN.2014.2384492 |
| [12] |
FENG Kaiqiang, LI Jie, ZHANG Xi, et al. An improved strong tracking cubature Kalman filter for GPS/INS integrated navigation systems[J]. Sensors, 2018, 18(6): 1919. DOI:10.3390/s18061919 |
| [13] |
LI Qian, BEN Yueyang, YU Fei, et al. System reset of transversal strapdown INS for ship in polar region[J]. Measurement, 2015, 60(2015): 247. DOI:10.1016/j.measurement.2014.10.020 |
| [14] |
黄德鸣, 程禄. 惯性导航系统[M]. 北京: 国防工业出版社, 1986: 175. HUANG Deming, CHENG Lu. Inertialnavigation system[M]. Beijing: National Defense Industry Press, 1986: 175. |
| [15] |
高伟, 史宏洋, 张鑫, 等. 基于位置信息的捷联惯导系统综合校正技术[J]. 华中科技大学学报(自然科学版), 2014, 42(6): 101. GAO Wei, SHI Hongyang, ZHANG Xin, et al. Comprehensive correction technology of strapdown inertial navigation system based on position information[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2014, 42(6): 101. DOI:10.13245/j.hust.140620 |
| [16] |
张鑫. 长航时捷联惯导系统综合校正方法[J]. 舰船电子工程, 2014, 34(2): 47. ZHANG Xin. Anovel comprehensive calibration method for long-endurance strapdown inertial navigation system[J]. Ship Electronic Engineering, 2014, 34(2): 47. DOI:10.3969/j.issn.1672-9730.2014.02.013 |
| [17] |
丰璐.长航时惯导系统的阻尼和综合校正技术研究[D].北京: 北京理工大学, 2016 FENG Lu. Research ondamping and comprehensive calibration techniques for long-term inertial navigation system[D]. Bejing: Beijing Institute of Technology, 2016 |
| [18] |
杨晓东, 邓太光. 平台式惯导系统两点校的常值误差分析[J]. 交通运输工程学报, 2011, 11(3): 100. YANG Xiaodong, DENG Taiguang. Constant error analysis of two-point comprehensive calibration in gimbaled inertial navigation system[J]. Journal of Traffic and Transportation Engineering, 2011, 11(3): 100. DOI:10.369/j.issn.1672-9730.2014.02.013 |
 2020, Vol. 52
2020, Vol. 52


