2. 空军工程大学 研究生学院, 西安 710051
2. Graduate College, Air Force Engineering University, Xi'an 710051, China
飞机在着陆过程中容易发生飞行事故, 其事故主要集中在着陆缓冲、滑跑减速和偏航纠偏等方面, 尤其是由于飞机自身结构的不完全对称性、机场跑道的凹凸和侧风扰动等原因, 飞机在滑跑过程中往往会相对于跑道中轴位置发生一定的偏航,若不及时修正偏航角,很可能导致飞机冲出跑道, 酿成事故.总体来看, 飞机滑跑纠偏过程是一个涉及飞行员、飞行指挥员、刹车系统、机载设备、空管法规以及外界环境等的典型复杂系统, 关于这一复杂系统的安全性分析对航空兵部队或航空公司有效预防和减少事故的发生有着重要意义.
传统安全性分析方法主要有故障树分析(FTA)[1]、事故树分析(ETA)[2]和故障模式及影响分析(FMEA)[3]等, 上述方法都是从线性角度对各失效部件进行独立分析, 忽略了各子系统之间的耦合性和协调性, 尤其是对设计缺陷、软件出错、协调能力不足、人为差错和非线性等问题[4]缺乏准确的描述与分析, 致使在复杂过程和复杂系统的安全性分析中具有很大的局限性.基于系统理论的安全性分析方法通过考虑部件或子系统之间的相互作用, 运用系统分析方法开展安全性研究, 主要有以下3种方法:1)基于分层社会-技术模型(HSTM)[5]的方法; 2)基于功能共振事故模型(FRAM)[6]的方法; 3)基于系统理论事故模型及过程(STAMP)[7]的方法.基于HTSM的方法着重关注系统运行过程中的社会-技术因素对安全的影响, 利用分层控制结构系统地分析事故原因, 但该方法是以假定存在线性因果事件链为前提的.基于FRAM的方法将系统运行过程分解为若干个运行单元进行性能波动分析, 并根据各单元之间的交联关系对整个系统进行安全性分析, 但该方法难以识别因系统设计缺陷而导致的安全问题.基于STAMP的方法将安全问题转化为控制问题而非可靠性问题, 通过施加安全约束、建立分层控制结构和分析过程模型以识别系统生命周期各阶段存在的不安全控制行为, 分析事故原因.该方法已成功应用于航空航天[8-9]、能源化工[10]、交通运输[11]和组织管理[12]等安全领域.
本文从控制的角度建立了考虑人机协调的全电差动刹车系统STAMP模型, 对飞机差动刹车纠偏过程进行了STPA分析, 对识别出的不安全控制行为进行了定性分析, 并通过建模仿真从定量角度提出了安全约束, 验证了STAMP/STPA方法在飞机全电差动刹车纠偏过程安全性分析中的可行性.
1 STAMP/STPA基本原理Leveson[13]于2004年提出系统理论事故模型及过程(STAMP), 认为安全性是系统的一种涌现特性, 并从控制的角度来研究复杂系统的安全问题, 通过确保满足安全约束这一控制目标以实现系统安全性.一个完整的STAMP模型通常由安全约束、分层控制结构和过程模型3部分组成.其中,安全约束未施加或未执行往往是导致事故发生的重要原因, 其约束主要包括物理定律、法律及策略等用于限制组件控制行为的安全机制; 系统的安全运行需要不同层次控制结构之间的交互、沟通和协调, 通过高层向低层施加控制要求或约束和低层向高层反馈信息或沟通的方式以确保整个系统的安全性, 控制行为的不恰当或不充足、控制行为未执行或执行不充分、反馈信息缺失或错误等都可能造成事故发生; 过程模型是控制理论的重要组成部分, 当过程模型或人工控制器的心智模型与被控系统不匹配时, 往往会导致组件交互事故或人为差错事故.基于以上基本概念, STAMP模型从控制反馈回路的角度将事故的致因大致分为:1)不恰当的控制输入、控制算法和过程模型; 2)被控过程行为失效或执行器故障; 3)控制器和决策者之间的沟通、协调冲突.同时, 控制结构中所涉及的外界干扰也是导致事故发生的重要原因.
系统理论过程分析(STPA)[14]是一种基于STAMP模型的安全分析方法, 该方法首先从全局角度确定系统级事故和危险, 然后根据所建立的分层控制结构进行不安全控制行为(UCA)识别, 通过识别UCA, 进一步分析控制反馈回路以完成事故的致因分析, 最后针对事故产生的原因对系统提出安全约束及要求.其中, UCA主要分为4种类型[15]:1)未提供安全所要求的控制行为; 2)提供了不恰当或错误的控制行为; 3)提供的控制行为时序错乱, 过早或过迟; 4)提供的控制行为时效性过长或过短.
2 全电差动刹车系统STAMP建模不同于传统的液压刹车系统, 全电差动刹车系统[16]通过电传机构传递电信号的方式控制刹车装置, 以完成差动刹车纠偏.该系统主要由刹车控制器、电作动控制器(EMA控制器)、电作动机构(EMA)、机轮速度传感器、力矩传感器、机轮刹车装置等组成, 其结构原理如图 1所示.
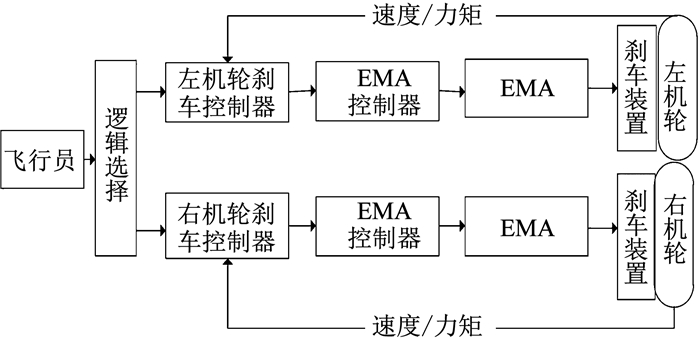
|
图 1 全电差动刹车系统结构原理 Fig. 1 Structural principle of all-electric differential braking system |
飞机进入跑道后发生一定的偏转和侧移, 首先, 飞行员综合考虑环境信息、管制员指令信息、飞机自身状态信息和自身操作经验, 选择滑跑纠偏模式, 采用人工控制的方式踩动刹车踏板提供飞机偏差信号; 然后, 利用逻辑选择开关将飞机偏差信号转化为左(或右)侧机轮刹车、右(或左)侧机轮不刹车的刹车信号, 并传递至左(或右)机轮刹车控制器; 左(或右)机轮刹车控制器结合机轮速度传感器、力矩传感器传来的速度信号和力矩信号对刹车信号做进一步分析, 将控制信号传递至EMA控制器; EMA控制器进一步将控制信号作用于EMA上, 从而控制左(或右)机轮刹车装置进行刹车.当左(或右)机轮发生滑动摩擦、右(或左)机轮正常滑行发生滚动摩擦时, 由于滑动摩擦的滑移率大于滚动摩擦滑移率(滑移率为零), 导致左(或右)机轮所受的摩擦力大于右(或左)机轮, 从而两机轮因产生相对飞机重心的偏航力矩使飞机向左(或右)发生偏转, 完成飞机右(或左)偏纠正.
此外, 在差动刹车纠偏过程中, 其正常运行还依赖于其他系统的正常工作, 比如EMA控制器的正常运行依赖于电源系统的运行状态, 仪表信息的正常显示依赖于电源系统和GPS系统的运行状态.
通过对飞机全电差动刹车纠偏过程的原理描述, 进一步梳理整个控制系统所涉及的控制对象、输入/输出信号、控制器、执行器和控制/反馈关系, 建立考虑人机协调的全电差动刹车系统STAMP模型, 如图 2所示.通过对STAMP模型中控制反馈回路的系统分析, 从控制缺陷、反馈缺陷和协调缺陷3个方面分析滑跑纠偏过程中的安全问题, 同时也综合考虑人为因素和外界环境的干扰.
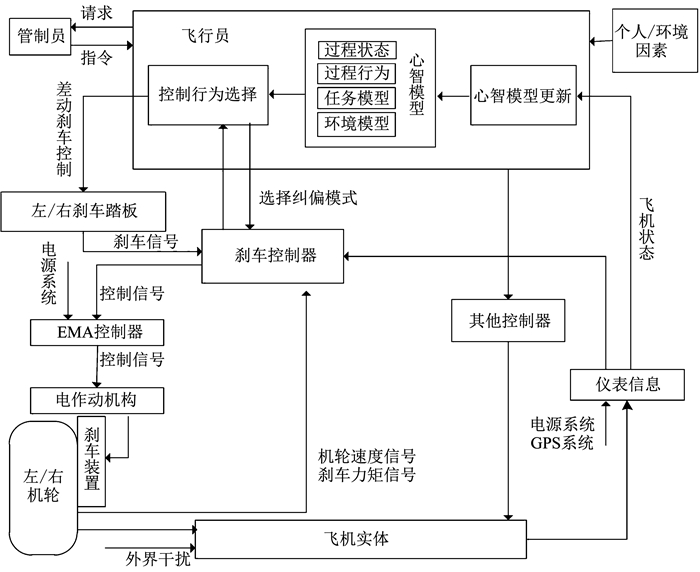
|
图 2 全电差动刹车系统STAMP模型 Fig. 2 STAMP model of all-electric differential braking system |
全电差动刹车纠偏过程中的系统级事故通常分为飞机损伤、人员伤亡以及地面设备、设施损坏等3种类型.飞机损伤(A-1)是指由于飞机的落地姿态、飞行员的操作失误、空中交通管制(air traffic control, ATC)信息提供不准确等原因导致滑跑纠偏效果差或未纠偏, 最终使得机体、机翼或者其他子系统偏出跑道而受损; 人员伤亡(A-2)是指在滑跑纠偏过程中出现不可控的情况而导致飞行员、乘客或者其他地面人员伤亡; 地面设备、设施损坏(A-3)是指在滑跑纠偏过程中地面保障设备、固定设施或地面飞机等损坏, 具体见表 1.
| 表 1 全电差动刹车纠偏过程的系统级事故 Tab. 1 System level accident of all-electric differential braking correction process |
全电差动刹车纠偏过程的系统级危险主要包括飞机偏出跑道(H-1)、飞机与地面设施碰撞(H-2)和飞机失控(H-3)3种.每个系统级危险可能导致的系统级事故见表 2.
| 表 2 全电差动刹车纠偏过程的系统级危险 Tab. 2 System level risk of all-electric differential braking correction process |
飞机偏出跑道(H-1)可能是由于差动刹车控制执行不充分、飞行员反应速度过慢、对飞机本身的状态认识不准确等原因造成的, 一般在飞行员控制速度的情况下, 不会出现人员伤亡情况, 但通常会造成飞机损伤(A-1)或地面设备、设施损坏(A-3);飞机与地面设施碰撞(H-2)主要是由于飞行员未及时提供差动刹车动作、ATC信息提供不准确等原因导致飞机滑跑纠偏过程中侧偏距离较大, 与跑道周边地面保障设施发生碰撞, 造成飞机损伤(A-1)、人员伤亡(A-2)以及地面设备、设施受损(A-3);飞机失控(H-3)主要是由于存在强侧风等其他危险因素导致飞行员实施了错误的控制行为或飞机发生故障, 从而使飞机进入失控状态, 造成飞机损伤(A-1)、人员伤亡(A-2)以及地面设备、设施受损(A-3).
3.3 不安全控制行为的识别为保证差动刹车系统的安全运行, 需要对整个系统控制回路的各组成部分进行分析,进而识别出可能导致危险的不安全控制行为.飞机在地面滑跑过程中, 必须在短时间内实现差动刹车控制以完成飞机纠偏, 本文旨在识别飞行员提供差动刹车动作所产生的不安全控制行为, 基于STPA方法将不安全控制行为分为4类, 主要包括未提供或错误提供差动刹车动作、过早或过晚提供差动刹车动作、差动刹车动作作用时间过短或过长、差动刹车系统组件失效等, 具体见表 3.
| 表 3 差动刹车动作的不安全控制行为 Tab. 3 Unsafe control action of differential braking |
根据STAMP控制缺陷分类[17], 从控制缺陷、反馈缺陷和协调缺陷3个方面建立全电差动刹车系统控制反馈回路, 如图 3所示.
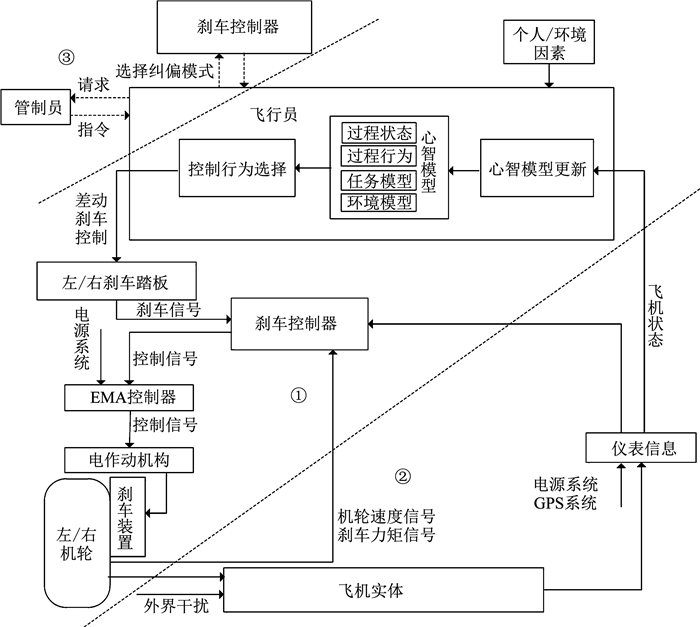
|
图 3 全电差动刹车系统控制反馈回路 Fig. 3 Control feedback loop of all-electric differential braking system |
图 3中①包含了飞行员、刹车踏板、刹车控制器、EMA控制器、电作动机构、刹车装置和机轮, 可以用来表示控制缺陷.图 3中②包含了飞机实体、相关传感器和仪表信息, 可以用来表示反馈缺陷.图 3中③包含了管制员、飞行员和刹车控制器, 它们之间的交互表示协调缺陷, 具体致因分析见表 4.
| 表 4 致因分析 Tab. 4 Accident-causing analysis |
本文以文献[18]提出的飞机地面滑跑模型为例, 对飞机全电差动刹车纠偏过程进行建模仿真.在MATLAB/SIMULINK环境下构建飞机地面滑跑模型[18], 主要包括:机体动力学模型、电作动机构模型、机轮模型和刹车装置模型.各子模型之间的控制关系如图 4所示.
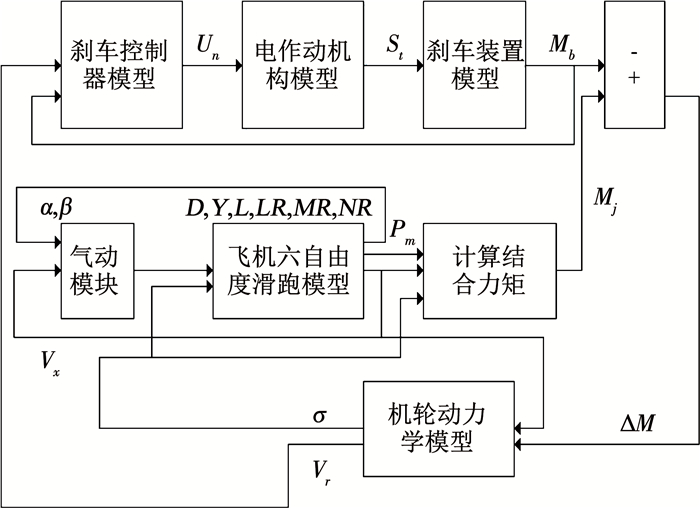
|
图 4 飞机地面滑跑控制系统 Fig. 4 Schematic diagram of control system for aircraft ground sliding |
飞机机体动力学模型由力方程组、力矩方程组、角运动方程组和线运动方程组构成, 具体如下.
力方程组为
| $ \left\{ \begin{array}{l} {{\dot v}_x} = \left( { - D{m_{11}} + Y{m_{12}} - L{m_{13}} + {f_x}\cos \psi - {f_y}\sin \psi + } \right.\\ \left. {\;\;\;\;\;\;\;{T_x}\cos {\theta _s}\cos \psi + {T_z}\sin {\theta _s}\cos \psi } \right)/m, \\ {{\dot v}_y} = \left( { - D{m_{21}} + Y{m_{22}} - L{m_{23}} + {f_x}\sin \psi - {f_y}\cos \psi + } \right.\\ \left. {\;\;\;\;\;\;{T_x}\cos {\theta _s}\sin \psi + {T_z}\sin {\theta _s}\sin \psi } \right)/m, \\ {{\dot v}_z} = \left( { - D{m_{31}} + Y{m_{32}} - L{m_{33}} + mg + {T_x}\cos {\theta _s}\cos \psi + } \right.\\ \left. {\;\;\;\;\;\;{T_z}\sin {\theta _s}\cos \psi } \right)/m. \end{array} \right. $ |
力矩方程组为
| $ \left\{ {\begin{array}{*{20}{l}} {{M_x} = \dot p{I_x} - \dot r{I_{xz}} + qr\left( {{I_z} - {I_y}} \right) - pq{I_{xz}}, }\\ {{M_y} = \dot q{I_y} + pr\left( {{I_x} - {I_z}} \right) + \left( {{p^2} - {r^2}} \right){I_{xz}}, }\\ {{M_z} = \dot r{I_z} - \dot p{I_{xz}} + pq\left( {{I_y} - {I_x}} \right) + qr{I_{xz}}.} \end{array}} \right. $ |
角运动方程组为
| $ \left\{ {\begin{array}{*{20}{l}} {\dot \theta = q\cos \varphi - r\sin \varphi , }\\ {\dot \varphi = p + (r\cos \varphi + q\sin \varphi )\tan \varphi , }\\ {\dot \psi = (r\cos \varphi + q\sin \varphi )/\cos \varphi .} \end{array}} \right. $ |
线运动方程组为
| $ \left\{ {\begin{array}{*{20}{l}} {\dot x = {v_x}, }\\ {\dot y = {v_y}, }\\ {\dot z = {v_z}.} \end{array}} \right. $ |
式中:
电作动机构模型主要分为无刷直流电机模型和机电作动器模型.
1) 无刷直流电机的数学模型为
| $ \left\{ {\begin{array}{*{20}{l}} {{U_d} = {I_d}{R_d} + L\frac{{{\rm{d}}{I_d}}}{{{\rm{d}}t}} + E, }\\ {E = {C_e}{n_d}.} \end{array}} \right. $ |
式中:Id为电枢电流; Rd为总电阻; L为绕组电感; E为电机电势; Ud为电枢电压; Ce为电势系数; nd为电机转速.
2) 机电作动器的数学模型为
| $ {T_{\rm{M}}} = {J_M}{\dot \omega _h} + {T_L}. $ |
式中:
刹车装置模型为
| $ {M_b} = \left\{ {\begin{array}{*{20}{l}} {0, }&{{p_b} < {p_0};}\\ {{k_2}\left( {{p_b} - {p_0}} \right), }&{{p_0} \le {p_b} < {M_1}/{k_2} + {p_0};}\\ {{M_1}, }&{{M_1}/{k_2} + {p_0} \le {p_b} < rp;}\\ {{M_1}, }&{rp \le {p_b} < {M_1}/{k_1} + {p_0};}\\ {{k_1}\left( {{p_b} - {p_0}} \right), }&{{M_1}/{k_1} + {p_0} \le {p_b} \le {p_m}.} \end{array}} \right. $ |
式中:Mb为刹车力矩; p0为最小刹车压力; pb为刹车压力; k1、k2分别为力矩的斜率; rp为上次输入压力; M1为上次输出力矩; pm为最大刹车压力.
4.1.4 机轮模型机轮的转动主要由刹车力矩和结合力矩共同控制, 从而影响机轮转动过程中的角速度、角加速度和线速度.
| $ \left\{ {\begin{array}{*{20}{l}} {\dot \omega = \frac{1}{{{J_r}}}\left( {{M_j} - {M_b}} \right) + \frac{{{{\dot V}_{zx}}}}{{{R_g}, }}}\\ {{v_r} = \omega {R_g}.} \end{array}} \right. $ |
式中:
本文主要针对飞机全电差动刹车纠偏过程中的UCA1、UCA2和UCA5这3种不安全控制行为进行仿真分析.其中, 仿真时间20 s, 机场跑道宽度48 m, 飞机翼展38 m, 飞机着陆滑跑的初始速度72 m/s, 侧偏距离大于5 m视为冲出跑道, 外在干扰为飞机着陆后存在1°初始偏航角或1 m/s持续侧风.
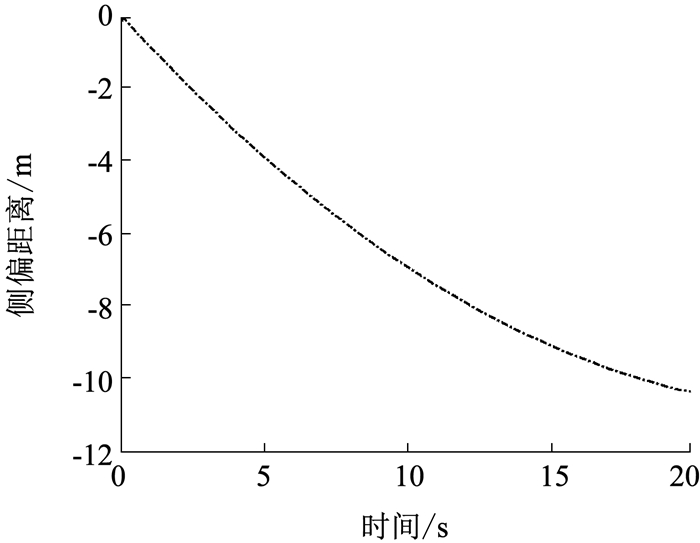
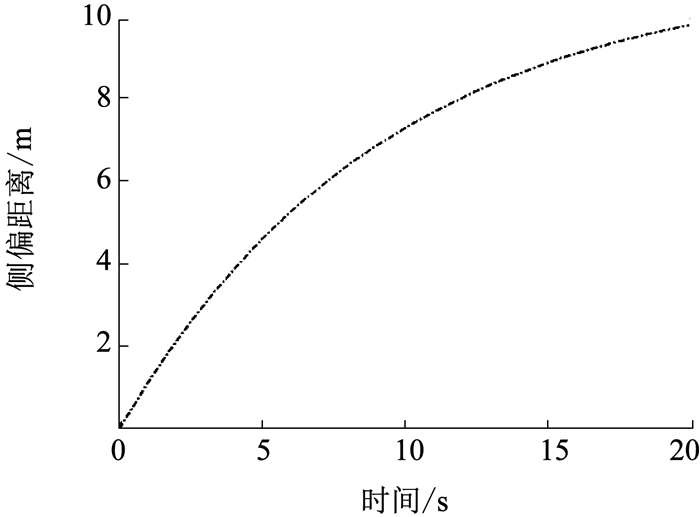
对飞机存在偏航角且未提供差动刹车动(UCA1)和存在侧风且未提供差动刹车动作(UCA2)分别进行仿真分析.从图 5、6中可以看出, 在1°初始偏航角或1 m/s持续侧风的情况下, 飞行员未提供差动刹车动作, 飞机在5 s后会发生偏出跑道的危险.由此可见, 即使在很小的初始偏航角或持续侧风干扰下, 飞行员如果不提供差动刹车动作进行纠偏,飞机很可能冲出跑道,与跑道周边的设备、设施发生碰撞并造成人员伤亡.
|
图 5 1°偏航角情形下的侧偏距离-时间曲线 Fig. 5 Offset distance-time curve of 1° yaw angle |
|
图 6 1 m/s持续侧风情形下的侧偏距离-时间曲线 Fig. 6 Offset distance-time curve of 1 m/s continuous crosswind |
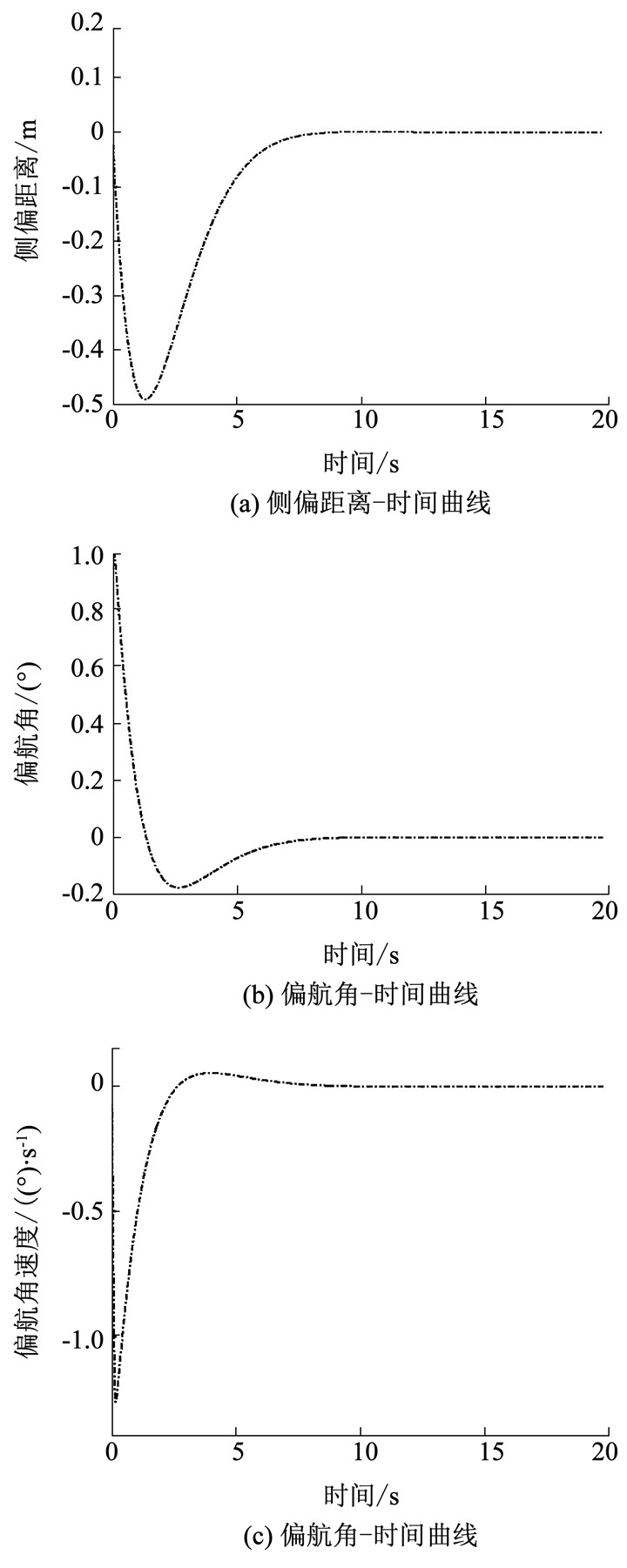
在1°初始偏航角(不考虑侧风影响)的情况下对飞机进行差动刹车纠偏, 从图 7(a)、图 7(b)、图 7(c)中可以看出, 侧偏距离、偏航角和偏航角速度大约需要10 s的时间归零, 从而完成纠偏.
|
图 7 1°偏航角情形下的相关时间曲线 Fig. 7 Correlation time curves of 1°yaw angle |
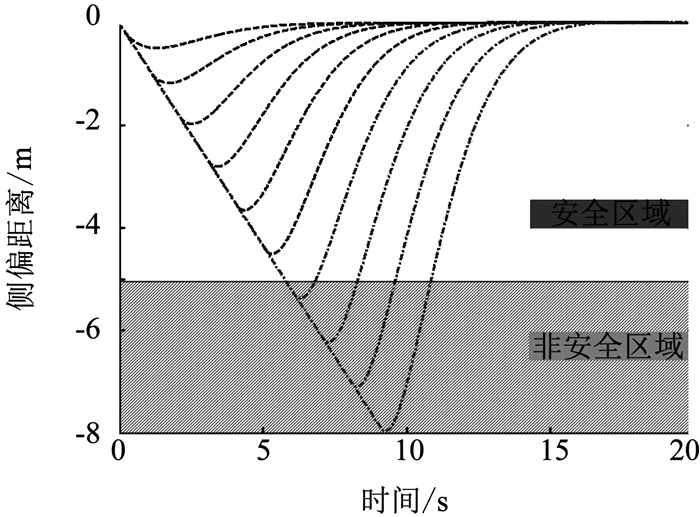
对飞机在地面滑跑x秒后, 提供差动刹车动作(UCA5)进行仿真分析.图 8表示在1°初始偏航角情况下, 差动刹车动作延迟0, 1, 2, …, 9 s时的侧偏距离-时间曲线, 阴影部分是非安全区域.由仿真结果可以看出, 当差动刹车动作延迟大于5 s时飞机会偏出跑道.因此, 该不安全控制行为的安全约束应设置为控制动作延迟不得大于5 s.
|
图 8 考虑延迟的侧偏距离-时间曲线 Fig. 8 Offset distance-time curves considering delay |
通过UCA1、UCA2和UCA5这3种不安全控制行为的仿真结果可以看出, 对在着陆滑跑阶段发生侧偏的飞机及时进行差动刹车纠偏是十分必要的, 尤其是要尽可能地降低差动刹车动作延迟时间, 以防止纠偏过程中飞机偏出跑道, 发生事故.
综述所述,从安全性的角度对滑跑纠偏过程做进一步分析.飞机在着陆滑跑阶段出现偏航时, 要确保飞行员、管制员和飞机差动刹车系统三者之间的及时沟通和协调, 并对外界复杂环境和突发情况做出有效判断, 同时正确认识和处理反馈信息, 按照空管法规以正确的操作规范完成差动刹车纠偏, 从而预防和减少事故的发生.
5 结论1) 从控制的角度进行了飞机全电差动刹车系统STAMP建模, 采用STPA方法对滑跑纠偏过程进行了安全性分析, 综合考虑了各部件或子系统之间的交互性、协调性以及人为差错等原因, 识别出更多潜在的不安全控制行为, 并从控制缺陷、反馈缺陷和协调缺陷3个方面了做出了详细的致因分析.
2) 针对部分不安全控制行为进行了仿真分析, 从定量角度验证了STAMP/STPA方法的有效性, 并制订了确保系统安全的定量化安全约束, 对航空装备安全性分析具有重要的参考价值.
| [1] |
NEUMANN P. Safeware: System safety and computers[J]. ACM SIGSOFT Software Engineering Notes, 1995, 20(5): 90. DOI:10.1145/217030.565656 |
| [2] |
郑磊, 胡剑波. 基于STAMP/STPA的机轮刹车系统安全性分析[J]. 航空学报, 2017, 38(1): 320144. ZHENG Lei, HU Jianbo. Safety analysis of wheel brake system based on STAMP/STPA[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(1): 320144. DOI:10.7527/S1000-6893.2016.0178 |
| [3] |
CHIOZZA M L, PONZETTI C. FMEA: A model for reducing medical errors[J]. Clinica Chimica Acta, 2009, 404(1): 75. DOI:10.1016/j.cca.2009.03.015 |
| [4] |
MAHAJAN H S, BRADLEY T, PASRICHA S. Application of systems theoretic process analysis to a lane keeping assist system[J]. Reliability Engineering & System Safety, 2017, 167: 177. DOI:10.1016/j.ress.2017.05.037 |
| [5] |
RASMUSSEN J. Risk management in a dynamic society: A modelling problem[J]. Safety Science, 1997, 27(2/3): 183. DOI:10.1016/S0925-7535(97)00052-0 |
| [6] |
ERIK H. The changing nature of risk[J]. Biological Bulletin, 2008, 19(3): 179. DOI:10.2307/1535963 |
| [7] |
PLACKE M S. Application of STPA to the integration of multiple control systems: A case study and new approach[D]. Cambridge, MA: Massachusetts Institute of Technology, 2014
|
| [8] |
ALLISON C K, REVELL K M, STANTON N, et al. Systems theoretic accident model and process (STAMP) safety modelling applied to an aircraft rapid decompression event[J]. Safety Science, 2017, 98: 159. DOI:10.1016/j.ssci.2017.06.011 |
| [9] |
ISHIMATSU T, LEVESON N G, THOMAS J P, et al. Hazard analysis of complex spacecraft using systems-theoretic process analysis[J]. Journal of Spacecraft & Rockets, 2014, 51(2): 509. DOI:10.2514/1.A32449 |
| [10] |
SCHMID D. Pilot homicide-suicide: A system-theoretic process analysis (STPA) of germanwings GWI18G[C]//International Conference on Applied Human Factors and Ergonomics. Cham: Springer, 2018: 53. DOI: 10.1007/978-3-319-93885-1_6
|
| [11] |
BAGSCHIK G, STOLTE T, MAURER M. Safety analysis based on systems theory applied to an unmanned protective vehicle[J]. Procedia Engineering, 2017, 179: 61. DOI:10.1016/j.proeng.2017.03.096 |
| [12] |
THORNBERRY C L. Extending the human controller methodology in systems-theoretic process analysis(STPA)[D]. Cambridge, MA: Massachusetts Institute of Technology, 2014
|
| [13] |
LEVESON N. A new accident model for engineering safer system[J]. Safety Science, 2004, 42(4): 237. DOI:10.1016/S0925-7535(03)00047-X |
| [14] |
DONG A R. Application of CAST and STPA to railroad safety in China[D]. Cambridge, MA: Massachusetts Institute of Technology, 2012
|
| [15] |
THOMAS J, SUO Dajiang. STPA-based method to identify and control feature interactions in large complex systems[J]. Procedia Engineering, 2015, 128: 12. DOI:10.1016/j.proeng.2015.11.499 |
| [16] |
廖俊侠.飞机全电刹车系统性能研究与仿真分析[D].南京: 南京航空航天大学, 2009 LIAO Junxia. Aircraft electric brake system performance analysis and simulation[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2009 |
| [17] |
STRINGFELLOW M V, LEVESON N. Accident analysis and hazard analysis for human and organizational factors[J]. Journal of Nuclear Medicine, 2010, 33(11): 72. DOI:10.1177/875647939200800608 |
| [18] |
冀美珊.飞机全电刹车系统的建模与滑跑纠偏控制研究[D].南京: 南京航空航天大学, 2012 JI Meishan. Research on modeling and taxiing rectification control of aircraft electric braking system[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012 |
 2020, Vol. 52
2020, Vol. 52


