2. 中国兵器工业集团203所, 西安 710065
2. No. 203 Research Institute of China Ordnance Industries, Xi'an 710065, China
在现代战争中,为了提高导弹的毁伤效果,往往希望导弹在命中目标时能够保持特定的攻击角度,例如:为了攻击坦克或军舰的薄弱部位,通常要求导弹以一定的落角命中目标;对于逆轨拦截高速运动目标,则要求弹道导弹能够对来袭弹头进行迎头拦截.因此,研究带有落角约束的末制导律具有重要的意义.
针对含有落角约束的拦截打击问题,相关学者在传统比例导引律的基础上提出了许多新的研究方法.文献[1]通过在传统比例导引律的视线角速度项上增加一个偏置量,以实现落角约束的要求.文献[2]则进一步利用能量最小准则优化了偏置参数,提高了制导律的控制效率,使得优化后的偏置比例导引律更适合于大气层外拦截.文献[3]针对静止目标,通过调整制导系数使得比例导引律满足期望的攻击角度,同时为了进一步提高大范围落角约束的适应性,引入了两阶段制导系数切换策略,取得了不错的制导效果.文献[4]则进一步将文献[3]中的方法扩展到了目标运动的情形.随着控制理论的发展,越来越多的学者基于现代控制理论提出了新型的末制导律.文献[5]改进并拓展了圆轨迹导引算法,提出了一种适应再入飞行器速度大小变化的带有落角约束的新型制导律.文献[6]利用模型预测静态规划技术,设计了弹道导弹再入末制导律,该制导律可以在满足落角约束的基础上对静止和机动目标进行打击,同时避免了运动模型的线性化,具有较高的制导精度.基于滑模控制理论和动态面控制方法,文献[7]围绕机动目标的打击问题,设计了一种考虑自动驾驶仪动态特性的带角度约束制导律.文献[8]采用扩张干扰观测器来估计导弹的速度及目标的机动信息,设计了带角度约束的有限时间收敛末制导律.
最优控制可以保证特定性能的最优性,同时还可以较为方便地处理各种约束条件,在制导律的设计中有着较大的优势,因此越来越多的学者将最优控制理论应用于带有落角约束的末制导律的设计中.文献[9]首先将末制导问题转化为线性二次型问题,然后应用次优理论设计了再入式飞行器带有落角约束的末制导律.通过求解能量最优控制问题,文献[10]同时研究了控制系统为一阶惯性环节和无惯性环节的落角约束最优制导律,为了提高制导精度,文献[10]还给出了3种剩余飞行时间的估算方法.基于最优控制理论,同时考虑目标机动的情形,文献[11]为反坦克导弹和反舰导弹设计了落角约束最优制导律.文献[12]考虑了导弹具有轴向加速度的情形,应用Schwarz不等式方法,设计了一种带有重力辅助的最优落角约束末制导律.
在基于最优控制的制导律设计中,控制能量被广泛用作性能函数,其中控制能量的加权函数对制导效果有着直接的影响,不同的加权函数会使导弹产生不同的飞行轨迹和制导指令分布.文献[13]以指数函数作为加权函数,设计了防空导弹的最优制导律.考虑了空气密度的变化,通过合理地设计指数函数,使得导弹在飞行高度增加的过程中,逐渐提高控制能量的权重,以此来限制制导指令,使导弹在接近目标的过程中,需用过载逐步趋向于零.文献[14-15]将剩余飞行时间n次方的倒数作为加权函数,设计了带有落角约束的最优末制导律,该制导律可使导弹过载在制导末端趋于小值,提高了导弹在制导末端的抗干扰能力.文献[16]则对制导初始指令的分布进行了着重考虑,设计了一种Gaussian加权函数,该加权函数可以使导弹过载在导引起始阶段保持较小的值,进而降低了导弹对初始状态误差的敏感度.文献[17]设计了一种基于正弦函数加权的落角约束最优制导律,通过调节正弦函数的周期和相位,该制导律可以实现导弹在制导始端和末端均产生较小的过载.文献[18]应用Schwarz不等式方法,研究了带有任意加权函数的最优制导律的一般表达式,但是为了能够得到解析解,该方法要求加权函数的逆的一次到三次积分都能求出解析表达式.上述研究主要是采用极小值原理和Schwarz不等式等方法来求解最优控制问题,这种方法精度较高,但对于复杂的问题,该方法推导过程较为繁琐.文献[19]利用黎卡提方程来求解最优制导律,但在一般情况下,求解黎卡提方程的解析解难度较大,为此,文献[20]使用黎卡提方程的稳态解来求解最优制导律,这种方法降低了求解难度,但只是一种近似的处理方法,有一定的局限性.针对上述问题,文献[21]采用滚动时域的方法,在每一个制导周期内,通过实时优化飞行弹道以获取最优制导律,避免了求解黎卡提方程,且对于复杂的问题具有较好的处理能力.但是该方法需要循环调用寻优算法来求解非线性规划问题,优化迭代的计算量较大,效率较低,实际应用中具有一定的局限性.
鉴于加权函数对制导性能有着很大的影响,若加权函数可以根据不同的需求灵活设计,则能在很大程度上提高制导效果.比如,不局限于现有文献,考虑其他更为复杂形式的加权函数,甚至在不同制导阶段采用不同形式的加权函数,构造分段形式的加权函数.基于此,本文研究一类基于双曲正切函数的加权函数,采用间接Gauss伪谱法,设计一种新型的落角约束最优制导律.该制导律在推导过程中不依赖于加权函数的具体形式,因此可以非常方便地处理复杂形式的加权函数(如分段形式),很大程度上提高了加权函数的设计自由度.
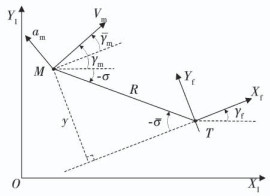
1 相对运动方程考虑图 1所示的二维平面内弹目相对运动几何关系图,图中:OXIYI为惯性坐标系,TXfYf为落角坐标系,该坐标系的原点取为目标点,并由惯性坐标系旋转期望的落角γf而来;M、T分别为导弹和目标;Vm、γm分别为导弹的运动速度和弹道倾角;am为垂直于导弹速度矢量的加速度;R、σ分别为弹目相对距离和视线角.γm、σ -分别为落角坐标系内导弹的弹道倾角和视线角,其中γm也表示落角误差.根据图中的几何关系,可知:
|
图 1 弹目相对运动几何 Fig. 1 Homing engagement between missile and target |
| $ \left\{ {\begin{array}{*{20}{l}} {{{\bar \gamma }_{\rm{m}}} = {\gamma _{\rm{m}}} - {\gamma _{\rm{f}}},}\\ {\bar \sigma = \sigma - {\gamma _{\rm{f}}}.} \end{array}} \right. $ | (1) |
根据图 1中所描述的运动关系,可以得到落角坐标系内的弹目相对运动方程为
| $ \left\{ {\begin{array}{*{20}{l}} {\dot y\left( t \right) = {V_{\rm{m}}}\left( t \right)\sin {{\bar \gamma }_{\rm{m}}}\left( t \right),}\\ {{{\dot {\bar \gamma} }_{\rm{m}}}\left( t \right) = {a_{\rm{m}}}\left( t \right)/{V_{\rm{m}}}\left( t \right),} \end{array}} \right. $ | (2) |
式中y为落角坐标系内导弹的法向脱靶量.假设导弹的运动速度Vm为常值,同时落角坐标系内的弹道倾角γm为小量,则式(2)可线性化为
| $ \left\{ {\begin{array}{*{20}{l}} {\dot y\left( t \right) = {V_{\rm{m}}}{{\bar \gamma }_{\rm{m}}}\left( t \right),}\\ {{{\dot {\bar \gamma} }_{\rm{m}}}\left( t \right) = {a_{\rm{m}}}\left( t \right)/{V_{\rm{m}}}.} \end{array}} \right. $ | (3) |
根据式(3),可得矩阵形式的弹目相对运动方程为
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{x}}(t) = \mathit{\boldsymbol{Fx}}(t) + \mathit{\boldsymbol{G}}u(t),}\\ {\mathit{\boldsymbol{x}}(0) = {\mathit{\boldsymbol{x}}_0},} \end{array}} \right. $ | (4) |
其中:
| $ \mathit{\boldsymbol{x}} \buildrel \Delta \over = {\left[ {\begin{array}{*{20}{l}} y&{{{\bar \gamma }_{\rm{m}}}} \end{array}} \right]^{\rm{T}}},u \buildrel \Delta \over = {a_{\rm{m}}},\mathit{\boldsymbol{F}} \buildrel \Delta \over = \left[ {\begin{array}{*{20}{l}} 0&{{V_{\rm{m}}}}\\ 0&0 \end{array}} \right],\mathit{\boldsymbol{G}} \buildrel \Delta \over = \left[ {\begin{array}{*{20}{c}} 0\\ {1/{V_{\rm{m}}}} \end{array}} \right]. $ |
注意到,式(4)所描述的线性化的相对运动方程在最优制导律的相关研究中得到了广泛的应用[10, 14, 16-17].根据图 1的几何关系,可以看出,若要满足终端的零脱靶量以及落角约束的要求,则需要满足y(tf)=0以及γm(tf)=0,其中tf为终端时刻.为了满足上述条件,构造如下形式的有限时间最优控制问题:在[t0, tf]时间内,寻求控制量u(t),使得导弹在满足动力学约束(4)的条件下,使如下的性能指标最小.
| $ J = \frac{1}{2}{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {{t_{\rm{f}}}} \right){\mathit{\boldsymbol{S}}_{\rm{f}}}\mathit{\boldsymbol{x}}\left( {{t_{\rm{f}}}} \right) + \frac{1}{2}\int_{{t_0}}^{{t_{\rm{f}}}} {\frac{{{u^2}(\tau )}}{{{T_{\rm{h}}}(\tau )}}{\rm{d}}\tau } . $ | (5) |
式中:t0为初始时刻;Sf为正定的对角矩阵,用于控制终端状态量;Th(t)为控制能量的加权函数,该函数可以有效地改变导弹的运动轨迹及制导指令的分布.本文基于双曲正切函数设计不同的加权函数,以实现不同的制导效果.下面给出了3种形式的加权函数,其中w, t1, ts和τσ分别为设计参数.
| $ {T_{{\rm{h}}1}}(t) = \frac{1}{2}\left[ {\frac{{{{\rm{e}}^{4.6\left( {t - {t_1}} \right)/w}} - 1}}{{{{\rm{e}}^{4.6\left( {t - {t_1}} \right)/w}} + 1}}} \right] + \frac{1}{2}, $ | (6) |
| $ {T_{{\rm{h}}2}}(t) = - \frac{1}{2}\left[ {\frac{{{{\rm{e}}^{4.6\left( {t - {t_1}} \right)/w}} - 1}}{{{{\rm{e}}^{4.6\left( {t - {t_1}} \right)/w}} + 1}}} \right] + \frac{1}{2}, $ | (7) |
| $ {T_{{\rm{h}}3}}(t) = \left\{ {\begin{array}{*{20}{l}} {\frac{1}{2}\left[ {\frac{{{{\rm{e}}^{4.6\left( {t - {t_1}} \right)/w}} - 1}}{{{{\rm{e}}^{4.6\left( {t - {t_1}} \right)/w}} + 1}}} \right] + \frac{1}{2},{t_0} \le t \le {t_{\rm{s}}};}\\ {{{\rm{e}}^{ - \frac{{{{\left( {t - {t_0}} \right)}^2}}}{{2\tau _\sigma ^2}}}},{t_{\rm{s}}} < t \le {t_{\rm{f}}}.} \end{array}} \right. $ | (8) |
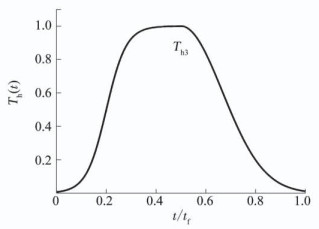
图 2、3分别给出了加权函数的变化曲线,其中函数Th1(t)和Th2(t)对应的设计参数的取值为w=tf/3, t1=tf/2;函数Th3(t)对应的设计参数的取值为w=tf/6, t1=tf/2, ts=tf/2, τσ=tf/6.从图 2中可以看出,函数Th1在制导初始段取值很小,但随着时间的增加,其值不断增大.由于式(5)中加权函数处于分母的位置,故而Th1对初始控制能量的权重最大.这种形式的加权函数将产生很小的初始过载指令,可降低末制导开始时的过载指令突变,有助于中末制导的平稳交接.Th2的变化规律与Th1正相反,即对终端控制能量的权重最大.这种形式的加权函数将产生很小的末端过载,可提供更多的过载裕量以抵抗导引末段可能存在的各种外界干扰.而Th3则兼有Th1和Th2的优点,将在导引始端和末端均产生很小的过载.此外注意到,式(8)中所示的加权函数Th3为分段函数,其综合了双曲正切函数以及文献[16]中所提出的Gaussian加权函数.这种复杂形式的加权函数在现有文献中罕有研究,也给问题的求解带来了较大的难度.为此,本文推导了一种新型的制导律,可以非常容易地处理上述复杂的加权函数.

|
图 2 加权函数Th1和Th2变化曲线 Fig. 2 Curves of weighting functions Th1 and Th2 |
|
图 3 加权函数Th3变化曲线 Fig. 3 Curve of weighting function Th3 |
由最优控制理论,可构造如下的Hamiltonian函数:
| $ H = \frac{1}{2}\frac{{{u^2}(t)}}{{{T_{\rm{h}}}(t)}} + \mathit{\boldsymbol{\lambda }}{(t)^{\rm{T}}}\left[ {\mathit{\boldsymbol{Fx}}(t) + \mathit{\boldsymbol{G}}u(t)} \right], $ |
其中λ(t)为协态变量,并满足如下的协态方程:
| $ \mathit{\boldsymbol{\dot \lambda }}(t) = - \frac{{\partial H}}{{\partial \mathit{\boldsymbol{x}}(t)}} = - {\mathit{\boldsymbol{F}}^{\rm{T}}}\mathit{\boldsymbol{\lambda }}(t), $ | (9) |
其横截条件为
| $ \mathit{\boldsymbol{\lambda }}({t_{\rm{f}}}) = {\mathit{\boldsymbol{S}}_{\rm{f}}}\mathit{\boldsymbol{x}}({t_{\rm{f}}}), $ | (10) |
根据极小值原理,有
| $ \frac{{\partial H}}{{\partial u(t)}} = 0, $ |
从而得到最优控制量为
| $ {u^*}(t) = - \frac{1}{{{T_{\rm{h}}}{{(t)}^{ - 1}}}}{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{\lambda }}(t). $ | (11) |
将式(11)代入式(4),并根据式(9),可得如下的两点边值问题:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot x}}(t) = \frac{{\partial H}}{{\partial \mathit{\boldsymbol{\lambda }}(t)}} = \mathit{\boldsymbol{Fx}}(t) - \mathit{\boldsymbol{G}}\frac{1}{{{T_{\rm{h}}}{{(t)}^{ - 1}}}}{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{\lambda }}(t),}\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{x}}\left( {{t_0}} \right) = {\mathit{\boldsymbol{x}}_0};}\\ {\mathit{\boldsymbol{\dot \lambda }}(t) = - \frac{{\partial H}}{{\partial \mathit{\boldsymbol{x}}(t)}} = - {\mathit{\boldsymbol{F}}^{\rm{T}}}\mathit{\boldsymbol{\lambda }}(t),\mathit{\boldsymbol{\lambda }}\left( {{t_{\rm{f}}}} \right) = {\mathit{\boldsymbol{S}}_{\rm{f}}}\mathit{\boldsymbol{x}}\left( {{t_{\rm{f}}}} \right).} \end{array}} \right. $ | (12) |
针对式(12)所示的带有复杂形式加权函数Th(t)的两点边值问题,较难获得解析解,这种情况下,可通过积分黎卡提微分方程来求得最优控制量,但这种方式需要大量的计算,且对于稍微复杂的系统,整个积分也变得更为困难,实际应用中限制较多.为此,本文采用间接Gauss伪谱法来求解.引入变量τ对时间t进行如下变换:
| $ \tau = \frac{2}{{{t_{\rm{f}}} - {t_0}}}t - \frac{{{t_{\rm{f}}} + {t_0}}}{{{t_{\rm{f}}} - {t_0}}}, $ |
从而将区间[t0, tf]转换为[-1, 1],故而式(12)变为
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot x}}(\tau ) = \frac{{{t_{\rm{f}}} - {t_{\rm{0}}}}}{2}\left[ {\mathit{\boldsymbol{Fx}}(t) - \mathit{\boldsymbol{G}}\frac{1}{{{T_{\rm{h}}}{{(t)}^{ - 1}}}}{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{\lambda }}(\tau )} \right],}\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{x}}\left( { - 1} \right) = {\mathit{\boldsymbol{x}}_0},}\\ {\mathit{\boldsymbol{\dot \lambda }}(t) = - \frac{{{t_{\rm{f}}} - {t_{\rm{0}}}}}{2}{\mathit{\boldsymbol{F}}^{\rm{T}}}\mathit{\boldsymbol{\lambda }}\left( \tau \right),\mathit{\boldsymbol{\lambda }}\left( 1 \right) = {\mathit{\boldsymbol{S}}_{\rm{f}}}\mathit{\boldsymbol{x}}\left( 1 \right).} \end{array}} \right. $ | (13) |
间接Gauss伪谱法的主要思想是通过构造全局插值多项式来近似x(τ)和λ(τ),进而将两点边值问题(13)转换为代数方程,求解这些代数方程即可得到最优控制量.为此,构造如下的插值多项式来近似状态量x(τ)为
| $ \mathit{\boldsymbol{x}}\left( \tau \right) \approx \mathit{\boldsymbol{X}}\left( \tau \right) = \mathit{\boldsymbol{x}}\left( { - 1} \right){L_0}\left( \tau \right) + \sum\limits_{k = 1}^N \mathit{\boldsymbol{x}} \left( {{\tau _k}} \right){\mathit{\boldsymbol{L}}_k}\left( \tau \right), $ | (14) |
其中, Lk(τ)=
| $ \mathit{\boldsymbol{\dot x}}\left( \tau \right) \approx \mathit{\boldsymbol{\dot X}}\left( \tau \right) = \mathit{\boldsymbol{x}}\left( { - 1} \right){{\dot L}_0}\left( \tau \right) + \sum\limits_{k = 1}^N \mathit{\boldsymbol{x}} \left( {{\tau _k}} \right){{\dot L}_k}\left( \tau \right), $ | (15) |
构造如下的插值多项式来近似协态量λ(τ)为
| $ \mathit{\boldsymbol{\lambda }}\left( \tau \right) \approx \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}\left( \tau \right) = \sum\limits_{k = 1}^N \mathit{\boldsymbol{\lambda }} \left( {{\tau _k}} \right)L_k^ * \left( \tau \right) + \mathit{\boldsymbol{\lambda }}(1)L_{N + 1}^*(\tau ), $ | (16) |
其中, Lk*(τ)=
| $ \mathit{\boldsymbol{\dot \lambda }}\left( \tau \right) \approx \mathit{\boldsymbol{ \boldsymbol{\dot \varLambda} }}\left( \tau \right) = \sum\limits_{k = 1}^N \mathit{\boldsymbol{\lambda }} \left( {{\tau _k}} \right)\dot L_k^ * \left( \tau \right) + \mathit{\boldsymbol{\lambda }}(1)\dot L_{N + 1}^*(\tau ). $ | (17) |
根据Gauss求积公式[22],状态量x(τ)的末端值x(1)可通过下式计算:
| $ \begin{array}{l} \mathit{\boldsymbol{x}}\left( 1 \right) = \mathit{\boldsymbol{x}}\left( { - 1} \right) + \frac{{{t_{\rm{f}}} - {t_0}}}{2}\sum\limits_{k = 1}^N {{w_k}} \left[ {\mathit{\boldsymbol{F}}x\left( {{\tau _k}} \right) - } \right.\\ \;\;\;\;\;\;\;\;\;\left. {\mathit{\boldsymbol{G}}\frac{1}{{{T_{\rm{h}}}{{(\tau )}^{ - 1}}}}{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{\lambda }}\left( {{\tau _k}} \right)} \right], \end{array} $ | (18) |
式中wk为Gauss求积系数.结合式(10)和式(18),则协态量的末端值λ(1)可进一步表示为
| $ \begin{array}{l} \mathit{\boldsymbol{\lambda }}(1) = {\mathit{\boldsymbol{S}}_{\rm{f}}}\mathit{\boldsymbol{x}}( - 1) + {\mathit{\boldsymbol{S}}_{\rm{f}}}\frac{{{t_{\rm{f}}} - {t_0}}}{2} \cdot \\ \;\;\;\;\;\;\;\;\;\sum\limits_{k = 1}^N {{w_k}} \left[ {\mathit{\boldsymbol{F}}x\left( {{\tau _k}} \right) - \mathit{\boldsymbol{G}}\frac{1}{{{T_{\rm{h}}}{{(\tau )}^{ - 1}}}}{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{\lambda }}\left( {{\tau _k}} \right)} \right]. \end{array} $ | (19) |
定义Di=
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\bar D}}_i^*{\mathit{\boldsymbol{S}}_{\rm{f}}}{\mathit{\boldsymbol{x}}_0} + \mathit{\boldsymbol{\bar D}}_i^*{\mathit{\boldsymbol{S}}_{\rm{f}}}\frac{{{t_{\rm{f}}} - {t_{\rm{0}}}}}{2}\sum\limits_{k = 1}^N {{w_k}} \left[ {\mathit{\boldsymbol{F}}{x_k} - \mathit{\boldsymbol{G}}\frac{1}{{{T_{{\rm{hk}}}}^{ - 1}}}{\mathit{\boldsymbol{G}}^{\rm{T}}}{\mathit{\boldsymbol{\lambda }}_k}} \right] + \\ \sum\limits_{k = 1}^N {{\mathit{\boldsymbol{\lambda }}_k}} \mathit{\boldsymbol{D}}_{ik}^* = - \frac{{{t_{\rm{f}}} - {t_0}}}{2}{\mathit{\boldsymbol{F}}^{\rm{T}}}{\mathit{\boldsymbol{\lambda }}_i},\\ {\mathit{\boldsymbol{x}}_0}{{\mathit{\boldsymbol{\bar D}}}_i} + \sum\limits_{k = 1}^N {{\mathit{\boldsymbol{x}}_k}{\mathit{\boldsymbol{D}}_{ik}}} = \frac{{{t_{\rm{f}}} - {t_0}}}{2}\left[ {\mathit{\boldsymbol{F}}{\mathit{\boldsymbol{x}}_i} - \mathit{\boldsymbol{G}}\frac{1}{{{T_{{\rm{h}}i}}^{ - 1}}}{\mathit{\boldsymbol{G}}^{\rm{T}}}{\mathit{\boldsymbol{\lambda }}_i}} \right]. \end{array} \right. $ | (20) |
式中:i=1, …, N, k=1, …, N,
| $ {{\mathit{\boldsymbol{\bar D}}}_i} = - \sum\limits_{k = 1}^N {{\mathit{\boldsymbol{D}}_{ik}}} ,\mathit{\boldsymbol{D}}_{ik}^* = - \frac{{{w_k}}}{{{w_i}}}{\mathit{\boldsymbol{D}}_{ki}},\mathit{\boldsymbol{\bar D}}_i^* = - \sum\limits_{k = 1}^N {\mathit{\boldsymbol{D}}_{ik}^*} . $ | (21) |
由于矩阵中D的元素可以通过下式离线计算:
| $ {\mathit{\boldsymbol{D}}_{ik}} = {{\dot L}_i}\left( {{\tau _k}} \right) = \sum\limits_{l = 0}^N {\frac{{\prod\limits_{j = 0,j \ne i,l}^N {\left( {{\tau _k} - {\tau _j}} \right)} }}{{\prod\limits_{j = 0,j \ne i}^N {\left( {{\tau _i} - {\tau _j}} \right)} }}} , $ |
因此,结合式(21),矩阵D, D*及D*中的元素均可离线获得.
记
| $ \left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\tilde {\bar D}}}}^ * }{\mathit{\boldsymbol{x}}_0} + \mathit{\boldsymbol{\tilde D}}_ + ^*\mathit{\boldsymbol{ \boldsymbol{\tilde \varLambda} }} + \mathit{\boldsymbol{\tilde A\tilde X}} = {\bf{0}},}\\ {\mathit{\boldsymbol{\tilde {\bar D}}}{\mathit{\boldsymbol{x}}_0} + {{\mathit{\boldsymbol{\tilde D}}}_ - }\mathit{\boldsymbol{\tilde X}} + \mathit{\boldsymbol{\tilde B \boldsymbol{\tilde \varLambda} }} = {\bf{0}},} \end{array}} \right. $ | (22) |
其中:
| $ {{\mathit{\boldsymbol{\tilde {\bar D}}}}^*} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\bar D}}_1^*{\mathit{\boldsymbol{S}}_{\text{f}}}} \\ \vdots \\ {\bar D_N^*{\mathit{\boldsymbol{S}}_{\text{f}}}} \end{array}} \right] \in {\mathbb{R}^{nN \times n}},\mathit{\boldsymbol{\tilde {\bar D}}} = \left[ {\begin{array}{*{20}{c}} {{{\bar D}_1}{\mathit{\boldsymbol{I}}_n}} \\ \vdots \\ {{{\mathit{\boldsymbol{\bar D}}}_N}{\mathit{\boldsymbol{I}}_n}} \end{array}} \right] \in {\mathbb{R}^{nN \times N}}, $ |
| $ \mathit{\boldsymbol{\tilde D}}_ + ^ * = \left[ {\begin{array}{*{20}{c}} {D_{11}^*{\mathit{\boldsymbol{I}}_n}}&{D_{12}^*{\mathit{\boldsymbol{I}}_n}}& \cdots &{D_{1N}^*{\mathit{\boldsymbol{I}}_n}} \\ {D_{21}^*{\mathit{\boldsymbol{I}}_n}}&{D_{22}^*{\mathit{\boldsymbol{I}}_n}}& \cdots &{D_{2N}^*{\mathit{\boldsymbol{I}}_n}} \\ \vdots & \vdots & \ddots & \vdots \\ {D_{N1}^*{\mathit{\boldsymbol{I}}_n}}&{D_{N2}^*{\mathit{\boldsymbol{I}}_n}}& \cdots &{D_{NN}^*{\mathit{\boldsymbol{I}}_n}} \end{array}} \right] - \frac{{{t_{\text{f}}} - {t_0}}}{2}\left[ {\begin{array}{*{20}{c}} {\bar D_1^*{\mathit{\boldsymbol{S}}_{\text{f}}}{w_1}\mathit{\boldsymbol{G}}\frac{1}{{T_{{\text{h}}1}^{ - 1}}}{\mathit{\boldsymbol{G}}^{\text{T}}} - {\mathit{\boldsymbol{F}}^{\text{T}}}}&{\bar D_1^*{\mathit{\boldsymbol{S}}_{\text{f}}}{w_2}\mathit{\boldsymbol{G}}\frac{1}{{T_{{\text{h}}2}^{ - 1}}}{\mathit{\boldsymbol{G}}^{\text{T}}}}& \cdots &{\bar D_1^*{\mathit{\boldsymbol{S}}_{\text{f}}}{w_N}\mathit{\boldsymbol{G}}\frac{1}{{T_{{\text{h}}N}^{ - 1}}}{\mathit{\boldsymbol{G}}^{\text{T}}}} \\ {\bar D_2^*{\mathit{\boldsymbol{S}}_{\text{f}}}{w_1}\mathit{\boldsymbol{G}}\frac{1}{{T_{{\text{h}}1}^{ - 1}}}{\mathit{\boldsymbol{G}}^{\text{T}}}}&{\bar D_2^*{\mathit{\boldsymbol{S}}_{\text{f}}}{w_2}\mathit{\boldsymbol{G}}\frac{1}{{T_{{\text{h2}}}^{ - 1}}}{\mathit{\boldsymbol{G}}^{\text{T}}} - {\mathit{\boldsymbol{F}}^{\text{T}}}}& \cdots &{\bar D_2^*{\mathit{\boldsymbol{S}}_{\text{f}}}{w_N}\mathit{\boldsymbol{G}}\frac{1}{{T_{{\text{h}}N}^{ - 1}}}{\mathit{\boldsymbol{G}}^{\text{T}}}} \\ \vdots & \vdots & \ddots & \vdots \\ {\bar D_N^*{\mathit{\boldsymbol{S}}_{\text{f}}}{w_1}\mathit{\boldsymbol{G}}\frac{1}{{T_{{\text{h1}}}^{ - 1}}}{\mathit{\boldsymbol{G}}^{\text{T}}}}&{\bar D_N^*{\mathit{\boldsymbol{S}}_{\text{f}}}{w_2}\mathit{\boldsymbol{G}}\frac{1}{{T_{{\text{h2}}}^{ - 1}}}{\mathit{\boldsymbol{G}}^{\text{T}}}}& \cdots &{\bar D_N^*{\mathit{\boldsymbol{S}}_{\text{f}}}{w_N}\mathit{\boldsymbol{G}}\frac{1}{{T_{{\text{h}}N}^{ - 1}}}{\mathit{\boldsymbol{G}}^{\text{T}}} - {\mathit{\boldsymbol{F}}^T}} \end{array}} \right] \in {\mathbb{R}^{nN \times nN}}, $ |
| $ {{\mathit{\boldsymbol{\bar D}}}_ - } = \left[ {\begin{array}{*{20}{c}} {{D_{11}}{\mathit{\boldsymbol{I}}_n}}&{{D_{12}}{\mathit{\boldsymbol{I}}_n}}& \cdots &{{D_{1N}}{\mathit{\boldsymbol{I}}_n}} \\ {{D_{21}}{\mathit{\boldsymbol{I}}_n}}&{{D_{22}}{\mathit{\boldsymbol{I}}_n}}& \cdots &{{D_{2N}}{\mathit{\boldsymbol{I}}_n}} \\ \vdots & \vdots & \ddots & \vdots \\ {{D_{N1}}{\mathit{\boldsymbol{I}}_n}}&{{D_{N2}}{\mathit{\boldsymbol{I}}_n}}& \cdots &{{D_{NN}}{\mathit{\boldsymbol{I}}_n}} \end{array}} \right] - \frac{{{t_{\text{f}}} - {t_0}}}{2}\left[ {\begin{array}{*{20}{c}} { - \mathit{\boldsymbol{F}}}&{{{\bf{0}}_n}}& \cdots &{{{\bf{0}}_n}} \\ {{{\bf{0}}_n}}&\mathit{\boldsymbol{F}}& \cdots &{{{\bf{0}}_n}} \\ \vdots & \vdots & \ddots & \vdots \\ {{0_n}}&{{0_n}}& \cdots &\mathit{\boldsymbol{F}} \end{array}} \right] \in {\mathbb{R}^{nN \times nN}}, $ |
| $ \mathit{\boldsymbol{\tilde A}} = \frac{{{t_{\text{f}}} - {t_0}}}{2}\left[ {\begin{array}{*{20}{c}} {\bar D_1^*{\mathit{\boldsymbol{S}}_{\text{f}}}{w_1}\mathit{\boldsymbol{F}}}&{\bar D_1^*{\mathit{\boldsymbol{S}}_{\text{f}}}{w_2}\mathit{\boldsymbol{F}}}& \cdots &{\bar D_1^*{\mathit{\boldsymbol{S}}_{\text{f}}}{w_N}\mathit{\boldsymbol{F}}} \\ {\bar D_2^*{\mathit{\boldsymbol{S}}_{\text{f}}}{w_1}\mathit{\boldsymbol{F}}}&{\bar D_2^*{\mathit{\boldsymbol{S}}_{\text{f}}}{w_2}\mathit{\boldsymbol{F}}}& \cdots &{\bar D_2^*{\mathit{\boldsymbol{S}}_{\text{f}}}{w_N}\mathit{\boldsymbol{F}}} \\ \vdots & \vdots & \ddots & \vdots \\ {\bar D_N^*{\mathit{\boldsymbol{S}}_{\text{f}}}{w_1}\mathit{\boldsymbol{F}}}&{\bar D_N^*{\mathit{\boldsymbol{S}}_{\text{f}}}{w_2}\mathit{\boldsymbol{F}}}& \cdots &{\bar D_N^*{\mathit{\boldsymbol{S}}_{\text{f}}}{w_N}\mathit{\boldsymbol{F}}} \end{array}} \right] \in {\mathbb{R}^{nN \times nN}},\mathit{\boldsymbol{\tilde B}} = \frac{{{t_{\text{f}}} - {t_0}}}{2}\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{G}}\frac{1}{{T_{{\text{h}}1}^{ - 1}}}{\mathit{\boldsymbol{G}}^{\text{T}}}}&{{{\bf{0}}_n}}& \cdots &{{{\bf{0}}_n}} \\ {{{\bf{0}}_n}}&{\mathit{\boldsymbol{G}}\frac{1}{{T_{{\text{h2}}}^{ - 1}}}{\mathit{\boldsymbol{G}}^{\text{T}}}}& \cdots &{{{\bf{0}}_n}} \\ \vdots & \vdots & \ddots & \vdots \\ {{{\bf{0}}_n}}&{{{\bf{0}}_n}}& \cdots &{\mathit{\boldsymbol{G}}\frac{1}{{T_{{\text{h}}N}^{ - 1}}}{\mathit{\boldsymbol{G}}^{\text{T}}}} \end{array}} \right] \in {\mathbb{R}^{nN \times nN}}. $ |
记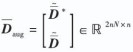
| $ {{\mathit{\boldsymbol{\bar D}}}_{{\rm{aug}}}}{\mathit{\boldsymbol{x}}_0} + {\mathit{\boldsymbol{D}}_{{\rm{aug}}}}\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{ \boldsymbol{\tilde \varLambda} }}}\\ {\mathit{\boldsymbol{\tilde X}}} \end{array}} \right] = {\bf{0}}, $ | (23) |
求解式(23)可得:
| $ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{ \boldsymbol{\tilde \varLambda} }}}\\ {\mathit{\boldsymbol{\tilde X}}} \end{array}} \right] = - \mathit{\boldsymbol{D}}_{{\rm{aug}}}^{ - 1}{{\mathit{\boldsymbol{\bar D}}}_{{\rm{aug}}}}{\mathit{\boldsymbol{x}}_0}. $ | (24) |
给定初始状态x0,通过上式可以得到N个Gauss节点上的状态量xi及协态量λi,i=1, …, N.由于Gauss节点并不包含边界点,因此式(24)无法提供协态量的初值λ(-1).考虑到协态量的末端值λ(1)是已知的,因此λ(-1)可通过如下的Gauss求积公式计算得到:
| $ \mathit{\boldsymbol{\lambda }}( - 1) = \mathit{\boldsymbol{\lambda }}(1) - \frac{{{t_{\rm{f}}} - {t_0}}}{2}\sum\limits_{k = 1}^N {{w_k}} {\mathit{\boldsymbol{F}}^{\rm{T}}}{\mathit{\boldsymbol{\lambda }}_k}. $ |
至此,τ0=-1, τ1, …, τN+1节点上的协态量均已求出,根据式(11)便可得到每个离散节点上的最优控制量为
| $ u_i^* = - \frac{1}{{T_{{\rm{h}}i}^{ - 1}}}{\mathit{\boldsymbol{G}}^{\rm{T}}}{\mathit{\boldsymbol{\lambda }}_i}.(i = 0, \cdots ,N + 1) $ | (25) |
上述推导过程并未对加权函数有所限制,也不依赖加权函数的具体形式,因此,所提方法可以非常方便地处理各种复杂加权函数.此外,该方法不需要任何的积分或迭代运算,只根据初始状态量x0即可通过式(25)方便地求出[t0, tf]区域内各节点上的最优控制量,相比于传统反向积分黎卡提微分方程的方法,计算量小,易于工程在线计算.由于式(25)得到的是开环最优解,无法抑制外界扰动的影响.为此,采用滚动时域方法,具体步骤如下.
步骤1 初始化离散节点的数量N,初始化当前时刻为初始时刻t0,给定期望落角γf.
步骤2 根据目标点的位置坐标及导弹的当前位置坐标计算弹目距离R,采用公式tgo=R/Vm计算得到剩余飞行时间tgo,进而得到tf=t0+tgo.
步骤3 计算矩阵Daug和Daug,同时结合式(1),根据期望落角γf以及导弹位置坐标和弹道倾角等信息,计算落角坐标系内的导弹状态量x0.
步骤4 根据式(25)计算[t0, tf]区域内各节点上的最优控制量ui(i=0, …, N+1),只取t0时刻对应的控制量u0,并将其应用于导弹动力学模型中,计算得到下一时刻t′以及状态量.
步骤5 判断是否命中目标.如果没有命中目标,则将当前时刻t′作为初始时刻,即t′=t0,将当前状态量作为初始状态量,重复步骤2~4,直至命中目标.
3 仿真结果分析本文通过数字仿真在不同条件下展示所提制导律的性能.在仿真中,导弹的初始位置取为(0 m, 0 m),目标的位置取为(5 000 m, 0 m),导弹速度Vm=200 m/s,导弹的初始弹道倾角γm(0)=45°;Gauss节点数N=10,Sf=diag([1×105, 1×105]).为了对比说明所提制导律的效果,在同等条件下,对文献[10]中提出的最优制导律(optimal guidance law, OGL)和文献[24]中提出的偏置比例导引律(biased proportional navigation guidance, BPNG)也进行了仿真计算.
图 4给出了在期望落角γf=-45°条件下,不同加权函数对应的弹道曲线和制导指令变化曲线.从图 4中可以看出在不同的加权函数作用下,导弹均能满足给定的落角约束,以期望的落角去攻击目标.但是,不同的加权函数明显地改变了导弹的运动轨迹以及制导指令的分布.Th1(t)在导引初始段产生了很小的制导指令,这主要是因为Th1(t)对初始控制能量的加权最大所致;这种类型的制导指令可有效降低制导律对初始状态误差的敏感度.由于Th2(t)的变化规律与Th1(t)相反,对末端控制能量的加权最大,因此随着导弹趋近于目标,其对应的制导指令也趋向于零,这有助于提高制导律在导引末端的抗干扰能力,即可提供更多的过载裕量来抵抗外界干扰.而Th3(t)则在导引始端和末端均提供了很小的制导指令,因此该加权函数不仅能降低制导律对初始状态误差的敏感度,而且还可以提高导弹的末端抗干扰能力.由于本文算法并不依赖于加权函数的具体形式,因此在实际工程应用中,可进一步灵活设计加权函数的变化规律,以实现不同的制导要求.此外,从图 4中还可以看出,传统的OGL虽然能够以能量最优的方式导引导弹以期望的落角命中目标,但是其初始及末端导引指令较大. BPNG虽然也能够保证导弹在满足落角约束的条件下命中目标,但其在弹道末段产生了很大的过载.因此,若要满足不同的制导需求,上述两种方法有一定的局限性.

|
图 4 不同加权函数条件下的制导效果 Fig. 4 Guidance performance for different weighting functions |
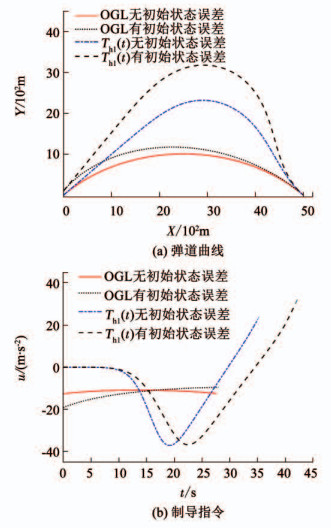
为了进一步考察初始初始状态误差对制导指令的影响,图 5给出了γm(0)存在10°误差以及ym(0)存在100 m误差下,OGL和Th1(t)的对比仿真结果.从图 5中可以看出,当存在较大的初始状态误差时,传统的OGL产生的制导指令在初始阶段变化较大,而本文的制导律则可使得制导指令在初始阶段始终保持很小的值,这样的特点在中末制导的平滑交接中具有一定的优势.
|
图 5 考虑初始状态误差的制导效果 Fig. 5 Guidance performance considering initial state errors |
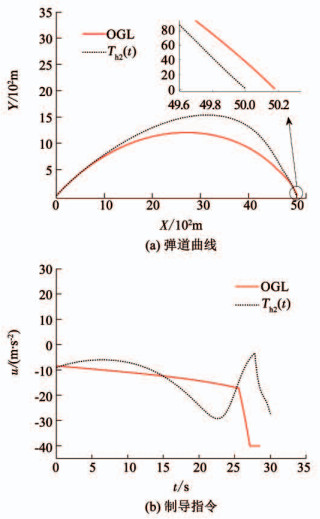
为了进一步展示制导律在导引末端的抗干扰能力,图 6给出了末端存在阵风的情况下,OGL和Th2(t)的对比仿真结果.其中当弹目距离小于500 m时,沿ox轴正向对导弹施加25 m/s的阵风.从图 6中可以看出,两种制导律在弹道末端均产生了额外的制导指令以抵抗阵风的干扰.由于OGL在弹道末端的需用过载较大,在附加额外的过载指令后产生了饱和现象,进而导致了接近20 m的脱靶量.而本文的制导律在弹道末端的需用过载很小,在附加额外的过载指令后仍有一定的裕量,从而很好地保证了最终的命中精度.
|
图 6 考虑末端风干扰的制导效果 Fig. 6 Guidance performance considering terminal wind disturbance |
图 7给出了期望落角分别为-10°, -30°, -60°和-90°的条件下,加权函数Th3(t)对应的弹道曲线和制导指令变化曲线.在这4种场景下,最终落角分别为-10.026°, -30.023°, -59.988°和-90.011°,可以很好地满足相应的落角约束.从图 7(a)可以看出,导弹在不同场景下也均能准确命中目标.从图 7(b)可以看出,在不同的落角约束情况下,加权函数Th3(t)均能保证在导引始端和末端产生很小的制导指令.上述结果表明,虽然本文制导律是基于线性化模型推导而来的,但其对较大范围内的落角约束具有较好的适应性.

|
图 7 不同落角约束下Th3(t)加权函数的制导效果 Fig. 7 Guidance performance for Th3(t) with different impact angle constraints |
为了进一步验证加权函数对制导效果的影响,以加权函数Th3(t)为例,选取不同的设计参数进行仿真分析.具体参数见表 1,每个算例对应的加权函数Th3(t)的外形曲线如图 8所示,仿真结果如图 9所示.
| 表 1 加权函数Th3(t)的参数取值 Tab. 1 Values for design parameters of Th3(t) |

|
图 8 不同参数条件下的加权函数Th3(t)曲线 Fig. 8 Curves of Th3(t) with different parameters |

|
图 9 Th3(t)在不同参数条件下的制导效果 Fig. 9 Guidance performance for Th3(t) with different parameters |
从图 8中可以看出,通过调整设计参数w, t1, ts和τσ的值,可以灵活地改变Th3(t)的外形,进而控制不同区域内控制能量的权重系数.从算例1到算例3,加权函数对导引始段和末段的控制能量的约束逐渐宽松,即要求较小的控制量在始末段内持续的时间逐渐变小.
从图 9可以看出,在3种算例下,导弹均能以期望的落角命中目标,但其运动轨迹和制导指令的分布却有所不同.在算例1中,导引始末段内制导指令在较长时间内保持了较小的值,导引中段内指令的值则相对较大.而在算例3中,制导指令在导引开始时增长较快,这样可使导弹更快地向目标收敛,这和图 9(a)中的弹道曲线的规律是一致的,在导引中段所需的制导指令则较小.从以上结果可以看出,通过不断收紧导引始末段内Th3(t)的取值,有助于降低导弹对初始状态误差的敏感度、提高末端的抗干扰能力,但同时也提高了导引中段内导弹的过载要求.由于本文方法在推导中不依赖于加权函数的具体形式,因此在实际应用中,可针对不同的需求,灵活调整相应参数,以获得满意的制导效果.此外,不局限于本文所给出的几种类型的加权函数,为了实现某些特定的制导要求,还可设计其他更为复杂的加权函数,因此,本文方法给制导律的设计带来了很大的自由度.
4 结论1) 结合极小值原理和Gauss伪谱离散方法,将最优末制导问题转换为一系列的代数方程进行求解,该方法避免了直接法中的寻优过程以及间接法中的求解黎卡提微分方程,不需要进行繁琐的积分运算.
2) 采用双曲正切加权函数,通过合适地调整加权函数的曲线形状,可以灵活调整不同阶段控制能量的权重,进而改变导弹的飞行轨迹和制导指令分布,不仅能降低制导律对初始状态误差的敏感度,而且还可以提高导弹的末端抗干扰能力.
3) 所提制导律在推导中不依赖于加权函数的具体形式,可非常方便地处理各种复杂形式的加权函数,如分段非光滑加权函数,为不同制导需求下设计末制导律提供了很大的自由度.
| [1] |
KIM B S, LEE J G, HAN H S. Biased PNG law for impact with angular constraint[J]. IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(1): 277. DOI:10.1109/7.640285 |
| [2] |
李君龙, 胡恒章. 最优偏置比例导引[J]. 宇航学报, 1998, 19(4): 75. LI Junlong, HU Hengzhang. Optimal biased proportional navigation[J]. Journal of Astronautics, 1998, 19(4): 75. |
| [3] |
RATNOO A, GHOSE D. Impact angle constrained interception of stationary targets[J]. Journal of Guidance, Control, and Dynamics, 2008, 31(6): 1816. DOI:10.2514/1.37864 |
| [4] |
RATNOO A, GHOSE D. Impact angle constrained guidance against nonstationary nonmaneuvering targets[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(1): 269. DOI:10.2514/1.45026 |
| [5] |
胡锡精, 黄雪梅. 具有碰撞角约束的三维圆轨迹制导律[J]. 航空学报, 2012, 33(3): 508. HU Xijing, HUANG Xuemei. Three-dimensional circular guidance law with impact angle constraints[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(3): 508. |
| [6] |
魏鹏鑫, 荆武兴, 高长生. 具有落角约束的弹道导弹再入末制导律设计[J]. 哈尔滨工业大学学报, 2013, 45(9): 23. WEI Pengxin, JING Wuxing, GAO Changsheng. Design of the reentry terminal guidance law with constraint of impact angle for ballistic missile[J]. Journal of Harbin Institute of Technology, 2013, 45(9): 23. |
| [7] |
熊少锋, 王卫红, 刘晓东, 等. 考虑导弹自动驾驶仪动态特性的带攻击角度约束制导律[J]. 控制与决策, 2015, 30(4): 585. XIONG Shaofeng, WANG Weihong, LIU Xiaodong, et al. Impact angle guidance law considering missile's dynamics of autopilot[J]. Control and Decision, 2015, 30(4): 585. DOI:10.13195/j.kzyjc.2014.0281 |
| [8] |
张皎, 杨旭, 刘源翔. 基于扩张干扰观测器的带攻击角约束制导律[J]. 北京航空航天大学学报, 2015, 41(12): 2256. ZHANG Jiao, YANG Xu, LIU Yuanxiang. Guidance law with impact angle constraints based on extended disturbance observer[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(12): 2256. DOI:10.13700/j.bh.1001-965.2015.0013 |
| [9] |
KIM M, GRIDER K V. Terminal guidance for impact attitude angle constrained flight trajectories[J]. IEEE Transactions on Aerospace and Electronic Systems, 1973, AES-9(6): 852. DOI:10.1109/taes.1973.309659 |
| [10] |
RYOO C K, CHO H, TAHK M J. Optimal guidance laws with terminal impact angle constraints[J]. Journal of Guidance, Control, and Dynamics, 2005, 28(4): 724. DOI:10.2514/1.8392 |
| [11] |
SONG T L, SHIN S J, CHO H. Impact angle control for planar engagements[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(4): 1439. DOI:10.1109/7.805460 |
| [12] |
HE Shaoming, LEE C H. Gravity-turn-assisted optimal guidance law[J]. Journal of Guidance, Control, and Dynamics, 2018, 41(1): 171. DOI:10.2514/1.G002949 |
| [13] |
BEN-ASHER J, FARBER N, LEVINSON S. New proportional navigation law for ground-to-air systems[J]. Journal of Guidance, Control, and Dynamics, 2003, 26(5): 822. DOI:10.2514/2.5118 |
| [14] |
RYOO C K, CHO H, TAHK M J. Time-to-go weighted optimal guidance law with impact angle constraints[J]. IEEE Transactions on Control Systems Technology, 2006, 14(3): 483. DOI:10.1109/TCST.2006.872525 |
| [15] |
OHLMEYER E J, PHILLIPS C A. Generalized vector explicit guidance[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(2): 261. DOI:10.2514/1.14956 |
| [16] |
LEE J I, JEON I S, LEE C H. Command-shaping guidance law based on a Gaussian weighting function[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(1): 772. DOI:10.1109/TAES.2013.120353 |
| [17] |
LEE C H, LEE J I, TAHK M J. Sinusoidal function weighted optimal guidance laws[J]. Proceedings of the Institute of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2015, 229(3): 534. DOI:10.1177/0954410014537470 |
| [18] |
张友安, 黄诘, 孙阳平. 带有落角约束的一般加权最优制导律[J]. 航空学报, 2014, 35(3): 848. ZHANG Youan, HUANG Jie, SUN Yangping. Generalized weighted optimal guidance laws with impact angle constraints[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(3): 848. DOI:10.7527/51000-6893.2013.0364 |
| [19] |
窦磊, 杨新民. 大着地角卫星制导炸弹最优制导律研究[J]. 南京理工大学学报(自然科学版), 2010, 34(3): 314. DOU Lei, YANG Xinmin. Optimal guidance law of satellite guided bombs with large landing angle[J]. Journal of Nanjing University of Science and Technology (Natural Science), 2010, 34(3): 314. DOI:10.14177/j.cnki.321397n.2010.03.026 |
| [20] |
侯明善. 精确对地攻击姿态约束最优末制导设计[J]. 兵工学报, 2008, 29(1): 63. HOU Mingshan. Optimum terminal guidance for air-to-ground missile with impact angle constraint[J]. Acta Armamentarii, 2008, 29(1): 63. DOI:10.3321/j.issn:1000-1093.2008.01.014 |
| [21] |
ZHANG Limin, SUN Mingwei, CHEN Zengqiang, et al. Receding horizon trajectory optimization with terminal impact specifications[J]. Mathematical Problems in Engineering, 2014, 604705. DOI:10.1155/2014/604705 |
| [22] |
DAVIS P J, RABINOWITZ P. Methods of numerical integration[M]. 2rd ed. San Diego, CA: Academic Press, 1984.
|
| [23] |
BENSON D A. A Gauss pseudospectral transcription for optimal control[D]. Cambridge, Mass: Massachusetts Institute of Technology, 2005
|
| [24] |
KIM B S, LEE J G, HAN H S. Biased PNG law for impact with angular constraint[J]. IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(1): 277. DOI:10.1109/7.640285 |
 2020, Vol. 52
2020, Vol. 52


