2. 空军工程大学 研究生学院, 西安 710051;
3. 中国卫星海上测控部, 江苏 江阴 214431
2. Graduate College, Air Force Engineering University, Xi'an 710051, China;
3. China Satellite Maritime TT&C Department, Jiangyin 214431, Jiangsu, China
为确保无人机的飞行安全, 需根据态势信息进行航迹规划[1].UAV在飞行时既要能够及时感知并迅速规避威胁, 威胁或是静态的(如山峰、建筑等), 或是动态的(如有人机、UAV等), 又要保证某种目标函数达到最优[2].实际的飞行航迹可采用直线和恒定半径弧的组合来模拟[3], 亦可在上述组合中加入回旋弧[4]; Dubins曲线[5]、Ferguson样条[6]和B样条[7]也可模拟实际航迹.航迹避障可在目标函数中添加惩罚函数来实现[8]; 也可将威胁视为规则的形状[9].经过多年研究, 航迹规划求解方法繁多[10].Voronoi图可用于航迹规划[11], 但存在两个缺点, 一是不能对具有非零区域的威胁区建模, 二是不能生成光滑航迹; 采用分段优化RRT方法时[12], 虽然航迹代价和算法运行时间有所降低, 但生成非平滑航迹, 航迹的精确跟踪性较差; 群智能算法由于具有鲁棒性强、易于实现、适应性强等优点, 现已广泛应用[13].遗传算法作为典型代表, 通过选择、交叉和变异等操作来搜索最优航迹[14], 但收敛到最优解的效率较低[15], 实时性较差.
本文针对规划空间存在诸多静态和动态威胁的情形, 采用滚动时域优化策略生成最优航迹序列和子序列; 结合约束条件和目标函数, 利用负梯度下降法搜索航路点[16]; 应用遗传算法对每个子序列进行规划, 使其收敛到局部最优解, 经反复滚动迭代可得近似全局最优航迹, 同时利用控制点优化的贝塞尔曲线, 生成平滑航迹.
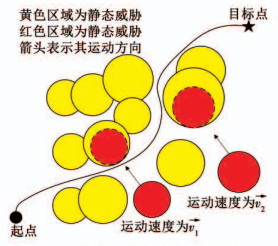
1 问题描述以小型固定翼无人机为例, 为其快速规划出一条从起点至目标点并顺利规避大量静态和动态威胁区的航迹, 同时使某种目标函数在约束条件下达到最优.将空域指定为二维平面, 无人机初始位置为(x0, y0), 目标点位置为(xf, yf), 空域中有n个静态威胁, 其中心位置坐标为(xcs, ycs)、半径为rs, 随机地分布在规划空间; 动态威胁区的中心位置为(xcd, ycd)、数量为q、半径为rd、运动速度为v →.空域中威胁区位置示意图如图 1所示.黄色圆形区域为静态威胁, 红色圆形区域为动态威胁, 箭头表示其运动方向, v → 1、v → 2为其运动速度, 黑色实线表示规划出的航迹.
|
图 1 静态与动态威胁位置示意 Fig. 1 Static and dynamic threat location schematic sketch |
本文采用二次型贝塞尔曲线对实际航迹进行建模, 同时定义了3种目标函数:航迹长度、飞行时间和油耗代价.采用滚动时域策略生成最优航迹序列和子序列, 每个子序列的目标函数达到最优即可构成近似全局最优.故每个目标函数均为两项之和, 即经滚动优化的航迹长度、飞行时间、油耗代价和最后一个子序列的末端控制点与目标点间的最优值.
2.1 航迹模型采用二次型贝塞尔曲线对航迹进行建模为
| $B(t)=(1-t)^{2} P_{0}+2(1-t) t P_{1}+t^{2} P_{2}, 0 \leqslant t \leqslant 1. $ |
曲线上任意点的一阶导数的推导, 从而会简化某些约束条件(如最小转弯半径)的计算, 即
| $B^{\prime}(t)=2(1-t)\left(P_{1}-P_{0}\right)+2 t\left(P_{2}-P_{1}\right), 0 \leqslant t \leqslant 1. $ |
式中:P0、P1、P2分别为航迹子序列上的首端、中端和末端控制点.
与其他航迹建模的方法相比, 贝塞尔曲线既能够快速地计算出曲率, 又能够减少控制变量的数量.对于每个子序列, 第1个控制点设置为前一子序列的末端控制点, 即P0(i)=P0(i-1).针对首个子序列, P0=(x0, y0).每个子序列均包含2个未知控制点, 故每个子序列包含4个控制变量.
2.2 航迹长度最优在构建航迹长度最优目标函数Flength时, 既要使每个子序列的航迹长度最优, 又要使最后一个子序列末端控制点与目标点间的长度最优, 则航迹总长度最优.当子序列的个数为m时, Flength为
| $F_{\text {length}}=\sum\limits_{i=1}^{m} l_{i}+l_{f}. $ | (1) |
式中:li为第i个子序列的长度,lf为目标点与最后子序列末端控制点间的长度, 即
| $l_{f}=\sqrt{\left(x_{f}-x_{f, \mathrm{m}}\right)^{2}+\left(y_{f}-y_{f, \mathrm{m}}\right)^{2}}, $ |
式中(xf, m, yf, m)为最后子序列末端控制点.li很难精确进行计算, 故采用数值积分法进行估算.
2.3 飞行时间最优采用类似的方法定义飞行时间最优目标函数, 既要使每个子序列耗时最优, 又要保证UAV以最大速度从最后子序列末端控制点直飞至目标点.若每个子序列的耗时均为Δtime, 则第1项耗时为mΔtime, 第2项耗时为lf/Vmax, 则Ftime为
| $F_{\text {time }}=m \Delta_{\text {time }}+l_{f} / V_{\max }, $ |
式中Vmax为最大飞行速度.
2.4 油耗代价最优为定义油耗代价最优目标函数Fenergy, 首先定义每千米消耗的能量Ereq为
| $E_{\mathrm{req}}=D_{\mathrm{est}} / \eta_{\mathrm{overall}}. $ |
式中:Dest为UAV所受阻力, ηoverall为推进效率.
采用Carson法估算阻力[17], Carson法综合考虑了空气密度、UAV质量、天线发射器面积、翼展、速度等参数.除速度外都是常数, 故Dest可表示为速度的函数.为使问题简化, 将η(V)也表示为速度的函数[18], 即
| $\eta(V)=\left\{\begin{array}{l}0.06\;V, 0 \leq V \leq 10 ; \\ 0.000\;01, V\geqslant20 ; \\ -0.0024 V^{3}+0.008 V^{2}-0.9V+3.6, \text {others.}\end{array}\right. $ |
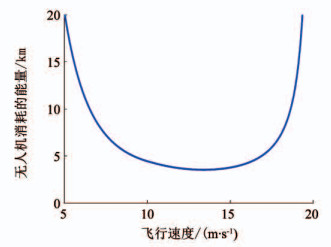
Ereq随着飞行速度的变化而不断改变, 如图 2所示.将min(Ereq)表示为(D/η)opt, 则从最后子序列末端控制点飞至目标点所需的最小能量为lf(D/η)opt.由式(1)可推导出Fenergy为
|
图 2 Ereq与飞行速度的关系 Fig. 2 Relationship between Ereq and flight speed |
| $F_{\text {energy }}=\sum\limits_{i=1}^{m}\left[\int_{0}^{l_{i}}\left(D_{i} / \eta_{i}\right) \mathrm{d} x\right]+l_{f}(D / \eta)_{\text {opt }}, $ |
式中(Di/ηi)为第i个子序列的Ereq.为提高实时性, 采用数值积分法估算第1项的数值.
2.5 威胁区约束假设威胁区的作用距离为Tdmax, 为能够迅速规避静态和动态威胁, 需要计算子序列上UAV的位置与每个威胁的距离.若其小于Tdmax, 则此威胁对航迹规划有影响; 然后对子序列进行离散化, 使航迹上的每个点均满足威胁约束.若以Δt=0.1 s在t=[0, 1]s上进行采样, 则静态威胁约束为
| $r_{s} \leqslant \sqrt{\left(x(t)_{i}-x_{c s}\right)^{2}+\left(y(t)_{i}-y_{c s}\right)^{2}}. $ | (2) |
动态威胁约束的推导与式(2)相似, 但动态威胁区的圆心位置随着时间在不断变化.
2.6 飞行约束本文考虑了常见的气动约束、最小速度和最大速度等飞行约束.由于分段优化策略在相同时间间隔内进行, 故每个航迹子序列的最大长度与最大速度有关、最小长度与最小速度有关.取Δtime=1 s、Vmin=10 m/s、Vmax=15 m/s, 则最大长度为lmax=15 m, 最小长度为lmin=10 m.则每个航迹子序列的长度为
| $l_{\min } \leqslant l_{\mathrm{est}, i} \leqslant l_{\max }. $ | (3) |
为使航迹能够满足飞行条件, 则航迹的最小曲率k大于等于最小转弯半径rturn, 即
| $k \geqslant r_{\mathrm{turn}}. $ | (4) |
为模拟真实的飞行状态, 应防止飞行方向瞬时改变.故要求当前航迹子序列末端控制点的一阶导数等于下一航迹子序列起始控制点的一阶导数, 即
| $B^{\prime}(t=1)_{i-1}=B^{\prime}(t=0)_{i}. $ | (5) |
滚动时域控制(亦称模型预测控制)是滚动时域优化策略的渊源, 其思想是将时间离散化.针对每一离散化时刻, 未来系统的状态模型可由当前系统的状态模型预测, 根据未来系统的状态模型构建约束优化问题模型, 最优控制序列通过实时求解约束优化问题模型得到.作用于系统的实际控制信号仅为当前采样时刻最优控制序列中的第1项, 其余各项均没有实际的作用.在下一采样时刻, 循环往复上述过程, 随着时间的递增而滚动推进.现在的工业过程控制[19]、飞行器控制[20]都有滚动时域控制的身影.
3.1 航迹初步优化究其本质, UAV动态方程具有非线性.为使问题简化, 本文采用线性近似模型, 将UAV视作质点, 则UAV离散时间线性动态模型为
| $\left[\begin{array}{l}\boldsymbol{p} \\ \boldsymbol{v}\end{array}\right]_{k+1}=\boldsymbol{A}\left[\begin{array}{l}\boldsymbol{p} \\ \boldsymbol{v}\end{array}\right]_{k}+\boldsymbol{B a}_{k}, $ | (6) |
其中: $\boldsymbol{A}=\left[\begin{array}{ll}\boldsymbol{I}_{2} & \Delta t \boldsymbol{I}_{2} \\ \boldsymbol{0}_{2} & \boldsymbol{I}_{2}\end{array}\right]$, $\boldsymbol{B}=\left[\begin{array}{c}(\Delta t)^{2} \boldsymbol{I}_{2} / 2 \\ \Delta t \boldsymbol{I}_{2}\end{array}\right]$.
式中: p(k)=[x y]T为UAV在直角坐标系中的位置向量; v(k)=[ẋ ẏ]T为速度向量; a(k)=[ẍ ÿ]T为加速度向量. 02、I2分别为2×2零阵和单位阵; xk=[pkT vkT]∈R4为第k个离散时刻的状态向量; uk=ak为第k个离散时刻的输入向量, 采样周期为Δt.
综合考虑飞行和威胁约束, 利用滚动时域优化策略, 以某种目标函数JT来建立无人机自主避障航迹规划数学模型, 即
| $\min \limits_{x_{\mathrm{m}}, u_{\mathrm{m}}} J_{\mathrm{T}}=\left\{\begin{array}{l}F_{\text {length }}, \\ F_{\text {time }}, \\ F_{\text {energy }}.\end{array}\right. $ | (7) |
| ${\rm{s. t.}} \boldsymbol{x}_{m+j+1|m}=\boldsymbol{A} \boldsymbol{x}_{m+j | m}+\boldsymbol{B} \boldsymbol{u}_{m+j | m}, \forall j=0, \cdots, T-1, $ | (8) |
| ${\mathit{\boldsymbol{x}}_{m + 0|m}} = {\mathit{\boldsymbol{\hat x}}_{m|m - 1}}, {\mathit{\boldsymbol{\hat x}}_{1|0}} = \left( {{x_0}, {y_0}} \right), $ | (9) |
| $\boldsymbol{u}_{m+j | m} \in \boldsymbol{U}, \quad \forall j=0, \cdots, T-1, $ | (10) |
| $\boldsymbol{p}_{m+j|m} \notin \boldsymbol{O}, \quad \forall j=1, \cdots, T. $ | (11) |
式中:T为规划时域和控制时域的长度; xm+j|m为m时刻UAV动态约束方程(8)对m+j时刻状态的预测.由式(6)确定UAV动态约束方程(8), 初始条件为式(9).由飞行约束式(3)、(4)、(5)确定控制输入式(10), 由式(2)间接确定自主避障约束式(11).由于存在计算时间滞后, 故对当前时刻进行的航迹规划必须在前一时刻求得.
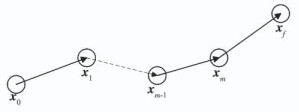
当前m时刻的状态序列{$\mathit{\boldsymbol{\hat x}}$m+0|m, $\mathit{\boldsymbol{\hat x}}$m+1|m, …, $\mathit{\boldsymbol{\hat x}}$m+T|m}和最优控制序列{um+0|m, um+1|m, …, um+T-1|m}可通过求解上述模型得到.根据滚动时域控制原理, 在m时刻, 仅有控制信号um+0|m实际作用于系统; 在m+1时刻, 仅有控制信号u(m+1)+0|(m+1)作用于系统.随着时间推进反复滚动得到最优航迹序列x0, x1, …, xm-1, xm, 最终指向目标点xf=(xf, yf), 如图 3所示.
|
图 3 最优航迹序列组成的轨迹 Fig. 3 A trajectory consisting of an optimal sequence of paths |
本文研究的航迹规划不是全局规划, 而是将起点至目标点的航迹进行分段优化, 模拟了UAV的有限视场.由于UAV只能通过自身的传感器感知附近的威胁, 故只进行局部规划.采用滚动优化策略, 每个子序列的最优航迹通过求解一个有限时域内约束优化问题得出, 经反复滚动可得由若干个局部最优航迹构成的近似全局最优航迹.
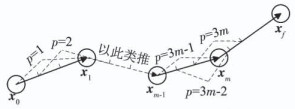
综合考量算法运行时间和目标函数为最优时, 针对最优航迹序列之间的航迹, 对其进行滚动优化, 生成3个航迹子序列; 尔后对其进行重新分组, 如图 4所示.每组中有3个子序列, 每次只优化第1个子序列.当对最后一段航迹(xm-1, xm)中第2个子序列进行优化时, 分组中最后一个子序列的长度取0.75lmax并指向目标点.同理, 也采用此方法优化(xm-1, xm)中最后一个子序列.该方法减少了航迹优化的收敛时间, 因为前一组优化的后两个子序列可直接用于下一组优化的前两个子序列.虽然增加了算法的运行时间, 但却提高了其鲁棒性.
|
图 4 航迹子序列重组示意 Fig. 4 Schematic diagram of recombination of path sub-sequences |
针对每个子序列, 采用遗传算法(GA)对其进行规划.GA从问题的解集(种群)开始搜索, 解集中的每个解是由基因经特定编码构成的个体, 一定数目的个体组成种群.GA的流程如下:①编码; ②生成初始种群; ③适应度函数f的计算; ④选择、交叉与变异; ⑤终止条件; ⑥解码.
设航向角为θ, Δθ为航向转角, Δθmax为最大航向转角, 飞行速度为v, 则
| $\left\{\begin{array}{l}\dot{x}=v \cos \theta, \\ \dot{y}=v \sin \theta.\end{array}\right. $ | (12) |
当(x(t)i, y(t)i)附近的威胁区对航迹规划无影响时, 适应度函数仅为目标函数, 即
| $f^{i}=\left\{\begin{array}{l}F_{\text {length, }} \\ F_{\text {time, }} \\ F_{\text {energy.}}\end{array}\right. $ |
利用负梯度下降法可推导出(x(t)i, y(t)i)的航向角迭代公式为
| ${\theta}_{i}^{n+1}={\theta}_{i}^{n}-\nabla {f}^{i}\left({\theta}_{i}^{n}\right), $ | (13) |
式中n为迭代次数.
设最大迭代次数为nmax.当迭代次数达到nmax时, 可得航向角θi.下一航路点坐标和航向角可由式(6)和式(12)确定.
当(x(t)i, y(t)i)处周围的威胁区对航迹规划有影响时, 适应度函数为两项之和, 即
| $f^{i}=\left\{\begin{array}{l}F_{\text {length }} \\ F_{\text {time }} \\ F_{\text {energy }}\end{array}\right\}+\sum\limits_{j=1}^{M} {\rm{e}}^{-\lambda_{i}\left[\left(x(t)_{i}-x_{c j}\right)^{2}+\left(y(t)_{i}-y_{c j}\right)^{2}\right]}. $ |
式中:$\sum\limits_{j=1}^{M}$e-λi[(x(ti-xcj)2+(y(t)i-ycj)2]为(x(t)i, y(t)i)的威胁代价FT; M为(x(t)i, y(t)i)附近威胁的总个数; λi为调节系数; (xcj, ycj)为威胁区的中心坐标.
同理, 根据式(13)求取当前航向角θi, 由式(6)和式(12)确定下一航路点坐标和航向角.
3.4 自主避障航迹规划流程自主避障航迹规划流程如图 5所示.
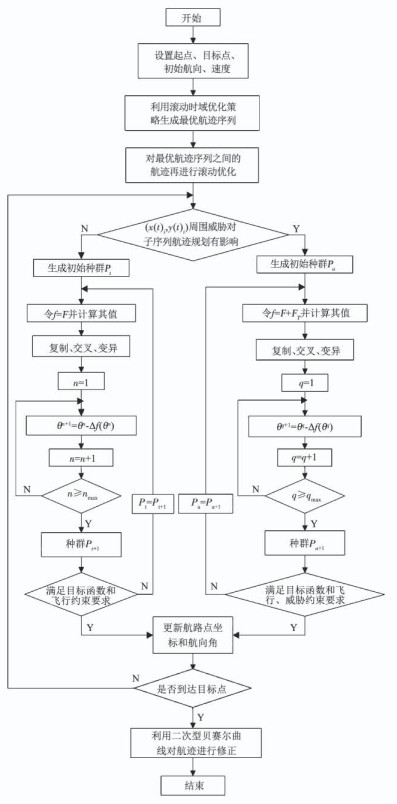
|
图 5 自主避障航迹规划流程 Fig. 5 Flow chart of path planning for autonomous obstacle avoidance |
实验仿真在Windows 10操作系统, 处理器为Intel酷睿i5 4200M, 内存为4 GB的Laptop上采用Matlab 2016b进行编程仿真.规划空间为100 m×100 m的空域, 起点为(0, 0) m, 目标点为(100, 100) m, 静态威胁区数量为40≤n≤60, (5, 5)m≤(xcs, ycs)≤(95, 95) m为其中心坐标, 3 m≤rs≤7 m为威胁半径, 动态威胁区的中心位置、数量、半径、运动速度将在具体的仿真中设定.GA的种群规模为100, 交叉概率为0.8, 变异概率为0.05, 最大迭代次数为50 000.
4.1 不同目标函数的多重静态威胁规避仿真在规划空间随机地分布着50个静态威胁, 威胁的半径为3 m≤rj≤6 m.采用本文所提出的算法, 调用fmincon求解器, 为UAV规划出一条从起点至目标点, 同时使目标函数达到最优的自主避障航迹.
当油耗代价最优时, 规划方案如图 6所示.
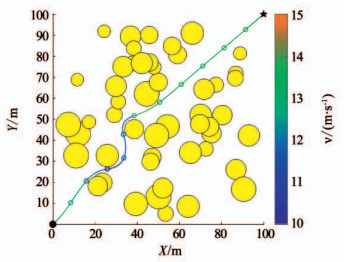
|
图 6 油耗代价为最优时的规划方案 Fig. 6 Path planning scheme with optimal fuel consumption cost |
从图 6可以看出, UAV能成功的避开静态威胁从起点飞至目标点.图 2中, 当飞行速度大约为13.5 m/s时, Ereq达到最小, 进而油耗代价达到最小.故规划的航迹颜色较多地对应速度条中13~14 m/s之间的颜色, 而其余的颜色分布主要是满足飞行约束的要求.
受篇幅所限, 其余目标函数的规划方案就不一一列举了.当规划空间仅存静态威胁时, 不同目标函数的油耗代价、时间代价和航迹代价的对比见表 1.
| 表 1 不同目标函数的代价对比 Tab. 1 Cost comparison of different objective functions |
由表 1可知, 当某目标函数为最优时, 相应代价最小, 但另两种代价会比相应目标函数为最优时的相应代价偏大.
4.2 不同目标函数的动态威胁规避仿真规划空间存在5个静态威胁和2个动态威胁, 动态威胁的圆心位置分别为(100 m, 90 m)、(70 m, 80 m), 半径均为10 m, 运动速度均为v1=(-8 m/s, -8 m/s).基于本文所提出的算法, 当油耗代价目标函数最优时, 规划出一条从起点至目标点的自主避障航迹.规划方案如图 7所示.图 7中, 蓝色虚线圆形表示动态威胁下一时刻所处的位置, 红色小方块表示其运动轨迹, 实线表示已规划的航迹, 虚线表示待规划的航迹.
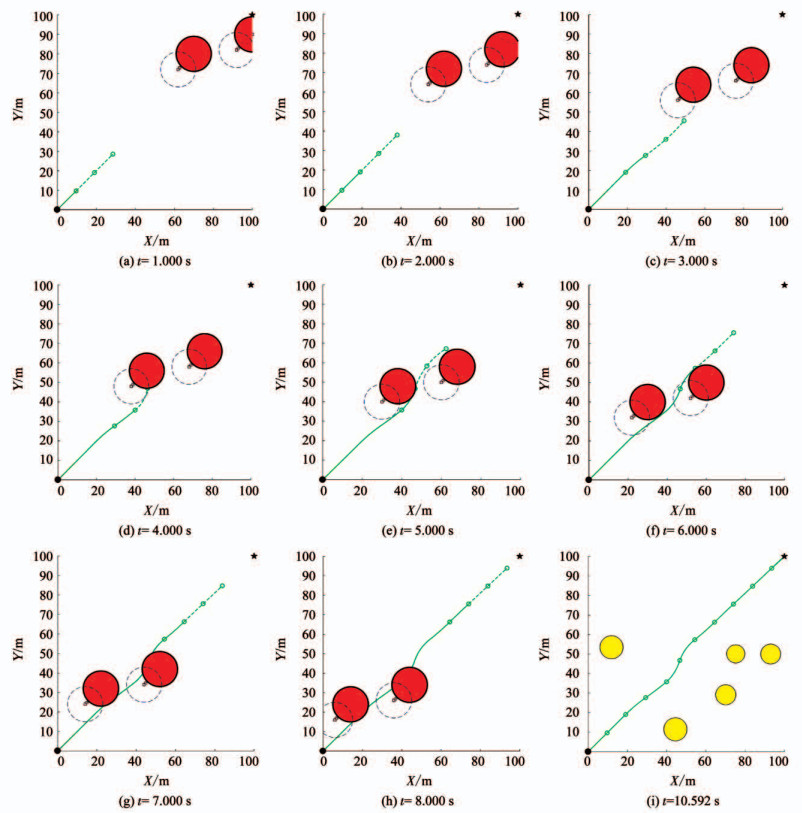
|
图 7 油耗代价最优动态威胁规避方案 Fig. 7 Optimal dynamic threat avoidance scheme for fuel consumption cost |
从图 7可以看出, 在满足油耗代价最优的情形下既可以规避空域的动态威胁, 又可以规避静态威胁, 能为UAV规划出一条从起点至目标点的可行航迹.验证了算法的有效性和模型的合理性.
当规划空间同时存在动态和静态威胁时, 不同目标函数的航迹代价、油耗代价、时间代价的对比见表 2.
| 表 2 存在动态威胁时不同目标函数的代价对比 Tab. 2 Cost comparison of different objective functions in the presence of dynamic threats |
由表 2可知, 当某一目标函数为最优时, 相应的代价最小, 另两种代价相比于其他目标函数为最优的代价偏大.此外, 油耗代价相差较大, 是因为UAV在规避动态威胁时要做大量的机动才能规划出一条可行航迹.
4.3 不同子序列个数对比仿真针对静态威胁规划空间, 其数量、中心位置、半径的设置与不同目标函数的多重静态威胁规避仿真相同.将最优航迹子序列的个数分别取1、2、3、4、5、6, 则在滚动优化的每个时间间隔内分别有0、1、2、3、4、5个前瞻性规划段; 当规划空间仅存动态威胁时, 其中心位置、数量、半径和运动速度与不同目标函数的动态威胁规避仿真设置相同, 子序列个数的设置与上述静态威胁规划空间相同.以航迹长度最优为目标函数, 比较子序列个数不同的情况下航迹长度与算法的运行时间, 如图 8所示.
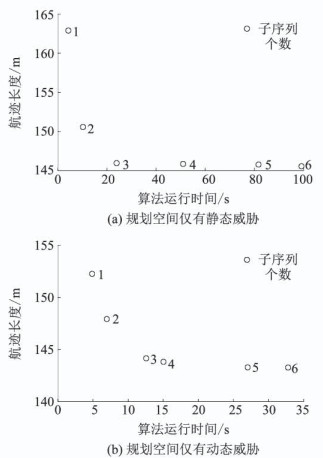
|
图 8 不同子序列个数对航迹长度的影响 Fig. 8 Effect of the number of different sub-sequences on path length |
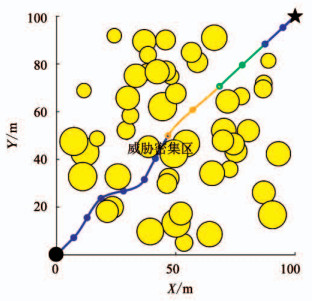
从图 8可以看出, 当子序列个数增加时, 虽然航迹长度更短, 但却增加了算法的运行时间.当子序列个数>3时, 并不会明显地缩短航迹长度, 但运行时间却显著增加.同时当子序列个数为1和2时, 通常会规划出不能令人满意的航迹, 如图 9所示.
|
图 9 子序列个数为2时的航迹规划 Fig. 9 Path planning when the number of sub-sequences is 2 |
从图 9可以看出, 当子序列个数为2时, 虽然可规划出一条可行航迹, 但会穿越威胁密集区.此时若按此航迹执行任务, UAV损伤概率将会增加.经综合分析可知, 当子序列个数为3时, 航迹长度既能达到相对最小, 又能规划出一条令人满意的航迹.
4.4 局部规划与全局规划对比仿真针对同一规划空间, 分别采用本文所提出的算法(局部航迹规划算法)和全局航迹规划算法, 规划出一条既满足约束条件又能使目标函数达到最优的实际可飞航迹.全局航迹规划指的是采用滚动优化策略生成的从起点至目标点的最优航迹序列, 经平滑处理形成的飞行航迹.
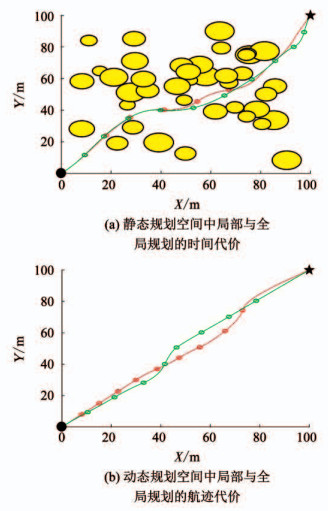
对于以下两种情况:1)规划空间仅随机地分布着40个静态威胁, 其半径、中心位置坐标与不同目标函数的多重静态威胁规避仿真设置相同, 以时间代价最优为目标函数; 2)规划空间仅存在两个动态威胁, 其半径、中心位置坐标、运动速度与不同目标函数的动态威胁规避仿真设置相同, 以航迹代价最优为目标函数.分别采用局部规划方法和全局规划方法对其进行自主避障航迹规划, 如图 10所示.红色实线表示局部规划, 绿色实线表示全局规划.
|
图 10 局部规划与全局规划的比较 Fig. 10 Comparison between local and global planning |
从图 10可以看出, 局部规划航迹与全局规划航迹的差别并不大, 说明局部规划可充分表征全局规划, 故本文所提出的算法可近似规划出全局最优航迹.同时针对同一规划空间, 在相应目标函数达到最优时, 局部规划与全局规划方法的收敛时间见表 3.
| 表 3 局部规划与全局规划方法的收敛时间 Tab. 3 Convergence time of local and global planning method |
由表 3可知, 局部规划算法规划出一条可飞航迹的收敛时间均少于全局规划算法的收敛时间, 说明本文所提出的算法提高了航迹规划的效率, 实时性更强.
5 结论1) 借鉴滚动时域控制思想并进行深入分析, 将其演化为航迹规划的优化策略.先后采用滚动优化策略生成最优航迹序列和子序列, 经反复滚动迭代优化可规划出一条从起点至目标点的航迹.
2) 综合考虑威胁和飞行约束, 利用负梯度下降法搜索航路点, 同时利用控制点优化贝塞尔曲线对航迹进行处理, 获得符合实际要求的飞行航迹.
3) 本文针对规划空间存在诸多静态和动态威胁的情形, 提出了一种基于滚动时域的无人机自主避障航迹规划方法.与全局规划方法相比, 该方法减少了算法的收敛时间, 实时性更强, 并且能够近似表征全局最优航迹.
| [1] |
LIN Yucong, SARIPALLI S. Sampling-based path planning for UAV collision avoidance[J]. IEEE Transactions on Intelligent Transportation Systems, 2017, 18(11): 3179. DOI:10.1109/TITS.2017.2673778 |
| [2] |
宗群, 王丹丹, 邵士凯, 等. 多无人机协同编队飞行控制研究现状及发展[J]. 哈尔滨工业大学学报, 2017, 49(3): 1. ZONG Qun, WANG Dandan, SHAO Shikai, et al. Research status and development of multi UAV coordinated formation flight control[J]. Journal of Harbin Institute of Technology, 2017, 49(3): 1. DOI:10.11918/j.issn.0367-6234.2017.03.001 |
| [3] |
YAO Min, ZHAO Min. Unmanned aerial vehicle dynamic path planning in an uncertain environment[J]. Robotica, 2015, 33(3): 611. DOI:10.1017/S0263574714000514 |
| [4] |
FRAICHARD T, SCHEUER A. From Reeds and Shepp's to continuous-curvature paths[J]. IEEE Transactions on Robotics, 2004, 20(6): 1025. DOI:10.1109/TRO.2004.833789 |
| [5] |
GAO Xianzhong, HOU Zhongxi, ZHU Xiongfeng, et al. The shortest path planning for manoeuvres of UAV[J]. Acta Polytechnical Hungarica, 2013, 10(1): 221. |
| [6] |
MANSYRY E, NIKOOKAR A, SALEHI M E. Artificial Bee Colony optimization offerguson splines for soccer robot path planning[C]//First RSI/ISM International Conference on Robotics and Mechatronics. Tehran, Iran: IEEE, 2013: 85. DOI: 10.1109/ICRoM.2013.6510086
|
| [7] |
齐乃明, 孙小雷, 董程, 等. 航迹预测的多无人机任务规划方法[J]. 哈尔滨工业大学学报, 2016, 48(4): 32. QI Naiming, SUN Xiaolei, DONG Cheng, et al. Mission planning based on path prediction for multiple UAVs[J]. Journal of Harbin Institute of Technology, 2016, 48(4): 32. DOI:10.11918/j.issn.0367-6234.2016.04.005 |
| [8] |
王怿, 祝小平, 周洲, 等. 3维动态环境下的无人机路径跟踪算法[J]. 机器人, 2014, 36(1): 83. WANG Yi, ZHU Xiaoping, ZHOU Zhou, et al. UAV path following in 3D dynamic environment[J]. Robot, 2014, 36(1): 83. DOI:10.3724/SP.J.1218.2014.00083 |
| [9] |
CUI Lei, ZHANG Longfei, ZHANG Yanhong. Study on modeling threat for flight path planning of UAV[J]. Machine Tool & Hydraulics, 2017, 45(24): 149. DOI:10.3969/j.issn.1001-3881.2017.24.026 |
| [10] |
唐强, 张翔伦, 左玲. 无人机航迹规划算法的初步探究[J]. 航空计算技术, 2003, 33(1): 125. TANG Qiang, ZHANG Xianglun, ZUO Ling. Initial study on the path planning's algorithms for unmanned aerial vehicles[J]. Aeronautical Computer Technique, 2003, 33(1): 125. DOI:10.3969/j.issn.1671-654X.2003.01.033 |
| [11] |
史红玉, 刘淑芬. 基于Voronoi图的无人机航路改进规划[J]. 吉林大学学报(理学版), 2018, 56(4): 945. SHI Hongyu, LIU Shufen. Unmanned aerial vehicle route improvement planning based on Voronoi diagram[J]. Journal of Jilin University (Science Edition), 2018, 56(4): 945. DOI:10.13413/j.cnki.jdxblxb.2018.04.29 |
| [12] |
李文广, 孙世宇, 李建增, 等. 分段优化RRT的无人机动态航迹规划算法[J]. 系统工程与电子技术, 2018, 40(8): 1786. LI Wenguang, SUN Shiyu, LI Jianzeng, et al. UAV dynamic path planning algorithm based on segmentated optimization RRT[J]. Systems Engineering and Electronics, 2018, 40(8): 1786. DOI:10.3969/j.issn.1001-506X.2018.08.17 |
| [13] |
MAC TT, COPOT C, TRAN D T, et al. Heuristic approaches in robot path planning: A survey[J]. Robotics and Autonomous Systems, 2016, 86: 13. DOI:10.1016/j.robot.2016.08.001 |
| [14] |
TISDALE J, KIM Z, HEDRIK J K. Autonomous UAV path planning and estimation[J]. IEEE Robotics & Automation Magazine, 2009, 16(2): 35. DOI:10.1109/MRA.2009.932529 |
| [15] |
ASCO A, ATKIN J A D, BURKE E K. An evolutionary algorithm for the over-constrained airport baggage sorting station assignment problem[C]//Proceedings of the 9th International Conference on Simulated Evolution and Learning. Berlin, Heidelberg: Springer, 2012: 32. DOI: 10.1007/978-3-642-34859-4_4
|
| [16] |
王强, 张建军. 潜射无人机海上突防航迹规划方法[J]. 水雷战与舰船防护, 2017, 25(3): 24. WANG Qiang, ZHANG Jianjun. Sea penetration route planning method for submarine-launched UAV[J]. Mine Warfare & Ship Self-Defence, 2017, 25(3): 24. |
| [17] |
CARSON B H. Fuel efficiency of small aircraft[J]. Journal of Aircraft, 1982, 19(6): 473. DOI:10.2514/3.57417 |
| [18] |
唐伟, 宋笔锋, 曹煜, 等. 微小型电动垂直起降无人机总体设计方法及特殊参数影响[J]. 航空学报, 2017, 38(10): 220972. TANG Wei, SONG Bifeng, CAO Yu, et al. Preliminary design method for miniature electric-powered vertical take-off and landing unmanned airial vehicle and effects of special parameters[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(10): 220972. DOI:10.7527/S1000-6893.2017.220972 |
| [19] |
KWON W H, HAN S. Receding horizon control: Model predictive control for state models[M]. London: Springer-Verlag, 2005: 17. DOI:10.1007/b136204
|
| [20] |
PRODAN I, OLARU S, BENCATEL R, et al. Receding horizon flight control for trajectory tracking of autonomous aerial vehicles[J]. Control Engineering Practice, 2013, 21(10): 1334. DOI:10.1016/j.conengprac.2013.05.010 |
 2020, Vol. 52
2020, Vol. 52


