2. 昆明船舶设备研究试验中心, 昆明 650051
2. Kunming Ship Equipment Research and Experiment Center, Kunming 650051, China
高空科学气球按其工作原理不同分为零压气球和超压气球.其中零压气球飞行时长受日照、环境温度、环境压力大小影响较大,必须不断释放压舱物和排气以维持气球高度.以往研究多数针对零压气球,尤其20世纪后半叶简称“大型零压气球年代”.相对于飞行高度经常发生变化的零压气球,超压气球囊体能承受由超热引起的正压力差,有助于气球在相对稳定高度长时间飞行[1-4].NASA在1997年提出的“ULDB”计划更是对超压气球的价值给出了肯定.“ULDB”计划全面采用超压气球,最终要实现的目标是大型超压气球(体积约6.23万m3),其飞行高度35 km,有效载重1 500 kg,飞行时长达到100 d以上.该目标在接近传统零压气球的最大升限和载重能力基础上,将飞行时长大大延长,曾被评为NASA最疯狂的计划之一.“ULDB”采用南瓜形设计,但由于技术难度较大计划延迟多年,分别于2005年、2008年进行了体积为17.6万m3超压气球和19.8万m3超压气球.后者更是达到了载重681 kg,飞行时长11 d,飞行高度30 km以上的数据[5-6].图 1为早期的“ULDB”概念气球.设计出有更大载荷、更高升限、更长驻空时间的超压气球一直都是研究学者追求的目标.

|
图 1 “ULDB”概念气球 Fig. 1 "ULDB"concept balloon |
针对超压气球设计时要考虑的耐压极限问题,先进囊体材料的出现会明显提高超压气球抗压能力.此外,也考虑从结构形态以及裁剪形式入手,尽可能地提高气球抗压能力以最大化发挥材料性能.传统气球设计中,通过在气球囊体上布置加强筋来分担膜面上包括外载荷在内的大部分纵向力,当气球承受较小的内压时相邻绳索间的囊体仍为简单平面,内压较大时能使囊体发生变形而隆起而形成小曲率半径的“鼓包”[7-8].基于囊体膜面应力大小理论,内压一定时,减小超压气球囊体某方向上曲率半径,能有效降低膜面应力.对此,Yajima等[9]提出一种称为3-D裁剪设计概念,设计时留有幅宽余值,加工时通过收边等方式在无膜面伸长变形时就已经形成鼓包.
本文提出的滑动索膜结构超压气球,在囊体外布置滑动绳索,在完成外形设计后,还可通过绳索施加预紧力的方式就能形成不同深度囊体鼓包[10].对囊体结构超压气球设计与分析中的膜面截面曲线的确定方法进行了研究,为便于工程实践,在设计超压气球时考虑纵向曲率半径变化对膜面应力分布产生的影响,对原设计的膜截面曲线采用椭圆曲线进行修正设计,降低同一纬度的囊体上应力差值.在球形设计上进一步提高了超压气球的抗压能力.
1 理论分析 1.1 膜面应力由充气气囊膜面受力静平衡分析,王文隽等[11]推导得到气球膜面张力的理论值,假设膜面单元上两垂直方向曲率半径R1与R2有如下关系:
| $R_{1}=n \cdot R_{2}, $ |
式中n为囊体两垂直方向曲率半径比值.
由膜面单元静平衡得到,囊体上这两方向应力值为:
| $\sigma_{1}=\frac{\Delta P \cdot R_{2}}{t \cdot\left(\frac{1}{n^{2}}+1\right)}, \sigma_{2}=\frac{\Delta P \cdot R_{2}}{t \cdot\left(\frac{1}{n}+n\right)}. $ | (1) |
式中:t为囊体厚度;ΔP为囊内外压力差.
假设气球囊体为各向同性材料,刘龙斌等[12]提出利用Von-mises应力定量描述平流层飞艇囊体受力情况.经推导气球囊体上Von-mises应力可依据:
| $\sigma_{v}=\frac{\rho_{1} \cdot \Delta P}{t \cdot\left(1+n^{2}\right)} \cdot \sqrt{n^{4}-n^{3}+n^{2}}, $ | (2) |
式中ρ1为囊体其中较小曲率半径值(文中为环向曲率半径值).
1.2 索膜结构膜面形状分析张建等[13]对气枕式充气膜结构受载时形态进行了分析,但滑动索膜结构超压气球膜面纵向曲率半径沿环向发生变化,为均匀化其膜面应力分布,并提高超压气球抗压能力,首先应分析纵向变化曲率对平衡膜面单元形状的影响.
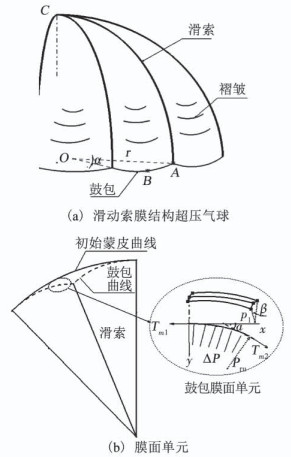
如图 2所示,取一段受载荷为ΔP的囊体膜面微元,该膜面微元纵向弧长dsl=1,且纵向曲率半径为ρl,圆心角(纵向单元中线转角)为β, 环向曲率半径为ρm,其值根据设计曲线不同随x变化有不同值.膜面单元在y轴有力平衡:
|
图 2 膜面单元平衡形状分析 Fig. 2 Analysis of the equilibrium shape of the membrane surface element |
| $T_{m 2} \cdot \sin (\alpha)=\Delta P \cdot x \cdot \mathrm{d} s_{l}-T_{l}. $ | (3) |
式中:Tl为纵向囊体膜面拉力在y轴方向的分力; Tm为单元沿膜面环向的张力; α为ρm对应的环向角度增量.
由式(1)得到Tl及Tm的值如下:
| $T_{l}=\frac{\Delta P \cdot \rho_{m} \cdot \mathrm{d} s_{m}}{\left(n+\frac{1}{n}\right) \cdot \rho_{l}}, T_{m 2}=\frac{\Delta P \cdot \rho_{m}}{1+\left(\frac{1}{n}\right)^{2}} \cdot \mathrm{d} s_{l}, $ |
式中dsm为环向微元弧长.
代入式(3),利用单元中线方程y=f(x)代替环向曲线方程,化简可得:
| $\frac{\Delta P \cdot\left(1+y^{2}\right) \cdot y^{\prime}}{1+\left(\frac{1}{n}\right)^{2}}=\Delta P \cdot x y^{\prime \prime}-\frac{\Delta P}{1+n^{2}} \mathrm{d} s_{m} \cdot y^{\prime \prime}. $ | (4) |
1) 当设计膜面纵向曲率半径ρl=∞,也即膜面为可展面,展开形状为矩形, 式(4)可变为
| $\Delta P \cdot\left(1+y^{2}\right) \cdot y^{\prime}=\Delta P \cdot x y^{\prime \prime}, $ |
积分可解得
| $y^{\prime}=\frac{x}{\sqrt{k^{2}-x^{2}}}, $ |
式中k为实常数.
即平衡时曲面仍为直纹柱面,膜面环向曲线为圆弧,圆弧大小为设计值.
2) 当纵向曲率半径ρl≥ρm且为有限值时,滑索施加预紧力后形成的鼓包曲面:
| $\frac{\Delta P \cdot\left(1+y^{2}\right) y^{\prime}}{1+\left(\frac{1}{n}\right)^{2}}=\Delta P \cdot x y^{\prime \prime}-\frac{\Delta P}{1+n^{2}} \cdot \mathrm{d} s_{m} \cdot y^{\prime \prime}. $ |
为便于解方程,假设膜面长度dsm近似等于x,也即假设膜面微元足够小,化简可得:
| $\frac{d x}{x}=\frac{d y^{\prime}}{y^{\prime}\left(1+y^{\prime 2}\right)}. $ |
说明在膜面单元足够小以至单元较大曲率半径是定值,则充气平衡状态下它的垂直方向截面曲线近似圆弧曲线,此时圆弧大小不光取决于设计值,还与纵向曲率半径有关[14].
当囊体膜面纵向曲率半径ρl确定时,能得到相应平衡状态下的环向曲率半径ρm,其值的确定应视具体囊体尺寸与环境压力等有关.滑动索膜结构超压气球的单幅蒙皮上,其经向的曲率半径却是变化的,引起囊体上同一纬度的应力大小存在差异,其平衡状态下膜面的截面曲线与标准圆弧存在一定差异.
2 正球形超压气球球形设计正球形气球由于其几何模型较为简单,且在膜面面积一定时,其体积能得到最大值,所以在科学气球中得到广泛应用[15].以较为简单的正球形超压气球为分析对象,在球形设计中考虑了鼓包的隆起带来的囊体纵向曲率半径的变化,进行环向截面曲线的修正设计,以希望达到真正的囊体上应力均匀分布.
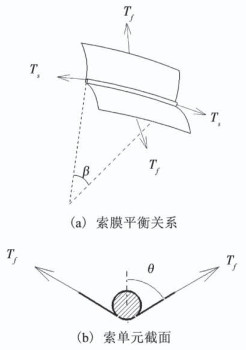
2.1 加强筋受力分析加强筋能有效分担囊体受力,加强筋轴向力随高度变化也会不同,取长度为1个单位的加强筋单元分析,设该加强筋单元对应的圆心角为β.在加强筋单元中垂线方向上,加强筋对囊体的作用力与囊体环向力在该方向上的合力平衡.如图 3所示,平衡方程为
|
图 3 索膜单元 Fig. 3 Cable membrane unit |
| $2 T_{s} \cdot \sin \alpha=2 T_{f} \cdot \cos \theta. $ |
式中:Tf为膜面单元切向张力; α为该位置点的囊体纵向曲率的1/2, 即α=β/2, 由于α足够小,所以sinα≈α,即
| $T_{s}=2 T_{f} \cdot \cos \theta \cdot \rho, $ | (5) |
式中ρ为该位置点的囊体纵向曲率半径.
| $T_{f}=2 t \sigma_{\mathrm{环}} \cdot \cos \theta, $ | (6) |
式中t为膜面厚度,综合式(1)、(5)、(6)可得:
| $T_{s}=\frac{2 \cdot \Delta P \cdot R_{z}}{1+\frac{1}{n^{2}}} \cdot \cos \theta \cdot \rho, $ |
式中n、ρ随纬度的增加而逐渐减小,θ则随纬度增加而逐渐增大,所以加强筋轴向力随纬度增加逐渐降低,最大值位于赤道面上.若不考虑在较高载荷作用下而发生的囊体膨胀,在顶点处(如图 2中C点),理论的值为θ值趋近90°,若按设计ρ为有限值,此时在顶点处绳索力为趋近于0.根据膜面应力受力分析,顶点处膜面接近球面,此时膜面纵向应力近似等于膜面环向应力值[16]如
| $\sigma_{纵}=\frac{\Delta P \cdot R_{2}}{2 t}. $ |
此处加强筋轴向应力远小于囊体膜面纵向应力,又绳索拥有远高于膜面的弹性模量,所以在高纬度位置,理论上的膜面纵向应变远大于加强筋.
若采用加强筋与膜面固定连接形式,将不利于膜面与加强筋间纵向力的传递.而滑动的索膜结构能很好地改善这一点,更有利于膜面应力传递,使纵向形变更均匀.
2.2 滑动索膜结构超压气球设计 2.2.1 赤道面截面曲线设计滑动索膜结构超压气球理论应力最大值位于赤道面上,故可在初步球形设计时以赤道面的膜面截面曲线为参考.
滑动索膜结构超压气球设计时,先采用传统的曲线设计,即囊体赤道截面设计曲线假设为圆心角更大的小半径圆弧,如图 4所示,不同的绳索径向收紧量dl会形成不同大小圆弧曲线.在寻找鼓包设计曲线之前基于一点假设:设计时超压球的横截面曲线周长不变,即绳索数量N确定后,单个鼓包截面曲线弧长为2πR/N.而该坐标系下,仅需知道圆弧圆心纵坐标与半径r,设原设计曲线的圆心角为α,依据dl可确定圆弧通过一点,再有圆弧长度相等假设,此时控制圆弧曲线由下式确定:

|
图 4 滑动索膜结构气球设计 Fig. 4 Design of balloon with sliding cable membrane structure |
| $\left\{\begin{array}{l}r \frac{\alpha}{2}=\frac{{\rm{ \mathsf{ π} }} R}{N}, \\ (R-d l) \sin \frac{\rm{ \mathsf{ π} }}{N}=r \sin \frac{\alpha}{2}.\end{array}\right. $ |
变形后曲线方程如图 4所示,假定柔性囊体蒙皮在沿圆弧方向应变均匀,假设变形后圆弧半径为r′,对应的圆心角为α′,则鼓包最高点应变、环向应力值为:
| $\varepsilon = \frac{{{\alpha ^\prime }{r^\prime } - (2{\rm{ \mathsf{ π} }}/N)R}}{{(2{\rm{ \mathsf{ π} }}/N)R}}, \sigma = \frac{{{r^\prime }\Delta P}}{t}. $ |
根据应力应变关系,因此有
| $E = \frac{\sigma }{\varepsilon } = \frac{{{r^\prime }\Delta P}}{t}\frac{{(2\pi /N)R}}{{{\alpha ^\prime }{r^\prime } - (2\pi /N)R}}, $ |
由此得到ΔP与α′的关系.
其纵向曲线依据滑索增强气球成形分析,考虑绳索汇接在球体两端或端部法兰盘的存在,假设绳索上、下两端高度差不变,dl为0时,其绳索曲线为圆弧;dl为非零值时,即绳索收紧后囊体纵向截面曲线为椭圆.
如图 5所示,绳索的收紧使得绳索纵向曲线变化.但仍要求在上、下两点处切线水平,左、右两点处切线竖直.

|
图 5 滑动索膜结构绳索曲线 Fig. 5 Cable curve of sliding cable membrane structure |
当dl较小时,由原方程x2+z2=R2,收紧后方程$\frac{x^{2}}{m^{2}}+z^{2}=1$,其中代入(R-dl, 0)点坐标.求得绳索收紧后曲线方程如下:
| $\frac{x^{2}}{\left(1-\frac{d l}{R}\right)^{2}}+z^{2}=R^{2}. $ |
同理,滑索增强结构超压气球膜面最大纵向截面曲线也可近似为一椭圆.以赤道面内单幅囊体分析,靠近绳索处,其纵向曲率半径更大,n更大,其Von-mises应力更大,而离绳索越远处,其Von-mises应力越小.
值得注意的是,对滑动索膜结构超压气球,绳索的收缩量对气球体积的影响也应该考虑,实际工况中对浮力有较高要求的,dl不能太大.
2.2.2 滑索索膜结构气球修正设计根据传统鼓包截面曲线圆弧设计,针对不同球体尺寸,能得到相应的最佳径向收缩量dl.为得到囊体应力均匀化的理想模型,根据式(2),调整鼓包截面曲线不同部位的曲率半径r大小,能间接影响n值,进而使囊体上应力分布得到相应调整.
式(2)中,若囊体纵向曲率半径为定值,随着ρ1的增大,囊体上Von-mises应力增大,在相同的囊体纵向曲率半径下,减小ρ1能相应降低囊体上Von-mises应力值.故提出用图 6中的椭圆曲线代替原设计中的圆弧曲线,降低A点环向曲率半径,增大B点处囊体环向曲率半径,能使原设计囊体上最小应力处应力水平升高,最大应力处应力水平降低,即降低了囊体同一纬度上应力变化幅值.

|
图 6 滑动索膜结构气球修正设计 Fig. 6 Modified design of balloon with sliding cable membrane structure |
已知椭圆曲线过A、B、B′3点,为便于计算将B、B′点处的法线夹角设为2α,充气超压变形后的截面曲线在B′点处的切线与OB的夹角记为δ,椭圆圆心O′位置不同所得曲线不同.亦即图中m的大小控制着曲线形状.此处,为控制椭圆长轴在x轴方向,m应小于(R-dl)·cos$\left({\frac{{\rm{ \mathsf{ π} }}}{N}} \right)$,但m必须大于R/2.设局部坐标系x′O′y下椭圆方程如下:
| $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1, $ |
曲线经过A、B两点,解得参数为
| $\left\{\begin{array}{l}b=r\left(1-\cos \left(\frac{\alpha}{2}\right)\right)+(R-d l) \cos \left(\frac{\rm{ \mathsf{ π} }}{N}\right)-m, \\ a=\frac{b x}{\sqrt{b^{2}-y^{2}}}, \end{array}\right. $ | (7) |
由A、B两点曲率半径解得相应的m值.
3 算例分析以原始形状为正球形,直径D=4 m,绳索数目N=16为例,通过圆弧设计理论分析,分别以赤道截面上蒙皮曲线上与球心径向距离最大(B点)、最小(A点)两点为参考点,通过比较不同球形设计参数得到的参考点理论应力值,得到相应的最佳球形设计参数dl.
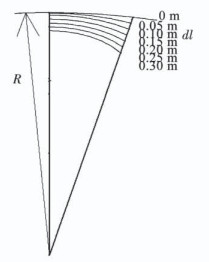
3.1 圆弧曲线设计考虑避免直径4 m正球因dl太大导致的球体体积损失以及从实践经验出发,分别取dl为0、0.05、0.10、0.15、0.20、0.25、0.30 m,代入式(7)中,可分别求得相应曲线的r与α,如图 7所示.因为赤道平面为危险截面,考虑此处囊体鼓包最高点(B点)应力σmin及最低点(A点)应力σmax由式(2)求得,相关参数见表 1.
|
图 7 不同dl时原设计曲线 Fig. 7 Original design curve at different dl values |
| 表 1 不同dl值时设计曲线几何参数 Tab. 1 Geometric parameters of design curves with different dl values |
体积也随dl增大而减小,假定成形鼓包后体积与原正球(dl=0时)形的体积比为λ=Vi/V0.期望能在体积变化较小情况下能明显降低膜面应力,如图 8所示,在理论上当dl=0.05 m时,其体积相对于原正球形气球减小4.5 ‰左右,但最大理论应力却减小1/2.

|
图 8 不同dl时体积损失 Fig. 8 Volume loss at different dl values |
利用Abaqus建立有限元模型时,采用对称条件,取两相邻单幅膜片的一半及绳索曲线为Assembly.试验中的超压气球为延缓蒙皮材料在紫外线照射下的老化现象,经常会在蒙皮材料最外层会镀上一层光滑的铝膜.绳索与蒙皮之间的摩擦力非常小,前期形状设计的仿真中可以假设索、膜间的接触为理想的无摩擦形式,建立绳索与膜面间的理想光滑模型.在完成形状设计后,再展开真实索、膜间的摩擦系数对索、膜匹配性的影响分析.利用惯性释放(Inertia relief)技术,模拟气球的浮空状态[17].气球压力载荷ΔP=0.032 MPa, 分析使用囊体与绳索材料参数见表 2.
| 表 2 超压气球材料参数 Tab. 2 Material parameters of super-pressure balloon |
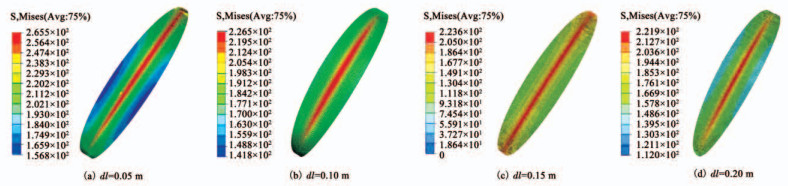
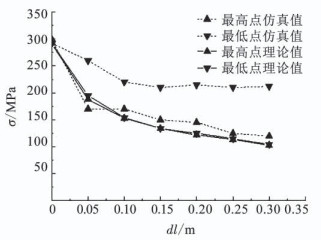
图 9为原设计球形的分析应力分布云图,记膜面中线上点(图 6中B点)为最高点,靠近绳索的点(图 6中A点)为最低点.图 10所示,理论分析中,随着dl的增大,囊体Von-mises应力逐渐减小,在0≤dl≤0.10时,应力随dl增大而降低最明显.在单幅囊体中线上点(最高点)的应力仿真值与理论值能很好地吻合,绳索附近囊体(最低点)应力其仿真值随dl的增大呈降低趋势,但效果不明显.尤其当dl≥0.05时,绳索附近囊体应力值在200 MPa附近浮动.
|
图 9 原设计球形应力云图 Fig. 9 Stress cloud of the original design |
|
图 10 不同dl时应力值 Fig. 10 Stress values for different dl values |
仿真值曲线与理论曲线走势基本一致,其中理论值为膜面无非线性形变时的理想数值,在载荷较小时,其数值大小与仿真值很接近.当考虑由大载荷引起的膜面变形时,由于绳索与膜面的弹性模量差值很大,分析中近似认为囊体截面上绳索位置不变,但膜面在发生明显几何变形后形成更小的半径和更大的圆心角(如图 4),位于绳索附近的膜面,变形后环向曲率半径更小,但纵向曲率半径不变,也即n更大,从图 10可以看出,图 6中A点位置的仿真值会比理论值大.
根据式(3)的Von-mises应力表达式,减小绳索附近囊体的环向曲率半径,能降低绳索附近囊体Von-mises应力.这也正是修正设计的内容.
以圆弧曲线设计囊体截面曲线,使单幅囊体同一纬度上环向曲率半径处处相等,但是囊体上最低点处较大的纵向曲率半径使此处的Von-mises应力更大,当内压达到抗压极限大小时,绳索附近囊体最先破坏,在绳索勒深dl较大时尤为明显.为此提出修正设计方案,按等极限压差的设计要求,采用椭圆曲线代替原囊体截面圆弧曲线,使单幅囊体同一纬度上的应力差值更小.
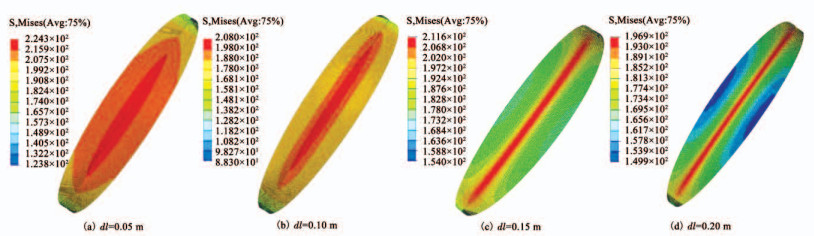
3.4 修正设计分析针对该型尺寸超压气球,对不同dl下,依据式(7),计算得相应的修正曲线的m见表 3.建立有限元模型仿真,修正设计后的应力分布云图与应力数值大小分别如图 11、12所示.
|
图 11 不同dl时修正设计后应力云图 Fig. 11 Stress of the modified design at different dl values |
|
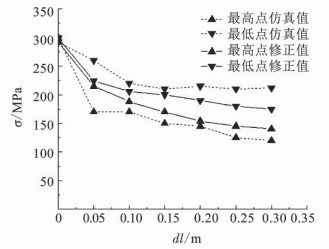
图 12 不同dl时修正设计应力值 Fig. 12 Stress values of the modified design at different dl values |
| 表 3 不同dl时修正曲线几何参数值 Tab. 3 Correction curve geometric parameter values for different dl values |
从图 12可以看出,修正后同一纬度的膜面应力最大、最小值介于原设计膜面最大、最小应力值之间,能直接减小应力峰谷差值,即膜面应力沿环向分布更均匀,在dl=0.05 m时,用该修正方法设计的膜面,最大应力明显降低,膜面应力分布效果明显优于修正前.
3.5 摩擦系数影响分析选取dl=0.05 m的球形超压气球,经过形状修正设计以后的几何模型,分别建立摩擦系μ=0.1~0.8的索、膜滑动接触模型,模型材料、载荷及其他条件均与前述相同,表 4为接触模型中不同摩擦系数下的索、膜上应力值及共节点模型的索、膜应力值,图 13为对应折线图,图中横坐标为摩擦系数.

|
图 13 摩擦系数对索、膜受力的影响 Fig. 13 Effect of friction coefficient on cable and membrane stress |
| 表 4 不同摩擦系数下索、膜应力值 Tab. 4 Cable and membrane stress values under different friction coefficients MPa |
由表 4可以看出,在摩擦系数超过0.2以后,该滑动模型数据近似等于共节点模型.这一结论也可为后续分析作参照,当索、膜材料间摩擦系数超过0.2时,仿真分析可近似简化成共节点模型.
如图 13所示,滑动索膜结构超压气球的索、膜间摩擦系数对膜面应力分布影响很小,但从绳索轴向应力结果考虑,当摩擦系数值小于0.2时,绳索的轴向应力随着摩擦系数的增大而增大,当摩擦系数大于0.2时,绳索轴向应力值稳定在789 MPa附近.可见当索、膜材料接触处的光滑度主要在摩擦系数较小时影响绳索的受力.实际制造中应在接触部位选用尽量光滑的涂层材料.
4 结论1) 滑动索膜结构超压气球以滑动绳索结构代替了与囊体固定的加强筋结构,能有效避免出现球膜与加强筋黏接处出现局部应力集中,滑动的绳索更有利于传递膜面载荷,使球膜上应力分布更均匀.
2) 滑动索膜结构超压气球,在初步设计中均假设囊体环向截面曲线为圆弧,以此能通过理论分析得到相应的最佳球形尺寸设计,再通过该修正理论设计能进一步使膜面应力分布均匀,提高气球的抗压能力.实际应用中也可以参照南瓜气球设计与制作过程.依据修正分析得到相应的幅面,再采用相应的裁剪工艺,使膜面在焊连后就达到最优设计形状.
3) 索、膜间的摩擦系数在较小的范围内对绳索轴向应力有一定影响,选择更光滑的涂层材料能进一步降低绳索应力.对于直径4 m正球形超压气球而言,摩擦系数大于0.2时,滑动模型与共节点模型近似.
4) 未来的研究中,在滑动索膜增结构超压气球设计理论分析时,可考虑随绳索收紧而产生的膜面褶皱的临界状态时绳索与囊体的匹配关系,获取滑动索膜结构超压气球的最佳超压值.
| [1] |
YAJIMA N. Survey of balloon design problems and prospects for large super-pressure balloons in the next century[J]. Advances in Space Research, 2002, 30(5): 1183. DOI:10.1016/S0273-1177(02)00531-8 |
| [2] |
BAGINSKI F, BRAKKE K, FARLEY R. Predicting the deployment pressure in an ascending pumpkin balloon[C]//Proceedings of the 11th AIAA Aviation Technology, Integration, and Operations (ATIO) Conference. Virginia Beach, VA: AIAA, 2013: 409. DOI: 10.2514/6.2011-6831
|
| [3] |
CATHEY H M. The NASA super pressure balloon: A path to flight[J]. Advances in Space Research, 2009, 44(1): 23. DOI:10.1016/j.asr.2009.02.013 |
| [4] |
顾逸东, 姜鲁华.科学气球的发展和应用[C].厦门: 全国空间探测学术交流会论文集, 2010 GU Yidong, JIANG Luhua. The development and application of scientific balloons[C]. Xiamen: National Space Exploration Academic Exchange Conference, 2010 |
| [5] |
CATHEY H M. Evolution of the NASA Ultra Long Duration Balloon[C]//AIAA Balloon Systems Conference. Williamsburg, VA: AIAA, 2007.DOI: 10.2514/6.2007-2615
|
| [6] |
SMITH M S, CATHEY H M. Test flights of the revised ULDB design[C]//AIAA 5th Aviation, Technology, Integration, and Operations Conference. Arlington, Virginia: AIAA, 2005. DOI: 10.2514/6.2005-7471
|
| [7] |
YAJIMA N. A new design and fabrication approach for pressurized balloon[J]. Advances in Space Research, 2000, 26(9): 1357. DOI:10.1016/S0273-1177(00)00060-0 |
| [8] |
PAGITZ M. Stability of lobed super pressure balloons during ascent[J]. Journal of Aircraft, 1971, 48(6): 2042. DOI:10.2514/1.C031436 |
| [9] |
YAJIMA N, IZUTSU N, HONDA H, et al. Three-dimensional gore design concept for high-pressure balloons[J]. Journal of Aircraft, 2012, 38(4): 738. DOI:10.2514/2.2825 |
| [10] |
杨其, 赵海涛, 王全保, 等. 索网囊体结构超压气球的设计与分析[J]. 上海交通大学学报, 2015, 49(9): 1411. YANG Qi, ZHAO Haitao, WANG Quanbao, et al. Design and analysis of super-pressure balloon with a cable-net envelope structure[J]. Journal of Shanghai Jiaotong University, 2015, 49(9): 1411. DOI:10.16183/j.cnki.jsjtu.2015.09.024 |
| [11] |
王文隽, 李勇, 姚伟, 等. 飞艇气囊压力与蒙皮张力的估算[J]. 宇航学报, 2007, 28(5): 1109. WANG Wenjun, LI Yong, YAO Wei, et al. Estimation of the relationship between the pressure in airship ballonet and the tension in its envelope[J]. Journal of Astronautics, 2007, 28(5): 1109. DOI:10.3321/j.issn.1000-1328.2007.05.007 |
| [12] |
刘龙斌, 吕明云, 肖厚地, 等. 基于压差梯度的平流层飞艇艇囊应力计算和仿真[J]. 北京航空航天大学学报, 2014, 40(10): 1386. LIU Longbin, LV Mingyun, XIAO Houdi, et al. Calculation and simulation of stratospheric airship capsule stress considering the pressure gradient[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(10): 1386. DOI:10.13700/j.bh.1001-5965.2013.0629 |
| [13] |
张建, 杨庆山, 李波. 气枕式充气膜结构形态与受力分析[J]. 哈尔滨工业大学学报, 2008, 40(12): 2020. ZHANG Jian, YANG Qingshan, LI Bo. Form-state and loading analyses of air-rated cushion membrane structures[J]. Journal of Harbin Institute of Technology, 2008, 40(12): 2020. DOI:10.3321/j.issn:0367-6234.2008.12.036 |
| [14] |
段有恒.索膜结构张拉及加载全过程仿真分析研究[D].北京: 北京交通大学, 2012. DUAN Youheng. Cable-membrane structure stretching and loading whole course simulating computation[D]. Beijing: Beijing Jiaotong University, 2012 |
| [15] |
YAJIMA N, IZUTSU N, HONDA H. Structure variations of pumpkin balloon[J]. Advances in Space Research, 2004, 33(10): 1694. DOI:10.1016/j.asr.2003.09.048 |
| [16] |
BARG M C, LEE J, BAGINSKI F. Modeling the equilibrium configuration of a piecewise-orthotropic pneumatic envelope with applications to pumpkin-shaped balloons[J]. Siam Journal on Applied Mathematics, 2011, 71(1): 20. DOI:10.1137/100795875 |
| [17] |
陈召涛, 孙秦. 惯性释放在飞行器静气动弹性仿真中的应用[J]. 飞行力学, 2008, 26(5): 71. CHEN Zhaotao, SUN Qin. Applications of inertia relief method in aircraft static aeroelasticity[J]. Flight Dynamics, 2008, 26(5): 71. |
 2020, Vol. 52
2020, Vol. 52


