2. 岩土及地下工程教育部重点实验室(同济大学),上海 200092
2. Key Laboratory of Geotechnical and Underground Engineering (Tongji University), Ministry of Education, Shanghai 200092, China
钻孔灌注桩在竖向成孔过程中所形成的钻孔孔壁自由面,会使孔周地层径向应力得到释放,往往导致钻孔孔壁收缩和产生塌孔、断桩等现象,影响桩身质量.考虑土体径向应力的卸荷效应在钻孔灌注桩桩基工程中不可忽视.径向卸荷引起的柱孔收缩与不同深度的径向土压力有密切关系,很多学者对土压力进行了研究.Tatiana等[1]综合比较了柱孔孔周土压力分布的理论公式及实验进展.马英明[2]总结了如下3个土压力计算理论:平面挡土墙主动土压力理论,如似液地压公式,但该公式不能反映孔径的影响;拱效应理论,如夹心墙土压力公式,该理论表明水平土压力随深度呈指数函数变化,到一定深度趋于一定值;空间轴对称极限平衡理论,该理论考虑了土体圆环效应,如Berezantsev土压力公式.郑榕明等[3]在Berezantsev土压力公式的基础上对Haar-Von Karman假定进行了修正,引入了变量的土压力系数,最后求解出主动土压力的通解.Cheng等[4-5]在计算挡土墙土压力时考虑了墙土壁面摩擦、边坡角度、超荷载和土体黏聚等因素,得到了主动土压力特征方程的数值解.Liu等[6]假定侧压力系数为线性变化,采用切向应力系数的滑移线方法,得到了轴对称条件下的单桩桩周主动土压力表达式.Prater[7]采用轴对称条件下的库伦楔形理论,假定孔周土体呈圆锥形破坏面,求解了土体径向和切向的土压力值.赵春风等[8]采用弹性徐变理论来描述混凝土变形特性,得到钻孔灌注桩深部桩周径向土压力随时间变化的解析式.陈志坚等[9]通过桩身混凝土对桩周土挤密作用的模型试验研究,给出了钻孔灌注桩桩侧压力的分布和变化规律.另一方面,对于小孔扩张理论的研究虽已较多[10-11],但对于钻孔收缩的研究并不多见.Yu等[12-13]考虑土体的剪胀性,推导了柱(球)孔收缩的孔周应力位移场的大应变解,解释了砂土中的旁压卸载实验.温世游等[14]考虑了土体的应变软化特性,推导出孔周存在弹性区、软化区和塑性区的柱(球)孔收缩理论解.温世游等[15]忽略了塑性区的弹性变形,得到了排水条件下球形空腔收缩问题的弹塑性解答.以上研究多集中于桩身土压力的确定或某一断面问题的解答,未对钻孔过程中径向应力松弛导致的孔壁收缩形成的沿深度方向塑性区范围及孔壁位移变化情况进行研究.
Zhao等[16]采用弹脆塑性软化模型对黏性土中钻孔径向卸荷沿深度方向变化的问题进行了理论推导,但该文只探讨了黏性土体情况.文献[17]考虑了土体静止侧压力系数K0的影响,采用相关联流动法则,对钻孔收缩过程中孔周存在两种应力状态而产生两个塑性区的情况进行了分析,但该工况局限于摩尔库伦屈服准则中.
基于此,采用平面应变条件下的SMP屈服准则,考虑塑性变形的非相关联流动法则,结合Berezantsev土压力公式和夹心墙土压力公式,推导了无黏性土钻孔卸荷收缩过程中的孔周应力场位移场的解析解,得到了孔周塑性区半径和孔壁位移沿钻孔深度方向的理论表达式,分析了不同参数对其的影响,对比了忽略塑性区弹性变形的结果.所得结论有助于对实际工程中钻孔灌注桩成孔卸荷的机理认识.
1 水平土压力的确定土压力公式采用Berezantsev土压力公式[18](别氏公式)以及夹心墙土压力公式,在无黏性土中别氏公式为
| $ {p_0} = \gamma {a_0}\frac{{\tan \left( {{{45}^\circ } - \frac{\phi }{2}} \right)}}{{\alpha - 1}}\left[ {1 - {{\left( {\frac{{{a_0}}}{{{r_{\rm{b}}}}}} \right)}^{(\alpha - 1)}}} \right]. $ | (1) |
其中:rb=a0+z·tan$\left(45^{\circ}-\frac{\phi}{2}\right)$;α=2tan ϕ·tan$\left(45^{\circ}-\frac{\phi}{2}\right)$.
对于不含水或者弱含水的无黏性土层,夹心墙土压力公式为[2]
| $ {p_0} = \frac{{\gamma {r_{\rm{u}}}}}{{\tan \phi }}\left( {1 - \exp \left( { - \frac{{\lambda z\tan \phi }}{{{r_{\rm{u}}}}}} \right)} \right). $ | (2) |
式中:λ为侧压力系数, λ=tan2(45°-ϕ/2);ϕ为内摩擦角; γ为土体重度; ru为钻孔的初始半径.
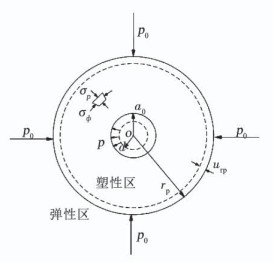
2 问题描述及力学模型无限半空间土体中轴对称的柱孔收缩问题,可视为平面应变问题, 计算模型见图 1.土体中初始水平地应力为p0,柱形孔初始半径为a0.在钻孔卸荷过程中随着孔内压力p的减小,钻孔半径由a0变为a,孔周区域的土体先产生弹性变形,当p减小到临界压力时,土体进入塑性状态,从原来的整体弹性状态转变为弹塑性状态,此时定义塑性区半径为rp,弹性与塑性区交界面位移为urp,对应的径向应力为临塑压力py.且规定应力、应变以压为正.
|
图 1 柱孔收缩力学模型平面图 Fig. 1 Mechanical model of cylindrical borehole contraction |
平衡方程、几何方程和物理方程分别为
| $ \frac{{\partial {\sigma _\rho }}}{{\partial \rho }} + \frac{{{\sigma _\rho } - {\sigma _\phi }}}{\rho } = 0. $ | (3) |
| $ \left\{ {\begin{array}{*{20}{l}} {{\varepsilon _\rho } = - \frac{{{\rm{d}}{u_\rho }}}{{{\rm{d}}\rho }},}\\ {{\varepsilon _\phi } = - \frac{{{u_\rho }}}{\rho }.} \end{array}} \right. $ | (4) |
| $ \left\{ {\begin{array}{*{20}{l}} {{\varepsilon _\rho } = \frac{{1 - {v^2}}}{E}\left( {{\sigma _\rho } - \frac{\mu }{{1 - \mu }}{\sigma _\phi }} \right),}\\ {{\varepsilon _\phi } = \frac{{1 - {v^2}}}{E}\left( {{\sigma _\phi } - \frac{\mu }{{1 - \mu }}{\sigma _\rho }} \right).} \end{array}} \right. $ | (5) |
平面应变条件下无黏性土的SMP准则[19]为
| $ \begin{array}{l} \frac{{{\sigma _\phi }}}{{{\sigma _\rho }}} = {R_{{\rm{ps}}}} = \frac{1}{4}\left\{ {\sqrt {8{{\tan }^2}\phi + 9} + } \right.\\ \;\;\;\;\;\;\;\;\;{\left. {\sqrt {8{{\tan }^2}\phi + 6 - 2\sqrt {8{{\tan }^2}\phi + 9} } - 1} \right\}^2}. \end{array} $ | (6) |
式中:σρ为土体径向应力,σϕ为土体环向应力;在缩孔问题中σρ为小主应力,σϕ为大主应力,即Rps为大小主应力之比.ϕ为土体内摩察角,由三轴压缩试验测得.
应力边界条件为
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _{\rho (\rho = a)}} = p,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {7{\rm{a}}} \right)}\\ {{\sigma _{\rho (\rho = \infty )}} = {p_0}.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {7{\rm{b}}} \right)} \end{array}} \right. $ |
结合式(3)~(5)及式(7b),易求解出弹性区的应力位移场如下:
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _\rho } = {p_0} + \left( {{p_y} - {p_0}} \right){{\left( {\frac{{{r_{\rm{p}}}}}{\rho }} \right)}^2},}\\ {{\sigma _\phi } = {p_0} - \left( {{p_y} - {p_0}} \right){{\left( {\frac{{{r_{\rm{p}}}}}{\rho }} \right)}^2},} \end{array}} \right. $ | (8) |
| $ {u_\rho } = \frac{{{p_y} - {p_0}}}{{2G}}{\left( {\frac{{{r_{\rm{p}}}}}{\rho }} \right)^2}\rho . $ | (9) |
将式(8)代入SMP屈服准则式(6),得弹塑性界面径向应力为
| $ {p_y} = {\sigma _{\rho \left( {\rho = {r_{\rm{p}}}} \right)}} = \frac{{2{p_0}}}{{1 + {R_{{\rm{ps}}}}}}. $ | (10) |
塑性区应力同时满足应力平衡微分方程和SMP屈服准则,将式(6)代入式(3)得
| $ {\sigma _\rho } = K{\rho ^{\left( {{R_{{\rm{ps}}}} - 1} \right)}}, $ | (11) |
式中K为积分常数.
将应力边界条件式(7a)和式(10)代入式(11),可得积分常数为
| $ K = {p_y}r_{\rm{p}}^{\left( {1 - {R_{{\rm{ps}}}}} \right)} = p{a^{\left( {1 - {R_{{\rm{ps}}}}} \right)}}. $ | (12) |
则塑性区径向、环向应力为
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _\rho } = K{\rho ^{\left( {{R_{{\rm{ps}}}} - 1} \right)}} = p{{\left( {\frac{\rho }{a}} \right)}^{\left( {{R_{{\rm{ps}}}} - 1} \right)}},}\\ {{\sigma _\phi } = {R_{{\rm{ps}}}}K{\rho ^{\left( {{R_{{\rm{ps}}}} - 1} \right)}} = {R_{{\rm{ps}}}}p{{\left( {\frac{\rho }{a}} \right)}^{\left( {{R_{{\rm{ps}}}} - 1} \right)}}.} \end{array}} \right. $ | (13) |
塑性区采用非相关联流动法则
| $ \left\{ \begin{array}{l} F = {\sigma _\phi } - \beta {\sigma _\rho } = 0\\ \beta = \frac{1}{4}\left\{ {\sqrt {8{{\tan }^2}\psi + 9} + } \right.\\ {\left. {\sqrt {8{{\tan }^2}\psi + 6 - 2\sqrt {8{{\tan }^2}\psi + 9} } - 1} \right\}^2}, \end{array} \right. $ | (14) |
其中ψ为土体剪胀角.
则有
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{d}}\varepsilon _\rho ^{\rm{p}} = {\rm{d}}\lambda \frac{{\partial F}}{{\partial {\sigma _\rho }}} = - \beta {\rm{d}}\lambda ,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {15{\rm{a}}} \right)}\\ {{\rm{d}}\varepsilon _\phi ^{\rm{p}} = {\rm{d}}\lambda \frac{{\partial F}}{{\partial {\sigma _\phi }}} = {\rm{d}}\lambda ,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {15{\rm{b}}} \right)}\\ {{\rm{d}}\varepsilon _z^{\rm{p}} = {\rm{d}}\lambda \frac{{\partial F}}{{\partial {\sigma _z}}} = 0.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {15{\rm{c}}} \right)} \end{array}} \right. $ |
由式(15c),结合弹塑性边界的初始时刻塑性应变为0的条件可得竖向塑性应变为0,即εzp=0.根据平面假定,无论孔周土体为何种状态,其应变值均应等于地基初始竖向应变值,即εzp+εze=εz0,其中εz0为未钻孔时地基土初始竖向应变.根据弹性物理方程,εz0的表达式为εz0=[σz0-μ(σρ0+σϕ0)]/E, 其中σρ0=σϕ0=p0=K0σz0,K0为土体静止侧压力系数,故可得εze=εz0.
联立塑性区弹性物理方程得竖向应力为
| $ {\sigma _z} = \left( {\frac{1}{{{K_0}}} - 2\mu } \right){p_0} + \mu \left( {{\sigma _\rho } + {\sigma _\phi }} \right). $ | (16) |
将上式代入塑性区弹性物理方程,且结合应力分量公式(13),可得
| $ \left\{ \begin{array}{l} \varepsilon _\phi ^{\rm{e}} = \frac{1}{E}\left[ {\left( {{R_{{\rm{ps}}}} - {R_{{\rm{ps}}}}{\mu ^2} - \mu - {\mu ^2}} \right)K{r^{\left( {{R_{{\rm{ps}}}} - 1} \right)}} - } \right.\\ \;\;\;\;\;\;\;\left. {\left( {\frac{1}{{{K_0}}} - 2\mu } \right)\mu {p_0}} \right],\\ \varepsilon _\rho ^{\rm{e}} = \frac{1}{E}\left[ {\left( {1 - {\mu ^2} - {R_{{\rm{ps}}}}\mu - {R_{{\rm{ps}}}}{\mu ^2}} \right)K{r^{\left( {{R_{{\rm{ps}}}} - 1} \right)}} - } \right.\\ \;\;\;\;\;\;\;\;\left. {\left( {\frac{1}{{{K_0}}} - 2\mu } \right)\mu {p_0}} \right]. \end{array} \right. $ | (17) |
由式(15a)、(15b),且根据初始屈服时各向塑性应变为0的条件可得
| $ \varepsilon _\rho ^{\rm{p}} + \beta \varepsilon _\phi ^{\rm{p}} = 0. $ | (18) |
根据塑性区的应变关系式及上式(18)得
| $ {\varepsilon _\rho } + \beta {\varepsilon _\phi } = \varepsilon _\rho ^{\rm{e}} + \beta \varepsilon _\phi ^{\rm{e}}. $ | (19) |
将几何方程(4)以及式(17)代入上式得
| $ \frac{{{\rm{d}}{u_\rho }}}{{{\rm{d}}\rho }} + \beta \frac{{{u_\rho }}}{\rho } = - t{\rho ^{\left( {{R_{{\rm{ps}}}} - 1} \right)}} - h. $ | (20) |
其中
| $ \left\{ {\begin{array}{*{20}{l}} {t = - \frac{1}{E}\left( {1 - {\mu ^2} - \mu {R_{{\rm{ps}}}} - {\mu ^2}{R_{{\rm{ps}}}} + \beta {R_{{\rm{ps}}}} - \beta {R_{{\rm{ps}}}}{\mu ^2} - } \right.}\\ {\;\;\;\;\left. {\beta \mu - \beta {\mu ^2}} \right)K,}\\ {h = \frac{1}{E}\left( {1 + \beta } \right)\left( {\frac{1}{{{K_0}}} - 2\mu } \right)\mu {p_0},} \end{array}} \right. $ |
解之得
| $ {u_\rho } = C{\rho ^{ - {R_{{\rm{ps}}}}}} - \frac{t}{{2\beta }}{\rho ^{{R_{{\rm{ps}}}}}} - \frac{h}{{\beta + 1}}\rho , $ | (21) |
上式为塑性区位移公式,其中C为待解参数.
在弹塑性界面ρ=rp处,由径向位移相等的条件,结合式(9)可得
| $ C = \left( {\frac{{{p_{\rm{y}}} - {p_0}}}{{2G}} + \frac{h}{{\beta + 1}}} \right)r_{\rm{p}}^{\left( {1 + {R_{{\rm{ps}}}}} \right)} + \frac{t}{{2\beta }}r_{\rm{p}}^{2{R_{{\rm{ps}}}}}, $ | (22) |
则塑性区位移为
| $ \begin{array}{*{20}{c}} {{u_\rho } = \left( {\frac{{{p_y} - {p_0}}}{{2G}} + \frac{h}{{\beta + 1}}} \right)r_{\rm{p}}^{\left( {1 + {R_{ps}}} \right)}{\rho ^{ - {R_{{\rm{ps}}}}}} + }\\ {\frac{t}{{2\beta }}r_{\rm{p}}^{2{R_{{\rm{ps}}}}}{\rho ^{ - {R_{{\rm{ps}}}}}} - \frac{t}{{2\beta }}{\rho ^{{R_{{\rm{ps}}}}}} - \frac{h}{{\beta + 1}}\rho .} \end{array} $ | (23) |
对于柱孔收缩而言,孔壁位移满足条件
| $ u\left( a \right) = a - {a_0}. $ | (24) |
式中:a0和a分别为柱形孔壁的初始和当前半径; u(a)为柱形孔壁位移,其在文中是相对位移,为钻孔初始半径和当前半径的差值.结合式(12)、(23)和(24)可解得a.
3.3 忽略塑性区弹性变形的位移解答文献[15]提到, 在柱孔收缩过程产生塑性区的回弹模量数量级通常在106~107,可忽略弹性变形的影响.为了对比本文的解答,当忽略塑性区中的弹性变形时,式(19)变为
| $ {\varepsilon _\rho } + \beta {\varepsilon _\phi } = 0. $ | (25) |
将几何方程式(4)代入上式,根据弹塑性交界处位移相等的条件,可得塑性区位移为
| $ {u_\rho } = \frac{{{p_0}\left( {1 - {R_{{\rm{ps}}}}} \right)}}{{2G\left( {1 + {R_{{\rm{ps}}}}} \right)}}{\left( {\frac{{{r_{\rm{p}}}}}{\rho }} \right)^{\left( {1 + \beta } \right)}}\rho , $ | (26) |
则孔壁的位移为
| $ \begin{array}{l} u\left( a \right) = \frac{{{p_0}\left( {1 - {R_{{\rm{ps}}}}} \right)}}{{2G\left( {1 + {R_{{\rm{ps}}}}} \right)}}{\left( {\frac{{{r_{\rm{p}}}}}{a}} \right)^{(1 + \beta )}}a = \\ \;\;\;\;\;\;\;\frac{{{p_0}\left( {1 - {R_{{\rm{ps}}}}} \right)}}{{2G\left( {1 + {R_{{\rm{ps}}}}} \right)}}{\left( {p\frac{{1 + {R_{{\rm{ps}}}}}}{{2{p_0}}}} \right)^{\frac{{1 + \beta }}{{1 - {R_{{\rm{ps}}}}}}}}a. \end{array} $ | (27) |
结合式(24)可解得a.
| $ 1 - \frac{{{a_0}}}{a} = \frac{{{p_0}\left( {1 - {R_{{\rm{ps}}}}} \right)}}{{2G\left( {1 + {R_{{\rm{ps}}}}} \right)}}{\left( {p\frac{{1 + {R_{{\rm{ps}}}}}}{{2{p_0}}}} \right)^{\frac{{1 + \beta }}{{1 - {R_{{\rm{ps}}}}}}}}. $ | (28) |
根据解出的a值,结合式(12)可得出塑性区半径rp值.
4 分析与讨论 4.1 卸荷因子的确定当钻孔内压力p小于临塑压力py时,孔周才开始出现塑性区,即p≤py,结合式(10)得
| $ p \le 2{p_0}/\left( {1 + {R_{{\rm{ps}}}}} \right). $ | (29) |
上式即钻孔卸荷孔周产生塑性变形的条件.
令p=np0,则
| $ n \le \frac{2}{{1 + {R_{{\rm{ps}}}}}}, $ | (30) |
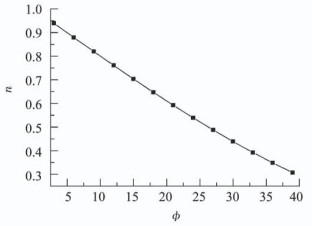
式中n为正数, 定义为卸荷因子.结合屈服准则式(6)以及式(30),可得内摩擦角ϕ与卸荷因子n的关系如图 2所示,可以看出,卸荷因子n是一个只与内摩擦角ϕ呈反比例关系的函数,且n随ϕ的增大非线性减小.
|
图 2 内摩察角ϕ与卸荷因子n的关系 Fig. 2 Relation between internal friction angle ϕ and unloading factor n |
联立式(10)、(12)可得rp与a的关系式如下:
| $ \frac{{{r_{\rm{p}}}}}{a} = {\left( {\frac{p}{{{p_{\rm{y}}}}}} \right)^{\frac{1}{{1 - {R_{{\rm{ps}}}}}}}} = {\left( {p\frac{{1 + {R_{{\rm{ps}}}}}}{{2{p_0}}}} \right)^{\frac{1}{{1 - {R_{{\rm{ps}}}}}}}} = {\left( {\frac{{n\left( {1 + {R_{{\rm{ps}}}}} \right)}}{2}} \right)^{\frac{1}{{1 - {R_{{\rm{ps}}}}}}}}. $ | (31) |
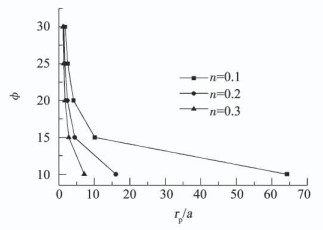
由式(31)可知,在无黏性土中钻孔形成弹塑性变形时,塑性区半径rp与孔壁缩孔后当前半径a的比值是一个与内摩察角ϕ、卸荷因子n有关的定值,其与深度方向无关,可见在无黏性土中竖向成孔,自立深度为零,须采取护壁措施.三者的关系如图 3所示,在相同内摩擦角情况下,rp/a随着卸荷因子n的增大而增大;相同卸荷因子情况下,rp/a值随内摩擦角减小而增大.特别地,当n和ϕ很小时,rp/a值急剧变化.ϕ=10°情况下,rp/a值在n=0.1和0.3时分别为64.29和7.13;ϕ=15°时rp/a值则为10.1(n=0.1)和2.75(n=0.3).可见卸荷因子和内摩擦角对塑性区半径有很大影响,ϕ、n值越小,其对rp/a值的影响越明显.
|
图 3 rp/a与内摩察角ϕ、卸荷因子n的关系 Fig. 3 Relation between internal friction ϕ and rp/a with different values of unloading factor n |
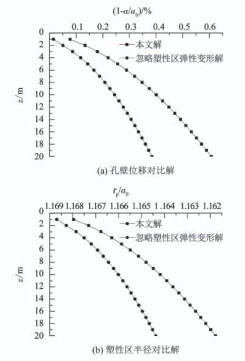
本节对比了忽略塑性区弹性变形的解答,孔壁位移和塑性区半径沿深度方向的关系见图 4.采用上海某高架工程静载试桩处⑤2层砂土的力学参数为[20]:内摩察角ϕ=26°,土体重度Υ=19.6 kN/m3,压缩模量E=12.43 MPa, 泊松比0.3,剪胀角ψ=5°.钻孔深度z=20 m,钻孔初始半径a0=0.5 m.土压力p0采用别列赞采夫土压力公式(别氏公式),令卸荷因子n=0.5.取静止侧压力系数K0=1-sin ϕ[21].
|
图 4 忽略塑性区弹性变形的孔壁位移及孔周塑性区半径对比解 Fig. 4 Comparison between the present solution and the solution of ignoring the elastic deformation in plastic zone with regard to borehole wall displacement and plastic zone radius |
由图 4可知,无黏性土钻孔卸荷过程中,孔壁位移沿深度逐渐增加,而孔周塑性区半径沿深度呈减小趋势,且塑性区半径值十分小,这与黏性土的结果[16]有较大差距,可见在无黏性土中钻孔产生的孔壁塑性区沿深度变化不明显.另外,忽略塑性区弹性变形的沿深度方向孔壁位移解小于本文解答;塑性区半径解则略大于本文解答,在z=20 m处,1-a/a0的本文解及忽略塑性区弹性变形解分别为0.607%和0.385%;rp/a0值为1.161和1.164.由此可知,在砂土等无黏性土中忽略塑性区弹性变形的解答相对不保守,需谨慎应用于工程实际中.
5.2 参数分析为了研究参数的影响,取别氏公式和夹心墙土压力公式获得钻孔沿深度方向的孔壁位移.令p=0.4 p0,考虑如下4种因素:卸荷过程、钻孔半径、剪胀性及内摩擦角.取基本参数如上算例相同.由于塑性区半径沿深度方向的变化很小,变化值几乎为0,在此不作特别分析.
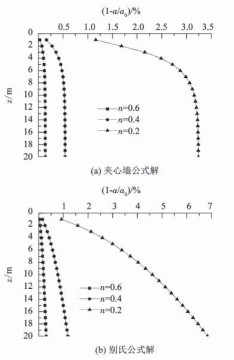
5.2.1 卸荷程度的影响为了研究钻孔过程卸荷效应的影响,取卸荷因子n分别为0.2, 0.4, 0.6,孔壁位移随钻孔深度z的变化如图 5所示.
|
图 5 卸荷程度对孔壁位移的影响 Fig. 5 Effect of unloading on borehole wall displacement |
由图 5可以看出,孔壁位移受卸荷过程影响明显,在同一深度下,随着卸荷的增加,孔壁径向位移也随之增大;在同一卸荷条件下,别氏公式解中孔壁位移随钻孔深度z呈非线性增大;夹心墙公式解中则趋于收敛, 且沿深度方向的孔壁位移数值大体上小于别氏公式解, 在z=20 m处,n=0.6时的孔壁位移值为0.139%(夹心墙公式)和0.304%(别氏公式); 当卸荷到n=0.2时,孔壁位移值为3.243%(夹心墙公式)和6.842%(别氏公式),可见土压力公式的选择对钻孔卸荷缩孔问题有很大的影响.特别地,当卸荷程度相同时,孔壁位移的增大幅度不一样,当n由0.4变为0.2时孔壁位移的增大幅度大于n由0.6卸荷至0.4时的孔壁位移增大幅度.夹心墙公式中,n由0.6卸荷至0.4时的孔壁位移增大幅度为(0.542-0.139)/0.139=2.9,n=0.4变为n=0.2卸荷时孔壁位移的增大幅度为(3.243-0.542)/0.542=4.98;别氏公式中,n=0.6变为n=0.4卸荷时孔壁位移的增大幅度为(1.181-0.304)/0.304=2.88,n=0.4变为n=0.2卸荷时孔壁位移的增大幅度为(6.842-1.181)/1.181=4.79.别氏公式的孔壁位移增大幅度较夹心墙公式解略小.
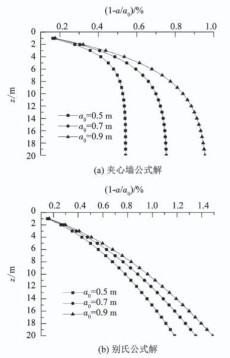
5.2.2 钻孔半径的影响将钻孔半径分别取为a0=0.5,0.7和0.9 m,孔壁位移沿深度方向的变化曲线如图 6所示.可以看出,孔壁位移在同一深度下随着钻孔半径的增大而增大,且均随着钻孔深度的增加而增加.在钻孔孔底处,0.9 m钻孔半径的孔壁位移与钻孔初始半径比值较0.5 m钻孔半径增大0.412%(夹心墙公式)和0.308%(别氏公式).在同一钻孔半径下,别氏公式的孔壁位移沿深度方向的增大幅度要大于夹心墙公式,当a0=0.9 m时,别氏公式中1-a/a0为1.488%(z=20 m),夹心墙公式则为0.954%(z=20 m).
|
图 6 钻孔半径对孔壁位移的影响 Fig. 6 Effect of borehole radius on borehole wall displacement |
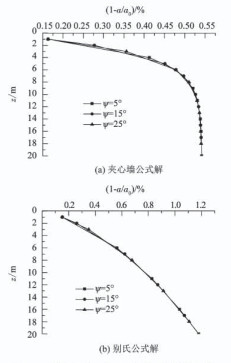
为了研究剪胀角对钻孔过程中孔壁位移的影响,取ψ分别为5°, 15°, 25°,孔壁位移与初始孔径比值沿深度方向的关系如图 7所示.可以看出,不同剪胀角的孔壁位移沿深度方向的曲线几乎重合.在夹心墙公式中,当ψ=25°时钻孔孔底位置的1-a/a0为0.539%;当ψ=5°时,1-a/a0为0.542%.在别氏公式中,当ψ=25°时钻孔孔底位置的1-a/a0为1.177%;当ψ=5°时,1-a/a0为1.181%.可知随着剪胀角的增大,孔壁位移值减小,但变化很小,甚至到了可忽略不计的地步.可知剪胀角对钻孔孔壁位移的影响很小,可忽略不计.另外,可知1-a/a0沿深度增大而增大.
|
图 7 剪胀角对孔壁位移的影响 Fig. 7 Effect of dilation angle on borehole wall displacement |
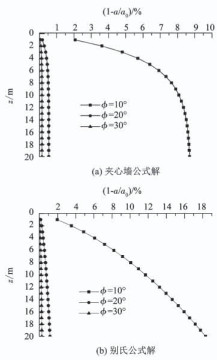
将内摩擦角分别取ϕ=10°,20°和30°,孔壁位移随钻孔深度z的变化值如图 8所示.
|
图 8 内摩擦角对孔壁位移的影响 Fig. 8 Effect of internal friction angle on borehole wall displacement |
由图 8可以看出,在同一深度下孔壁径向位移随内摩擦角的减小而增大,特别地,当ϕ=10°时,孔壁位移较ϕ=20°大大增大.在z=20 m处,ϕ=10°时的孔壁位移值为8.704%(夹心墙公式)和18.318%(别氏公式); ϕ=20°时的孔壁位移值为0.542%(夹心墙公式)和1.181%(别氏公式); 当ϕ=30°时,孔壁位移值为0.148%(夹心墙公式)和0.280%(别氏公式),可知无黏性土的内摩擦角对径向卸荷钻孔缩孔解影响很大,内摩擦角越小,对孔壁位移的影响程度越明显.
6 结论1) 基于SMP屈服准则和非相关联流动法则,推导了在无黏性土中竖向钻孔径向卸荷引起的孔周应力场位移场解析式(8)、(13),(9)、(23).
2) 卸荷因子n只与内摩擦角ϕ有关,且随着ϕ的增大而减小;rp/a是只与ϕ和n有关的定值,与深度方向无关,故在无黏性土中竖向钻孔的自立深度为0.
3) 忽略塑性区弹性变形的柱孔收缩位移解相对偏小,而塑性区半径解相对偏大,故忽略塑性区弹性变形的解答在工程应用中不保守.
4) 参数n、a0和ϕ对孔壁位移值有明显影响.其中n和ϕ存在临界值,本文的算例取n=0.4,ϕ=20°,n和ϕ超过该值,孔壁位移显著增大;ψ对孔壁位移的影响十分有限,可忽略不计.
5) 两种土压力下的孔壁位移沿深度方向相差较大,夹心墙土压力所得位移解在孔口浅表位置较快收敛,Berezantsev土压力以抛物曲线趋向孔端.故钻孔中的土压力选取还需与现场实测值相结合.
| [1] |
TATIANA T, MOHAMED A M. Comparative evaluation of methods to determine the earth pressure distribution on cylindrical shafts: A review[J]. Tunnelling and Underground Space Technology, 2010, 25(2): 188. DOI:10.1016/j.tust.2009.11.001 |
| [2] |
马英明. 立井厚表土层地压的理论与实践[J]. 中国矿业学院学报, 1979(1): 45. MA Yingming. Theory and practice of ground pressure on shaft due to thick overburden[J]. Journal of China University of Mining and Technology, 1979(1): 45. |
| [3] |
郑榕明, 胡亚元. 竖井衬砌主动土压力在一般环向压应力系数下的简化滑移线解[J]. 岩土工程学报, 2005, 27(1): 110. ZHENG Rongming, HU Yayuan. Active earth pressure on circular shaft lining obtained by simplified slip line solution with general tangential stress coefficient[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(1): 110. DOI:10.3321/j.issn:1000-4548.2005.01.019 |
| [4] |
CHENG Yunmin, HU Yayuan, WEI Weibin. General axisymmetric active earth pressure by method of characteristics: Theory and numerical formulation[J]. International Journal of Geomechanics, 2007, 7(1): 1. DOI:10.1061/(ASCE)1532-3641(2007)7:1(1) |
| [5] |
LIU Faqian, WANG Jianhua. A generalized slip line solution to the active earth pressure on circular retaining walls[J]. Computers and Geotechnics, 2008, 35(2): 155. DOI:10.1016/j.compgeo.2007.06.002 |
| [6] |
LIU Faqian, WANG Jianhua. Axi-symmetric active earth pressure obtained by the slip line method with a general tangential stress coefficient[J]. Computers and Geotechnics, 2009, 36(1): 352. DOI:10.1016/j.compgeo.2008.02.002 |
| [7] |
PRATER E G. Examination of some theories of earth pressure on shaft linings[J]. Canadian Geotechnical Journal, 1977, 14(1): 91. DOI:10.1139/t77-007 |
| [8] |
赵春风, 王学知, 赵洪平, 等. 考虑混凝土性质变化灌注桩深部土压力分析[J]. 同济大学学报(自然科学版), 2009, 37(7): 878. ZHAO Chunfeng, WANG Xuezhi, ZHAO Hongping, et al. Analysis of deep earth pressure around cast-in-place pile considering concrete property variation[J]. Journal of Tongji University (Natural Science), 2009, 37(7): 878. DOI:10.3969/j.issn.0253-374x.2009.07.006 |
| [9] |
陈志坚, 刘艳军. 超长灌注桩对桩周土挤密作用的模型试验研究[J]. 岩土力学, 2008, 29(12): 3277. CHEN Zhijian, LIU Yanjun. Model experimental research on compacting effect of concreting for overlength and large-diameter bored pile[J]. Rock and Soil Mechanics, 2008, 29(12): 3277. DOI:10.3969/j.issn.1000-7598.2008.12.018 |
| [10] |
ZHAO Chunfeng, FEI Yi, ZHAO Cheng, et al. Analysis of expanded radius and internal expanding pressure for undrained cylindrical cavity expansion[J]. International Journal of Geomechanics, 2018, 18(2): 04017139. DOI:10.1061/(ASCE)GM.1943-5622.0001058 |
| [11] |
綦春明, 莫斌, 聂春龙, 等. 饱和土体柱形扩孔时大变形不排水统一解析解[J]. 岩石力学与工程学报, 2008, 28(4): 827. QI Chunming, MO Bin, NIE Chunlong, et al. Unified analytical solutions for cylindrical expansion in saturated soil under large deformation and undrained conditions[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 28(4): 827. |
| [12] |
YU Haisui, HOUSLBY G T. A large strain analytical solution for cavity contraction in dilatant soils[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1995, 19(7): 793. |
| [13] |
YU Haisui. Interpretation of pressuremeter unloading tests in sands[J]. Geotechnique, 1996, 46(1): 17. |
| [14] |
温世游, 陈云敏, 李夕兵. 考虑应变软化特性的缩孔解析解[J]. 岩石力学与工程学报, 2002(21): 2432. WEN Shiyou, CHEN Yunmin, LI Xibing. Analytical solutions for contracting cavities with strain softening considered[J]. Chinese Journal of Rock Mechanics and Engineering, 2002(21): 2432. |
| [15] |
温世游, 陈云敏, 唐晓武, 等. 排水条件下球形空腔收缩问题的弹塑性分析[J]. 岩石力学与工程学报, 2004, 23(13): 2251. WEN Shiyou, CHEN Yunmin, TANG Xiaowu, et al. Elastoplastic analysis on contraction of spherical cavity under drainage[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(13): 2251. DOI:10.3321/j.issn:1000-6915.2004.13.023 |
| [16] |
ZHAO Chunfeng, YANG Yanzong, ZHAO Cheng, et al. Analytical solution for borehole contraction caused by radial unloading[J]. KSCE Journal of Civil Engineering, 2013, 17(1): 60. DOI:10.1007/s12205-013-1209-9 |
| [17] |
ZHAO Chunfeng, FEI Yi, ZHAO Cheng, et al. Mohr-Coulomb criterion-based theoretical solutions for borehole contraction in the anisotropic initial stress condition[C]//Proceedings of GeoShanghai 2018 International Conference: Fundamentals of Soil Behaviours. Singapore: Springer, 2018: 442
|
| [18] |
BEREZANTZEV V G. Earth pressure on the cylindrical retaining wall[J]. Proceedings of Brussels Conference on Earth Pressure Problems, 1958(2): 21. |
| [19] |
罗汀, 姚仰平, 松冈元. 基于SMP准则的土的平面应变强度公式[J]. 岩土力学, 2000, 21(4): 390. LUO Ting, YAO Yangping, MATSUOKA H. Soil strength equation in plane strain based on SMP[J]. Rock and Soil Mechanics, 2000, 21(4): 390. DOI:10.3969/j.issn.1000-7598.2000.04.020 |
| [20] |
杨砚宗.砂土考虑卸荷效应的钻孔灌注桩试验与理论研究[D].上海: 同济大学, 2011 YANG Yanzong. Study on the test and method of bored pile in sand with unloading[D]. Shanghai: Tongji University, 2011 |
| [21] |
OKOCHI Y, TATSUOKA F. Some factors affecting K0-values of sand measured in tri-axial cell[J]. Soils Found, 1984, 24(3): 52. DOI:10.3208/sandf1972.24.3_52 |
 2020, Vol. 52
2020, Vol. 52


