2. 北京科技大学 土木与资源工程学院,北京 100083;
3. 中条山有色金属集团有限公司 铜矿峪矿,山西 运城 043706;
4. 中条山有色金属集团有限公司 设计院,山西 运城 043700
2. School of Civil & Environment Engineering, University of Science and Technology Beijing, Beijing 100083, China;
3. Tongkuangyu Mine, Zhongtiaoshan Non-ferrous Metals Group Co., Ltd., Yuncheng 043706, Shanxi, China;
4. Zhongtiaoshan Design Institute, Zhongtiaoshan Non-ferrous Metals Group Co., Ltd., Yuncheng 043700, Shanxi, China
自然崩落法是一种大规模、低成本和高效率的采矿方法,其凿岩工程量小,生产能力大,是地下采矿方法中唯一能够与露天采矿相媲美的比较经济的采矿方法[1-3].自然崩落法是在某一阶段矿体底部进行拉底,即采用以凿岩爆破的普通回采工艺采出10 m左右薄层矿体,为上部矿体崩落创造自由空间并使其失去支撑,从而上部矿体在自然应力的作用下产生崩落并将破碎的矿石在重力作用下从底部结构放出[4-5].自然崩落法适用于地表允许崩落、矿石价值不高、矿石节理裂隙发育的厚大矿体开采中[6].由于自然崩落法可以带来巨大的经济效益,解决自然崩落法开采的技术难题并推广其应用具有重要意义.
自然崩落法的底部结构是指拉底水平和出矿水平之间一系列巷道和工程的总称,所有采下的矿石都需经过底部结构由装运设备运出采场[7].底部结构的稳定性至关重要,是自然崩落法能否成功运用的关键因素之一.
国内外学者对自然崩落法底部结构的稳定性和地压显现相关理论方法进行了研究.Trueman等[8-11]研究了拉底方式、构造应力、底部结构高度等因素对自然崩落法底部结构的影响,并提出了控制措施.丁亦敏[12]通过监测铜矿峪矿在自然崩落法拉底和崩落过程中底部结构的受力,分析了自然崩落法开采过程中底部结构应力变化特征;Diering等[13-16]采用三维有限元数值模拟的方法研究了自然崩落法开采过程中底部结构的稳定性,并提出了支护措施;周航[17]采用颗粒流程序PFC2D和压力拱理论研究了自然崩落法拉底崩落过程中压力拱的演化规律.
在自然崩落法矿山实际生产中,水平地应力比较大的条件下,随着拉底爆破的推进,底部结构地压灾害演化会呈现反复来压的特征,但在以往的研究中并没有真正揭示高水平地应力下自然崩落法底部结构地压灾害的演变特征和机理.本文以中条山集团铜矿峪矿为背景,采用三维有限差分软件FLAC3D对深部高水平应力下自然崩落法拉底过程中底部结构应力的时空演化特征和规律进行了分析,并与现场地压灾害发生实际情况进行了对比,揭示了底部结构地压灾害演变的机理,对矿山底部结构稳定性的维护具有重要意义.
1 地压灾害演变特征中条山集团铜矿峪矿床主要以斑铜矿为主,矿床由百余条矿体组成,其中4#和5#矿体为主采矿体.4#和5#矿体平面上为巨大透镜状,沿倾斜为似板状,倾角40°~60°. 4#矿体平均厚度95 m,最大厚度151 m,5#矿体平均厚度97 m,最大厚度155 m.矿区内主要含矿岩石为变石英晶屑凝灰岩.铜矿峪矿设计采用后退式拉底自然崩落法开采,底部结构超前于拉底层掘进,由于矿体倾角较缓,为了充分回收矿石,减少损失率,充分发挥自然崩落法的优势,使矿体更为经济地回收出来,在两个矿体分别布设一个主层和两个副层来回收矿石.
采用应力解除法对原岩应力进行测量,测得的地应力最大主应力位于水平方向,且与矿体走向近乎一致,夹角较小.由于矿体在水平方向呈现条带状分布,走向长度较长,倾向长度较短,为了便于工程开拓和多点出矿,出矿穿脉与矿体走向基本垂直布置.由于采用后退式拉底方式,底部结构的掘进需要超前于拉底,但随着拉底爆破的推进和采深的增加,底部结构面临的地压灾害日益严重,表现为出矿穿脉和装矿进路收敛变形,甚至垮塌,如图 1、2所示.根据回顾历年地压灾害区域的演化过程,统计分析地压显现区域(历年典型破坏位置统计见表 1),可以发现底部结构地压显现呈现以下规律:1)随着拉底爆破的进行,在推进线附近地压显现比较明显,主要表现为出矿穿脉和装矿进路收敛变形,甚至垮塌;2)随着拉底爆破的推进,一些地压显现区域会呈现反复来压,拉底推进线后方也出现一定比例的地压破坏,表现为出矿穿脉和装矿进路的反复破坏,如在矿山实际生产中拉底推进线推进到510出矿穿脉附近时,8~10号聚矿沟之间的出矿穿脉段在2014年3月份变形严重,在同年7月份对出矿穿脉进行加固支护,恢复出矿,在8月份拉底推进线前移后,510出矿穿脉8~10号聚矿沟之间的出矿穿脉段再次发生破坏;3)随着拉底爆破推进范围的增大,地压显现呈现加重趋势.

|
图 1 出矿穿脉坍塌 Fig. 1 Collapse of the ore-drawing transverse drift |

|
图 2 装矿进路钢拱架压弯 Fig. 2 Bending of the steel arch in loading roadway |
| 表 1 典型地压显现位置统计 Tab. 1 Statistics of typical ground pressure occurrence locations |
研究采用三维有限差分软件FLAC3D构建数值模型,模型范围取自于自然崩落法矿山实际开采范围,根据后退式拉底实际开采顺序进行开挖模拟,然后分析底部结构应力变化规律,并与现场实际灾变过程进行对比,从而分析底部结构灾变机理.
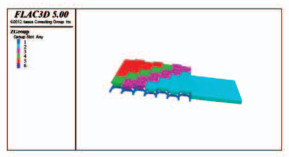
2.1 模型大小根据现场实际工程布置,建立FLAC3D数值模型,模型整体如图 3所示,模型内部如图 4所示,采场巷道名称如图 5所示,模型走向长510 m,垂直走向长310 m,高度310 m,共计2 773 845个单元.根据研究内容及建模单元数量计算难度限制,出矿水平共布设8条出矿穿脉,59条出矿进路和聚矿沟,出矿水平埋深550 m.聚矿沟长13 m,高10 m,下宽6.4 m,上宽11 m,出矿穿脉和装矿进路净断面为3.8 m×3.2 m(宽×高).

|
图 3 模型整体结构图 Fig. 3 Overall structure diagram of the model |
|
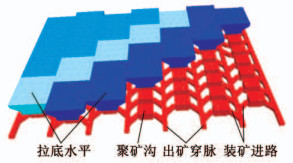
图 4 模型内部拉底和底部结构图 Fig. 4 Undercut and extraction level excavations of the model |
|
图 5 采场巷道名称 Fig. 5 Names of roadways in stope |
本次计算采用Mohr-Coulomb破坏准则,但其不能有效描述岩体中节理、裂隙及结构面对岩体强度的影响,而Hoek-Brown准则可以准确表征含有大量节理、裂隙的岩体材料的破坏,故通过Hoek-Brown准则换算出与其等效的Mohr-Coulomb破坏准则中的黏聚力和内摩擦角,从而使Mohr-Coulomb破坏准则更好地适用于数值模型中的工程岩体.
在FLAC3D中,Mohr-Coulomb破坏准则发生剪切屈服的条件为fs=σ1-σ3Nφ+2c
最大主应力σ1为负数时,σ1的值越小表示压应力越大,最小主应力σ3的值为正值时,σ3越大表示拉应力越大.由上述公式可知,压应力和拉应力越大,岩体越易达到fs < 0的条件,即发生剪切屈服;最小主应力σ3的值越大即拉应力越大,岩体越易达到ft>0的条件,即发生拉伸屈服.
2.3 力学参数、边界条件与地应力施加在铜矿峪矿进行矿岩现场取芯,然后制作成标准岩石试件,进行实验室测试.将测定的岩石参数进行一定程度的折减弱化,从而得到能用于数值模拟的工程岩体的参数.模拟需要的物理力学参数见表 2.
| 表 2 FLAC3D模拟岩体的物理参数 Tab. 2 Physical and mechanical parameters of rock mass simulated by FLAC3D |
数值模型内的垂直应力随深度线性变化,根据矿体埋藏深度和平均岩体密度(ρ=2 740 kg/m3),模型上部施加垂直方向应力,内部施加实测地应力,模型侧面限制水平移动,模型底面限制垂直移动.模型内部施加的实测地应力是通过应力解除法在测量区域未受采矿影响前获取的,先根据矿山地质条件、开采现状和施工条件选取测点,然后利用应力解除法测得各个测点的孔壁弹性应变,根据应力应变关系和实测的岩石弹性常数求解岩体应力.采用最小二乘法对所有测点的最大水平主应力、最小水平主应力和垂直主应力值进行线性回归,得出了各个主应力值随埋深的变化规律.将矿山实际所得的地应力拟合方程进行坐标转换,成为本文数值模型内部可以施加的地应力方程如下:
| $\sigma_{x}=22.895\;4-0.039\;9Z, \\ \sigma_{y}=11.648\;4-0.020\;4Z, \\ \sigma_{z}=14.660\;0-0.026\;9Z. $ |
本文建立的数值模型的模拟过程如下:
1) 导入模型,施加初始应力和边界条件,形成初始平衡,此时为矿岩处于原岩应力状态;
2) 底部结构开挖,分析底部结构和出矿水平的应力状态;
3) 拉底分3步阶梯式推进(如图 4所示),矿山为了便于出矿和拉底的管理,拉底呈阶梯型沿矿体对角线方向水平推进,为了便于数值模拟,将矿山已有拉底空间根据年推进线近似划分了4个单元,图 4中每个颜色代表 1个单元,从右向左依次推进,只推进3个单元,第1个单元近似等于3年的拉底面积,第2、3个单元分别近似等于1年的拉底面积.分别分析拉底后底部结构和出矿水平的应力状态.
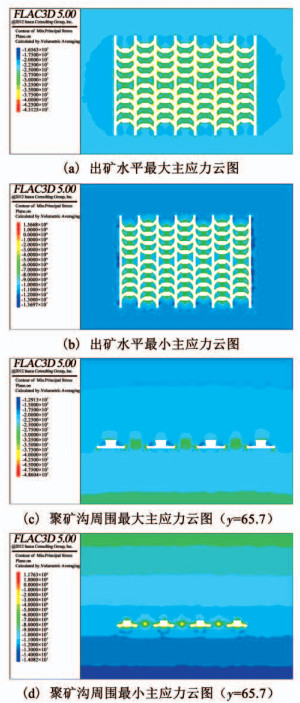
3 结果及分析 3.1 模拟结果 3.1.1 底部结构开挖后应力状态出矿穿脉、聚矿沟和装矿进路开挖后,即形成底部结构,此时出矿水平周围最大主应力和最小主应力云图分别如图 6(a)、图 6(b)所示,聚矿沟周围最大主应力和最小主应力云图分别如图 6(c)、图 6(d)所示,所有云图中红色表示高应力区.
|
图 6 底部结构开挖后模型应力云图 Fig. 6 Stress contour of the model after extraction level excavations formation |
底部结构形成后,出矿水平和聚矿沟周围最大主应力云图中最大值为负值,所以是以压应力的形式存在的,主要集中在出矿穿脉和装矿进路的交叉口位置,最大应力值大小为38.4 MPa,由于巷道开挖后,其周围的岩体完整性降低,而且由三向应力状态变为两向应力状态,所以岩体强度会降低很多.由Mohr-Coulomb破坏准则可知,fs=σ1-σ3Nφ+2c
出矿水平和聚矿沟周围最小主应力云图中最大值为正值,所以以拉应力为主,主要集中出矿穿脉和装矿进路的交叉口位置,最大应力值大小为1.58 MPa,由于矿区内的凝灰岩脆性很高延展性很差,而且含有节理的岩体的抗拉强度会远小于岩石试件的抗拉强度,由于巷道开挖后,其周围的岩体完整性降低,所以抗拉强度会降低很多.由Mohr-Coulomb破坏准则可知,ft=σ3-σt>0时,岩体会发生拉伸屈服,因此随着拉应力升高会逐渐达到拉伸破坏条件,故交叉口位置也易发生拉破坏.
综上所述,在底部结构形成后,应力集中位置主要在出矿穿脉和装矿进路交叉口位置,应加强交叉口位置的巷道支护,但对于底部结构整体而言并没有大范围处于应力集中区,所以底部结构初步形成后整体稳定性不受影响.
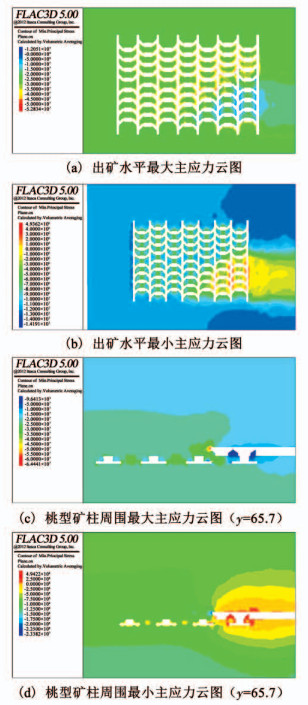
3.1.2 第1步拉底推进后应力状态底部结构上方拉底层进行第1步推进后,推进面积为18 000 m2,形成桃型矿柱,此时出矿水平周围最大主应力和最小主应力云图分别如图 7(a)、图 7(b)所示,桃型矿柱周围最大主应力和最小主应力云图分别如图 7(c)、图 7 (d)所示.
|
图 7 第1步拉底后模型应力云图 Fig. 7 Stress contour of the model after the first step undercutting |
第1步拉底推进后,底部结构范围内最大主应力的高应力区为压应力,主要集中在拉底推进线前方底部结构,最大应力大小为52.8 MPa,尤其是推进线前方的装矿进路和出矿穿脉的周围应力值较高.由压力拱理论可知,这是由于压力拱在推进线前方的应力集中造成的.拉底推进后,位于拉底层下方的底部结构压应力比最初底部结构形成时明显减小,也验证了压力拱理论,开挖后岩体压力会向空间四周转移.初次拉底后底部结构最大压应力相比最初底部结构形成时增大37.5%,由Mohr-Coulomb破坏准则可知,随着压应力的增加推进线前方的底部结构容易发生剪切破坏.
拉底推进后,底部结构范围内最小主应力高应力区为拉应力,主要集中部位为拉底层下方出矿穿脉和桃型矿柱周围,最大值达到4.94 MPa,位于拉底层下方高应力集中区域范围也有明显扩大,未拉底前拉应力高应力区主要集中在出矿穿脉和装矿进路交叉口位置,拉底推进后,位于拉底层下方的桃型矿柱和出矿穿脉两帮都处于拉应力的高应力集中区,底部结构大范围处于受拉的状态.第1步拉底推进后拉应力值比最初底部结构施工后明显增大,增加了2倍,由Mohr-Coulomb破坏准则可知,随着拉应力的增加拉底空间下方的底部结构容易发生拉伸破坏.这主要是矿区水平主应力较高造成的,开挖空间受到高水平主应力的挤压,从而产生较高的拉应力.
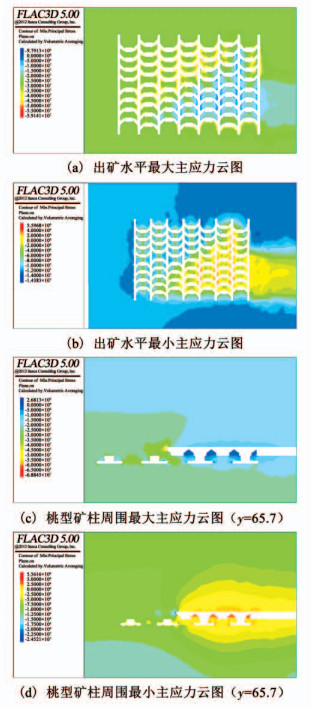
3.1.3 第2步拉底推进后应力状态底部结构上方拉底层第2步推进面积为7 650 m2,两步推进面积达到25 650 m2,此时出矿水平周围最大主应力和最小主应力云图分别如图 8(a)、图 8(b)所示,桃型矿柱周围最大主应力和最小主应力云图分别如图 8(c)、图 8(d)所示.
|
图 8 第2步拉底后模型应力云图 Fig. 8 Stress contour of the model after the second step undercutting |
第2步拉底推进后,底部结构范围内最大主应力的高应力区依然为压应力,拉底推进线前方底部结构最大压应力大小增加到57.3 MPa,比初次拉底推进时增加8.5%.由压力拱理论可知,随着压力拱跨度的增大,压力拱需要承担的上覆岩层的质量增加,所以压力拱范围内应力增加.第2步拉底推进后,原来处于推进线前方底部结构的高应力区压应力得到释放,变为4 MPa,也验证了压力拱理论,开挖后岩体压力会向空间四周转移.
第2步拉底推进后,底部结构范围内最小主应力高应力区依然为拉应力,高应力区依然在拉底层下方出矿穿脉和桃型矿柱周围,最大拉应力值达到5.6 MPa,比第1步拉底后的拉应力值增加20%.原来在推进线前方处于压应力高应力区范围内的底部结构在拉底推进后位于拉应力的高应力区范围,此时底部结构由受压的状态变为受拉的状态.由Mohr-Coulomb破坏准则可知,在拉底推进线前方的底部结构易发生剪切破坏,随着拉底的推进,此处底部结构经历了压应力释放到拉应力集中的阶段,逐渐转为拉伸破坏,这就是高水平应力下自然崩落法底部结构在同一位置反复来压的原因.
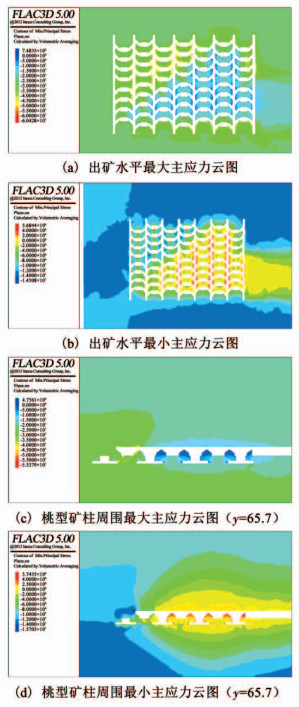
3.1.4 第3步拉底推进后应力状态底部结构上方拉底层第3步推进面积为4 500 m2,3步推进面积达到30 150 m2,此时出矿水平周围最大主应力和最小主应力云图分别如图 9(a)、图 9(b)所示,桃型矿柱周围最大主应力和最小主应力云图分别如图 9(c)、图 9(d)所示.
|
图 9 第3步拉底后模型应力云图 Fig. 9 Stress contour of the model after the third step undercutting |
第3步拉底推进后,底部结构范围内最大主应力的高应力区依然为压应力,拉底推进线前方底部拉底推进时增加5.4%.第3步拉底推进后,原来处于第2步推进线前方底部结构的高应力区压应力得到释放,变为4 MPa.
第3步拉底推进后,底部结构范围内最小主应力高应力区依然为拉应力,高应力区依然在拉底层下方出矿穿脉和桃型矿柱周围,最大拉应力值达到5.74 MPa,比第2步拉底后的拉应力值增加2.5%,拉应力增加幅度变小.原来在第2步推进线前方处于压应力高应力区范围内的底部结构在拉底推进后位于拉应力的高应力区范围,底部结构由受压的状态变为受拉的状态.
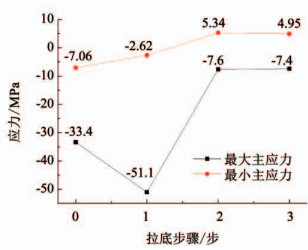
3.2 应力演化规律分析在数值仿真模拟过程中布置应力监测点,监测每一步开挖后的应力状态,可以发现底部结构同一位置(第1步拉底推进线前方出矿穿脉和装矿进路交叉口位置,X=179,Y=103.1,Z=1)在拉底前后的应力变化规律如图 10所示,图中第0步为形成底部结构未拉底时的应力状态,第1步为初次拉底推进,监测点位于拉底推进线前方,经过第2、3步拉底后,监测点位于拉底层下方的底部结构.
|
图 10 拉底前后底部结构同一位置应力变化规律 Fig. 10 Stress variation law of extraction level excavations at the same position before and after undercutting |
从图 10中可以发现,在第1步拉底推进后,推进线前方底部结构最大主应力值由拉底前的33.4 MPa迅速增加到51.1 MPa,符号为负,此时推进线前方的底部结构处于压应力集中的区域,经过第2步拉底后,此时监测点位置底部结构位于拉底层下方,此时压应力迅速降低到7.6 MPa,而最小主应力变成正值,增加到5.34 MPa,处于受拉的状态,此时监测点位置底部结构处于拉应力集中区域.
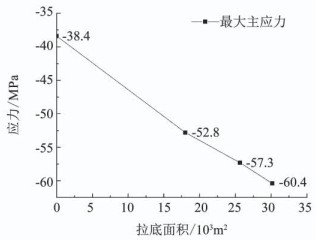
推进线前方底部结构最大主应力最大值随拉底面积的增加的变化规律如图 11所示.拉底面积为0时,表示形成底部结构未拉底时应力状态.从图 11中可发现随拉底面积的不断增加,推进线前方的最大主应力值不断增加,压应力集中程度逐渐明显.
|
图 11 最大主应力随拉底面积的增加的变化规律 Fig. 11 Variation law of maximum principal stress with the increase of undercut area |
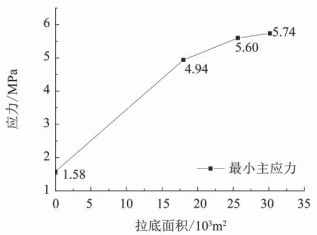
底部结构最小主应力最大值随拉底面积的增加的变化规律如图 12所示.拉底面积为0时,表示形成底部结构未拉底时的应力状态,拉应力集中的高应力区位于拉底层下方的底部结构.从图 12中可以发现随着拉底面积的不断增加,推进线后方的最小主应力值不断增加,拉应力集中程度逐渐明显.
|
图 12 最小主应力随拉底面积的增加的变化规律 Fig. 12 Variation law of minimum principal stress with the increase of undercut area |
通过数值仿真模拟研究可以发现在高水平应力下的自然崩落法开采过程中,随着拉底爆破的推进,底部结构的受力呈现“先受压,后受拉”的应力变化规律.自然崩落法采矿拉底后,会在拉底空间周围形成压力拱,空间形态近似为长轴在拉底推进的方向,短轴沿着拉底推进线方向的鸡蛋形厚壁结构.采场就被这个结构所包围,压力拱内岩体处于应力升高区.随着拉底面积的不断增加,拉底空间上方压力拱承担的上覆岩层质量不断增加,推进线前方底部结构所受压应力就会不断增加,集中程度就会变得更加明显,由Mohr-Coulomb破坏准则可知,fs=σ1-σ3Nφ+2c
根据现场调研,对历史地压显现次数和面积进行统计,研究发现530中段底部结构地压显现发生在拉底推进线附近的次数有5次,影响面积达4 300 m2,发生在拉底推进线后方的重复地压显现有3次,影响面积达2 500 m2.现场调研的地压显现规律与数值模拟研究得出的地压演化规律一致.
5 结论1) 随着拉底爆破的推进,推进线前方的底部结构逐渐产生压应力集中,而且随着拉底面积增加,压应力集中程度更加明显,当推进线前方的底部结构所受的压应力逐渐增大达到岩体剪切破坏条件时,就会出现地压破坏现象.拉底推进过后,拉底空间下方的底部结构,压应力集中得到释放.
2) 位于拉底层下方的底部结构呈现拉应力集中,随着拉底面积增加,拉应力集中程度更加明显,当底部结构所承受的拉应力不断增加达到岩体拉伸破坏条件时,就会再次出现地压破坏现象.
3) 在高水平应力下,自然崩落法底部结构会呈现“先受压,后受拉”应力规律,随着拉底面积的增加,压应力和拉应力集中程度越来越明显,在实际生产中呈现底部结构反复来压的现象.
| [1] |
HURTADO J P, DÍAZ N, ACUNA E I, et al. Shock losses characterization of ventilation circuits for block caving production levels[J]. Tunnelling and Underground Space Technology, 2014, 41: 88. DOI:10.1016/j.tust.2013.11.010 |
| [2] |
WOO K S, EBERHARDT E, ELMO D, et al. Empirical investigation and characterization of surface subsidence related to block cave mining[J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 61: 31. DOI:10.1016/j.ijrmms.2013.01.015 |
| [3] |
PIERCE M E. Forecasting vulnerability of deep extraction level excavations to draw-induced cave loads[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2019, 11(3): 527. DOI:10.1016/j.jrmge.2018.07.006 |
| [4] |
SANCHEZ V, CASTRO R, PALMA S. Gravity flow characterization of fine granular material for block caving[J]. International Journal of Rock Mechanics and Mining Sciences, 2019, 114: 24. DOI:10.1016/j.ijrmms.2018.12.011 |
| [5] |
RAFIEE R, ATAEI M, KHALOOKAKAIE R, et al. Numerical modeling of influence parameters in cavabililty of rock mass in block caving mines[J]. International Journal of Rock Mechanics and Mining Sciences, 2018, 105: 22. DOI:10.1016/j.ijrmms.2018.03.001 |
| [6] |
王青, 任凤玉. 采矿学[M]. 2版. 北京: 冶金工业出版社, 2011. WANG Qing, REN Fengyu. Mining science[M]. 2nd ed. Beijing: Metallurgical Industry Press, 2011. |
| [7] |
XIA Zhiyuan, TAN Zhuoying, PEI Qingyan, et al. Ground pressure damage evolution mechanism of extraction level excavations induced by poor undercutting in block caving method[J]. Geotechnical and Geological Engineering, 2019, 37(3): 1. DOI:10.1007/s10706-019-00921-1 |
| [8] |
TRUEMAN R, PIERCE M, WATTIMENA R. Quantifying stresses and support requirements in the undercut and production level drifts of block and panel caving mines[J]. International Journal of Rock Mechanics and Mining Sciences, 2002, 39(5): 617. DOI:10.1016/S1365-1609(02)00060-6 |
| [9] |
FLORES G. A new mining sequence to minimise stability problems in block caving mines[D]. Golden, CO: Colorado School of Mines, 1993
|
| [10] |
者亚雷, 侯克鹏, 程涌, 等. 自然崩落法底部结构应力状态研究[J]. 金属矿山, 2018(2): 61. ZHE Yalei, HOU Kepeng, CHENG Yong, et al. Research on bottom structural stress state by natural caving method[J]. Metal Mine, 2018(2): 61. DOI:10.19614/j.cnki.jsks.201802011 |
| [11] |
梁江波, 刘华武, 冯兴隆. 自然崩落法超前拉底数值模拟研究[J]. 矿业研究与开发, 2017, 37(2): 93. LIANG Jiangbo, LIU Huawu, FENG Xinglong. Numerical simulation study on advanced undercutting in block caving method[J]. Mining Research and Development, 2017, 37(2): 93. |
| [12] |
丁亦敏. 自然崩落法底部结构应力分布的研究[J]. 有色金属(矿山部分), 1995(3): 20. DING Yimin. Research on stress distribution of extraction level excavations in block caving method[J]. Non-ferrous Metals (Mine Part), 1995(3): 20. |
| [13] |
DIERING J, STACEY T. Three-dimensional stress analysis: A practical tool for mining problems[C]//Proceedings of the 20th International Symposium on the Application of Computers and Mathematics in the Mineral Industries. Johannesburg, SAIMM: APCOM, 1987: 33
|
| [14] |
ESTERHUIZEN G. Three-dimensional stress analysis of block caving layouts[C]//Proceedings of the 20th International Symposium on the Application of Computers and Mathematics in the Mineral Industries. Johannesburg, SAIMM: APCOM, 1987: 43
|
| [15] |
范文录, 刘育明, 葛启发. 自然崩落法拉底过程底部结构稳定性研究[J]. 中国矿山工程, 2017, 46(1): 1. FAN Wenlu, LIU Yuming, GE Qifa. Study on bottom structure stability in the undercutting process of block caving[J]. China Mining Engineering, 2017, 46(1): 1. |
| [16] |
王宁, 韩志型. 金川贫矿区自然崩落法采场底部结构的稳定性[J]. 有色金属, 2004, 56(3): 79. WANG Ning, HAN Zhixing. Base stability of Jingchuan lean ore area mining by natural caving method[J]. Nonferrous Metals, 2004, 56(3): 79. |
| [17] |
周杭.基于PFC2D自然崩落法底部结构受力变化规律研究[D].昆明: 昆明理工大学, 2017 ZHOU Hang. Research on force change law ofextraction level excavations based on PFC2D block caving method[D]. Kunming: Kunming University of Science and Technology, 2017 |
 2020, Vol. 52
2020, Vol. 52


