2. 中海石油(中国)有限公司 北京研究中心开发研究院, 北京 100028;
3. 俄克拉荷马大学 石油与地质工程学院,俄克拉荷马州 诺曼 73019
2. Development Research Department, China National Offshore Oil Corporation Research Institute, Beijing 100028, China;
3. School of Petroleum and Geological Engineering, University of Oklahoma, Norman 73019, OK, USA
纳米孔隙中流体赋存与流动规律与非常规油气开发[1]、污水净化[2]等诸多工程问题直接相关,深入研究流体分子与纳米孔隙之间的相互作用具有重要意义,其中以水分子在纳米孔隙中吸附和流动特征的研究尤为常见[3].物理实验[4-5]发现纳米孔隙表面结构直接影响水分子在纳米孔隙中的赋存与流动,但是由于受到研究尺度的限制并不能从机理上进行解释,制约着工程技术的进一步发展[6].所以,非常有必要从微观尺度对上述现象进行深入研究,以便更好的指导工程实际.
近年来,分子动力学模拟快速发展被广泛的应用于与表界面性质相关的研究[7-9].它不仅能够观察到实验中难以捕捉的微观现象,更能够从分子水平上揭示微观现象的本质.其中,作为最简单但最关键的水分子在各种矿物表面的吸附特征和机理研究已经广泛开展.Lardge等[10]利用密度泛函理论和从头算分子模拟结合研究水分子与方解石(10.4)表面的反应机理,揭示不同覆盖度下水分子在方解石表面的吸附特征.Du等[11]利用分子动力学模拟研究水分子在滑石表面的吸附结构和吸附状态.Picaud等[12]利用分子动力学模拟研究水分子在羟基化石墨表面的吸附,发现H2O-OH相互作用较弱,水分子易聚集成团簇.Ou等[13]利用分子动力学模拟研究水分子在云母(001)表面凝聚和吸附现象,发现两层水分子具有不同的吸附特征.Koparde等[14]利用分子动力学模拟研究水分子在不同尺度的TiO2纳米颗粒表面的吸附,水分子在纳米颗粒表面形成双层结构.上述研究多基于理想晶体表面,但实际中由于溶蚀、机械外力等作用导致矿物晶体表面普遍存在缺陷[15-16].表面缺陷的存在直接影响物质吸附,Keller等[17]利用分子动力学模拟研究水分子和乙醇分子在不同形态的方解石表面的吸附结构,提出台阶的存在增大水分子替代乙醇分子的可能.Spagnoli等[18]利用分子动力学模拟研究水分子与理想和非理想方解石表面的反应特征并计算表面离子溶解的自由能.Guo等[19]研究硬脂酸钾分子在类金刚石表面的吸附,研究3种不同的表面形态对吸附的影响.当前,关于表面结构对于吸附影响的研究仍多局限于选择不同常见矿物表面进行对比分析[20-22],鲜有研究涉及到晶体表面不同缺陷类型对分子吸附的影响.此外,当前研究多以分析表面形态对吸附影响现象为主,鲜有研究从机理方面进行解释.
本文利用分子动力学模拟研究方解石表面结构对于水分子吸附的影响.首先,研究方解石表面结构类型和尺寸对水分子吸附的影响.其次,分析水分子在存在表面缺陷的纳米狭缝中的吸附特征.最后,结合方解石表面悬键特征和表面能定量解释方解石表面结构对水分子吸附的影响.本文从分子尺寸研究方解石表面结构对水分子吸附的影响规律,从理论上解释方解石表面结构处强吸附的机理,为后续研究致密储层中纳米孔隙中油水赋存与流动规律奠定基础.
1 模型建立与模拟方法 1.1 模型的建立利用Materials Studio软件中Forcite模块和Amorphous Cell模块完成分子动力学模拟中的体系构建、结构优化和动力学弛豫,利用COMPASS力场[23-24]描述原子间相互作用,作为第1个从头算力场已被证明能够准确的预测有机和无机物质之间的相互作用,势能函数为
| $ \begin{array}{l} {E_{{\rm{total}}}} = \sum\limits_{{\rm{bond}}} {{E_{\rm{b}}}\left( b \right) + } \sum\limits_{_{{\rm{angle}}}} {{E_\theta }\left( \theta \right) + } \\ \sum\limits_{_{{\rm{dihedral}}}} {{E_\varphi }\left( \varphi \right) + } \sum\limits_{_{{\rm{cross}}}} {E\left( {b, \theta , \varphi } \right) + } \\ \sum\limits_{{\rm{out - of - plane}}} {{E_\chi }\left( \chi \right) + } {E_{{\rm{ele}}}} + {E_{{\rm{vdw}}}}. \end{array} $ | (1) |
式中:前5项为成键相互作用,分别为键长、键角、二面角、交叉项和离平面的势能函数;b、θ、φ、χ分别为键长、键角、二面角和离平面振动的角度;最后2项表示非键相互作用,分别为静电相互作用
方解石晶体属于三方晶系,空间群为R3c,六方晶胞,晶胞中包含Ca、O、C等元素,晶胞参数为a=b=0.499 nm, c=1.706 nm, α=β=90°, γ=120°.{104}表面为最常见的方解石晶体生长面具有最低的表面能和最稳定的结构,所以选取{104}表面[25-27]用以研究水分子的吸附规律.首先,建立尺寸为2.05 nm×3.92 nm的理想{104}表面包含4层分子,通过删除和添加分子构造凸起和空位结构.将包含275个水分子的水分子单元置于{104}表面构造水单元-方解石表面二元体系,研究表面结构对于水分子吸附的影响;此外,建立尺寸为4.02 nm×7.49 nm的理想方解石表面包含5层分子,而后通过删除和添加方式在每个{104}表面构建两种不同尺度的凸起和空位缺陷.将包含1 200个水分子的水分子单元置于方解石表面构造水单元-方解石表面二元体系研究表面缺陷尺寸对水分子吸附的影响;还有,建立2个尺寸为2.41 nm×7.98 nm的理想方解石表面分别包含4层分子,在方解石表面的不同位置通过删除和添加分子构造不同的凸起和空位结构.分别将包含800个和1 200个水分子的水分子单元置于两个包含不同表面结构的方解石表面之间构造方解石表面-水单元-方解石表面三元体系,研究水分子在纳米狭缝中的赋存特征,纳米狭缝间距2.421 nm.
1.2 分子动力学模拟过程首先,对建立的水单元-方解石表面二元体系及方解石表面-水单元-方解石表面三元体系通过Smart Minimizer方法进行20 000步的结构优化,以减少原子间不合理接触.而后,基于结构优化后的二元和三元体系进行分子动力学模拟,模拟条件如下:选择NVT系综,分子初始速度按照Maxwell-Boltzmann分布随机产生,运用Velocity-Verlet[28]算法求解牛顿运动方程.体系温度设置为298 K,采用Andersen恒温模式[29].长程静电作用力计算采用Ewald求和方法[30],范德华相互作用计算采用Atom Based方法,截断半径设置为1.25 nm,截断能以外的分子间相互作用能按平均密度近似方法进行校正.为了保证体系结构的完整性,模拟过程中方解石表面所有原子固定.模拟步长为1.0 fs,对上述体系进行5 ns的分子动力学模拟.最终,确保体系达到平衡,采用最后500 ps的统计平均值来计算相关参量,分析方解石表面结构对水分子吸附的影响.
2 结果与讨论 2.1 表面形态对水分子吸附的影响图 1(a)、图 1(b)分别为理想方解石表面水分子吸附平衡构象和对应密度分布图.由图 1(a)、图 1(b)可知, 水分子在理想方解石表明的吸附存在明显的分层特征.在方解石表面附近,水分子排列规则、密度大,存在明显的稳定吸附层;随着逐渐远离方解石表面,水分子排列逐渐无序,密度逐渐降低,具有明显的扩散吸附层特征,研究结果与Wolthers等[31]和Wang等[32]相一致.Ca(CaCO3)-O(H2O)径向分布函数同样说明问题,如图 1(c)所示,径向分布函数在0.273 nm时径向分布函数高达21.357,即水分子出现概率最高,说明该范围内水分子的数量相对较多并且水分子排列更为规则、紧密.
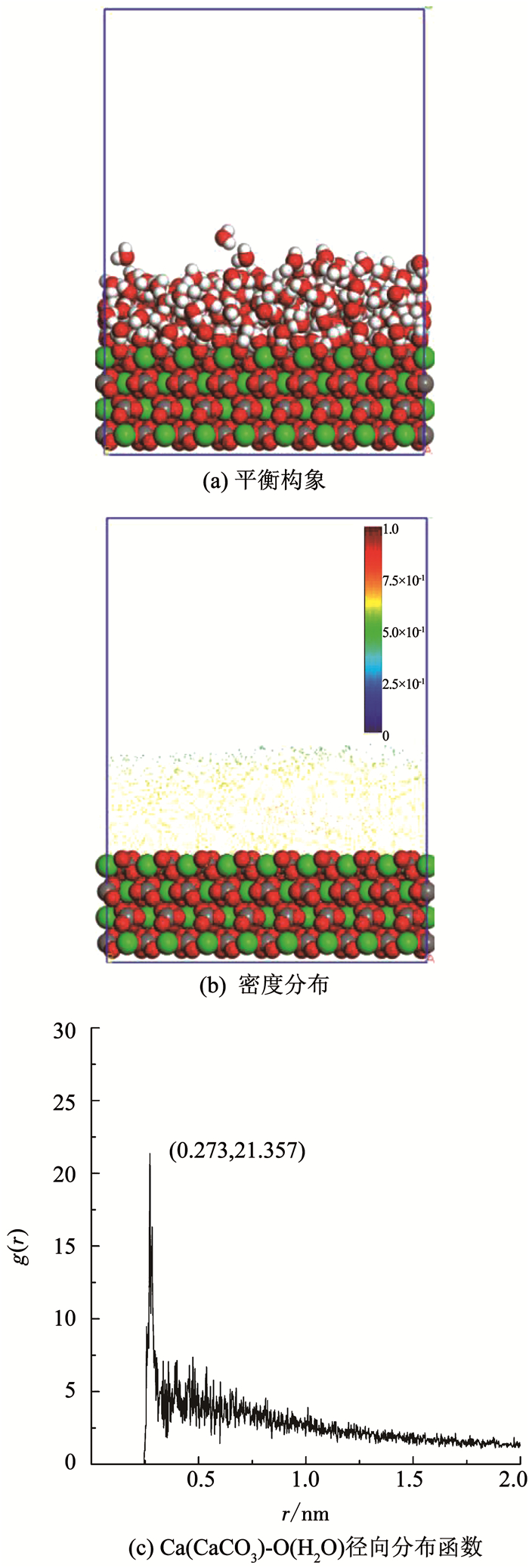
|
图 1 理想方解石表面水分子吸附特征 Fig. 1 Adsorption characteristics of water molecules on ideal calcite surface |
图 2(a)、图 2(b)分别为水分子在凸起方解石表面的吸附平衡构象和对应密度分布图.由图 2(a)、图 2(b)可知, 凸起方解石表面水分子的分布具有明显的局域性,水分子在凸起部分异常聚集,吸附量和吸附密度远高于水平部分.特别是,凸起的顶点部分最为明显.图 2(c)发现Ca(CaCO3)-O(H2O)径向分布函数显示在0.273 nm处水分子径向分布函数高达27.188,远高于理想方解石表面的21.357,即水分子在表面凸起部分的吸附更多,排列更为紧密.
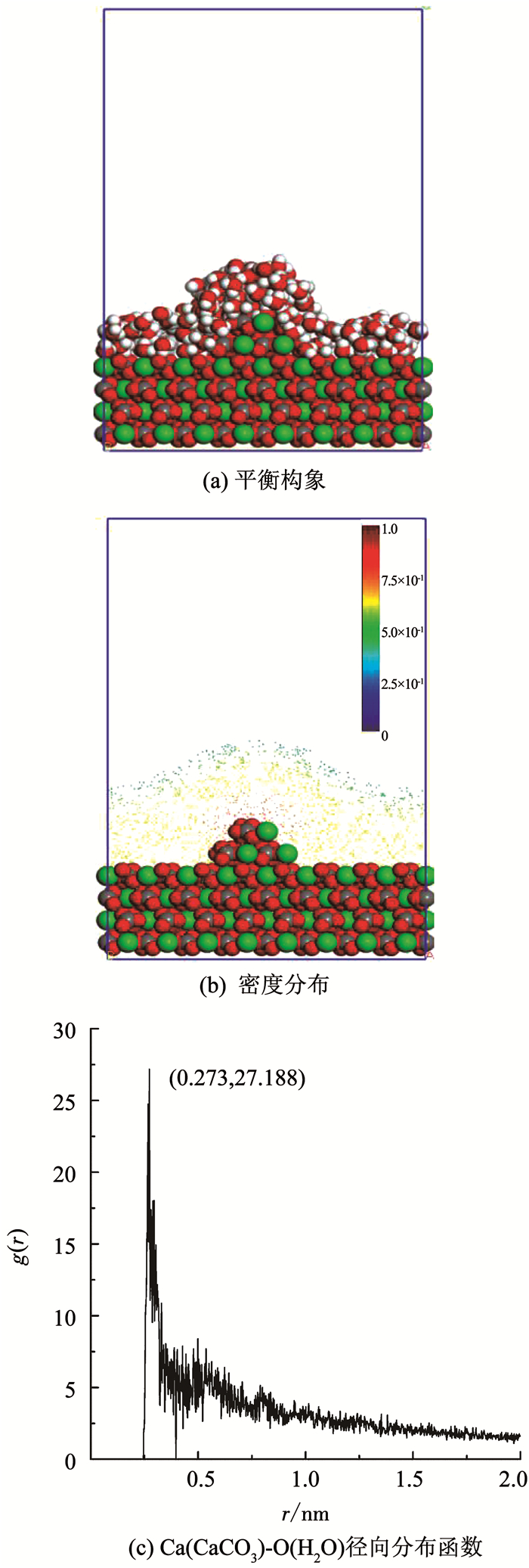
|
图 2 凸起方解石表面水分子吸附特征 Fig. 2 Adsorption characteristics of water molecules on protrude calcite surface |
图 3(a)、图 3(b)分别为水分子在空位方解石表面的吸附平衡构象和对应密度分布图.由图 3(a)、图 3(b)可知,水分子在空位方解石表面的吸附同样存在较强局域性,空位部分水分子异常聚集形成明显的吸附凸起,吸附量和吸附密度远高于与之竞争的理想表面部分.图 3(c)径向分布函数中空位方解石表面Ca(CaCO3)-O(H2O)径向分布函数在0.272 nm处达到峰值24.001,表面空位的存在增强了水分子在方解石表面的吸附的局域性与差异性.
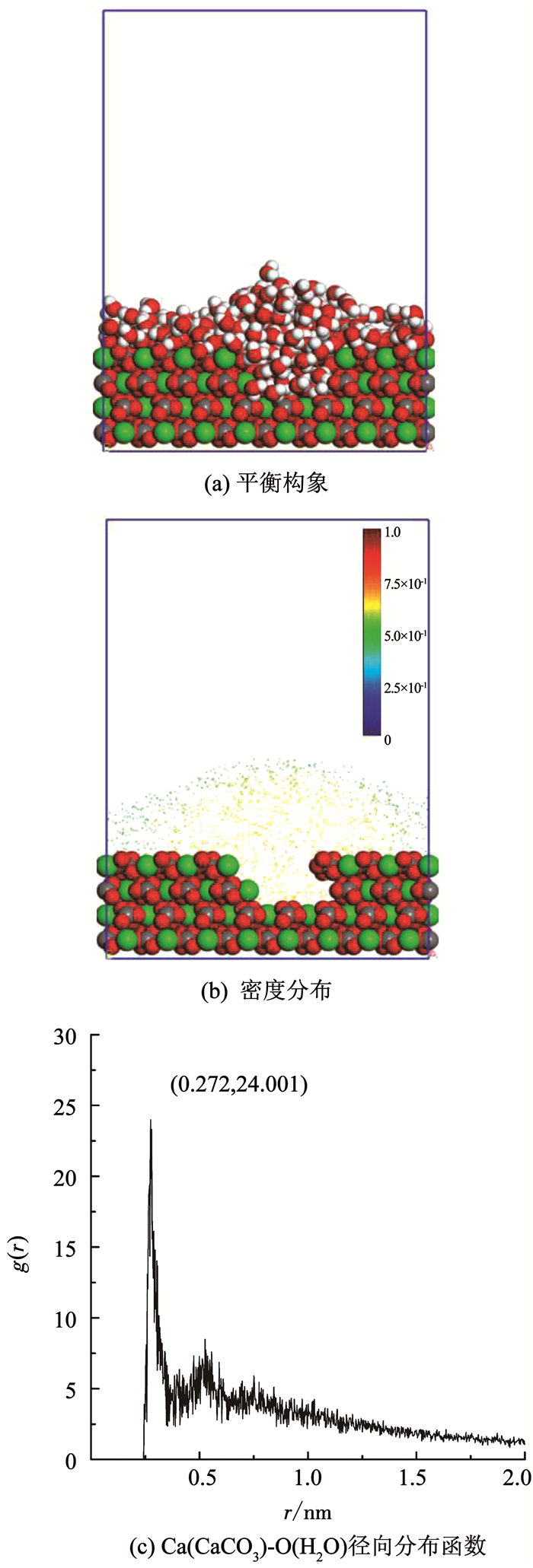
|
图 3 空位方解石表面水分子吸附特征 Fig. 3 Adsorption characteristics of water molecules on vacant calcite surface |
图 4(a)、图 4(b)分别为水分子在凸起、空位和理想水平等3种结构的方解石表面的吸附平衡构型和密度分布图.由图 4(a)、图 4(b)可知, 方解石表面结构直接影响水分子的吸附和分布特征.空位和凸起的存在使得水分子在方解石表面的吸附存在明显的局域性,空位和凸起处水分子的吸附量和吸附密度远高于理想水平表面部分.特别的,距离空位和凸起部分越近,水分子的排列越规则,密度越大,研究结论与Keller等[17]结果一致.因此,水分子在方解石表面吸附机理研究中必须充分考虑表面结构的影响.
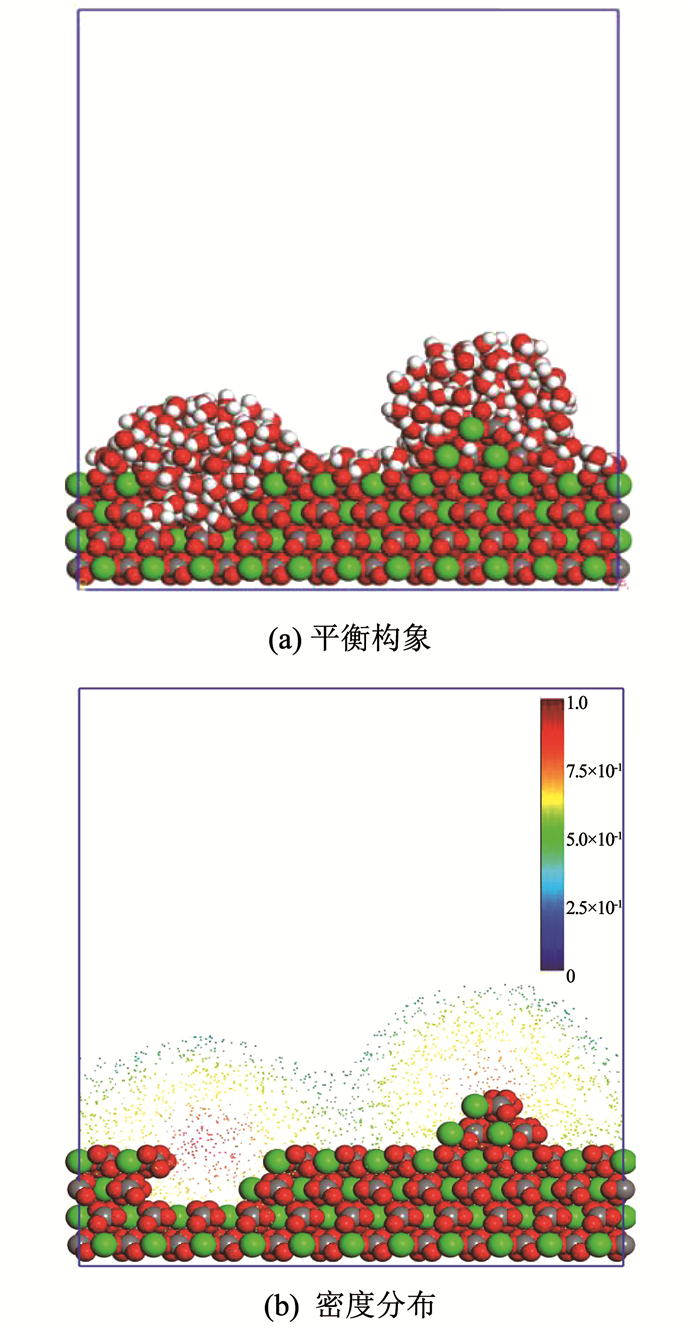
|
图 4 水分子在不同形态的方解石表面的吸附特征 Fig. 4 Adsorption characteristics of water molecules on calcite surface with different structures |
表面形态对水分子吸附的影响研究了凸起、空位和理想方解石表面水分子吸附特征,分析表面结构对于水分子吸附的重要影响.由于受到周围环境以及自身性质的影响,实际方解石晶体表面发育不同尺寸的表面结构[31-32],接下来,研究水分子在不同结构类型、不同结构尺寸的方解石表面吸附特征,分析结构尺寸对水分子吸附的影响.
图 5(a)、图 5(b)分别为水分子在两种不同尺寸的凸起方解石表面的吸附平衡构型和密度分布图.由图 5(a)、图 5(b)可知, 方解石表面凸起的尺寸对水分子吸附影响较大.凸起尺寸越大对水分子的吸附作用越明显,越多的水分子吸附到表面凸起周围,凸起周围水分子密度越高、排列越紧密.
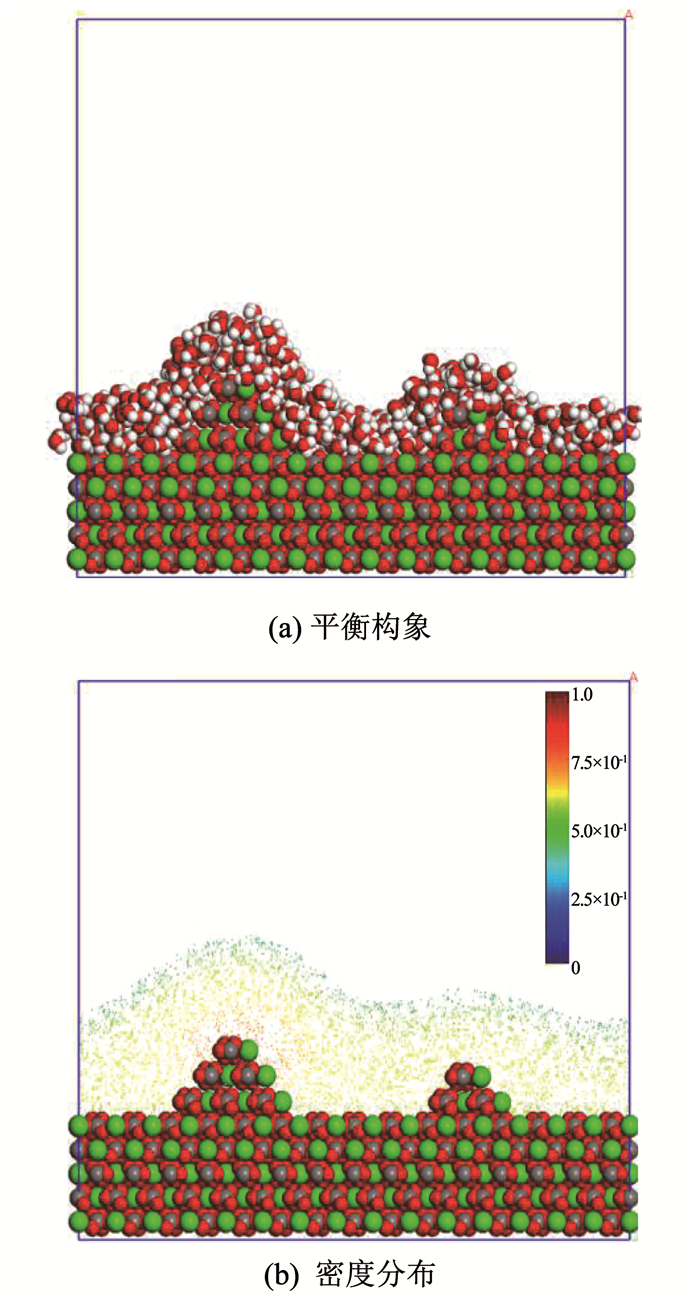
|
图 5 水分子在不同尺寸凸起方解石表面的吸附特征 Fig. 5 Adsorption characteristics of water molecules on calcite surface with different protrude scales |
图 6(a)、图 6(b)分别为水分子在两种不同尺寸的空位方解石表面的吸附平衡构型和密度分布图.由图 6(a)、图 6(b)可知, 方解石表面空位尺寸对水分子的吸附存在明显影响.方解石表面空位尺寸越大,对水分子吸附作用越强,水分子的聚集作用越明显,排列越规则、密度越大,形成的吸附凸起越大.
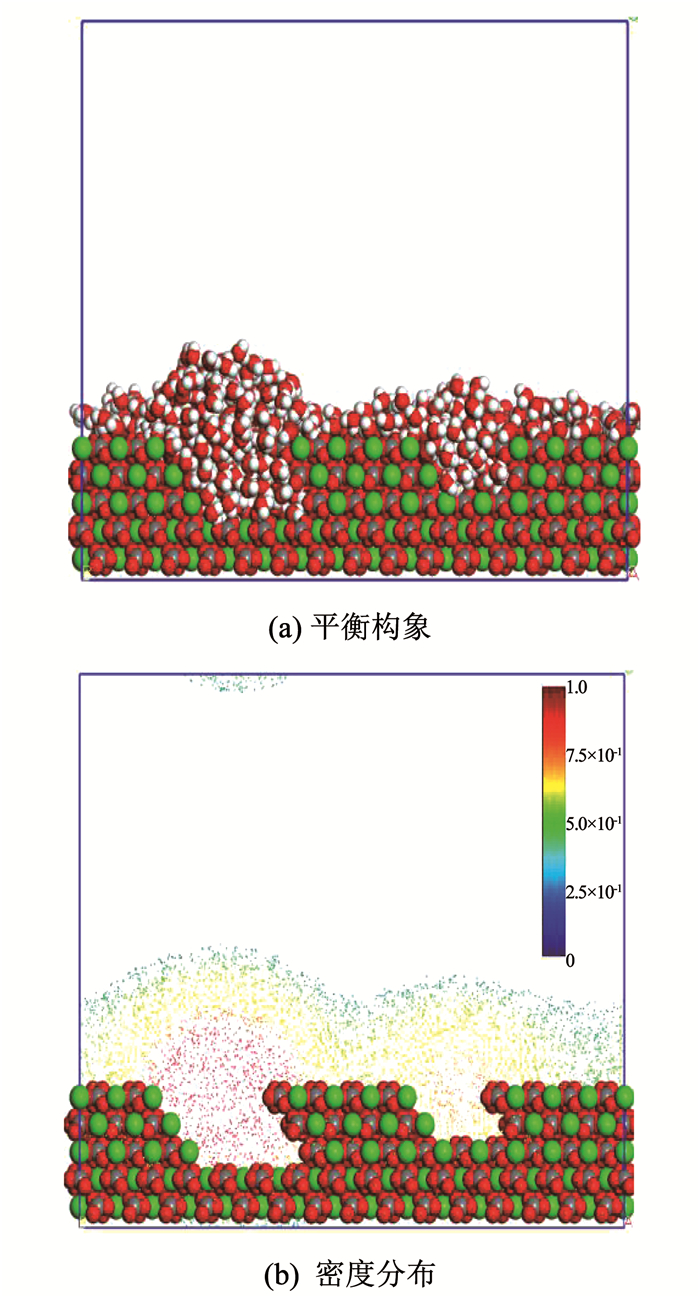
|
图 6 水分子在不同尺寸空位方解石表面吸附特征 Fig. 6 Adsorption characteristics of water molecules on calcite surface with different vacant scales |
图 7为800水分子在方解石纳米狭缝(理想和结构表面)中的吸附特征.由图 7(a)、图 7(b)可知, 当纳米狭缝之间包含800个水分子时,水分子均匀吸附到理想方解石表面密度最高,随着逐渐远离方解石表面密度逐渐降低,中间存在明显的连续流动空间.由图 7(c)、图 7(d)可知, 水分子在结构方解石表面吸附显示出较强的局域性,与单一结构方解石表面类似,水分子优先在方解石表面结构部位吸附,凸起和空位处水分子密度远高于理想方解石表面.纳米狭缝中两侧凸起相互对应位置,由于空间构型特点加上水分子的优先聚集,两个凸起部位吸附的水分子已经相互结合并形成密度较大的稳定水膜,将纳米狭缝内的连续流动空间阻断.凸起与空位处吸附的水分子之间存在明显的交换通道,一定程度上阻断流动空间.两个空位部分均形成了明显的吸附凸起,但是由于空间位置的限制,水分子稳定吸附于各自表面.综上所述,纳米狭缝内表面结构的存在直接影响狭缝内部水分子吸附和赋存规律,结构部位吸附的水分子结合成为水膜阻断连续流动空间,直接造成水锁效应.
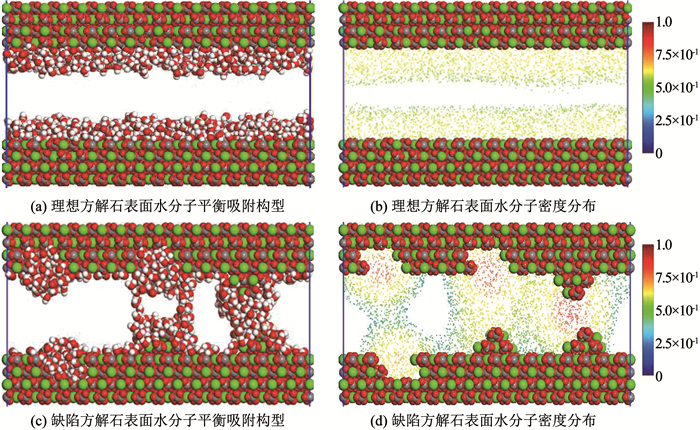
|
图 7 800个水分子纳米狭缝中的分布特征 Fig. 7 Distribution characteristics of 800 water molecules in nano-slit |
当纳米狭缝中水分子量到达1 200个,水分子吸附特征如图 8所示.由图 8(a)、图 8(b)可知, 理想方解表面水分子吸附特征变化不大,方解石表面水分子的排列最紧密、密度最大.随着逐渐原理方解石表面水分子密度稳定降低. 图 8(c)、图 8(d)可知, 随着纳米狭缝中水分子数量的增多,狭缝表面形态对于水分子吸附特征的影响加剧.纳米狭缝中表面凸起对应的部分的水锁效应更加明显,连续流动空间被进一步阻断.凸起与空位对应的部分形成的水分子交换通道进一步增强,水分子密度进一步增加.空位对应部分,水分子聚集效应增强伴随着密度的明显增加,之间的自由空间逐渐减小有相连的趋势.因此,纳米狭缝中方解石表面结构的存在造成了水分子在方解石表面吸附的局域性,结构部位形成的水膜阻断纳米孔隙中流动通道,形成明显的水锁效应.
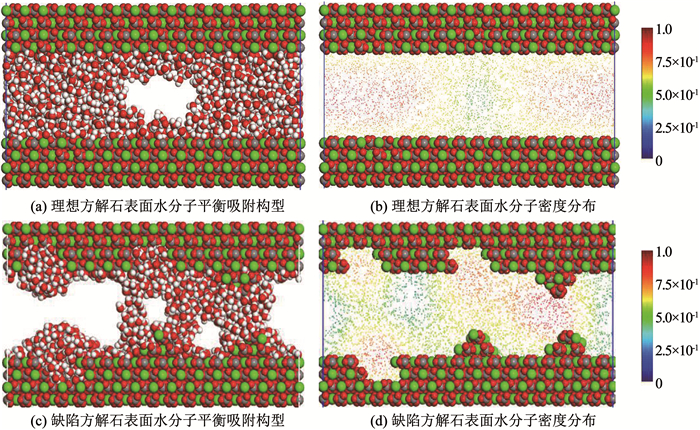
|
图 8 1 200个水分子在纳米狭缝中的分布特征 Fig. 8 Distribution characteristics of 1 200 water molecules in nano-slit |
晶体处于稳定状态时内部所有原子的成键轨道被电子充满,体系处于最低能量状态,难以发生化学反应[33].当沿某一方向切开晶体时,表面的原子失去了与之成键的邻位原子,点阵平面被截断,形成表面悬键[34].悬键的出现造成晶体表面高能态,表面趋于吸附环境中分子以重新达到最低能量状态,在此过程中晶体表面的高能悬键与环境分子相互作用.所以,晶体表面的悬键特征是控制晶体表面活性的关键[35-36].
文献[10, 25, 37]研究发现,H2O分子化学吸附于CaCO3(104)表面,二者之间存在电子交换和化学键的形成,其中H2O中的O原子和CaCO3(104)表面的Ca原子之间存在电子交换形成离子键,H2O中H原子和CaCO3(104)表面的O原子之间存在较弱的氢键作用.因此,水分子在方解石表面吸附特征直接与方解石表面Ca和O原子的成键特征有直接关系,以Ca原子为主.
3.2 方解石表面高能悬键特征图 9(a)为方解石晶胞内部原子结构图.图 9中可知, 方解石属于三方晶系,空间群为R3c,六方晶胞,a=b=0.499 nm,c=1.706 nm,α=β=90°,γ=120°. Ca2+与周围6个CO32-离子中的O结合为6配位,形成不规则八面体,Ca-O键长为0.235 nm. C与O形成3配位,C-O键长为0.128 nm,如图 9(b)所示.当前状态为方解石晶体最稳定状态,任何破坏当前体系内部配位状态的因素都将造成晶体高能态的出现.
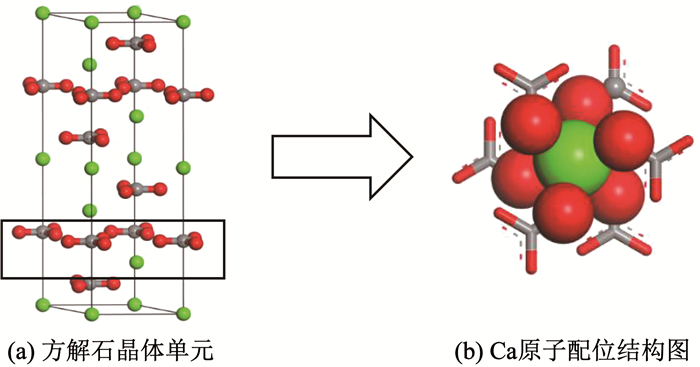
|
图 9 方解石晶体单元及内部原子配位结构 Fig. 9 Calcite crystal units and internal atomic coordination structure |
图 10为理想方解石表面、凸起和空位方解石表面所出现的悬键类型.由图 10(a)、图 10(d)可知, 理想CaCO3(104)表面Ca原子配位数为5,即每个Ca原子存在1个悬键可以与水分子相互作用.由图 10(b)、图 10(e)可知, CaCO3(104)表面凸起部位的Ca原子配位数仅有3个,对应每个Ca原子有3个悬键;CaCO3(104)表面空位部分的Ca原子配位数同样仅有3个,如图 10(c)、图 10(e)对比发现, CaCO3(104)表面的凸起和空位部位的悬键数量远高于理想方解石表面.因此,凸起和空位方解石表面和水分子反应能力和对水分子吸附能力远强于理想方解石表面.
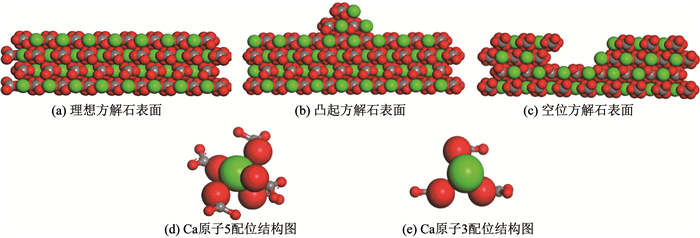
|
图 10 理想和缺陷方解石表面悬键特征 Fig. 10 Characteristics of dangling bonds on ideal and structured calcite surface |
为了定量表征方解石表面悬键与水分子吸附之间的相互关系,计算3种不同方解石表面的悬键数量以及悬键密度,确定方解石表面悬键数量对水分子吸附的影响见表 1.由表 1可知:不同方解石表面的悬键密度存在差异,其中理想CaCO3(104)表面悬键数量为48个,表面悬键密度为5.098 nm-2;凸起方解石表面悬键数量为72个,密度为6.716 nm-2远高于理想方解石表面;空位方解石表面悬键数量高达78个,悬键密度为7.275 nm-2.对比非常明显,凸起和空位方解石表面的悬键数量和悬键密度远高于理想方解石表面,说明二者表面有更多的水分子吸附位.因此,水分子在凸起和缺陷方解石表面的吸附作用更强,水分子密度和排列紧密程度远高于理想方解石表面.
| 表 1 3种不同结构的方解石表面悬键特征统计 Tab. 1 Characteristics of dangling bonds on three different calcite surfaces |
晶体沿某一方向断裂之后,表面层原子具有不饱和的价键,键能得不到补偿,使得表面质点较本体内质点具有额外的势能,称为表面能[38-39].表面能是表征表面活性的重要参数,表面能越小,表面的稳定性越高[40].此外,表面能受到表面结构影响较大,即使同一晶面,原子排列不同也会造成表面能不同,表面稳定性不同.因此,本文通过研究理想方解石表面、凸起和空位方解石表面的表面能,对比分析三者稳定性的强弱,解释水分子的吸附差异机理.表面能计算公式为
| $ {E_{{\rm{surface}}}} = \frac{{{E_{{\rm{slab}}}} - \left( {{N_{{\rm{slab}}}}/{N_{{\rm{bulk}}}}} \right) \times {E_{{\rm{bulk}}}}}}{A}. $ | (2) |
式中:Esurface为表面能; Eslab、Ebulk分别为表面模型和晶体原胞的总能量;Nslab、Nbulk分别为表面模型与原胞模型的原子数;A为表面模型面积.
计算可知,理想方解石表面、凸起和空位方解石表面的表面能存在较大差异.其中,理想方解石表面的表面能为0.581 J/m2,空位方解石表面的表面能0.734 J/m2,凸起方解石表面的表面能为0.721 J/m2.对比发现,理想方解石表面能远小空位和凸起方解石表面,即三者中理想方解石表面最为稳定,对水分子吸附作用相对较弱,空位方解石表面表面能最大,表面活性最强,对水分子吸附作用最强.
综上所述,研究发现理想方解石表面悬键密度远低于结构方解石表面,也就意味着相同条件下结构方解石表面具有更多的悬键可以与水分子反应,因此,结构方解石表面能够吸附更多的水分子.此外,理想方解石表面能远低于结构方解石表面,表面结构的存在活化了方解石表面,高能结构方解石表面倾向于吸附更多的水分子以降低表面能量.悬键密度和表面能共同解释了结构方解石表面对水分子吸附强度远高于理想方解石表面的现象.
4 结论1) 方解石表面结构对于水分子吸附具有重要影响,水分子优先在方解石表面结构处聚集吸附,吸附强度与密度远高于理想方解石表面处.
2) 方解石表面结构的尺寸对水分子吸附有较大影响,结构尺寸越大对水分子吸附越强.纳米狭缝中水分子在凸起和空位处快速聚集,形成的吸附凸起结合为水膜阻断流动空间,水锁作用明显.
3) 空位表面、凸起表面和理想表面对应的悬键密度和表面能依次为7.275 nm-2和0.734 J/m2、6.716 m-2和0.721 J/m2、5.098 nm-2和0.581 J/m2.空位表面和凸起表面具有更多的反应活性位点、更强的反应活性,因此,水分子优先吸附于空位表面和凸起表面.
| [1] |
SUN Zheng, SHI Juntai, WU Keliu, et al. Transport capacity of gas confined in nanoporous ultra-tight gas reservoirs with real gas effect and water storage mechanisms coupling[J]. International Journal of Heat and Mass Transfer, 2018, 126: 1007. DOI:10.1016/j.ijheatmasstransfer.2018.05.078 |
| [2] |
WIERZBICKA E, SYREK K, SULKA G D, et al. The effect of foil purity on morphology of anodized nanoporous ZrO2[J]. Applied Surface Science, 2016, 388: 799. DOI:10.1016/j.apsusc.2016.02.178 |
| [3] |
BAGHERI A, NAZARIA A, SANJAYA J G, et al. Molecular simulation of water and chloride ion diffusion in nanopores of alkali-activated aluminosilicate structures[J]. Ceramics International, 2018, 44(17): 20723. DOI:10.1016/j.ceramint.2018.08.067 |
| [4] |
ARISTILDE L, GALDI S M, KELCH S E, et al. Sugar-influenced water diffusion, interaction, and retention in clay interlayer nanopores probed by theoretical simulations and experimental spectroscopies[J]. Advances in Water Resources, 2017, 106: 24. DOI:10.1016/j.advwatres.2017.03.014 |
| [5] |
GU Zhen, WANG Huifeng, YING Yilun, et al. Ultra-low noise measurements of nanopore-based single molecular detection[J]. Science Bulletin, 2017, 62(18): 1245. DOI:10.1016/j.scib.2017.09.005 |
| [6] |
BALANNEC B, GHOUF A, SZYMCZYK A. Nanofiltration performance of conical and hourglass nanopores[J]. Journal of Membrane Science, 2018, 552(15): 336. DOI:10.1016/j.memsci.2018.02.026 |
| [7] |
曾凡林, 孙毅, 周玉. 有机材料的分子模拟模型(Ⅰ):单分子链的构建[J]. 哈尔滨工业大学学报, 2009, 41(10): 95. ZENG Fanlin, SUN Yi, ZHOU Yu. Molecular simulation models for organic materials (Ⅰ): A single molecular chain[J]. Journal of Harbin Institute of Technology, 2009, 41(10): 95. |
| [8] |
曾凡林, 孙毅, 周玉. 有机材料的分子模拟模型(Ⅱ):模拟元胞的构建[J]. 哈尔滨工业大学学报, 2010, 42(2): 242. ZENG Fanlin, SUN Yi, ZHOU Yu. Molecular simulation models for organic materials(Ⅱ): A simulation cell[J]. Journal of Harbin Institute of Technology, 2010, 42(2): 242. |
| [9] |
LU Gui, WANG Xiaodong, DUAN Yuanyuan. A critical review of dynamic wetting by complex fluids: from newtonian fluids to non-newtonian fluids and nanofluids[J]. Advances in Colloid and Interface Science, 2016, 236: 43. DOI:10.1016/j.cis.2016.07.004 |
| [10] |
LARDGE J S, DUFFY D M, GILLAN M J. Investigation of the interaction of water with the calcite (10.4) surface using ab initio simulation[J]. Journal of Physical Chemistry C, 2009, 113(17): 7207. DOI:10.1021/jp806109y |
| [11] |
DU Hao, MILLER J D. A molecular dynamics simulation study of water structure and adsorption states at talc surfaces[J]. International Journal of Mineral Processing, 2007, 84(1/2/3/4): 172. DOI:10.1016/j.minpro.2006.09.008 |
| [12] |
PICAUD S, COLLIGNON B, HOANG P N M, et al. Molecular dynamics simulation study of water adsorption on hydroxylated graphite surfaces[J]. Journal of Physical Chemistry B, 2006, 110(16): 8398. DOI:10.1021/jp056889t |
| [13] |
OU Xinwen, WANG Xiaofeng, LIN Zhang, et al. Heterogeneous condensation of water on the mica (001) surface: A molecular dynamics simulation work[J]. Journal of Physical Chemistry C, 2017, 121(12): 6813. DOI:10.1021/acs.jpcc.7b00855 |
| [14] |
KOPARDE V N, CUMMINGS P T. Molecular dynamics study of water adsorption on TiO2 nanoparticles[J]. Journal of Physical Chemistry C, 2007, 111(19): 6920. DOI:10.1021/jp0666380 |
| [15] |
De LEEUW N H, PARKER S C, HARDING J H. Molecular dynamics simulation of crystal dissolution from calcite steps[J]. Physical Review B, 1999, 60(19): 13792. DOI:10.1103/PhysRevB.60.13792 |
| [16] |
KRISTENSEN R, STIPP S L S, REFSON K. Modeling steps and kinks on the surface of calcite[J]. Journal of Chemical Physics, 2004, 121(17): 8511. DOI:10.1063/1.1775771 |
| [17] |
KELLER K S, OLSSON M H M, YANG M, et al. Adsorption of ethanol and water on calcite: Dependence on surface geometry and effect on surface behavior[J]. Langmuir, 2015, 31(13): 3847. DOI:10.1021/la504319z |
| [18] |
SPAGNOLI D, KERISIT S, PARKER S C. Atomistic simulation of the free energies of dissolution of ions from flat and stepped calcite surfaces[J]. Journal of Crystal Growth, 2006, 294(1): 103. DOI:10.1016/j.jcrysgro.2006.05.030 |
| [19] |
GUO Shusen, CAO Yongzhi, SUN Tao, et al. Influence of surface morphology on adsorption of potassium stearate molecules on diamond-like carbon substrate: A molecular dynamics study[J]. Applied Surface Science, 2018, 441: 708. DOI:10.1016/j.apsusc.2018.02.039 |
| [20] |
NADA H. Difference in the conformation and dynamics of aspartic acid on the flat regions, step edges, and kinks of a calcite surface: A molecular dynamics study[J]. Journal of Physical Chemistry C, 2014, 118(26): 14335. DOI:10.1021/jp502332c |
| [21] |
SUJITH K S, RAMACHANDRAN C N. Effect of surface roughness on adsorption and distribution of methane at the water-methane interface[J]. Journal of Molecular Liquids, 2018, 266(15): 856. DOI:10.1016/j.molliq.2018.06.119 |
| [22] |
KREKELBERG W P, SHEN V K, ERRINGTON J R, et al. Impact of surface roughness on diffusion of confined fluids[J]. Journal of Chemical Physics, 2011, 135(15): 154502. DOI:10.1063/1.3651478 |
| [23] |
SUN Huai. COMPASS: An ab initio force-field optimized for condensed phase applications-overview with details on alkane and benzene compounds[J]. Journal of Physical Chemistry B, 1998, 102(38): 7338. DOI:10.1021/jp980939v |
| [24] |
MCQUAID M J, SUN Huai, RIGBY D. Development and Validation of COMPASS force field parameters for molecules with aliphatic azide chains[J]. Journal of Computational Chemistry, 2004, 25(1): 61. DOI:10.1002/jcc.10316 |
| [25] |
柴汝宽, 刘月田, 王俊强, 等. 第一性原理研究H2O分子在CaCO3(104)表面吸附[J]. 原子与分子物理学报, 2018, 35(6): 1075. CHAI Rukuan, LIU Yuetian, WANG Junqiang, et al. First principles study on the adsorption of H2O molecule on CaCO3(104) surface[J]. Journal of Atomic and Molecular Physics, 2018, 35(6): 1075. DOI:10.3969/j.issn.1000-0364.2018.06.030 |
| [26] |
GAO Zhiyong, LI Chengwei, SUN Wei, et al. Anisotropic surface properties of calcite: A consideration of surface broken bonds[J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 2017, 520(5): 53. DOI:10.1016/j.colsurfa.2017.01.061 |
| [27] |
MEDEIROS S K, ALBUQUERQUE E L, MAIA F F, et al. Electronic and optical properties of CaCO3 calcite, and excitons in Si@CaCO3 and CaCO3@SiO2 core-shell quantum dots[J]. Journal of Physics D: Applied Physics, 2007, 40(18): 5747. DOI:10.1088/0022-3727/40/18/036 |
| [28] |
MARTYS N S, MOUNTAIN R D. Velocity verlet algorithm for dissipative-particle-dynamics-based models of suspensions[J]. Physical Review E (Statistical Physics Plasmas Fluids & Related Interdisciplinary Topics), 1999, 59(3): 3733. DOI:10.1103/physreve.59.3733 |
| [29] |
HUNENBERGER P H. Thermostat algorithms for molecular dynamics simulations[J]. Advances in Polymer Science, 2005, 173: 105. DOI:10.1007/b99427 |
| [30] |
WELLS B A, CHAFFEE A L. Ewald summation for molecular simulations[J]. Journal of Chemical Theory and Computation, 2015, 11(8): 3684. DOI:10.1021/acs.jctc.5b00093 |
| [31] |
WOLTHERS M, DI TOMMASO D D, DU Z, et al. Calcite surface structure and reactivity: Molecular dynamics simulations and macroscopic surface modelling of the calcite-water interface[J]. Physical Chemistry Chemical Physics, 2012, 14(43): 15145. DOI:10.1039/C2CP42290E |
| [32] |
WANG Jianwei, KALINICHEY A G, KIRKPATRICK R J, et al. Structure, energetics, and dynamics of water adsorbed on the muscovite (001) surface: A molecular dynamics simulation[J]. Journal of Physical Chemistry B, 2005, 109(33): 15893. DOI:10.1021/jp045299c |
| [33] |
SÖNGEN H, REISCHL B, MIYATA K, et al. Resolving point defects in the hydration structure of calcite (10.4) with three-dimensional atomic force microscopy[J]. Physical Review Letters, 2018, 120(11): 116101. DOI:10.1103/PhysRevLett.120.116101 |
| [34] |
LIU C Z, LIN C H, YEH M S, et al. Surface modification and planar defects of calcium carbonates by magnetic water treatment[J]. Nanoscale Research Letters, 2010, 5(12): 1982. DOI:10.1007/s11671-010-9736-5 |
| [35] |
LINDSAY R, DURR H A, WINCOTT P L, et al. Dangling-bond adsorption site for potassium on Si(100)-(2×1)[J]. Physical Review B, 1995, 51(16): 11140. DOI:10.1103/PhysRevB.51.11140 |
| [36] |
GAO Zhiyong, FAN Ruiying, RALSTON J, et al. Surface broken bonds: An efficient way to assess the surface behavior of fluorite[J]. Minerals Engineering, 2019, 130: 15. DOI:10.1016/j.mineng.2018.09.024 |
| [37] |
KERISIT S, PARKER S C, HARDING J H. Atomistic simulation of the dissociative adsorption of water on calcite surfaces[J]. Journal of Physical Chemistry B, 2003, 107(31): 7676. DOI:10.1021/jp034201b |
| [38] |
De LEEUW N H, PARKER S C. Surface structure and morphology of calcium carbonate polymorphs calcite, aragonite, and vaterite: An Atomistic Approach[J]. Journal of Physical Chemistry B, 1998, 102(16): 2914. DOI:10.1021/jp973210f |
| [39] |
GAO Zhiyong, SUN Wei, HU Yuehua, et al. Anisotropic surface broken bond properties and wettability of calcite and fluorite crystals[J]. Transactions of Nonferrous Metals Society of China, 2012, 22(5): 1203. DOI:10.1016/S1003-6326(11)61306-X |
| [40] |
De LEEUW N H, COOPER T G. A computational study of the surface structure and reactivity of calcium fluoride[J]. Journal of Materials Chemistry, 2003, 13(1): 93. DOI:10.1039/B208004D |
 2020, Vol. 52
2020, Vol. 52


