2. 天津大学 环境科学与工程学院,天津 300350
2. School of Environmental Science and Engineering, Tianjin University, Tianjin 300350, China
中国疆域幅员辽阔,同一建筑热工设计分区内由于温度及太阳辐射强度的差异,建筑能耗水平及其重要影响参数会有所不同[1],在建筑节能设计中不可视同一律,而寒冷地区由于需要兼顾冬季供暖和夏季制冷因此不确定性更强.研究中,局部法[2-3]、Morris法[4-6]、Sobol法[4]等多种敏感性分析均可用于建筑能耗相关模型以筛选重要参数,但就分析结果对能耗表现的优化效果却鲜有提及.
本文着眼于设计阶段,并将办公建筑室内环境营造负荷(包含全年供暖制冷负荷、电器及照明用电负荷)的影响因素作为研究对象,分别以北京、兰州、喀什、拉萨4个寒冷地区为气候背景实施Morris全局敏感性分析;之后采用相关性判定[6]对负荷进行优化,并与NSGA-Ⅱ算法的优化结果进行对比;旨在指出寒冷地区局域气候下建筑负荷的敏感性特征差异,并在此基础上评价基于Morris敏感性分析的优化效果.
1 方法敏感性分析可用于获取参数对结果的影响性排名,但局部法并不适用于建筑能耗相关模型的非线性特征,虽可得到重要参数集合却不推荐用于获取敏感度排名[7-9].文中所用Morris全局敏感性分析因计算成本低、模型适应性强[9-11],且对参数与结果的相关性有定性的描述[6, 10]而常被用于分析建筑能耗模型.相比于稳健性较好的基于方差的全局敏感性分析(如:Sobol法),在不要求因素间定量相关性描述的情况下,Morris法仅需Sobol法计算成本的几十分之一即可得到与其基本一致的参数敏感度排名[10-11].
Morris敏感性分析中,输出结果函数y(x)定义为
| $ y\left( x \right) = y\left( {{x_1}, {x_2}, {x_3}, \cdots , {x_k}} \right), $ |
式中,输入参数x的取值范围需映射到量纲一的区间[0, 1]并等分为p水平(本文p=4),即构成k维p水平的样本空间.之后根据OAT(one-factor-at-one-time)策略生成参数样本,其数量常采用轨迹进行计量,每个轨迹中的k+1个样本在运算后可得到参数的局部敏感度[12],即元素效应EEi为
| $ E{E_i} = \frac{{\left[ {y\left( x \right) - {y^i}\left( x \right)} \right]}}{\Delta }. $ |
式中:i∈{1, 2, 3, …, k};y(x)、yi(x)分别为xi变化前、后的输出结果;Δ为xi变化前后对应在量纲一的区间[0, 1]上的取值之差.
在对多轨迹实施运算后,可通过元素效应均值μ来表达参数的全局敏感度,但当参数相关性较强时,μ会因正负元素效应抵消而无法客观地反映参数重要性;因此,更推荐采用μ*表达敏感度[12].μ的正、负则可用来表达参数与结果的正、负相关性,配合相关性指标σ/μ*可对参数与结果的相关形式进行描述[6],进而对取值范围内的参数最优值进行判定(见表 1),相关公式定义如下:
| $ \mu = \frac{{\sum\limits_{i = 1}^r {E{E_i}} }}{r}, $ |
| $ {\mu ^*} = \frac{{\sum\limits_{i = 1}^r {\left| {E{E_i}} \right|} }}{r}, $ |
| $ \sigma = \sqrt {\frac{{\sum\limits_{i = 1}^r {{{\left| {E{E_i} - \mu } \right|}^2}} }}{r}} . $ |
| 表 1 参数的相关性描述 Tab. 1 Correlation description of parameters |
式中:r为轨迹数;σ为EEi的标准偏差;μ*为EEi的绝对均值,即敏感度.
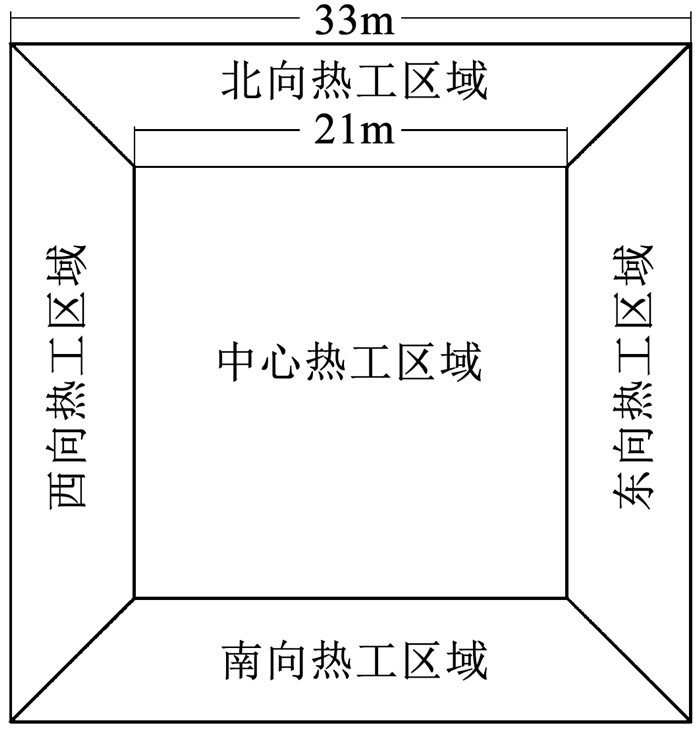
2 模型及相关参数说明模型为6层正方形办公建筑,总建筑面积6 534 m2、层高3.6 m,EnergyPlus中的热区划分如图 1所示.
|
图 1 办公建筑热区划分 Fig. 1 Partition of thermal zone in office building |
模型输入参数以围护结构热工参数为主,辅以室内负荷参数、室内供暖制冷设定温度等(共计42个).由于针对设计初期,并未对暖通空调参数做过多探讨;此外,为减少参数数量采用等效法将围护结构简化为单一结构层.
表 2中,通过结构厚度、导热系数、比热容、密度对非透明围护结构的热工性能进行描述,并将屋顶及外墙的传热系数通过导热系数和厚度控制在GB 50189―2015《公共建筑节能设计标准》规定[13]中寒冷地区的限值以内,楼板、地面、内墙则参考常规构造.室内供暖制冷设定温度、外窗及室内负荷参数取值见表 3,其中外表面空气渗透率约相当于2~7级门窗气密性[14].表皮辐射参数设定见表 4,其中太阳辐射吸收系数代表结构表皮对太阳辐射的吸收能力(波长在0.300~2.537 μm的辐射),而吸热系数则针对构件间的辐射换热(波长大于2.500 μm的辐射).
| 表 2 非透明围护结构参数取值 Tab. 2 Parameter setting of non-transparent envelop structure |
| 表 3 外窗、室内负荷、供暖制冷设定温度参数取值 Tab. 3 Parameter setting of window, internal loads, and set-point temperatures |
| 表 4 结构表皮辐射相关参数设定 Tab. 4 Setting of radiation-related parameters of structure surface |
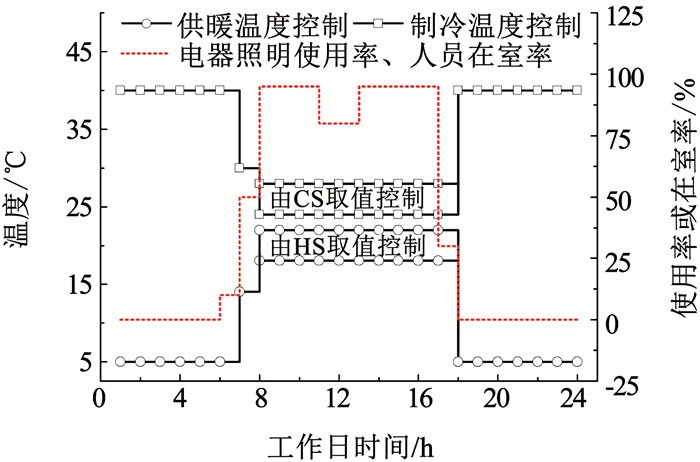
图 2为北京、兰州地区办公建筑运行设定,其中系统高负荷运行时段设为8:00-18:00,但喀什及拉萨由于与北京所属时区差异较大,因此需分别延后1.5 h和1.0 h.此外,人体活动水平及人均新风量分别设为100 W ·人-1和30 m3·(h·人)-1.
|
图 2 标准建筑运行设定 Fig. 2 Standard setting of building operation |
Morris敏感性分析中负荷模型的输出结果包含建筑供暖负荷、制冷负荷、电器及照明用电负荷;为表征建筑能耗水平将其合并为建筑室内环境营造负荷,并以单位面积全年累计量的形式进行分析.
2.3 气候参数中国寒冷地区地域广阔,室外温度、太阳辐射强度、以及局部气候上会存在一定差异,因此筛选地理跨度(经度、纬度、海拔)较大的4所城市作为气候背景,分别为北京、兰州、喀什、拉萨,其地理及气候信息见表 5.
| 表 5 各地区地理及气候信息(数据源自文献[15]) Tab. 5 Information of geography and climate of each region(data from literature[15]) |
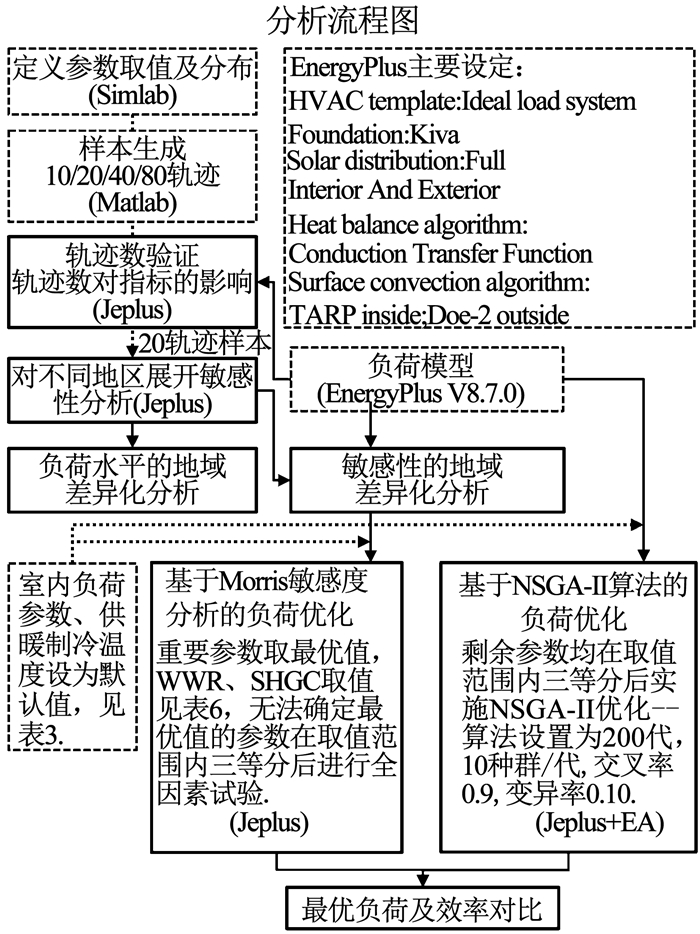
图 3为本文分析流程图,包含EnergyPlus中的基础设定及各步骤所需软件,其中批量模拟通过EnergyPlus和Jeplus实现.
|
图 3 分析流程图 Fig. 3 Flow chart of analysis |
Morris敏感性分析中,结果的准确性取决于样本对样本空间的全局性表达,而这与样本数量及采样方法关联较大.文中所用SU(sampling uniformity)采样法从300组样本中筛选出欧几里得距离最大的一组,并视其具有最佳全局性[16].而另一方面,由于模型、参数数量及取值的不同,轨迹数的确定还需单独验证.
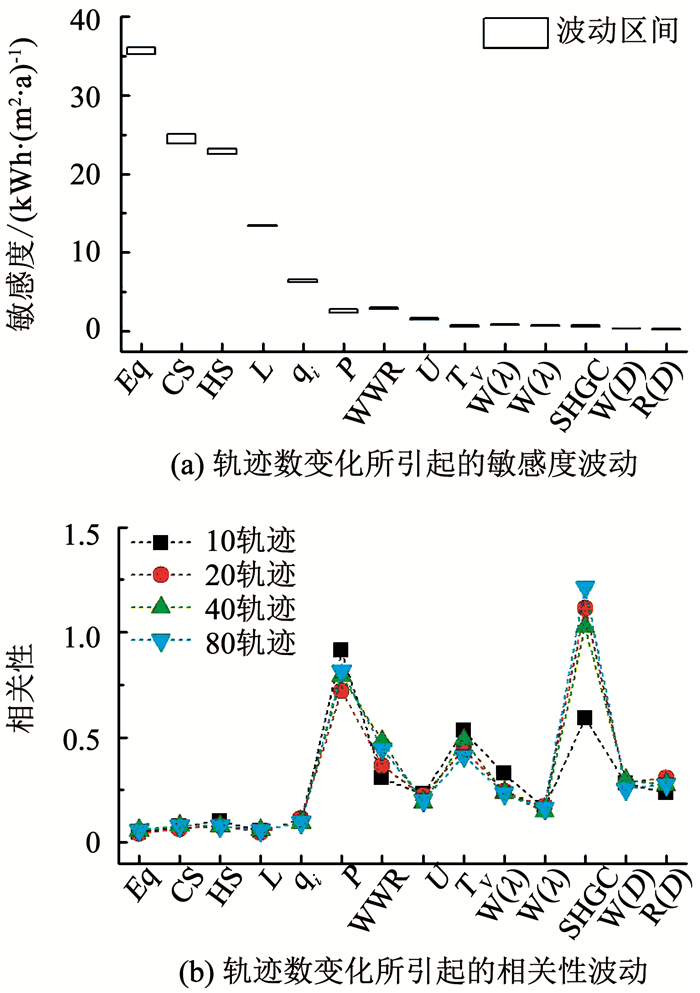
基于Morris法的建筑能耗分析中多采用不低于10轨迹的样本[5, 10],因此前期分析中通过SU采样法生成10、20、40、80轨迹数样本,并针对室内环境营造负荷(北京气候)实施敏感性分析.结果显示:对于敏感度排名前1/3的参数,轨迹数变化所引起的敏感度波动微弱,基本可忽略不计(图 4(a));相比之下,相关性受影响较大,但在20轨迹时已趋于稳定(图 4(b)),可用于后续分析.
|
图 4 轨迹数对敏感度和相关性的影响 Fig. 4 Impact of trajectory number on sensitivity and correlation indices |
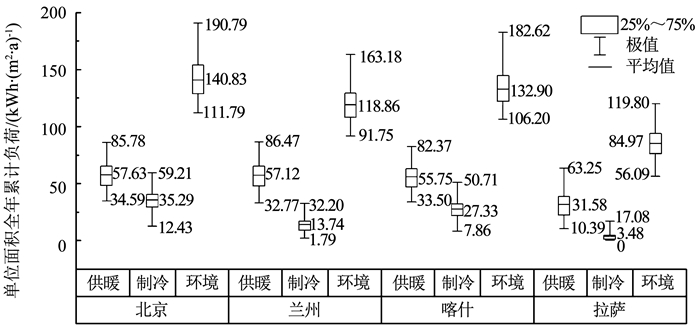
全局样本下,各地区建筑负荷分布如图 5所示.就室内环境营造负荷的整体水平而言,北京>喀什>兰州>拉萨,其间的差距主要源自各地区的供暖和制冷负荷.与制冷负荷不同,采暖度日数并不能很好地反映当地的供暖负荷水平,尤其是在采暖度日数最高的拉萨地区(3 425 ℃·d)反而供暖负荷水平最低,单位面积全年累计供暖负荷均值仅为31.6 kWh·(m2·a)-1.
|
图 5 敏感性分析中各地区建筑负荷分布 Fig. 5 Distributions of building loads in each region in the sensitivity analysis |
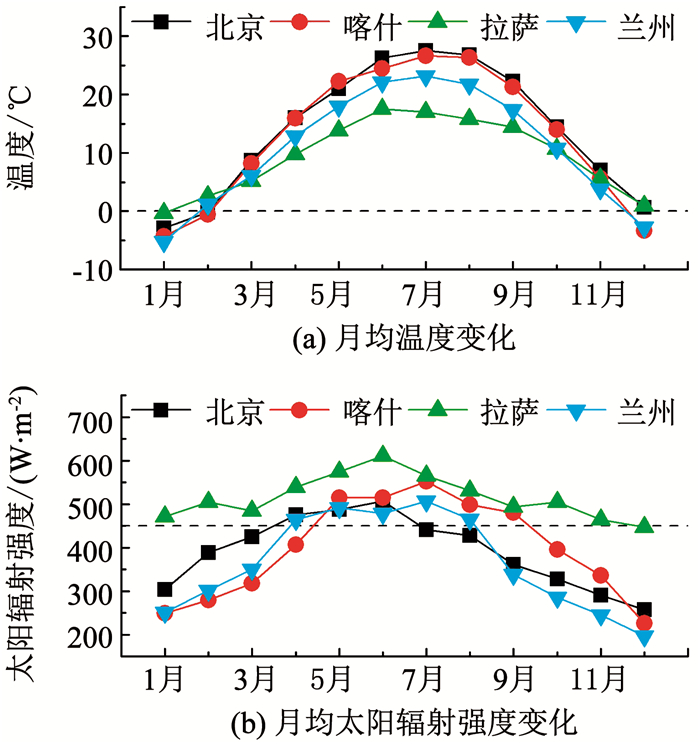
该现象与工作时段当地温度及太阳辐射强度有关.图 6中可见拉萨地区在工作时段±2 h内(此处考虑延迟作用)的室外温度月均值在冬季最低约为0 ℃,明显高于其他3个地区;不仅如此,当地该时段的冬季太阳辐射强度月均值大于450 W/m2,同样高于其他地区.在此综合作用下,拉萨表现出最低的供暖负荷水平.
|
图 6 温度、太阳辐射强度月均值(数据源自文献[17]) Fig. 6 Monthly mean value of temperature and solar radiation intensity(data from literature[17]) |
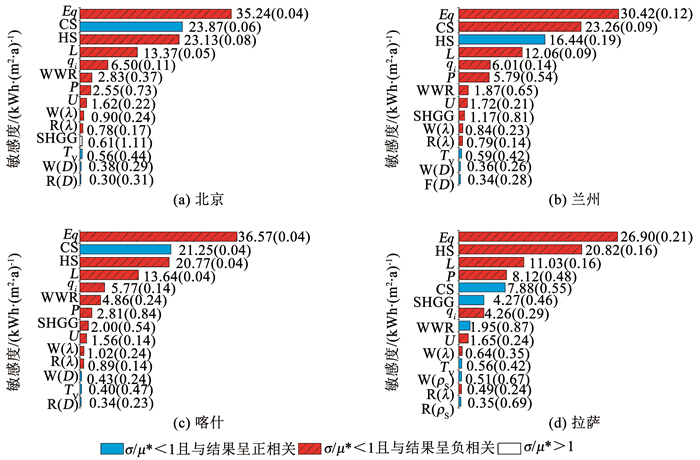
为排除低敏感参数的干扰,将各地区敏感度排名前1/3的参数定义为高敏感参数并做进一步分析(如图 7所示).4个地区中,室内负荷参数及供暖制冷设定温度排名靠前,且除人均占建筑面积(P)外均可视为与室内环境营造负荷呈线性相关.排名靠后的围护结构参数中,导热相关参数,如:U、R(λ)、W(D),与室内环境营造负荷在各地区均为单调相关且正负相关性一致,因此具有相同的最优值.
|
图 7 高敏感参数敏感度及相关性(括号内为相关性) Fig. 7 Sensitivity and correlation indices of high-sensitivity parameters (bracket: correlation index) |
敏感性的地域差异则主要表现在两方面,首先是拉萨地区辐射相关参数影响的突显,图 7(d)中可见屋顶及外墙的外表面太阳辐射吸收系数与其结构平均导热系数的敏感度相近.另外,WWR和SHGC与负荷的正、负相关性存在地域差异,如WWR在北京、兰州、喀什均与室内环境营造负荷呈正相关而在拉萨却为负相关,对此需考虑朝向并做进一步分析.
表 6、7为各朝向外围热区中SHGC和WWR对室内环境营造负荷的敏感度以及根据相关性确定的取值范围内最优值;可见,相比于图 7中的建筑整体敏感度,二者对外围空间负荷的影响有显著提升,其中SHGC多在南向影响最强(喀什为西向);而WWR多为西向最强(拉萨为南向).对于最优值,二者多数情况下都存在朝向差异或不确定性,仅在拉萨(SHGC: 0.52)和喀什(WWR: 0.25)分别表现出相同的各朝向最优值.
| 表 6 SHGC在不同朝向的敏感度及最优值 Tab. 6 Sensitivity and optimal value of SHGC in different orientations in each region |
| 表 7 WWR在不同朝向的敏感度及最优值 Tab. 7 Sensitivity and optimal value of WWR in different orientations in each region |
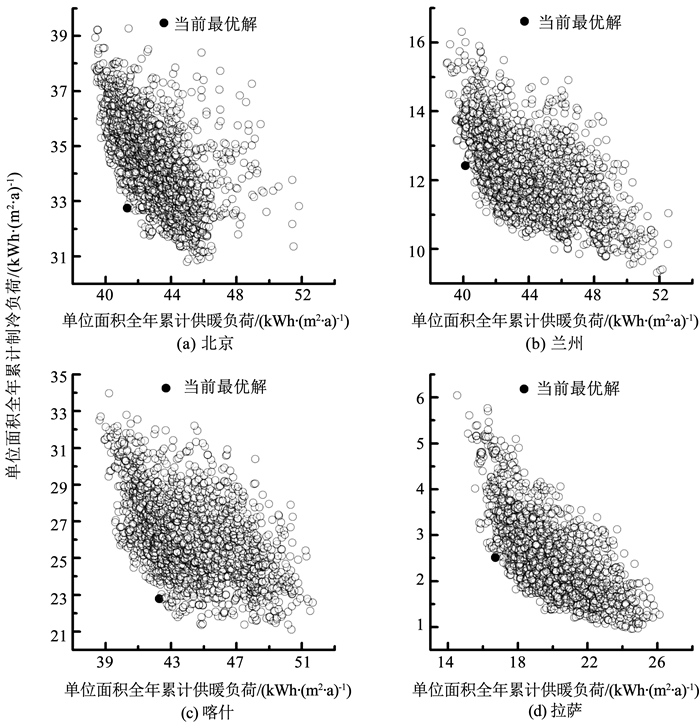
在对各朝向外围空间实施Morris敏感性分析后,无法确定最优值的参数已仅剩个别外窗参数,数量较少——北京0个、兰州2个、喀什1个、拉萨3个(见表 6).此时可对该类参数采用全因素试验来获取最优室内环境营造负荷.为评价该方法的优化表现,将NSGA-Ⅱ算法的优化结果及耗时与之进行对比,操作流程及设定如图 3所示.由于室内负荷参数取值已经固定,图 8中着重突显NSGA-Ⅱ算法对供暖及制冷负荷的优化效果,可见200代(10种群/代)时的帕累托前沿重叠度已较高,继续优化的意义不大.表 8中可见与耗时逾6 h的NSGA-Ⅱ优化结果相比,基于Morris敏感性分析的最优解更小,且总耗时可至少降低1/3(约2 h).此外,由全因素试验所得不确定参数的最优值如下:兰州(SHGC东: 0.52,SHGC西: 0.52),喀什(SHGC南: 0.52),拉萨(WWR北: 0.33,WWR东: 0.33,WWR西: 0.25).
|
图 8 NSGA-Ⅱ算法优化所得各地供暖制冷负荷分布 Fig. 8 Heating and cooling loads distribution of NSGA-Ⅱ optimization in different regions |
| 表 8 最优室内环境营造负荷及总耗时对比 Tab. 8 Comparison of optimal indoor environmental construction loads and total time consumption |
1) 相比于敏感度(μ*),相关性(σ/μ*)受样本数量影响更为显著;若单纯考虑敏感度,样本数量可酌情降低,文中基于SU采样法的样本数量可至少从20降至10轨迹.
2) 采暖度日数并不能很好地反映寒冷地区办公建筑的供暖负荷水平,更应综合考虑工作时段室外温度及太阳辐射强度.
3) 围护结构参数中,辐射相关参数在太阳能资源丰富地区应予以重视.以拉萨为例,外墙及屋顶外表面太阳辐射吸收系数对室内环境营造负荷的影响可接近相应结构的平均导热系数.
4) 在节能标准[13]对寒冷地区建筑围护结构的热工性能限定下,各地屋顶、外墙的导热系数和厚度以及外窗传热系数与室内环境营造负荷均表现为单调相关且正负相关性稳定.而另一方面,相比于敏感度的朝向差异,SHGC和WWR的相关性在地域及朝向上的差异会直接影响对参数最优值的判断,在节能设计中应予以重视.
5) 200代(10种群/代)的NSGA-Ⅱ优化结果可证实基于Morris敏感性分析的优化在节能设计中的有效性,且显示出其效率上的优势.
| [1] |
刘大龙, 刘加平, 张习龙, 等. 青藏高原气候条件下的建筑能耗分析[J]. 太阳能学报, 2016, 37(8): 2167. LIU Dalong, LIU Jiaping, ZHANG Xilong, et al. Building energy consumption analysis in climate condition of Tibetan plateau[J]. Acta Energiae Solaris Sinica, 2016, 37(8): 2167. DOI:10.3969/j.issn.0254-0096.2016.08.041 |
| [2] |
刘立, 刘丛红, 吴迪, 等. 天津办公建筑空间设计因素节能分析与优化[J]. 哈尔滨工业大学学报, 2018, 50(4): 181. LIU Li, LIU Conghong, WU Di, et al. Energy saving analysis and optimization of geometric factors of office buildings in Tianjin[J]. Journal of Harbin Institute of Technology, 2018, 50(4): 181. DOI:10.11918/j.issn.0367-6234.201608092 |
| [3] |
杨柳, 侯立强, 李红莲, 等. 空调办公建筑能耗预测回归模型[J]. 西安建筑科技大学学报(自然科学版), 2015, 47(5): 707. YANG Liu, HOU Liqiang, LI Honglian, et al. Regression models for energy consumption prediction in air-conditioned office building[J]. Journal of Xi'an University of Architecture & Technology (Natural Science Edition), 2015, 47(5): 707. DOI:10.15986/j.1006-7930.2015.05.017 |
| [4] |
MASTRUCCI A, PÉREZ-LÓPEZ P, BENETTO E, et al. Global sensitivity analysis as a support for the generation of simplified building stock energy models[J]. Energy and Buildings, 2017, 149: 368. DOI:10.1016/j.enbuild.2017.05.022 |
| [5] |
HEISELBERG P, BROHUS H, HESSELHOLT A, et al. Application of sensitivity analysis in design of sustainable buildings[J]. Renewable Energy, 2009, 34(9): 2030. DOI:10.1016/j.renene.2009.02.016 |
| [6] |
SANCHEZ D G, LACARRIÉRE B, MUSY M, et al. Application of sensitivity analysis in building energy simulations: Combining first-and second-order elementary effects methods[J]. Energy and Buildings, 2014, 68(1): 741. DOI:10.1016/j.enbuild.2012.08.048 |
| [7] |
DELGARM N, SAJADI B, AZARBAD K, et al. Sensitivity analysis of building energy performance: A simulation-based approach using OFAT and variance-based sensitivity analysis methods[J]. Journal of Building Engineering, 2018, 15: 181. DOI:10.1016/j.jobe.2017.11.020 |
| [8] |
HEMSATH T L, BANDHOSSEINI K A. Sensitivity analysis evaluating basic building geometry's effect on energy use[J]. Renewable Energy, 2015, 76: 526. DOI:10.1016/j.renene.2014.11.044 |
| [9] |
KRISTENSEN M H, PETERSEN S. Choosing the appropriate sensitivity analysis method for building energy model-based investigations[J]. Energy and Buildings, 2016, 130: 166. DOI:10.1016/j.enbuild.2016.08.038 |
| [10] |
MENBERG K, HEO Y, CHOUDHARY R. Sensitivity analysis methods for building energy models: Comparing computational costs and extractable information[J]. Energy and Buildings, 2016, 133: 433. DOI:10.1016/j.enbuild.2016.10.005 |
| [11] |
NGUYEN A T, REITER S. A performance comparison of sensitivity analysis methods for building energy models[J]. Building Simulation, 2015, 8(6): 651. DOI:10.1007/s12273-015-0245-4 |
| [12] |
SALTELLI A, RATTO M, ANDRES F, et al. Global sensitivity analysis: The primer[M]. England: John Wiley & Sons Ltd, 2008. DOI:10.1002/9780470725184.ch6
|
| [13] |
中国建筑科学研究院.公共建筑节能设计标准: GB 50189―2015[S].北京: 中国建筑工业出版社, 2015 China Academy of Building Research. Designstandard for energy efficiency of public buildings: GB 50189―2015[S]. Beijing: China Architecture & Building Press, 2015 |
| [14] |
中华人民共和国国家质量监督检验检疫总局.建筑外门窗气密、水密、抗风压性能分级及检测方法: GBT 7106―2008[S].北京: 中国标准出版社, 2015 General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China. Graduations and test methods of air permeability, water tightness, wind load resistance performance for building external windows and doors: GBT 7106―2008[S]. Beijing: Standards Press of China, 2015 |
| [15] |
中华人民共和国住房和城乡建设部.民用建筑热工设计规范: GB 50176―2016[S].北京: 中国建筑工业出版社, 2016 Ministry of Housing and Urban-Rural Construction of the People's Republic of China. Code for thermal design of civil building: GB 50176―2016[S]. Beijing: China Architecture & Building Press, 2016 |
| [16] |
KHARE Y P, MUÑOZ-CARPENA R, ROONEY R W, et al. A multi-criteria trajectory-based parameter sampling strategy for the screening method of elementary effects[J]. Environmental Modelling & Software, 2015, 64: 230. DOI:10.1016/j.envsoft.2014.11.013 |
| [17] |
EnergyPlus. EnergyPlus软件官方网站[DB/OL].[2019-05-13]. https://www.energyplus.net/weather
|
 2020, Vol. 52
2020, Vol. 52


