2. 西安建筑科技大学 建筑学院, 西安 710055;
3. 西安建筑科技大学 机电工程学院, 西安 710055
2. School of Architecture, Xi'an University of Architecture and Technology, Xi'an 710055, China;
3. School of Mechanical and Electrical Engineering, Xi'an University of Architecture and Technology, Xi'an 710055, China
到达地面的太阳辐射分为直射辐射和散射辐射,散射辐射主要受大气成分、云量的影响;准确可靠的散射辐射数据是建筑能耗模拟、负荷计算、遮阳设计、太阳能利用的基础,计算斜面的太阳辐射数据也需要水平面的直射、散射辐射数据做支撑.使用高精度的测量设备实时采集是获得准确、足量数据的最有效的方法,但限于资金和维护等问题,中国辐射观测台站较少. 1993年,辐射观测站调整为98个,其中仅有17个台站记录了水平面散射辐射数据,并且呈现了东多稀少、平原多山地少的分布特征[1];在已有的观测台站中,连续记录超过10年的数据大多集中在20世纪80~90年代初,近20年的直、散辐射数据严重匮乏.因此,亟需选择适当的模型计算中国不同地区散射辐射数据.
散射辐射模型的研究起源于20世纪60年代,发展至今,出现了上百篇相关计算方法的研究,总结起来,主要为建立散射比(水平面日散射辐射与水平面日总辐射之比)或散射率(定义为水平面散射辐射与水平面天文辐射之比)与晴空指数、日照时数比、云量等气象因子之间的相关关系,包括单个因子的线性、多项式、指数、对数、幂函数形式以及考虑多因子综合作用的多项式形式.根据计算尺度的不同,可分为月均值与日值,其中计算月均值的模型较多,日值模型包含在月均值模型中,详见表 1.
| 表 1 日散射辐射模型类别及表达式 Tab. 1 Classification and expression of daily diffuse radiation estimation models |
这些研究多以实测数据进行模型的建立或对模型进行修正,采用误差分析方法评价模型的优劣,进而得到适合这一地区的最优模型,包括模型形式及经验系数.由于地区气候差异性,没有得到统一的模型;例如,Boukelia等[17]基于阿尔及利亚地区,发现以晴空指数为输入参数的二次或三次多项式形式最准确;Jamil等[18]认为以晴空指数、日照时数比为输入参数的一次函数适合印度地区;Sabzpooshani等[19]发现基于日照时数比的三次多项式最适合伊朗伊斯法罕地区月均散射辐射的计算.李峥嵘等[20]研究得到了适合上海地区的日散射辐射模型;马年骏等[21]研究表明,考虑晴空指数、日照百分率的模型估算精度优于单一晴空指数的分段函数模型;冯巍等[22]以北京地区数据为基础,验证了Erbs、张晴原等10种模型的计算精度,得出晴空指数是影响散射辐射估算精度的最主要因素,考虑晴空指数为输入参数的分段函数最准确.相关研究[17, 23]证实,这类模型的经验系数与地理位置有很大的关系,具有显著的地区差异性,对于缺少观测台站的西部及偏远的农村地区,在应用此类模型计算日散射辐射时,其经验系数取多少合适,尚有待研究.文献[23-25]在计算总辐射时,在温度、日照时数、相对湿度等气象参数的基础上,加入了纬度、海拔高度等地理参数的修正,结果表明,修正后的模型准确度有所降低,但可以满足计算精度的要求,实现了总辐射数据的“从无到有”;文献[17]根据阿尔及利亚6个城镇的散射辐射、气象数据,拟合了散射比与日照时数比、晴空指数的关系,但这是一种平均化状态,弱化了纬度、海拔高度对太阳辐射的影响.因此,本文根据观测台站的辐射数据建立模型经验系数与地理参数关系,以计算未观测站点的散射辐射数据.本文以实测数据进行不同模型在不同地区的适应性分析,以准确度相对较高、形式简单的模型为基础,建立考虑纬度、海拔高度等地理参数修正的模型,对比修正前后模型的准确度,验证此类方法的可行性.
1 数据与方法 1.1 数据来源文中所用到的数据均来自中国国家气象信息中心日值气象、辐射数据集,建模所涉及到的数据包括水平面日总辐射、水平面日散射辐射及日照时数等气象要素.选择北京等17个台站2000—2017年观测数据,其中,每个台站前10年数据用来建模,后4年数据用来验证,各个台站经纬度等基本信息及建模、验证数据时间段见表 2.
| 表 2 17个台站的基本信息 Tab. 2 Basic information of the 17 stations |
测量技术和设备精度都会带来误差,所以在建模之前有必要对散射辐射数据进行质量控制,本文采用Younes等[26]提出的散射包络线法筛选出异常的散射辐射数据.该方法包括如下步骤: 1)删除kt、kdf落在[0, 1]区间以外的值;2)将剩下的数据根据kt分成10个相等的数据带,对于每一个数据带b,求出相应散射比的平均值kdf, b和标准偏差σb,做出两条上、下包络线,下包络线flow是10对(ktb, kdf, b- 2σb)数据的二次拟合曲线,上包络线fup是10对(ktb,kdf, b+2σb)数据的二次拟合曲线,其中ktb是每个数据带b中晴空指数的中值,若散点在上、下包络线范围之外则属于异常数据.
文中以北京(54511)为例,按照上述方法分别计算得到上、下包络线,将包络线与散点图叠加,如图 1所示,上、下包络线之外的数据则为异常数据.将17个台站依次完成质量控制,将异常数据删去,其余通过质量控制的数据将用于后续建模与模型验证.
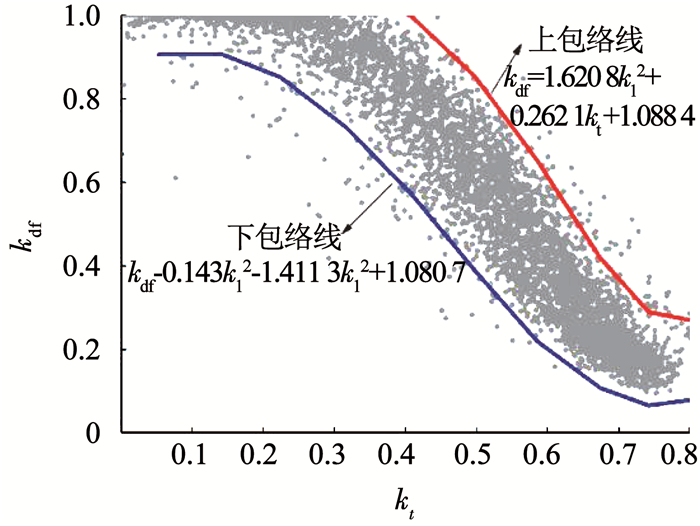
|
图 1 散射辐射数据质量控制图 Fig. 1 Quality control chart of diffuse radiation data |
文献[27-28]证实散射率模型的准确度低于散射比模型,加入日平均温度和相对湿度的多因子的散射比模型并不能显著提高模型准确度.因此本文不再考虑散射率模型,而是选择散射比模型,模型的输入参数为单一的晴空指数、日照时数比以及晴空指数、日照时数比共同作用的模型,模型形式为多项式函数、对数形式、指数形式,共12个模型,具体见表 3.
| 表 3 日散射辐射推测模型汇总表 Tab. 3 Summary of daily diffuse radiation models |
为了比较模型的优劣,引入了3个评价指标,分别为平均绝对误差百分比(MAE)、均方根误差百分比(RMSE)和决定系数(R2),计算如下:
| $ {\rm{MAE = }}\left( {\frac{1}{n}\sum\limits_{i = 1}^n {\left| {{I_{e, i}} - {I_{m, i}}} \right|} } \right)/\overline I \times 100\% , $ |
| $ {\rm{RMSE = }}\left( {\sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{I_{e, i}} - {I_{m, i}}} \right)}^2}} } } \right)\overline I \times 100\% , $ |
| $ {R^2} = 1 - \frac{{\sum\limits_{i = 1}^n {{{\left( {{I_{m, i}} - {I_{e, i}}} \right)}^2}} }}{{\sum\limits_{i = 1}^n {{{\left( {{I_{m, i}} - \overline I } \right)}^2}} }}. $ |
式中:Ie, i为模型计算值,MJ·m-2;Im, i为实测值,MJ·m-2;I为实测值的平均值,MJ·m-2;n为数据总量.
MAE、RMSE越小越好.R2数值范围介于-∞~1之间,R2越接近于1越好;R2接近于0表示计算值接近实测平均值,总体结果可信,但估算误差较大;R2 < 0,表示计算值小于实测值,结果不可信.
2 结果与讨论 2.1 单站点模型以上述17个台站质量控制后的数据进行模型适应性研究,选择相应的数据建模,拟合17个模型的经验系数,如图 2所示;依据相应时间段的数据进行模型验证,依次计算模型的R2、MAE和RMSE值,按晴空指数由低到高排序,绘制不同模型的MAE、RMSE及R2,结果如图 3~5所示.
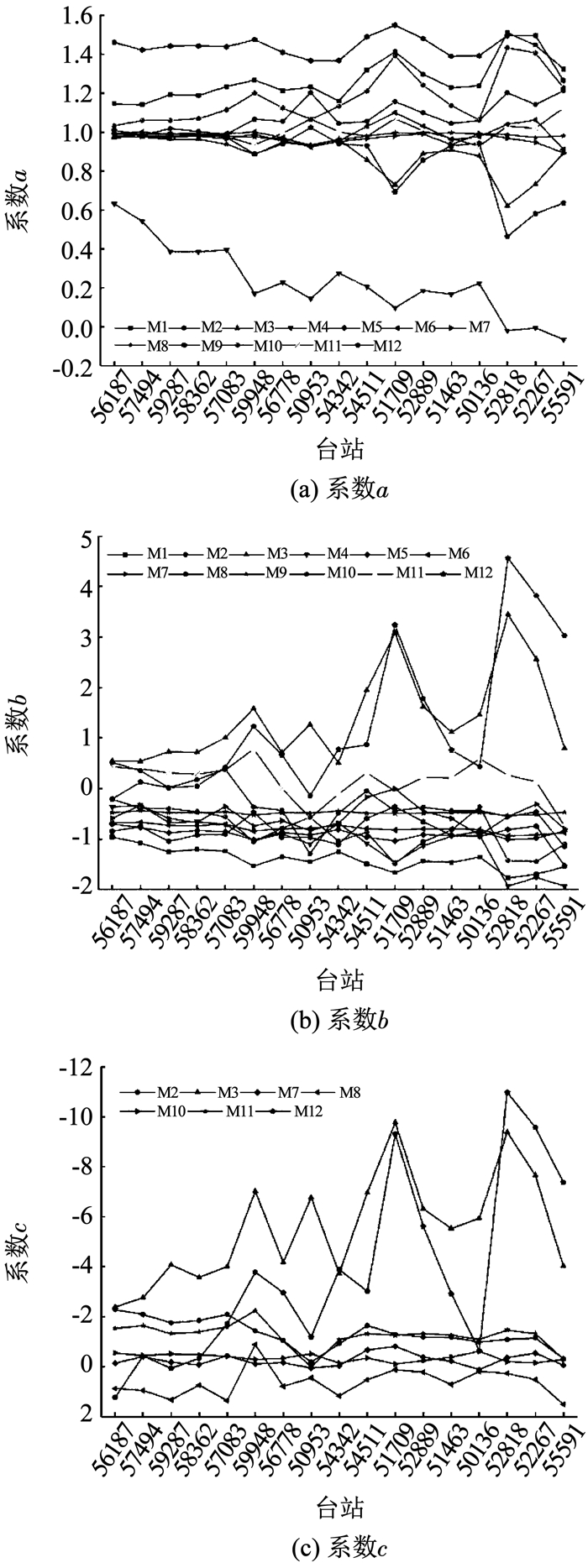
|
图 2 M1~M12的经验系数 Fig. 2 Empirical coefficient of M1~M12 |
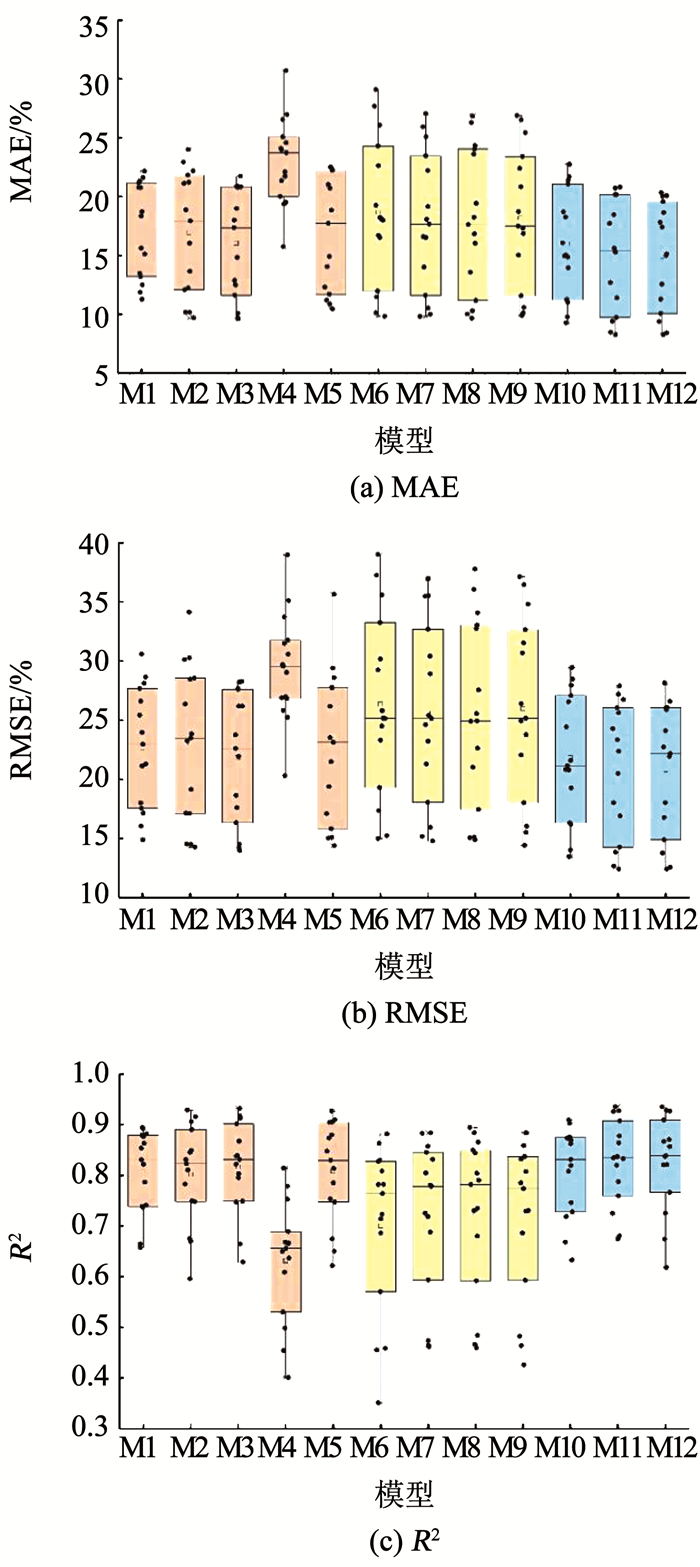
|
图 3 12个模型的误差评价指标 Fig. 3 Evaluation index of the 12 models |
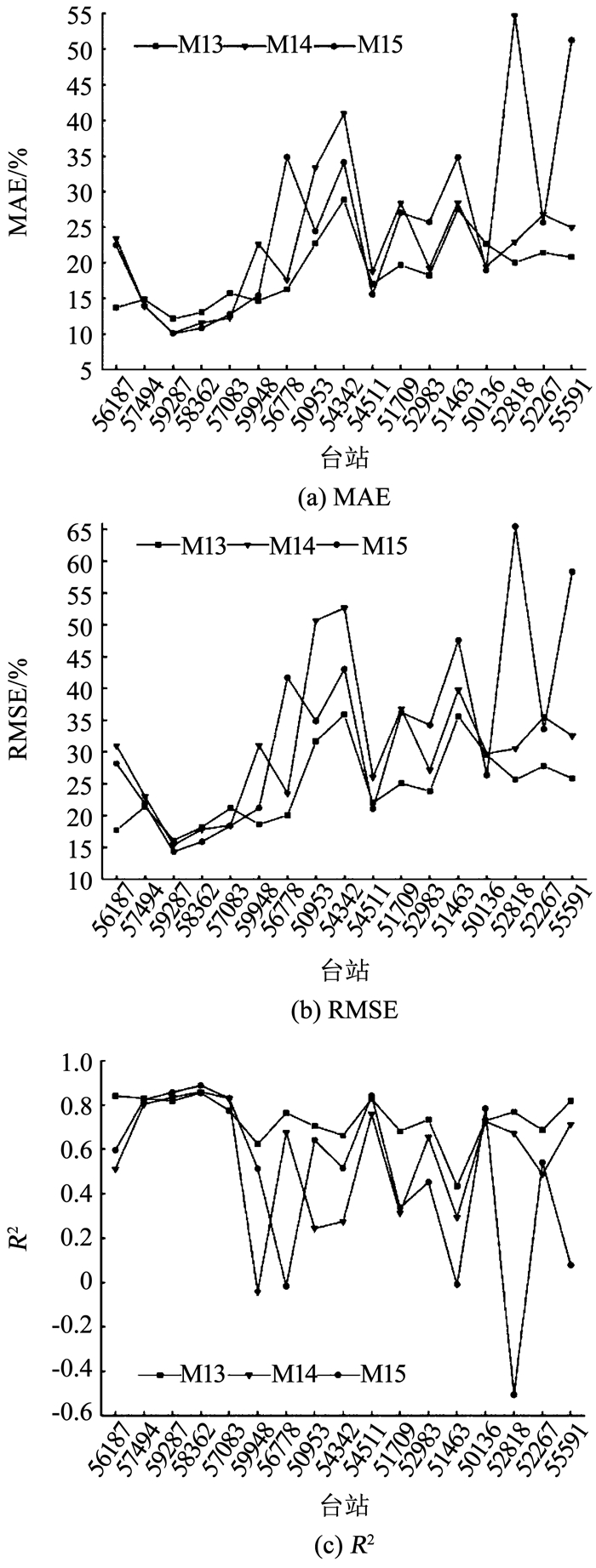
|
图 4 修正模型误差指标 Fig. 4 Evaluation index of the modified model |
|
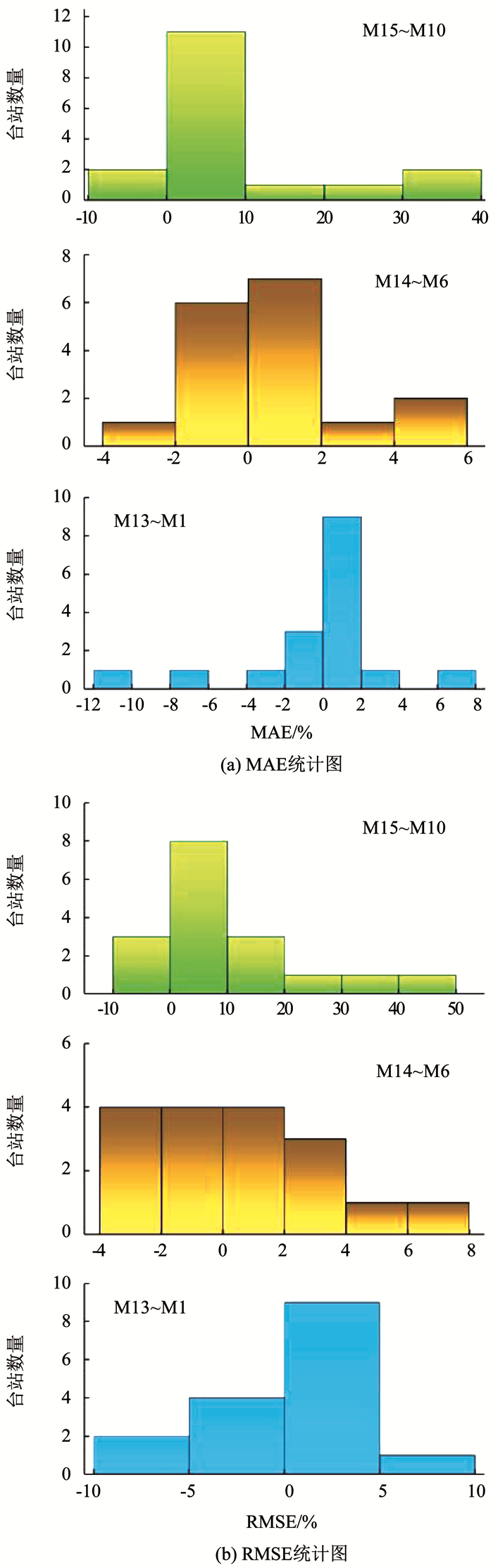
图 5 修正模型与单站点模型误差指标差值的统计图 Fig. 5 Statistical chart of the difference of error index between modified and individual model |
以系数a、b、c为例分析模型经验系数的差异,如图 2所示,模型的经验系数具有台站差异性,尤其以包含晴空指数为变量模型M1、M2、M3、M4、M12最为明显,这与文献[23]的研究结果是一致的.
分析图 3(a)~图 3(c)可知:3类模型的R2,以晴空指数、日照时数比为输入参数的模型最大、波动小,其次是以晴空指数为输入参数的模型,最后是以日照时数比为输入参数的模型,MAE、RMSE的数值与R2有相反的变化趋势,表明以晴空指数、日照时数比为输入参数的模型准确度最高,其次是以晴空指数为输入参数的模型,以日照时数比为输入参数的模型准确度最低.文献[18]以印度地区2013—2016年间的数据分析以晴空指数、日照时数比为输入参数的模型的准确度,得到了相同的结果.
比较同类模型之间不同形式对准确度的影响.对比以晴空指数为输入参数的模型(M1,M2,M3,M4,M5)可知:各个台站的R2由小到大的顺序依次是对数模型、指数模型、多项式模型,MAE、RMSE变化趋势相反;在多项式形式中,二次、三次的MAE、RMSE低于一次函数形式;二次、三次的MAE、RMSE、R2基本重合.对比以日照时数比为输入参数以及以晴空指数、日照时数比为输入参数的双变量模型发现,多项式模型MAE、RMSE要低于其他形式,而在多项式模型中,二次、三次之间MAE、RMSE的差异较小.上述分析表明:多项式形式要优于对数、指数等形式;在多项式模型中,增加自变量的次数可以提高模型的准确度,但二次到三次不明显.
2.2 修正模型由上述分析可知,模型的准确度随地区而变化,此外,模型的经验系数具有地区差异性,对于无辐射观测台站地区,其经验系数多少合适,是未知的,能否寻找经验系数与地理参数的关系,以解决无观测台站的辐射数据.相关研究证实散射辐射的变化与纬度、经度、海拔高度密切相关,挑选单站点模型中准确度相对较高、形式相对简单的模型,即M1、M6、M10,利用多元回归分析建立模型经验系数与纬度(φ)、经度(β)、海拔高度(H)关系式,本文称为修正模型,以M13~M15表示,模型经验系数见表 4.为便于和单站点模型对比,计算修正后的模型与单站点模型(即M13与M1、M14与M6、M15与M10)误差指标的差值以及在17个台站的平均值,结果如图 4、5所示, 以17个台站后4年的数据进行验证,计算3个模型的误差指标,如图 6所示.
| 表 4 修正模型经验系数 Tab. 4 Empirical coefficient of the modified model |
|
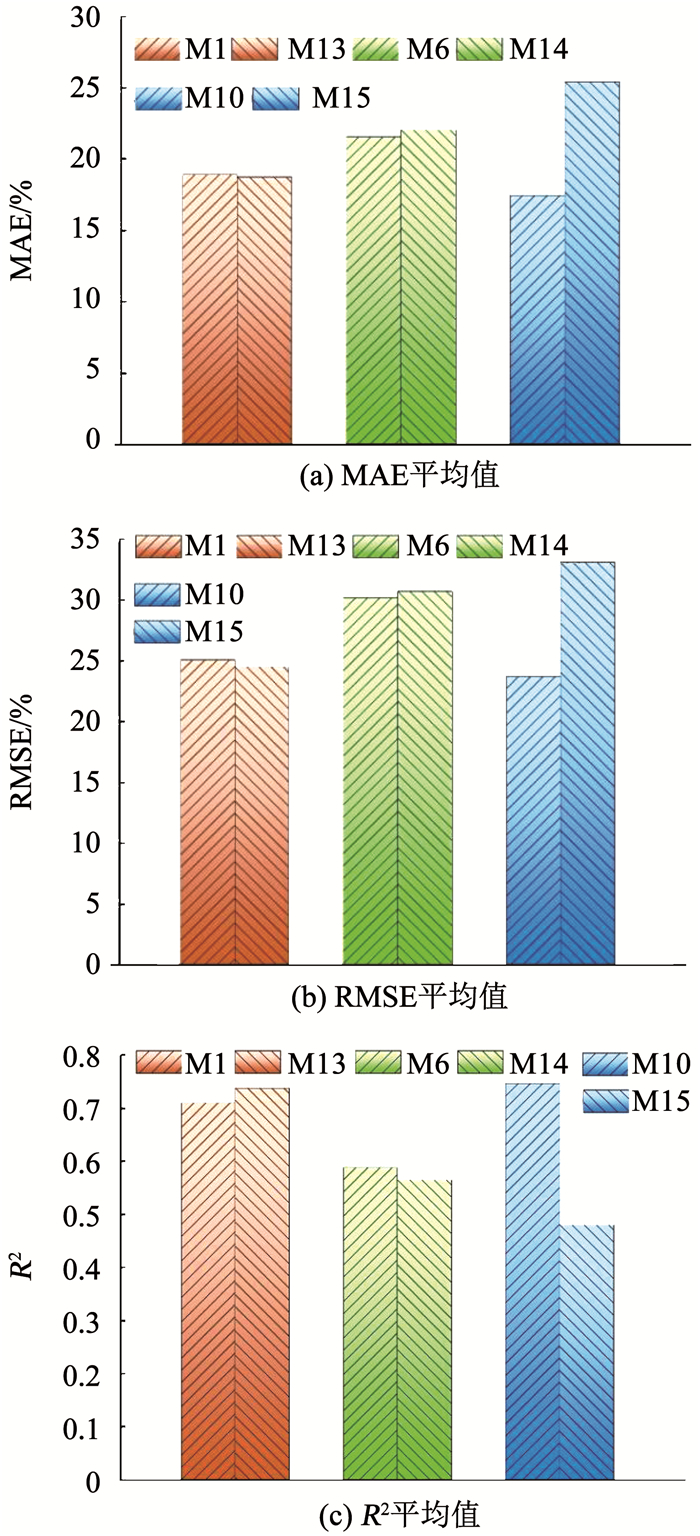
图 6 修正模型与单站点模型误差指标的平均值 Fig. 6 Mean error index of the modified and individual model |
M13、M14、M15之间对比可知,除57494、59287、58362、57083台站外,M15的MAE、RMSE明显高于M13、M14,R2低于M13、M14,如图 4所示;结合误差指标平均值进行分析(图 6),M15的MAE、RMSE最大,R2最小;结果表明,基于晴空指数、日照时数比模型的准确度低于基于晴空指数、日照时数比的单一输入参数模型.
计算修正前后模型之间误差指标(即M13与M1、M14与M6、M15与M10)的差值,并做17个台站的统计图,如图 5所示,对于3类模型,大多数台站的单站点模型的MAE、RMSE要低于修正模型;基于晴空指数模型(M1、M13)的MAE、RMSE的差异最小,分别分布在-0.12%~0.08%、-0.1%~0.1%之间;基于晴空指数、日照时数比双变量模型(M10、M15)的MAE、RMSE的差异最大,分别分布在-10%~40%、-10%~50%之间;将空间扩展模型与单站点模型在17个台站的误差指标值进行平均,如图 6所示,发现基于晴空指数修正模型(M13)的MAE、RMSE均低于单站点模型,R2高于单站点模型(M1);而另两类修正模型的MABE、RMSE均高于单站点模型,分布高出0.48%、7.98%、4.80%、9.37%;上述对比说明,基于晴空指数修正模型的准确度稍高于单站点模型,其他修正模型准确度低于单站点模型.
3 结论1) 以中国17个辐射观测台站2000年—2017年的实测数据为基础,建立12个单站点模型,采用误差分析的方法对比不同模型的准确度;分析表明:多项式模型的准确度高于对数、指数形式;一次函数的准确度低于二次、三次函数形式,二次与三次函数无明显差异;以晴空指数、日照时数比为输入参数的模型最准确,基于晴空指数的模型次之,基于日照时数比的模型最差.
2) 以单站点模型中表现较好形式简单的模型(M1、M6、M10)为基础,建立3个包含地理信息(纬度、经度、海拔高度)的修正模型,数据分析表明,基于晴空指数的模型最准确,基于日照时数比模型次之,基于晴空指数、日照时数比模型最差.
3) 建议用本文提出的方法确定散射辐射模型的经验系数,采用基于晴空指数的一次函数模型计算散射辐射.
| [1] |
CHEN Jilong, LIU Hongbin, WU Wei, et al. Estimation of monthly solar radiation from measured temperatures using support vector machines-A case study[J]. Renewable Energy, 2011, 36(1): 413. DOI:10.1016/j.renene.2010.06.024 |
| [2] |
Al-MOHAMAD A. Global, direct and diffuse solar-radiation in Syria[J]. Applied Energy, 2004, 79(2): 191. DOI:10.1016/j.apenergy.2003.12.011 |
| [3] |
TARHAN S, SARI A. Model selection for global and diffuse radiation over the Central Black Sea (CBS) region of Turkey[J]. Energy Conversion and Management, 2005, 46(4): 605. DOI:10.1016/j.enconman.2004.04.004 |
| [4] |
El-SEBAⅡ AA, Al-HAZMI F S, Al-GHAMDI A A, et al. Global, direct and diffuse solar radiation on horizontal and tilted surfaces in Jeddah, Saudi Arabia[J]. Applied Energy, 2010, 87(2): 568. DOI:10.1016/j.apenergy.2009.06.032 |
| [5] |
BAKIRCI K. Models for the estimation of diffuse solar radiation for typical cities in Turkey[J]. Energy, 2015, 82: 827. DOI:10.1016/j.energy.2015.01.093 |
| [6] |
NADJEM B, KADA B, ZAKI A M, et al. A new empirical model for forecasting the diffuse solar radiation over Sahara in the Algerian Big South[J]. Renewable Energy, 2018, 117: 530. DOI:10.1016/j.renene.2017.10.081 |
| [7] |
BARBARO S, CANNATA G, COPPOLONO S, et al. Diffuse solar radiation statistics for Italy[J]. Solar Energy, 1981, 26(5): 429. DOI:10.1016/0038-092x(81)90222-x |
| [8] |
JAIN P C. A model for diffuse and global irradiation on horizontal surfaces[J]. Solar Energy, 1990, 45(5): 301. DOI:10.1016/0038-092x(90)90015-5 |
| [9] |
PANDEY C K, KATIYAR A K. A comparative study to estimate daily diffuse solar radiation over India[J]. Energy, 2009, 34(11): 1792. DOI:10.1016/j.energy.2009.07.026 |
| [10] |
Al-HAMDANI N, Al-RIAHI M, TAHIR K. Estimation of the diffuse fraction of daily and monthly average global radiation for Fudhaliyah, Baghdad (Iraq)[J]. Solar Energy, 1989, 42(1): 81. DOI:10.1016/0038-092x(89)90132-1 |
| [11] |
COLLARES-PEREIRA M, RABL A. The average distribution of solar radiation correlations between diffuse and hemispherical and between daily and hourly insolation values[J]. Solar Energy, 1979, 22(2): 155. DOI:10.1016/0038-092x(79)90100-2 |
| [12] |
LI Maofen, LIU Hongbin, GUO Pengtao, et al. Estimation of daily solar radiation from routinely observed meteorological data in Chongqing, China[J]. Energy Conversion and Management, 2010, 51(12): 2575. DOI:10.1016/j.enconman.2010.05.021 |
| [13] |
BASHAHU M. Statistical comparison of models for estimating the monthly average daily diffuse radiation at a subtropical African site[J]. Solar Energy, 2003, 75(1): 43. DOI:10.1016/s0038-092x(03)00213-5 |
| [14] |
HAYDAR A, BALLI O, HEPBASLI A. Estimating the horizontal diffuse solar radiation over the Central Anatolia region of Turkey[J]. Energy Conversion and Management, 2006, 47(15/16): 2240. DOI:10.1016/j.enconman.2005.11.024 |
| [15] |
LI Huashan, BU Xianbiao, LONG Zhen, et al. Calculating the diffuse solar radiation in regions without solar radiation measurements[J]. Energy, 2012, 44(1): 611. DOI:10.1016/j.energy.2012.05.033 |
| [16] |
KARAKOTI I, DAS P K, SINGH S K. Predicting monthly mean daily diffuse radiation forIndia[J]. Applied Energy, 2012, 91(1): 412. DOI:10.1016/j.apenergy.2011.10.012 |
| [17] |
BOUKELIA T E, MECIBAH M S, MERICHE I E. General models for estimation of the monthly mean daily diffuse solar radiation (Case study: Algeria)[J]. Energy Conversion and Management, 2014, 81: 211. DOI:10.1016/j.enconman.2014.02.035 |
| [18] |
JAMIL B, AKHTAR N. Comparative analysis of diffuse solar radiation models based on sky-clearness index and sunshine period for humid-subtropical climatic region of India: A case study[J]. Renewable and Sustainable Energy Reviews, 2017, 78: 336. DOI:10.1016/j.rser.2017.04.073 |
| [19] |
SABZPOOSHANI M, MOHAMMADI K. Establishing new empirical models for predicting monthly mean horizontal diffuse solar radiation in city of Isfahan, Iran[J]. Energy, 2014, 69: 571. DOI:10.1016/j.energy.2014.03.051 |
| [20] |
李峥嵘, 姚万祥, 赵群, 等. 水平面日太阳散射辐射模型对比研究[J]. 太阳能学报, 2013, 34(5): 794. LI Zhengrong, YAO Wanxiang, ZHAO Qun, et al. Study on the comparison of models for daily diffuse solar radiation on a horizontal surface[J]. Acta Energiae Solar is Sinica, 2013, 34(5): 794. DOI:10.3969/j.issn.0254-0096.2013.05.011 |
| [21] |
马年骏, 李芬, 边泽强, 等. 太阳辐射直散分离模型的改进及应用[J]. 水电能源科学, 2016, 34(4): 211. MA Nianjun, LI Fen, BIAN Zeqiang, et al. Comparative study of solar beam-diffuse radiation separated model[J]. Water Resources and Power, 2016, 34(4): 211. |
| [22] |
冯巍, 董宏, 杨柳, 等. 太阳辐射直散分离模型比较研究——以北京地区为例[J]. 土木建筑与环境工程, 2015, 37(1): 12. FENG Wei, DONG Hong, YANG Liu, et al. Comparison of the fraction model of direct and diffuse solar radiation-Taking Beijing area as anexample[J]. Journal of Civil, Architectural & Environment Engineering, 2015, 37(1): 12. DOI:10.11835/j.issn.1674-4764.2015.01.003 |
| [23] |
LI Maofen, TANG Xiaoping, WU Wei, et al. General models for estimating daily global solar radiation for different solar radiation zones in mainland China[J]. Energy Conversion and Management, 2013, 70(70): 139. DOI:10.1016/j.enconman.2013.03.004 |
| [24] |
LIU Yanfeng, ZHOU Yong, WANG Dengjia, et al. Classification of solar radiation zones and general models for estimating the daily global solar radiation on horizontal surfaces in China[J]. Energy Conversion and Management, 2017, 154: 168. DOI:10.1016/j.enconman.2017.10.043 |
| [25] |
ZHOU Jin, WU Yezheng, YAN Gang. General formula for estimation of monthly average daily global solar radiation in China[J]. Energy Conversion and Management, 2005, 46(2): 257. DOI:10.1016/j.enconman.2004.02.020 |
| [26] |
YOUNES S, CLAYWELL R, MUNNEER T. Quality control of solar radiation data: Present status and proposed new approaches[J]. Energy, 2005, 30(9): 1533. DOI:10.1016/j.energy.2004.04.031 |
| [27] |
于瑛, 杨柳, 陈猛, 等. 日散射辐射推算模型在中国的适用性研究[J]. 太阳能学报, 2018, 39(11): 3005. YU Ying, YANG Liu, CHEN Meng, et al. Applicability of estimation models for diffuse solar radiation in China[J]. Acta Energiae Solaris Sinica, 2018, 39(11): 3005. |
| [28] |
EL-SEBAⅡ A A, AL-AGEL F. Estimation of horizontal diffuse solar radiation from common meteorological parameters: A case study for Jeddah, Saudi Arabia[J]. International Journal of Ambient Energy, 2013, 34(2): 92. DOI:10.1080/01430750.2012.740423 |
 2020, Vol. 52
2020, Vol. 52


