随着人民生活水平的不断提高,人们对室内空气质量要求也越来越高,而居住建筑主要依靠自然通风方式来满足室内空气质量的要求.相关文献研究发现,随着窗户开口面积的增大,房间的通风效果随之增强[1-2].然而随着汽车数量的持续增长,交通噪声带来的影响也越来越大.在欧盟地区,超过40%的居民几乎全天受到交通噪声的干扰,其中20%的居民受到的交通噪声污染超过65 dB(A)[3].对于临街居住的居民而言,开窗实现室内自然通风与营造舒适的室内声环境是相互矛盾的举措.因此,既要隔声降噪,又要满足室内空气质量要求是居住建筑研究中亟需解决的问题之一.
为此,国内外学者主要针对自然隔音通风窗的性能进行深入研究与分析.Kang等[4]将透明微穿孔薄膜应用到交错结构窗户的玻璃上,不仅增强了室内采光能力,同时避免了吸声材料的二次污染.Nishimura等[5]设计了一种通风与照明结构交错的窗户,虽然其可以防雨降噪以及通风采光,但该类窗户整体降噪性能并不突出.Yu等[6]采用有限元的方法,研究了上下交错开口整体通风的隔声窗的声学性能.Huang等[7]、Kwon等[8]对安装控制源的隔声通风窗进行研究,但其降噪效果依赖于控制精度.
综上所述,虽然隔音通风窗的设计及研究成果取得了较大进展,但其实际通风效果不利于调控,受室外气象条件影响较大,且内部结构较为复杂.针对现有隔音通风窗的不足之处,本文设计了一种新型隔音通风装置[9-10],该装置具有内部结构简单,通风量相对稳定的优点.本文通过实验对装置的隔声性能和通风效果进行研究,并建立Simulink仿真模型对影响装置通风效果的参数进行优化分析.
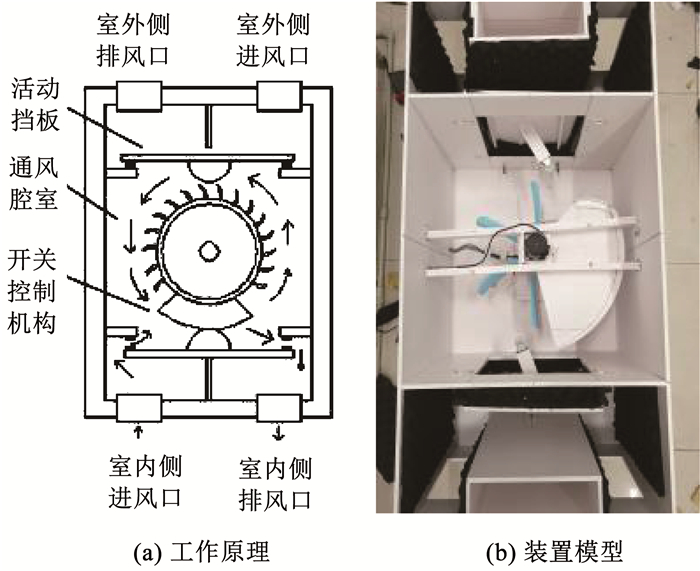
1 装置工作原理及模型介绍隔音通风装置的工作原理如图 1(a)所示,装置室内侧和室外侧分别设有进风口、排风口以及活动挡板,装置中部的通风腔室内设有动力机构和开关控制机构,譬如扇形机构.工作时,依靠动力机构上的叶片产生气流进行通风,同时控制机构控制室内侧和室外侧的活动挡板周期性地启闭,确保装置在工作过程中,始终只有室内侧或室外侧与通风腔室进行空气交换,而室内侧和室外侧并没有直接连通.故装置在保持通风换气的同时,隔断了室外噪声通过风道传递到室内的路径,从而能够最大程度地起到隔音降噪的作用.
|
图 1 隔音通风装置的原理及模型 Fig. 1 Schematic and model of sound insulation ventilation device |
装置模型如图 1(b)所示,装置尺寸为0.9 m(长)×0.5 m(宽)×0.4 m(高), 其中通风腔室尺寸为0.5 m(长)× 0.5 m(宽)×0.4 m(高),室内侧及室外侧风口尺寸均为0.135 m(宽)×0.250 m(高).通风腔室的中部及底部分别设置了直流电机1(功率为28 W,转速为20 r/min)和带调速器(功率为6 W)的直流电机2(功率为25 W,转速为1 620 r/min).
2 研究 2.1 系统介绍实验系统包括隔音通风装置(如图 1所示)和房间模型.为研究装置的隔声性能和通风效果,实验中搭建了一个尺寸为1.0 m(长)×1.0 m(宽)×1.0 m(高)的房间模型,房间一侧下部设置了一开口,用于与实验装置连接,其尺寸与实验装置横截面尺寸一致.此外,房间另一侧中部设置了一个带玻璃板的开口,用于模拟房间窗户,其尺寸为0.25 m(宽)× 0.25 m(高).
2.2 方案设计隔声实验测试了5种工况下的房间噪声值以及不同频率环境噪声下的房间隔声效果.5种工况分别为:1)开启窗户;2)关闭窗户;3)关闭装置;4)启动装置(50%风量);5)启动装置(100%风量).其中,前2种工况下,房间下侧开口均未与实验装置连接,并作密封处理.而后3种工况下,房间窗户均处于关闭状态.
通风实验测试了启动装置工况下的通风口风速以及关闭窗户和启动装置工况下,房间CO2体积分数随时间的变化,其中采样间隔为5 min.
2.3 测点布置及主要仪器通风口风速测量采用在通风口对角线均匀布置5个测点的方案.由于噪声计和CO2检测仪的尺寸相对较大,且无可伸缩的探头,而测量过程中需保证房间的气密性,故CO2体积分数以及噪声的测量均采用在房间中心处布置一个测点的方案.
主要实验仪器及规格型号见表 1所示.
| 表 1 实验仪器及规格型号 Tab. 1 Experimental instrument and specification |
装置室内侧和室外侧活动挡板的轮流启闭导致房间噪声值呈周期性变化.环境噪声越大,房间噪声值的周期性变化越弱,房间噪声值的波动幅度最大约1.5 dB.为方便分析起见,文中启动装置工况下的房间噪声值取一个周期内房间噪声的平均值.
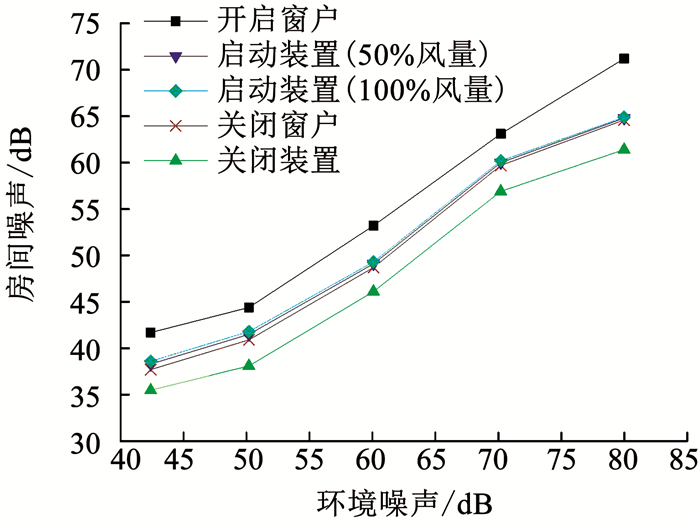
由图 2可知,随着环境噪声的增大,各工况下(开启窗户、关闭窗户、关闭装置、启动装置)的房间噪声值均上升.其中,开启窗户时房间噪声值比关闭窗户时高4~6 dB,启动装置时房间噪声值比关闭装置时高2~3 dB.由于装置室内侧及室外侧均设有隔音棉,因此图 2显示,关闭装置时房间噪声值比关闭窗户时低2~3 dB,说明安装该装置后,房间的隔声效果得以改善.从图 2中可知,关闭窗户、启动装置(50%风量)以及启动装置(100%风量)这3种工况下的房间噪声值相当.
|
图 2 不同工况下的房间噪声 Fig. 2 Room noise under different working conditions |
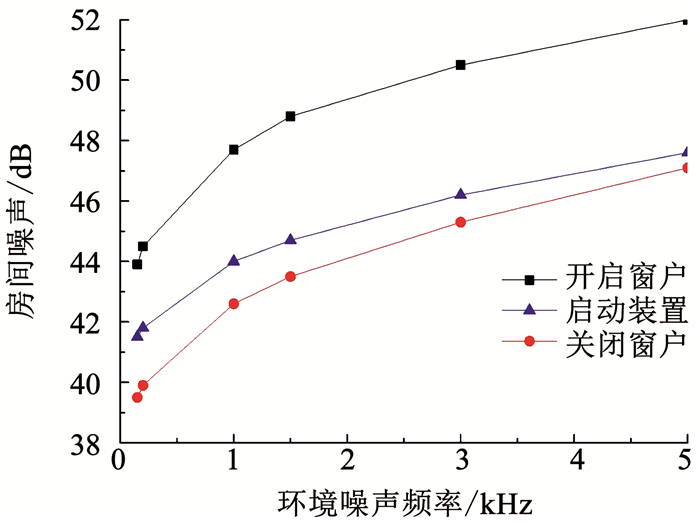
噪声按频率可以分为低频噪声、中频噪声以及高频噪声.其中频率在200 Hz以下的噪声属于低频噪声,500~2 000 Hz属于中频噪声,2 000~16 000 Hz属于高频噪声[11].为分析环境噪声频率对装置隔声效果的影响,实验中分别选取了频率为150、200、1 000、1 500、3 000、5 000 Hz的环境噪声,结果如图 3所示.在开启窗户和关闭窗户(均未安装装置)工况下,房间噪声随着环境噪声频率的上升而增大,说明了房间对于中、高频噪声的隔声效果较差.随着环境噪声频率的上升,启动装置和关闭窗户工况下,房间噪声的差值减小,说明了该装置对于中、高频噪声的隔声效果较好.
|
图 3 不同频率环境噪声下的房间隔声效果 Fig. 3 Sound insulation effect of the room under ambient noise of different frequencies |
实验中测试了开关控制机构转动10圈所需时间为30 s,即其转动周期为3 s,其中室内侧和室外侧与通风腔室的通风换气时间均为1 s.此外,实验期间电机平均功率为0.06 kW.
通风口风速测量结果显示,装置室内侧进、排风口的平均风速分别为0.17 m/s和0.19 m/s,装置室外侧进、排风口的平均风速分别为0.18 m/s和0.21 m/s,说明装置4个通风口的风量基本相等.由于装置存在少量的渗透风量,因此室内侧及室外侧进风口的平均风速比排风口低约0.03 m/s.装置室内侧和室外侧空气阻力不相等,导致室内侧进、排风口的平均风速均比室外侧低约0.02 m/s.
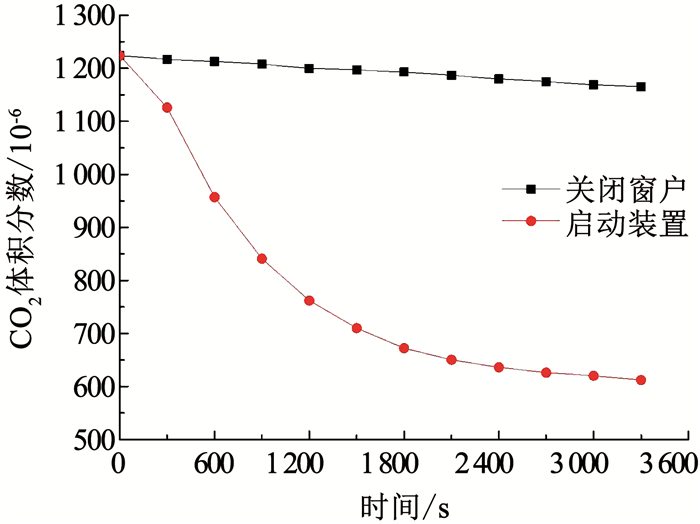
在对装置通风效果和房间自然渗透通风效果的实验研究中,被测房间CO2体积分数初始值为1 224×10-6,实验室环境CO2体积分数为610×10-6,测试时间为3 300 s.房间CO2体积分数随时间的变化如图 4所示,启动装置时,在0~1 500 s内,房间CO2体积分数下降速度较快,而在1 500~3 300 s内,CO2体积分数下降速度较慢,最后稳定在612×10-6左右,与实验室环境CO2体积分数相近.由此可见,当装置通风量一定时,房间与实验室环境的CO2体积分数差越大,装置通风效果越好.关闭窗户时,房间CO2体积分数在自然渗透作用下缓慢下降,3 300 s时房间CO2体积分数为1 165×10-6.由此可见,与装置通风效果相比,房间自然渗透通风效果较差,难以满足室内空气品质要求.
|
图 4 装置通风效果和房间自然渗透通风效果的对比 Fig. 4 Comparison between the ventilation effect of the device and the ventilation effect of natural infiltration of the room |
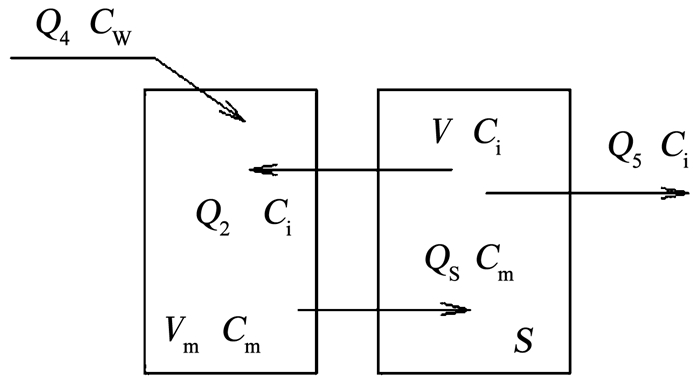
国内外学者已建立了大量的建筑通风模型及计算模型,包括良好混合化学反应器模型[12]、混合因子模型[13]、多区域模型[14]以及双层皮幕墙自然通风模型[15]等.这些通风模型的局限性在于,室内送风CO2体积分数是相对稳定的,而该装置的送风CO2体积分数是变化的.因此,本文建立了一种适合于该装置的新型隔音通风模型(如图 5所示)及装置新风量计算模型.
|
图 5 装置室内侧通风模型 Fig. 5 Indoor side ventilation model of the device |
根据CO2质量守恒定律,装置室外侧通风模型方程为
| $ {V_{\rm{m}}} = \frac{{{\rm{d}}{C_{\rm{m}}}}}{{{\rm{d}}t}} = {Q_{\rm{w}}}{C_{\rm{w}}} + {Q_3}{C_{\rm{w}}} - {Q_1}{C_{\rm{m}}}, $ |
同理装置室内侧通风模型方程为:
| $ V\frac{{{\rm{d}}{C_{\rm{i}}}}}{{{\rm{d}}t}} = {Q_{\rm{s}}}{C_{\rm{m}}} + {Q_2}{C_{\rm{i}}} - {Q_5}{C_{\rm{i}}} + S, $ |
| $ {V_{\rm{m}}} = \frac{{{\rm{d}}{C_{\rm{m}}}}}{{{\rm{d}}t}} = {Q_2}{C_{\rm{i}}} + {Q_4}{C_{\rm{w}}} - {Q_{\rm{s}}}{C_{\rm{m}}}, $ |
装置新风量计算模型方程为
| $ V\frac{{{\rm{d}}{C_{\rm{i}}}}}{{{\rm{d}}t}} = {Q_{{\rm{w1}}}}{C_{\rm{w}}} + {Q_{{\rm{w}}1}}{C_{\rm{i}}} + S. $ |
式中:Vm为通风腔室体积;Cm为通风腔室CO2体积分数;t为时间;Qw为室外侧进风量;Cw为新风CO2体积分数;Q3为室外侧渗透进风量;Q1为室外侧排风量;V为房间体积;Ci为房间CO2体积分数;Qs为室内侧排风量;Q2为室内侧进风量;Q5为房间渗透排风量;Q4为室内侧渗透进风量;Qw1为装置新风量;S为房间CO2散发量.
由于通风腔室及房间CO2体积分数分布是非均匀的,故计算时需对其进行离散化处理.为了便于研究,对隔音通风模型作如下的简化和假设:
1) 4个通风口的风量相等;
2) 忽略房间的渗透排风量;
3) 通风腔室及房间CO2体积分数均匀分布.
简化后,装置室外侧通风模型方程为
| $ {V_{\rm{m}}}\frac{{{\rm{d}}{C_{\rm{m}}}}}{{{\rm{d}}t}} = {Q_{\rm{w}}}\left( {{C_{\rm{w}}} - {C_{\rm{m}}}} \right), $ |
同理,装置室内侧通风模型方程为:
| $ V\frac{{{\rm{d}}{C_{\rm{i}}}}}{{{\rm{d}}t}} = {Q_{\rm{s}}}\left( {{C_{\rm{m}}} - {C_{\rm{i}}}} \right) + S, $ |
| $ {V_{\rm{m}}}\frac{{{\rm{d}}{C_{\rm{m}}}}}{{{\rm{d}}t}} = {Q_{\rm{s}}}\left( {{C_{\rm{w}}} - {C_{\rm{m}}}} \right), $ |
装置新风量计算模型方程为
| $ {Q_{{\rm{w}}1}} = \left( {V\frac{{{\rm{d}}{C_{\rm{i}}}}}{{{\rm{d}}t}} - S} \right)/\left( {{C_{\rm{w}}} - {C_{\rm{i}}}} \right). $ |
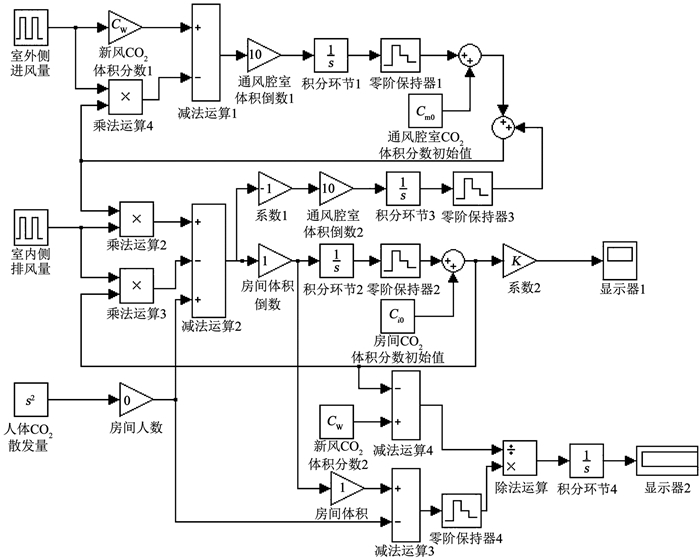
根据简化的隔音通风模型方程以及装置新风量计算模型方程来建立Simulink仿真模型.如图 6所示,Simulink仿真模型从上到下可分为装置室外侧通风模型、装置室内侧通风模型以及装置新风量计算模型.
|
图 6 Simulink仿真模型 Fig. 6 Simulink simulation model |
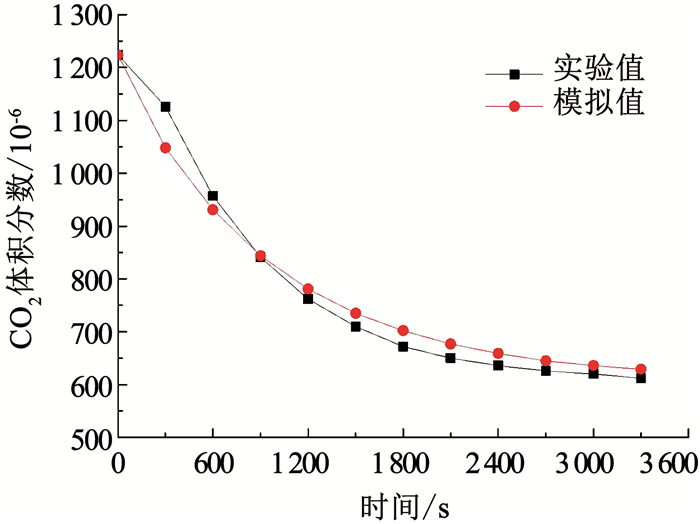
根据实验结果分别设置仿真模型中各参数值,其中人体CO2散发量取5.46×10-6m3/(人· s)[16-17].Simulink模拟结果如图 7所示,房间CO2体积分数的实验值与模拟值存在一致的规律性,误差均在±7%以内,表明了Simunlink仿真模型能较好地反映装置的通风效果.
|
图 7 模拟值与实验值的对比 Fig. 7 Comparison between simulated and measured values |
通风量和通风腔室体积均影响装置的经济性、合理性以及适用性.因此,通过研究装置通风量及通风腔室体积对装置通风效果的影响规律,为装置的优化设计提供参考.仿真模型中的新风CO2体积分数取400×10-6,初始时刻房间及通风腔室的CO2体积分数均取1 000×10-6,房间尺寸取4 m(长)×3 m(宽)×3 m(高),模拟时间取7 200 s.
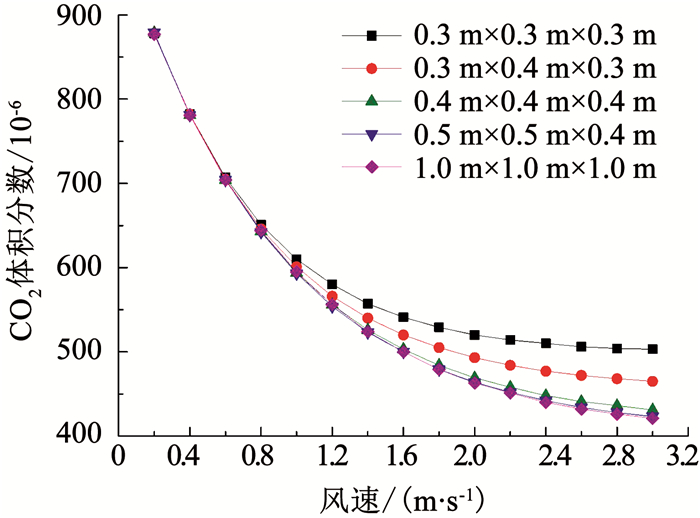
图 8所示的数据均为房间在7 200 s这一时刻的CO2体积分数.从图 8中可发现,当通风腔室体积一定时,随着风速的增大,房间CO2体积分数下降量的增加率逐渐减小.当风速增大到某个值后,房间CO2体积分数下降量的增加率几乎保持不变.这是由于通风腔室CO2体积分数与房间CO2体积分数接近相等,导致通风腔室CO2体积分数基本达到饱和状态,即装置的通风效果已基本失效.故本文规定当风速增大到某个临界值后,房间CO2体积分数下降量的增加率小于3%时,该临界值对应的通风量称为装置的经济通风量.
|
图 8 通风量及通风腔室体积对装置通风效果的影响 Fig. 8 Influence of ventilation volume and ventilation chamber volume on ventilation effect of the device |
当风速一定时,随着通风腔室体积的增大,房间CO2体积分数下降量的增加率逐渐减小.当通风腔室体积增大到某个值后,房间CO2体积分数下降量的增加率几乎保持不变.虽然通风腔室体积增大可以有效避免通风腔室CO2体积分数达到饱和状态,但装置通风效果主要取决于通风量.因此继续增大通风腔室体积,装置通风效果基本保持不变.故本文假定当通风腔室体积增大到某个临界值后,房间CO2体积分数下降量的增加率小于3%时,该临界值称为装置的经济通风腔室体积.
综上所述,当通风腔室体积与经济通风量匹配时,装置的经济性最佳.从图 8可发现,尺寸为0.5 m(长)×0.5 m(宽)×0.4 m(高)的通风腔室的经济通风量对应的风速约为2.0 m/s,结合通风实验结果可知,实验装置的经济性并非最佳.因此,实验装置的优化方案为:根据实际叶片尺寸,合理地减小通风腔室体积并增大装置通风量.
3.5 装置通风效果模拟某尺寸为4 m(长)×3 m(宽)×3 m(高)的单人间卧室,作息时间为22:00~8:00. 22:00时刻房间CO2体积分数取600×10-6,通风腔室及室外新风CO2体积分数均取400×10-6.采取装置通风效果的影响因素分析的优化方案,在仿真模型中调整实验装置尺寸为0.65 m(长)×0.45 m(宽)×0.30 m(高),通风腔室尺寸为0.45 m(长)×0.45 m(宽)×0.30 m(高),调整电机转速使通风口风速达0.7 m/s.模拟结果表明,在22:00~8:00的作息时间段内,卧室CO2体积分数较好地控制在1 030×10-6以内,新风量能达到351.6 m3,即35.16 m3/h.
4 结论1) 装置运行时室内噪声值与关闭窗户时相当,表明装置在实现通风的同时,还具有良好的隔声效果.尤其对于中、高频环境噪声,装置的隔声效果更理想.
2) 通风实验表明,Simunlink仿真模型能较好地反映装置的通风效果.当通风腔室体积与经济通风量匹配时,装置的经济性最佳.
3) 仿真结果表明,采用进一步优化后的装置,单人间卧室新风量能达到35.16 m3/h,室内CO2体积分数可控制在1 030×10-6范围内,满足室内空气质量要求.
| [1] |
VISAGAVEL K, SRINIVASAN P S S. Analysis of single side ventilated rooms by varying the width of the window opening using CFD[J]. Solar Energy, 2009, 83(1): 2. DOI:10.1016/j.solener.2008.06.004 |
| [2] |
王巧宁, 官燕玲, 陆齐力. 房间内部不同阻隔方式风压自然通风风洞试验[J]. 太阳能学报, 2016, 37(3): 666. WANG Qiaoning, GUAN Yanling, LU Qili. Wing tunnel test on wind natural ventilation building with different partitions[J]. Acta Energiae Solaris Sinica, 2016, 37(3): 666. DOI:10.3969/j.issn.0254-0096.2016.03.021 |
| [3] |
CARLESJ L, BARRIO I L, LUCIO J V. Sound influence on landscape values[J]. Landscape and Urban Planning, 1999, 43(4): 191. DOI:10.1016/S0169-2046(98)00112-1 |
| [4] |
KANG J, BROCKLESBY M W. Feasibility of applying micro-perforated absorbers in acoustic window systems[J]. Applied Acoustics, 2005, 66(2): 669. DOI:10.1016/j.apacoust.2004.06.011 |
| [5] |
NISHIMURA Y, NISHIMURA S, NISHIMURA T, et al. Sound propagation in soundproofing casement windows[J]. Applied Acoustics, 2009, 70(9): 1160. DOI:10.1016/j.apacoust.2009.04.006 |
| [6] |
YU Xiang, LAU S K, CHENG Li, et al. A numerical investigation on the sound insulation of ventilation windows[J]. Applied Acoustics, 2017, 117: 113. DOI:10.1016/j.apacoust.2016.11.006 |
| [7] |
HUANG Huahua, QIU Xiaojun, KANG Jian. Active noise attenuation in ventilation windows[J]. Journal of the Acoustical Society of America, 2011, 130(1): 176. DOI:10.1121/1.3596457 |
| [8] |
KWON B, PARK Y. Interior noise control with an active window system[J]. Applied Acoustics, 2013, 74(5): 647. DOI:10.1016/j.apacoust.2012.11.005 |
| [9] |
卢军, 谢柱维, 梁朔, 等.一种室内隔音通风装置: 201810149495.2[P].2018-07-17 LU Jun, XIE Zhuwei, LIANG Shuo, et al. Indoor sound insulation and ventilation device: 201810149495.2[P]. 2018-07-17 |
| [10] |
卢军, 谢柱维, 梁朔, 等.一种建筑室内隔断式降噪通风方法: 201810149549.5[P]. 2018-07-27 LU Jun, XIE Zhuwei, LIANG Shuo, et al. Indoor partition type noise reduction ventilation method for building: 201810149549.5[P]. 2018-07-27 |
| [11] |
徐珺.新型吸声材料对变电站低频噪声降噪降噪机制的研究[D].北京: 华北电力大学, 2018 XU Jun. Study on the noise reduction mechanism of low frequency noise in substation with new absorbing materials[D]. Beijing: North China Electric Power University, 2018 |
| [12] |
SHAIR F H, HEITNER K L. Theoretical model for relating indoor pollutant concentrations to those outside[J]. Environmental Science & Technology, 1974, 8(5): 444. DOI:10.1021/es60090a006 |
| [13] |
ESMEN N A. Characterization of contaminant concentrations in enclosed spaces[J]. Environmental Science & Technology, 1978, 12(3): 337. DOI:10.1021/es60139a011 |
| [14] |
HOLFORD J M, HUNT G R. Fundamental atrium design for natural ventilation[J]. Building and Environment, 2003, 38(3): 409. DOI:10.1016/s0360-1323(02)00019-7 |
| [15] |
王京南, 陈友明, 王衍金, 等. 双层皮幕墙自然通风模型与实验验证[J]. 太阳能学报, 2018, 39(6): 1543. WANG Jingnan, CHEN Youming, WANG Yanjin, et al. Natural ventilation model and experiment verification of double shin curtain wall[J]. Acta Energiae Solaris Sinica, 2018, 39(6): 1543. DOI:10.3969/j.issn.0254-0096.2018.06.009 |
| [16] |
NG M O, QU Ming, ZHENG Pengxuan, et al. CO2-based demand controlled ventilation under new ASHRAE Standard 62.1-2010: A case study for a gymnasium of an elementary school at West Lafayette, Indiana[J]. Energy and Buildings, 2011, 43(11): 3216. DOI:10.1016/j.enbuild.2011.08.021 |
| [17] |
谢柱维, 郑洁, 卢军, 等. 基于人体疲劳状态的需求控制通风研究[J]. 暖通空调, 2018, 48(8): 30. XIE Zhuwei, ZHENG Jie, LU Jun, et al. Demand controled ventilation based on human fatigue state[J]. Heating Ventilating & Air Conditioning, 2018, 48(8): 30. DOI:10.3969/j.issn.1002-8501.2018.08.005 |
 2020, Vol. 52
2020, Vol. 52


