2. 北京工业大学, 北京 100000
2. Beijing University of Technology, Beijing 100000, China
组合测试是一种重要的黑盒测试技术[1-4],利用更少的测试数据量,可以发现更多的由参数之间的相互作用引起的系统故障.通过对任意t个参数全部取值组合的覆盖,可以发现几乎100%的系统故障,因此又被称为“伪穷举测试”[5].
在实际测试中,参数之间往往存在约束条件,限制了参数之间的取值关系[6-8].这种情况下,组合测试的测试数据集被称为t维约束覆盖数组,其可覆盖任意t个参数之间满足约束的取值组合.t=2的约束覆盖数组被称为2维约束覆盖数组,因为其规模小,所以最为常用.为了提高实际测试的效率,2维约束覆盖数组的规模应尽可能的小,最好找到理论上最小规模的2维约束覆盖数组.然而找到规模最小的2维约束覆盖数组已被证明是NP完全(Non-deterministic Polynomial Complete,NPC)问题[9-10],因此为减少生成时间,很多测试数据搜索算法被应用到寻找规模最小或近似最小的2维约束覆盖数组.经典算法有HSS[11]、SA_SAT[12]、mAETG_SAT[13]、PICT、TestCover、IPOG[14]、IPOG-F[15]、CTWT[16]等.前两个算法属于启发式算法,其余算法属于贪心算法.
为了评价这些算法的性能,需要将这些算法生成的2维约束覆盖数组的规模与理论上的最小值进行比较.目前可以得出的理论最小值是任意两个参数之间满足约束的取值组合数的最大值,然而这个值只表示了约束下需要覆盖的取值组合数,并没有考虑约束的影响.由于约束的影响,2维约束覆盖数组不仅要考虑需要覆盖的取值组合数,还要考虑约束情况,约束的存在使得原本可以在一条测试数据中覆盖的取值组合,要被拆开放到多条测试数据中,这样就增加了测试数据的数目,导致2维约束覆盖数组的规模增加,因此2维约束覆盖数组最小规模要考虑约束的影响.
本文提出一种禁忌边分解方法,可以将描述被测系统输入配置的图分解成两个子图,通过计算覆盖两个子图中全部顶点的子覆盖数组的规模和剩余需要覆盖的取值组合数,与单纯计算需要覆盖的取值组合数相比,提升了2维约束覆盖数组的最小规模.提升的最小规模可以用于评价现有算法生成的2维约束覆盖数组,比较生成的2维约束覆盖数组的规模与理论最小规模之间的差距,同时最小规模有助于判断生成的2维约束覆盖数组是否真实存在.
1 基本概念假设一个被测系统具有k个参数,分别为P1, P2, …, Pk,每个参数分别对应v1, v2, …, vk个取值,即对于任意参数Pi(1≤i≤k)其有vi个取值,具体表示为集合{0, 1, …, vi-1},简记为[0, vi-1],各个参数之间取值均相互独立.记参数集合P={P1, P2, …, Pk},取值个数集合V={v1, v2, …, vk},配置空间模型(Configuration Space Model,CSM)M= < P, V>,组合测试根据被测系统的配置空间模型来构造测试数据集.
定义1 (约束覆盖数组,约束混合覆盖数组)[17]:设A是一个n×k的矩阵,约束元组f=(a1, a2, …, ak)是一个k维向量,用于限制取值组合的出现,ai∈[0, vi-1]∪[x](1≤i≤k),如果约束中没有指定第j个参数的取值,则aj=x.对任意一个出现在测试数据中,且不会引起测试数据中出现约束元组的t维组合I={(Pi1, ai1), (Pi2, ai2), …, (Pit, ait)},aij∈[0, vij-1](1≤j≤t),如果A至少存在一行r,使得A[r, ij]=aij且不覆盖约束元组,则称A为约束覆盖数组(Constrained Covering Array,CCA),记为CCA(n; t, k, v; F),其中F是约束元组f的全集.
没有覆盖约束元组的测试数据和测试数据集是满足约束一致性的,A和A中的测试数据都是满足约束一致性的.当参数的取值个数不同时,A被称为约束混合覆盖数组(Constrained Mixed Covering Array,CMCA),记为CMCA(n; t, (v1, v2, …, vk), F).
在记录CCA或者CMCA时,可以把一些具有相同值域的项合并,如CMCA(n; t, (v1, v2, …, vk), F)可以表示为CMCA(n; t, s1p1s2p2…srpr, F),其中
定义2 (带有禁忌边的覆盖数组)[9]设A是一个n×k的带有禁忌边的覆盖数组(Covering Array with Forbidden Edges,CAFE),表示为CAFE(n, G),其中G=G(g1, g2, …, gk)是参数取值构成的图,gi(1≤i≤k)是图中第i列顶点的集合,E(G)是G中的边集,简记为E或EG.对A中任意一列,其取值范围为[0, |gi|-1].对任意的不属于同一列的两个顶点ai∈[0, |gi|-1]和bj∈[0, |gj|-1](i≠j),如果{ai, bj}∉E(G)且满足约束一致性,则A中一定存在一行r,使得A [r, i]=a,A [r, j]=b.
E中的边就是约束,在图中被称为边或禁忌边.CAFE(n, G)是力度为2的约束覆盖数组.N或NG用来表示对应于图G的覆盖力度为2的带有禁忌边的覆盖数组的最小规模.从图G中容易得出如下式所示关系式:
| $ N_{G} \geqslant \max _{1 \leqslant i<j \leqslant k}\left(\left|g_{i}\right|\left|g_{j}\right|-\left|E_{i j}\right|\right). $ | (1) |
式(1)中Eij表示图G中第i列和第j列中满足约束一致性的边,NG的下限是图G中任意两列满足约束一致性的取值组合个数的最大值.
定义3 (顶点子图)Gi, a是图G的一个子图,移除了图G中第i列除了a之外的全部顶点(1≤i≤k),并且移除了与第i列中顶点a构成边的顶点.
定义4 (顶点带禁忌边的覆盖数组) A是顶点子图Gi, a的一个n×k的顶点带有禁忌边的覆盖数组,顶点带有禁忌边的覆盖数组简记为CAFE(n, Gi, a),对顶点子图Gi, a中的任意一个顶点bj,A中一定存在一行r满足约束一致性且A[r, j]=b.
定义5 (两列的取值组合个数)Ii, j(AGi, a)表示CAFE(n, Gi, a)中覆盖的第i列和第j列的取值组合个数.如果取值组合重复出现,则只记录一次.
2 基于禁忌边分解方法的约束覆盖数组最小规模下限的提升式(1)在估计NG的范围时,只是根据两个参数之间满足约束的取值组合数进行估计,并没有依据实际的约束的特点进行估计,因此得出的NG的范围较为宽泛,通过对禁忌边进行分解可以更准确的估计NG的范围.
通过对图中的边进行分解,进一步分析组合约束对其余取值的限制关系,可以更为准确的得到CAFE(n, G)的最小规模NG的下限,式(2)所示为对G中的一条边(ai, bj)进行分解得到的NG的下限.
| $ \begin{array}{c} N_{G} \geqslant \max _{1 \leqslant i<j \leqslant k, \left(a_{i}, b_{j}\right) \in E_{i j}}\left(\left|g_{i}\right|\left|g_{j}\right|-\left|E_{i j}\right|+N_{G_{i, a}}+\right.\\ \left.N_{G_{j, b}}-\boldsymbol{I}_{i, j}\left(\boldsymbol{A}_{G_{i, a}}\right)-\boldsymbol{I}_{i, j}\left(\boldsymbol{A}_{G_{j, b}}\right)\right). \end{array} $ | (2) |
如式(2)所示,(ai, bj)是图G中的任意一条边,基于边(ai, bj)中的两个顶点可以从图G中分出两个顶点子图Gi, a和Gj, b. AGi, a和AGj, b是Gi, a和Gj, b对应的两个顶点带禁忌边的约束覆盖数组,NGi, a和NGj, b是AGi, a和AGj, b的规模,Ii, j(AGi, a)和Ii, j(AGj, b)是AGi, a和AGj, b中i和j两列参数的取值组合数.
式(2)的含义有如下两种解释:
1) 为了覆盖第i列和第j列参数的|gi||gj|-|Eij|个取值组合,CAFE(n, G)规定一定包含顶点ai与第j列参数的全部满足约束的取值组合和顶点bj与第i列参数的全部满足约束的取值组合,这两组参数取值组合分别在规模最小的AGi, a和AGj, b中被覆盖,然而CAFE(n, G)中仍有|(|gi||gj|-|Eij|-Ii, j(AGi, a)-Ii, j(AGj, b)个满足约束的取值组合需要覆盖,加上已经生成的规模NGi, a+NGj, b,即得到NG的下限.
2) 因为最终生成的覆盖数组中一定覆盖了包含顶点ai与第j列参数的全部满足约束一致性的取值组合,和顶点bj与第i列参数的全部满足约束的取值组合,所以规模最小的AGi, a和AGj, b一定存在于CAFE(n, G)中,原本CAFE(n, G)的最小规模为|gi||gj|-|Eij|,但是为了覆盖其中的Ii, j(AGi, a)个参数取值组合,需要增加的测试数据规模为NGi, a-Ii, j(AGi, a),为了覆盖Ii, j(AGj, b)个参数取值组合,需要增加的测试数据规模为NGj, b-Ii, j(AGj, b),所以为了覆盖|gi||gj|-|Eij|个取值组合,至少还要在其基础上增加NGi, a+NGj, b-Ii, j(AGi, a)-Ii, j(AGj, b)条测试数据.
以一个有4个参数的被测系统为例,其第1个参数有2个取值(0和1),其余参数有3个取值(0、1和2),其中参数2和参数3的取值组合(0,0)、参数2和参数4的取值组合(2,2)、参数3和参数4的取值组合(1,1)是约束,如图 1所示.
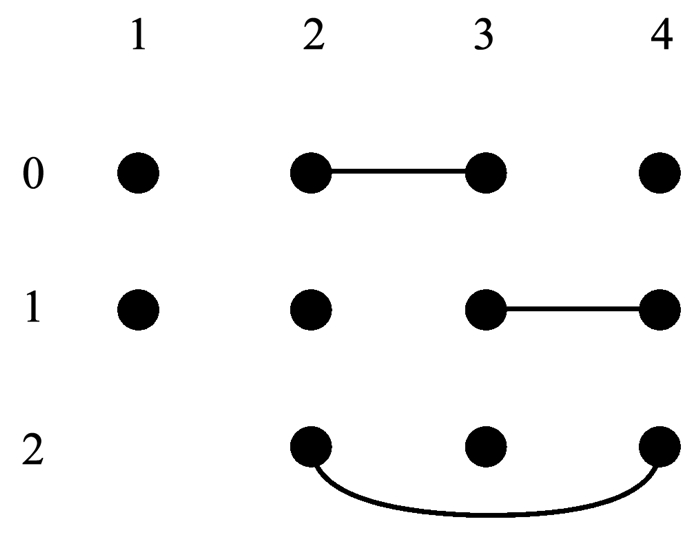
|
图 1 被测系统参数及取值配置对应图举例 Fig. 1 Example graph of the parameters and value configurations of the system under test |
为其生成带有禁忌边的覆盖数组时,按照式(1)的结论,可以得出NG≥9-1=8.然而在实际构造带有禁忌边的约束覆盖数组时,由于约束的存在,需要增加一定的测试数据才能覆盖8个取值组合,其最小规模为10,如表 1所示.为了证明其最小规模为10,采用禁忌边分解方法首先对图进行分解,然后计算需要覆盖的参数间的取值组合数.
| 表 1 带有禁忌边的覆盖数组举例 Tab. 1 Example of the covering array with forbidden edge |
图 2和图 3分别是顶点子图G2, 0和G3, 0,在G2, 0中移除了与第2个参数顶点0同一列的其他取值,同时移除了与顶点0构成边的其余参数的顶点,参数3的顶点0.同理可得G3, 0.表 2和表 3分别是对应顶点子图G2, 0和G3, 0的CAFE(3, G2, 0)和CAFE(3, G3, 0),记为AG2, 0和AG3, 0,其规模都为3.因为每个顶点子图中,参数4最多有3个取值,所以覆盖这两个顶点子图中的全部顶点(取值)至少需要3条测试数据.所以AG2, 0和AG3, 0都具有最小规模,且覆盖的参数2和参数3的取值组合数I2, 3(AG2, 0)和I2, 3(AG3, 0)都是2,所以由式(2)可得NG≥3×3-1+3+3 -2-2=10,从另外的两个边着手也可以得到相同的NG的下限,因此可以得出NG的下限就是10.
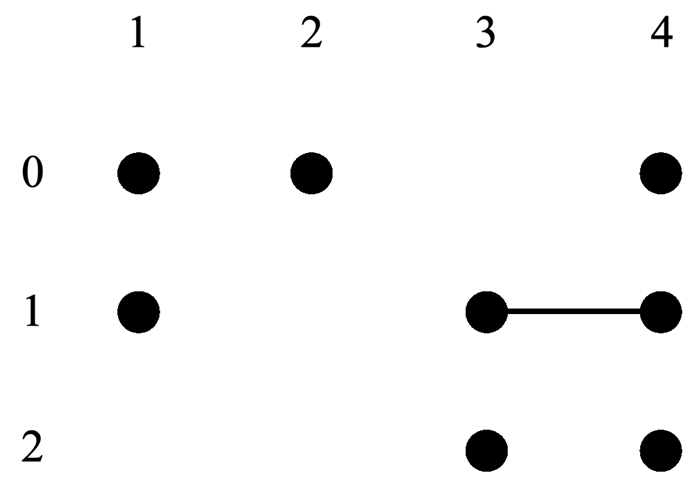
|
图 2 G2, 0 Fig. 2 G2, 0 |
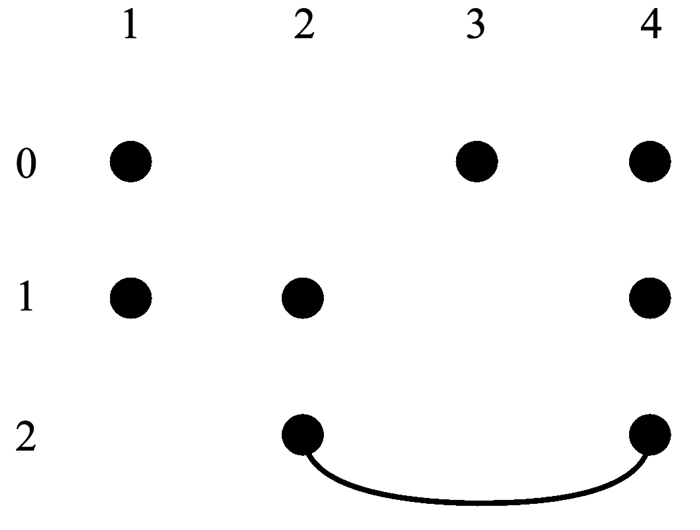
|
图 3 G3, 0 Fig. 3 G3, 0 |
| 表 2 CAFE(3, G2, 0) Tab. 2 CAFE(3, G2, 0) |
| 表 3 CAFE(3, G3, 0) Tab. 3 CAFE(3, G3, 0) |
根据对图中边进行分解计算CAFE(n, G)的最小规模下限的过程,可以得出如下推论:
如果一个图满足下面3个条件:
1) 所有的列具有相同的顶点数,即被测系统的每个参数具有相同的取值个数|g1|=|g2|=…=|gk|=g;
2) 参数i和j之间只有一条边(ai, bj),a, b∈[0, g-1],i, j∈[1, k]且i≠j;
3) 不存在任意顶点cl,c∈[0, g-1]且l∈[1, k],使得(cl, ai), (cl, bj)∉EG.
则有如下关系:
| $ \begin{aligned} N_{G} \geqslant &\left|g_{i}\right|\left|g_{j}\right|-1+\left|g_{i}\right|-\left(\left|g_{i}\right|-1\right)+\\ &\left|g_{j}\right|-\left(\left|g_{j}\right|-1\right)=\left|g_{i}\right|\left|g_{j}\right|+1=g^{2}+1 \end{aligned} $ |
上述推论的证明过程与上例计算NG的过程相同.该推论可以用一个简单的例子来理解,假设图G中每一列都有g个顶点,G中没有边时NG≥g2.假设存在一个带约束的禁忌覆盖数组AG覆盖了全部参数的取值组合,其规模为g2,当G中有一条边时,AG 中一定存在至少一行违反了约束,违反约束的行至少要被扩展成两行才能满足约束,所以CAFE(n, G)的规模至少要增加1,因此,带有一条边的图G满足NG≥g2+1.
3 试验结果与分析本文利用禁忌边分解方法给出5个典型被测系统的2维约束覆盖数组的最小规模的下限,典型的被测系统的配置如表 4所示,这些系统来自于文献[11]和[16].现有算法生成的2维约束覆盖数组的规模如表 5所示.禁忌边分解方法给出的最小规模的下限如表 6所示.通过与生成的约束覆盖数组的规模进行比较,可以看出除了HSS为第2个被测系统生成的规模16小于下限17,其余结果都大于等于给出的下限.小于基于禁忌边分解方法给出的最小规模下限的约束覆盖数组一定不存在,可通过实际的生成过程来说明.
| 表 4 被测系统的配置 Tab. 4 Configurations of the systems under test |
| 表 5 现有算法生成的2维约束覆盖数组的规模 Tab. 5 Sizes of the 2-way constrained covering arrays generated by the existing algorithms |
| 表 6 禁忌边分解方法给出的最小规模的下限 Tab. 6 Lower bounds of the minimum sizes obtained by the forbidden edge decomposing method |
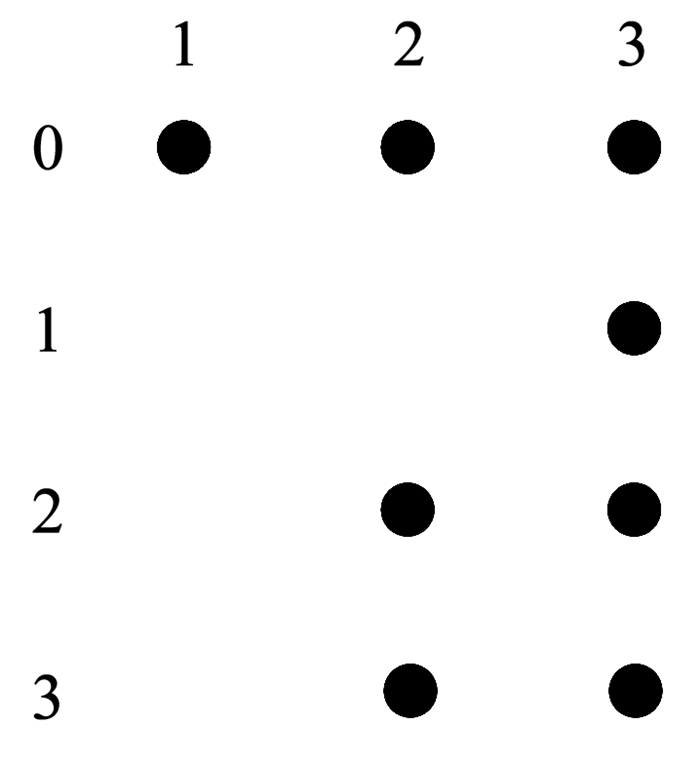
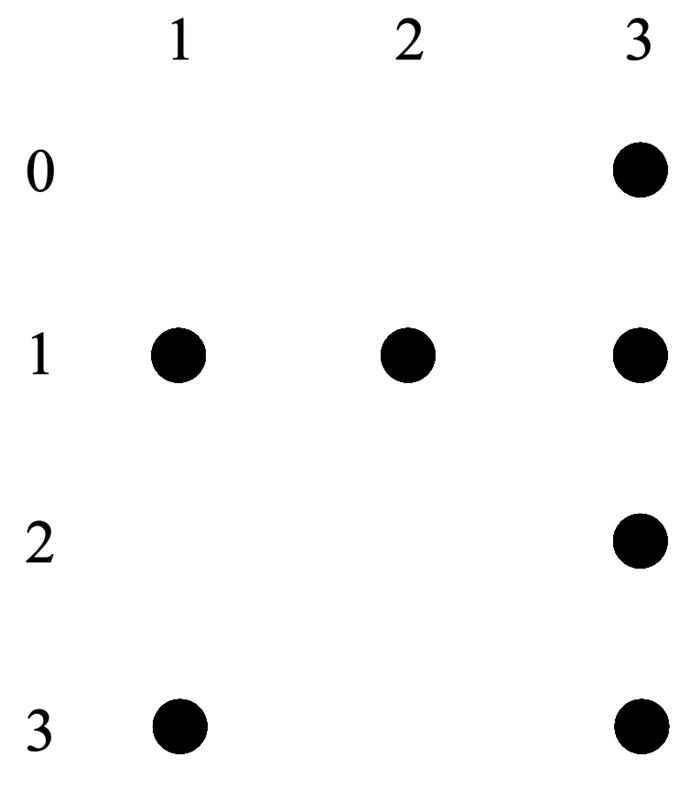
图 4是第2个被测系统参数及取值配置对应的图,图 5和图 6是选取其中第1个参数的值0和第2个参数的值1构成的两个顶点子图.对应这两个顶点子图,能得到表 7和表 8给出的CAFE(4, G1, 0)和CAFE(4, G2, 1),记为AG1, 0和AG2, 1,其规模都为4,表中覆盖了第1个参数和第2个参数的5个取值组合,但是仍有9个取值组合没有被覆盖,如表 9所示.所以可得出NG≥4+4+9=17,即第2个被测系统的约束覆盖数组规模的最小值不能小于17.违反禁忌边分解方法给出的最小规模的下限时,覆盖数组一定不存在,没有违反也不一定能够说明约束覆盖数组不存在,此时只有得到实际生成的约束覆盖数组才能进行验证.
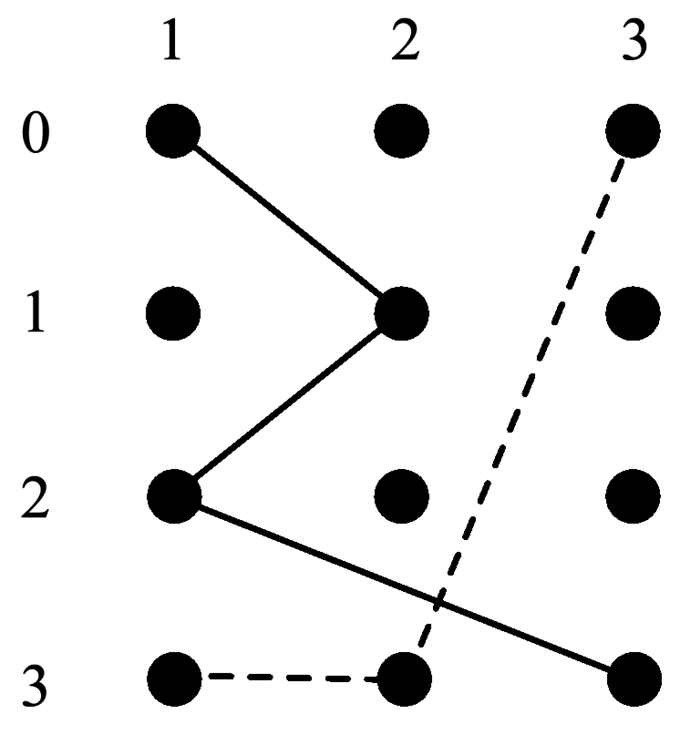
|
图 4 第2个被测系统参数及取值配置对应 Fig. 4 Graph of the parameters and value configurations of the 2nd system under test |
|
图 5 第2个被测系统的G1, 0 Fig. 5 G1, 0 of the 2nd system under test |
|
图 6 第2个被测系统的G2, 1 Fig. 6 G2, 1 of the 2nd system under test |
| 表 7 第2个被测系统的CAFE(4, G1, 0) Tab. 7 CAFE(4, G1, 0) of the 2nd system under test |
| 表 8 第2个被测系统的CAFE(4, G2, 1) Tab. 8 CAFE(4, G2, 1) of the 2nd system under test |
| 表 9 第2个被测系统的未被覆盖的取值组合 Tab. 9 Uncovered value combinations of the 2nd system under test |
本文提出了一种分析2维约束覆盖数组最小规模的禁忌边分解方法.通过将图分解成两个顶点子图,生成两个顶点带有禁忌边的覆盖数组,计算其规模和剩余需要覆盖的取值组合数,提升了2维约束覆盖数组的最小规模.该方法能够得到提升的2维约束覆盖数组的最小规模,更逼近真实值.生成的最小规模可以用于评价现有算法生成的2维约束覆盖数组,有助于判断其是否真实存在.
| [1] |
KACKER R N, KUHN D R, LEI Yu, et al. Combinatorial testing for software:An adaptation of design of experiments[J]. Measurement, 2013, 46(9): 3745. DOI:10.1016/j.measurement.2013.02.021 |
| [2] |
聂长海. 组合测试研究进展[J]. 中国科技论文, 2017, 12(20): 2391. NIE Changhai. The latest research development of combinatorial testing[J]. China Science Paper, 2017, 12(20): 2391. DOI:10.3969/j.issn.1002-137X.2010.03.001 |
| [3] |
KUHN D R, BRYCE R C, DUAN Feng, et al. Combinatorial testing:Theory and practice[J]. Advances in Computers, 2015, 99: 1. DOI:10.1016/bs.adcom.2015.05.003 |
| [4] |
ZHANG Jian, ZHANG Zhiqiang, MA Feifei. Automatic generation of combinatorial test data[M]. Berlin and Heidelberg, Germany: Springer, Berlin, Heidelberg, 2014: 1. DOI:10.1007/978-3-662-43429-1
|
| [5] |
KUHN D R, WALLACE D R, GALLO A M. Software fault interactions and implications for software testing[J]. IEEE Transactions on Software Engineering, 2004, 30(6): 418. DOI:10.1109/TSE.2004.24 |
| [6] |
AHMED B S, ZAMLI K Z, AFZAL W, et al. Constrained interaction testing:A systematic literature study[J]. IEEE Access, 2017, 5: 25706. DOI:10.1109/ACCESS.2017.2771562 |
| [7] |
YU Libin, DUAN Feng, LEI Yu, et al. Constraint handling in combinatorial test generation using forbidden tuples[C]//Proceedings of the 2015 IEEE Eighth International Conference on Software Testing, Verification and Validation Workshops. Washington DC, USA: IEEE Computer Society, 2015: 1. DOI: 10.1109/ICSTW.2015.7107441
|
| [8] |
YAMADA A, BIERE A, ARTHO C, et al. Greedy combinatorial test case generation using unsatisfiable cores[C]//Proceedings of the 31st IEEE/ACM International Conference on Automated Software Engineering. New York, USA: ACM New York, 2016: 614. DOI: 10.1145/2970276.2970335
|
| [9] |
DANZIGER P, MENDELSOHN E, MOURA L, et al. Covering arrays avoiding forbidden edges[J]. Theoretical Computer Science, 2009, 410(52): 5403. DOI:10.1016/j.tcs.2009.07.057 |
| [10] |
MALTAIS E, MOURA L. Finding the best CAFE is NP-hard[C]//Proceedings of the 9th Latin American Conference on Theoretical Informatics. Berlin, Germany: Springer-Verlag, 2010: 356. DOI: 10.1007/978-3-642-12200-2_32
|
| [11] |
ALSEWARI A R A, ZAMLI K Z. Design and implementation of a harmony-search-based variable-strength t-way testing strategy with constraints support[J]. Information and Software Technology, 2012, 54(6): 553. DOI:10.1016/j.infsof.2012.01.002 |
| [12] |
GARVIN B J, COHEN M B, DWYER M B. Evaluating improvements to a meta-heuristic search for constrained interaction testing[J]. Empirical Software Engineering, 2011, 16(1): 61. DOI:10.1007/s10664-010-9135-7 |
| [13] |
COHEN M B, DWYER M B, SHI Jiangfan. Constructing interaction test suites for highly-configurable systems in the presence of constraints:A greedy approach[J]. IEEE Transactions on Software Engineering, 2008, 34(5): 633. DOI:10.1109/TSE.2008.50 |
| [14] |
LEI Yu, KACKER R, KUHN D R, et al. IPOG: A general strategy for t-way software testing[C]//Proceedings of the 14th Annual IEEE International Conference and Workshops on the Engineering of Computer-Based Systems. Washington DC, USA: IEEE Computer Society, 2007: 549. DOI: 10.1109/ECBS.2007.47
|
| [15] |
MICHAEL F, JIM L, YU Lei, et al. Refining the in-parameter-order strategy for constructing covering arrays[J]. Journal of Research of the National Institute of Standards and Technology, 2008, 113(5): 287. DOI:10.6028/jres.113.022 |
| [16] |
LI Longshu, CUI Yingxia, YANG Yun. Combinatorial test cases with constraints in software systems[C]//Proceedings of the 2012 IEEE 16th International Conference on Computer Supported Cooperative Work in Design. New York, USA: IEEE, 2012: 195. DOI: 10.1109/CSCWD.2012.6221818
|
| [17] |
GALINIER P, KPODJEDO S, ANTONIOL G. A penalty-based Tabu search for constrained covering arrays[C]//Proceedings of the Genetic and Evolutionary Computation Conference. New York, USA: ACM New York, 2017: 1288. DOI: 10.1145/3071178.3071324
|
 2020, Vol. 52
2020, Vol. 52


