2. 中国空间技术研究院西安分院, 西安 710000
2. China Academy of Space Technology (Xi'an), Xi'an 710000, China
极化敏感阵列的自适应波束形成技术能够同时利用极化信息和空域信息完成滤波,相比传统标量阵列的纯空域滤波具有更加优良的抗干扰能力,使其在重要的军事、民事等领域具有广泛的应用前景[1-2].四元数具有4个正交基,特别适用于极化敏感阵列的信号建模及信号处理,因此其在极化敏感阵列上得到了广泛的应用[3-4].文献[5]提出的四元数MVDR(Quaternion Minimum Variance Distortionless Response, Q-MVDR)算法在干扰噪声协方差矩阵(interference-plus-noise covariance matrix, IPNCM)及期望信号导向矢量精确已知时具备优越的性能.然而,在实际应用中,许多非理想因素不可忽视.如:由指向误差、阵元位置误差带来的期望信号导向矢量失配[6-8];精确的IPNCM难以获得,利用采样协方差矩阵代替,在期望信号较强时,会出现信号相消现象,引起算法性能急剧下降[9-10].因此,对基于四元数的鲁棒自适应波束形成算法(Robust Adaptive Beamforming, RAB)进行研究十分必要.
在RAB算法方面,文献[11-12]利用对角加载(Diagonal Loading, DL)技术改善了对导向矢量误差的敏感性,但是并没有准则来确定最优加载量.针对此问题,文献[13-14]提出的迭代RAB算法、基于收缩失配估计的RAB算法避免了加载量的求解,并提高了在导向矢量失配时算法的鲁棒性.但是,以上RAB算法都有一个共同的缺点:由于训练数据中包含期望信号成分,当期望信号较强时,算法性能下降.因此,文献[15]利用Capon空间功率谱估计器对与期望信号分离的区域进行积分重构得到了IPNCM,去除训练数据中的期望信号成分,在波束形成领域实现了有价值的创新,为RAB技术的发展提供了一种新思路.但是该算法忽略了干扰信号的功率,并且需要利用CVX工具包求解二次约束二次规划问题,不易实现.在该算法的基础上,文献[16-18]提出的改进算法利用斜投影、去除残余噪声等方法在一定程度上提高了重构IPNCM的精度,以及导向矢量失配时的鲁棒性,但在这两方面仍具有一定的改进空间.
综上,在标量阵列、强期望信号条件下,矩阵重构类方法极大地提升了波束形成算法的鲁棒性.但是在极化敏感阵列方面,已有研究成果尚未有效解决强期望信号和导向矢量失配情况下性能下降的问题.本文针对此问题,提出一种基于四元数矩阵重构的鲁棒波束形成算法,该算法利用四元数完成信号建模,将协方差矩阵重构方法扩展到四元数域,结合四元数信号子空间投影方法,完成了对极化敏感阵列最优权矢量的求解.仿真实验表明,在强期望信号和导向矢量失配时,本文算法表现出较好的鲁棒性.
1 四元数信号模型 1.1 四元数基础将复数在四维空间上进行扩展,可以得到四元数,比较常用的是Hamilton四元数.其定义四元数q由4个分量组成,一个实部和3个虚部[19],可以表示成如下形式
| $ q = a + {\rm{i}}b + {\rm{j}}c + {\rm{k}}d. $ |
式中i, j, k都是虚部单位,满足
| $ {{\rm{i}}^2} = {{\rm{j}}^2} = {{\rm{k}}^2} = {\rm{ijk}} = - 1, {\rm{ij}} = {\rm{k}}, {\rm{ji}} = - {\rm{k, }} $ |
| $ {\rm{ki}} = {\rm{j}}, {\rm{ik}} = - {\rm{j}}, {\rm{ik}} = {\rm{i}}, {\rm{kj}} = - {\rm{i, }} $ |
四元数具有如下性质:
1) 四元数q的共轭q=a-ib-jc-kd;
2) 四元数q的模
3) 四元数q的逆q-1=q /|q2|.
一个四元数q可以表示成2个复数q1,q2相加的形式如:q=q1+iq2,其中q1=a+jc,q2=b+jd,且q1,q2唯一.
1.2 四元数信号模型为了简化阐述,文中假设接收极化波为完全极化波,阵列工作在理想环境下.
极化敏感阵列由相互正交的M个电偶极子对构成,阵列结构如图 1所示,整个阵列可以分为2个子阵,分别由沿x轴和y轴方向放置的电偶极子组成,接收来自x轴和y轴方向的电场分量.各个阵元沿y轴构成均匀线阵,阵元间距为d.
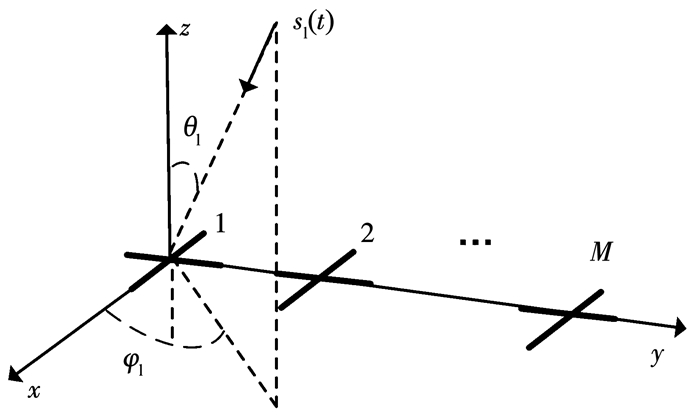
|
图 1 交叉偶极子均匀线阵 Fig. 1 Crossed dipole uniform line array |
假设空间有L+1个远场窄带信号{sl(t)}l=0L入射到阵列上,其中包含1个期望信号和L个干扰信号,入射俯仰角为θl,方位角为φl,极化幅角与相角分别为γl,ηl,信号波长为λ.为方便表述且不失一般性,令φl=90°,ηl=90°,则第l个信号的空域导向矢量和极化域导向矢量可以分别表示为
| $ {\mathit{\boldsymbol{a}}_{\rm{s}}}\left( {{\theta _l}} \right) = {{\rm{e}}^{ - {\rm{j}}\left( {m - 1} \right)\frac{{2{\rm{ \mathit{ π} }}}}{\lambda }d\sin {\theta _l}}}\left( {m = 1, 2, \cdots M} \right), $ |
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{a}}_{\rm{p}}}\left( {{\theta _l}, {\gamma _l}} \right) = \left[ {\begin{array}{*{20}{c}} { - \sin {\varphi _l}}&{\cos {\theta _l}\cos {\varphi _l}}\\ {\cos {\varphi _l}}&{\cos {\theta _l}\sin {\varphi _l}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\cos {\gamma _l}}\\ {\sin {\gamma _l}{e^{{\rm{j}}{\eta _l}}}} \end{array}} \right] = }\\ {\left[ {\begin{array}{*{20}{c}} { - \cos {\gamma _l}}\\ {{\rm{j}}\cos {\theta _l}\sin {\gamma _l}} \end{array}} \right] \buildrel \Delta \over = \left[ {\begin{array}{*{20}{l}} {a_{\rm{p}}^x\left( {{\theta _l}, {\gamma _l}} \right)}\\ {a_{\rm{p}}^y\left( {{\theta _l}, {\gamma _l}} \right)} \end{array}} \right].} \end{array} $ |
式中:apx是沿x轴方向偶极子的极化响应,apy是沿y轴方向的偶极子的极化响应.
根据偶极子方向,可将阵列分为垂直、水平偶极子两个子阵,这两个子阵上第l个信号的导向矢量可表示为
| $ {\mathit{\boldsymbol{a}}_{x, l}} = a_{\rm{p}}^x \cdot {\mathit{\boldsymbol{a}}_{\rm{s}}}, $ |
| $ {\mathit{\boldsymbol{a}}_{y, l}} = a_{\rm{p}}^y \cdot {\mathit{\boldsymbol{a}}_{\rm{s}}}. $ |
则两个子阵的输出x1(t)和x2(t)分别为
| $ {\mathit{\boldsymbol{x}}_1}\left( t \right) = \sum\limits_{l = 0}^L {{\mathit{\boldsymbol{a}}_{x, l}}{s_l}\left( t \right)} + {\mathit{\boldsymbol{n}}_1}\left( t \right), $ |
| $ {\mathit{\boldsymbol{x}}_2}\left( t \right) = \sum\limits_{l = 0}^L {{\mathit{\boldsymbol{a}}_{y, l}}{s_l}\left( t \right)} + {\mathit{\boldsymbol{n}}_2}\left( t \right). $ |
式中:n1(t)和n2(t)分别为两个子阵中与信号相统计独立的高斯白噪声矢量.
四元数具有4个正交基,极化敏感阵列的每个阵元有两个正交分量,整个阵列的输出可以表示成四元数的形式,保持了各分量之间固有的正交特性.四元数域极化敏感阵列的输出可表示为
| $ \begin{array}{l} \mathit{\boldsymbol{x}}\left( t \right) = {\mathit{\boldsymbol{x}}_1}\left( t \right) + {\rm{i}}{\mathit{\boldsymbol{x}}_2}\left( t \right) = \\ \;\;\;\;\;\;\;\;\;\sum\limits_{l = 0}^L \mathit{\boldsymbol{a}} \left( {{\theta _l}, {\gamma _l}} \right){s_l}\left( t \right) + \mathit{\boldsymbol{n}}\left( t \right). \end{array} $ | (1) |
式中:
在波束形成中,式(1)一般表示为
| $ \mathit{\boldsymbol{x}}\left( t \right) = {\mathit{\boldsymbol{a}}_0}{s_0}\left( t \right) + \sum\limits_{l = 1}^L {{\mathit{\boldsymbol{a}}_l}} {s_l}\left( t \right) + \mathit{\boldsymbol{n}}\left( t \right). $ |
式中:a0为期望信号导向矢量,s0(t)为期望信号,al, (l=1, 2, …L)为干扰信号导向矢量,sl(t), (l=1, 2, …, L)为干扰信号.
四元数域的协方差矩阵R∈HM×M为
| $ \mathit{\boldsymbol{R}} = E\left\{ {\mathit{\boldsymbol{x}}\left( t \right){\mathit{\boldsymbol{x}}^ \triangleleft }\left( t \right)} \right\} = \sigma _0^2{\mathit{\boldsymbol{a}}_0}\mathit{\boldsymbol{a}}_0^ \triangleleft + {\mathit{\boldsymbol{R}}_{{\rm{j}} + {\rm{n}}}}. $ |
式中:σ02为期望信号功率,Rj+n为干扰噪声协方差矩阵,(·)⊲表示四元数的共轭转置.
干扰噪声协方差矩阵Rj+n定义为
| $ {\mathit{\boldsymbol{R}}_{{\rm{j}} + {\rm{n}}}} = \sum\limits_{l = 1}^L {\sigma _l^2} {\mathit{\boldsymbol{a}}_l}\mathit{\boldsymbol{a}}_l^ \triangleleft + \sigma _{\rm{n}}^2{\mathit{\boldsymbol{I}}_M}. $ | (2) |
式中:σl2为第l个干扰信号的功率,σn2为噪声功率,IM为单位阵.
1.3 Q-MVDR波束形成算法Q-MVDR算法的最优权矢量w∈HM×1可以依据最大输出信干噪比(max signal-to-interference-plus-noise ratio, MSINR)准则转化为如下问题求得
| $ \mathop {\min }\limits_\mathit{\boldsymbol{w}} {\mathit{\boldsymbol{w}}^ \triangleleft }{\mathit{\boldsymbol{R}}_{{\rm{j}} + {\rm{n}}}}\mathit{\boldsymbol{w}}~{\rm{ s}}{\rm{.t }}~{\mathit{\boldsymbol{w}}^ \triangleleft }{\mathit{\boldsymbol{a}}_0} = 1. $ | (3) |
利用拉格朗日乘子法求解式(3),解得四元数域最优权矢量的表达式为
| $ \mathit{\boldsymbol{w}} = \frac{{\mathit{\boldsymbol{R}}_{{\rm{j}} + {\rm{n}}}^{ - 1}{\mathit{\boldsymbol{a}}_0}}}{{\mathit{\boldsymbol{a}}_0^ \triangleleft \mathit{\boldsymbol{R}}_{{\rm{j}} + {\rm{n}}}^{ - 1}{\mathit{\boldsymbol{a}}_0}}}. $ | (4) |
但是在实际应用中Rj+n难以得到,通常用K个快拍数据的采样协方差矩阵
| $ {\mathit{\boldsymbol{w}}_{{\rm{Q}} - {\rm{MVDR}}}} = \frac{{{{\mathit{\boldsymbol{\hat R}}}^{ - 1}}{{\mathit{\boldsymbol{\hat a}}}_0}}}{{\mathit{\boldsymbol{\hat a}}_0^ \triangleleft {{\mathit{\boldsymbol{\hat R}}}^{ - 1}}{{\mathit{\boldsymbol{\hat a}}}_0}}}. $ | (5) |
式中
针对强期望信号时,MVDR算法出现性能下降并且会加重导向矢量失配的问题,文献[15]提出复数域标量阵列的重构IPNCM的方法,本文将其扩展到四元数域
| $ {{\mathit{\boldsymbol{\hat R}}}_{{\rm{j}} + {\rm{n}}}} = \int_{\mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}} {\frac{{\mathit{\boldsymbol{a}}\left( \theta \right){\mathit{\boldsymbol{a}}^ \triangleleft }\left( \theta \right)}}{{{\mathit{\boldsymbol{a}}^ \triangleleft }\left( \theta \right){{\mathit{\boldsymbol{\hat R}}}^{ - 1}}\mathit{\boldsymbol{a}}\left( \theta \right)}}{\rm{d}}\theta } . $ | (6) |
式中:Θ为干扰信号区域,a(θ), θ∈Θ为导向矢量.但是该方法没有严格按照Rj+n的定义求解,会导致与理论的Rj+n产生误差.针对该问题,本文在此基础上,提出一种基于四元数矩阵重构的鲁棒波束形成算法.
算法首先对
| $ {{\mathit{\boldsymbol{\hat R}}}_{{\rm{j}} + {\rm{n}}}} = \sum\limits_{i = 1}^M {{\gamma _i}} {\mathit{\boldsymbol{b}}_i}\mathit{\boldsymbol{b}}_i^ \triangleleft = {\mathit{\boldsymbol{B}}_{\rm{s}}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{\rm{s}}}\mathit{\boldsymbol{B}}_{\rm{s}}^ \triangleleft + {\mathit{\boldsymbol{B}}_{\rm{n}}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{\rm{n}}}\mathit{\boldsymbol{B}}_{\rm{n}}^ \triangleleft . $ | (7) |
式中:γi, i=1, 2, …, M是按降序排列的
第l个干扰信号的导向矢量位于Bs各列矢量bi张成的干扰子空间,即可用Bs各列线性表示
| $ {\mathit{\boldsymbol{A}}_{\rm{B}}} \buildrel \Delta \over = \left\{ {{{\mathit{\boldsymbol{\hat a}}}_l}\left| {{{\mathit{\boldsymbol{\hat a}}}_l}} \right. = {\mathit{\boldsymbol{B}}_{\rm s}}{\mathit{\boldsymbol{\alpha }}_{\rm{B}}}, \forall {\mathit{\boldsymbol{\alpha }}_{\rm{B}}} \in {R^{P \times 1}}} \right\}. $ |
式中:∀ αB∈RP×1为系数向量,R为实数集.
然后对采样协方差矩阵
| $ \mathit{\boldsymbol{\hat R = }}\sum\limits_{i = 1}^M {{\lambda _i}} {\mathit{\boldsymbol{e}}_i}\mathit{\boldsymbol{e}}_i^ \triangleleft \mathit{\boldsymbol{ = }}{\mathit{\boldsymbol{E}}_{\rm{s}}}{\mathit{\boldsymbol{A}}_{\rm{s}}}\mathit{\boldsymbol{E}}_{\rm{s}}^ \triangleleft + {\mathit{\boldsymbol{E}}_{\rm{n}}}{\mathit{\boldsymbol{A}}_{\rm{n}}}\mathit{\boldsymbol{E}}_{\rm{n}}^ \triangleleft . $ | (8) |
式中:λi, i=1, 2, …, M是按降序排列的
第l个干扰信号的导向矢量也可以用Es线性表示
| $ {\mathit{\boldsymbol{A}}_{\rm{E}}} \buildrel \Delta \over = \left\{ {{{\mathit{\boldsymbol{\hat a}}}_l}\left| {{{\mathit{\boldsymbol{\hat a}}}_l}} \right. = {\mathit{\boldsymbol{E}}_s}{\mathit{\boldsymbol{\alpha }}_{\rm{E}}}, \forall {\mathit{\boldsymbol{\alpha }}_{\rm{E}}} \in {R^{\left( {L + 1} \right) \times 1}}} \right\}, $ |
式中∀αE∈R(L+1)×1为系数向量.
通过以上分析,第l个干扰信号的导向矢量估计
首先构造一个初始向量为
| $ {\mathit{\boldsymbol{a}}_{L + 1}} = {\mathit{\boldsymbol{P}}_{\rm{B}}}{\mathit{\boldsymbol{P}}_{\rm{E}}}{\mathit{\boldsymbol{a}}_L}. $ |
当L趋近于∞时,aL收敛于真实的导向矢量,即:a∞=PBPEa∞.根据文献[20],a∞的求解问题可以等价为对矩阵PBPE中特征值为1的特征向量的求解问题,有
| $ \begin{array}{*{20}{c}} {{\rm eig}{_{\max }}\left( {{\mathit{\boldsymbol{P}}_{\rm{B}}}{\mathit{\boldsymbol{P}}_{\rm{E}}}} \right) \le {\rm eig}{_{{\rm{max}}}}\left( {{\mathit{\boldsymbol{P}}_{\rm{B}}}} \right)\mathop {\max }\limits_{{\mathit{\boldsymbol{u}}^ \triangleleft }\mathit{\boldsymbol{u}} = 1} {\mathit{\boldsymbol{P}}_{\rm{E}}}\mathit{\boldsymbol{u}} = }\\ {\mathop {\max }\limits_{{\mathit{\boldsymbol{u}}^ \triangleleft }\mathit{\boldsymbol{u}} = 1} \mathit{\boldsymbol{u}}{\mathit{\boldsymbol{P}}_{\rm{E}}}\mathit{\boldsymbol{u}} = {\rm eig}{_{{\rm{max}}}}\left( {{\mathit{\boldsymbol{P}}_{\rm{E}}}} \right) = 1.} \end{array} $ |
式中eigmax()代表矩阵的最大特征值.矩阵PBPE的最大特征值为1.
得到
| $ {{\mathit{\boldsymbol{\hat a}}}_l} = \sqrt M \gamma \left( {{\mathit{\boldsymbol{P}}_{\rm{B}}}{\mathit{\boldsymbol{P}}_{\rm{E}}}} \right). $ | (9) |
式中:PB=BsBs⊲,PE=EsEs⊲,γ(PBPE)表示矩阵PBPE的最大特征值对应的特征向量.
最后,利用Capon谱估计器得到第l个干扰信号的功率
| $ \mathit{\boldsymbol{\hat \sigma }}_l^2 = \frac{1}{{\mathit{\boldsymbol{\hat a}}_l^ \triangleleft {{\mathit{\boldsymbol{\hat R}}}^{ - 1}}{{\mathit{\boldsymbol{\hat a}}}_l}}}. $ | (10) |
式(2)中,噪声功率σn2未知,其可以用
| $ {{\mathit{\boldsymbol{\tilde R}}}_{{\rm{j}} + {\rm{n}}}} = \sum\limits_{l = 1}^L {\hat \sigma _l^2} {{\mathit{\boldsymbol{\hat a}}}_l}\mathit{\boldsymbol{\hat a}}_l^ \triangleleft + \mathit{\boldsymbol{\hat \sigma }}_{\rm{n}}^2{\mathit{\boldsymbol{I}}_M}. $ | (11) |
将
| $ {\mathit{\boldsymbol{w}}_{{\rm{Q}} - {\rm{Re}c}}} = \frac{{\mathit{\boldsymbol{\tilde R}}_{{\rm{j}} + {\rm{n}}}^{ - 1}{{\mathit{\boldsymbol{\hat a}}}_0}}}{{\mathit{\boldsymbol{\hat a}}_0^ \triangleleft \mathit{\boldsymbol{\tilde R}}_{{\rm{j}} + {\rm{n}}}^{ - 1}{{\mathit{\boldsymbol{\hat a}}}_0}}}. $ | (12) |
当导向矢量失配时,
| $ {\mathit{\boldsymbol{w}}_{{\rm{Proposed}}}} = {\mathit{\boldsymbol{P}}_{\rm{E}}}{\mathit{\boldsymbol{w}}_{{\rm{Q}} - {\rm{Re}c}}} = {\mathit{\boldsymbol{E}}_{\rm{s}}}\mathit{\boldsymbol{E}}_{\rm{s}}^ \triangleleft {\mathit{\boldsymbol{w}}_{{\rm{Q}} - {\mathop{\rm Re}\nolimits} c}}. $ |
式中PE为投影矩阵,该投影运算使得权矢量的范数减小,同时满足
易知,EsEs⊲+EnEn⊲=IM,将wQ-Rec分解为两个正交的分量
| $ {\mathit{\boldsymbol{w}}_{{\rm{Q}} - {\mathop{\rm Re}\nolimits} c}} = {\mathit{\boldsymbol{E}}_{\rm{s}}}\mathit{\boldsymbol{E}}_{\rm{s}}^ \triangleleft {\mathit{\boldsymbol{w}}_{{\rm{Q}} - {\mathop{\rm Re}\nolimits} c}} + {\mathit{\boldsymbol{E}}_{\rm{n}}}\mathit{\boldsymbol{E}}_{\rm{n}}^ \triangleleft {\mathit{\boldsymbol{w}}_{{\rm{Q}} - {\mathop{\rm Re}\nolimits} c}}. $ |
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{w}}_{{\rm{Proposed}}}^ \triangleleft {{\mathit{\boldsymbol{\hat a}}}_0} = {{\left( {{\mathit{\boldsymbol{E}}_{\rm{s}}}\mathit{\boldsymbol{E}}_{\rm{s}}^ \triangleleft {\mathit{\boldsymbol{w}}_{{\rm{Q}} - {\mathop{\rm Re}\nolimits} c}} + {\mathit{\boldsymbol{E}}_{\rm{n}}}\mathit{\boldsymbol{E}}_{\rm{n}}^ \triangleleft {\mathit{\boldsymbol{w}}_{{\rm{Q}} - {\mathop{\rm Re}\nolimits} c}}} \right)}^ \triangleleft }{{\mathit{\boldsymbol{\hat a}}}_0} = }\\ {{{\left( {{\mathit{\boldsymbol{E}}_{\rm{s}}}\mathit{\boldsymbol{E}}_{\rm{s}}^ \triangleleft {\mathit{\boldsymbol{w}}_{{\rm{Q}} - {\mathop{\rm Re}\nolimits} c}}} \right)}^ \triangleleft }{{\mathit{\boldsymbol{\hat a}}}_0}, } \end{array} $ |
得到最优权矢量
| $ {\mathit{\boldsymbol{w}}_{{\rm{Proposed}}}} = {\mathit{\boldsymbol{E}}_{\rm{s}}}\mathit{\boldsymbol{E}}_{\rm{s}}^ \triangleleft {\mathit{\boldsymbol{w}}_{{\rm{Q}} - {\mathop{\rm Re}\nolimits} c}}. $ | (13) |
综上,本文提出的基于四元数矩阵重构的鲁棒波束形成算法,具体步骤如下
步骤1:利用式(8)对
步骤2:利用式(6)重构
步骤3:根据干扰信号个数,利用式(9)和(10)得到干扰信号的导向矢量和功率的估计值;
步骤4:利用式(11)和(12)得到重构的
步骤5:利用式(13)将wQ-Rec向四元数信号子空间EsEs⊲投影,得到最优权值wProposed.
3 算法性能分析定义四元数波束形成器信干噪比损失[20]为
| $ L = \frac{{{S_{{\rm{out}}}}}}{{{S_{{\rm{CBF}}}}}} = \frac{{\sigma _{\rm{n}}^2{{\left| {{\mathit{\boldsymbol{w}}^ \triangleleft }{\mathit{\boldsymbol{a}}_0}} \right|}^2}}}{{M{\mathit{\boldsymbol{w}}^ \triangleleft }{\mathit{\boldsymbol{R}}_{{\rm{j}} + {\rm{n}}}}\mathit{\boldsymbol{w}}}}. $ | (14) |
式中:阵列输出Sout=σ02|w⊲a0|2/w⊲Rj+nw,SCBF=Mσ02/σn2.Sout与期望信号的强度有关,而信干噪比损失L不再依赖于期望信号的强度.
将式(4)代入式(14)得到最优波束形成器的信干噪比损失为
| $ {L_{{\rm{opt}}}} = \frac{{\sigma _{\rm{n}}^2}}{M}\mathit{\boldsymbol{a}}_0^ \triangleleft \mathit{\boldsymbol{R}}_{{\rm{j}} + {\rm{n}}}^{ - 1}{\mathit{\boldsymbol{a}}_0}. $ |
最优波束形成器的输出SINR可以表示为
| $ {S_{{\rm{opt}}}} = \sigma _0^2\mathit{\boldsymbol{a}}_0^ \triangleleft \mathit{\boldsymbol{R}}_{{\rm{j}} + {\rm{n}}}^{ - 1}{\mathit{\boldsymbol{a}}_0} = {L_{{\rm{opt}}}}{S_{{\rm{CBF}}}}. $ | (15) |
在强期望信号和导向矢量失配情况下,算法性能严重下降的原因有以下两种情况:
1) 训练数据中不含期望信号时导向矢量失配的权矢量为
| $ {\mathit{\boldsymbol{w}}_{{\rm{{\rm mis}}}}} = \frac{{\mathit{\boldsymbol{R}}_{{\rm{j}} + {\rm{n}}}^{ - 1}{{\mathit{\boldsymbol{\hat a}}}_0}}}{{\mathit{\boldsymbol{\hat a}}_0^ \triangleleft \mathit{\boldsymbol{R}}_{{\rm{j}} + {\rm{n}}}^{ - 1}{{\mathit{\boldsymbol{\hat a}}}_0}}}, $ | (16) |
将式(16)代入Sout,得到
| $ \begin{array}{*{20}{c}} {{S_{{\rm{{\rm mis}}}}} = \frac{{\sigma _0^2{{\left| {\mathit{\boldsymbol{w}}_{{\rm mis}}^ \triangleleft {\mathit{\boldsymbol{a}}_0}} \right|}^2}}}{{\mathit{\boldsymbol{w}}_{{\rm mis}}^ \triangleleft {\mathit{\boldsymbol{R}}_{{\rm{j}} + {\rm{n}}}}{\mathit{\boldsymbol{w}}_{{\rm mis}}}}} = }\\ {\sigma _0^2\mathit{\boldsymbol{a}}_0^ \triangleleft \mathit{\boldsymbol{R}}_{{\rm{j}} + {\rm{n}}}^{ - 1}{\mathit{\boldsymbol{a}}_0}\frac{{{{\left| {{{\mathit{\boldsymbol{\hat a}}}^ \triangleleft }\mathit{\boldsymbol{R}}_{{\rm{j}} + {\rm{n}}}^{ - 1}{\mathit{\boldsymbol{a}}_0}} \right|}^2}}}{{\left( {\mathit{\boldsymbol{\hat a}}_0^ \triangleleft \mathit{\boldsymbol{R}}_{{\rm{j}} + {\rm{n}}}^{ - 1}{{\mathit{\boldsymbol{\hat a}}}_0}} \right)\left( {{\mathit{\boldsymbol{a}}^ \triangleleft }\mathit{\boldsymbol{R}}_{{\rm{j}} + {\rm{n}}}^{ - 1}{\mathit{\boldsymbol{a}}_0}} \right)}}, } \end{array} $ | (17) |
定义
| $ {S_{{\rm{{\rm mis}}}}} = {S_{{\rm{opt}}}}{\cos ^2}\left( {{{\mathit{\boldsymbol{\hat a}}}_0}, {\mathit{\boldsymbol{a}}_0}, \mathit{\boldsymbol{R}}_{{\rm{j}} + {\rm{n}}}^{ - 1}} \right), $ |
则信干噪比损失为
| $ {L_{{\rm{{\rm mis}}}}} = {\cos ^2}\left( {{{\mathit{\boldsymbol{\hat a}}}_0}, {\mathit{\boldsymbol{a}}_0}, \mathit{\boldsymbol{R}}_{{\rm{j}} + {\rm{n}}}^{ - 1}} \right), $ |
结合式(15)得
| $ {S_{{\rm{{\rm mis}}}}} = {S_{{\rm{CBF}}}}{L_{{\rm{opt}}}}{L_{{\rm{{\rm mis}}}}}. $ |
可见,此时由导向矢量失配引起的信干噪比损失与期望信号强度无关,当失配角较小时,Lmis接近为1.
2) 训练数据中含有期望信号时导向矢量失配,信干噪比损失为
| $ {L_{{\rm{sp}}}} = \frac{1}{{1 + \left( {2{S_{{\rm{opt}}}} + S_{{\rm{opt}}}^2} \right){{\sin }^2}\left( {{{\mathit{\boldsymbol{\hat a}}}_0}, {\mathit{\boldsymbol{a}}_0}, \mathit{\boldsymbol{R}}_{{\rm{j}} + {\rm{n}}}^{ - 1}} \right)}}, $ | (18) |
并且有
| $ {S_{{\rm{{\rm mis}}} + {\rm{sp}}}} = {S_{{\rm{{\rm mis}}}}}{L_{{\rm{sp}}}} = {S_{{\rm{CBF}}}}{L_{{\rm{opt}}}}{L_{{\rm{{\rm mis}}}}}{L_{{\rm{sp}}}}. $ |
由式(18)可知,此时的信干噪比损失与期望信号强度有关,期望信号越强,信干噪比损失越大,甚至会出现强期望信号时的输出SINR比弱期望信号时还要低的现象,这就是强期望信号引起性能下降的原因所在.此外,导向矢量失配对算法性能的影响比不含期望信号时大[21].
本文算法首先严格按照IPNCM的定义式,并利用子空间方法去除了期望信号成分,重构出高精度的
| $ \begin{array}{*{20}{c}} {{S_{{\rm{Proposed}}}} = \frac{{\sigma _0^2{{\left| {\mathit{\boldsymbol{w}}_{{\rm{Proposed}}}^ \triangleleft {\mathit{\boldsymbol{a}}_0}} \right|}^2}}}{{\mathit{\boldsymbol{w}}_{{\rm{Proposed}}}^ \triangleleft {\mathit{\boldsymbol{R}}_{{\rm{j}} + {\rm{n}}}}{\mathit{\boldsymbol{w}}_{{\rm{Proposed}}}}}} = }\\ {\frac{{\sigma _0^2{{\left| {\mathit{\boldsymbol{\tilde a}}_0^ \triangleleft \mathit{\boldsymbol{R}}_{{\rm{j}} + {\rm{n}}}^{ - 1}{\mathit{\boldsymbol{a}}_0}} \right|}^2}}}{{\mathit{\boldsymbol{\tilde a}}_0^ \triangleleft \mathit{\boldsymbol{\tilde R}}_{{\rm{j}} + {\rm{n}}}^{ - 1}{\mathit{\boldsymbol{R}}_{{\rm{j}} + {\rm{n}}}}\mathit{\boldsymbol{\tilde R}}_{{\rm{j}} + {\rm{n}}}^{ - 1}{{\mathit{\boldsymbol{\tilde a}}}_0}}} \approx \frac{{\sigma _0^2{{\left| {\mathit{\boldsymbol{\tilde a}}_0^ \triangleleft \mathit{\boldsymbol{R}}_{{\rm{j}} + {\rm{n}}}^{ - 1}{\mathit{\boldsymbol{a}}_0}} \right|}^2}}}{{\mathit{\boldsymbol{\tilde a}}_0^ \triangleleft \mathit{\boldsymbol{\tilde R}}_{{\rm{j}} + {\rm{n}}}^{ - 1}{{\mathit{\boldsymbol{\tilde a}}}_0}}}, } \end{array} $ |
化简得
| $ {L_{{\rm{Proposed}}}} = {\cos ^2}\left( {{{\mathit{\boldsymbol{\tilde a}}}_0}, {\mathit{\boldsymbol{a}}_0}, \mathit{\boldsymbol{R}}_{{\rm{j}} + {\rm{n}}}^{ - 1}} \right), $ |
修正后的导向矢量
| $ {S_{{\rm{Proposed}}}} \approx {S_{{\rm{opt}}}}{L_{{\rm{Proposed}}}} \approx {S_{{\rm{opt}}}}. $ |
因此,本文算法的输出SINR接近于最优值.
4 仿真分析仿真条件:由8个偶极子构成的均匀线阵,阵元数M=8,阵元间距d=λ/2,采样快拍数K=200,期望信号参数为(θ0, γ0)=(0°, 10°),导向矢量失配误差为2°,S=10 dB,干扰信号参数为(θ1, γ1)=(50°, 20°),I=30 dB.
在以上仿真条件下,将本文算法(Proposed)与四元数域PCMR-Q-MVDR算法[17]、CCMR-Q-MVDR算法[15]、对角加载(DL-Q-MVDR)算法[11]、Q-MVDR算法[5]和最优(Optimal)算法进行对比分析,考察算法方向图、输出信干噪比等方面的性能.
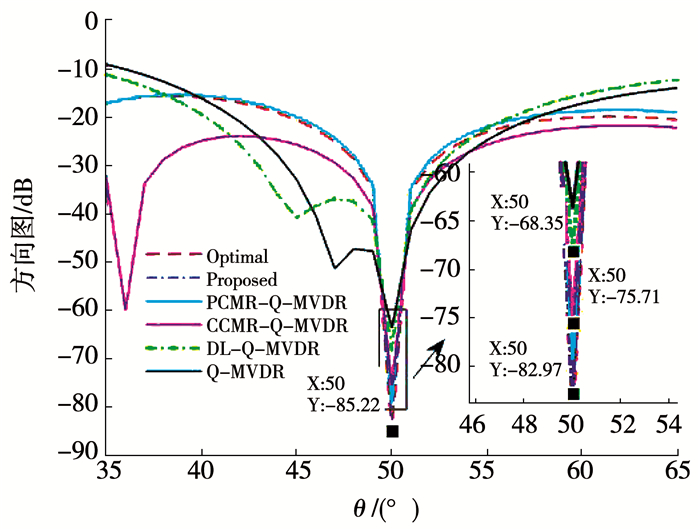
4.1 强期望信号时不同算法方向图比较本实验考察强期望信号情况下,不同算法的方向图对比,仿真结果如图 2所示.

|
图 2 强期望信号时方向图的对比 Fig. 2 Comparison of beampatterns in strong desired signal case |
由图 2可知,DL-Q-MVDR和Q-MVDR算法出现期望信号相消的现象,即:期望信号方向产生了零陷;CCMR-Q-MVDR算法在期望信号方向出现较小的估计偏差;本文算法和PCMR-Q-MVDR算法都精确对准期望信号并具有较低的旁瓣.
为便于比较不同算法产生的零陷深度,将图 2中干扰附近区域放大如图 3所示.由图 3可知,本文算法由于严格依据定义式重构得到
|
图 3 强期望信号时干扰零陷深度的对比 Fig. 3 Comparison of interference depth in strong desired signal case |
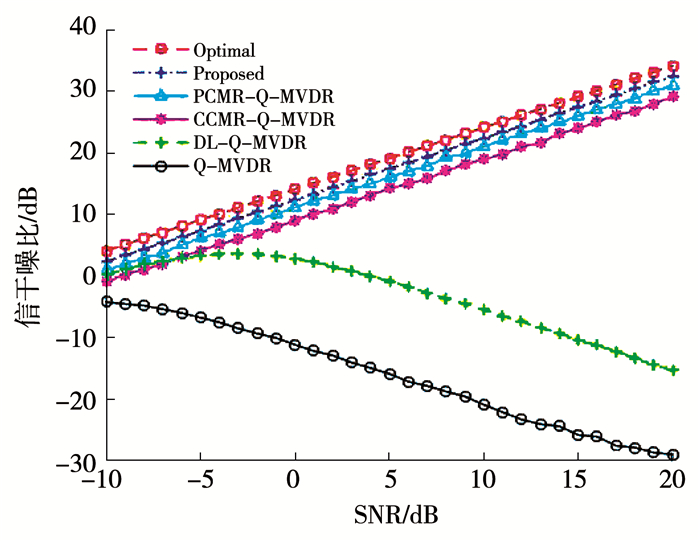
本实验在导向矢量失配条件下,考察不同算法输出SINR随输入SNR的变化情况.仿真条件改变S=-10 dB~20 dB,进行500次蒙特卡洛独立实验,仿真结果如图 4所示.
|
图 4 输出SINR与输入SNR的变化曲线 Fig. 4 Variation curves of output SINR with input SNR |
由图 4可知,Q-MVDR算法在SNR很小时,性能已经出现下降;DL-Q-MVDR算法虽然一定程度上改善了算法的性能,但是当SNR>0 dB时,算法性能也明显下降;本文算法、PCMR-Q-MVDR和CCMR-Q-MVDR算法由于重构出IPNCM,输出SINR随着输入SNR线性增加.本文算法相比其他两种重构类算法,具有更高的输出SINR,并接近于最优值.
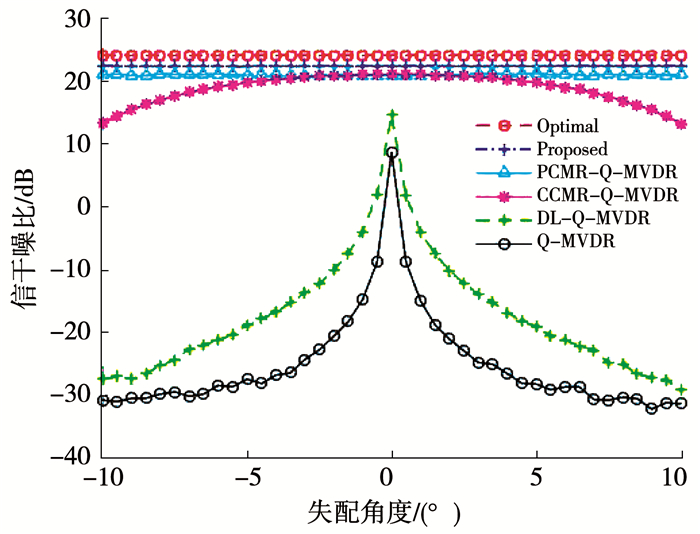
4.3 输出信干噪比与失配角度的关系本实验在强期望信号条件下,对不同算法输出SINR与失配角度的关系进行仿真.仿真条件改变失配角度为-10°~10°,进行500次蒙特卡洛独立实验,仿真结果如图 5所示.
|
图 5 期望信号失配时输出SINR与失配角度关系 Fig. 5 Correlation between output SINR and mismatch angle in the case of desired signal steering vector mismatch |
由图 5可知,Q-MVDR算法即使很小的失配角度,就会引起性能严重恶化;DL-Q-MVDR算法一定程度上提高了对失配角度的敏感性,但当失配角度大于2°时,算法性能严重下降;CCMR-Q-MVDR算法进一步提高了对失配角度的敏感性,但当失配角度大于5°时,性能也出现明显下降;本文算法和PCMR-Q-MVDR算法都对失配角度不敏感,但本文算法具有更高的输出SINR,当失配角度较大时,依旧较接近于最优值.
以上仿真实验表明,本文提出的基于四元数矩阵重构的鲁棒波束形成算法,在强期望信号和导向矢量失配时的输出SINR均能收敛于最优值.这说明通过重构
针对在强期望信号和导向矢量失配的情况下,Q-MVDR算法性能下降的问题,提出了一种基于四元数矩阵重构的鲁棒波束形成算法.该算法首先利用四元数矩阵重构方法得到IPNCM的精确估计;然后利用四元数特征空间投影对导向矢量失配误差进行修正.仿真结果表明,本文算法在强期望信号和导向矢量失配同时存在时,能够保证期望信号方向波束增益无损失的同时,实现对干扰的有效抑制;算法始终具有较高的输出SINR,有效地提高了算法的鲁棒性.
| [1] |
JO O, KIM J, YOON J, et al. Exploitation of dual-polarization diversity for 5G millimeter-wave MIMO beamforming systems[J]. IEEE Transactions on Antennas and Propagation, 2017, 65(12): 6646. DOI:10.1109/TAP.2017.2761979 |
| [2] |
FABIANI B M, SILVEIRA E S, PINA M V P, et al. Nonlinear constrained beamforming algorithm for circularly polarized phased arrays[J]. IEEE Antennas & Wireless Propagation Letters, 2018, 17(9): 1692. DOI:10.1109/LAWP.2018.2863544 |
| [3] |
LIU Wei. Channel equalization and beamforming for quaternion-valued wireless communication systems[J]. Journal of the Franklin Institute, 2016, 354(18): 8721. DOI:10.1016/j.jfranklin.2016.10.043 |
| [4] |
ZHANG Xirui, LIU Wei, XU Yougen, et al. Quaternion-valued robust adaptive beamformer for electromagnetic vector-sensor arrays with worst-case constraint[J]. Signal Processing, 2014, 104: 274. DOI:10.1016/j.sigpro.2014.04.006 |
| [5] |
TAO Jianwu, CHANG Wenxiu. The MVDR beamformer based on hypercomplex processes[C]//Proceedings of 2012 International Conference on Computer Science and Electronics Engineering. Piscataway: IEEE, 2012: 273. DOI: 10.1109/ICCSEE.2012.430
|
| [6] |
李文兴, 毛晓军, 翟助群. 抗导向矢量失配的零陷展宽波束形成算法[J]. 哈尔滨工业大学学报, 2016, 48(11): 116. LI Wenxing, MAO Xiaojun, ZHAI Zhuqun. Null broadening beamforming against steering vector mismatch[J]. Journal of Harbin Institute of Technology, 2016, 48(11): 116. DOI:10.11918/j.issn.0367-6234.2016.11.018 |
| [7] |
CHEN Peng, YANG Yixin, WANG Yong, et al. Adaptive beamforming with sensor position errors using covariance matrix construction based on subspace bases transition[J]. IEEE Signal Processing Letters, 2019, 26(1): 19. DOI:10.1109/LSP.2018.2878948 |
| [8] |
HUANG Junsheng, SU Hongtao, YANG Yang. Low-complexity robust adaptive beamforming method for MIMO radar based on covariance matrix estimation and steering vector mismatch correction[J]. IET Radar, Sonar & Navigation, 2019, 13(5): 712. DOI:10.1049/iet-rsn.2018.5416 |
| [9] |
LI Zhihui, ZHANG Yongshun, GE Qichao, et al. Middle subarray interference covariance matrix reconstruction approach for robust adaptive beamforming with mutual coupling[J]. IEEE Communications Letters, 2019, 23(4): 664. DOI:10.1109/LCOMM.2019.2899874 |
| [10] |
ZHENG Zhi, ZHENG Yan, WANG Wenqin, et al. Covariance matrix reconstruction with interference steering vector and power estimation for robust adaptive beamforming[J]. IEEE Transactions on Vehicular Technology, 2018, 67(9): 8495. DOI:10.1109/TVT.2018.2849646 |
| [11] |
ER M H, NG B C. A new approach to robust beamforming in the presence of steering vector errors[J]. IEEE Transactions on Signal Processing, 1994, 42(7): 1826. DOI:10.1109/78.298291 |
| [12] |
MESTRE X, LAGUNAS M A. Finite sample size effect on minimum variance beamformers:Optimum diagonal loading factor for large arrays[J]. IEEE Transactions on Signal Processing, 2006, 54(1): 69. DOI:10.1109/TSP.2005.861052 |
| [13] |
HASSANIEN A, VOROBYOV S A, WONG K M. Robust adaptive beamforming using sequential quadratic programming:An iterative solution to the mismatch problem[J]. IEEE Signal Processing Letters, 2008, 15: 733. DOI:10.1109/LSP.2008.2001115 |
| [14] |
RUAN Hang, DE LAMARE R C. Robust adaptive beamforming using a low-complexity shrinkage-based mismatch estimation algorithm[J]. IEEE Signal Processing Letters, 2014, 21(1): 60. DOI:10.1109/LSP.2013.2290948 |
| [15] |
GU Yujie, LESHEM A. Robust adaptive beamforming based on interference covariance matrix reconstruction and steering vector estimation[J]. IEEE Transactions on Signal Processing, 2012, 60(7): 3881. DOI:10.1109/TSP.2012.2194289 |
| [16] |
ZHU Xingyu, YE Zhongfu, XU Xu, et al. Covariance matrix reconstruction via residual noise elimination and interference powers estimation for robust adaptive beamforming[J]. IEEE Access, 2019, 7: 53262. DOI:10.1109/ACCESS.2019.2912402 |
| [17] |
ZHANG Xue, LIU Shuai, YAN Fenggang, et al. Robust adaptive beamforming based on covariance matrix reconstruction against steering vector mismatch[C]//Proceedings of 2019 IEEE/CIC International Conference on Communications in China (ICCC). Piscataway: IEEE, 2019: 283. DOI: 10.1109/ICCChina.2019.8855940
|
| [18] |
AI Xiaoyu, GAN Lu. Robust adaptive beamforming with subspace projection and covariance matrix reconstruction[J]. IEEE Access, 2019, 7: 102149. DOI:10.1109/ACCESS.2019.2930750 |
| [19] |
JIANG Mengdi, LIU Wei, LI Yi. Adaptive beamforming for vector-sensor arrays based on a reweighted zero-attracting quaternion-valued LMS algorithm[J]. IEEE Transactions on Circuits and Systems, 2016, 63(3): 274. DOI:10.1109/TCSII.2015.2482464 |
| [20] |
ZHANG F, ZHANG Q. Eigenvalue inequalities for matrix product[J]. IEEE Transactions on Automatic Control, 2006, 51(9): 1506. DOI:10.1109/TAC.2006.880787 |
| [21] |
王永良, 丁前军, 李荣锋. 自适应阵列处理[M]. 北京: 清华大学出版社, 2009: 14. WANG Yongliang, DING Qianjun, LI Rongfeng. Adaptive array processing[M]. Beijing: Tsinghua University Press, 2009: 14. |
 2020, Vol. 52
2020, Vol. 52


