超密集网络(UDN)通过在宏小区的覆盖区域内密集部署小小区基站(SBS)，实现了热点增强、消除覆盖忙点、提高系统容量的目的^[1-3]，UDN已成为满足5G系统超高容量需求的关键技术之一^[4-5].但SBS的多样化、密集化和随机化带来了严重的系统干扰问题^[6].

研究结果表明有效的功率分配策略可以抑制干扰并提高系统吞吐量^[7-8]，但功率优化问题通常是非凸的.采用博弈论建模可将非凸问题转化为各种凸问题.此外，基于博弈论设计的分布式算法往往需要较少的信道状态信息(CSI).因此，国内外学者对UDN中基于博弈论的功率分配方案进行了广泛研究，包括非合作场博弈^[9-10]、斯坦伯格博弈^[11-12]、平均场博弈^[13-14]及联盟博弈^[15]等.

文献[9]采用了带有惩罚因子的非合作博弈模型，并提出了基于虚拟小区本地信息的功率分配算法.文献[11]采用斯坦伯格博弈对双层异构网络进行建模, 针对密集部署场景提出了非统一定价的功率分配策略.文献[13]提出了一种基于平均场博弈的分布式功率控制方法以最大化系统能效，研究中考虑了用户的移动性和终端设备的电量储备.但上述的研究成果仍有一些不足之处：无法判断博弈模型的NE与原非凸优化问题最优解之间的关系；没有对用户受到的干扰进行约束以保证服务质量(QOS)；所提出的迭代算法没有在理论上证明收敛性.

本文通过设计一种动态定价使得博弈的纳什均衡点(NE)是原优化问题的驻点，并引入干扰功率约束条件以保证宏小区用户的QOS.在此博弈论框架下，提出了适用于两层异构UDN中的功率分配算法，并证明了收敛性.

1 系统模型

考虑UDN中的上行传输场景，在宏基站(MBS)的覆盖范围内随机部署若干个SBS.设系统中的小小区数量为N，每个小小区与宏小区共享相同的频带.由于采用正交频分多址，小区内每个时频资源块上只有一个接入用户，因此小区内干扰可忽略不计.但是，同一时频资源块上不同小区间的用户存在严重干扰.系统模型如图 1所示，为了简洁清晰，图中只画出了部分干扰链路.

假设每个用户随机分布在每个小小区的覆盖区域内，且所有用户(即终端)和基站都配备单天线.发射功率向量p=(p₁, p₂, …, p_n, …, p_N－1, p_N)，其中p_n是小小区n中用户的发射功率，由于发射功率限制，p_n的最大值为p_n^max.宏小区中用户的发射功率为p^m.另外，小小区i和SBS j的用户之间的信道功率增益是h_ij，小小区i和MBS的用户之间的信道功率增益为h_i^sm，并且h_i^ms表示宏小区用户和SBS i之间的信道功率增益.假设所有信道功率增益是独立同分布的，建模为d^－αβ²，其中d是发射机和接收机之间的距离，α是路径损耗指数，β是具有零均值和单位方差的瑞利衰落系数，即β~CN(0, 1).

在上述框架下，小小区n在给定频谱上的信干燥比(SINR)为

$ {\chi _n} = \frac{{{p_n}{h_{n, n}}}}{{\sum\limits_{i \ne n} {{p_i}} {h_{i, n}} + {p^{\rm{m}}}h_n^{{\rm{ms}}} + {w_n}}}. $

式中w_n为加性高斯白噪声.则小小区n的传输速率为

$ {R_n} = B{\log _2}\left( {1 + {\chi _n}} \right). $

来自所有小小区用户的跨层干扰严重影响宏小区用户的QOS，因此，通过引入干扰功率约束Q来限制跨层干扰，即

$ \sum\limits_{i = 1}^N {{p_i}} h_i^{{\rm{sm}}} \le Q. $

则系统和速率最大化问题，即问题P1为

$ \mathop {\max }\limits_p {R_{{\rm{sum}}}}\left( \mathit{\boldsymbol{p}} \right) = \sum\limits_{n = 1}^N {{R_n}} \left( \mathit{\boldsymbol{p}} \right), $

(1)

$ {\rm{s}}.\;{\rm{t}}.\;\;0 < {p_n} < p_n^{\max }, \forall 1 \le n \le N, $

$ \sum\limits_{i = 1}^N {{p_i}} h_i^{{\rm{sm}}} \le Q. $

显然，问题P1是非凸的，获得其全局最优解是一项具有挑战性的任务.在下节中将采用非合作博弈模型将问题P1解耦为N个凸的子问题.

2 博弈论建模 2.1 非合作博弈模型

将每个用户建模为博弈论的参与者，非合作博弈可以表示为G=[C, {ρ_n|n∈C}, {U_n|n∈C}].C={1, 2, …, N}是一组博弈参与者.参与者n的可用策略集为$ \rho_{n}=\left\{p_{n} | 0<p_{n}<p_{n}^{\max }, p_{n}+\sum\limits_{i \neq n} p_{i} h_{i}^{\mathrm{sm}} \leqslant Q\right\}$.U_n为参与者n的效用函数

$ {U_n}\left( {{p_n}\left| {{\mathit{\boldsymbol{p}}_{ - n}}} \right.} \right) = {R_n}\left( {{p_n}\left| {{\mathit{\boldsymbol{p}}_{ - n}}} \right.} \right) + {\lambda _n}{p_n}. $

式中p_－n=(p₁, …, p_n－1, p_n+1, …, p_N)表示除了参与者n之外，所有参与者的传输策略.λ_n可以看作是发射功率的一种动态价格，它由下式给出

$ {\lambda _n} = \sum\limits_{i \ne n} {\frac{\partial }{{\partial {p_n}}}} {R_i}\left( \mathit{\boldsymbol{p}} \right). $

显然，U_n为p_n的凸函数，所以可得到式(1)中小小区和速率R_sum(p)的凸近似形式，即

$ {{\tilde R}_{{\rm{sum}}}}\left( \mathit{\boldsymbol{p}} \right) \buildrel \Delta \over = \sum\limits_{n = 1}^N {{U_n}} \left( {{p_n}\left| {{\mathit{\boldsymbol{p}}_{ - n}}} \right.} \right). $

(2)

在上述非合作博弈模型下，式(2)可以分解为N个凸的子问题，每个子问题如问题P2所示

$ \begin{array}{*{20}{c}} {\mathop {\max }\limits_{{p_n}} {U_n}\left( {{p_n}\left| {{\mathit{\boldsymbol{p}}_{ - n}}} \right.} \right), \forall n \in C;}\\ {{\rm{s}}.\;{\rm{t}}.\;\;0 < {p_n} < p_n^{\max };}\\ {{p_n} + \sum\limits_{i \ne n} {{p_i}h_i^{{\rm{sm}}}} \le Q.} \end{array} $

(3)

因此，和速率最大化问题可以等同于最大化每个小小区的传输速率.使用凸优化方法求得问题P2的全局最优解为

$ {b_n} = \arg \mathop {\max }\limits_{{p_n} \in {\rho _n}} {U_n}\left( {{p_n}\left| {{\mathit{\boldsymbol{p}}_{ - n}}} \right.} \right). $

2.2 纳什均衡点

定义1 ：当且仅当每个参与者的发射功率是相应于其他参与者发射功率的最佳策略，即p_n^*=b_n, ∀n∈C，则此时所有参与者的发射功率p^*是博弈G的纳什均衡点.

一旦达到纳什均衡点，则没有参与者会试图改变其传输战略，因为

$ {U_n}\left( {p_n^ * \left| {\mathit{\boldsymbol{p}}_{ - n}^ * } \right.} \right) \ge {U_n}\left( {{p_n}\left| {\mathit{\boldsymbol{p}}_{ - n}^ * } \right.} \right), \forall n \in C. $

定理1 ：博弈模型G的每个NE是非凸问题P1的驻点，反之亦然.

具体证明可参考文献[16].众所周知，优化问题的全局或局部最优解必然是优化问题目标函数的驻点.因此，通过找到博弈模型G的NE就可能获得原始非凸优化问题的局部最优解，甚至是全局最优解.

3 功率分配方案 3.1 基于全局信息的功率分配算法

由于个体效用函数U_n和约束集ρ_n是凸的，因此问题P2是典型的凸优化问题.问题P2的拉格朗日函数由下式给出

$ \begin{array}{*{20}{c}} {{L_n}\left( {{p_n}, {\mu _1}, {\mu _2}, {\mu _3}} \right) = - {R_n}\left( {{p_n}\left| {{\mathit{\boldsymbol{p}}_{ - n}}} \right.} \right) - {\lambda _n}{p_n} + }\\ {{\mu _1}\left( {{p_n} - p_n^{\max }} \right) - {\mu _2} + {\mu _3}\left( {{p_n} + \sum\limits_{i \ne n} {{p_i}} h_i^{{\rm{sm}}} - Q} \right).} \end{array} $

拉格朗日对偶函数为

$ {g_n}\left( {{\mu _1}, {\mu _2}, {\mu _3}} \right) = \mathop {\inf }\limits_{{p_n}} {L_n}\left( {{p_n}, {\mu _1}, {\mu _2}, {\mu _3}} \right). $

由于满足强对偶条件，即对偶间隙为零，因此可通过求解KKT条件，得到问题P2的最优解的解析表达式，即

$ {b_n} = \max \left\{ {0, \min \left\{ {p_n^Q, p_n^{{\rm{op}}}, p_n^{\max }} \right\}} \right\}, $

(4)

$ p_n^Q = \frac{1}{{h_n^{{\rm{sm}}}}}\left( {Q - \sum\limits_{i \ne n} {{p_i}} h_i^{{\rm{sm}}}} \right), $

(5)

$ p_n^{{\rm{op}}} = \frac{1}{{\sum\limits_{i \ne n} {\frac{{{h_{ii}}{p_i}{h_{ni}}}}{{{\sigma _i}\left( {{\sigma _i} + {h_{ii}}{p_i}} \right)}}{p_i}h_i^{{\rm{sm}}}} }} - \frac{{{\sigma _n}}}{{{h_{{\rm{nn}}}}}}. $

(6)

式中σ_j, ∀j∈C为小小区j的用户经历的干扰加噪声为

$ {\sigma _j} = \sum\limits_{i \ne j} {{p_i}} {h_{i, j}} + {p^{\rm{m}}}h_j^{{\rm{ms}}} + {w_j}, \forall j \in C. $

(7)

利用解析解设计的GIPA算法，算法流程如下：

输入:发射功率向量p，步长r，常数ε和δ.

1) 初始化:设置初始值p⁰, r⁰∈(0, 1], ε∈(0, 1)和δ.

2) while $\left|\tilde{R}_{\text {sum }}\left(\boldsymbol{p}^{t+1}\right)-\tilde{R}_{\text {sum }}\left(\boldsymbol{p}^{t}\right)\right|<\delta $

3) 不满足终止条件, 令t←t+1

4) 给定当前t时刻发射功率向量p^t, 每个用户根据式(4)计算其最优发射功率b_n^t, n∈C.

5) 通过p^t+1=p^t+r^t(b^t-p^t)更新发射功率，其中b^t=(b₀^t, b₁^t, …, b_N^t)..

6) 通过r^t+1=r^t(1-εr^t)更新步长.

7) 计算$\tilde{R}_{\text {sum }}\left(\boldsymbol{p}^{t+1}\right) $.

8) end

9) 令p^*=p^t+1.

输出:发射功率p^*.

在每次迭代中，给定当前发射功率向量p^t，每个用户通基于全局CSI通过式(4)来计算其最佳发射功率.然后通过步骤5、6分别更新发射功率向量和步长.直到满足终止条件，即$ | \tilde{R}_{\text {sum }}\left(\boldsymbol{p}^{t+1}\right)-\tilde{R}_{\text {sum }}\left(\boldsymbol{p}^{t}\right) |<\delta$，其中δ是任意小的正数，即可获得博弈模型G的NE.

3.2 收敛性分析

定理2：通过GIPA算法，发射功率向量p^t收敛到博弈模型G的NE，并且$\tilde{R}_{\text {sum }}\left(\boldsymbol{p}^{t+1}\right) $收敛到有限值.

证明：系统和速率近似函数$\tilde{R}_{\text {sum }}\left(\boldsymbol{p}\right) $在可行域上是Lipschitz连续的，因此存在一个正数η，使得

$ \left\| {{{\tilde R}_{sum}}\left( {{\mathit{\boldsymbol{p}}^{t + 1}}} \right) - {{\tilde R}_{{\rm{sum}}}}\left( {{\mathit{\boldsymbol{p}}^t}} \right)} \right\| \le \eta \left\| {{\mathit{\boldsymbol{r}}^t}\left( {{\mathit{\boldsymbol{b}}^t} - {\mathit{\boldsymbol{p}}^t}} \right)} \right\|. $

基于下降引理^[17]，可得到以下不等式

$ \begin{array}{*{20}{c}} {{{\tilde R}_{{\rm{sum}}}}\left( {{\mathit{\boldsymbol{p}}^{t + 1}}} \right) \le {{\tilde R}_{{\rm{sum}}}}\left( {{\mathit{\boldsymbol{p}}^t}} \right) + {r^t}{{\tilde R}_{{\rm{sum}}}}{{\left( {{\mathit{\boldsymbol{p}}^t}} \right)}^{\rm{T}}}\left( {{\mathit{\boldsymbol{b}}^t} - {\mathit{\boldsymbol{p}}^t}} \right) + }\\ {\frac{{\eta {{\left( {{r^t}} \right)}^2}}}{2}{{\left\| {{\mathit{\boldsymbol{b}}^t} - {\mathit{\boldsymbol{p}}^t}} \right\|}^2}.} \end{array} $

(8)

b^t－p^t是函数$\tilde{R}_{\text {sum }}\left(\boldsymbol{p}\right) $在p^t处的下降方向，则

$ {{\tilde R}_{{\rm{sum}}}}{\left( {{\mathit{\boldsymbol{p}}^t}} \right)^{\rm{T}}}\left( {{\mathit{\boldsymbol{b}}^t} - {\mathit{\boldsymbol{p}}^t}} \right) \le - \tau {\left\| {{\mathit{\boldsymbol{b}}^t} - {\mathit{\boldsymbol{p}}^t}} \right\|^2}, $

(9)

式中τ是一个正数.由式(8)和(9)，可得

$ {{\tilde R}_{{\rm{sum}}}}\left( {{\mathit{\boldsymbol{p}}^{t + 1}}} \right) \le {{\tilde R}_{{\rm{sum}}}}\left( {{\mathit{\boldsymbol{p}}^t}} \right) - {r^t}\left( {\tau - \frac{{\eta {r^t}}}{2}} \right){\left\| {{\mathit{\boldsymbol{b}}^t} - {\mathit{\boldsymbol{p}}^t}} \right\|^2}. $

因为r^t→0，当t足够大时，即t≥t，可找到一个正数ψ使得

$ {{\tilde R}_{{\rm{sum}}}}\left( {{\mathit{\boldsymbol{p}}^{t + 1}}} \right) \le {{\tilde R}_{{\rm{sum}}}}\left( {{\mathit{\boldsymbol{p}}^t}} \right) - {r^t}\psi {\left\| {{\mathit{\boldsymbol{b}}^t} - {\mathit{\boldsymbol{p}}^t}} \right\|^2}. $

因为$\tilde{R}_{\text {sum }}\left(\boldsymbol{p}\right) $是有界的，应用Robbins-Siegmund定理^[18]，可知$\tilde{R}_{\text {sum }}\left(\boldsymbol{p}\right) $收敛到一个有限值且下式成立.

$ \sum\limits_{t \ge \bar t} {{r^t}} {\left\| {{\mathit{\boldsymbol{b}}^t} - {\mathit{\boldsymbol{p}}^t}} \right\|^2} < \infty . $

因为$ \sum\limits_{t \geqslant \bar{t}} r^{t} \rightarrow \infty$则$ \lim\limits_{t \rightarrow \infty}\left\|\boldsymbol{b}^{t}-\boldsymbol{p}^{t}\right\|=0$，即，p^*=p^t.证毕.

3.3 基于局部信息的功率分配算法

GIPA算法的每次迭代过程中，每个用户需要其他用户的发射功率和全局CSI来计算其最优功率策略.在每次迭代中每个用户所需的信令数量为N²+3N-1，因此当小小区的数量增加时，信令开销是巨大的.

为减少信令开销，提出LIPA算法.LIPA的迭代过程与GIPA算法相同，但步骤4中求解b_n^t的计算方法略有不同，并且式(5)~(7)中的h_ij(i≠j)和h_i^sm分别用h_ij(i≠j)和h_i^sm替换.h_ij(i≠j)和h_i^sm是近似信道功率增益，其中忽略了瑞利衰落的影响并且用基站之间的距离代替用户与基站之间的距离.

由于基站之间的距离是恒定的，因此在迭代过程中不必重复发送.使用LIPA算法，每次迭代每个用户需要的信令数为3N-1，包括：1)其他用户的传输功率.2)小小区用户与其SBS之间的信道功率增益h_ii.3)宏小区用户和SBS之间的信道功率增益h_i^ms.

4 仿真分析

假设w_n=w，∀n∈C，且p_n^max=p^max, ∀n∈C.主要仿真参数如表 1所示.

将文献[9]中基于惩罚因子的功率分配(PFPA)算法和文献[11]中基于非统一定价的功率分配(NPPA)算法作为对比算法.将平均每个小小区的频谱效率作为衡量指标.

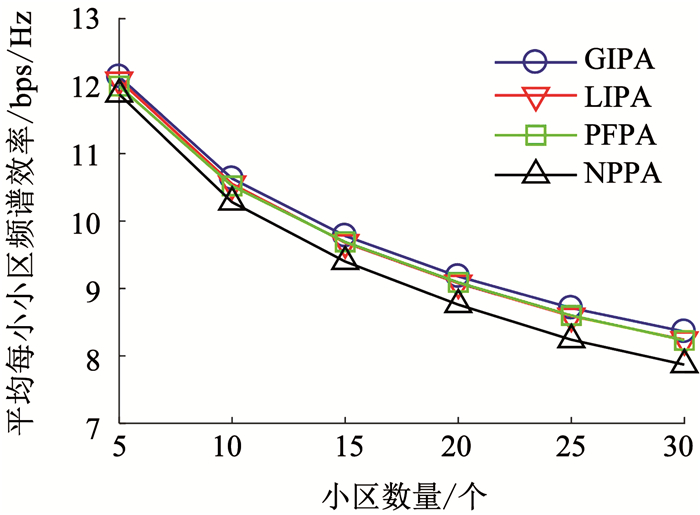
图 2中的仿真结果是通过蒙特卡罗方法获得的，共进行了10 000次实验.如图 2所示，提出的GIPA算法所实现的平均每个小小区频谱效率要高于对比算法.所提出的LIPA算法的性能与PFPA算法几乎相同.

图 3显示了不同算法的收敛性能.尽管由于采用动态价格，GIPA算法的收敛速度略慢于PFPA算法，但在达到收敛后，平均每个小小区所获得的频谱效率更高.LIPA算法具有与GIPA算法相似的收敛性能.由于NPPA算法的求解过程不需要迭代，因此它在图中是一条水平线.

图 4显示了干扰功率约束Q对功率分配算法性能的影响.当Q < -55 dBm时，所提出的算法的性能随着Q的增加而提高.当Q>-55 dBm时，所提出算法获得的平均频谱效率保持恒定，这是因为Q>-55 dBm时，可以忽略式(3)中的约束条件.

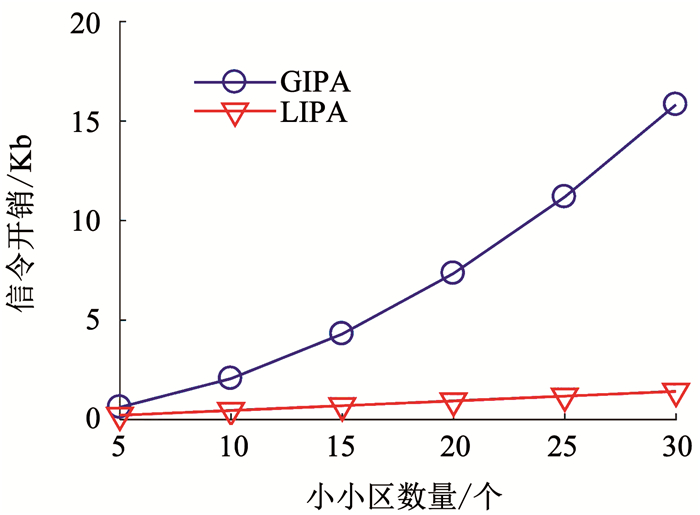
图 5对比了所提算法每次迭代时每个用户所需的信令开销.这里假设传输一个浮点数需要16比特.可以看出，随着小小区的数量增加，GIPA算法的信令开销显着增加，而LIPA算法的信令开销增加缓慢.

5 结论

本文研究了频谱共享两层超密集网络的功率分配策略.采用非合作博弈将非凸系统和率最大化问题解耦为若干凸子问题，并引入了干扰功率约束以保证宏小区用户的QoS.每个用户可通过最大化基于动态定价的效用函数来获得当前的最佳发射功率.基于此非合作博弈模型，提出了迭代式的GIPA算法和LIPA算法.仿真结果表明，GIPA算法比对比方法具有更好的传输性能，LIPA算法在保证较好的传输性能的前提下有效地减少了信令开销.