2. 苏州大学 机电工程学院, 江苏 苏州 215021;
3. 哈尔滨工业大学 金属精密热加工国家级重点实验室, 哈尔滨 150001
2. School of Mechanical and Electrical Engineering, Soochow University, Suzhou 215021, Jiangsu, China;
3. National Key Laboratory for Precision Hot Processing of Metals, Harbin Institute of Technology, Harbin 150001, China
屈服准则是判别材料是否发生塑性变形的基本方程,也是求解材料成形所需外力必须求解的方程,它的开发与应用一直是塑性成形领域中一项基本而重要的研究内容.1864年,在冲裁和挤压实验的基础上,Tresca提出了最大剪应力理论[1],为材料的屈服特性提供了基本的理论解释.Tresca屈服准则数学表达简单,取得了广泛应用,但其忽略了中间主应力的影响,通常会给出偏低的力学参数结果.1913年,von Mises认为偏差应力二次不变量达到一定值,金属将从弹性变形过渡到塑性变形[2-3],并基于这一假设提出了Mises屈服准则.然而,该准则的表达式是非线性的,不便于复杂力学方程的联解计算.1951年,Drucker和Prager[4]将静水压力的影响添加到Mises公式中,从而提出了一种他们自己的屈服准则.Haigh和Westgarrd[5]为了在三维应力空间中统一以上各种形式的屈服准则,提出了三维应力空间的概念,实现了屈服准则的几何学表示.1983年,俞茂宏[6]提出了双剪应力(TSS)屈服准则.该准则假定当两个较大的主剪应力之和达到临界值时,材料发生屈服,通常被用来预测力学参数的上限[7].2005年,俞茂宏等[8]认为双剪应力屈服准则虽然考虑了中间主应力的影响,但忽略了最小剪应力对材料强度的影响,继而又提出了三剪应力屈服准则.最近,Zhu[9]通过平均Tresca屈服准则的最大剪应力和Mises屈服准则等效剪应力,提出一种加权平均屈服准则,称为平均剪应力(ASSY)屈服准则.为了解释延性和脆性材料的屈服条件,Barsanescu[10]将最大应变能和最大畸变能作为修正系数,提出了修正后的Mises屈服准则.对于均质各向同性材料,Gu[11]对于拉伸和压缩不同情况提出了两种屈服公式.他认为形状变化和体积膨胀会导致材料失效,而体积收缩(如静水压力)会阻碍失效.Pei等人[12]在应力坐标系中引入了一个由三个法向应力组成的法向应力空间来表示应力张量和材料结构之间的相互作用,并在此基础上提出了基于几何因子而非代数张量的各向异性准则来描述岩石的各向异性抗剪强度.基于以上研究可见,Tresca屈服准则通常给出下限解,TSS屈服准则通常给出上限解;Mises屈服准则的精度高,但其公式是非线性的,很难用于获得的力学参数的解析解.因此,寻求逼近Mises圆的线性屈服准则,并进行工程应用具有很重要的意义.
厚板广泛应用于工程机械、输油管道、海洋平台等结构的承载件,如何精确获得厚板轧制力、轧制力矩关系到工艺的设计与优化,具有重要的研究价值.非线性轧制功率泛函积分求解困难是造成目前轧制力解析困难的根源,早在1973年小林史郎[13]就对三维轧制过程建立了总功率泛函的积分框架,但未求出解析结果,只给出了相应的数值结果.1980年,Kato等[14]提出一种简化的加权速度场,也仅获得了相应的轧制力与轧制力矩的数值解.王振范等[15]采用三维流函数法解析了塑性加工问题,分析和建立了考虑宽展的平辊轧制模型.李涛等[16]采用了Hill屈服准则研究了正交异性材料平面应力问题的应力场和速度场,得出应力场和速度场的特征线处处重合的结果.赵德文等[17]提出一种简化的二维流函数速度场,通过应用应变矢量内积法以及共线矢量内积法,获得了轧制过程中各项功率以及轧制力与轧制力据的解析解.章顺虎等[18]提出一种考虑了轧制渗透率的新型速度场来分析特厚板轧制.研究表明,考虑轧制渗透率可以使轧制力与轧制力矩模型更加精确.根据以上研究可见,通过解析法建立速度场可以对厚板轧制问题进行有效的分析,且有利于轧制参数的优化处理.然而,已有速度场未能准确描述厚板轧制时纵横流动特性(即变形金属沿轧制方向和宽度方向的速度分布规律),相应的力能参数解析也鲜见报道.
为了解决以上问题,本文拟开发一逼近非线性Mises屈服准则的线性屈服准则,并计算其相应的比塑性功率.随后,利用导出的比塑性功率解析提出的厚板轧制椭圆速度场.通过能量计算,获得了相应的内部变形功率、摩擦功率以及剪切功率,再经变分获得了轧制力矩与轧制力的解析解,并与实验数据进行对比分析.
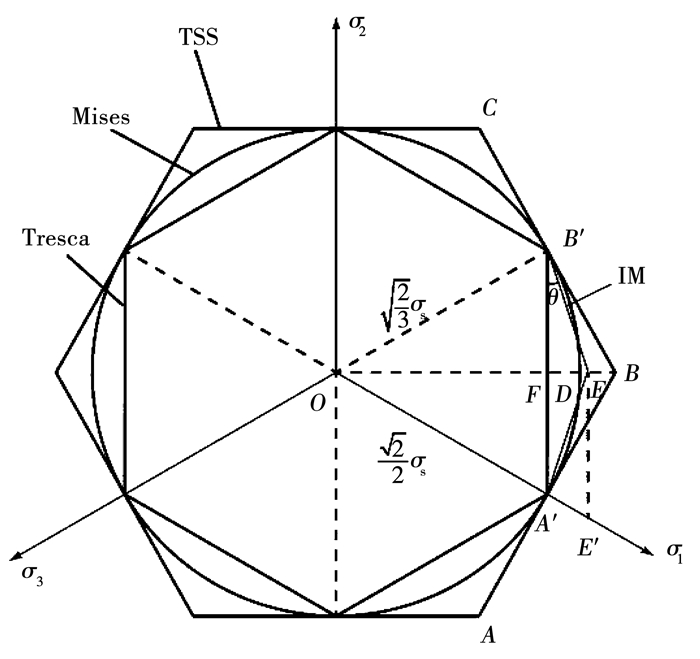
1 积分中值屈服准则 1.1 屈服准则表达式Mises屈服准则的轨迹是一个在π平面上的圆,它的外接六边形(TSS)和内接六边形(Tresca)之间的十二边形可用作对Mises圆的线性逼近.如图 1所示,设线段BF上有一动点E,B′F与B′E之间的夹角∠FB′E设为θ,则当θ=0°时,对应Trasca屈服轨迹B′F;当θ=30°时,对应TSS屈服轨迹B′B.
|
图 1 π平面上的屈服轨迹 Fig. 1 Different loci on the π-plane |
已知Mises圆的半径
| $ \begin{matrix} f\left( \theta \right)={B}'E={B}'F/\cos \theta =\frac{3}{\text{ }\!\!\pi\!\!\text{ }}\overset\frown{{B}'D}/\cos \theta = \\ {{\sigma }_{\text{s}}}/\left( \sqrt{6}\cos \theta \right), {{0}^{{}^\circ }}\le \theta \le {{30}^{{}^\circ }}. \\ \end{matrix} $ |
由积分中值定理,可得平均化后的新轨迹长度为
| $ B'E = \frac{1}{{\left( {\frac{{\rm{ \mathit{ π} }}}{6} - 0} \right)}}\int_0^{\frac{{\rm{ \mathit{ π} }}}{6}} {\left[ {{\sigma _{\rm{s}}}/\left( {\sqrt 6 \cos \theta } \right)} \right]{\rm{d}}\theta } = 0.428{\sigma _{\rm{s}}}, $ |
基于上式,可得
| $ FE = \sqrt {B'{E^2} - B'{F^2}} = 0.129{\sigma _{\rm{s}}}, $ |
Mises屈服轨迹上的偏差矢量模长为
| $ OD = OB' = \sqrt 6 /3{\sigma _{\rm{s}}}, $ |
积分中值屈服准则的偏差矢量模长为
| $ OE = 0.837{\sigma _{\rm{s}}}, $ |
所以两者之间的误差为
| $ \Delta = \left( {\frac{{\sqrt 6 }}{3} - 0.837} \right)/\frac{{\sqrt 6 }}{3} = - 2.46\% . $ |
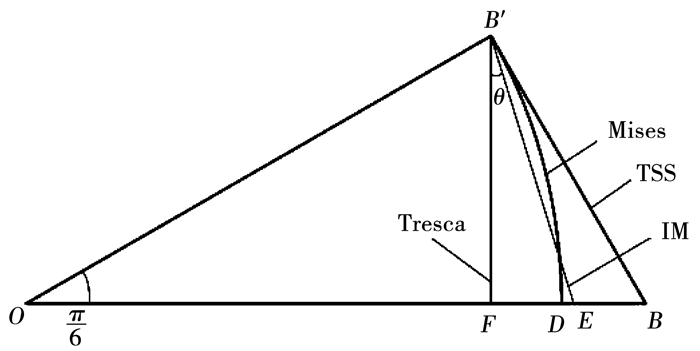
可见,积分中值准则的偏差矢量模长较Mises屈服准则增加了2.46%,即E点在B、D之间,如图 2所示.
|
图 2 积分中值屈服准则在误差三角形内轨迹 Fig. 2 Locus of the integral mean value yield criterion in the error triangle |
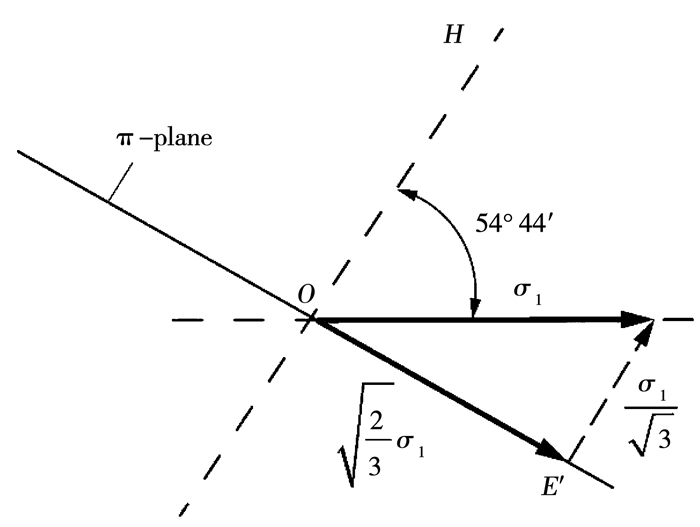
下面建立图 1中直线A′E、B′E的应力方程.图 3为主应力分量σ1在π平面上的投影,其中E点的应力状态为
|
图 3 σ1在π平面上的投影 Fig. 3 Trajectory of σ1 on the π-plane |
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _1} = \frac{{OE \times \sqrt 3 }}{{\sqrt 2 \cos {{30}^\circ }}} = 1.1831{\sigma _{\rm{s}}}, }\\ {{\sigma _3} = 0, }\\ {{\sigma _2} = \frac{{{\sigma _1} + {\sigma _3}}}{2} = 0.5916{\sigma _{\rm{s}}}.} \end{array}} \right. $ |
假定A′E线满足如下方程
| $ {\sigma _1} - {a_1}{\sigma _2} - {a_2}{\sigma _3} - c = 0. $ | (1) |
当材料屈服时有c=σs、a1+a2=1,代入应力分量式可得
| $ {a_1} = 0.309, {a_2} = 0.691. $ | (2) |
将式(2)代入式(1),可得A′E的方程为
| $ {\sigma _1} - 0.309{\sigma _2} - 0.691{\sigma _3} = {\sigma _s}, {\sigma _2} \le \frac{1}{2}\left( {{\sigma _1} + {\sigma _3}} \right). $ | (3) |
同理,轨迹B′E的方程可确定为
| $ 0.691{\sigma _1} + 0.309{\sigma _2} - {\sigma _3} = {\sigma _{\rm{s}}}, {\sigma _2} \ge \frac{1}{2}\left( {{\sigma _1} + {\sigma _3}} \right). $ | (4) |
式(3)、(4)即为新的屈服准则的数学表达式,它是主应力分量的线性组合.因该准则的轨迹边长B′E由积分中值定理计算而得,故称为积分中值屈服准则,简称IM屈服准则.
由图 2可知,积分中值屈服准则的轨迹在π平面上与Mises圆相交,各顶角计算如下:
| $ \left\{ {\begin{array}{*{20}{l}} {\angle FB'E = {{17.598}^\circ }, }\\ {\angle OB'E = {{60}^\circ } + {{17.598}^\circ } = {{77.598}^\circ }, }\\ {\angle OEB' = {{180}^\circ } - {{30}^\circ } - {{77.598}^\circ } = {{72.402}^\circ }, }\\ {2\angle OB'E = {{155.196}^\circ }, 2\angle OE{B^\prime } = {{144.804}^\circ }.} \end{array}} \right. $ | (5) |
由图 1和式(5)表明,积分中值屈服准则的轨迹是与Mises圆相交的等边非等角的十二边形,轨迹的6个顶点在Mises圆上,内接点顶角为155.196°,另外6个顶点位于Mises圆的外侧,相距0.02σs,顶角为144.804°;十二边形的边长为0.428σs.
1.2 比塑性功率设应力分量σij满足f(σij)=0且
| $ {{\dot \varepsilon }_{ij}} = {\rm{d}}\lambda \frac{{\partial f}}{{\partial {\sigma _{ij}}}} = d\lambda {{\sigma '}_{ij}}. $ | (6) |
假设有λ≥0,μ≥0,由式(3)与(6)得
| $ \begin{array}{l} {{\dot \varepsilon }_1}:{{\dot \varepsilon }_2}:{{\dot \varepsilon }_3} = 1:\left( { - 0.301} \right):\left( { - 0.691} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\lambda :( - 0.309)\lambda :( - 0.691)\lambda . \end{array} $ |
同理,由式(4)与(6)得
| $ \begin{array}{l} {{\dot \varepsilon }_1}:{{\dot \varepsilon }_2}:{{\dot \varepsilon }_3} = 0.691:0.309:\left( { - 1} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0.691\mu :0.309\mu :\left( { - \mu } \right). \end{array} $ |
将以上两式所得结果进行线性组合有
| $ \begin{array}{l} {{\dot \varepsilon }_1}:{{\dot \varepsilon }_2}:{{\dot \varepsilon }_3} = (\lambda + 0.691\mu ):0.309(\mu - \lambda ):\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;( - 0.691\lambda - \mu ), \end{array} $ |
取
| $ {{\dot \varepsilon }_2} = 0.309(\mu - \lambda ), {{\dot \varepsilon }_3} = - (0.691\lambda + \mu ), $ |
其中
| $ \begin{array}{*{20}{c}} {{{\dot \varepsilon }_{\max }} - {{\dot \varepsilon }_{\min }} = 1.691(\lambda + \mu ), }\\ {(\lambda + \mu ) = \frac{{1000}}{{1691}}\left( {{{\dot \varepsilon }_{\max }} - {{\dot \varepsilon }_{\min }}} \right).} \end{array} $ | (7) |
在顶点E处,注意到σ2=(σ1+σ3)/2,所以可由式(10)和式(11)得
| $ {\sigma _1} - {\sigma _3} = \frac{{2000}}{{1691}}{\sigma _{\rm{s}}}. $ | (8) |
因此,从式(7)和式(8)可得积分中值屈服准则比塑性功率为
| $ \begin{array}{*{20}{c}} {D\left( {{{\dot \varepsilon }_{ij}}} \right) = {\sigma _1}{{\dot \varepsilon }_1} + {\sigma _2}{{\dot \varepsilon }_2} + {\sigma _3}{{\dot \varepsilon }_3} = {\sigma _1}{{\dot \varepsilon }_1} + \frac{{{\sigma _1} + {\sigma _3}}}{2}{{\dot \varepsilon }_2} + }\\ {{\sigma _3}{{\dot \varepsilon }_3} = 0.8455\left( {{\sigma _1} - {\sigma _3}} \right)(\mu + \lambda ) = }\\ {\frac{{1691}}{{2000}} \times \frac{{2000}}{{1691}}{\sigma _s} \times \frac{{1000}}{{1691}}\left( {{{\dot \varepsilon }_{\max }} - {{\dot \varepsilon }_{\min }}} \right) = }\\ {\frac{{1000}}{{1691}}{\sigma _{\rm{s}}}\left( {{{\dot \varepsilon }_{\max }} - {{\dot \varepsilon }_{\min }}} \right) = }\\ {0.591{\sigma _{\rm{s}}}\left( {{{\dot \varepsilon }_{\max }} - {{\dot \varepsilon }_{\min }}} \right).} \end{array} $ | (9) |
Tresca与TSS屈服准则的塑性功率表达式分别为[19]
| $ D\left( {{{\dot \varepsilon }_{ij}}} \right) = \frac{2}{3}{\sigma _{\rm{s}}}\left( {{{\dot \varepsilon }_{\max }} - {{\dot \varepsilon }_{\min }}} \right), $ | (10) |
| $ D\left( {{{\dot \varepsilon }_{ij}}} \right) = \frac{1}{2}{\sigma _{\rm{s}}}\left( {{{\dot \varepsilon }_{\max }} - {{\dot \varepsilon }_{\min }}} \right). $ | (11) |
将式(20)与式(21)、(22)进行比较,比塑性功率误差为
| $ \left\{ {\begin{array}{*{20}{l}} {{\Delta _{{\rm{Tresca}}}} = \left( {0.591 - \frac{1}{2}} \right)/\frac{1}{2} = 18.20\% , }\\ {{\Delta _{{\rm{TSS}}}} = \left( {0.591 - \frac{2}{3}} \right)/\frac{2}{3} = - 11.29\% .} \end{array}} \right. $ |
可见,使用积分中值屈服准则比塑性功率的计算值较Tresca屈服准则提高了18.20%,而比TSS屈服准则降低了11.29%.
1.3 实验验证在主应力状态为σ1≥σ2≥σ3时,Lode引入了应力状态参数用以对比不同的屈服准则,并评价了中间主应力对屈服的影响,该参数为[20]
| $ \mu = \frac{{2{\sigma _2} - {\sigma _1} - {\sigma _3}}}{{{\sigma _s}}}. $ |
将上式分别代入Tresca准则、Mises准则、TSS屈服准则和IM屈服准则可得它们的Lode参数表达式如下:
| $ \frac{{{\sigma _1} - {\sigma _3}}}{{{\sigma _s}}} = 1, $ |
| $ \frac{{{\sigma _1} - {\sigma _3}}}{{{\sigma _s}}} = \frac{2}{{\sqrt {3 + {\mu ^2}} }}, $ |
| $ \frac{{{\sigma _1} - {\sigma _3}}}{{{\sigma _s}}} = \left\{ {\begin{array}{*{20}{l}} {\frac{{4 + \mu }}{3}, - 1 \le \mu \le 0;}\\ {\frac{{4 - \mu }}{3}, 0 \le \mu \le 1, } \end{array}} \right. $ |
| $ \frac{{{\sigma _1} - {\sigma _3}}}{{{\sigma _s}}} = \left\{ {\begin{array}{*{20}{l}} {\frac{{2000 + 309\mu }}{{1691}}, - 1 \le \mu \le 0;}\\ {\frac{{2000 - 309\mu }}{{1691}}, 0 \le \mu \le 1.} \end{array}} \right. $ |
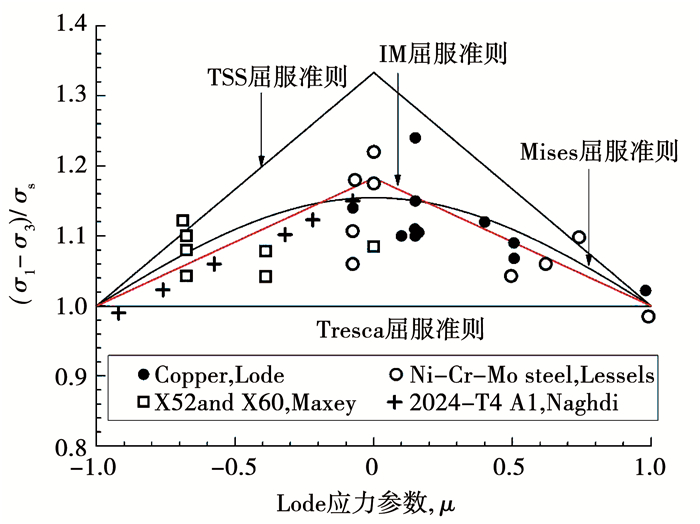
基于以上方程,结合不同实验数据[20-23],可以得到对比图 4.
|
图 4 屈服准则实验结果对比 Fig. 4 Comparison between various yield criteria and experimental data |
由图可知,Tresca屈服准则提供了实验数据的下界,而TSS屈服准则提供了上界;IM屈服准则计算值则介于TSS准则与Tresca准则之间,相交于Mises准则.可见,IM屈服准则与实验数据较一致,提供了较合理的中间结果.
2 轧制力解析 2.1 椭圆速度场对于厚板轧制,当轧板宽度b与其厚度h的比值大于10时,宽度方向的金属流动可以忽略,轧制过程可以视为二维平面变形问题[24].
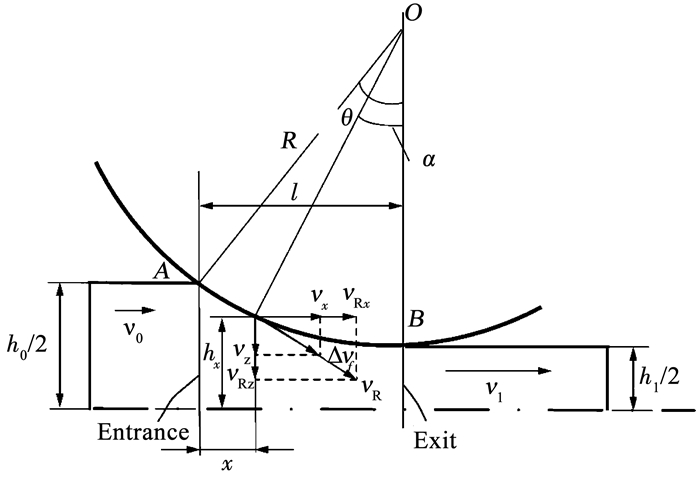
如图 5所示,h0为轧件入口厚度,h1为出口厚度,R为轧辊半径,O点为轧辊中心,v0为入口速度,v1为出口速度.θ为接触角,α为中性角,x为中性点位置距变形区入口长度,hx为中性点处轧件厚度.中性点处轧件切向速度与此处轧辊的切向速度相等,切向速度不连续量与摩擦功均为零.根据图中的几何关系,接触弧方程、参数方程以及其一阶及二阶导数可表示为
|
图 5 厚板轧制变形示意 Fig. 5 Rolling deformation diagram of heavy plate |
| $ \left\{ {\begin{array}{*{20}{l}} {z = {h_x} = R + {h_1} - {{\left[ {R - {{(l - x)}^2}} \right]}^{1/2}}, }\\ {z = {h_\alpha } = R + {h_1} - R\cos \alpha .} \end{array}} \right. $ | (12) |
| $ l - x = R\sin \alpha dx = - R\cos \alpha d\alpha , $ |
| $ h_x^\prime = - \tan \alpha h_x^{\prime \prime } = {\left( {R{{\cos }^3}\alpha } \right)^{ - 1}}. $ |
由式(12)可知边界条件如下:
| $ \left\{ {\begin{array}{*{20}{l}} {x = 0, \alpha = \theta :{h_x} = {h_\alpha } = {h_\theta } = {h_0}, h_x^\prime = - \tan \theta ;}\\ {x = l, \alpha = \theta :{h_x} = {h_\alpha } = {h_1}, h_x^\prime = 0.} \end{array}} \right. $ |
对于展宽轧制,由于l/h≤1、b/h≥10,入口至出口的宽度函数bx可看作常数,因此
| $ y = {b_x} = {b_1} = {b_0} = b. $ |
本文假定轧制时金属流动水平速度分量从入口到出口按椭圆方程分布,则可提出如下二维速度场:
| $ \left\{ \begin{array}{l} {v_x} = {v_0}\sqrt {1 + \frac{{\left( {v_1^2 - v_0^2} \right){x^2}}}{{{l^2}v_0^2}}} , \\ {v_y} = 0, \\ {v_z} = {v_x}\tan \alpha = {v_x}\frac{{h_x^\prime }}{{{h_x}}}z = {v_0}\sqrt {1 + \frac{{\left( {v_1^2 - v_0^2} \right){x^2}}}{{{l^2}v_0^2}}} \cdot \frac{{h_x^\prime }}{{{h_x}}}z. \end{array} \right. $ |
这一速度场既考虑了轧件宽向速度近似为0的特点,又考虑了水平速度分量逐渐增大的特点.根据体积不变条件v0h0b=v1h1b,故可令h0/h1=η,即v1=ηv0.因此,该速度场可以简写成如下形式:
| $ \left\{ \begin{array}{l} {v_x} = {v_0}\sqrt {1 + \left( {{\eta ^2} - 1} \right)\frac{{{x^2}}}{{{l^2}}}} , \\ {v_y} = 0, \\ {v_z} = {v_0}\sqrt {1 + \left( {{\eta ^2} - 1} \right)\frac{{{x^2}}}{{{l^2}}}} \cdot \frac{{h_x^\prime }}{{{h_x}}}z. \end{array} \right. $ | (13) |
式中,vx、vy、vz分别是轧制方向、展宽方向以及压下方向的速度分量.根据几何方程,可得
| $ \left\{ \begin{array}{l} {{\dot \varepsilon }_x} = \frac{{d{v_x}}}{{dx}} = \frac{{{v_0}\left( {{\eta ^2} - 1} \right)x}}{{{l^2}\sqrt {1 + \left( {{\eta ^2} - 1} \right)\frac{{{x^2}}}{{{l^2}}}} }} = {{\dot \varepsilon }_{\max }}, \\ {{\dot \varepsilon }_y} = 0, \\ {{\dot \varepsilon }_z} = - {{\dot \varepsilon }_{\max }} = - \frac{{{v_0}\left( {{\eta ^2} - 1} \right)x}}{{{l^2}\sqrt {1 + \left( {{\eta ^2} - 1} \right)\frac{{{x^2}}}{{{l^2}}}} }} = {{\dot \varepsilon }_{\min }}. \end{array} \right. $ | (14) |
式中
| $ U = {v_x}{h_x}b = {v_n}{h_n}b = {v_{\rm{R}}}\cos {\alpha _n}b\left( {R + {h_1} - R\cos {\alpha _n}} \right) = {v_1}{h_1}b. $ | (15) |
在式(13)和式(14)中,由于
代入式(9)表示的IM屈服准则比塑性功率至下式,可得轧制时内部变形功率为
| $ \begin{array}{*{20}{c}} {{N_{\rm{d}}} = 4\int_0^l {\int_0^{{h_x}} 0 } .591{\sigma _s}\left( {{{\dot \varepsilon }_{\max }} - {{\dot \varepsilon }_{\min }}} \right)b{\rm{d}}x{\rm{d}}z = }\\ {4b\int_0^l {\int_0^{{h_x}} 0 } .591{\sigma _{\rm{s}}} \cdot 2{{\dot \varepsilon }_{\max }}{\rm{d}}x{\rm{d}}z = }\\ {4.731{\sigma _{\rm{s}}}b\int_0^l {\int_0^{{h_{\rm{r}}}} {\frac{{{v_0}\left( {{\eta ^2} - 1} \right)x}}{{{l^2}\sqrt {1 + \left( {{\eta ^2} - 1} \right)\frac{{{x^2}}}{{{l^2}}}} }}} } {\rm{d}}x{\rm{d}}z = }\\ {4.731{\sigma _{\rm{s}}}b\int_0^l {\frac{{\left( {{\eta ^2} - 1} \right)x}}{{{l^2}v_x^2}}{h_x}{v_x}{\rm{d}}x} = }\\ {4.731{\sigma _{\rm{s}}}U \cdot \ln \eta .} \end{array} $ | (16) |
根据轧辊辊面方程
| $ {N_{\rm{f}}} = 4mkb\int_0^l \Delta {v_{\rm{f}}}\sqrt {1 + {{\left( {h_x^\prime } \right)}^2}} {\rm{d}}x, $ |
| $ \Delta {v_{\rm{f}}} = {v_x}\sqrt {1 + {{\left( {h_x^\prime } \right)}^2}} - {v_{\rm{R}}} = {v_x}\sec \alpha - {v_{\rm{R}}}. $ |
式中:Δvf为速度不连续量.剪切屈服强度
上式可写成共线矢量内积形式,即
| $ \begin{array}{*{20}{c}} {{N_{\rm{f}}} = 4\int_0^l {{\tau _{\rm{f}}}} \cdot \Delta {v_{\rm{f}}}{\rm{d}}F = }\\ {4\int_0^l {\left( {{\tau _{{\rm{f}}x}} \cdot \Delta {v_x} + {\tau _{{\rm{fz}}}} \cdot \Delta {v_{\rm{z}}}} \right)} \sqrt {1 + {{\left( {h_x^\prime } \right)}^2}} b{\rm{d}}x = }\\ {4mkb\int_0^l {\left( {\Delta {v_x}\cos \alpha + \Delta {v_{\rm{z}}}\cos \gamma } \right)} \sec \alpha {\rm{d}}x.} \end{array} $ | (17) |
由图 5知,Δvf与坐标轴之间的方向余弦分别为
| $ \left\{ \begin{array}{l} \cos \alpha = \pm {\left[ {R - {{(l - x)}^2}} \right]^{1/2}}/R, \\ \cos \gamma = \pm \left( {l - x} \right)/R = \sin \alpha , \\ \cos \beta = 0. \end{array} \right. $ | (18) |
将式(18)代入到式(17)中,得
| $ \begin{array}{*{20}{c}} {{N_{\rm{f}}} = 4mkb\left[ {\int_0^l {\cos } \alpha \left( {{v_{\rm{R}}}\cos \alpha - {v_x}} \right)\sec \alpha {\rm{d}}x + } \right.}\\ {\left. {\int_0^t {\sin } \alpha \left( {{v_{\rm{R}}}\sin \alpha - {v_x}\tan \alpha } \right)\sec \alpha {\rm{d}}x} \right] = }\\ {4mkb\left[ {{v_{\rm{R}}}R\left( {\theta - 2{a_n}} \right) + \frac{{UR}}{{b{h_m}}}\ln \frac{{{{\tan }^2}\left( {\frac{{\rm{ \mathit{ π} }}}{4} + \frac{{{a_n}}}{2}} \right)}}{{\tan \left( {\frac{{\rm{ \mathit{ π} }}}{4} + \frac{\theta }{2}} \right)}}} \right].} \end{array} $ | (19) |
由式(12)与(13)可知,x=l,h′x=b′x=0;vy|x=l= vz|x= l=0.因此可得
由于在出口截面上不消耗剪切功率,因此入口截面上消耗的剪切功率即为总剪切功率
| $ \begin{array}{*{20}{c}} {{N_{\rm{s}}} = 4\int_0^{{h_0}} k \left| {\Delta {v_z}} \right|b{\rm{d}}z = }\\ {4k\int_0^{{h_0}} {\frac{{{v_0}\Delta h}}{{l{h_0}}}bz{\rm{d}}z} = \frac{{2kU\Delta h}}{l}.} \end{array} $ | (20) |
总功率泛函Φ等于
| $ \mathit{\Phi } = {N_{\rm{d}}} + {N_{\rm{f}}} + {N_{\rm{s}}}. $ |
因此,将式(16)、式(19)与式(20)相加可得
| $ \begin{array}{*{20}{c}} {\mathit{\Phi } = 4.731{\sigma _{\rm{s}}}U \cdot \ln \eta + \frac{{2kU\Delta h}}{l} + }\\ {4mkb\left[ {{v_{\rm{R}}}R\left( {\theta - 2{a_n}} \right) + \frac{{UR}}{{b{h_{\rm{m}}}}}\ln \frac{{{{\tan }^2}\left( {\frac{{\rm{ \mathit{ π} }}}{4} + \frac{{{a_n}}}{2}} \right)}}{{\tan \left( {\frac{{\rm{ \mathit{ π} }}}{4} + \frac{\theta }{2}} \right)}}} \right].} \end{array} $ |
由式(15)、式(16)、式(19)与式(20),对中性角αn求导可得:
| $ \begin{array}{*{20}{c}} {\frac{{{\rm{d}}U}}{{{\rm{d}}{\alpha _n}}} = {v_x}{h_x}b = {v_n}{h_n}b = {v_{\rm{R}}}bR\sin 2{\alpha _n} - }\\ {{v_{\rm{R}}}b\left( {R + {h_1}} \right)\sin {\alpha _n} = N, } \end{array} $ |
| $ \frac{{{\rm{d}}{N_d}}}{{{\rm{d}}{\alpha _n}}} = 4.731{\sigma _{\rm{s}}}N \cdot \ln \eta , $ |
| $ \frac{{{\rm{d}}{N_f}}}{{{\rm{d}}{\alpha _n}}} = 4mk\left[ {\frac{{NR}}{{{h_m}}}\ln \frac{{{{\tan }^2}\left( {\frac{{\rm{ \mathit{ π} }}}{4} + \frac{{{a_n}}}{2}} \right)}}{{\tan \left( {\frac{{\rm{ \mathit{ π} }}}{4} + \frac{\theta }{2}} \right)}} + \frac{{2UR}}{{{h_{\rm{m}}}\cos {a_n}}} - 2{v_{\rm{R}}}bR} \right], $ |
| $ \frac{{{\rm{d}}{N_{\rm{s}}}}}{{{\rm{d}}{\alpha _n}}} = \frac{{2kN\Delta h}}{l}, $ |
因此,对于总功率有
| $ \frac{{{\rm{d}}\mathit{\Phi }}}{{{\rm{d}}{\alpha _n}}} = \frac{{{\rm{d}}{N_{\rm{d}}}}}{{{\rm{d}}{\alpha _n}}} + \frac{{{\rm{d}}{N_{\rm{f}}}}}{{{\rm{d}}{\alpha _n}}} + \frac{{{\rm{d}}{N_{\rm{s}}}}}{{{\rm{d}}{\alpha _n}}}. $ | (21) |
求解上式可得摩擦因子m的理论表达式为
| $ m = \frac{{N\left( {4.731{\sigma _{\rm{s}}}\ln \eta + \frac{{2k\Delta h}}{l}} \right)}}{{4k\left[ {\frac{{NR}}{{{h_{\rm{m}}}}}\ln \frac{{{{\tan }^2}\left( {\frac{{\rm{ \mathit{ π} }}}{4} + \frac{{{a_n}}}{2}} \right)}}{{\tan \left( {\frac{{\rm{ \mathit{ π} }}}{4} + \frac{\theta }{2}} \right)}} + \frac{{2UR}}{{{h_{\rm{m}}}\cos {a_n}}} - 2{v_{\rm{R}}}bR} \right]}}. $ | (22) |
将式(21)确定的αn及式(22)确定的m代入到下式可得轧制力矩、轧制力和应力状态系数解析解:
| $ \left\{ {\begin{array}{*{20}{l}} {{M_{\min }} = \frac{R}{{2{v_{\rm{R}}}}}{\mathit{\Phi }_{\min }}, }\\ {{F_{\min }} = \frac{{{M_{\min }}}}{{\chi \sqrt {2R\Delta h} }}, }\\ {{n_\sigma } = \frac{{{F_{\min }}}}{{4blk}}.} \end{array}} \right. $ | (23) |
式中力臂参数χ可以参考文献[25],一般对于热轧大约为0.5,冷轧大约0.45.
2.6 实验验证与分析讨论在国内某厂开展了现场轧制实验.轧机的工作直径为1 120 mm,连铸坯的尺寸为219 mm×3 200 mm×2 290 mm.从第1~第5道次由于轧件宽厚比>10,所以这些轧制道次的轧件宽度不变,满足平面变形条件.第1~5道次的轧制速度分别为2.29 m/s,2.45 m/s,2.57 m/s,2.75 m/s和2.91 m/s;力臂系数χ分别取0.62,0.63,0.61,0.66和0.63;相应的轧制温度分别为919℃,911℃,903℃,896℃和890℃.每道次轧件的出口厚度以及每道次轧制力可以在线实测.材料为Q345R钢,其变形抗力模型为[26]
| $ \begin{array}{l} {\sigma _{\rm{s}}} = 3583.195{{\rm{e}}^{ - 2.233 \times {{10}^{ - 3}}T}} \cdot {\varepsilon ^{0.42437}} \cdot \\ \;\;\;\;\;\;\;{{\dot \varepsilon }^{ - 0.3486 \times {{10}^{ - 3}}T + 0.46339}}, \end{array} $ |
| $ T = t + 273. $ |
式中:ε为等效应变、
上述道次的轧制力矩和轧制力可由式(23)计算.解析计算结果与实测结果如表 1所示.
| 表 1 解析轧制力、力矩与实测结果比较 Tab. 1 Comparison of analytical rolling force and torque with measured results |
在表 1中,Δ1为实测轧制力FM与由本文速度场计算的解析轧制力FA的相对误差,最大误差为5.3%;Δ2为实测轧制力矩MM与由本文速度场计算的解析轧制力矩MA的相对误差,平均误差为6.04%,仅有一组误差为13.7%.以上的各误差均小于工程允许的15%要求,具有较好的预测精度,能够为工艺优化提供理论指导.
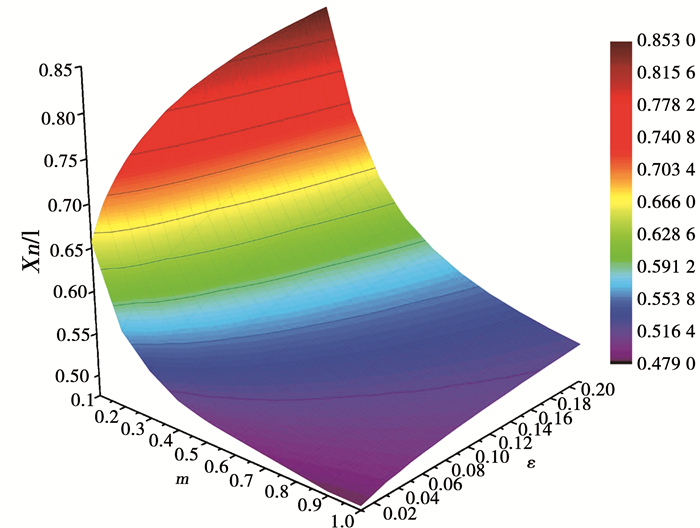
3 分析与讨论图 6表示了中性点位置Xn/l与摩擦因子m以及压下率ε(真应变)之间的关系.如图所示,随着m的增加,中性点位置逐渐向入口处移动,但随ε的增加,中性点向出口移动.
|
图 6 中性点位置与摩擦因子以及压下率的关系 Fig. 6 Relationship among the neutral point position, the friction factor, and relative reduction |
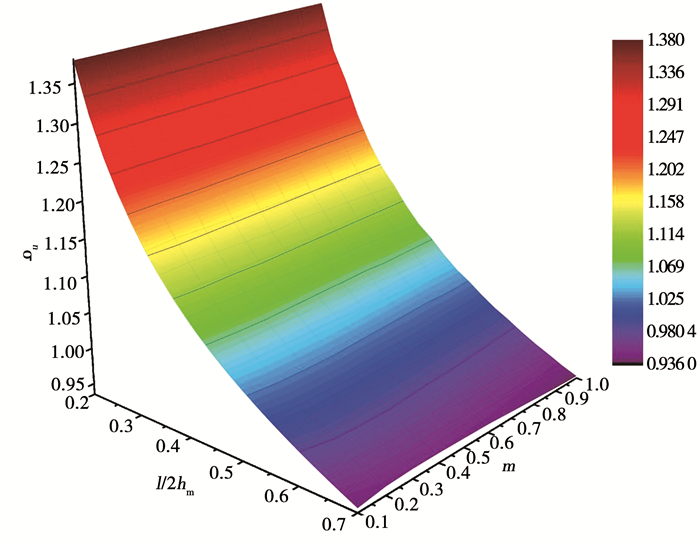
图 7表示了应力状态系数nσ与形状因子l/2hm以及摩擦因子m之间的关系.可以看出,随着形状因子的增加,nσ有明显减小.而摩擦因子m对nσ的影响较小,说明摩擦功率对总功率的影响很小.
|
图 7 应力状态系数与形状因子以及摩擦因子的关系 Fig. 7 Relationship among the stress state coefficient, the shape factor, and the friction factor |
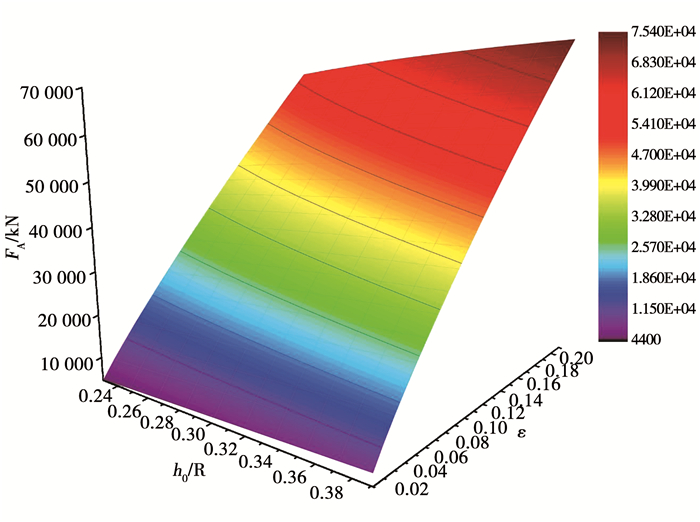
图 8表示了解析轧制力FA与厚径比h0/R以及压下率ε之间的关系.可以看出,轧制力随着压下率的增加以及厚径比的增加而增加.
|
图 8 轧制力与厚径比以及压下率的关系 Fig. 8 Relationship among the rolling force, the thickness to diameter ratio, and relative reduction |
1) 本文提出的积分中值屈服准则是关于主应力分量的线性组合,它的屈服轨迹为一个相交于Mises圆的等边非等角十二边形,边长为0.428σs,顶角为155.196°与144.804°.通过对比实验数据,发现IM屈服准则的结果与实验数据吻合程度高,给出了合理的中间结果.
2) 本文建立了一种新型的二维轧制速度场,该速度场满足运动许可条件,它能反映厚板轧制时轧件的纵横流动特点.通过运算,获得了内部变形功率、摩擦功率以及剪切功率的表达式,并获得了轧制力、轧制力矩的解析解.通过对比实测数据,理论轧制力与轧制力矩与实测值吻合较好,轧制力误差不大于5.3%,轧制力矩误差在6%左右,最大误差为13.7%.由此可见本文采用IM屈服准则解析椭圆速度场的方法是可行的.
3) 对各种轧制参数的变化规律对比发现,摩擦因子m增加,中性点向入口移动;压下率ε的增加会导致中性点位置向出口方向移动,也会导致轧制力的增加;变形区形状因子l/2hm的增加会降低应力状态系数,而轧板厚径比h0/R的增大会引起轧制力增加.
| [1] |
TRESCA H. Memoir on the flow of solid bodies under strong pressure[J]. Comptes-Rendus de l'Académie des Sciences, 1864, 59: 754. |
| [2] |
MISES R V. Mechanik der festen Körper im plastisch-deformablen Zustand[J]. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse, 1913, 1913(4): 582. |
| [3] |
MISES R V. Mechanik der plastischen Formänderung von Kristallen[J]. Zamm-Journal of Applied Mathematics & Mechanics, 1928, 8(3): 161. DOI:10.1002/zamm.19280080302 |
| [4] |
DRUCKER DC, PRAGER W. Soil mechanics and plastic analysis or limit design[J]. Quarterly of Applied Mathematics, 1952, 10(2): 157. DOI:10.1090/qam/48291 |
| [5] |
YU Maohong. Advances in strength theories for materials under complex stress state in the 20th century[J]. Applied Mechanical Reviews, 2002, 55(3): 169. DOI:10.1115/1.1472455 |
| [6] |
俞茂宏. 双剪理论及其应用[M]. 北京: 科学出版社, 1998. YU Maohong. Twin shear theory and its applications[M]. Beijing: Academic Press, 1998. |
| [7] |
YU Maohong. Twin shear stress yield criterion[J]. International Journal of Mechanical Sciences, 1983, 25(1): 71. DOI:10.1016/0020-7403(83)90088-7 |
| [8] |
胡小荣. 材料三剪屈服准则研究[J]. 工程力学, 2006, 23(4): 6. HU Xiaorong. Research on triple-shear yield criterion for materials[J]. Engineering Mechanics, 2006, 23(4): 6. DOI:10.3969/j.issn.1000-4750.2006.04.002 |
| [9] |
ZHU Xiankui, LEIS B N. Average shear stress yield criterion and its application to plastic collapse analysis of pipelines[J]. International Journal of Pressure Vessels & Piping, 2006, 83(9): 663. DOI:10.1016/j.ijpvp.2006.06.001 |
| [10] |
BARSANESCU P D, COMANICI A M. von Mises hypothesis revised[J]. Acta Mechanica, 2017, 228(2): 433. DOI:10.1007/s00707-016-1706-2 |
| [11] |
GU Jiefei, CHEN Puhui. A failure criterion for homogeneous and isotropic materials distinguishing the different effects of hydrostatic tension and compression[J]. European Journal of Mechanics-A/Solids, 2018, 70: 15. DOI:10.1016/j.euromechsol.2018.01.013 |
| [12] |
PEI Jianyong, EINSTEIN H H, WHITTLE A J. The normal stress space and its application to constructing a new failure criterion for cross-anisotropic geomaterials[J]. International Journal of Rock Mechanics and Mining Sciences, 2018, 106: 364. DOI:10.1016/j.ijrmms.2018.03.023 |
| [13] |
小林史郎ら. マトリツワス法による刚-塑性体变形の解析[J]. 塑性と加工, 1973, 14(153): 770. KOBAYASHI Shiro. Analysis of elastic-plastic fracture forms by matrix method[J]. Plasticity and Processing, 1973, 14(153): 770. |
| [14] |
KATO K, OSAKADA K. Finite element simulation of three dimensional deformation in shape rolling[J]. International Journal for Numerical Methods in Engineering, 1990, 30: 1431. DOI:10.1002/nme.1620300807 |
| [15] |
王振范, 木内学. 三维流函数法解析在塑性加工中的应用[J]. 哈尔滨工业大学学报, 2000(5): 93. WANG Zhenfan, MANABU Kiuchi. Application of 3D fluxional function to metal forming[J]. Journal of Harbin Institute of Technology, 2000(5): 93. DOI:10.1007/s10011-000-0335-3 |
| [16] |
李涛. 正交异性材料在R.Hill屈服准则下平面应力问题的特征场(h>2)[J]. 工程力学, 2002, 19(4): 123. LI Tao. Characteristic field of plane stress problem for the orthotropic materials[J]. Journal of Harbin Institute of Technology, 2002, 19(4): 123. DOI:10.3969/j.issn.1000-4750.2002.04.026 |
| [17] |
ZHAO Dewen, ZHANG Shunhu, LI Canming, et al. Rolling with simplified stream function velocity and strain rate vector inner product[J]. Journal of Iron and Steel Research, International, 2012, 19(3). DOI:10.1016/S1006-706X(12)60068-5 |
| [18] |
ZHANG Shunhu, DENG Lei, ZHANG Qinyu, et al. Modeling of rolling force of ultra-heavy plate considering the influence of deformation penetration rate[J]. International Journal of Mechanical Sciences, 2019, 159: 373. DOI:10.1016/j.ijmecsci.2019.05.048 |
| [19] |
ZHANG Shunhu, GAO Siwei, WU Guijing, et al. A weighted average yield criterion and its applications to burst failure of pipeline and three-dimensional forging[J]. Journal of Manufacturing Processes, 2017, 28: 243. DOI:10.1016/j.jmapro.2017.06.006 |
| [20] |
LODE W. Versucheüber den Einfluß der mittleren Hauptspannung auf das Fließen der Metalle Eisen, Kupfer und Nickel[J]. Zeitschrift für Physik A Hadrons and Nuclei, 1926, 36(11): 913. DOI:10.1007/BF01400222 |
| [21] |
LESSELLS J M, MACGREGOR C W. Combined stress experiments on a nickel-chrome-molybdenum steel[J]. Journal of the Franklin Institute, 1940, 230(2): 163. DOI:10.1016/S0016-0032(40)90729-3 |
| [22] |
NAGHDI P M, ESSENBURG F Jr, KOFF W. An experimental study of initial and subsequent yield surfaces in plasticity[J]. Applied Mechanica, 1958, 25: 201. |
| [23] |
MAXEY W A. Measurement of yield strength in the mill expander[C]//Proceedings of the Fifth Symposium Online Pipe Research. Houston: [s.n.], 1974: 20
|
| [24] |
PITTMAN J F T, ZIENKIEWICZ O C, WOOD R D, et al. Numerical analysis of forming processes[M]. New York: John Wiley and Sons, 1984.
|
| [25] |
HARRIS J N, JOHN Noel. Mechanical working of metals:Theory and practice[M]. Oxford: Pergamon Press, 1983.
|
| [26] |
ZHANG Shunhu. Linearization of yield criterion and its engineering applications[M]. Beijing: Metallurgical Industry Press, 2018.
|
 2020, Vol. 52
2020, Vol. 52


