光学式三维测量具有高精度测量、非接触性、无损测量等优点,已被广泛用于逆向工程、生物与医学工程、工业检测、质量控制等领域[1-5].其中相位测量轮廓术(PMP)[6-7]具有点对点相位计算及全场分析等优点,更倍受业界青睐.在PMP系统中,带有相移量的正弦条纹由投影装置将其逐一投射到被测物体表面,由成像装置逐一对应采集被物体表面调制的变形相移条纹,最后由数据处理装置对采集的数据进行处理,得到物体表面的相位分布[8].要得到被测物体的真实高度,就要建立相位到高度的映射关系.相位—高度映射关系的待定系数,可由成像装置光心与投影装置光心之间的距离,参考面与投影装置光心之间的距离以及两装置光轴之间的夹角等系统结构参数确定,这种需要测量系统结构参数的高度校准方法为显式校准[9-10],但在实际测量中很难精确测量这些参数值.通常通过建立相位-高度映射关系,由已知平面高度与测得的对应相位来标定映射关系中的待定系数,这种高度校准方法为隐式校准[11-13],避免了直接测量系统结构参数困难的问题.
传统的相位—高度映射算法要求成像装置光轴与投影装置光轴共面且交于参考面内的一点,成像装置光轴平行于参考平面的法线,参考面平行于两装置光心的连线,但在测量中要全部满足这些条件是很苛刻的,在搭建系统时很难精确实现.为此,业界学者对搭建的测量系统结构进行了改进,并提出了相应的相位—高度映射算法.文献[14]介绍了相位—高度的映射关系,并且证明了当投影装置光轴和成像装置光轴不共面时,传统的相位—高度的映射关系也是适用的,但仍然要求参考面必须平行于投影装置光心与成像装置光心的连线.文献[15]提出既不用保证参考面平行于投影装置光心与成像装置光心的连线,也不要求成像装置光轴垂直参考面,但两光轴必须共面且交于参考面一点的相位—高度映射关系.本文在传统的相位—高度映射算法的基础上,提出一种新的具有宽松约束的相位—高度映射算法.这种算法不要求投影光心和成像光心的连线平行于参考平面,也不要求投影光轴与成像光轴共面且交于参考面一点,只要保证成像装置光轴垂直于参考平面,即可实现相位到高度的映射.通过数学模型推导发现所提相位—高度映射中的待定系数不仅与系统的结构参数有关,也与参考平面的相位分布有关.
1 PMP测量原理投影装置将带有相移量的正弦条纹投影到被测物体表面,其光强I(x, y)为[16]
| $ I(x,y) = R(x,y)[A(x,y) + B(x,y)\cos (\varphi (x,y) + \delta )]. $ | (1) |
式中:R(x, y)为物体表面不均匀的反射率,A(x, y)为背景光强,B(x, y)为条纹对比度,ϕ(x, y)为受物体高度调制的相位分布,δ为条纹每次的相移量.对于N(N≥3)步相移法,光强In(x, y)为
| $ \begin{array}{*{20}{c}} {{I_n}(x,y) = R(x,y)[A(x,y) + B(x,y)\cos (\varphi (x,y) + }\\ {\left. {\left. {\frac{{2n{\rm{ \mathsf{ π} }}}}{N}} \right)} \right],(n = 1,2 \cdots N).} \end{array} $ | (2) |
式中n为N步相移法的步数,由式(2)计算可得相位ϕ(x, y)为
| $ \varphi (x,y) = \arctan \left[ {\frac{{\sum\limits_1^N {{I_n}} (x,y)\sin \left( {\frac{{2n{\rm{ \mathsf{ π} }}}}{N}} \right)}}{{\sum\limits_1^N {{I_n}} (x,y)\cos \left( {\frac{{2n{\rm{ \mathsf{ π} }}}}{N}} \right)}}} \right]. $ |
此时相位ϕ(x, y)被截断在反正切函数的主值范围(-π, π]内,因而是不连续的,需要进行相位展开将其恢复成原有的相位分布,连续相位分布记为φ(x, y).要由物体的相位分布得到物体的三维形貌,需要建立相位—高度的映射关系.
2 宽松约束的相位—高度映射算法传统相位—高度映射算法和所提相位—高度映射算法的测量光路如图 1(a)、(b)所示:

|
图 1 测量原理 Fig. 1 Schematic of the measuring method |
在图 1(a)中,DLP为数字投影装置,CCD为成像装置,P是DLP的光心,E是CCD的光心,PO是投影装置的光轴,EO是CCD的光轴并垂直于参考面,PO和EO相交于参考平面上的O点,D是物体上的任一点.l是投影装置光心到参考平面上O点的距离、d是两装置光心之间的距离、L是CCD光心与参考面之间的距离、θ是投影装置光轴和CCD光轴之间的夹角,它们都是系统的结构参数.从图 1(a)分析可知,要求投影装置的光心和CCD的光心连线与参考平面平行,并且要求两光轴共面并交于参考面一点.
图 1(b)中的P点、E点、A点、B点、D点、l以及L和图 1(a)中相同.DLP的光轴PO与参考面相交于O点,CCD的光轴EO′垂直于参考面并交于O′点,EF平行于OO′,平面PGH平行于参考面,交FO于G点,交EO′于H点.P点到G点之间的距离为d,DLP的光轴PO与FO之间的夹角为θ.由于DLP和CCD的光心和光轴都是不可见的,因此在实验中很难保证DLP与DLP光心的连线恰好平行于参考面,也难以保证两装置的光轴共面且恰好相交于参考平面上一点.而在图 1(b)中,不再要求两装置的光心连线平行于参考平面,也不再要求两光轴共面且交于参考面上一点,只需保证CCD的光轴垂直于参考平面,以便于建立图像坐标与世界坐标的简单映射.因而图 1(b)所示测量光路约束更宽松,更易于搭建.
根据图 1(a)所示的测量光路图,文献[14]推导出物体上任一点D点的高度h(即DB)为
| $ \frac{1}{h} = {a_1} + {b_1}\frac{1}{\varphi }. $ | (3) |
式中φ为D点的相位,考虑到CCD探测器的阵列特性,式(3)可被写为
| $ \frac{1}{{h(x,y)}} = {a_1}(x,y) + {b_1}(x,y)\frac{1}{{\varphi (x,y)}}. $ |
文献[14]提出当系统结构一定时,a1(x, y)和b1(x, y)应该是恒定不变的,可由标定获得.后来,文献[13]提出要考虑镜头畸变的影响,式(3)被修正为
| $ \begin{array}{*{20}{c}} {\frac{1}{{h(x,y)}} = {a_1}(x,y) + {b_1}(x,y)\frac{1}{{\varphi (x,y)}} + }\\ {{c_1}(x,y)\frac{1}{{{\varphi ^2}(x,y)}}.} \end{array} $ | (4) |
式(4)在PMP系统中经常用于系统标定,以下简称为Li′s算法.
从图 1(b)可看出,两装置的光心连线PE与参考平面不平行, 且PO与EO′不共面,推导物体表面任一点D点的高度h的过程如下:
当采用远心光路的PMP系统时,在参考平面上看到的投影正弦光栅是等周期分布的,其周期为p0,在参考平面上的相位分布φ(x)是坐标x的线性函数[17],记为
| $ \varphi (x) = Kx = \frac{{2{\rm{ \mathsf{ π} }}}}{{{p_0}}}x. $ |
当PMP系统是发散光路时,正弦光栅被投影到参考平面上,φ(x)是x的非线性函数,但是参考平面上每一点相对于参考点O的相位值是唯一的且单调变化的.此时参考平面上条纹周期的分布为[18]
| $ \frac{1}{{p(x)}} = \frac{{\cos \theta }}{{{p_0}}}\left( {1 - \frac{{2x\sin \theta }}{l}} \right). $ | (5) |
从式(5)可看出,参考平面上的条纹周期p(x)与x成非线性的关系,各点的周期分布随点的变化而改变.这种非线性给各点的相位计算带来了不便.因此,在计算参考面上各点的相位值时,将其映射到周期p0上.同样,在计算物体上各点的相位时,也将其映射到周期p0上,测得的物体上各点相位与对应点在参考平面上的相位差,即反映了物体高度的相位信息.因此,可得图 1(b)中参考平面上A,B,C点的相位ϕ:
| $ {\varphi _{\rm{A}}} = \frac{{2{\rm{ \mathsf{ π} }}}}{{{p_0}}}\overline {OA} ,{\varphi _{\rm{B}}} = \frac{{2{\rm{ \mathsf{ π} }}}}{{{p_0}}}\overline {OB} ,{\varphi _{\rm{C}}} = \frac{{2{\rm{ \mathsf{ π} }}}}{{{p_0}}}\overline {OC} . $ | (6) |
由于D点被投射到参考平面A点处,A点与D点具有相同的相位,即
| $ {\varphi _{\rm{D}}} = {\varphi _{\rm{A}}} = \frac{{2{\rm{ \mathsf{ π} }}}}{{{p_0}}}\overline {OA} . $ | (7) |
由三角形BCD和OCF相似可得出
| $ \frac{{\overline {BC} }}{{\overline {OC} }} = \frac{{\overline {BD} }}{{\overline {OF} }}. $ | (8) |
结合式(6)、式(7)以及
| $ \frac{h}{L} = \frac{{{\varphi _{\rm{C}}} - {\varphi _{\rm{B}}}}}{{{\varphi _{\rm{C}}}}}. $ |
再由三角形BDA和PPA′相似可得出
| $ \frac{{\overline {BA} }}{{\overline {P'A} }} = \frac{{\overline {BD} }}{{\overline {P'P} }}. $ | (9) |
将
| $ \frac{1}{h} = \frac{1}{{l\cos \theta }} + \frac{{2{\rm{ \mathsf{ π} }}}}{{{p_0}}}\tan \theta \frac{1}{{{\varphi _{CD}}}} + \frac{{l\cos \theta - L{\varphi _C}}}{{Ll\cos \theta {\varphi _{CD}}}}. $ | (10) |
| $ 令\left\{ {\begin{array}{*{20}{l}} {{a_2} = \frac{1}{{l\cos \theta }},}\\ {{b_{21}} = \frac{{2{\rm{ \mathsf{ π} }}}}{{{p_0}}}\tan \theta ,}\\ {{b_{22}} = \frac{{l\cos \theta - L}}{{Ll\cos \theta }}.} \end{array}} \right. $ | (11) |
式(10)即可写为
| $ \frac{1}{h} = {a_2} + {b_{21}}\frac{1}{{{\varphi _{{\rm{CD}}}}}} + {b_{22}}\frac{{{\varphi _{\rm{C}}}}}{{{\varphi _{{\rm{CD}}}}}}. $ | (12) |
式中:φC为参考平面的相位分布,φCD为物体上各点的连续相位与参考平面上对应点相位的差值.
当两装置的光心连线平行于参考平面且O与O′重合时,图 1(b)与图 1(a)相同,此时从图 1(a)中可知lcos θ=L,由式(11)可知,b22=0,即式(12)可化为式(3).表明图 1(a)所示测量光路是图 1(b)所示测量光路的一个特例.
从式(12)可知,所提出的相位—高度的映射算法不仅与系统的结构参数有关,还与参考面上的相位分布有关.所提算法对应的系统结构,不要求投影装置光心和成像装置光心的连线平行于参考平面,也不要求投影光轴与成像光轴共面,使得系统的搭建更加容易.所以为了得到物体的真实高度,实现相位到高度的映射,所提算法相比传统的算法更具优势.当考虑CCD探测器的阵列特性,可将式(12)表达为
| $ \begin{array}{*{20}{c}} {\frac{1}{{h(x,y)}} = {a_2}(x,y) + {b_{21}}(x,y)\frac{1}{{\varphi (x,y)}} + }\\ {{b_{22}}(x,y)\frac{{{\varphi _{\rm{C}}}(x,y)}}{{\varphi (x,y)}}.} \end{array} $ | (13) |
式(13)φC(x, y)为参考平面的相位,可事先通过测量参考平面得到并存于计算机.因此,在标定a2(x, y)、b21(x, y)和b22(x, y)时,则需要测量4个或者4个以上已知高度的平面(包括参考平面),以求出所测平面的连续相位,将平面的高度和对应的相位代入式(13)中,求得对应的a2(x, y)、b21(x, y)和b22(x, y)即完成标定.
3 实验及分析搭建的实验装置如图 2所示,其中使用的数字光投影仪型号为PLED-W200 DLP,成像系统CCD型号为MVC1 000MF.测量前利用型号为Zolix TSA300-B的电动平移台带动一个标准平面沿z轴移动并结合CCD图像,反复调整CCD,直至CCD光轴垂直标准平面.

|
图 2 实验装置 Fig. 2 Experimental setup |
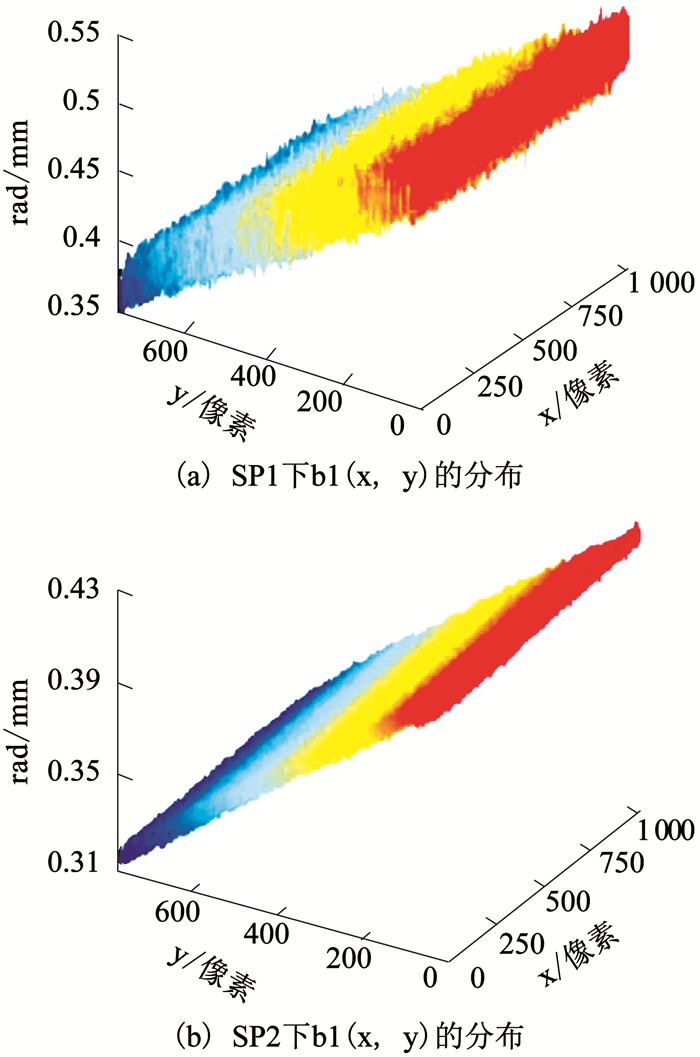
通过计算机产生周期为20像素的768×1 024大小的正弦光栅图,采用5步相移技术.使用标准平面相对于参考面沿z轴移动预设高度的方法进行参数标定.考虑到CCD各像元之间的灵敏度差异性和随机误差的影响,a1(x, y),b1(x, y)和c1(x, y)应该呈现具有一定波动厚度的特征分布.在大量的系统标定实验结果中选取两组不同结构参数下b1(x, y)的分布图如图 3所示.图 3(a)为结构参数1(Structural Parameters 1, SP1)下的实验结果,图 3(b)结构参数2(Structural Parameters 2, SP2)下的实验结果.
|
图 3 b1(x, y)分布 Fig. 3 The corresponding calibrated distributions of b1(x, y) |
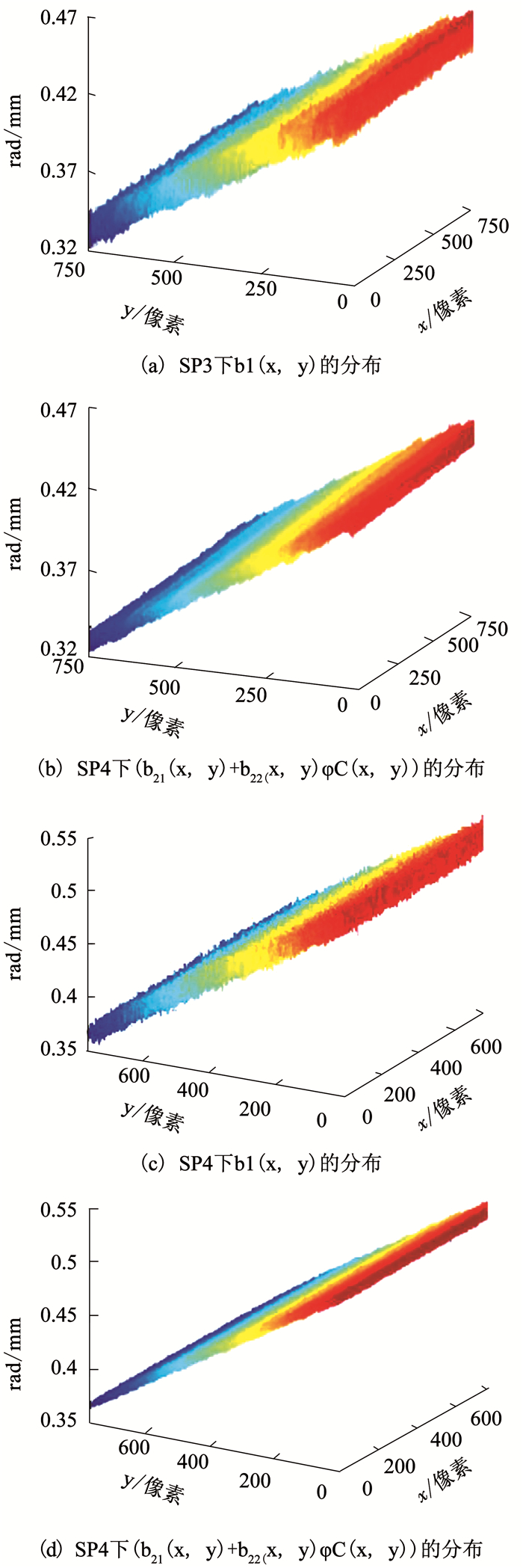
从图 3可看出,在不同结构参数下,b1(x, y)具有不同的波动厚度且呈现不同的倾斜角度特征.在式(13)中1/φ(x, y)的系数可写为b21(x, y)+ b22(x, y)φC(x, y),为了比较两者的区别,通过大量的实验,发现b21(x, y)+ b22(x, y)φC(x, y)是呈有一定波动厚度且有一定倾角的斜平面的特征分布.两组代表性的不同结构参数下的实验结果如图 4所示,图 4(a)~(b)为结构参数3(Structural Parameters 3, SP3)下的实验结果,图 4(c)~(d)为改变DLP和CCD的位置后重新测量的结果,即结构参数4(Structural Parameters 4, SP4)下的一组实验结果.
|
图 4 两组不同结构参数(SP3和SP4)下验证b1(x, y)与b21(x, y)+b22(x, y)φC(x, y)的关联性的实验结果 Fig. 4 Experimental results of the correlation between b1(x, y) and b21(x, y)+b22(x, y)φC(x, y) under two groups of structure parameters SP3 and SP4 |
图 4(a)为SP3下b1(x, y)的分布,b1(x, y)是一个具有一定倾角的斜面且具有一定波动厚度,正如上图 3中所示.图 4(b)为SP3下b21(x, y)+ b22(x, y)φC(x, y)的分布,也是一个具有一定倾角且有一定波动厚度的斜平面.由图 4(a)和图 4(b)可知,二者的倾斜角大致相同,但是后者的斜面波动厚度明显小于前者且表面更光滑.由于波动厚度是由测量误差等因素引入的,波动厚度越小则表征测量精度越高.由此可知,运用1/φ(x, y)的系数为b21(x, y)+ b22(x, y)φC(x, y)的式(13)进行相位到高度的映射,重建效果更好,精度更高.
为了证明上述实验的可重复性,对测量系统的结构参数进行了多次改变,即随意改变投影装置和成像装置的位置,然后进行测量.图 4(c)、(d)为代表SP4下的一组实验数据.结果同样表明,图 4(d)和图 4(c)的倾斜角基本相同,但仍然是后者的斜平面的波动厚度明显小于前者.
通过对上述实验结果的分析可知:在相同的结构参数下,利用所提算法式(13)进行标定得到的b21(x, y)+b22(x, y)φC(x, y)的分布,其斜面波动厚度要明显小于利用式(4)标定得到的b1(x, y)的分布的波动厚度.正如上文所说波动厚度是由测量误差等因素引入的,波动厚度越小表征测量精度越高.因此,可表明所提算法在测量精度上要优于传统的算法,且所搭建的测量系统结构也更易于实现.
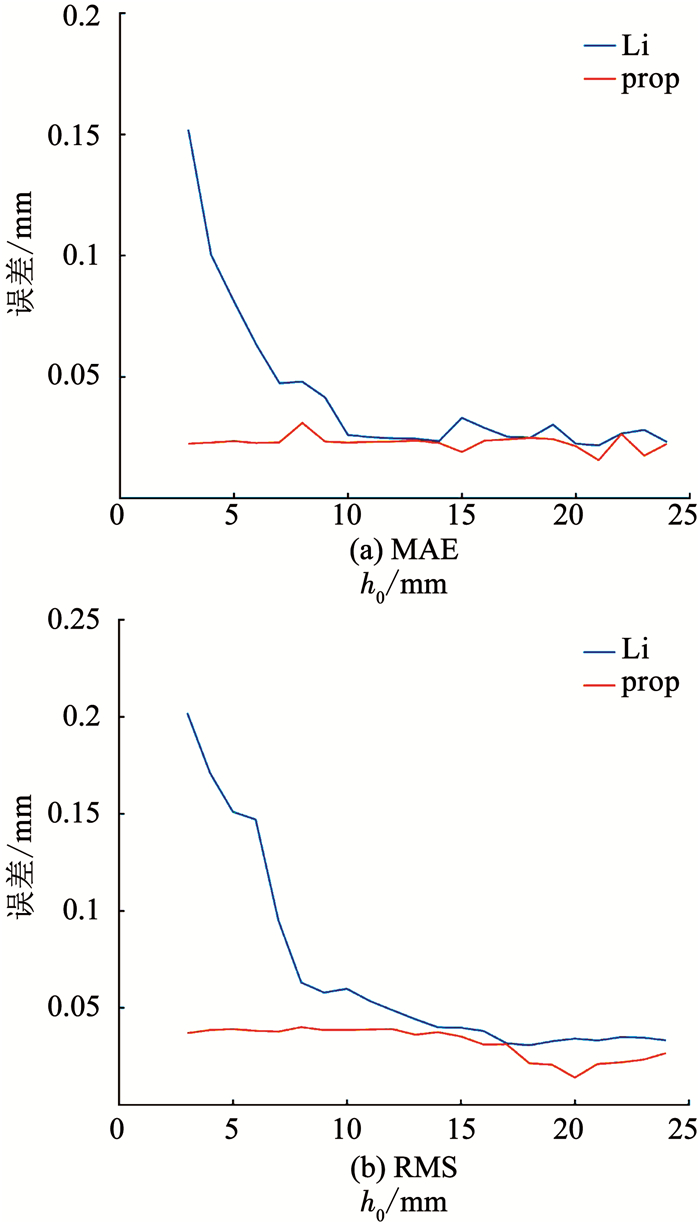
为了验证所提测量方法的精确性,测量3 mm到24 mm等若干已知高度平面的相位分布,并分别通过式(4)和式(13)进行相位高度映射.得到平均绝对误差(MAE)和均方根误差(RMS)的对比结果如图 5所示.表 1中列出其中3 mm、8 mm、16 mm 3个测量结果,包括平面真实高度h0,由两种算法恢复出平面的平均高度havg,平均绝对误差(MAE)和均方根误差(RMS).
|
图 5 各平面的平均绝对误差(MAE)和均方根误差(RMS)对比 Fig. 5 Comparison of MAE and RMS of each plane |
| 表 1 对已知高度平面测量复结果对比 Tab. 1 Comparison of measuring results of the planes with known heightsmm |
从表 1和图 5可看出,所提算法所恢复平面的平均高度都比Li′s算法更接近平面的真实高度,同时平面的平均绝对误差和均方根误差也均小于Li′s算法.在高度平面较低的区域,Li′s算法恢复平面的精度较低,随着测量平面高度的增加,Li′s算法所恢复平面的精度逐步提高并在测量高度大于10 mm的平面时,其精度逐渐趋于稳定,但仍低于所提算法的精度.而所提算法一直保持了较好的测量精度,较之更加稳定.因此可得,所提的相位—高度映射算法的准确性和可重复性都要优于Li′s相位—高度映射算法.
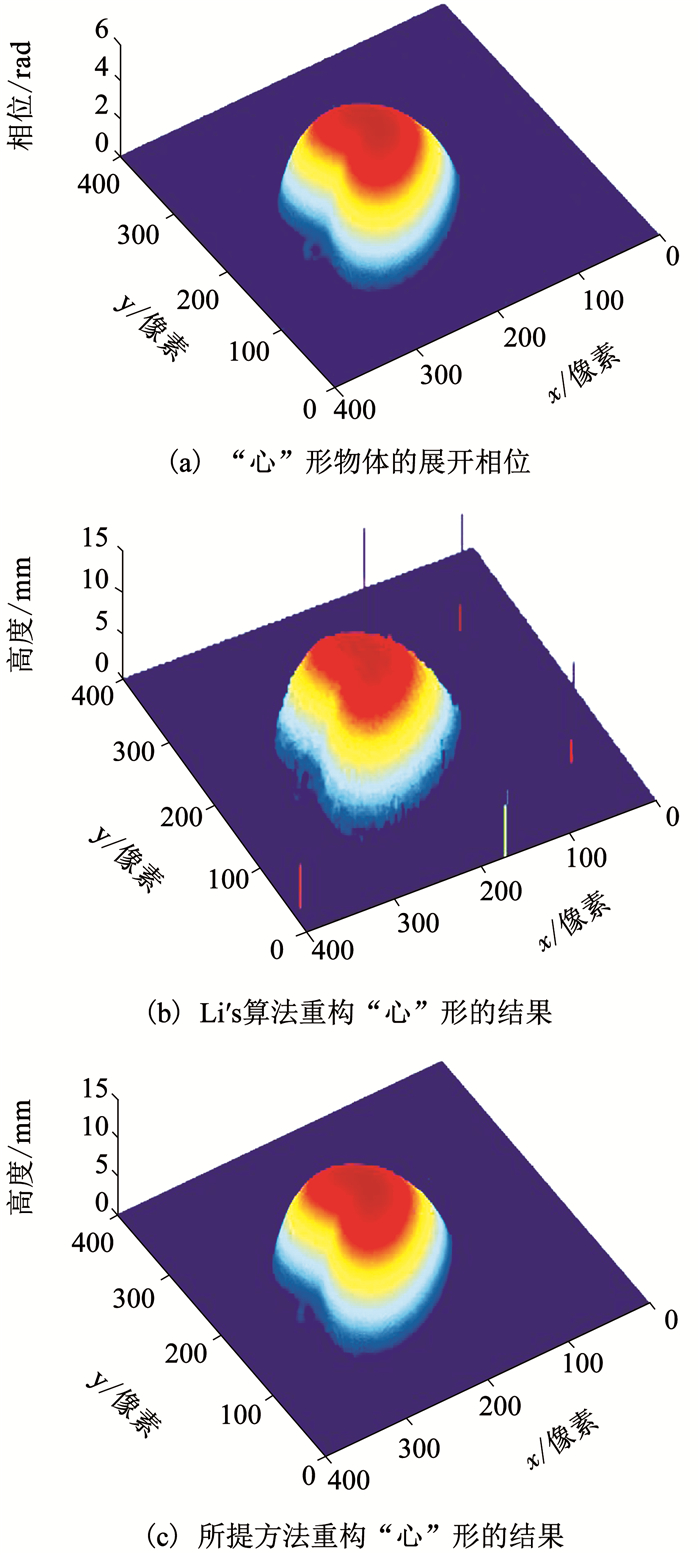
为了验证该方法的实用性,对如图 6(a)中所示的“心”形物体进行了三维形貌的测量.图 6(b)为由CCD采集所得的一帧物体变形条纹,图 6(c)为根据采集所得物体变形条纹中得到的物体截断相位的信息分布.图 8为分别采用Li′s算法和所提算法来实现相位到高度的映射对比效果.图 8(a)为所测“心”形物体的连续相位信息分布,图 8(b)为Li′s算法重构出的三维物体形貌.图 8(c)为所提算法重构出的三维物体形貌.

|
图 6 “心”形物体测量数据 Fig. 6 Measured data of the heart-shaped object |
|
图 8 “心”形物体相位到高度的重构结果 Fig. 8 Reconstruction of the heart-shaped object |
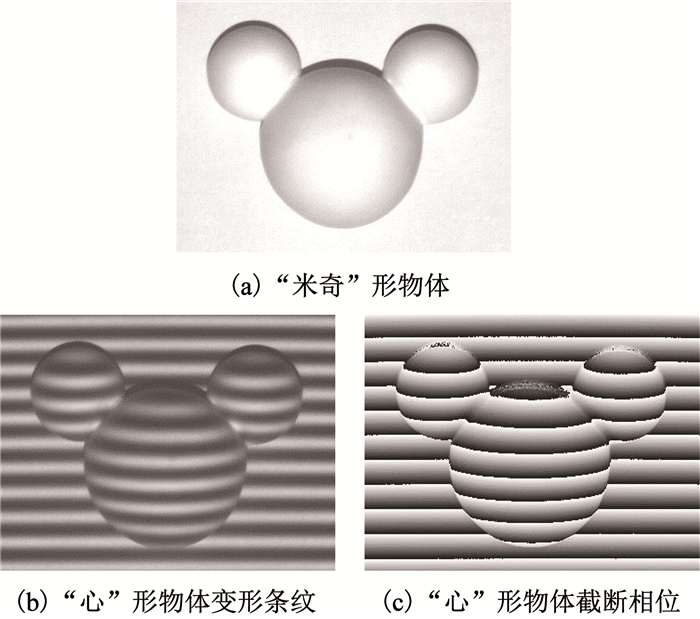
为了验证该方法在不同特征环境下的可重复性,对如图 7(a)中所示的“米奇”形物体进行了三维形貌的测量.图 7(b)为由CCD采集所得的一帧物体变形条纹,图 7(c)为根据采集所得物体变形条纹中得到的物体截断相位的信息分布.图 9为分别采用Li′s算法和所提算法来实现相位到高度的映射对比效果.图 9(a)为所测“米奇”形物体的连续相位信息分布,图 9(b)为Li′s算法重构出的三维物体形貌.图 9(c)为所提算法重构出的三维物体形貌.
|
图 7 “米奇”形物体测量数据 Fig. 7 Measured data of the Mickey-shaped object |
|
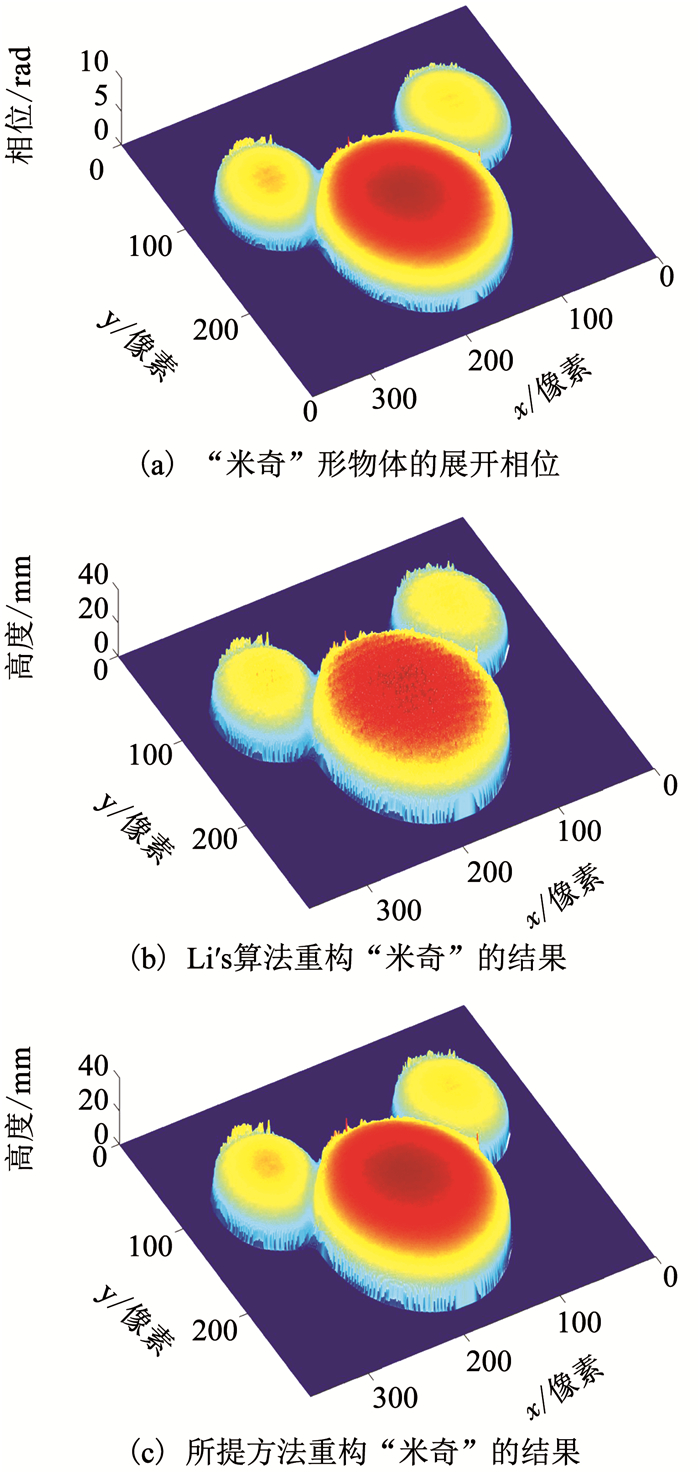
图 9 “米奇”形物体相位到高度的重构结果 Fig. 9 Reconstruction of the Mickey-shaped object |
由图 8(b)可看出,Li′s算法虽然恢复出了物体的三维形貌,但是在一些局部区域出现了毛刺,使得在这些点上相位到高度的映射呈现难以对应的关系,并且在图 8(b)中所重构出的物体表面出现了一定失真.而由图 8(c)可看出,所提算法很好地恢复了物体面形,整体没有出现毛刺现象,而且表面轮廓也比较光滑,使测量的精度得到了保证,有效实现了相位到高度的一一映射.对于高度更高的“米奇”形物体,由图 9(b)可看出,Li′s算法所重构出物体的三维面形存在一定程度的失真,而由图 9(c)可看出,所提算法所重构的面形区域则更加光滑,尤其是在面形顶部区域.并且所提算法的测量精度也较Li′s算法的高,综上可得,所提出相位—高度映射算法在实现相位到高度的映射效果上要优于Li′s算法.
4 结论本文从实验系统的实际光路出发,考虑到实际光路难以精确达到理想模型要求,提出了一种新的具有宽松约束的相位—高度映射算法.这种算法既不需要满足成像装置光轴与投影装置光轴共面且交于参考面内的一点,参考面平行于两装置光心的连线的要求,也不需要满足两光轴必须共面且交于参考面一点的要求.只要求成像装置光轴垂直于参考平面,即可实现相位到高度的映射.理论分析和实验验证发现,当投影装置光心与成像装置光心的连线不平行于参考平面时,相位—高度映射不只与系统的结构参数有关,还与参考平面的相位分布有关.完成了对比测量实验,在对高度分别为3 mm、8 mm和16 mm的平面测量中,使用传统算法进行的相位—高度映射时,其平均绝对误差和均方根误差最大可达0.152 mm和0.202 mm.而使用所提算法进行的相位—高度映射时,其平均绝对误差和均方根误差最大不超过0.031 mm和0.040 mm,有效验证了所提算法的准确性和可重复性.通过“心”形物体的面形测量验证了所提算法的实用性.
| [1] |
陈超, 於燕琴, 黄淑君, 等. 三维小视场成像系统[J]. 红外与激光工程, 2016, 45(8): 0824002. CHEN Chao, YU Yanqin, HUANG Shujun, et al. 3D small-field imaging system[J]. Infrared and Laser Engineering, 2016, 45(8): 0824002. DOI:10.3788/IRLA201645.0824002 |
| [2] |
刘巍, 王亮, 樊超楠, 等. 大型高温锻件在线视觉测量图像匹配方法[J]. 激光与红外, 2016, 46(11): 1414. LIU Wei, WANG Liang, FAN Chaonan, et al. Image matching method for online vision measurement of large forgings[J]. Laser&Infrared, 2016, 46(11): 1414. DOI:10.3969/j.issn.1001-5078.2016.11.023 |
| [3] |
赵亚龙, 刘守起, 张启灿. GPU加速三维面形测量[J]. 红外与激光工程, 2018, 47(3): 317003. ZHAO Yalong, LIU Shouqi, ZHANG Qican. 3D shape measurement accelerated by GPU[J]. Infrared and Laser Engineering, 2018, 47(3): 317003. DOI:10.3788/IRLA201847.0317003 |
| [4] |
白素琴, 史金龙, 钱强, 等. 采用可编程逻辑控制器的大型物体三维扫描重建[J]. 光学精密工程, 2017, 25(4): 1044. BAI Suqin, SHI Jinlong, QIAN Qiang, et al. 3D scanning and reconstruction of large objects based on PLC[J]. Optics and Precision Engineering, 2017, 25(4): 1044. DOI:10.3788/OPE.20172504.1044 |
| [5] |
吴庆阳, 曾增, 张佰春, 等. 一种新的360°三维测量系统及标定技术[J]. 中国激光, 2017, 44(4): 0404002. WU Qingyang, ZENG Zeng, ZHANG Baichun, et al. A 360° three-dimensional measurement system and its calibration[J]. Chinese Journal of Lasers, 2017, 44(4): 0404002. DOI:10.3788/cjl201744.0404002 |
| [6] |
CHEN Fang, BROWN G M, SONG Mumin. Overview of 3-D shape measurement using optical methods[J]. Optical Engineering, 2000, 39(1): 10. DOI:10.1117/1.602438 |
| [7] |
许幸芬, 曹益平, 彭旷, 等. 基于相位预测的在线三维测量像素匹配方法[J]. 光学学报, 2016, 36(6): 0612005. XU Xingfen, CAO Yiping, PENG Kuang, et al. On-line three-dimensional measurement based on phase prediction[J]. Acta Optica Sinica, 2016, 36(6): 0612005. DOI:10.3788/aos201636.0612005 |
| [8] |
李勇, 苏显渝, 吴庆阳. PMP系统中一种新的相位-高度映射算法[J]. 光电工程, 2007, 34(2): 79. LI Yong, SU Xianyu, WU Qingyang. New phase-height mapping algorithm in PMP system[J]. Opto-Electronic Engineering, 2007, 34(2): 79. DOI:10.3969/j.issn.1003-501X.2007.02.017 |
| [9] |
张旭, 李祥, 屠大维. 相位高度的显函数模型及其标定[J]. 光学精密工程, 2015, 23(8): 2384. ZHANG Xu, LI Xiang, TU Dawei. Explicit phase height model and its calibration[J]. Optics and Precision Engineering, 2015, 23(8): 2384. DOI:10.3788/OPE.20152308.2384 |
| [10] |
MAO Xianfu, CHEN Wenjing, SU Xianyu. Improved Fourier-transform profilometry[J]. Applied Optics, 2007, 46(5): 664. DOI:10.1364/AO.46.000664 |
| [11] |
陈雨婷, 曹益平, 陈澄, 等. 基于不等占空比二元光栅的相位测量轮廓术[J]. 光学学报, 2018, 38(8): 0815021. CHEN Yuting, CAO Yiping, CHEN Cheng, et al. Phase measurement profilometry based on binary gratings with Unequal Duty Cycle[J]. Acta Optica Sinica, 2018, 38(8): 0815021. DOI:10.3788/aos201838.0815021 |
| [12] |
ZHOU Duo, WANG Zhangying, GAO Nan, et al. Virtual fringe projection system with nonparallel illumination based on iteration[J]. Measurement Science&Technology, 2017, 28(6). DOI:10.1088/1361-6501/aa6597 |
| [13] |
李万松, 苏礼坤, 苏显渝. 相位检测面形术在大尺度三维面形测量中的应用[J]. 光学学报, 2000, 20(6): 792. LI Wansong, SU Likun, SU Xianyu. Phase-mapping profilometry in big scale measurement[J]. Acta Optica Sinica, 2000, 20(6): 792. DOI:10.3321/j.issn:0253-2239.2000.06.013 |
| [14] |
ZHOU W S, SU Xianyu. A direct mapping algorithm for phase-measuring profilometry[J]. Journal of Modern Optics, 1994, 41(1): 89-94. DOI:10.1080/09500349414550101 |
| [15] |
肖焱山, 曹益平, 武迎春. 条纹投影轮廓术中新的相位高度映射算法[J]. 中国激光, 2011, 38(12): 188. XIAO Yanshan, CAO Yiping, WU Yingchun. A new phase-to-height mapping algorithm in fringe projection profilometry[J]. Chinese Journal of Laser, 2011, 38(12): 188. DOI:10.3788/CJL201138.1208004 |
| [16] |
SRINIVASAN V, LIU H C, HALIOUA M. Automated phase-measuring profilometry of 3-D diffuse objects[J]. Applied Optics, 1984, 23(18): 3150. |
| [17] |
苏显渝, 李继陶, 曹益平, 等. 信息光学[M]. 2版. 北京科学出版社, 2011: 317. SU Xianyu, LI Jitao, CAO Yiping, et al. Information Optics[M]. Beijing: Science Press, 2011: 317. |
| [18] |
SPAGNOLO G S, GUATTARI G, SAPIA C, et al. Contouring of artwork surface by fringe projection and FFT analysis[J]. Optics&Lasers in Engineering, 2000, 33(2): 141. DOI:10.1016/s0143-8166(00)00023-3 |
 2020, Vol. 52
2020, Vol. 52


