2. 中国科学院大学, 北京 100049;
3. 重庆机电职业技术大学, 重庆 400036;
4. 贵州大学, 贵阳 550025
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Chongqing Vocational and Technical University of Mechatronics, Chongqing 400036, China;
4. Guizhou University, Guiyang 550025, China
日常生活中数字图像的使用量在互联网的飞速发展下保持爆炸式增长,图像压缩是解决数字图像高效存储以及在有限带宽下高效传输的关键技术之一.图像压缩去除图像中的冗余信息以较少的比特表示原来的像素矩阵,分为有损压缩与无损压缩两类[1].无损压缩如游程编码[2]、霍夫曼编码[3]等压缩率较低但不会造成数据失真,适用于医疗、军事等领域中使用的特定图像,要求高保真度与真实性.有损压缩如矢量量化[4]、分型图像压缩[5]、小波变换编码[6]、块截断编码[7]等,这些算法压缩率高但会产生失真效果,适用于日常工作、生活等领域中使用的一般图像,可接受一定数据失真.
块截断编码(Block Truncation Coding, BTC)是Mitchel等[7]提出的一种简单高效的有损灰度图像压缩算法,同时也广泛应用在图像检索[8]、数据隐藏[9]、图像认证[10]、数字水印[11]等领域.BTC将图像分成不重叠的子块,每个子块压缩为一个位图与两个量化值.为进一步降低BTC压缩灰度图像的失真效果,很多基于BTC的改进算法被提出,例如Mitchell等[12]提出的绝对矩块截断编码(Absolute Moment Block Truncation Coding, AMBTC)和L. Hui等[13]提出的自适应块截断编码等.对于彩色图像,直接使用传统的BTC算法需要对R, G, B通道平面进行处理,将每个图像块压缩为3个位图与6个量化值,压缩率偏低.Wu等[14]针对此问题提出了单位图块截断编码(Single Bitmap Block Truncation Coding, SBBTC),将R, G, B通道平面的位图压缩成一个公共位图,算法有效的提升了BTC的压缩率,但重构图像失真度较高,权重平面(Weighted Plane, W-plane)是其中一个简单有效的方法.基于Wu等[14]的工作,Tai等[15]提出基于Hopfield神经网络的单位图块截断编码,算法通过Hopfield神经网络优化生成公共位图,重构图像的失真度低于Wu等[14]的算法.随后,Tai等[16]又提出基于遗传算法的单位图块截断编码(GA-AMBTC),通过遗传算法优化生成公共位图,该算法重构图像的视觉质量优于之前的算法.之后,Chang等[17]提出基于渐进搜索的单位图块截断编码(GSBTC),Cui等[18]提出了基于猫群算法的单位图块截断编码(CSO-BTC).最近,Li等[19]提出基于二进制蚁群算法的单位图块截断编码(BACO-BTC),使用二进制蚁群算法优化生成公共位图.GSBTC与BACO-BTC计算量较低,但生成的公共位图为近似优化值,生成重构图像的质量难以达到最优效果,GA-AMBTC与CSO-BTC通过遗传算法与猫群算法可以得到最优值,但需要的算法迭代轮数较高.
烟花算法是谭营等[20]在2010年提出的群体智能优化算法,算法通过烟花的爆炸机制与变异机制平衡了局部搜索与全局搜索,具有较好的优化性能且应用广泛,如多模态函数优化[21]、复杂网络社区检测[22]等.为解决一些特殊离散问题,如多维背包问题[23]等,二进制形式烟花算法被提出.本文将烟花算法改进为二进制形式并结合W-plane方法,提出了基于二进制烟花算法的单位图块截断编码.与文献[23]中的二进制烟花算法不同,本文保留原始烟花算法对爆炸火花数目与爆炸半径的计算公式,在生成爆炸火花与高斯变异火花时均作了相应改进以提高算法的寻优效果.
1 相关理论 1.1 W-plane方法SBBTC是BTC的扩展,主要用于彩色图像的压缩.W-plane方法是一种传统的SBBTC方法,主要步骤如下:
1) 对彩色图像进行分块并计算每个块的像素均值.将图像分切成不重叠的子图像块,每个子图像块大小为m×m×3,由R, G, B通道平面构成,每个通道大小为m×m,m通常取4或8.用Rij, Gij, Bij分别表示子图像块中R, G, B通道平面在位置(i, j)处像素的灰度值,通过式(1)构造子图像块的权重平面并计算权重平面的像素均值w.
| $ \begin{array}{*{20}{c}} {{w_{ij}} = \frac{{{R_{ij}} + {G_{ij}} + {B_{ij}}}}{3},}\\ {\bar w = \frac{1}{{{m^2}}}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^m {{w_{ij}}} } .} \end{array} $ | (1) |
式中wij为权重平面在位置(i, j)处像素的灰度值;2)根据式(2),生成每个子图像块的公共位图,计算两个量化向量H,L.
| $ \begin{array}{*{20}{c}} {{b_{ij}} = \left\{ {\begin{array}{*{20}{l}} {1,{w_{ij}} \ge \bar w;}\\ {0,{w_{ij}} < \bar w.} \end{array}} \right.}\\ {\mathit{\boldsymbol{H}} = \frac{1}{q}\sum\limits_{{b_{ij}} = 1} {{\mathit{\boldsymbol{x}}_{ij}}} ,}\\ {\mathit{\boldsymbol{L}} = \frac{1}{{{m^2} - q}}\sum\limits_{{b_{ij}} = 0} {{\mathit{\boldsymbol{x}}_{ij}}} .} \end{array} $ | (2) |
式中xij=(Rij, Gij, Bij),q为公共位图中值为1元素的个数;
3)根据式(3)重构每个子图像块,通过子图像块组合成重构图像.
| $ {\mathit{\boldsymbol{c}}_{ij}} = \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{H}},}&{{b_{ij}} = 1;}\\ {\mathit{\boldsymbol{L}},}&{{b_{ij}} = 0.} \end{array}} \right. $ | (3) |
式中cij为重构子图像块在位置(i, j)处像素的灰度值向量.
1.2 烟花算法烟花算法有效地平衡了全局搜索与局部搜索,算法主要步骤如下:
1) 初始化N个烟花并评估每个烟花ri的适应度值,根据式(4)计算每个烟花的爆炸火花数目Si与爆炸半径Ai.
| $ \begin{array}{*{20}{c}} {{S_i} = {\rm{M}} \times \frac{{{y_{\max }} - f\left( {{r_i}} \right) + \varepsilon }}{{\sum\limits_{j = 1}^N {\left( {{y_{\max }} - f\left( {{r_j}} \right)} \right)} + \varepsilon }},}\\ {{A_i} = {\rm{\hat A}} \times \frac{{f\left( {{r_i}} \right) - {y_{\min }} + \varepsilon }}{{\sum\limits_{j = 1}^N {\left( {f\left( {{r_j}} \right) - {y_{\min }}} \right)} + \varepsilon }}.} \end{array} $ | (4) |
式中:M,
2) 根据Ai为每个烟花生成Si个爆炸火花,同时根据烟花生成一定数量高斯变异火花.
3) 将烟花、爆炸火花与高斯变异火花作为候选集,从中选择下一代N个烟花,候选集中适应度值最小的烟花被确定性选择为下一代烟花,其余N-1个烟花通过轮盘赌方法从候选集中选出.
4) 重复步骤1)~4)直到达到指定迭代轮数或满足预先设定的停止标准.
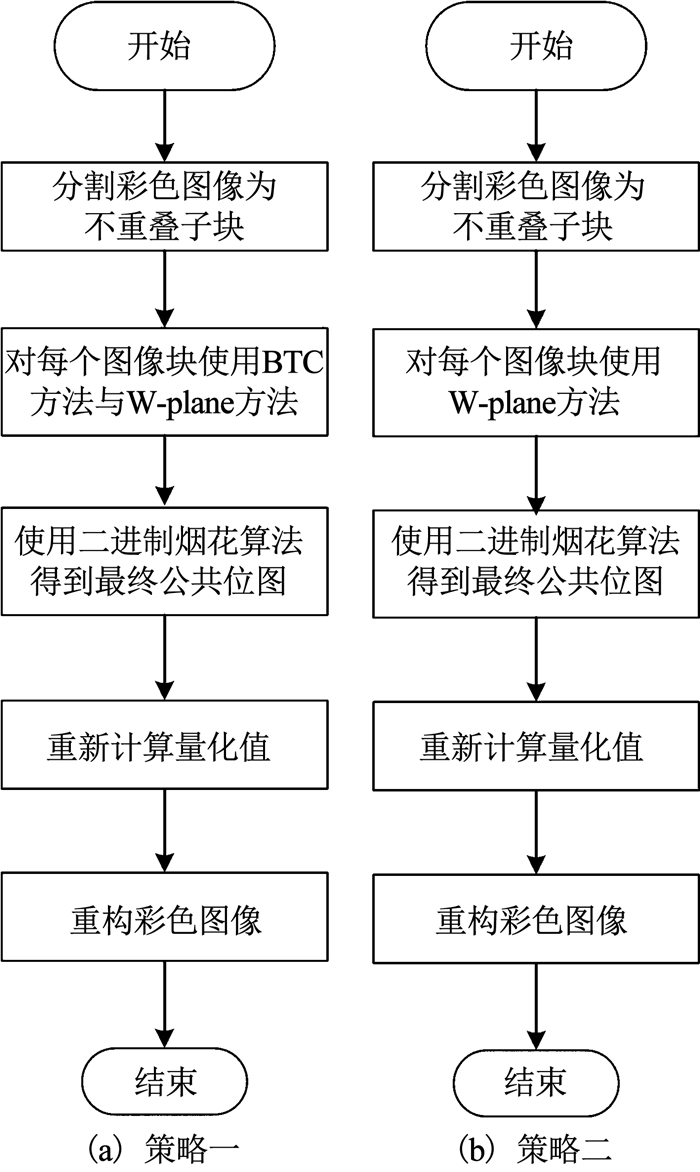
2 本文算法本文结合W-plane方法,基于二进制烟花算法提出了两种单位图块截断编码策略.两种策略的算法过程相互独立,各自得到的压缩图像精度不同,整体流程如图 1所示.两种策略主要区别在于子图像块预处理部分.策略一在处理子图像块时采用局部优化的思想,通过BTC方法确定公共位图中待优化元素.策略二采用全局优化的思想,将整个公共位图中的元素作为待优化元素.两种策略在得到待优化原素后,通过相同的优化方法与压缩方法对图像进行压缩与重构.
|
图 1 两种策略流程图 Fig. 1 Flow charts of the two strategies |
对于给定大小为M×N×3的彩色图像,将图像分成不重叠的子图像块,每个子图像块的大小为m×m×3,后续操作将在每个子图像块上进行.
2.2 子图像块预处理策略一采用局部优化思想对每个子图像块进行预处理.首先对子图像块R, G, B通道平面使用BTC方法得到相应的3个位图RP, GP, BP,根据式(5)生成子图像块初始公共位图BM并将其中值为α的元素个数记做nα,记录所有值为α元素的位置并将这些位置标记为L,同时将值为α的元素逐行记做长度为nα的向量s=(α, α, …, α).得到BM后,需对其中值为α的元素即s进行优化以生成最终公共位图,在进行优化之前先对s的值进行初始化.
| $ b_{ij}^{\rm{m}} = \left\{ {\begin{array}{*{20}{l}} {R_{ij}^{\rm{p}},R_{ij}^{\rm{p}} = G_{ij}^{\rm{p}} = B_{ij}^{\rm{p}};}\\ {\alpha ,{\rm{ else}}{\rm{. }}} \end{array}} \right. $ | (5) |
式中:bijm, Rijp, Gijp, Bijp为BM, RP, GP, BP在位置(i, j)处的值,α为自定义常数.
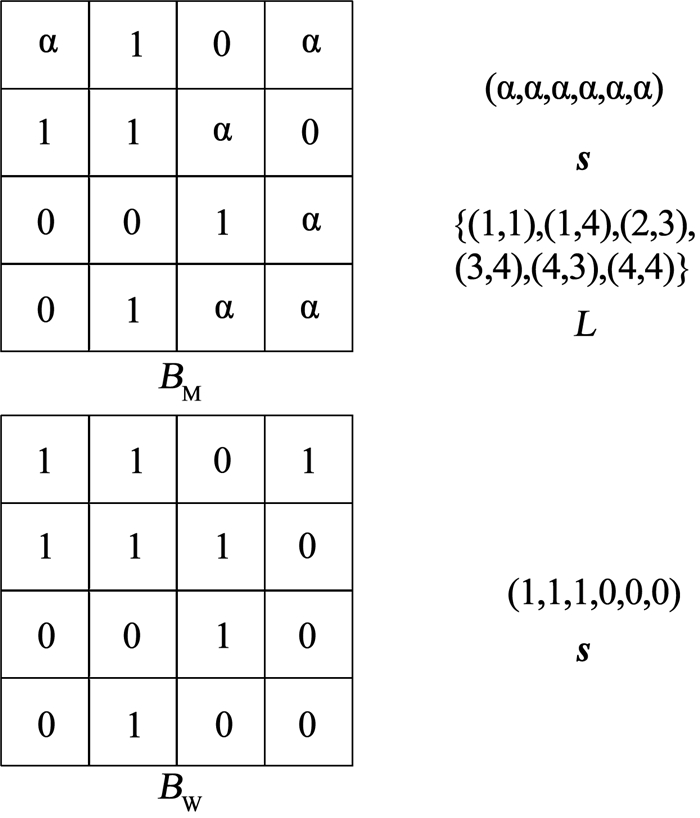
为保证初始化s不影响BM中其它元素值,策略一通过W-plane方法得到子图像块的位图BW,如图 2所示,使用BW中位置与L对应的nα个元素值初始化s.策略一使用W-plane方法初始化证明如下.
|
图 2 策略一初始化s示意 Fig. 2 Schematic diagram of initializing s for Strategy One |
令Wij, Rij, Bij, Gij为子图像块权重平面与R, G, B通道平面在位置(i, j)处像素的灰度值.W, R, B, G为图像块权重平面与R, G, B通道平面像素均值,通过式(6)计算.m×m为权重平面与通道平面大小.
| $ \bar R = \frac{1}{{{m^2}}}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^m {{R_{ij}}} } , $ |
| $ \bar G = \frac{1}{{{m^2}}}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^m {{G_{ij}}} } , $ |
| $ \bar B = \frac{1}{{{m^2}}}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^m {{B_{ij}}} } , $ |
| $ \begin{array}{*{20}{c}} {\bar W = \frac{1}{{{m^2}}}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^m {{W_{ij}}} } = }\\ {\frac{1}{{3{m^2}}}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^m {\left( {{R_{ij}} + {B_{ij}} + {G_{ij}}} \right)} } = \frac{1}{3}\left( {\bar R + \bar B + \bar G} \right).} \end{array} $ | (6) |
当
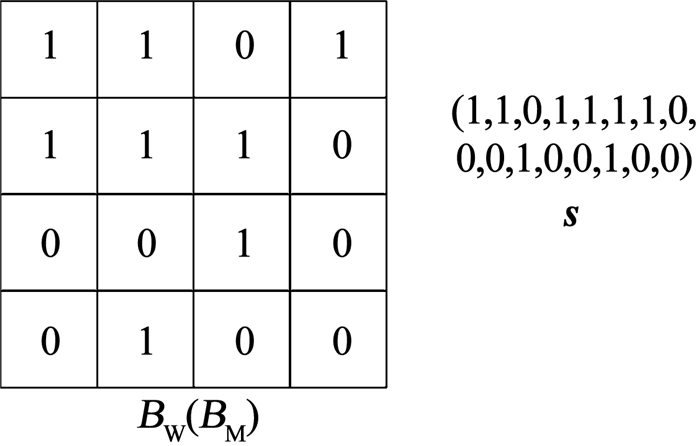
策略二采用全局优化思想对每个子图像块进行预处理.对子图像块使用W-plane方法得到权重平面的位图BW,并将其作为初始公共位图BM.如图 3所示,将BM元素逐行转换为向量s,向量长度为m2.
|
图 3 策略二初始化s示意 Fig. 3 Schematic diagram of initializing s for Strategy Two |
在子图像块预处理阶段得到向量s后,采用二进制烟花算法对s进行优化并得到其对应的位图与量化值.算法基于均方误差(Mean Squared Error, MSE)设计评价函数来计算每个烟花的适应度值,如式(7)所示.
| $ \begin{array}{*{20}{c}} {f\left( {{\mathit{\boldsymbol{X}}_i}} \right) = \sum\limits_{{T_{ij}} = 1} {\left( {{{\left( {{R_{ij}} - {c_{{\rm{RH}}}}} \right)}^2} + {{\left( {{G_{ij}} - {c_{{\rm{GH}}}}} \right)}^2} + } \right.} }\\ {\left. {{{\left( {{B_{ij}} - {c_{{\rm{BH}}}}} \right)}^2}} \right) + }\\ {\sum\limits_{{T_{ij}} = 0} {\left( {{{\left( {{R_{ij}} - {c_{{\rm{RL}}}}} \right)}^2} + } \right.} }\\ {\left. {{{\left( {{G_{ij}} - {c_{{\rm{GL}}}}} \right)}^2} + {{\left( {{B_{ij}} - {c_{{\rm{BL}}}}} \right)}^2}} \right).} \end{array} $ | (7) |
式中:Xi为烟花个体,Tij为Xi对应的位图TF在位置(i, j)处的值,cRH, cRL, cGH, cGL, cBH, cBL为Xi对应的6个量化值.
2.3.1 烟花种群初始化二进制烟花算法首先需要对烟花种群初始化.根据式(8)初始化N个烟花,烟花为二进制向量,维度为l.在策略一中,l的取值为nα,在策略二中,l的取值为m2.
| $ {\mathit{\boldsymbol{X}}_i} = \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{s}},i = 1;}\\ {d\left( {1,l} \right),2 \le i \le N.} \end{array}} \right. $ | (8) |
式中d()随机生成维度为l的二进制向量,Xi为烟花个体.
2.3.2 参数计算烟花种群初始化之后,计算每个烟花的适应度值与其生成的爆炸火花的数目、爆炸半径.
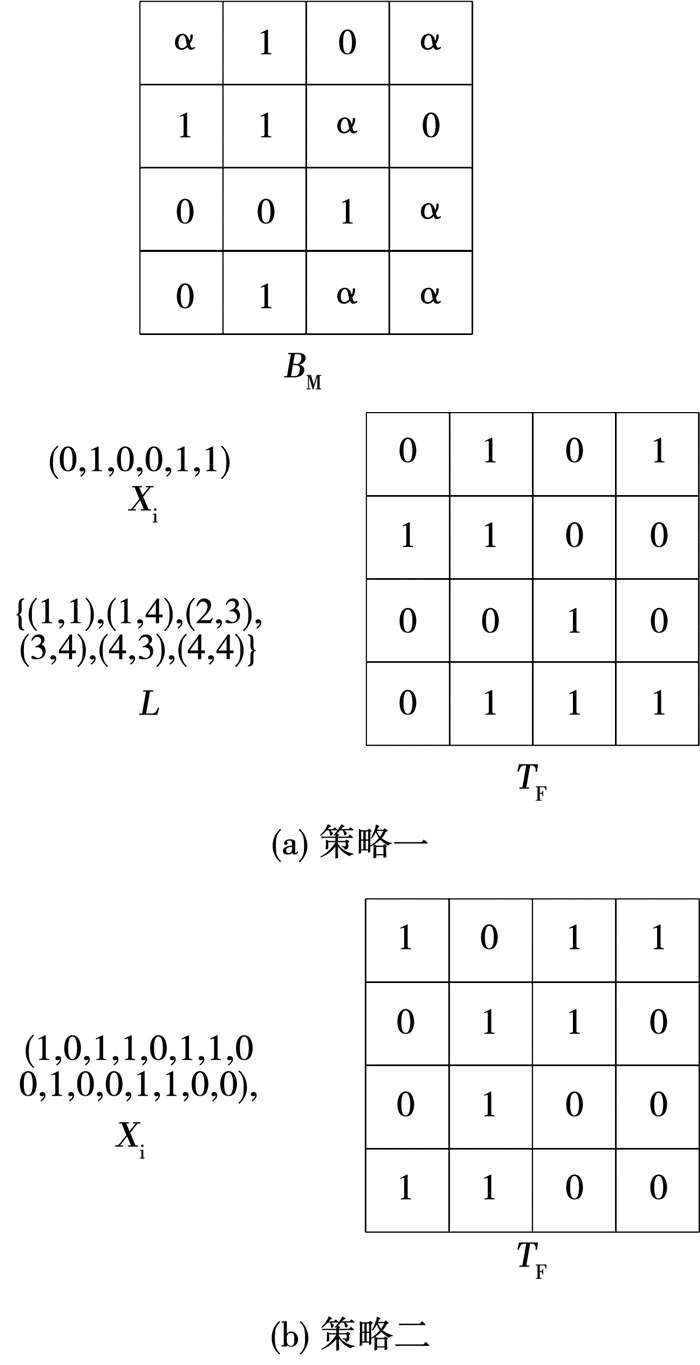
策略一将每个烟花的元素根据L记录的位置替换BM中值为α的元素,形成完整位图TF,见图 4(a).策略二将每个烟花按行生成完整位图TF, 见图 4(b).
|
图 4 完整位图生成过程 Fig. 4 Generation of the complete bitmap |
得到TF后,通过式(9)计算每个烟花对应的6个量化值cRH, cRL, cGH, cGL, cBH, cBL并根据式(7)计算每个烟花的适应度值.
| $ {c_{{\rm{RH}}}} = \left[ {\frac{1}{q}\sum\limits_{{T_{ij}} = 1} {{R_{ij}}} } \right],{c_{{\rm{RL}}}} = \left[ {\frac{1}{{{m^2} - q}}\sum\limits_{{T_{ij}} = 0} {{R_{ij}}} } \right], $ |
| $ {c_{{\rm{GH}}}} = \left[ {\frac{1}{q}\sum\limits_{{T_{ij}} = 1} {{G_{ij}}} } \right],{c_{{\rm{GL}}}} = \left[ {\frac{1}{{{m^2} - q}}\sum\limits_{{T_{ij}} = 0} {{G_{ij}}} } \right], $ |
| $ {c_{{\rm{BH}}}} = \left[ {\frac{1}{q}\sum\limits_{{T_{ij}} = 1} {{B_{ij}}} } \right],{c_{{\rm{BL}}}} = \left[ {\frac{1}{{{m^2} - q}}\sum\limits_{{T_{ij}} = 0} {{B_{ij}}} } \right]. $ | (9) |
式中q为TF中值为1元素的个数,[·]表示四舍五入取整.
得到每个烟花的适应度值后,通过式(10)计算每个烟花生成的爆炸火花数目Ai、爆炸半径Si.
| $ {A_i} = \left[ {\begin{array}{*{20}{c}} {{\rm{M}} \times \frac{{{y_{\max }} - f\left( {{\mathit{\boldsymbol{X}}_i}} \right) + \varepsilon }}{{\sum\limits_{j = 1}^N {\left( {{y_{\max }} - f\left( {{\mathit{\boldsymbol{X}}_j}} \right)} \right)} + \varepsilon }}} \end{array}} \right], $ |
| $ {S_i} = \left[ {l \times \frac{{f\left( {{\mathit{\boldsymbol{X}}_i}} \right) - {y_{\min }} + \varepsilon }}{{\sum\limits_{j = 1}^N {\left( {f\left( {{\mathit{\boldsymbol{X}}_j}} \right) - {y_{\min }}} \right)} + \varepsilon }}} \right] + 1. $ | (10) |
式中:M为固定常数50,ε是一个机器最小量,取值为2.220 4×e-16,ymax, ymin为当前烟花种群的最大适应度值与最小适应度值,l是Xi维度,在策略一中为nα,在策略二中为m2,[·]表示下界取整.
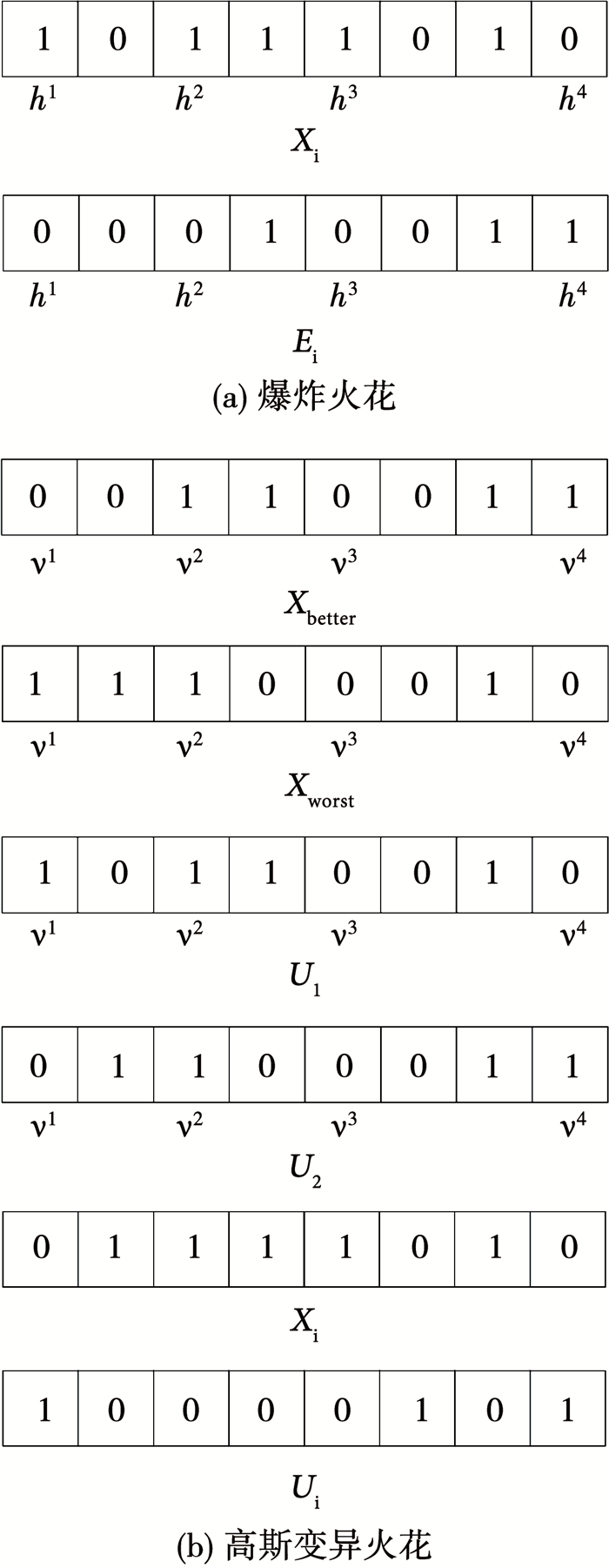
2.3.3 生成爆炸火花、高斯变异火花爆炸火花的生成见图 5(a),图中h表示爆炸范围记录.对每个烟花Xi,根据其爆炸半径Si随机生成Ai个爆炸范围,确定每个爆炸范围在Xi中的位置,对在爆炸范围内的元素通过式(11)进行变异得到Ai个爆炸火花E1, E2, …, EAi.
|
图 5 爆炸火花与高斯变异火花生成过程 Fig. 5 Generation of the sparks |
| $ {e_i} = \left\{ {\begin{array}{*{20}{l}} {\left| {{o_i} - 1} \right|,i \in h;}\\ {{o_i},{\rm{else}}{\rm{.}}} \end{array}} \right. $ | (11) |
式中:h为生成的爆炸范围,oi, ei为Xi与Ei在位置i处的元素值,|·|表示取绝对值.
高斯变异火花的生成如图 5(b)所示.通过N个烟花X1, X2, …, XN生成K个高斯变异火花U1, U2, …, UK,其中U1, U2由烟花中适应度值最大和最小的两个烟花Xbetter, Xworst根据随机产生的交叉范围记录v互换元素后生成,U3, …, UK由N个烟花中随机选取的K-2个烟花通过式(12)逐位变异生成.
| $ {u_i} = \left| {{o_i} - 1} \right|. $ | (12) |
式中ui为Ui在位置i处的元素值.
2.3.4 生成新一代烟花种群从烟花、爆炸火花和高斯变异火花中选取N个烟花作为新一代烟花种群.选出烟花、爆炸火花、高斯变异火花中适应度值最小的火花作为第1个新一代烟花,剩余N-1个新一代烟花使用轮盘赌方法从烟花、爆炸火花、高斯变异火花中选择.
2.3.5 输出优化值算法重复步骤2)~4),达到指定的迭代轮数niter后,将适应度值最小的烟花Xbest作为s的优化值,并输出与及与其对应的完整位图TF和6个量化值cRH, cRL, cGH, cGL, cBH, cBL.不同的niter会生成不同质量的Xbest,从而生成不同精度的压缩图像.如图 9所示,两种策略生成的压缩图像与原图之间的结构相似性指数(Structural Similarity Index, SSIM)值初期会随着迭代轮数的增加而提升.当算法迭代一定轮数后,两种策略生成的压缩图像与原图之间的SSIM会逐渐收敛,达到一个稳定值.从图 9(a)可看出,当分块大小为4×4时,策略一与策略二在迭代10轮后均达到收敛状态.从图 9(b)可看出,当分块大小为8×8时,策略一在迭代30轮后达到收敛状态,策略二在迭代35轮后达到收敛状态.由于分块大小为8×8时算法对应的搜索空间要大于4×4时搜索空间,因此在图 9中,策略一与策略二在分块大小为8×8时,达到收敛状态所需要的迭代轮数要多于分块大小为4×4时的迭代轮数.同时由于策略二为全局搜索方法,策略一为局部搜索方法,因此策略二中的搜索空间要大于策略一中的搜索空间,即策略二达到收敛状态所需的迭代轮数要高于策略一.
2.4 重构图像根据完整位图TF和6个量化值cRH, cRL, cGH, cGL, cBH, cBL,通过式(13)恢复子图像块.图 6为恢复子图像块的例子,其中cRH, cRL, cGH, cGL, cBH, cBL分别为235, 226, 182, 156, 255, 250.在恢复所有子图像块后,将所有子图像块组合成重构图像.
| $ R_{ij}^{\rm{r}} = \left\{ {\begin{array}{*{20}{l}} {{c_{{\rm{RH}}}},}&{{T_{ij}} = 1;}\\ {{c_{{\rm{RL}}}},}&{{T_{ij}} = 0,} \end{array}} \right. $ |
| $ G_{ij}^{\rm{r}} = \left\{ {\begin{array}{*{20}{l}} {{c_{{\rm{GH}}}},\quad {T_{ij}} = 1;}\\ {{c_{{\rm{GL}}}},\quad {T_{ij}} = 0,} \end{array}} \right. $ |
| $ B_{ij}^{\rm{r}} = \left\{ {\begin{array}{*{20}{l}} {{c_{{\rm{BH}}}},\quad {T_{ij}} = 1;}\\ {{c_{{\rm{BL}}}},\quad {T_{ij}} = 0.} \end{array}} \right. $ | (13) |
式中Rijr, Gijr, Bijr为重构子图像块中R, G, B通道平面在位置(i, j)处像素的灰度值.

|
图 6 子图像块恢复过程 Fig. 6 Recovery process of the blocks |
本文所提算法与W-plane、GA-AMBTC、GSBTC、BACO-BTC等算法都是对SBBTC压缩图像精度的改进,该算法在压缩比方面与SBBTC保持一致,因此本文的实验分析主要采用多种算法在压缩图像精度方面进行详尽对比分析.
仿真实验在MATLAB 2016a环境下完成,实验平台CPU为Inter Core i5 3.0 GHz,16 GB RAM.算法实验参数如表 1所示,使用测试图片如图 7所示,均为512×512的彩色图像,所有实验结果均取自算法运行10次后的均值.
| 表 1 实验参数 Tab. 1 Experiment parameters |

|
图 7 测试图片 Fig. 7 Test images |
本文所提算法是在W-plane方法[14]上的改进,为验证算法有效性,首先将两种策略与W-plane方法在图 7中测试图片上的结果进行比较.表 2、表 3分别为分块大小4×4与8×8时两种策略与W-plane方法生成压缩图像与原图的MSE,从表中实验结果可以看出两种策略的MSE均小于W-plane方法,表明所提算法的改进有效.
| 表 2 两种策略与W-plane重构图像MSE比较(4×4) Tab. 2 MSE for images reconstructed by W-plane method and two proposed schemes with block size 4×4 |
| 表 3 两种策略与W-plane重构图像MSE比较(8×8) Tab. 3 MSE for images reconstructed by W-plane method and two proposed schemes with block size 8×8 |
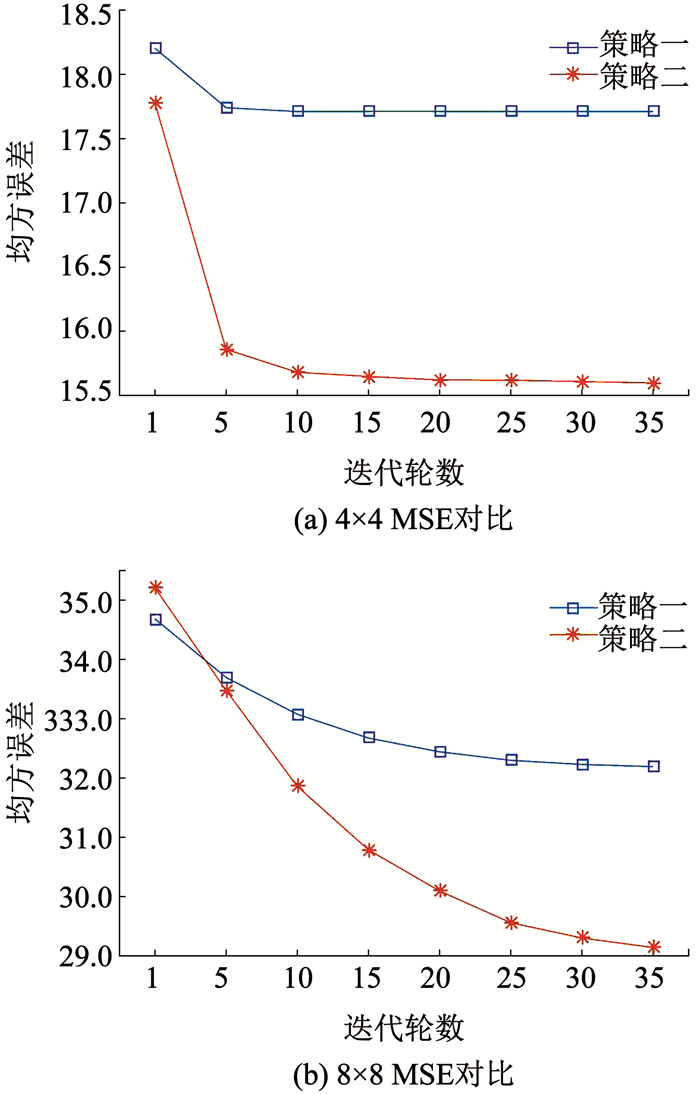
表 2、表 3中实验结果显示策略二生成压缩图像与原图之间的MSE小于策略一,为验证两种策略效果,将两种策略对图Fruits同时迭代35轮进行对比.图 8(a)为分块大小4×4时的MSE对比图,可以看出策略二MSE整体优于策略一,图 8(b)为分块大小8×8时的MSE对比图,策略二在最初几轮迭代中MSE高于策略一,接近第5轮迭代后策略二MSE值逐步小于策略一.
|
图 8 两种策略MSE对比 Fig. 8 Comparison of the MSE of the two strategies |
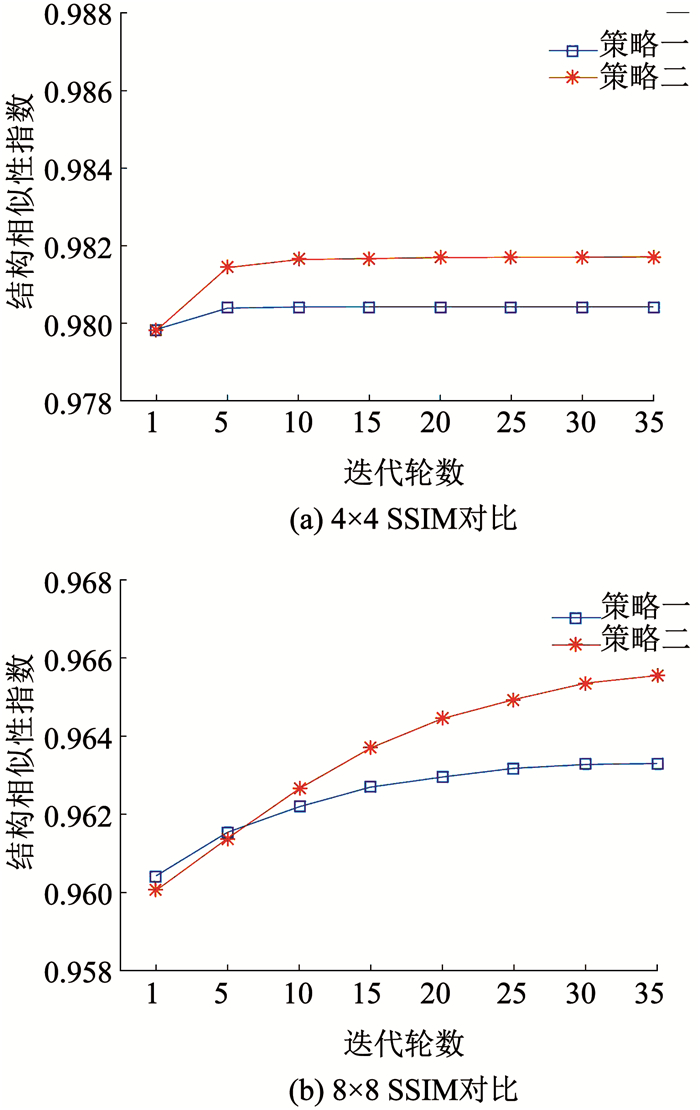
结构相似性指数(Structural Similarity Index, SSIM)用于衡量两张图片的相似度.图 9为两种策略生成压缩图与原图之间的SSIM对比图,图 9(a)的分块大小为4×4,其中策略二SSIM整体高于策略一,图 9(b)分块大小为8×8,其中策略二初始优化时SSIM略差于策略一,在迭代几轮后SSIM高于策略一.从对比结果可以看出,策略一由于采用局部优化的思想,优化位数少于策略二,因此策略一在迭代一定轮数后陷入局部最优,效果无法进一步提升,最终优化结果与策略二相比较差.
|
图 9 两种策略SSIM对比 Fig. 9 Comparison of the SSIM of the two strategies |
进一步验证文中所提算法有效性,将两种策略与GA-AMBTC[16]、GSBTC[17]、BACO-BTC[19]这3算法在图 7测试图片上的结果进行对比,其中GA-AMBTC染色体数目设为12,迭代轮数与本文算法相同,均为20轮,其余参数与文献[16]中一致.
图 11至图 14为文中所提两种策略与3种对比算法的压缩图局部区域对比,局部区域为Frymire中分别选取图的两块子图,即图 10中两个白色框选中的部分,图 11与图 12中各类算法的分块大小为4×4,图 13、14中各类算法的分块大小为8×8.由图 11可看出GA-AMBTC、BACO-BTC、策略一、策略二的压缩图视觉效果接近原图,其中策略二的噪点相比其它3种方法更少,图 12中GA-AMBTC、策略一、策略二的压缩图视觉效果与原图更为接近且3者视觉效果大致相同.由于图 13、14中实验选择的分块大小为8×8,因此各种方法得到的压缩图存在较明显的块效应,从图 13可看出GA-AMBTC、BACO-BTC、策略一、策略二与原图接近,其中策略二对于原图的细节保留更多,图 14可见GA-AMBTC、策略一、策略二的压缩图视觉效果优于其它两种,对原图的还原度更高.图 11至图 14表明相对与其它3种方法和策略一,策略二得到的压缩图对原图的细节保留度较好,压缩图与原图间的相似度更高,即本文算法有效,得到的位图与量化值更优.

|
图 10 视觉效果测试 Fig. 10 Test image for visual comparison |

|
图 11 细节对比图一(4×4) Fig. 11 Detail comparison diagram with block size 4×4 on area one |

|
图 12 细节对比图二(4×4) Fig. 12 Detail comparison diagram with block size 4×4 on area two |

|
图 13 细节对比图一(8×8) Fig. 13 Detail comparison diagram with block size 8×8 on area one |

|
图 14 细节对比图二(8×8) Fig. 14 Detail comparison diagram with block size 8×8 on area two |
表 4~表 7为图 7中所示测试图与通过文中所提两种策略和3种对比算法进行压缩后的压缩图之间的MSE与SSIM值,各类算法的分块大小在表 4、表 6中为4×4,在表 5、表 7中为8×8.
| 表 4 5种方法重构图像MSE比较(4×4) Tab. 4 MSE for images reconstructed by the five schemes with block size 4×4 |
| 表 5 5种方法重构图像MSE比较(8×8) Tab. 5 MSE for images reconstructed by the five schemes with block size 8×8 |
| 表 6 5种方法重构图像SSIM比较(4×4) Tab. 6 SSIM for images reconstructed by the five schemes with block size 4×4 |
| 表 7 5种方法重构图像SSIM比较(8×8) Tab. 7 SSIM for images reconstructed by the five schemes with block size 8×8 |
表 4中,策略一在测试图Pepper和Fruits上的MSE比BACO-BTC略高,平均MSE比3种对比算法略低,策略二MSE在整体上都低于其它算法.表 5中策略一在测试图Pepper、Fruits、Tiffany、Lenna上的MSE高于BACO-BTC,在测试图Tiffany上的MSE高于GA-AMBTC,平均MSE略低于3种对比算法,策略二MSE在整体上都低于其它算法.表 4与表 5结果表明本文所提策略二在相同迭代轮数下优于GA-AMBTC,同时优于策略一与其它两种对比算法.
表 6中策略一与策略二的SSIM值整体上都优于其它算法,表 7中策略一在测试图Fruits、Tiffany、Lenna上SSIM低于BACO-BTC,在测试图Tiffany上SSIM低于GA-AMBTC,策略二在测试图Tiffany上SSIM低于GA-AMBTC,两种策略在测试图上的平均SSIM均高于3种对比算法.表 6、7结果表明本文所提算法重构图像与原图的相似度高于其它算法,即本文所提算法有效且重构图像效果要好于3种对比算法.
4 结论本文针对彩色图像压缩需求,提出了一种基于二进制烟花算法的单位图块截断编码方法.该方法结合块截断编码特点将烟花算法改为二进制形式,以W-plane方法公共位图中的部分位与全部位作为初始化,采用局部优化与全局优化的思想进行两种不同的优化得到彩色图像的公共位图,在保证压缩比不变下提升重构图像与原图之间的相似度.实验结果表明,该方法可以有效地降低重构图像的失真度,提高重构图像的视觉质量.所提方法属于有损压缩,对不同大小和类型的彩色图像均可通过调整图像分块标准与子图像块大小来实现有效压缩.未来可在方法的子图像块预处理方面将两种策略进行融合,同时在优化算法方面进行简化改进,以提升算法整体效率.
| [1] |
RABBANI M, JONES P W. Digital image compression techniques[M]. Bellingham, Washington: SPIE, 1991: 6.
|
| [2] |
ROBINSON A H, CHERRY C. Results of a prototype television bandwidth compression scheme[J]. Proceedings of the IEEE, 1967, 55(3): 356. DOI:10.1109/PROC.1967.5493 |
| [3] |
HUFFMAN D A. A method for the construction of minimum-redundancy codes[J]. Proceedings of the IRE, 1952, 40(9): 1098. DOI:10.1109/JRPROC.1952.273898 |
| [4] |
GOLDBERG M, BOUCHER P, SHLIEN S. Image compression using adaptive vector quantization[J]. IEEE Transactions on Communications, 1986, 34(2): 180. DOI:10.1109/TCOM.1986.1096503 |
| [5] |
FISHER Y. Fractal image compression[J]. Fractals, 1994, 2(3): 347. DOI:10.1142/S0218348X94000442 |
| [6] |
ANTONINI M, BARLAUD M, MATHIEU P, et al. Image coding using wavelet transform[J]. IEEE Transactions on Image Processing, 1992, 1(2): 205. |
| [7] |
DELP E, MITCHELL O. Image compression using block truncation coding[J]. IEEE Transactions on Communications, 1979, 27(9): 1335. DOI:10.1109/TCOM.1979.1094560 |
| [8] |
GUO Jingming, PRASETYO H. Content-based image retrieval using features extracted from half-toning-based blocktruncation coding[J]. IEEE Transactions on Image Processing, 2014, 24(3): 1010. DOI:10.1109/TIP.2014.2372619 |
| [9] |
SUN Wei, LU Zheming, WEN Yuchun, et al. High performance reversible data hiding for block truncation coding compressed images[J]. Signal, Image and Video Processing, 2013, 7(2): 297. DOI:10.1007/s11760-011-0238-4 |
| [10] |
LIN Chiachen, HUANG Yuehong, TAI Weiliang. A novel hybrid image authentication scheme based on absolute moment block truncation coding[J]. Multimedia Tools and Applications, 2017, 76(1): 463. DOI:10.1007/s11042-015-3059-6 |
| [11] |
谢琨, 曾平, 郑海红, 等. 利用自适应有序抖动块截断编码的鲁棒水印[J]. 西安电子科技大学学报(自然科学版), 2015, 42(3): 198. XIE Kun, ZENG Ping, ZHENG Haihong, et al. Robust watermarking utilizing adaptive order dither block truncation coding[J]. Journal of Xidian University, 2015, 42(3): 198. DOI:10.3969/j.issn.1001-2400.2015.03.033 |
| [12] |
LEMA M, MITCHELL O. Absolute moment block truncation coding and its application to color images[J]. IEEE Transactions on Communications, 1984, 32(10): 1148. DOI:10.1109/tcom.1984.1095973 |
| [13] |
HUI Lucas. An adaptive block truncation coding algorithm for image compression[C]//Proceedings of International Conference on Acoustics, Speech, and Signal Processing.[S.l.]: IEEE, 1990: 2233
|
| [14] |
WU Yiyan, COLL D C. Single bitmap block truncation coding of color images[J]. IEEE Journal on Selected Areas in Communications, 1992, 10(5): 952. DOI:10.1109/49.139000 |
| [15] |
TAI Shenchuan, LIN Yihchuan, LIN Jungfeng. Single bitmap block truncation coding of color images using a Hop-field neural network[J]. Information Sciences, 1997, 103(1-4): 211. DOI:10.1016/S0020-0255(97)00054-6 |
| [16] |
TAI Shenchuan, CHEN Wenjan, CHENG Pojen. Genetic algorithm for single bitmap absolute moment block truncation coding of color images[J]. Optical Engineering, 1998, 37(9): 2483. DOI:10.1117/1.601772 |
| [17] |
CHANG Chinchen, WU Mingni. An algorithm for color image compression base on common bitmap block truncation coding[C]//Proceedings of the 6th Joint Conference on Information Science. North Carolina: Association for Intelligent Machinery (AIM), 2002: 964
|
| [18] |
CUI Shiyu, WANG Zhihui, TSAI Peiwei, et al. Single bitmap block truncation coding of color images using cat swarm optimization[M]. Berlin: Springer, 2013: 119.
|
| [19] |
LI Zhihong, JIN Qiang, CHANG Chinchen, et al. A common bitmap block truncation coding for color images based on binary ant colony optimization[J]. KSII Transactions on Internet and Information Systems (TIIS), 2016, 10(5): 2326. DOI:10.3837/tiis.2016.05.020 |
| [20] |
TAN Ying, ZHU Yuanchun. Fireworks algorithm for optimization[C]//Proceedings of International Conference in Swarm Intelligence. Berlin, Heidelberg: Springer, 2010: 355
|
| [21] |
LI Junzhi, TAN Ying. Loser-out tournament-based fireworks algorithm for multimodal function optimization[J]. IEEE Transactions on Evolutionary Computation, 2017, 22(5): 679. DOI:10.1109/TEVC.2017.2787042 |
| [22] |
GUENDOUZ M, AMINE A, HAMOU R M. A discrete modified fireworks algorithm for community detection in complex networks[J]. Applied Intelligence, 2017, 46(2): 373. DOI:10.1007/s10489-016-0840-9 |
| [23] |
薛俊杰, 王瑛, 孟祥飞, 等. 二进制反向学习烟花算法求解多维背包问题[J]. 系统工程与电子技术, 2017, 39(2): 451. XUE Junjie, WANG Ying, MENG Xiangfei, et al. Binary opposite backward learning fireworks algorithm for multidimensional knapsack problem[J]. Systems Engineering and Electronics, 2017, 39(2): 451. DOI:10.3969/j.issn.1001-506X.2017.02.33 |
 2020, Vol. 52
2020, Vol. 52


