2. 重庆邮电大学 通信与信息工程学院, 重庆 400065
2. School of Communication and Information Engineering, Chongqing University of Posts and Telecommunications, Chongqing 400065, China
分数阶微积分已有300多年的历史,自然界的物理现象大多以分数阶的形式存在,整数阶微分方程正好是分数阶微分方程的特例.与整数阶模型相比,分数阶模型更接近真实的世界,具有更诱人的发展前景,近年来已得到了越来越多的关注[1-2].值得注意的是,与只有固定翼混沌吸引子的分数阶混沌系统相比,具有多种多翼混沌吸引子共存的分数阶混沌系统显示出更复杂的动力学行为和更好的性能[3-4].在安全通信[5]和图像加密[6]中,此类分数阶混沌系统具有更高的序列复杂度以及更大的密钥空间,提高了系统安全性能.因此,发现和构造具有多种多翼混沌吸引子共存的低维分数阶混沌系统具有更大的价值.Zhou等人基于四翼整数阶忆阻混沌系统,构造了相应的分数阶忆阻系统,出现三翼与三翼、三翼与四翼混沌吸引子的共存[7];Borah和Roy设计了一种新的分数阶混沌系统,此系统具有三翼和四翼混沌吸引子共存[8];Xian等人构造了一个双翼与四翼混沌吸引子共存的分数阶混沌系统[9].目前,构造具有更多种多翼混沌吸引子共存的分数阶混沌系统仍然存在一定挑战.在已有文献中,能够产生双翼到四翼混沌吸引子共存的三维分数阶混沌系统还比较少见.
本文设计了一个新型三维分数阶混沌系统,对其进行了动力学分析.在q=0.98时,出现双翼、双翼、四翼等混沌吸引子的共存;q=0.83时,出现双翼、三翼、四翼等混沌吸引子的共存,表明系统具有丰富的混沌特性.与文献[10]和文献[11]相比,此系统不存在不光滑的非线性函数,更易于用硬件电路实现.对系统进行了Multisim模拟电路设计和仿真,仿真结果与数值分析相符,进一步验证了系统的混沌行为.基于分数阶Lyapunov稳定理论,设计了一个自适应同步控制器,仿真结果表明了所设计控制器的有效性.
1 系统模型及其特性 1.1 分数阶系统模型增广Lü系统[12]状态方程为
| $ \left\{ {\begin{array}{*{20}{l}} {\dot x = - (bc/(b + c))x - yz + d,}\\ {\dot y = by + xz,}\\ {\dot z = cz + xy.} \end{array}} \right. $ | (1) |
将式(1)中第一个方程右边添加非线性项-kx-9yz-d,第3个方程右边添加非线性项-9xy+y2.再根据Caputo分数阶积分定义,构建了一个新型三维分数阶混沌系统,系统状态方程为
| $ \left\{ {\begin{array}{*{20}{l}} {{D^q}x = - ax - 10yz,}\\ {{D^q}y = bx + xz,}\\ {{D^q}z = cz - 8xy + {y^2}.} \end{array}} \right. $ | (2) |
式中:x,y,z为系统状态变量,a,b为系统参数,q为系统阶数.
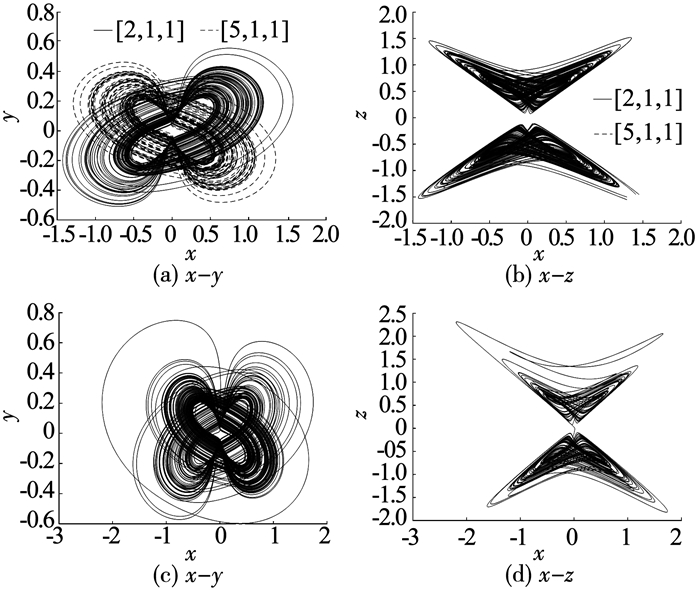
固定参数a=2,b=1,c=-0.78,取q=0.98,其最大Lyapunov指数(MAXLE)为1.065 96.利用预估-校正数值计算方法[13],结合matlab软件,得到系统的仿真相图.初始值为[2, 1, 1]、[5, 1, 1]和[6, 1, 1]时,分别得到两个孤立的双翼混沌吸引子和一个四翼混沌吸引子,其x-y面和y-z面如图 1所示.其中,图 1(a)和(b)中的蓝色部分为初始值[2, 1, 1]诱发的双翼混沌吸引子,红色部分为初始值[5, 1, 1]诱发的四翼混沌吸引子.
|
图 1 q=0.98时系统的相 Fig. 1 Phase diagram of the system at q=0.98 |
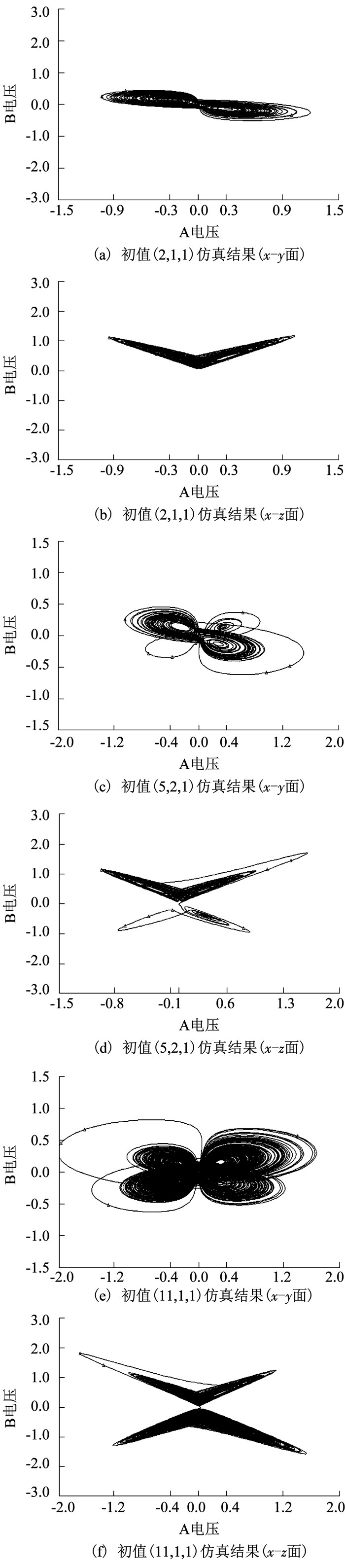
取q=0.83,其MAXLE为1.494 3.初始值为[2, 1, 1]、[5, 2, 1]和[11, 1, 1]时,分别得到双翼、三翼和四翼混沌吸引子,其x-y面和y-z面如图 2所示.

|
图 2 q=0.83时系统的相 Fig. 2 Phase diagram of the system at q=0.83 |
由此可见,系统阶数q=0.98时,系统有双翼、双翼、四翼等混沌吸引子共存;q=0.83时,系统有双翼、三翼、四翼等混沌吸引子共存,表明了阶数q对系统的混沌特性具有较大影响.
1.2 平衡点及其稳定性参数不变,令系统(2)方程式的左边等于0,即
| $ \left\{ {\begin{array}{*{20}{l}} {0 = - 2x - 10yz,}\\ {0 = y + xz,}\\ {0 = - 0.78z - 8xy + {y^2}.} \end{array}} \right. $ | (3) |
求得平衡点,如表 1所示.
| 表 1 系统的平衡点 Tab. 1 Equilibrium points of the system |
在平衡点
| $ \mathit{\boldsymbol{J}} = \left[ {\begin{array}{*{20}{c}} { - 2}&{ - 10\hat z}&{ - 10\hat y}\\ {\hat z}&1&{\hat x}\\ { - 8\hat y}&{2\hat y - 8\hat x}&{ - 0.78} \end{array}} \right]. $ |
令det(λE-J)=0,得到其特征多项式为
| $ f\left( \lambda \right) = {\lambda ^3} + {A_2}{\lambda ^2} + {A_1}\lambda + {A_0}. $ | (4) |
其中
| $ {A_2} = 1.78, $ |
| $ {A_1} = 8{{\hat x}^2} + 10{{\hat z}^2} - 80{{\hat y}^2} - 2\hat x\hat y - 1.22, $ |
| $ {A_0} = 16{{\hat x}^2} + 80{{\hat y}^2} + 7.8{{\hat z}^2} + 20{{\hat y}^2}\hat z - 4\hat x\hat y - 160\hat x\hat y\hat z - 1.56. $ |
若平衡点稳定,其特征值满足Re[λ] < 0.依据Routh-Hurwitz判据,当且仅当A2>0,A0>0,A2A1-A0>0时,平衡点稳定[14-15].求得每个平衡点所对应的特征值及平衡点的稳定性如表 2所示.
| 表 2 系统的平衡点稳定性 Tab. 2 Stability of equilibrium points of systems |
表 2表明,平衡点S1是第一类鞍点,S0,S2,S3和S4是第二类鞍点.混沌吸引子的环围绕第二类鞍点产生,第一类鞍点起到连接环的作用[16-17].
设λ是第二类鞍点的共轭复根,为使分数阶系统存在混沌吸引子,λ必须保持在不稳定区域.由文献[18]可得,需满足
| $ \left| {\arg \left( \lambda \right)} \right| < 0.5{\rm{ \mathit{ π} }}q. $ | (5) |
其中arg(λ)是特征值λ的辐角,所以有
| $ q > \frac{2}{{\rm{ \mathit{ π} }}}\left| {\arg \left( \lambda \right)} \right|. $ | (6) |
由此,a=2,b=1,c=-0.78时,可得分数阶系统(2)存在混沌吸引子的必要条件,即q>0.822 4.
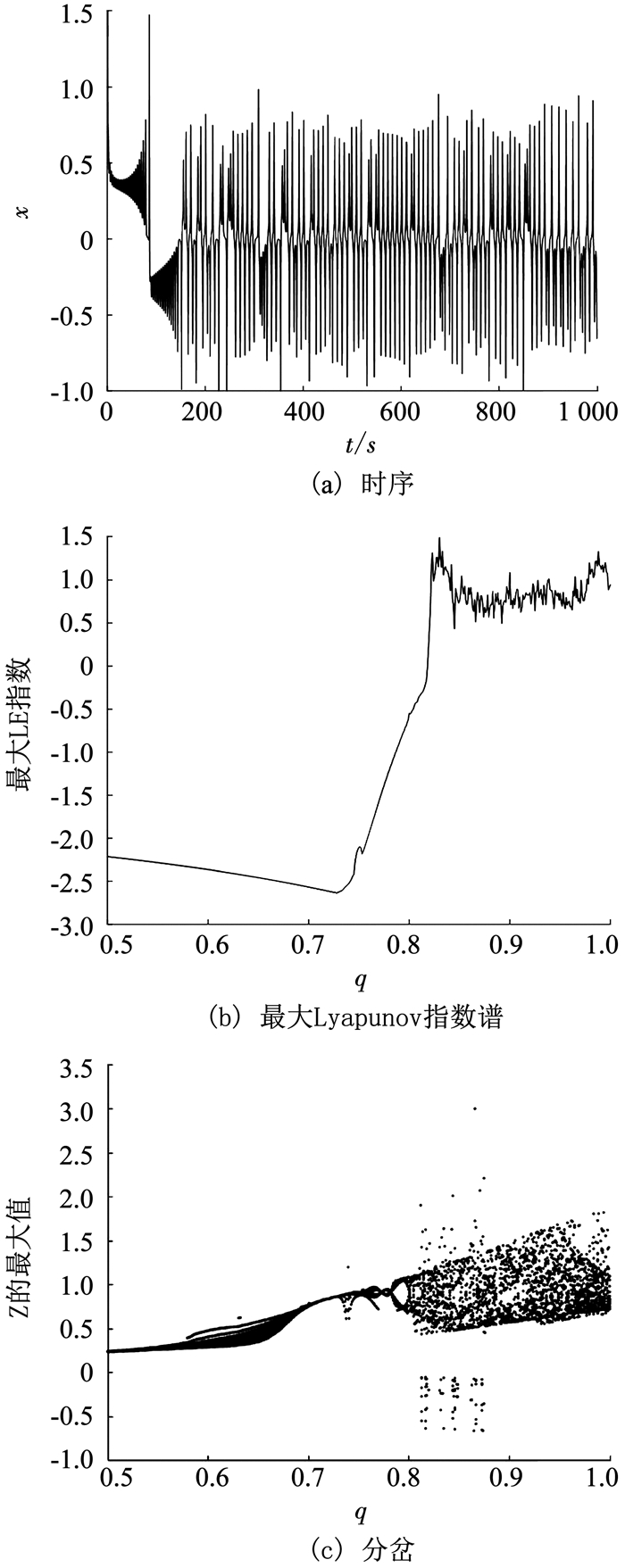
1.3 时序图参数不变,取q=0.83, 初始值为[5, 2, 1],得到相应的时序图,如图 3(a)所示,从图中能直观地看出系统的混沌行为.
|
图 3 系统的基本动力学分析 Fig. 3 Basic dynamics analysis of the system |
系统阶数的变化会改变平衡点的稳定性, 引起系统状态的变化.参数不变,选择阶数q为控制变量.采用Adams-Bashforth-Moulton数值算法的改进版本[19],初始值为[5, 2, 1]时,得到系统变量z随系统阶数q变化的最大Lyapunov指数谱和分岔图,如图 3(b)和图 3(c)所示.最大Lyapunov指数谱和分岔图可以比较直观地反映非线性动力学系统随阶数变化的动态特性.当最大Lyapunov指数>0的时候,系统处于混沌状态.由图 3(c)可知,当q∈ [0.5,0.819]时,系统处于周期状态;当q∈(0.819,1]时,系统处于混沌状态.q从0.5向1增加的过程中,结合图 3(c)可知,系统通向混沌的道路为倍周期分岔道路,进一步验证了q对系统具有较大影响.
2 系统的电路仿真参数不变,取初始值为[5, 2, 1],根据文献[20],当q=0.83时,分数阶算子逼近
| $ H\left( s \right) = \frac{{3.1869\left( {s + 0.1981} \right)(s + 5.181)(s + 87.72)}}{{(s + 0.01324)(s + 0.299)(s + 6.792)(s + 153.8)}}. $ | (7) |
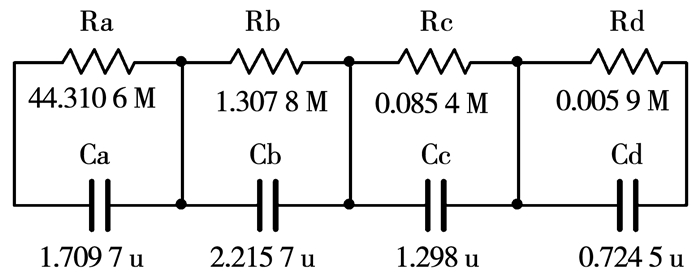
文献[19]中的分数阶等效串并联RC模块电路单元如图 4所示.
|
图 4 分数阶算子的等效电路模块 Fig. 4 Equivalent circuit module of the fractional order operator |
其中Ra=44.310 6 MΩ,Rb=1.307 8 MΩ,Rc=0.085 4 MΩ,Rd=0.005 9 MΩ,Ca=1.709 7 μF,Cb=2.215 7 μF,Cc=1.298 μF,Cd=0.724 5 μF.
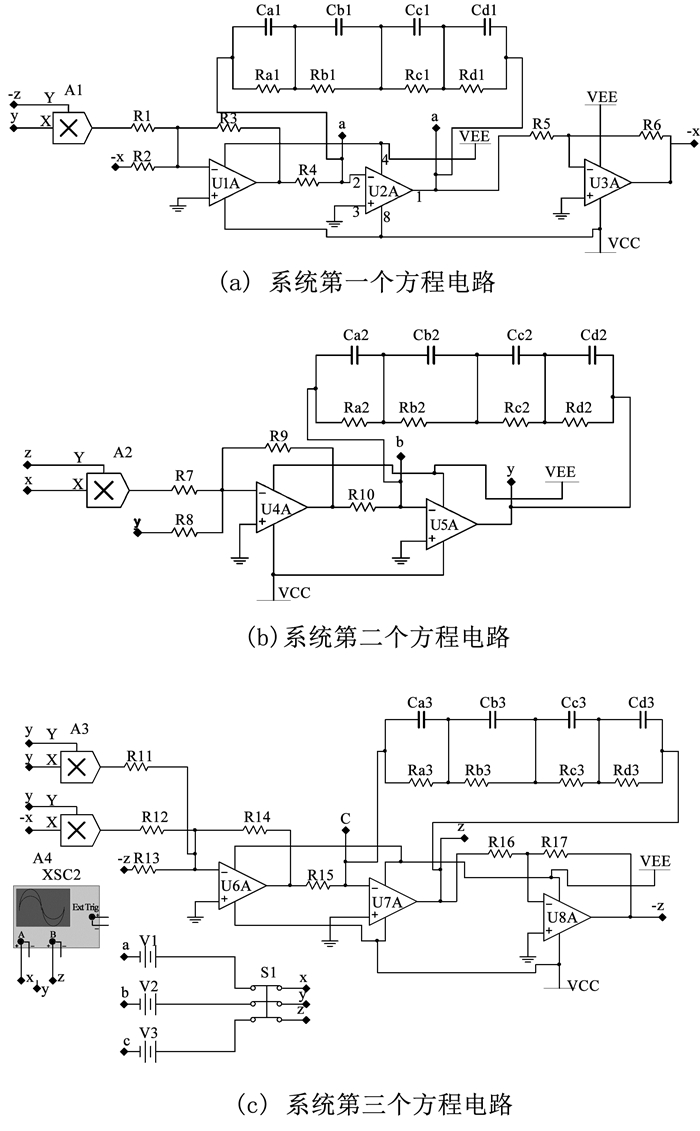
采用线性电阻、电容、LM2924N型运算放大器、MULTIPLIER模拟乘法器,其中乘法器的输出增益为1,从而设计出了系统的模拟电子电路,如图 5所示.运算放大器U1A相当于加法器,其输出端电压为vU1A=-(R3/R2)x-(R3/R1)yz,U2A相当于积分器,利用分数阶算子单元模块,得到
|
图 5 系统的电路原理 Fig. 5 Circuit schematic diagram of the system |
| $ {D^{0.83}}x = {v_{{\rm{U1A}}}} = - \left( {{R_3}/{R_2}} \right)x - \left( {{R_3}/{R_1}} \right)yz, $ | (8) |
同理
| $ {D^{0.83}}x = {v_{{\rm{U}}4{\rm{A}}}} = \left( {{R_9}/{R_7}} \right)xz + \left( {{R_9}/{R_8}} \right)y, $ | (9) |
| $ \begin{array}{*{20}{c}} {{D^{0.83}}x = {v_{{\rm{U}}6{\rm{A}}}} = - \left( {{R_{14}}/{R_{13}}} \right)z - \left( {{R_{14}}/{R_{12}}} \right)xy + }\\ {\left( {{R_{14}}/{R_{11}}} \right){y^2}.} \end{array} $ | (10) |
根据式(2)中的系数,a=2,b=1,c=-0.78,令R1=100 Ω,R2=500 Ω,R3=R7=R8=R9=1 kΩ,R5=R6=R16=R17=10 kΩ,R4=R10=R15=100 kΩ,R11=R14=1.56 kΩ,R12=195 Ω,R13=2 kΩ,Ra1=Ra2=Ra3=44.310 6 MΩ,Rb1=Rb2=Rb3=1.307 8 MΩ,Rc1=Rc2=Rc3=0.085 4 MΩ,Rd1=Rd2=Rd3=0.005 9 MΩ,Ca1=Ca2=Ca3=1.709 7 μF,Cb1=Cb2=Cb3=2.215 7 μF,Cc1=Cc2=Cc3=1.298 μF,Cd1=Cd2=Cd3=0.724 5 μF.
图 6为示波器上观察到的结果,可以看出实验结果与数值仿真结果完全相符,进一步验证了系统的混沌行为.
|
图 6 电路实验结果 Fig. 6 Experimental results of the circuit |
采用自适应控制方法[21-23]实现分数阶混沌系统的同步.令驱动系统为
| $ \left\{ {\begin{array}{*{20}{l}} {{D^{\rm{q}}}{x_1} = - a{x_1} - 10{x_2}{x_3},}\\ {{D^{\rm{q}}}{x_2} = b{x_2} + {x_1}{x_3},}\\ {{D^{\rm{q}}}{x_3} = c{x_3} - 8{x_1}{x_2} + x_2^2.} \end{array}} \right. $ | (11) |
其中x1,x2,x3为系统变量.响应系统为
| $ \left\{ {\begin{array}{*{20}{l}} {{D^{\rm{q}}}{y_1} = - a{y_1} - 10{y_2}{y_3} + {u_1},}\\ {{D^{\rm{q}}}{y_2} = b{y_2} + {y_1}{y_3} + {u_2},}\\ {{D^{\rm{q}}}{y_3} = c{y_3} - 8{y_1}{y_2} + y_2^2 + {u_3}.} \end{array}} \right. $ | (12) |
其中y1,y2,y3是状态变量,u1,u2,u3是自适应控制器.
令驱动系统(11)和响应系统(12)的同步误差为ei=yi-xi(i=1, 2, 3),则同步误差系统为
| $ \left\{ \begin{array}{l} {D^{\rm{q}}}{e_1} = - a{e_1} - 10{e_2}{e_3} - 10{e_2}{x_3} - \\ \;\;\;\;\;\;\;\;\;10{e_3}{x_2} + {u_1},\\ {D^{\rm{q}}}{e_2} = b{e_2} + {e_1}{e_3} + {e_1}{x_3} + \\ \;\;\;\;\;\;\;\;\;{e_3}{x_1} + {u_2},\\ {D^{\rm{q}}}{e_3} = c{e_3} - 8\left( {{e_1}{x_2} + {e_2}{x_1} + {e_1}{e_2}} \right) + \\ \;\;\;\;\;\;\;\;\;\;e_2^2 + 2{e_2}{x_2} + {u_3}. \end{array} \right. $ | (13) |
参数估计误差定义为
| $ \left\{ {\begin{array}{*{20}{l}} {{e_{\rm{a}}}(t) = a - \tilde a(t),}\\ {{e_{\rm{b}}}(t) = b - \tilde b(t),}\\ {{e_{\rm{c}}}(t) = c - \tilde c(t).} \end{array}} \right. $ | (14) |
对参数估计误差(14)求q阶导,得
| $ \left\{ {\begin{array}{*{20}{l}} {{D^{\rm{q}}}{e_{\rm{a}}}(t) = - {D^{\rm{q}}}\tilde a(t),}\\ {{D^{\rm{q}}}{e_{\rm{b}}}(t) = - {D^{\rm{q}}}\tilde b(t),}\\ {{D^{\rm{q}}}{e_{\rm{c}}}(t) = - {D^{\rm{q}}}\tilde c(t).} \end{array}} \right. $ | (15) |
设计系统的自适应控制器为
| $ \left\{ \begin{array}{l} {u_1} = \tilde a\left( t \right){e_1} + 18{e_3}{x_2} + 17{e_2}{x_3} + \\ \;\;\;\;\;\;9{e_2}{x_3} - {k_1}{e_1},\\ {u_2} = - \tilde b\left( t \right){e_2} + 7{e_3}{x_1} - {e_2}{e_3} - \\ \;\;\;\;\;\;2{e_3}{x_2} - {k_2}{e_2},\\ {u_3} = - \tilde c\left( t \right){e_3} - {k_3}{e_3}. \end{array} \right. $ | (16) |
式中k1, k2, k3为正的增益常数.
定义参数更新定律为
| $ \left\{ {\begin{array}{*{20}{l}} {{D^{\rm{q}}}\tilde a\left( t \right) = {\lambda _1}\left( { - e_1^2 + {e_{\rm{a}}}} \right),}\\ {{D^{\rm{q}}}\tilde b\left( t \right) = {\lambda _2}\left( {e_2^2 + {e_{\rm{b}}}} \right),}\\ {{D^{\rm{q}}}\tilde c\left( t \right) = {\lambda _3}\left( {e_3^2 + {e_{\rm{c}}}} \right).} \end{array}} \right. $ | (17) |
式中λ1, λ2, λ3为正的增益常数.
对于分数阶混沌系统,由参考文献[24]给出的分数阶Lyapunov稳定性理论,得出引理1.
引理1 对于分数阶系统
定理1 在自适应控制器(16)和参数更新定律(17)的作用下,同步误差系统(13)渐近稳定.
证明 构造J函数如下:
| $ J = \mathit{\boldsymbol{eP}}{D^{\rm{q}}}e = \left[ {e,{e_{\rm{a}}},{e_{\rm{b}}},{e_{\rm{c}}}} \right]\mathit{\boldsymbol{P}}{\left[ {{D^{\rm{q}}}e,{D^{\rm{q}}}{e_{\rm{a}}},{D^{\rm{q}}}{e_{\rm{b}}},{D^{\rm{q}}}{e_{\rm{c}}}} \right]^{\rm{T}}} $ |
其中,e为同步误差,ea, eb, ec为参数估计误差,P为实对称正定矩阵,选择正定矩阵P=diag(1, 1, 1, 1/λ1, 1/λ2, 1/λ3),λ1, λ2, λ3为特征值.
将同步误差系统(13)、参数估计误差(14)、自适应控制器(16)和参数更新定律(17)代入上式,简化可得
| $ \begin{array}{l} J = \left[ {e,{e_{\rm{a}}},{e_{\rm{b}}},{e_{\rm{c}}}} \right]\mathit{\boldsymbol{P}}{\left[ {{D^{\rm{q}}}e,{D^{\rm{q}}}{e_{\rm{a}}},{D^{\rm{q}}}{e_{\rm{b}}},{D^{\rm{q}}}{e_{\rm{c}}}} \right]^{\rm{T}}} = \\ \;\;\;\;\;{e_1}{D^{\rm{q}}}{e_1} + {e_2}{D^{\rm{q}}}{e_2} + {e_3}{D^{\rm{q}}}{e_3} + \left( {1/{\lambda _1}} \right){e_{\rm{a}}}{D^{\rm{q}}}{e_{\rm{a}}} + \\ \;\;\;\;\;\left( {1/{\lambda _2}} \right){e_{\rm{b}}}{D^{\rm{q}}}{e_{\rm{b}}} + \left( {1/{\lambda _3}} \right){e_{\rm{c}}}{D^{\rm{q}}}{e_{\rm{c}}} = \\ \;\;\;\;\; - ae_1^2 - 10{e_1}{e_2}{e_3} - 10{e_1}{e_2}{x_3} - 10{e_1}{e_3}{x_2} + \tilde a\left( t \right)e_1^2 - \\ \;\;\;\;\;{k_1}e_1^2 + 17{e_1}{e_2}{e_3} + 9{e_1}{e_2}{x_3} + 18{e_1}{e_3}{x_3} + be_2^2 + \\ \;\;\;\;\;{e_1}{e_2}{e_3} + {e_1}{e_2}{x_3} + {e_2}{e_3}{x_1} - \tilde b\left( t \right)e_2^2 - {e_2}{e_3}{x_1} + \\ \;\;\;\;\;8{e_2}{e_3}{x_1} - e_2^2{e_3} - 2{e_2}{e_3}{x_2} - {k_2}e_2^2 - ce_3^2 - \\ \;\;\;\;\;8{e_1}{e_2}{e_3} - 8{e_1}{e_3}{x_2} - 8{e_2}{e_3}{x_1} + e_2^2{e_3} + \\ \;\;\;\;\;2{e_2}{x_2}{e_3} - \tilde c\left( t \right)e_3^2 - {k_3}e_3^2 + \\ \;\;\;\;\;\left( {1/{\lambda _1}} \right){e_{\rm{a}}}{D^{\rm{q}}}{e_{\rm{a}}} + \left( {1/{\lambda _2}} \right){e_{\rm{b}}}{D^{\rm{q}}}{e_{\rm{b}}} + \left( {1/{\lambda _3}} \right){e_{\rm{c}}}{D^{\rm{q}}}{e_{\rm{c}}} = \\ \;\;\;\;\; - {e_{\rm{a}}}e_1^2 - {k_1}e_1^2 + {e_{\rm{b}}}e_2^2 - {k_2}e_2^2 + {e_{\rm{c}}}e_3^2 - {k_3}e_3^2 + \\ \;\;\;\;\;\left( {1/{\lambda _1}} \right){e_{\rm{a}}}{D^{\rm{q}}}{e_{\rm{a}}} + \left( {1/{\lambda _2}} \right){e_{\rm{b}}}{D^{\rm{q}}}{e_{\rm{b}}} + \left( {1/{\lambda _3}} \right){e_{\rm{c}}}{D^{\rm{q}}}{e_{\rm{c}}} = \\ \;\;\;\;\; - {k_1}e_1^2 - {k_2}e_2^2 - {k_3}e_3^2 - e_a^2 - e_b^2 - e_c^2. \end{array} $ |
显然,J≤0,据引理1误差系统渐近稳定.
证毕.
采用四阶Runge-Kutta算法,仿真步长为0.001.取q=0.83,a=2,b=1,c=-7.8,k1=k2=k3=20, λ1=λ2=λ3=20.x1(0)=1,x2(0)=2, x3(0)=3作为驱动系统(11)的初始条件;y1(0)=2, y2(0)=3, y3(0)=4作为响应系统(12)的初始条件;
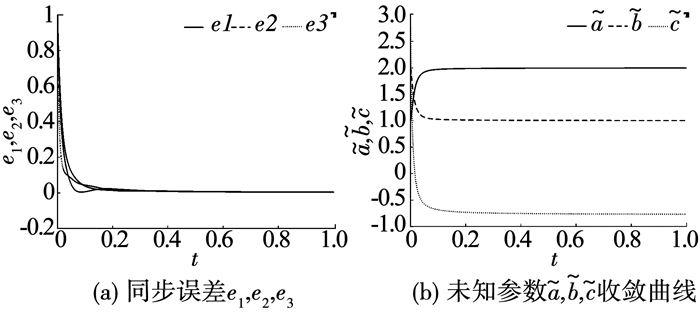
图 7描述了驱动系统(11)和响应系统(12)的同步误差e1, e2, e3和对系统未知参数的识别.结果表明响应系统与驱动系统在0.2 s内达到同步,在0.2 s内完成对未知参数
|
图 7 同步误差和未知参数收敛曲线 Fig. 7 Convergence curves of synchronization errors and unknown parameters |
本文设计了一个新型三维分数阶混沌系统,分析了此系统的动力学特性,系统具有复杂的动态行为,能够出现双翼、三翼、四翼等不同类型多翼混沌吸引子共存.对系统进行了Multisim模拟电路设计与仿真,仿真结果与数值分析相符,进一步验证了系统的混沌行为.基于分数阶Lyapunov稳定理论及定理1,设计了一个自适应同步控制器,仿真结果表明了所设计控制器的有效性.
| [1] |
KHAN A, KHATTER D, AGRAWAL N. Synchronization of a new fractional order chaotic system[J]. International Journal of Dynamics and Control, 2018, 6(4): 1585. DOI:10.1016/j.chaos.2018.05.015 |
| [2] |
孙美美, 胡云安, 韦建明. 一种新型不确定分数阶混沌系统滑模同步控制方式[J]. 电子科技大学学报, 2017, 46(3): 555. SUN Meimei, HU Yunan, WEI Jianming. A novel sliding mode synchronization method of uncertain fractional-order chaotic systems[J]. Journal of University of Electronic Science and Technology of China, 2017, 46(3): 555. DOI:10.3969/j.ssn.1001-0548.2017.03.013 |
| [3] |
MUNOZ-PACHECO J M, ZAMBRANO-SERRANO E, VOLOS C, et al. A fractional order chaotic system with a 3D grid of variable attractors[J]. Chaos Solitons & Fractals, 2018, 113: 69. DOI:10.1016/j.chaos.2018.05.015 |
| [4] |
LAI Qiang, NESTAR T, KENGNE J, et al. Coexisting attractors and circuit implementation of a new 4D chaotic system with two equilibria[J]. Chaos Solitons & Fractals, 2018, 107: 92. DOI:10.1016/j.chaos.2017.12.023 |
| [5] |
LI Ruiguo, WU Haining. Secure communication on fractional-order chaotic systems via adaptive sliding mode control with teaching-learning-feedback-based optimization[J]. Nonlinear Dynamics, 2018, 1. |
| [6] |
SHUKLA M K, SIVA D, MAHAJAN A, et al. A novel scheme of image encryption based on synchronization of fractional order chaotic systems[C]//Proceedings of 2018 International Conference on Intelligent Circuits and Systems (ICICS). Piscataway: IEEE, 2018: 433. DOI: 10.1109/ICICS.2018.00094
|
| [7] |
PING Z, KE M. An integer-order memristive system with two-to four-scroll chaotic attractors and its fractional-order version with a coexisting chaotic attractor[J]. Complexity, 2018, 2018: 1. DOI:10.1155/2018/4970152 |
| [8] |
BORAH M, ROY B K. An enhanced multi-wing fractional-order chaotic system with coexisting attractors and switching hybrid synchronisation with its nonautonomous counterpart[J]. Chaos, Solitons & Fractals, 2017, 102: 372. DOI:10.1016/j.chaos.2017.03.055 |
| [9] |
鲜永菊, 夏诚, 徐昌彪. 新混沌系统及其分数阶系统的自适应同步控制[J]. 控制理论与应用, 2018, 35(6): 159. XIAN Yongju, XIA Cheng, XU Changbiao. New chaotic system and the adaptive synchronization control of its fractional order system[J]. Control Theory & Applications, 2018, 35(6): 159. DOI:10.7641/CTA.2017.70567 |
| [10] |
ZHANG Chaoxia, YU Simin. Generation of multi-wing chaotic attractor in fractional order system[J]. Chaos, Solitons & Fractals, 2011, 44(10): 845. DOI:10.1016/j.chaos.2011.06.017 |
| [11] |
TANG Zilong, ZHANG Chaoxia, YU Simin. Design and circuit implementation of fractional-order multiwing chaotic attractors[J]. International Journal of Bifurcation and Chaos, 2012, 22(11): 1250269. DOI:10.1142/S0218127412502690 |
| [12] |
LYU Jinhu, CHEN Guangrong, CHENG Daizhan. A new chaotic system and beyond:The generalized Lorenz-like system[J]. International Journal of Bifurcation and Chaos, 2014, 14(5): 1507. DOI:10.1142/S021812740401014X |
| [13] |
DIETHELM K, FORD N J, FREED A D. A predictor-corrector approach for the numerical solution of fractional differential equations[J]. Nonlinear Dynamics, 2002, 29(1-4): 3. |
| [14] |
BASHKIRTSEVA I A, ZAITSEVA S. The phenomenon of stochastic excitability in the enzymatic reaction model[J]. Institute of Natural Science & Mathematics, 2018, 3. DOI:10.20537/vm180101 |
| [15] |
SAHA S, MAITI A, SAMATA G P. A Michaelis-Menten predator-prey model with strong Allee effect and disease in prey incorporating prey refuge[J]. International Journal of Bifurcation and Chaos, 2018, 28(06): 1850073. DOI:10.1142/S0218127418500736 |
| [16] |
周平, 危丽佳, 程雪峰. 一个分数阶混沌系统及其EWB仿真结果[J]. 西南大学学报(自然科学版), 2009, 31(1): 69. ZHOU Ping, WEI Lijia, CHENG Xuefeng. A fractional-order chaotic system and its simulation result electronic work-bench (EW-B)[J]. Journal of Southwest University (Natural Science), 2009, 31(1): 69. DOI:10.13718/j.cnki.xdzk.2009.01.014 |
| [17] |
OGATA K. Modern control engineering[M]. New Jersey: Prentice Hall, 2002.
|
| [18] |
TAVAZOEI M S, HAERI M. A necessary condition for double scroll attractor existence in fractional-order systems[J]. Physics Letters A, 2007, 367(1-2): 102. DOI:10.1016/j.physleta.2007.05.081 |
| [19] |
SOHAIL A, MAQBOOL K, ELLAHI R. Stability analysis for fractional-order partial differential equations by means of space spectral time Adams-Bashforth Moulton method[J]. Numerical Methods for Partial Differential Equations, 2018, 34(1): 19. DOI:10.1002/num.22171 |
| [20] |
邵书义.新型混沌系统的动力学分析、同步控制及应用[D].南京: 南京师范大学, 2014 SHAO Shuyi. Dynamic analysis, synchronous control and application of new chaotic system[D]. Nanjing: Nanjing Normal University, 2014 http://cdmd.cnki.com.cn/Article/CDMD-10319-1014343213.htm |
| [21] |
LUO Shaohua, LI Shaobo, TAJADDODIANFAR F. Chaos and adaptive control of the fractional-order magnetic-field electromechanical transducer[J]. International Journal of Bifurcation and Chaos, 2017, 27(13): 1750203. DOI:10.1142/S0218127417502030 |
| [22] |
LUO Shaohua, LI Shaobo, TAJADDODIANFAR F, et al. Adaptive synchronization of the fractional-order chaotic arch micro-electro-mechanical system via Chebyshev neural network[J]. IEEE Sensors Journal, 2018, 18(9): 3524. DOI:10.1109/JSEN.2018.2812859 |
| [23] |
LI Ruiguo, WU Haining. Adaptive synchronization control based on QPSO algorithm with interval estimation for fractional-order chaotic systems and its application in secret communication[J]. Nonlinear Dynamics, 2018, 1. |
| [24] |
HUANG Yu, WANG Dongfeng, ZHANG Jinying, et al. Controlling and synchronizing a fractional-order chaotic system using stability theory of a time-varying fractional-order system[J]. PloS One, 2018, 13(3). DOI:10.1371/journal.pone.0194112 |
 2020, Vol. 52
2020, Vol. 52


