近年来,大中型城市中市民打车难与出租车空载率高并存的矛盾现象愈来愈严重.交通高峰期,乘客候车时间过长容易导致抢车冲突的发生,出租车在路侧随意停靠载客的行为给周边交通增加了压力.增设出租车停靠站有利于引导司机文明停车,方便市民有序候车,有效提高出租车运营效率,改善交通拥堵.然而,出租车站点利用率低的问题仍不容忽视.一方面,设施监管不足导致停靠站常常被社会车辆占用或遮挡;另一方面,站点空间布局的不合理导致乘客的使用意愿较低.实际中,出租车停靠站通常设置在城市的出行热点区域, 但具体的站位选择则取决于交通管理者的经验以及对司机或乘客的抽样调查.缺乏科学严谨的决策准则,导致了出租车停靠站低利用率的现状.因此,合理解决出租车停靠站的布局问题,对改善出租车行业服务水平和运营效率具有十分重要的现实意义.
目前,与出租车运营相关的国内外研究主要集中在出租车服务策略[1]、驾驶员收入[2]、需求预测[3]等方面.在出租车停靠站设置问题上,国内研究大多倾向于对站点布设原则[4]、影响因素[5]、规模预测[6]的探讨与分析,而关于站点数量及空间布局的研究则相对较少.文献[7]结合GIS开发了出租车停靠站决策支持系统,建立模糊逻辑模型对安卡拉99个交通区的现有出租车站进行评价;文献[8]提出了基于最大覆盖的出租车停靠站选址模型,并结合出行者的不确定性交通行为和消费特点分析了模型的适用条件;文献[9]提出了基于乘客最短步行距离的出租车停靠站设置模型,依据站点的服务能力和路段的交通状况对站点的设置进行了分析;文献[10]针对出租车停靠站的空间布局问题提出了一种三阶段选址策略,以最小化乘客的出行成本和站点的建设成本为目标建立了站点选址模型.
本文基于出租车GPS轨迹数据,提取出行需求的时空动态特征,并结合设施的实际布设原则确定候选站点的分布位置.以政府的投入成本最低和公众的访问意愿最高为优化目标,建立出租车停靠站的双目标选址模型,并提出求解算法.通过成都市某商圈的案例研究验证选址方法的有效性,以期为交通及市政管理部门进行出租车停靠站的规划提供理论基础和技术支持.
1 出行需求估计 1.1 数据描述本文的数据来源是成都市1.3万余辆出租车在2014年8月的某一周内6:00~24:00时生成的GPS轨迹信息,经过对原始数据的预处理最终获取了3亿余条有效数据.研究所利用的字段主要包括:出租车编号(id)、定位时间(gps time)、经度(lng)、纬度(lat)、车载状态(status)等,数据样本示例见表 1.其中,车载状态为1时表示载客,0表示空载.通常将车载状态由连续0变为连续1时的第一个“1”的点视为上客点,相反地,将车载状态由连续1变为连续0时的第一个“0”的点视为下客点[11].论文在Microsoft SQL Sever 2008数据库环境下提取了出租车上、下客点数据集,乘客出行的OD信息为后续的需求估计及选址研究提供数据支持.
| 表 1 出租车GPS数据样本 Tab. 1 Sample of taxi GPS data |
为了保持出租车独特的灵活性与便利性的优势,站点候车的出行方式不可能均匀地应用在整个城市路网上,而仅适用于人车流量较大的热点出行区域.本文分三步对出租车的出行需求进行估计,见图 1.首先,选取一定的分割长度(R)将研究范围内的道路划分成相邻的网格,并标定其位置坐标.通常情况下,站点、站牌与信号交叉口的距离需≥50 m,因此,不宜包含交叉口及距离交叉口停止线50 m内的路段.同时,提取每个网格内的出租车上客点,统计出行频数Qi,见图 1(a).在此基础上,沿道路中线将网格分为上、下行两个方向的子网,判别原网格内上客点的出行方向以确定其所属子网,统计两侧子网的出行频数qai和qdi, 见图 1(b).根据出租车停靠站的实际布设原则,即沿道路两侧交错排列,选择上、下行方向上符合该位置特征的子网作为出租车出行需求的发生小区,并按奇偶顺序进行编码, 见图 1(c).分配未编码子网内的上客点至相邻需求小区,计算出行频数qi,有
| $ {q_i} = \left\{ \begin{array}{l} {q_{d\left( {i + 1} \right)}} + \frac{{{q_{d\left( {i + 2} \right)}}}}{2},i = 0;\\ {q_{a\left( {i + 1} \right)}} + {q_{ai}} + \frac{{{q_{a\left( {i + 2} \right)}}}}{2},i = 1;\\ {q_{d\left( {i + 1} \right)}} + \frac{{{q_{di}}}}{2} + \frac{{{q_{d\left( {i + 2} \right)}}}}{2},i = 2n\left( {n = 1,2, \cdots } \right);\\ {q_{a\left( {i + 1} \right)}} + \frac{{{q_{ai}}}}{2} + \frac{{{q_{a\left( {i + 2} \right)}}}}{2},i = 2n + 1\left( {n = 1,2, \cdots } \right). \end{array} \right. $ | (1) |
文献[10]的调查研究表明出租车出行的平均载客人数为2人, 因此,出行发生小区的实际需求量为2qi.为便于计算出行距离,假设出行需求均发生在各小区的几何中心处,并在该位置生成一个出租车停靠站候选点,实现将供需的空间关系特征应用于需求量估计与候选点确定的过程,见图 1(d).
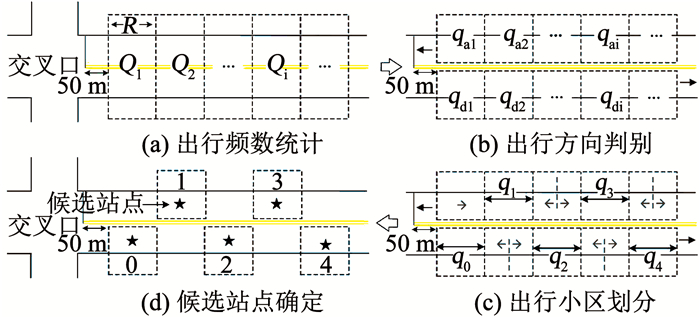
|
图 1 出租车出行需求估计与候选站点确定 Fig. 1 Taxi travel demands estimation and candidate stands identification |
出租车停靠站作为一种交通基础服务设施,其数量及位置的决策需要兼顾和平衡城市规划者和出行者双方的利益.从规划者的角度出发,在确保覆盖区域内全部出行需求的前提下,应尽量减少待建站点的数量以降低可能带来的用地改造、站牌和站位布设、以及后续的维护等成本,节约空间资源.从出行者的角度出发,应尽可能为每个站点找到合适的位置并分配乘客到一个特定的设施,以达到站点与乘客之间的出行成本最低,使服务的可达性及公众的出行满意度最高.因此,在综合考两者成本利益的基础上,确定出租车停靠站布局优化的双目标函数.
引入二元决策变量xj和yij,有:
| $ {x_j} = \left\{ \begin{array}{l} 0,\\ 1. \end{array} \right. $ | (2) |
式中:j表示候选点,J表示出租车停靠站候选点集合(j∈J),xj=0表示j点不设置出租车停靠站,xj=1表示在j点设置出租车停靠站.
| $ {y_{ij}} = \left\{ \begin{array}{l} 0,\\ 1. \end{array} \right. $ | (3) |
式中:i表示需求点,I表示需求点集合(i∈I),yij=0表示i的乘客不由j点服务,yij=1表示i的乘客由j点服务.
通过待建设施数量P反映规划者成本投入,则最小停靠站数量优化的目标函数表达式为
| $ \min P = \sum\limits_{j \in J} {{x_j}} . $ | (4) |
影响公众出行满意度最重要的因素是步行距离,其表现在出行的便捷性与可达性上.一般可以将满意度函数定义为网络距离上的非增函数,本文在出租车停靠站的选址研究中采用余弦分布函数[12]评价乘客对于出行距离的满意程度,其函数曲线见图 2,函数表达式为
| $ f\left( {{d_{ij}}} \right) = \left\{ \begin{array}{l} 1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{d_{ij}} < \delta - \sigma ;\\ \frac{1}{2} + \frac{1}{2}\cos \left( {\frac{{\rm{ \mathsf{ π} }}}{\sigma }\left( {{d_{ij}} - \frac{{2\delta - \sigma }}{2}} \right) + \frac{{\rm{ \mathsf{ π} }}}{2}} \right),\;\;\;\;\;{d_{ij}} \in \left[ {\delta - \sigma ,\delta } \right],\forall i \in I,j \in J;\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{d_{ij}} > \delta . \end{array} \right. $ | (5) |
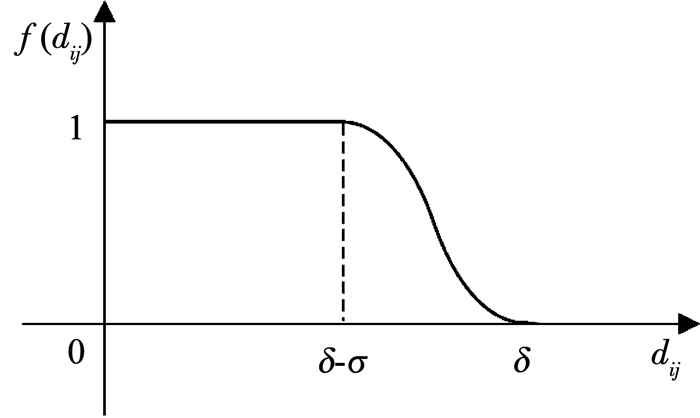
|
图 2 乘客出行距离满意度函数曲线 Fig. 2 Passenger satisfaction function curve for travel distance |
式中:δ表示乘客可接受的最大出行距离Dmax,σ表示满意度从1降为0的过程距离,本文σ=Dmax/2,dij表示需求点i与候选点j之间的出行距离.
通过乘客满意度的加权之和A反映公众出行意愿,则最大乘客满意度优化的目标函数表达式为
| $ \max A = \sum\limits_{t \in T} {\sum\limits_{i \in I} {\sum\limits_{j \in J} {{q_{it}}} } } \cdot {y_{ij}} \cdot f\left( {{d_{ij}}} \right). $ | (6) |
式中:t表示单位小时的时段,T表示时段的集合,qit表示需求点i在第t个时段的出行需求量.
2.2 影响因素及约束条件分析在对出租车停靠站进行选址决策时,设施服务对象即乘客与出租车是主要的考虑因素,二者与路网中需要布设的站点数量及位置有着紧密的关系.本文主要从这两个方面具体分析出租车停靠站选址的影响因素,从而确定双目标优化模型的约束条件.
2.2.1 乘客的出行需求通常在设有出租车停靠站的局部路网中,出租车被严格禁止在路侧随意停靠搭载乘客,乘客只能选择前往附近的站点乘车.因此,出租车停靠站的选址应充分考虑乘客的实际出行需求,保证研究区域内需求全覆盖的约束限制,即对任意一个出行需求点i,必有一个站点能够为其提供服务,有
| $ \sum\limits_{j \in J} {{y_{ij}}} = 1. $ | (7) |
此外,假设需求点i的乘客由站点j提供服务的前提是j点设有出租车停靠站,即
| $ {y_{ij}} \le {x_j},\;\;\;\;\forall i \in I,j \in J. $ | (8) |
出租车停靠站的服务半径具有局限性,这通常取决于公众的期望出行距离.出行者往往希望尽可能减小出行距离或时间,以实现快速乘车的目的.在禁止出租车以“招手即停”方式运营的区域内,乘客能够接受前往站点乘车的前提是出行距离处于其可接受的水平,一旦出行距离超出其预期阈值,便会引发乘客的抵触情绪,导致站点利用率下降.因此,出租车站点选址的过程中,需要添加约束以保证任意一个出行需求点i的乘客前往为其提供服务的站点j的步行距离不超过期望出行距离,即
| $ \sum\limits_{j \in J} {{d_{ij}}} {y_{ij}} \le {D_{\max }},\forall i \in I. $ | (9) |
式中:Dmax表示乘客可接受的最大步行距离,即期望出行距离.
2.2.3 站点的服务能力出租车停靠站供出租车停靠并搭载乘客,单位时间内站点能够服务的最大乘客数量由停车位数量和每个停车位在单位时间内的车辆周转量共同决定.每个站点实际覆盖的出行需求量与其自身的服务能力之间的供需关系,也是出租车停靠站优化布局中需要重点考虑的因素.
引入变量sj为出租车停靠站j的服务能力,有
| $ {s_j} = {p_j}{T_{{\rm{bb}}}}{n_{\rm{p}}}. $ | (10) |
式中:pj表示候选站点j的停车位数量,np表示每辆出租车的平均载客人数,Tbb表示每个停车位每小时能够服务的最大车辆数,在站点几何尺寸适当的条件下可通过下式[13]计算
| $ {T_{{\rm{bb}}}} = \frac{{3600\left( {g/C} \right)}}{{{t_{\rm{c}}} + \left( {g/C} \right){t_{\rm{d}}} + {Z_{\rm{a}}} \cdot {c_{\rm{v}}} \cdot {t_{\rm{d}}}}}. $ | (11) |
式中:g/C为每个信号周期内有效绿灯时间(在无信号交叉口及路段上的停车站为1.0),tc为连续两辆出租车之间的时间间隔(单位s),Za表示对应于在站点后排队概率的单边检验量,cv为停留时间的偏差系数,td表示平均停留时间(单位s).
当站点的服务人数超出其服务能力时,出租车供不应求,站内会产生乘客排队现象.为了避免供需失衡,选址优化时需要保证在任意时段t内站点j所覆盖的出行需求量不超过其最大服务能力,即
| $ \sum\limits_{i \in I} {{q_{it}}} {y_{ij}} \le {p_j}{T_{{\rm{bb}}}}{n_{\rm{p}}}{x_j},\forall j \in J,t \in T. $ | (12) |
本文在选址方案的决策过程中考虑了两个评价标准,建立了两个目标函数,即双目标优化问题.本文采用基于遗传算法的宽容分层序列法对模型进行求解,其基本思想是将多个目标函数按其重要程度排序,依次对各个目标函数求最优解,且将前一目标的最优解增加宽容值后作为新的约束加入到后一目标的优化过程中,迭代生成原问题的最优解[14-15].其中,各个子目标的优化采用遗传算法进行求解,通过种群生成、适应度评价、选择、交叉和突变五个基本步骤完成最优解的迭代搜索过程.算法流程包括:
Step 1:求解最小停靠站数量优化问题
| $ \min P = \sum\limits_{j \in J} {{x_j}} . $ |
s.t.式(2)、(3)、(7)、(8)、(9)、(12)获得最小待建站点数量P0.
Step 2:引入最小站点数量的宽容系数ε,添加约束条件,求解最大乘客满意度优化问题.
| $ \max A = \sum\limits_{t \in T} {\sum\limits_{i \in I} {\sum\limits_{j \in J} {{q_{it}}} } } \cdot {y_{ij}} \cdot f\left( {{d_{ij}}} \right), $ |
s.t.式(2)、(3)、(7)、(8)、(9)、(12)
| $ \sum\limits_{j \in J} {{X_j}} = \left\{ {{P_0}, \cdots ,{P_0} + \varepsilon } \right\}. $ |
获得最大乘客满意度A0,及双目标优化模型的最佳选址方案.
3 案例分析以成都市春熙路商圈为例,利用所建立模型对该区域的出租车停靠站进行重新选址,并将获取的布局方案和现有站点进行对比.
3.1 研究区域统计成都市出租车上、下客频数的日变化规律,结果见图 3.可以发现,一周内出租车出行的最大值和最小值分别出现在周五和周日.基于ArcGIS10.2,对周五的GPS数据集进行空间分析,建立50 m×50 m的渔网覆盖研究区域路网,两个高峰出行时段的可视化结果见图 4.
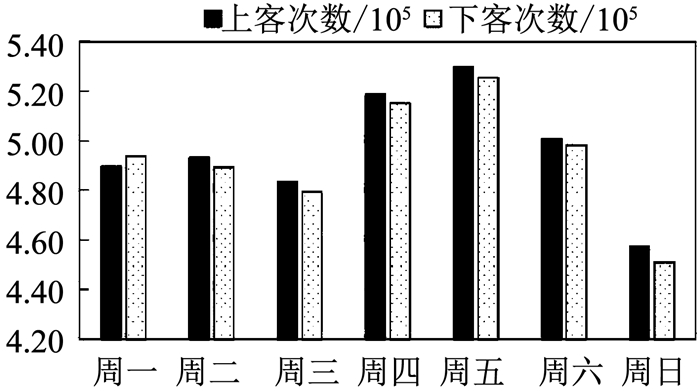
|
图 3 出租车上下客频数图 Fig. 3 Frequency of taxi picking up or dropping off passengers |
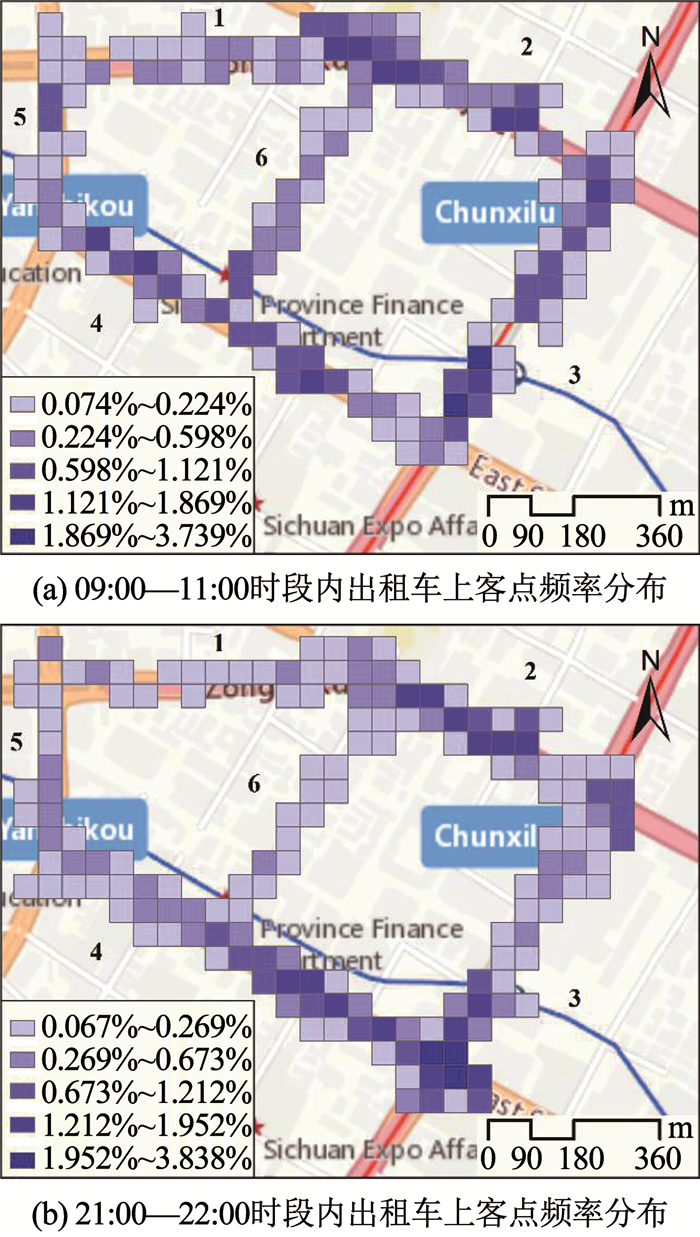
|
图 4 研究区域出租车上客点频率分布 Fig. 4 Frequency distribution of taxi pick-up points in the study area |
结果显示研究区域内的路段5、6出行频率相对较低,结合路网实际情况可知,路段6属于支路,不具备设置出租车停靠站的道路条件;路段5在现实中也并未被纳入布设站点的范围.本文仅选取1~4号出行热点路段进行选址研究,路段长度分别为543、457、487、720 m.
3.2 基本参数设定以长度R=50 m划分道路网格,获取到36个出行需求小区及出租车停靠站候选点,见图 5.现状出租车停靠站共有11处,分别位于2-10-11-11-19-21-22-23-26-26-27号小区,停车位数量分别为1-1-1-6-3-3-3-4-1-1-3,共27个停车位.乘客在路段1、2、4需利用过街天桥过街,为了简化研究,本文将该种过街方式的出行距离设定为Od= 100 m,路段3的过街距离为Rd=15 m.根据城市距离与过街距离计算需求点与候选点之间的距离矩阵D36×36,模型的其他相关参数设定见表 2,其中,出租车平均停留时间td参考文献[10]的实际调查结果.
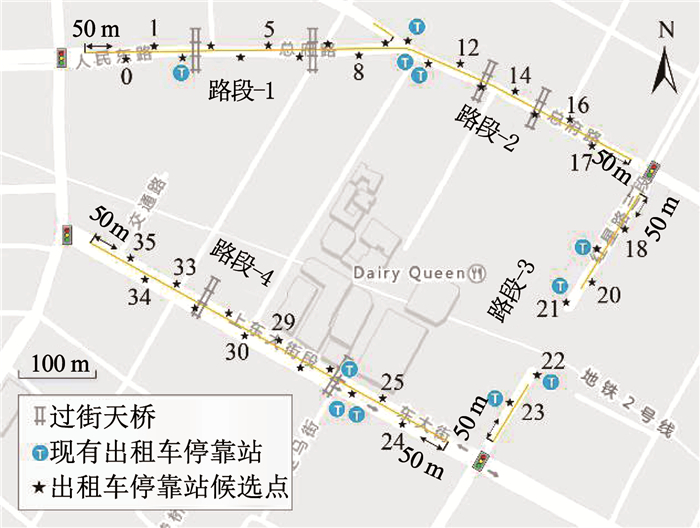
|
图 5 出行需求小区及候选站点分布 Fig. 5 Travel demand zone and candidate stands distribution |
| 表 2 模型基本参数设定 Tab. 2 Model basic parameters setting |
根据文献[16],公共交通站点服务半径通常以300 m计算,最大不超过500 m.事实上,出租车乘客对于乘车距离的容忍度往往小于公交车乘客,因此,本文将乘客可接受的最大步行距离Dmax从100 m增加到500 m,每次增加50 m,探讨不同期望出行距离对优化选址方案的影响,结果见表 3.可以发现,乘客可接受的最大步行距离与待建站点数量及停车位数量的关系整体呈现负相关趋势.这与我们的经验相符,较小的期望出行距离表示乘客不愿意步行较远的距离去乘坐出租车,因此需要在出行需求附近设置更多的站点.期望出行距离越大,表示乘客能够接受较远的距离,因此,会有更多的选择来决定站点的位置,为了使成本投入最小,最终方案的站点数量更小.对于站点数量相同的选址方案,可以发现乘客可接受的最大步行距离越大,乘客的出行满意度越高.上述结果验证了乘客可接受的最大步行距离对出租车停靠站的选址和乘客对出行距离的满意度有显著影响.
| 表 3 不同期望出行距离下的优化方案对比 Tab. 3 Comparison of optimal location schemes under different expected travel distances |
现状出租车停靠站在不同期望出行距离下的乘客满意度及需求覆盖率情况见表 4.可以看出,乘客出行满意度随着乘客可接受的最大步行距离的增大而提高,考虑主要原因是在站点数量及停车位数量不变的条件下,期望出行距离越大,乘客对于远距离乘车的容忍度越高,因此出行满意度也越大.但需要注意的是,现状出租车停靠站在期望出行距离小于500 m时无法覆盖研究区域内的全部出行需求.随着乘客期望出行距离的减小,未被覆盖的出行需求量逐渐增大,而优化后的选址方案能够保证出行需求的全覆盖.
| 表 4 不同期望出行距离下的现状出租车停靠站对比 Tab. 4 Comparison of existing taxi stands under different expected travel distances |
图 6为新的选址优化方案与现状出租车停靠站的对比.可以看出,当乘客可接受的最大步行距离大于等于200 m时,优化方案的站点数量和停车位数量始终小于现状数量,有效节省了规划者的成本投入及空间资源;当乘客可接受的最大步行距离小于200 m时,尽管优化方案的站点数量较高,但停车位的总数仍低于现状情况,同时保证了研究区域内的需求得到全部覆盖,而现状方案的需求覆盖率仅为70%,部分乘客的乘车需求无法得到满足.当Dmax≥300 m时,现状方案下的乘客出行满意度高于优化后的结果;当Dmax < 300 m时,优化方案下的乘客出行满意度较高,这与出租车乘客的期望出行距离较小的现实情况相符,验证了优化模型的有效性及适用性.
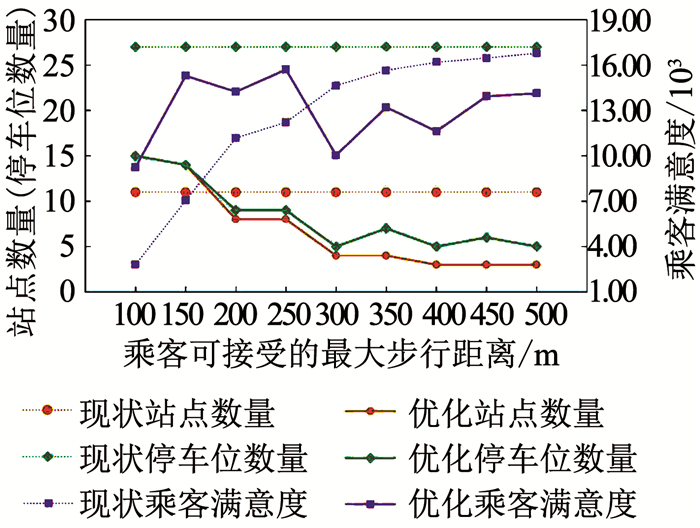
|
图 6 现状出租车停靠站与优化后的位置方案对比 Fig. 6 Comparison between the existing taxi stands and the optimized location scheme |
1) 根据出租车停靠站在道路空间上的布设原则,划分了出行需求发生小区;基于出租车GPS轨迹数据对乘客出行需求和候选站点的位置与数量进行了估计.
2) 构建了城市热点区域出租车停靠站双目标选址模型,从规划者的角度出发,以待建站点数量最小为目标,从使用者的角度出发,以出行距离满意度最大为目标.给出了基于遗传算法的布局优化模型求解方法,探讨了乘客可接受的最大出行距离对选址方案的影响.
3) 以成都市为例,运用所建立模型对春熙路商圈的出租车停靠站进行重新选址,结果表明,在乘客可接受的最大步行距离较小的情况下,双目标优化模型既能够保证以合理数量的站点覆盖全部的出行需求,又能使乘客的出行满意度较高,在节约政府投入成本的同时保证了公众出行意愿.
| [1] |
ZHANG Daqing, SUN Lin, LI Bin, et al. Understanding taxi service strategies from taxi GPS traces[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(1): 123. DOI:10.1109/tits.2014.2328231 |
| [2] |
QIN Guoyang, LI Tienan, YU Bin, et al. Mining factors affecting taxi drivers'incomes using GPS trajectories[J]. Transportation Research Part C Emerging Technologies, 2017, 79: 103. DOI:10.1016/j.trc.2017.03.013 |
| [3] |
MOREIRA-MATIAS L, GAMA J, FERREIRA M, et al. Predicting taxi-passenger demand using streaming data[J]. IEEE Transactions on Intelligent Transportation Systems, 2013, 14(3): 1393. DOI:10.1109/tits.2013.2262376 |
| [4] |
叶海飞. 出租车停靠站的设置方法[J]. 交通标准化, 2014, 42(15): 68. YE Haifei. Setting method of taxi stands[J]. Transportation Standardization, 2014, 42(15): 68. DOI:10.16503/j.cnki.2095-9931.2014.15.017 |
| [5] |
叶臻, 贺明光, 梁科科. 出租车服务站布局与城市形态协调性量化分析[J]. 武汉理工大学学报(交通科学与工程版), 2018, 42(2): 216. YE Zhen, HE Mingguang, LIANG Keke. Quantitative analysis of coordination between taxi service station layout and urban morphology[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2018, 42(2): 216. DOI:10.3963/j.issn.2095-3844.2018.02.010 |
| [6] |
叶海飞. 基于土地利用的出租车停靠规模预测方法[J]. 交通运输工程与信息学报, 2013, 37(4): 76. YE Haifei. Forecast method of the scale of taxi stands based on land use[J]. Journal of Transportation Engineering and Information, 2013, 37(4): 76. DOI:10.3969/j.issn.1672-4747.2013.04.013 |
| [7] |
OCALIR E V, ERCOSKUN O Y, TUR R. An integrated model of GIS and fuzzy logic (FMOTS) for location decisions of taxicab stands[J]. Expert Systems with Applications, 2010, 37(7): 4892. DOI:10.1016/j.eswa.2009.12.026 |
| [8] |
金雷, 谢秉磊. 基于上落客时空特征的出租车停靠站选址模型[J]. 交通运输系统工程与信息, 2015, 15(2): 182. JIN Lei, XIE Binglei. A location model for taxi stands based on spatial-temporal characteristics of taxi pick-ups and drop-offs[J]. Journal of Transportation Systems Engineering and Information Technology, 2015, 15(2): 182. DOI:10.16097/j.cnki.1009-6744.2015.02.028 |
| [9] |
齐林.基于GPS数据的出租车交通运行特性研究及应用[D].哈尔滨: 哈尔滨工业大学, 2013 QI Lin. Research and application on taxi traffic running performance based on GPS data[D]. Harbin: Harbin Institute of Technology, 2013 |
| [10] |
QU Zhaowei, WANG Xin, SONG Xianmin, et al. Location optimization for urban taxi stands based on taxi GPS trajectory big data[J]. IEEE Access, 2019, 7: 62273. DOI:10.1109/ACCESS.2019.2916342 |
| [11] |
曲昭伟, 王鑫, 宋现敏, 等. 基于出租车GPS大数据的城市热点出行路段识别方法[J]. 交通运输系统工程与信息, 2019, 19(2): 238. QU Zhaowei, WANG Xin, SONG Xianmin, et al. Urban hotspot travel section identification method based on taxi GPS large data[J]. Journal of Transportation Systems Engineering and Information Technology, 2019, 19(2): 238. DOI:10.16097/j.cnki.1009-6744.2019.02.034 |
| [12] |
马云峰.网络选址中基于时间满意的覆盖问题研究[D].武汉: 华中科技大学, 2005: 43 MA Yunfeng. Time-satisfaction-based covering location problems on network[D]. Wuhan: Huazhong University of Science and Technology, 2005: 43 |
| [13] |
美国交通研究委员会. 道路通行能力手册. HCM2000[M]. 北京: 人民交通出版社, 2007: 2713. Transportation Research Board. Highway capacity manual. HCM2000[M]. Beijing: China Communications Press, 2007: 2713. |
| [14] |
谭昌柏, 袁军, 周来水. 基于宽容分层序列法的飞机装配公差稳健设计技术[J]. 中国机械工程, 2012, 23(24): 2962. TAN Changbai, YUAN Jun, ZHOU Laishui. Robust tolerancing for aircraft assembly based on tolerant lexicographic method[J]. China Mechanical Engineering, 2012, 23(24): 2962. DOI:10.3969/j.issn.1004-132X.2012.24.014 |
| [15] |
孙智源, 陆化普. 考虑交通大数据的交通检测器优化布置模型[J]. 清华大学学报(自然科学版), 2016(7): 743. SUN Zhiyuan, LU Huapu. Optimal traffic sensor layout model considering traffic big data[J]. Journal of Tsinghua University (Science and Technology), 2016(7): 743. DOI:10.16511/j.cnki.qhdxxb.2016.24.025 |
| [16] |
中华人民共和国建设部.城市道路交通规划设计规范: GB/50220-95[S].北京: 中国计划出版社, 1995: 8 Ministry of Housing and Urban-Rural Development, PRC. Code for transport planning on urban road: GB/50220-95[S]. Beijing: China Planning Press, 1995: 8 |
 2020, Vol. 52
2020, Vol. 52


