由于加速度计的安装位置很难与载体摇摆参考点相重合，在角运动环境下加速度计输出会产生相对参考点的干扰加速度，即杆臂效应^[1-2].航姿参考系统(Attitude and Heading Reference System，AHRS)中加速度计测量重力加速度在载体系各坐标轴上的投影分量从而获取水平姿态角，同时修正陀螺漂移^[3-5].在静态条件下可获得较高的姿态测量精度.但在动态环境，叠加在加速度计敏感轴上的干扰加速度会对加速度计测姿精度造成极大影响.

根据现有文献，杆臂效应误差补偿研究可分为三类：1)低通滤波法，将杆臂效应视为高频干扰，通过低通滤波抑制杆臂效应误差.如文献^[6]采用FIR和IIR低通滤波方法对加速度计杆臂效应在频域内进行滤除.但低通滤波法无法滤除振动产生的直流分量.2)力学补偿法，将陀螺仪测量的角速度，以及对角速度微分得到的角加速度代入杆臂效应公式，分别补偿杆臂效应中的向心加速度项和切向加速度项.文献^[7-8]采用力学补偿法对弹载环境下的内外杆臂效应进行补偿.由于角加速度是通过对角速度测量值直接数值微分得到，微分运算会放大误差，进而引起切向加速度项误差放大.文献^[9]根据$\mathit{\boldsymbol{\dot \omega }} \times \mathit{\boldsymbol{r}} \bot \mathit{\boldsymbol{r}}$的特点，将加速度计的敏感轴沿杆臂r的矢量方向布置，避免了求解切向加速度项.但文献^[9]只能消除敏感轴与杆臂r矢量方向平行的加速度计上的切向加速度项，其他两轴加速度计上的切向加速度项仍不可忽略.3)当杆臂长度未知时，将杆臂长度扩充为系统的状态变量，以速度误差作为系统观测量，引入卡尔曼滤波对杆臂效应误差予以补偿^[10-16]，但现有文献均采用高精度的陀螺仪，以减少角速度及角加速度测量误差对杆臂效应估计的影响，而在AHRS系统里，MEMS陀螺仪的精度有限.受篇幅限制，本文仅考虑杆臂长度已知时，以解析方式补偿杆臂效应，未对杆臂效应的估计进行展开分析.

本文基于AHRS系统，通过对杆臂效应的误差机理以及现有滤波、补偿方法的不足进行分析，提出了一种改进的杆臂效应补偿方法，与现有方法相对比，显著提高了杆臂效应误差补偿精度.

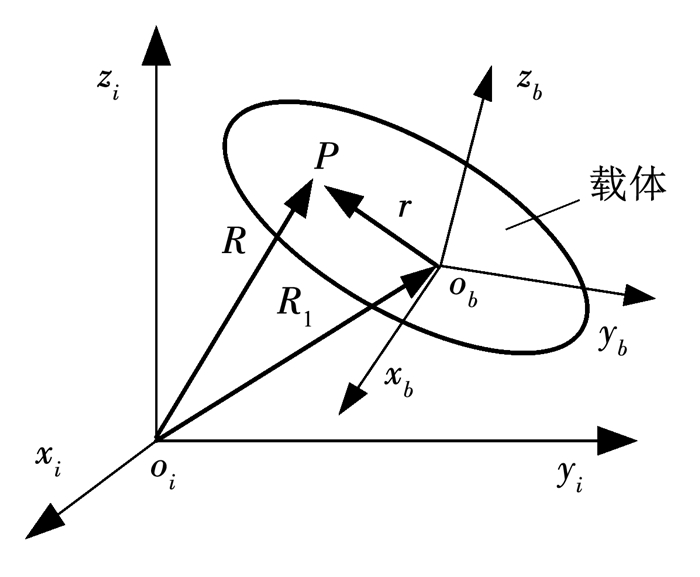
1 杆臂效应的误差机理

定义惯性坐标系(i系)为o_ix_iy_iz_i，载体坐标系(b系)为o_bx_by_bz_b，加速度计安装在载体P处，o_b点为载体的参考点，R为P点在惯性系中的位置矢量，R₁为载体参考点o_b在惯性系中的位置矢量，r为从载体参考点到P点的位置矢量，即为杆臂.位置示意图如图 1所示.

在角运动环境下，由于载体参考点o_b与加速度计安装点P不重合，在加速度计的输出中就含有相对参考点的杆臂效应误差，如式(1)所示

$ \mathit{\boldsymbol{f}}_{{\rm{ip}}}^{\rm{b}} = \mathit{\boldsymbol{f}}_{{\rm{ib}}}^{\rm{b}} + \mathit{\boldsymbol{\omega }}_{{\rm{ib}}}^{\rm{b}} \times \mathit{\boldsymbol{\omega }}_{{\rm{ib}}}^{\rm{b}} \times {\mathit{\boldsymbol{r}}^{\rm{b}}} + \mathit{\boldsymbol{\dot \omega }}_{{\rm{ib}}}^{\rm{b}} \times {\mathit{\boldsymbol{r}}^{\rm{b}}}. $

(1)

式中：f_iP^b为加速度计输出比力矢量在载体系b系下的投影，f_ib^b为载体参考点o_b的比力矢量在载体系b系下的投影，ω_ib^b为载体相对惯性坐标系的角速度在载体系b系下的投影.

杆臂效应引起的干扰加速度表示为

$ {\rm{ \mathsf{ δ} }}{\mathit{\boldsymbol{f}}^{\rm{b}}} = \mathit{\boldsymbol{\omega }}_{{\rm{ib}}}^{\rm{b}} \times \left( {\mathit{\boldsymbol{\omega }}_{{\rm{ib}}}^{\rm{b}} \times {\mathit{\boldsymbol{r}}^{\rm{b}}}} \right) + \mathit{\boldsymbol{\dot \omega }}_{{\rm{ib}}}^{\rm{b}} \times {\mathit{\boldsymbol{r}}^{\rm{b}}}. $

(2)

其中第1项定义为杆臂效应的向心加速度项，第2项定义为杆臂效应的切向加速度项.

杆臂效应对加速度计测姿的影响航姿参考系统中加速度计通过测量重力加速度在载体系各坐标轴上的投影分量来获取水平姿态角，以y轴为例

$ \gamma = \arcsin \left( {\frac{{f_y^{\rm{b}}}}{g}} \right). $

(3)

式中：f_y^b为y轴加速度计输出比力，γ为横滚角，g为重力加速度，g=9.8 m/s².

动态环境下杆臂效应会对加速度计测姿造成极大的影响.记叠加在y轴上的杆臂效应向心加速度项与切向加速度项分别为Δf₁, Δf₂.为简化分析，只考虑z轴上有角速度ω_ibz^b与角加速度$\dot \omega _{{\rm{ibz}}}^{\rm{b}}$，其余轴上角速度与角加速度为0.

$ \left\{ {\begin{array}{*{20}{l}} {\omega _{{\rm{ib}}z}^{\rm{b}} = \omega ;}\\ {\dot \omega _{{\rm{ib}}z}^{\rm{b}} = \dot \omega ;}\\ {\omega _{{\rm{ib}}y}^{\rm{b}} = \omega _{{\rm{ib}}x}^{\rm{b}} = \dot \omega _{{\rm{ib}}y}^{\rm{b}} = \dot \omega _{{\rm{ib}}x}^{\rm{b}} = 0;}\\ {{r_x} = r,{r_y} = {r_z} = 0.} \end{array}} \right. $

式中：ω_ibx^b, ω_iby^b为载体绕x, y轴转动的角速度，单位(°/s)，$\dot \omega _{{\rm{ib}}x}^{\rm{b}}$, $\dot \omega _{{\rm{ib}}y}^{\rm{b}}$为载体绕x, y轴转动的角加速度，单位(°/s²)，r_x, r_y, r_z为杆臂矢量r在x, y, z轴上的投影，单位(m)，记投影到y轴上的杆臂效应向心加速度项与切向加速度项分别为Δf₁, Δf₂.

由式(2)、(3)可以得到，杆臂效应造成的横滚角误差Δγ为

$ \Delta \gamma = \frac{{\Delta f}}{{g\cos \gamma }} = \frac{{\Delta {f_1}}}{{g\cos \gamma }} + \frac{{\Delta {f_2}}}{{g\cos \gamma }}. $

(4)

在横滚角γ=0°时，由Δf₁, Δf₂分别造成的横滚角误差Δγ₁, Δγ₂如图 2所示.

图 2中，Δγ₁为向心加速度造成的姿态误差；Δγ₂为切向加速度造成的姿态误差.由图 2可见随着角速度、角加速度以及杆臂长度的增加，杆臂效应相应增大，加速度计测姿误差也越大，只有通过对加速度计杆臂效应进行有效的补偿，才能保证AHRS系统测姿精度.

2 现有杆臂效应补偿方法的不足

目前处理杆臂效应的解析方法主要为低通滤波法和力学补偿法.在实际工程中二者应用广泛，但也存在其自身的不足.

2.1 低通滤波法的不足

从现有文献看，采用低通滤波法主要应用在初始对准场景中.此时载体一般没有大的角机动，只有微幅晃动(振动).该环境下的干扰频率远高于舒拉频率以及地球自转频率，可视为高频干扰^[6].但是低通滤波无法滤除振动产生的直流分量.

设在振动环境下，载体沿俯仰轴、横滚轴有频率相同，相位差为90°的角振动，即

$ \left\{ {\begin{array}{*{20}{l}} {\theta \left( t \right) = {\theta _{\rm{m}}}\sin \mathit{\Omega }t,}\\ {\gamma \left( t \right) = {\gamma _{\rm{m}}}\cos \mathit{\Omega }t,}\\ {\psi \left( t \right) = 0.} \end{array}} \right. $

(5)

式中：Ω为振动的角频率，θ为俯仰角，θ_m为俯仰角的振动幅值，γ为横滚角，γ_m为横滚角的振动幅值，ψ为方位角.

由欧拉角微分方程，振动环境下的角速度为

$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\omega }}_{{\rm{nb}}}^{\rm{b}} = \left[ {\begin{array}{*{20}{c}} {\omega _{{\rm{nb}}x}^{\rm{b}}}\\ {\omega _{{\rm{nb}}y}^{\rm{b}}}\\ {\omega _{{\rm{nb}}z}^{\rm{b}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0\\ {\dot \gamma }\\ 0 \end{array}} \right] + {\mathit{\boldsymbol{C}}_\gamma }\left[ {\begin{array}{*{20}{c}} {\dot \theta }\\ 0\\ 0 \end{array}} \right] + {\mathit{\boldsymbol{C}}_\gamma }{\mathit{\boldsymbol{C}}_\theta }\left[ {\begin{array}{*{20}{c}} 0\\ 0\\ { - \dot \psi } \end{array}} \right]}\\ { = \left[ \begin{array}{l} {\theta _{\rm{m}}}\mathit{\Omega }\cos \mathit{\Omega }t\cos \left( {{\gamma _{\rm{m}}}\cos \mathit{\Omega }t} \right)\\ - {\gamma _{\rm{m}}}\mathit{\Omega }\sin \mathit{\Omega }t\\ {\theta _{\rm{m}}}\mathit{\Omega }\cos \mathit{\Omega }t\cos \left( {{\gamma _{\rm{m}}}\cos \mathit{\Omega }t} \right) \end{array} \right].} \end{array} $

(6)

在微幅振动环境下，可以把θ, γ当作小角度处理，即

$ \mathit{\boldsymbol{\omega }}_{{\rm{nb}}}^{\rm{b}} = \left[ \begin{array}{l} {\theta _{\rm{m}}}\mathit{\Omega }\cos \mathit{\Omega }t\\ - {\gamma _{\rm{m}}}\mathit{\Omega }\sin \mathit{\Omega }t\\ {\gamma _{\rm{m}}}{\theta _{\rm{m}}}\mathit{\Omega }{\cos ^2}\mathit{\Omega }t \end{array} \right]. $

(7)

由于地球自转相对动态环境下的角速度可以忽略，因此可认为ω_ib^b≈ω_nb^b.将式(7)代入式(2)的向心加速度项中，可发现向心加速度项中存在直流分量：

$ \left\{ {\begin{array}{*{20}{l}} {\left( {\omega _{{\rm{ib}}x}^{\rm{b}}} \right)_{{\rm{DC}}}^2 = \theta _{\rm{m}}^2{\mathit{\Omega }^2}/2,}\\ {\left( {\omega _{{\rm{ib}}y}^{\rm{b}}} \right)_{{\rm{DC}}}^2 = \gamma _{\rm{m}}^2{\mathit{\Omega }^2}/2,}\\ {\left( {\omega _{{\rm{ib}}z}^{\rm{b}}} \right)_{{\rm{DC}}}^2 = 3\gamma _{\rm{m}}^2\theta _{\rm{m}}^2{\mathit{\Omega }^2}/8.} \end{array}} \right. $

(8)

由式(8)可见，振动环境下向心加速度项存在直流分量，依靠低通滤波无法将直流分量滤除.

对式(6)求角加速度，可得

$ \mathit{\boldsymbol{\dot \omega }}_{{\rm{nb}}}^{\rm{b}} = {\mathit{\Omega }^2}\left[ \begin{array}{l} - {\theta _{\rm{m}}}\sin \mathit{\Omega }t - \gamma _{\rm{m}}^2{\theta _{\rm{m}}}(\sin 3\mathit{\Omega }t + \sin \mathit{\Omega }t)/4\\ - {\gamma _{\rm{m}}}\cos \mathit{\Omega }t\\ - {\theta _{\rm{m}}}{\gamma _{\rm{m}}}\sin 2\mathit{\Omega t} \end{array} \right]. $

在振动环境下角加速度仍为振荡形式，通过低通滤波可滤除切向加速度.但在机动环境下，若角加速度也包含有直流项时，低通滤波无法滤除角加速度直流项.

2.2 力学补偿法的不足

力学补偿法通过陀螺仪输出获取角速度ω_ib^b补偿向心加速度项，通过对角速度ω_ib^b求微分获得角加速度$\mathit{\boldsymbol{\dot \omega }}_{{\rm{ib}}}^{\rm{b}}$补偿切向加速度项.但是向心加速度项的补偿会受限于陀螺测量精度，同时直接通过对陀螺仪输出值微分计算获取角加速度$\mathit{\boldsymbol{\dot \omega }}_{{\rm{ib}}}^{\rm{b}}$，不可避免会引起切向加速度项误差放大.令通过对陀螺输出值微分获得的角加速度为$\mathrm{\dot{\hat{ }\!\!\omega\!\!\text{ }}}_{\text{ib}}^{\text{b}}=\mathrm{ }\!\!\alpha\!\!\text{ }$，可表示为

$ \mathit{\boldsymbol{\hat \omega }}_{{\rm{ib}}}^{\rm{b}}\left( {t + \Delta T} \right) - \mathit{\boldsymbol{\hat \omega }}_{{\rm{ib}}}^{\rm{b}}\left( t \right) = \mathit{\boldsymbol{a}}\Delta T. $

(9)

式中:$\mathit{\boldsymbol{\widehat \omega }}_{{\rm{ib}}}^{\rm{b}}$为陀螺仪所测角速度，ΔT为采样间隔时间.式(9)两边求方差

$ var\left( {\mathit{\boldsymbol{\hat \omega }}_{{\rm{ib}}}^{\rm{b}}\left( {t + \Delta T} \right) - \mathit{\boldsymbol{\hat \omega }}_{{\rm{ib}}}^{\rm{b}}\left( t \right)} \right) = var\left( {\mathit{\boldsymbol{a}}\Delta T} \right). $

(10)

令${\mathop{\rm var}} \left( {\mathit{\boldsymbol{\widehat \omega }}_{{\rm{ib}}}^{\rm{b}}\left( {t + \Delta T} \right)} \right) = {\mathop{\rm var}} \left( {\mathit{\boldsymbol{\widehat \omega }}_{{\rm{ib}}}^{\rm{b}}\left( t \right)} \right) = {\mathit{\boldsymbol{Q}}_\omega }$，且不相关，则由方差性质，可得

$ var\left( \mathit{\boldsymbol{a}} \right) = 2{\mathit{\boldsymbol{Q}}_{\rm{ \mathsf{ ω} }}}/\Delta {T^2}. $

(11)

由此可看出微分求角加速度$\mathrm{\dot{\hat{ }\!\!\omega\!\!\text{ }}}_{ib}^{b}$误差会放大，且采样时间越短，噪声放大越严重.

3 一种改进的杆臂效应补偿方法

利用低通滤波法，杆臂效应中的向心加速度项会残存整流误差项；再者当角加速度也含有直流分量时，杆臂效应中的切向加速度项也会出现低通滤波无法滤除的整流误差.采用力学补偿法，向心加速度项的求解误差会受到陀螺测量误差的影响；而通过角速度微分获取角加速度，会引起切向加速度项误差激剧放大.考虑到多加速度计可以直接解析地求解角加速度^[17-18]，可避免角速度微分计算造成的误差放大.因此综合考虑低通滤波法、力学补偿法以及多加速度计解析求解法，提出一种改进的杆臂效应补偿方法见图 3.对于杆臂效应中的向心加速度，在低于给定角频率阈值工况下采用低通滤波法，在高于给定角频率阈值工况下采用力学补偿+低通滤波法.对杆臂效应中的切向加速度项，通过多加速度计解析求解角加速度.

3.1 基于角频率阈值判决的向心加速度项补偿

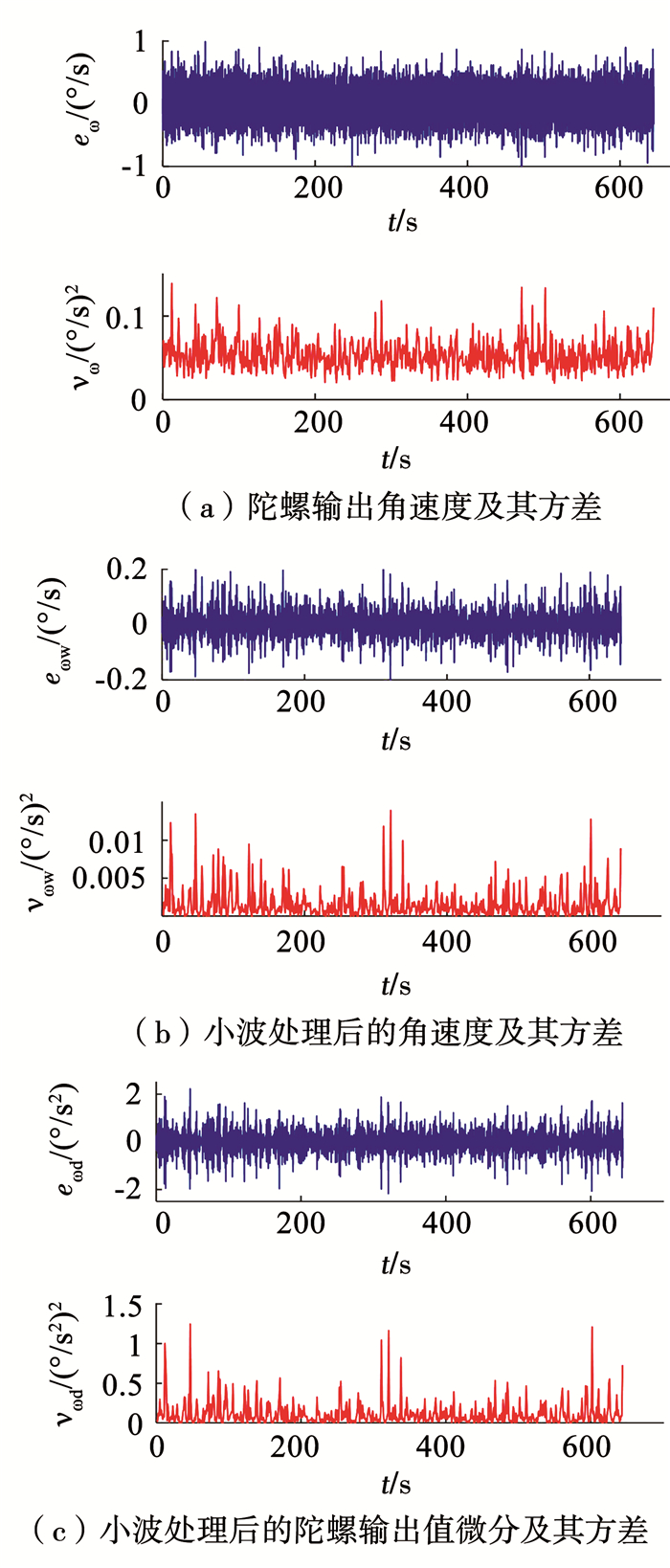
由于式(8)在振动环境下(ω_ibx^b)², (ω_iby^b)², (ω_ibz^b)²项会产生低通滤波无法滤除的直流分量.力学补偿法对这几项可由陀螺仪直接测量获取，令Δω_ibx^b=Δω_iby^b=Δω_ibz^b为陀螺仪测量误差.根据陀螺随机误差模型

$ \mathit{\boldsymbol{\hat \omega }}_{{\rm{ib}}}^{\rm{b}} = \mathit{\boldsymbol{\omega }}_{{\rm{ib}}}^{\rm{b}} + \Delta \mathit{\boldsymbol{\omega }}_{{\rm{ib}}}^{\rm{b}} = \mathit{\boldsymbol{\omega }}_{{\rm{ib}}}^{\rm{b}} + \mathit{\boldsymbol{b}} + \mathit{\boldsymbol{n}}. $

(12)

式中：$\mathit{\boldsymbol{\widehat \omega }}_{{\rm{ib}}}^{\rm{b}}$为陀螺仪测量角速度；ω_ib^b为真实的角速度；Δω_ib^b为角速度测量误差；b为陀螺仪常值偏差；n为陀螺仪随机漂移噪声.

$ \left\{ \begin{array}{l} \mathit{\boldsymbol{\hat \omega }}_{{\rm{ib}}}^{\rm{b}} = {\left[ {\begin{array}{*{20}{c}} {\hat \omega _{{\rm{ib}}x}^{\rm{b}}}&{\hat \omega _{{\rm{ib}}y}^{\rm{b}}}&{\hat \omega _{{\rm{ib}}z}^{\rm{b}}} \end{array}} \right]^{\rm{T}}},\\ \mathit{\boldsymbol{\omega }}_{{\rm{ib}}}^{\rm{b}} = {\left[ {\begin{array}{*{20}{c}} {\omega _{{\rm{ib}}x}^{\rm{b}}}&{\omega _{{\rm{ib}}y}^{\rm{b}}}&{\omega _{{\rm{ib}}z}^{\rm{b}}} \end{array}} \right]^{\rm{T}}},\\ \Delta \mathit{\boldsymbol{\omega }}_{{\rm{ib}}}^{\rm{b}} = {\left[ {\begin{array}{*{20}{c}} {\Delta \omega _{{\rm{ib}}x}^{\rm{b}}}&{\Delta \omega _{{\rm{ib}}y}^{\rm{b}}}&{\Delta \omega _{{\rm{ib}}z}^{\rm{b}}} \end{array}} \right]^{\rm{T}}},\\ \mathit{\boldsymbol{b}} = {\left[ {\begin{array}{*{20}{c}} {{b_x}}&{{b_y}}&{{b_z}} \end{array}} \right]^{\rm{T}}},\\ \mathit{\boldsymbol{n}} = {\left[ {\begin{array}{*{20}{l}} {{n_x}}&{{\mathit{n}_y}}&{{\mathit{n}_\mathit{z}}} \end{array}} \right]^{\rm{T}}}. \end{array} \right. $

则根据式(12)，经过小波去噪后，可认为

$ \Delta \omega _{{\rm{ib}}x}^{\rm{b}} = \Delta \omega _{{\rm{ib}}y}^{\rm{b}} = \Delta \omega _{{\rm{ib}}z}^{\rm{b}} = {b_x} = {b_y} = {b_z} = b. $

(13)

此时陀螺仪对(ω_ibx^b)²项的测量误差绝对值为

$ \left| {{{\left( {\hat \omega _{{\rm{ib}}x}^{\rm{b}}} \right)}^2} - {{\left( {\omega _{{\rm{ib}}x}^{\rm{b}}} \right)}^2}} \right| \approx \left| {2\Delta \omega _{{\rm{ib}}x}^{\rm{b}}\omega _{{\rm{ib}}x}^{\rm{b}}} \right| = \left| {2\omega _{{\rm{ib}}x}^{\rm{b}}b} \right|, $

(14)

将式(7)代入式(14)，即

$ \left| {2\omega _{{\rm{ib}}x}^{\rm{b}}b} \right| = \left| {2{\theta _{\rm{m}}}\Omega b\cos \Omega t} \right|, $

(15)

此时陀螺仪对(ω_iby^b)²项的测量误差绝对值为

$ \left| {{{\left( {\hat \omega _{{\rm{ib}}y}^{\rm{b}}} \right)}^2} - {{\left( {\omega _{{\rm{ib}}y}^{\rm{b}}} \right)}^2}} \right| \approx \left| {2\Delta \omega _{{\rm{ib}}y}^{\rm{b}}\omega _{{\rm{ib}}y}^{\rm{b}}} \right| = \left| {2\omega _{{\rm{ib}}y}^{\rm{b}}b} \right|, $

(16)

将式(7)代入式(16)，即

$ \left| {2\omega _{{\rm{ib}}y}^{\rm{b}}b} \right| = \left| { - 2{\gamma _{\rm{m}}}\Omega b\sin \Omega t} \right|, $

(17)

此时陀螺仪对(ω_ibz^b)²项的测量误差绝对值为

$ \left| {{{\left( {\hat \omega _{{\rm{ib}}z}^{\rm{b}}} \right)}^2} - {{\left( {\omega _{{\rm{ib}}z}^{\rm{b}}} \right)}^2}} \right| \approx \left| {2\Delta \omega _{{\rm{ib}}z}^{\rm{b}}\omega _{{\rm{ib}}z}^{\rm{b}}} \right| = \left| {2\omega _{{\rm{ib}}z}^{\rm{b}}b} \right|, $

(18)

将式(7)代入式(18)，即

$ \left| {2\omega _{{\rm{ib}}z}^{\rm{b}}b} \right| = \left| {{\gamma _{\rm{m}}}{\theta _{\rm{m}}}\Omega b\left( {1 + \cos 2\Omega t} \right)} \right|. $

(19)

由式(15)、式(17)可以看出采用力学补偿后(ω_ibx^b)², (ω_iby^b)²的计算误差仍为振荡形式，通过低通滤波没有整流误差.而由式(19)可以看出，力学补偿后(ω_ibz^b)²再经过低通滤波仍有残存整流误差|γ_mθ_mΩb|.

将力学补偿后的整流误差|γ_mθ_mΩb|与对应的通过低通滤波后残存整流误差3γ_m²θ_m²Ω²/8比较.

设角频率阈值Ω₀为

$ {\Omega _0} = 8\left| b \right|/\left( {3{\gamma _{\rm{m}}}{\theta _{\rm{m}}}} \right), $

(20)

当Ω≥Ω₀时，有

$ \left| {{\gamma _{\rm{m}}}{\theta _{\rm{m}}}\Omega b} \right| \le 3\gamma _{\rm{m}}^2\theta _{\rm{m}}^2{\Omega ^2}/8, $

(21)

而在Ω < Ω₀时，有

$ \left| {{\gamma _{\rm{m}}}{\theta _{\rm{m}}}\Omega b} \right| > 3\gamma _{\rm{m}}^2\theta _{\rm{m}}^2{\Omega ^2}/8. $

(22)

由式(21)、(22)可见，当角频率Ω大于角频率阈值Ω₀时，采用力学补偿+低通滤波法造成的残存整流误差小于直接采用低通滤波造成的整流误差；而在角频率Ω小于角频率阈值Ω₀时，直接采用低通滤波造成的整流误差小于采用力学补偿+低通滤波法造成的残存整流误差.

3.2 利用多加速度计补偿杆臂效应切向加速度项

因微分法求解角加速度会放大误差，而低通滤波无法滤除直流分量，因此提出两种利用多加速度计解析求解角加速度的改进方法.

3.2.1 6加速度计构型1

设置6加速度计构型，如图 4所示.6个加速度计安装在立方体6个面的中心，其敏感轴沿着每个面的对角线.令θ^b表示加速度计在载体系中敏感方向矢量，在6加速度计构型其中心位于P点，立方体的边长为2l时，由式(1)可得单个加速度计的输出表达式为

$ A = {\left( {{\mathit{\boldsymbol{\theta }}^{\rm{b}}}} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{f}}_{{\rm{i}}P}^{\rm{b}} + \mathit{\boldsymbol{\omega }}_{{\rm{ib}}}^{\rm{b}} \times \mathit{\boldsymbol{\omega }}_{{\rm{ib}}}^{\rm{b}} \times {\mathit{\boldsymbol{l}}^{\rm{b}}} + \mathit{\boldsymbol{\dot \omega }}_{{\rm{ib}}}^{\rm{b}} \times {\mathit{\boldsymbol{l}}^{\rm{b}}}} \right), $

(23)

该构型方案的安装参数矩阵

$ \left\{ \begin{array}{l} {\mathit{\boldsymbol{l}}^{\rm{b}}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{l}}_1^{\rm{b}}}& \cdots &{\mathit{\boldsymbol{l}}_6^{\rm{b}}} \end{array}} \right] = l\left[ {\begin{array}{*{20}{c}} 0&0&{ - 1}&1&0&0\\ 0&{ - 1}&0&0&1&0\\ { - 1}&0&0&0&0&1 \end{array}} \right],\\ {\mathit{\boldsymbol{\theta }}^{\rm{b}}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\theta }}_1^{\rm{b}}}& \cdots &{\mathit{\boldsymbol{\theta }}_6^{\rm{b}}} \end{array}} \right] = \frac{1}{{\sqrt 2 }}\left[ {\begin{array}{*{20}{c}} 1&1&0&0&{ - 1}&{ - 1}\\ 1&0&1&{ - 1}&0&1\\ 0&1&1&1&1&0 \end{array}} \right]. \end{array} \right. $

将安装参数矩阵代入式(23)，可得角加速度

$ \left[ {\begin{array}{*{20}{c}} {\dot \omega _{{\rm{ib}}x}^{\rm{b}}}\\ {\dot \omega _{{\rm{ib}}y}^{\rm{b}}}\\ {\dot \omega _{{\rm{ib}}z}^{\rm{b}}} \end{array}} \right] = \frac{{\sqrt 2 }}{{4l}}\left[ {\begin{array}{*{20}{c}} {{A_1} + {A_5} - {A_2} - {A_6}}\\ {{A_3} - {A_1} - {A_4} - {A_6}}\\ {{A_2} + {A_5} - {A_3} - {A_4}} \end{array}} \right]. $

(24)

根据式(24)，可由6个加速度计直接求解角加速度，避免了微分求解角加速度致使误差放大的问题.利用多加速度计求解角加速度$\mathit{\boldsymbol{\dot \omega }}_{{\rm{ib}}}^{\rm{b}}$的误差

$ \left[ {\begin{array}{*{20}{c}} {\Delta \dot \omega _{{\rm{ib}}x}^{\rm{b}}}\\ {\Delta \dot \omega _{{\rm{ib}}y}^{\rm{b}}}\\ {\Delta \dot \omega _{{\rm{ib}}z}^{\rm{b}}} \end{array}} \right] = \frac{{\sqrt 2 }}{{4l}}\left[ {\begin{array}{*{20}{c}} {\Delta {A_1} + \Delta {A_5} - \Delta {A_2} - \Delta {A_6}}\\ {\Delta {A_3} - \Delta {A_1} - \Delta {A_4} - \Delta {A_6}}\\ {\Delta {A_2} + \Delta {A_5} - \Delta {A_3} - \Delta {A_4}} \end{array}} \right]. $

(25)

3.2.2 6加速度计构型2

构型1中加速度计的布局相对6个基准面为倾斜安装.文献^[20]指出斜置IMU，存在大安装误差角，安装误差角二次项的影响不能忽略.文献^[21]指出斜装形式下的标定需要：1)设计倾斜的标定工装；2)设计专门的斜装标定算法.由此可见构型1中加速度计的布局对实际安装以及标定都带来一定的困难.文献^[22]指出正交双加速度计可消除安装误差角影响.文献^[23]中给出了一种便于安装的6加速度计构型，但该方案将多个加速度计安装在同一点，若采用体积较大的石英挠性加速度计，会产生较大的安装误差.为此设计了另一种构型：6加速度计构型2，如图 5所示.将各加速度计的安装位置移至各基准面的中心，避免了将多个加速度计安装在同一点造成的安装误差.各加速度计距离质心的距离均为l.同时构型2不存在大安装误差角问题.

该构型方案的安装参数矩阵

$ \left\{ \begin{array}{l} {\mathit{\boldsymbol{l}}^{\rm{b}}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{l}}_1^{\rm{b}}}& \cdots &{\mathit{\boldsymbol{l}}_6^{\rm{b}}} \end{array}} \right] = l\left[ {\begin{array}{*{20}{c}} 0&0&1&{ - 1}&0&0\\ { - 1}&1&0&0&0&0\\ 0&0&0&0&1&{ - 1} \end{array}} \right],\\ {\mathit{\boldsymbol{\theta }}^{\rm{b}}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\theta }}_1}}& \cdots &{{\mathit{\boldsymbol{\theta }}_6}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&0&0&0&1&1\\ 0&0&1&1&0&0\\ 1&1&0&0&0&0 \end{array}} \right]. \end{array} \right. $

代入式(23)，可得角加速度为

$ \left[ {\begin{array}{*{20}{c}} {\dot \omega _{{\rm{ib}}x}^{\rm{b}}}\\ {\dot \omega _{{\rm{ib}}y}^{\rm{b}}}\\ {\dot \omega _{{\rm{ib}}z}^{\rm{b}}} \end{array}} \right] = \frac{1}{{2l}}\left[ {\begin{array}{*{20}{c}} {{A_1} - {A_2}}\\ {{A_5} - {A_6}}\\ {{A_3} - {A_4}} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {\omega _{{\rm{ib}}y}^{\rm{b}}\omega _{{\rm{ib}}z}^{\rm{b}}}\\ {\omega _{{\rm{ib}}z}^{\rm{b}}\omega _{{\rm{ib}}x}^{\rm{b}}}\\ {\omega _{{\rm{ib}}x}^{\rm{b}}\omega _{{\rm{ib}}y}^{\rm{b}}} \end{array}} \right]. $

(26)

对比式(24)及式(26)可见，构型1的角加速度的求解只需利用加速度计即可求解，而构型2的角加速度的求解，还须引入陀螺测量角速度信息才能完成角加速度的求解.该构型方案求解角加速度$\mathit{\boldsymbol{\dot \omega }}_{{\rm{ib}}}^{\rm{b}}$的误差

$ \left[ {\begin{array}{*{20}{c}} {\Delta \dot \omega _{{\rm{ib}}x}^{\rm{b}}}\\ {\Delta \dot \omega _{{\rm{ib}}y}^{\rm{b}}}\\ {\Delta \dot \omega _{{\rm{ib}}z}^{\rm{b}}} \end{array}} \right] = \frac{1}{{2l}}\left[ {\begin{array}{*{20}{c}} {\Delta {A_1} - \Delta {A_2}}\\ {\Delta {A_5} - \Delta {A_6}}\\ {\Delta {A_3} - \Delta {A_4}} \end{array}} \right] - \left[ \begin{array}{l} \omega _{{\rm{ib}}y}^{\rm{b}}\Delta \omega _{{\rm{ib}}z}^{\rm{b}} + \omega _{{\rm{ib}}z}^{\rm{b}}\Delta \omega _{{\rm{ib}}y}^{\rm{b}}\\ \omega _{{\rm{ib}}z}^{\rm{b}}\Delta \omega _{{\rm{ib}}x}^{\rm{b}} + \omega _{{\rm{ib}}x}^{\rm{b}}\Delta \omega _{{\rm{ib}}z}^{\rm{b}}\\ \omega _{{\rm{ib}}x}^{\rm{b}}\Delta \omega _{{\rm{ib}}y}^{\rm{b}} + \omega _{{\rm{ib}}y}^{\rm{b}}\Delta \omega _{{\rm{ib}}x}^{\rm{b}} \end{array} \right], $

将式(7)代入，可得振动环境下，经低通滤波后，角加速度误差$\Delta \mathit{\boldsymbol{\dot \omega }}_{{\rm{ib}}}^{\rm{b}}$的整流残差为

$ \left[ {\begin{array}{*{20}{c}} {\Delta \dot \omega _{{\rm{ib}}x}^{\rm{b}}}\\ {\Delta \dot \omega _{{\rm{ib}}y}^{\rm{b}}}\\ {\Delta \dot \omega _{{\rm{ib}}z}^{\rm{b}}} \end{array}} \right] = \frac{1}{{2l}}\left[ {\begin{array}{*{20}{c}} {\Delta {A_1} - \Delta {A_2}}\\ {\Delta {A_5} - \Delta {A_6}}\\ {\Delta {A_3} - \Delta {A_4}} \end{array}} \right] - \frac{1}{{2l}}\left[ {\begin{array}{*{20}{c}} {{\gamma _{\rm{m}}}{\theta _{\rm{m}}}\Omega \Delta \omega _{{\rm{ib}}y}^{\rm{b}}}\\ {{\gamma _{\rm{m}}}{\theta _{\rm{m}}}\Omega \Delta \omega _{{\rm{ib}}x}^{\rm{b}}}\\ 0 \end{array}} \right]. $

(27)

相比构型1，构型2在振动环境下会有整流残差，且随着角频率、振幅的增加，其残留整流误差也随之增大.对比式(24)及式(26)，在角加速度项含有直流分量的情况下，构型1能很好地补偿切向加速度，而构型2求解角加速度的误差项中含有角速度信息，也即是构型2求解角加速度的误差会随着角速度的增大而增大.

4 仿真验证 4.1 杆臂效应向心加速度项补偿

设Δω_ibx^b=Δω_iby^b=Δω_ibz^b=0.2°/s为MEMS陀螺仪测量误差.俯仰角的振动幅值θ_m与横滚角的振动幅值γ_m范围为0°~10°，杆臂半径为r=1 m.分别采用低通滤波算法以及改进算法对杆臂效应向心加速度项进行仿真验算，如图 6所示.

由图 6可见，对于向心加速度的补偿，在角频率大于角频率阈值时，改进算法的残存整流误差小于低通滤波法残存整流误差.随着振幅增大，角频率阈值迅速减小，也即是在大振幅工况下，改进算法远胜于低通滤波法.

4.2 杆臂效应切向加速度项补偿

在实际工程上应用的MEMS加速度计其精度已达到1×10^-4 g^[19].因此在仿真中设定加速度计常值漂移服从Gauss分布，均方差为10^-4 g.

4.2.1 非振动低动态环境

仿真时间设为650 s，载体的角加速度取为${\left[ {\dot \omega _{{\rm{ib}}x}^{\rm{b}}\;\;\;\dot \omega _{{\rm{ib}}y}^{\rm{b}}\;\;\;\dot \omega _{{\rm{ib}}z}^{\rm{b}}} \right]^{\rm{T}}} = {\left[ {0.01\;\;0.01\;\;0.01} \right]^{\rm{T}}}\left( {^\circ /{{\rm{s}}^2}} \right)$，初始角速度取为${\left[ {\omega _{{\rm{ib}}x}^{\rm{b}}\;\;\;\omega _{{\rm{ib}}y}^{\rm{b}}\;\;\;\omega _{{\rm{ib}}z}^{\rm{b}}} \right]^{\rm{T}}} = {\left[ {0\;\;0\;\;0} \right]^{\rm{T}}}\left( {^\circ /{\rm{s}}} \right)$，内杆臂l为5 cm，由直接微分法、多加速度计构型1以及构型2求解杆臂效应的切向加速度项误差如图 7(a)所示(以x轴角加速度为例).

4.2.2 非振动高动态环境

角加速度为${\left[ {\dot \omega _{{\rm{ib}}x}^{\rm{b}}\;\;\;\dot \omega _{{\rm{ib}}y}^{\rm{b}}\;\;\;\dot \omega _{{\rm{ib}}z}^{\rm{b}}} \right]^{\rm{T}}} = {\left[ {0.5\;\;0.5\;\;0.5} \right]^{\rm{T}}}\left( {^\circ /{{\rm{s}}^2}} \right)$，其余仿真设置与非振动低动态环境一致.求解杆臂效应的切向加速度项误差如图 8(b)所示.

从图 7可见，构型1解析求解的切向加速度比直接微分法的精度提高了1个数量级.构型2的求解误差随着角速度的增大而增大，但在低动态环境下构型2的求解误差是可以接受的.在仿真650 s时，构型2的求解误差达到-0.042(m/s²)，与直接微分法的求解误差相仿，而此时角速度达到325(°/s).也即是除了高动态环境下，一般的工程应用也可采用构型2.

4.2.3 振动环境

设定振动频率范围为0~20 Hz，俯仰角的振幅θ_m与横滚角的振幅γ_m设为10°，仿真时间为40 s，两种加速度计构型在振动环境下的求解杆臂效应的切向加速度项误差如图 9所示(以x轴角加速度为例)

从图 9可看到，振动频率对构型1影响较小，而构型2的切向加速度误差随着振动频率增加而增大.结合图 7、图 8可看到，无论是振动环境或非振动环境，低动态或高动态，构型1的性能总是优于构型2.但是构型1的安装方式为斜置安装，需要设计专用的标定工装以及斜装标定算法，给工程实现带来一定的难度.构型2为正交安装，可以利用重力加速度的幅值平方g²作为参考基准，在标定过程中不受安装误差角的影响.同时无须设计专用标定工装，给工程实现带来一定便利.

实际工程中，惯性器件经过一定时间的使用其自身性能参数会随时间的推移与应用环境的变化而发生改变，同时在使用过程中由于摩擦、振动等因素的影响，惯性器件的安装位置、安装误差角也可能发生变化，需重新标定才能满足使用要求.因此对现场无精密标定设备、且工况为低振动、低动态环境，优先采用构型2.而高振动、高动态环境优先采用构型1.

4.2.4 内杆臂对多加速度计测姿的影响

由式(24)、式(26)可看到，多加速度计的内杆臂长度越长，多加速度计测姿精度越高.以非振动低动态环境下测姿为例，内杆臂l长度范围为1 cm~4 cm，构型1和构型2的切向加速度误差如图 9所示.

从图 9可以看到构型1和构型2内杆臂l越大，求解的角加速度误差越小.但是在实际工程中，仪器安装的空间总是有限的，为提高求解精度在有限的安装空间里应尽可能增大内杆臂长度.

5 结论

本文研究了杆臂效应误差对加速度计测姿精度的影响，针对低通滤波法与力学补偿法各自的不足，提出了一种改进的杆臂效应误差补偿方案.1)对向心加速度项，以振动角频率为判别标准，在低于给定角频率阈值时采用低通滤波法，在高于给定角频率阈值时采用力学补偿+低通滤波法.与传统的低通滤波法对比，改进算法显著提高了向心加速度项的补偿精度.2)对切向加速度项，设计了两种多加速度计构型方式，通过多加速度计解析求解角加速度，避免了角速度直接微分造成的误差放大.3)对加速度计构型1和构型2在三种工况环境下的求解精度进行了分析，同时根据构型1、构型2标定参数的难易，确定了构型1和构型2的适用范围.