随着卫星导航应用逐渐深入到社会生活以及军事应用的方方面面,导航接收机收到虚假信号得出错误的定时定位结果将导致重大灾难.尤其在导航战背景下,敌方有针对性施放的欺骗干扰信号可以改变无人机、导弹等载体的运动轨迹,使其到达欺骗干扰方指定的位置[1].如何有效检测欺骗干扰,从而保护己方导航接收机不受欺骗干扰影响,是当前GNSS领域的研究热点[2].
正常工作的导航接收机是自洽的,当欺骗干扰信号存在时会打破原有的参数特征.现有文献都是针对欺骗信号与真实信号在某一参数和特定属性上的区别进行设计.这些属性包括信号到达角[4]、伪距[5-6]、信号载噪比[7]、信号功率[8-9]、导航电文等[10-11].虽然这些方法对于某一类欺骗信号具有很强的检测能力,但是无法适应未来导航战中欺骗模式的快速更新变化.因此融合多种欺骗干扰检测手段是未来高可靠抗欺骗干扰导航接收机的必然选择.由于或融合规则实现简单且可靠性高,所以在工程中得到了广泛应用,但是某种检测器性能下降时,将直接导致融合后的欺骗检测性能大幅下降.融合检测方法在雷达领域研究较多且较为成熟,尤其是分布式检测理论的研究,所以这里参考了雷达领域信号检测相关研究成果,并结合导航领域实际应用场景,尤其是检测器性能实时变化且检测器先验信息未知的场景给出了一种性能实时评估的欺骗检测融合算法.该方法实时评估每一种欺骗检测器的性能,一旦发现某种检测器性能下降,则在融合过程中将该检测器剔除.在不同干扰场景下,采用该算法融合后的性能始终与参与融合中性能最优的检测器性能相当,检测适应能力大幅提高.理论上,该方法可以适用于任意数量,任意种类的欺骗检测方法融合,但为方便说明原理,本文选取了两种常用的欺骗检测方法,即相位差检测的欺骗信号检测算法和多普勒方差检测的欺骗信号检测算法.
1 欺骗信号检测算法 1.1 相位差检测的欺骗信号检测算法在接收机天线阵基线以及姿态条件已知的情况下(对固定安装的天线阵进行预先精密测定),通过卫星星历获取所跟踪卫星的精确位置,即可计算得到真实卫星信号到达天线阵的入射俯仰角以及方位角;通过精密时延标定,可以获取两副天线到达接收机信号处理端的时延差;再结合对接收机载波测量误差的估计,即可得到天线阵对真实卫星信号的测量相位差估计值.将接收机对接收到的实际信号相位差测量结果与真实卫星信号的测量相位差估计值相比较,如果误差超出一定的范围即可判定为欺骗干扰信号.
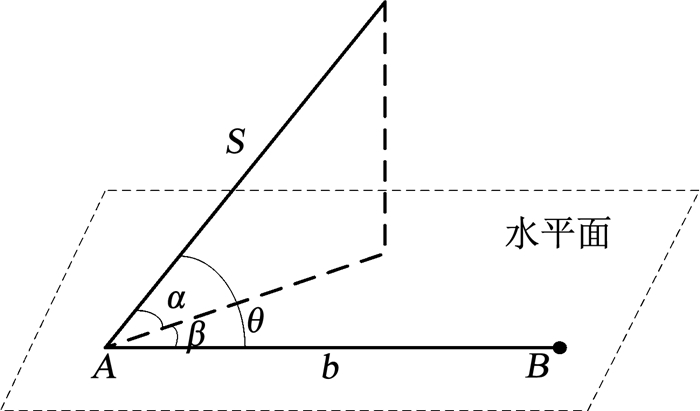
不失一般性,假定接收机天线阵处于水平面上并且以两天线间连线所在方向为方位角零度位置,那么信号入射关系见图 1.图中,A、B为两个天线阵元所处位置,b为天线基线长度,S为入射信号,α为入射信号俯仰角,β为入射信号方位角.根据三余弦定理,信号到达接收天线平面入射角θ为
| $ \cos \theta = \cos \alpha \cos \beta . $ | (1) |
|
图 1 信号入射角与天线阵位置关系 Fig. 1 Relation between the incident angle of signal and the position of antenna array |
可进一步改写为
| $ d\varphi = \left| b \right|\cos \alpha \cos \beta + C + \gamma $ |
式中:dφ为入射信号到两个阵元的相位差,C为天线间的时延差,γ为载波相位测量误差之和.
即同一路信号在两副天线上表现出的相位差与天线基线长度、信号入射俯仰角以及信号入射方位角相关.由文献[12]分析可知,天线阵载波相位差的误差源主要是天线间的时延差.因此,对单路信号相位差检测建立检验统计量ρ,其在真实卫星信号(假设H0)以及欺骗干扰信号(假设H1)条件下的概率分布为
| $ \left\{ \begin{array}{l} H0:\rho = d{\varphi _{{\rm{au}}}} - \widehat {d\varphi } \sim N\left( {0,\sigma } \right),\\ H1:\rho = d{\varphi _{{\rm{sp}}}} - \widehat {d\varphi } \sim N\left( {d{\varphi _{{\rm{sp}}}} - \widehat {d\varphi },\sigma } \right). \end{array} \right. $ |
式中:dφau为真实信号相位测量值,dφsp为欺骗信号相位测量值,
| $ {P_{{\rm{fa}}}} = 1 - \int_{ - {\rho _{{\rm{Th}}}}}^{{\rho _{{\rm{Th}}}}} {{p_{N\left( {0,\sigma } \right)}}} \left( x \right){\rm{d}}x. $ |
式中:pN(0, B)为真实信号下的相位差概率密度分布函数,欺骗信号的检测概率PD为
| $ {P_{\rm{D}}} = 1 - \int_{{\rho _{{\rm{Th}}}}}^\infty {{p_{N\left( {d{\varphi _{{\rm{sp}}}} - \widehat {d\varphi },\sigma } \right)}}} \left( x \right){\rm{d}}x. $ | (2) |
式中:
| $ d{\varphi _{{\rm{sp}}}} - \widehat {d\varphi } \approx 2\left| b \right| \cdot \left| {\sin \left[ {\frac{{{\theta _{{\rm{sp}}}} + {\theta _{{\rm{au}}}}}}{2}} \right]\sin \left[ {\frac{{{\theta _{{\rm{sp}}}} - {\theta _{{\rm{au}}}}}}{2}} \right]} \right|. $ | (3) |
式中下标sp与au分别为欺骗干扰信号和真实卫星信号.由上式可以看出,当欺骗干扰信号与真实卫星信号的相对于接收机天线阵的入射角相同或者对称时,式(3)恒为0,此时单路信号相位差检测无法正确鉴别欺骗信号与真实卫星信号.同时,当欺骗信号与真实信号入射角一定的条件下,天线阵的基线长度越大,H1条件下检验统计量的均值越大,因此天线阵基线长度越大,H0和H1条件下的概率密度分布函数间隔越大,欺骗干扰检测性能越好.
1.2 载波多普勒方差检测的欺骗信号检测算法第二种方法利用了接收机接收真实卫星信号的多普勒特性.接收信号的多普勒是由于卫星与接收机相对运动所致,如(4)式
| $ {f_{\rm{r}}} = {f_{\rm{c}}}\left( {1 - \frac{{{v_{\rm{r}}}}}{c}} \right). $ | (4) |
式中:fc为发射的载波频率,fr为接收机接收到的载波频率,vr为接收机与卫星的相对运动速度,c为光速.由于GNSS信号载波频率高,卫星速度快,因此可以产生±5 kHz范围内的多普勒频偏.如果GNSS接收机的晶振同样有±5 kHz的频偏,则相对频偏可以达到±10 kHz.对于静止终端来说,由卫星运动引起的多普勒频偏变化率最大不超过40 Hz每分钟,因此可以认为其多普勒频偏是线性的[13].对多普勒偏移测量值在一定范围加窗长度下求平均,加窗长度越长其线性度越好.再对接收真实卫星信号的多普勒求方差,其方差在很小的范围内波动,计算方差采用矩形窗如下式
| $ w\left( n \right) = \left\{ {\begin{array}{*{20}{l}} {1,}&{n \le K;}\\ {0,}&{n > K.} \end{array}} \right. $ |
式中:K为加窗长度,K大于100时,其方差的波动小于20 Hz2,即使K缩小为10时,其方差的波动也小于40 Hz2.存在欺骗信号下第i颗卫星的基带信号Si(t)为
| $ \begin{array}{*{20}{c}} {{S_i}\left( t \right) = {A_i}{d_i}\left( {t - {\tau _i}} \right){c_i}\left( {t - {\tau _i}} \right){{\rm{e}}^{j2{\rm{ \mathit{ π} }}t{f_{{\rm{d}},i}}}} + }\\ {{A_{{\rm{is}}}}{d_{{\rm{si}}}}\left( {t - {\tau _{{\rm{si}}}}} \right){c_i}\left( {t - {\tau _{{\rm{si}}}}} \right){{\rm{e}}^{j2{\rm{ \mathit{ π} }}t{f_{{\rm{ds}},i}}}} + \eta \left( t \right).} \end{array} $ |
式中:Ai为真实信号幅度,di为真实信号电文,τi为真实信号时延,ci第i颗卫星扩频码,fd, i为真实信号多普勒,Ais为欺骗信号幅度,dsi为欺骗信号电文,τsi为真实信号时延,fds, i为欺骗信号多普勒,η(t)为噪声.当多普勒方差超过门限则认为受到欺骗攻击.
根据文献[13]可知,接收真实信号的多普勒方差分布满足对数正态分布,因此,对载波多普勒方差检测建立检验统计量ρ,其在真实卫星信号(假设H0)以及欺骗干扰信号(假设H1)条件下的概率分布为
| $ \left\{ \begin{array}{l} H0:\rho \sim \frac{1}{{\rho \sigma \sqrt {2{\rm{ \mathit{ π} }}} }}{{\rm{e}}^{ - {{\left( {\log \rho - {\mu _{{\rm{au}}}}} \right)}^2}/2{\sigma ^2}}},\\ H1:\rho \sim \frac{1}{{\rho \sigma \sqrt {2{\rm{ \mathit{ π} }}} }}{{\rm{e}}^{ - {{\left( {\log \rho - {\mu _{{\rm{sp}}}}} \right)}^{2/2{\sigma ^2}}}}}. \end{array} \right. $ | (5) |
由(5)式可知,当欺骗信号与真实信号多普勒差异越大,该方法的检测性能越优.
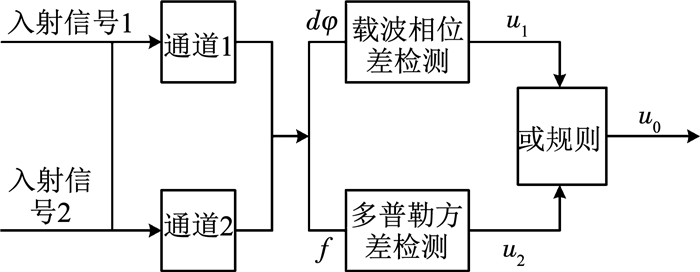
2 融合算法欺骗信号检测算法章节中介绍的两个检测方法,分别利用了真实信号与欺骗信号在到达角和载波多普勒上的差异.传统的融合方法只对每个检测器的检测结果进行融合,即只要其中一种方法检测结果为欺骗信号,则最终系统的检测结果即为欺骗信号,其检测框图见图 2,即为传统的分布式硬决策N-P检测融合系统,其中u1为载波相位差检测结果,u2为多普勒方差检测结果,u0为融合后的检测结果.
|
图 2 传统的检测融合方法 Fig. 2 Traditional detection fusion method |
假定融合后的虚警概率为Pf,若平均分配至每个检测器,则每个检测器虚警概率为
| $ \begin{array}{*{20}{c}} {{P_{\rm{d}}} = {f_1}\left( {1 - \sqrt {1 - {P_{\rm{f}}}} } \right) + {f_2}\left( {1 - \sqrt {1 - {P_{\rm{f}}}} } \right) - }\\ {{f_1}\left( {1 - \sqrt {1 - {P_{\rm{f}}}} } \right){f_2}\left( {1 - \sqrt {1 - {P_{\rm{f}}}} } \right).} \end{array} $ | (6) |
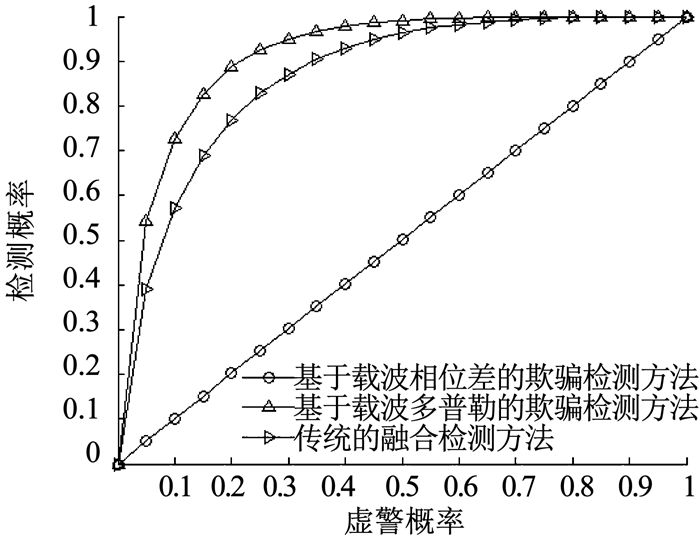
由(6)式可知,融合后的检测性能与上述两种检测方法其性能和欺骗信号的特性有关,当欺骗信号在到达角或载波多普勒方差上与真实信号比较接近时,其中一个方法的检测性能将大幅度地下降,直接采用传统的融合方法将会导致系统整体的检测性能下降,见图 3.
|
图 3 单独检测器和传统融合后检测器的性能曲线 Fig. 3 Performance curves of detector after fusion of individual and traditional detectors |
图 3中真实信号入射角为45°,欺骗信号入射角为46°,真实信号载波多普勒方差为14.86 Hz2,欺骗信号载波多普勒方差为20.52 Hz2.由图 3可知,当真实信号入射角和欺骗信号入射角非常接近时,载波相位差的欺骗检测方法基本无效.如果此时采用传统的融合方法,系统最终的检测性能反而低于单独使用载波多普勒方差的欺骗检测方法.
基于上述原因,本文设计了性能实时评估的融合检测算法.其基本思想为:融合算法实时对每个检测器的性能进行估计,当发现其中一个检测器性能明显较差时,系统将剔除该检测器,单独使用另一种检测器进行欺骗干扰检测.当两种检测器性能接近时,系统将同时使用两个检测器进行欺骗干扰检测.
性能实时评估的融合检测算法是利用各检测器判决结果和传统的融合中心全局判决结果之差的最近M个累积平均值来判定该检测器是否可用.具体方法如下:如果该平均值小于门限值λ(λ为一个0~1之间的常数),则认为该检测器可用,否则认为不可用,将其剔除.
该误差平均值的计算如下式
| $ E_i^k = \frac{1}{M}\sum\limits_{j = K - M + 1}^K {\left| {u_0^j - u_{i1}^j} \right|} . $ | (7) |
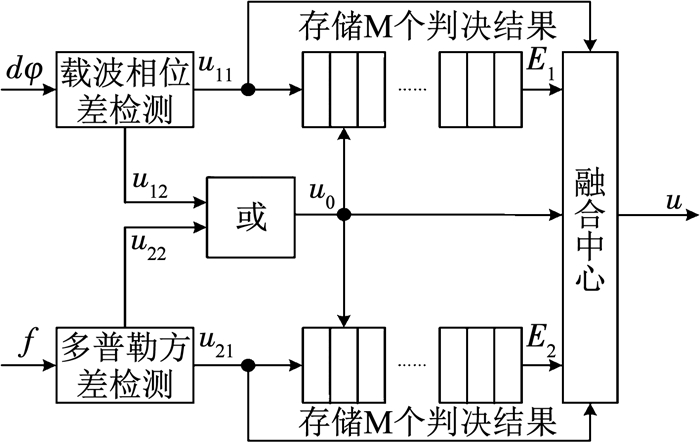
性能实时评估的融合检测算法的实现框图见图 4.
|
图 4 性能实时评估的检测融合方法 Fig. 4 Detection fusion method for real-time performance evaluation |
其中图中采用2个深度为M的FIFO来存储M个判决结果.下面结合图 4具体说明该算法的实现步骤:
步骤一:设定整个系统的虚警概率为Pf,在或规则下将Pf均分到两个检测器中,即两个检测器的虚警概率为
步骤二:两个检测器分别根据虚警概率Pf和
步骤三:两个检测器把根据Th11、Th21的检测结果u11和u21送入存储器,同时将根据门限Th12、Th22的检测结果u21和u22相或的结果u0送入存储器.
步骤四:根据(7)式计算每个检测器的误差平均值,将其分别与λ比较,判定该检测器的检测性能.
步骤五:如果两个检测器的检测性能都满足要求则采用u0作为检测结果输出,否则采用u11或者u21作为检测结果输出.
3 性能分析为了全面的分析该算法的性能,下面给出三种不同的应用场景:
场景一:真实信号的入射角为45°,欺骗信号的入射角为65°,真实信号多普勒方差均值为14.86 Hz2,欺骗信号多普勒方差均值为18.93 Hz2.
场景二:真实信号的入射角为45°,欺骗信号的入射角为65°,真实信号多普勒方差均值为14.86 Hz2,欺骗信号多普勒方差均值为15.33 Hz2.
场景三:真实信号的入射角为45°,欺骗信号的入射角为46°,真实信号多普勒方差均值为14.86 Hz2,欺骗信号多普勒方差均值为18.93 Hz2.
仿真参数设置见表 1.
| 表 1 仿真参数设置 Tab. 1 Setting of simulation parameters |
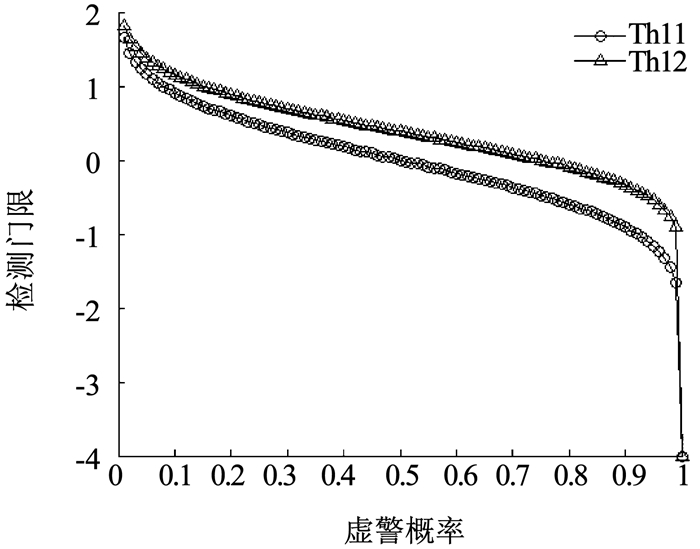
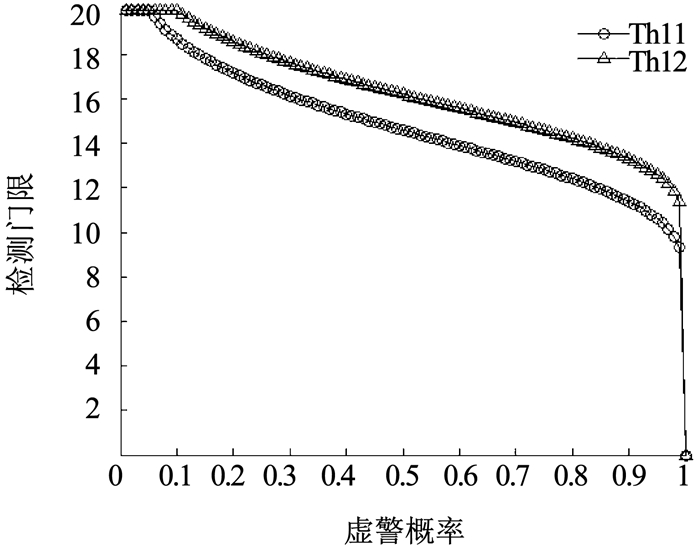
仿真过程中,不同虚警概率下载波相位差检测器和多普勒方差检测器的双门限见图 5、6.
|
图 5 载波相位差检测器的双门限 Fig. 5 Double threshold of carrier phase difference detector |
|
图 6 多普勒方差检测器的双门限 Fig. 6 Double threshold of Doppler variance detector |
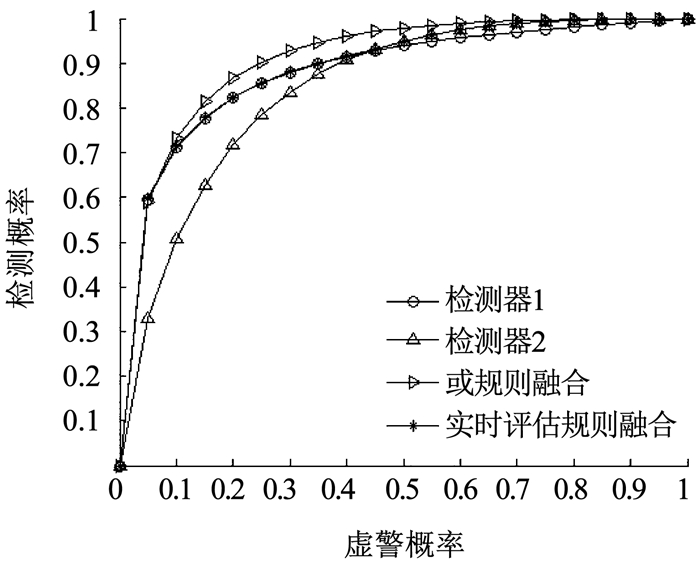
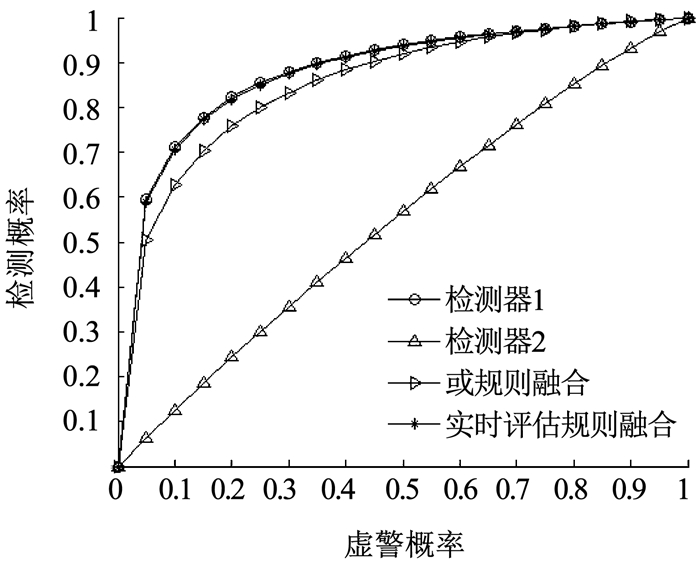
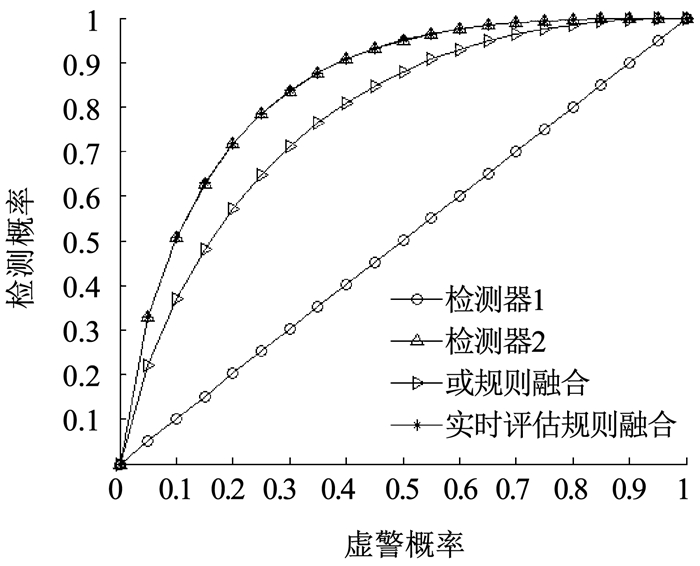
下面给出3种不同场景下各个方法的ROC曲线.其中检测器1为载波相位差检测方法,检测器2为多普勒方差检测方法.
根据图 7~9将不同场景下各种检测方法的性能汇总见表 2.由表 2可看出,在不同场景下,基于检测器性能实时评估的融合检测方法表现出良好的适应能力,在未知传感器先验信息以及传感器性能实时变化时均能保持系统整体的融合检测性能,验证了该算法性能具有很强的鲁棒性.
|
图 7 场景1下不同检测方法的性能比较 Fig. 7 Performance comparison of different detection methods in Scenario 1 |
|
图 8 场景2下不同检测方法的性能比较 Fig. 8 Performance comparison of different detection methods in Scenario 2 |
|
图 9 场景3下不同检测方法的性能比较 Fig. 9 Performance comparison of different detection methods in Scenario 3 |
| 表 2 不同场景下不同检测方法的性能比较 Tab. 2 Performance comparison of different detection methods in different scenarios |
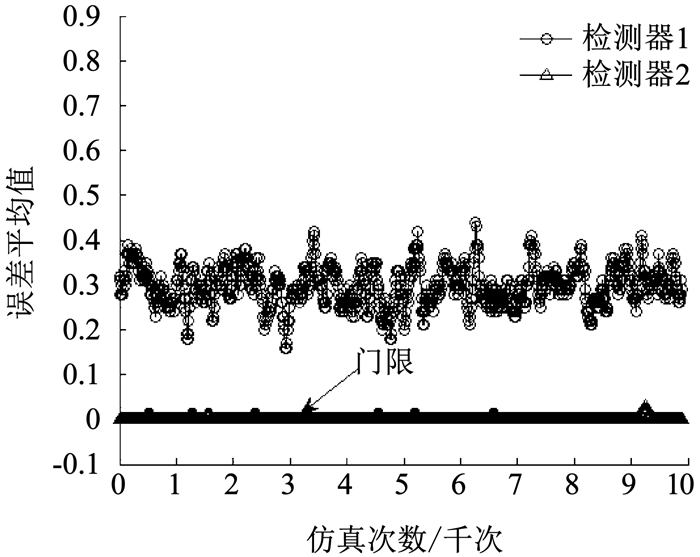
为更好地展现实时评估规则如何对两种检测器的性能进行评估,在场景3中,将虚警概率设为0.9,分别得到载波相位观测值、多普勒方差观测值见图 10、11,由图可以看出场景3下载波相位观测值检测概率低,而利用多普勒方差观测值检测概率高,两个检测器输出的误差平均值E1和E2见图 12,可以看出检测器1输出的误差平均值E1明显高于检测器2输出的误差平均值E2,故在融合算法中将检测器1的判决结果剔除,有效地保证了融合后的检测器性能.

|
图 10 场景3下载波相位观测值 Fig. 10 Carrier phase observations in Scenario 3 |

|
图 11 场景3下多普勒方差观测值 Fig. 11 Doppler variance observations in Scenario 3 |
|
图 12 场景3下两个检测器的误差均值 Fig. 12 Error means of two detectors in Scenario 3 |
本文针对检测器性能实时变化且先验信息未知的欺骗干扰检测场景,提出了一种性能实时评估的欺骗检测融合算法.通过实时评估各检测器性能,将检测性能低的检测器从融合算法中剔除,既保证了融合后的适应性,又避免因为某一个检测器性能偏低导致融合后整体性能下降.最后本文通过仿真比较了性能实时评估的欺骗检测融合算法与单独使用到相位差检测或者载波多普勒方差检测以及传统融合算法的性能.仿真结果表明,性能实时评估的欺骗检测融合算法与单独两种方法以及传统融合算法相比具有更高的检测性能和更广的适应能力.
| [1] |
张瑞华, 贾琼琼, 吴仁彪. 利用矢量跟踪环路的欺骗干扰检测与抑制方法[J]. 信号处理, 2018, 34(6): 688. ZHANG Ruihua, JIA Qiongqiong, WU Renbiao. Spoofing detection and suppression method by utilizing vector tracking loop[J]. Journal of Signal Processing, 2018, 34(6): 688. DOI:10.16798/j.issn.1003-0530.2018.06.007 |
| [2] |
黄龙, 吕志成, 王飞雪. 针对卫星导航接收机的欺骗干扰研究[J]. 宇航学报, 2012, 33(7): 884. HUANG Long, LYU Zhicheng, WANG Feixue. Spoofing pattern research on GNSS receivers[J]. Journal of Astronautics, 2012, 33(7): 884. DOI:10.3873/j.issn.1000-1328.2012.07.005 |
| [3] |
范广腾, 黄仰博, 伍微, 等. 惯导辅助的三元天线阵欺骗干扰检测算法[J]. 国防科技大学学报, 2017, 39(2): 91. FAN Guangteng, HUANG Yangbo, WU Wei, et al. Detection of spoofing threats by inertial assisted three elements antenna[J]. Journal of National University of Defense Technology, 2017, 39(2): 91. DOI:10.11887/j.cn.201702013 |
| [4] |
DANESHMAND S, JAFARNIA-JAHROMI A, BROUMANDON A, et al. A low-complexity GPS anti-spoofing method using a multi-antenna array[C]//Proceedings of the 25th International Technical Meeting of the Satellite Division of The Institute of Navigation. Nashville, Thennessee, USA: [s.n.], 2012: 1233
|
| [5] |
LEDVINA B M, BENCZE W J, et al. An in-line anti-spoofing device for legacy civil GPS receivers[C]//Proceedings of the Institute of Navigation International Technical Meeting. San Diego, Calif, USA: [s.n.], 2010: 698
|
| [6] |
史鹏亮, 靳文鑫, 吴舜晓. 实施转发GNSS欺骗干扰的选星方法研究[J]. 北京理工大学学报, 2019, 39(5): 524. SHI Pengliang, JIN Wenxin, WU Shunxiao. Research on satellite selection algorithm of GNSS repeater deception jamming[J]. Transaction of Beijing Institute of Technology, 2019, 39(5): 524. DOI:10.15918/j.tbit1001-0645.2019.05.015 |
| [7] |
JAFARNIA-JAHROMI A, BROUMANDAN A, NIELSEN J, et al. GPS vulnerability to spoofing threats and a review of antispoofing techniques[J]. International Journal of Navigation&Observation, 2012, 2012(9): 1. DOI:10.1155/2012/127072 |
| [8] |
PSIAKI M L, HUMPHREYS T E. GNSS spoofing and detection[J]. Proceedings of the IEEE, 2016, 104(6): 1258. DOI:10.1109/JPROC.2016.2526658 |
| [9] |
胡彦逢, 边少锋, 曹可劲, 等. GNSS接收机欺骗干扰功率控制策略[J]. 中国惯性技术学报, 2015, 23(2): 207. HU Yanfeng, BIAN Shaofeng, CAO Kejin, et al. Spoofing power control strategy for GNSS receiver[J]. Journal of Chinese Inertial Technology, 2015, 23(2): 207. DOI:10.13695/j.cnki.12-1222/o3.2015.02.013 |
| [10] |
HUMPHREYS T E, LEDVINA BM, PSIAKI ML, et al. Assessing the spoofing threat: Development of a portable GPS civilian spoofer[C]//Proceedings of the 21st International Technical Meeting of the Satellite Division of the Institute of Navigation. Savannah, Ga, USA: [s.n.], 2008: 2341
|
| [11] |
CHENG Xijun, XU Jiangning, CAO Kejin, et al. An authenticity verification scheme based on hidden messages for current civilian GPS signals[C]//Proceedings of the 4th International Conference on Computer Sciences and Convergence Information Technology. Piscataway: IEEE, 2009: 345
|
| [12] |
黄龙. GNSS接收机欺骗与抗欺骗关键技术研究[D].长沙: 国防科技大学, 2013 HUANG Long. Study on techniques of receiver spoofing and anti-spoofing for global navigation satellite system[D]. Changsha: National University of Defense Technology, 2013 |
| [13] |
JOVANOVIC A, BOTTERON C, FARINE PIERRE-ANDRÉ. Multi-test detection and protection algorithm against spoofing attacks on GNSS receivers[C]//Proceedings of Position, Location&Navigation Symposium-PLANS. Piscataway: IEEE, 2014: 1258. DOI: 10.1109/PLANS.2014.6851501
|
 2020, Vol. 52
2020, Vol. 52


