随着深度学习技术的发展,越来越多的传统机器学习方法与深度神经网络结合,在广告预测、影视音乐推荐等领域被研究和应用,并取得了显著的效果.其中,基于神经网络架构的推荐系统已经成为了重要的研究热点.
在传统推荐系统中协同过滤[1]是最常用的算法,基于用户对项目的评分数据,利用用户间或者项目间的相似度来预测未知评分.这一方法充分利用了用户、项目这些推荐主体间的关联行为,在相对稠密的数据集上简单而有效,但面对稀疏数据时性能严重退化.为了解决数据稀疏问题,Rendle等[2-4]提出因子分解机(Factorization Machines,FM),通过对特征数据进行组合来克服数据稀疏的情况,并将这个模型运用在推荐领域.FM局限于两个方面,其一是只对不同特征进行组合而未考虑同一领域的多个特征;其二是产生高阶特征非常困难.Juan等[5]提出的Field-aware Factorization Machine(FFM)对FM进一步优化,强化了一类特征在领域间的关系;Blondel等[6]提出Higher-order FM,优化了FM对高阶特征的交叉能力.但这些模型对于捕捉数据中潜在的高阶知识相比深度神经网络还是逊色很多,于是研究人员Shan、Cheng等[7]将特征工程与神经网络结合,其中Shan等[8]在2016年提出了Deep Crossing,让神经网络自主学习特征组合以实现了特征工程自动化;Cheng等[9]在同年提出了Wide&Deep,通过将交叉特征作为线性模型的输入与深度神经网络(DNN)联合训练线性模型来实现预测.考虑FM与DNN各自对特征处理的优势,研究人员尝试将两者进行结合,于是Wang等[10]在2017年提出了Deep & Cross Network (DCN),通过构建一个多层交叉网络来优化Deep Crossing与Wide&Deep对特征的选择和组合方法;Guo等[11]在2017年提出了DeepFM,为FM与DNN两部分共享同样的输入,其中FM部分学习低阶知识,DNN部分学习高阶知识;He等[12]在同年提出了Neural Factorization Machine (NFM),以FM为入口,再通过Bi-Interaction层从低阶特征中获得二阶特征交互.但由于FM与DNN都对数据标签需求较高,这些模型面对推荐领域的数据稀疏、特征稀缺等常见情境,往往耗费大量算力却无法提高精度.
尽管上述基于深度神经网络架构的模型[8-12]已经被广泛运用于点击率预测(CTR)、评分预测等推荐任务中,并取得了相比传统推荐方法更好的效果,但它们的瓶颈也非常明显:首先,模型基于对大量知识标签的组合学习,导致对源数据的标签类别数量需求较高,在标签类别稀少的情况下,推荐效果不如协同过滤;其次,神经网络模型更偏向于对性别、年龄段、类别等有直接意义的标签进行组合交叉学习并尝试挖掘知识,对于用户编号、项目编号等关联型索引标签不友好,无法快速学习到具体用户及项目所在粒度层面的关联知识;再次,由于不同标签对应不同的特征域,导致不同域的特征向量间没有直接相关性,进入神经网络的“黑盒”后直接对多个特征产生的结果进行表达,而单个特征的独立表达没有意义,这也使得模型的可移植性和拓展性受限.
为解决上述问题,本文提出一种多标签统一域嵌入方法,并以此设计实现了统一域嵌入的推荐模型,它可以在数据稀疏、标签类别稀少的情况下,有效提高推荐精度,减少训练时间.模型运用协同过滤和特征迁移方法的思想,通过一种领域粒度的可训练映射方法,将多领域特征映射到同一空间中,使得向量空间关系可以表达特征间的关联性.这一方法大大降低了模型在推荐预测任务中对源数据标签类别数量及稀疏性的要求,并且增强了模型的可拓展性及特征标签的可迁移性.
1 多标签统一域嵌入的推荐模型 1.1 模型框架本文提出多标签统一域嵌入的推荐模型(Multi-label Unified Domain Embedding Model,MUDEM),它以神经网络为基础进行架构,以用户对项目的历史行为数据为主要输入,通过网络训练预测用户对项目评分.
MUDEM的设计基于对两个核心思想的运用与拓展,即基于关联值的潜在聚类以及特征映射原理.基于关联值的潜在聚类来自于协同过滤方法[13],协同过滤在特征处理时会将同类项目间的标签量化后通过欧氏距离、余弦相似度、皮尔逊相关系数、Jaccard距离等方法计算出它们间的关联值(相似度),再基于关联值为目标项目推荐相似项目;在这个过程中,若将同类项目集合放入一个无限维空间中,令关联值越高的两个项目间的距离越近,那么可以认为这个项目集合根据关联值完成了聚类;但这个聚类受限于同领域的项目,对于不同领域的项目(例如用户集合与商品集合),特征标签无法在同一空间中表达,若可以将同领域的聚类拓展到多领域,那么就可以在这个空间中直接通过空间距离来表达跨领域项目间的关联值.特征映射是迁移学习中在特征层面迁移的一种实现方法[14],它通过寻找具有代表性特征,将源领域与目标域的特征变换到同样的空间中,若可以自适应地寻找这些领域到目标空间的最优映射方法,那么就解决了多领域在同一空间中聚类表达的问题.
本文提出特征领域粒度的可训练映射方法与神经网络的嵌入层方法相结合来实现上述拓展.在神经网络中通过嵌入层可以将推荐系统中常见的离散分类标签转换为低维特征向量,随着嵌入层的不断训练,对于单个标签的嵌入向量集合会趋向于“越相似,则越接近”的聚类效果,这个结果满足了基于关联值的潜在聚类的情境.再通过映射层将不同类别标签的嵌入向量投影到统一的欧式空间中(下文称这个空间为统一域).在映射层中每一类标签对应独立的映射系数,这些系数与神经网络同步训练,不断寻找当前领域到统一域的映射最优方法,这个方法将重要特征“放大”,次要特征“缩小”,并且映射后保留源领域的基本分布.模型由统一域中向量间的空间距离所计算的预测值与实际值的误差进行反向传播,从而驱动网络迭代训练.比较近年来的主流模型[10-12],这些模型主要以FM为基础来设计实现数据的嵌入以及关联知识的学习,导致高维度的离散标签在嵌入以及后续的无差别学习的流程中不能被神经网络良好的关注,当数据标签类别稀少时,可组合的特征匮乏,使得预测精度严重下降.MUDEM通过自适应的统一域映射方法与统一域空间的关联值聚类特性解决了这些问题,它一方面提升了对推荐主体间关联知识的关注,另一方面扩充了统一域标签的丰富性,从而优化了数据稀疏、标签类别稀少情境下的网络训练性能和预测精确度.
MUDEM的特点在于依靠神经网络来最优化特征域到统一域的合理映射,并在统一域中学习主体间的关联知识,其实现流程如下:
1) 预处理原始特征数据,将数据划分领域后分别进行One-hot编码;
2) 通过嵌入层将编码后的各个标签进行降维,获得特征向量表示;
3) 通过映射层,使各个特征向量在对应领域的映射池中从当前域嵌入到统一域;
4) 基于统一域中特征的空间关系,在输出层中获得同领域及跨领域的特征之间的关联值,并对关联值进行简单修正加权产生预测值;
5) 以损失函数计算预测值与实际值误差,通过反向传播算法调整嵌入层、映射层、输出层中的可训练系数,对预测模型进行迭代训练,实现评分预测.
模型结构主要由嵌入层、映射层和输出层三部分构成,以“用户-用户对项目的评分-项目”作为输入的最基础模型为例,其流程如图 1所示,图中深色底的部分拥有独立的可训练参数.

|
图 1 统一域嵌入模型流程图 Fig. 1 Flow chart of MUDEM |
在上述模型框架的基础上对其主要嵌入及映射流程进行数学定义.给出一个用户集合U={u1, u2, …, uN},另给出由M个项目组成的集合V={v1, v2, …, vM}.用户与项目间存在评价行为,即ui对vj的偏好值可以组成评分矩阵R={Ri, j}N×M.R非常稀疏,存在大量的空缺值表示该用户对该项目没有评价行为,需要模型进行预测.令eui为第i个用户的特征经过嵌入后的向量,则U中所有用户被嵌入后的集合为Ue={eu1, eu2, …, euN}.同样的,令evj表示第j个项目的嵌入后向量,则V中项目被嵌入后的集合为Ve.由于Ue与Ve所用的嵌入层不同,它们的向量也位于不同域的空间中,设通用映射方法为W,统一域空间为H,Ue与Ve的映射系数集合分别为α和β.若WαA→H表示将集合A中向量所在空间映射到空间H的过程,则上述流程的具体公式可以表达为
| $ \begin{align} & {{U}_{\text{e}}}\xrightarrow{W_{\alpha }^{U\to H}}U\prime \in H,~ \\ & {{V}_{\text{e}}}\xrightarrow{W_{\beta }^{U\to H}}V\prime \in H. \\ \end{align} $ |
MUDEM通过迭代训练,寻找不同标签所对应特征域到统一域的最优映射方法W,最终使得统一域向量的空间关系能较好的反映特征间的关联性.
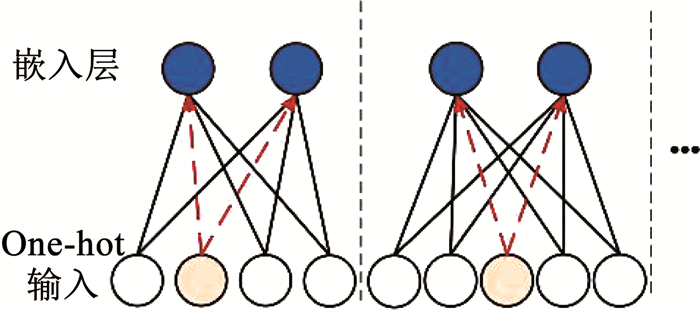
1.2 嵌入层模型推荐领域数据集含有大量的离散特征,需要对这些特征进行One-hot编码.但编码后数据极其稀疏,只有一个维度为1其余为0,直接输入神经网络会导致网络参数太多.利用FFM的思想,将特征分为不同领域,分别进行One-hot编码后送入嵌入层进行降维.如图 2所示,每个特征作为一个独立领域的One-hot编码被传递给嵌入层,将各个领域的嵌入向量设为相同长度k(图例中k为2).可知,一个领域特征的每个可能的离散值对应一种One-hot输入向量,这个向量在某个维度为1其余为0,在嵌入过程中仅计算维度为1部分对应的权重系数(图中用虚线表达)来获得嵌入结果.
|
图 2 特征嵌入方法 Fig. 2 Feature embedding method |
从神经网络模型来说,嵌入层作为入口层,本身也是可以被训练的.在网络反向传播的过程中,嵌入层参数不断更新优化以实现对原始特征的更准确表达,这个方法与自然语言处理中word2vec[15]的原理类似.
1.3 映射层模型映射层从嵌入层获得嵌入向量并对这些向量进行转换,每个领域的嵌入向量对应一个映射池,所有映射池遵循相同的映射规则但本身的权重参数相互独立.需要注意的是,映射层并不是对特征向量整体进行简单线性变换,而是通过对特征向量每个维度的值进行线性变换来实现向量各维的权重偏移.这里结合本文后续实验的评估,给出一种简单有效的基础映射方法如下:
| $ W\left( \mathit{\boldsymbol{x}} \right) = \mathit{\boldsymbol{a}}*{\mathit{\boldsymbol{x}}^{\rm{T}}} + \mathit{\boldsymbol{b}} = \left[ {\begin{array}{*{20}{c}} {{a_1}}\\ {{a_2}}\\ \vdots \\ {{a_k}} \end{array}} \right]*\left[ {\begin{array}{*{20}{c}} {{x_1}}\\ {{x_2}}\\ \vdots \\ {{x_k}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{b_1}}\\ {{b_2}}\\ \vdots \\ {{b_k}} \end{array}} \right]. $ |
式中:W为映射层的统一规则,k为模型所定义的嵌入向量长度,x为某特征嵌入向量的1×k的矩阵表达,a与b均是由可训练系数组成的k×1的矩阵,运算符*为哈达马积运算.
在网络训练前,需要对映射层设置初始化系数.在实验中发现,不同的初始化方法会对网络收敛速度与预测准确率产生影响,其中将向量尽量不作变换直接传递(即设置所有系数a接近1,系数b接近0)在收敛速度与准确率中取得了较好的平衡.在后续实验中,对该初始化的具体设置方法是:系数a初始化为μ=1.0,σ=0.025的正态分布,系数b初始化为0.这种初始化设置满足了训练初期嵌入向量到统一域的镜像投射,从而保留了嵌入向量的原始表达,对于网络的前向和反向传播来说都更加稳定.
在模型中,映射层承担嵌入向量空间与统一域的转换工作.每个领域会传入独立的映射池,即通过网络训练,每个领域都会有为本身所用的映射池系数.映射层的输出与输入的数据结构相同,是一个k长度的向量,它与同一任务的另一领域的映射后向量位于同一空间域中,为后续运算提供支持.由于映射层与嵌入层都可被训练,对两者进行对比分析:映射层作为向量转换的最后一步,在反向传播中系数受到的影响更大,并且会直接影响到后续训练中所有的该领域特征的统一域映射结果;而嵌入层受到的影响要小的多,因为在嵌入层模型中,原始特征的每一个可能的离散值对应一组独立的权重系数,网络优化只会影响到当前特征的当前值对应的嵌入系数.综上所述,映射层更关注整个特征空间与统一域空间的关联性,而嵌入层更关注特征的当前值转化为其嵌入向量的表达准确性,这个分析也是映射层的必要性和有效性的理论说明,通过设置“有/无映射层”的对比实验论证了这一点,具体实验结果请参见实验小节.
1.4 输出层模型输出层承担统一域中主体关联值计算与预测输出工作.由前置映射池传入数据,对两个(多个)向量进行关联运算.这里列举一种对于双领域任务基础模型的关联运算方法,也是在本文后续实验中所用的一种有效方法.求两个向量的欧式距离来表达它们间的关联性,公式如下
| $ d\left( {\mathit{\boldsymbol{X}},\mathit{\boldsymbol{Y}}} \right) = \sqrt {\sum\limits_{i = 1}^k {{{({x_i} - {y_i})}^2}} } . $ |
式中:xi为X的第i个元素,yi为Y的第i个元素,k为向量维度.
在输出预测评分前,放置一定的可训练参数及激活函数,用于处理模型预测值对于实际目标值的最终修正,这里需要说明的是,实际值是模型中统一域主体间期待的距离值,对于很多数据集的评价标签来说需要进行简单变换,例如用户对项目的偏好评分r在[0, 5]区间中,若认为最高分评价对应距离最近,可以简单设实际值为5-r.
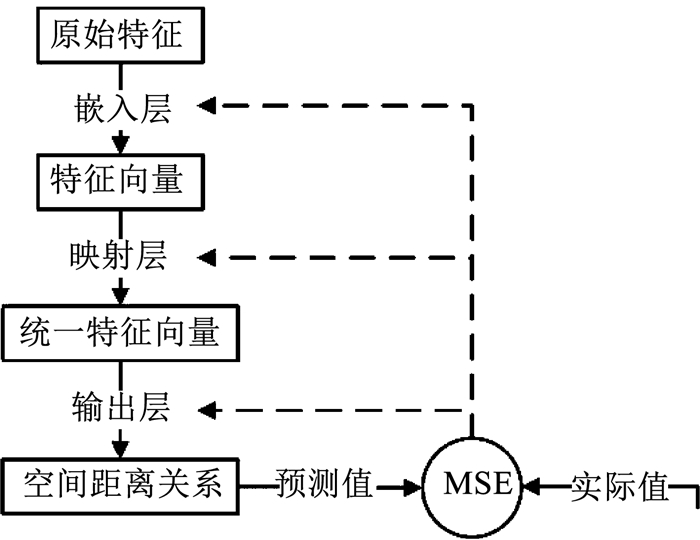
在训练中,网络根据输出层产生的预测值与实际值的均方误差MSE进行反向传播,以误差来驱动网络中权重系数的不断迭代.正向映射及反向优化的过程如图 3所示,原始特征在网络的正向传递中(图中由左至右)由嵌入层、映射层完成两次转换,再通过输出层获得统一域空间的距离关系并产生预测值,由损失函数计算的误差并反向传播(图中虚线表示)优化嵌入层、映射层、输出层中的可训练系数.
|
图 3 统一域嵌入方法 Fig. 3 Unified domain embedding method |
不同于传统推荐模型将多个特征进行联合或者分解后再求最优解的方法,将多个特征分别处理为统一域空间的特征表达后再求解,使各个特征相对独立.将不同领域间的历史评分值或者关联值作为相似度依据,模型在训练中会促使统一域中的高相似度特征在空间距离上不断接近.这个过程中,正向映射与反向传播组成闭环,实现了模型自适应求最优解的过程.
2 实验 2.1 数据集使用MovieLens[16]及Jester公用数据集进行实验评估:
1) MovieLens1M.包含6 040个用户对3 883部电影的1 000 209个评分,评分在[1, 5]区间.数据密度为4.26%,是较为稀疏的数据集.
2) MovieLens10M.包含69 878个用户对10 681部电影的10 000 054个评分,评分在[0.5, 5]区间.数据密度为1.33%,是相比1M更多稀疏的数据集
3) Jester.选择其1.7M规模数据集,包含59 132个用户对150则笑话的1 761 439个评分,评分在[-10, 10]区间.数据密度为31.50%,是相对稠密的数据集.
2.2 对比模型选择了DeepFM、DCN、NFM三个近年被提出的在推荐领域运用的典型深度学习预估网络模型,加之本文提出的MUDEM进行对比实验.
1) DeepFM模型[11].该模型将FM与DNN结构相结合,FM部分学习低阶知识,DNN部分学习高阶知识,最后在输出层融合低阶和高阶的特征组合实现综合预测,是典型的并行结构模型.
2) DCN模型[10].该模型通过一个多层的交叉网络中不断对特征进行交叉学习,每个层上明确地应用特征交叉,不需要手工特征工程;同时并行一个深度网络来组合预测.
3) NFM模型[12].该模型基于FM,结合DNN以提升FM捕捉特征间多阶交互信息的能力,它通过Bi-Interaction层从低阶特征中获得二阶特征交互,是一个串行结构模型.
4) MUDEM模型.本文提出的新模型.
2.3 评价指标从精确度和效率两个方面对模型进行评价.精确度方面选择均方根误差RMSE(Root Mean Square Error)[17]作为模型的评价指标.RMSE是常用的推荐性能评价指标,越小代表推荐精度越高,其公式如下
| $ {E_{{\rm{RMSE}}}} = \sqrt {\frac{1}{m}\sum\limits_{i = 1}^m {{{({x_i} - \mathop {{y_i}}\limits^ \wedge )}^2}} } . $ |
式中:m为待评价值的数量,yi为第i个实际值,
模型效率以网络训练稳定收敛的总耗时及网络参数数量来进行评估.收敛耗时越少,模型训练越高效;参数越少,模型越轻量.需要说明的是,在实验中对稳定收敛的控制定义是连续5次Epoch的过程中损失函数MSE值都不再下降.
2.4 模型训练MUDEM对嵌入向量映射后的空间关系的合理利用,使其在数据稀疏且类别标签稀少情景下有优于其它模型的表现.实验选取数据集中的“用户-项目-评价”三元组数据作为输入来对比各个模型效果,具体是:从MovieLens数据集中选择userId、movieId、rating标签;从Jester数据集中选择User ID、Item ID、Rating标签.选取标签后,对数据进行标准化预处理并随机打乱先后次序.
对同一数据集的所有模型设置相同的嵌入向量维度,使各个模型的参数规模接近,以保证模型间对比效果的公平性.同时,经过预先实验以及相关论文调研[10-12],对各个模型本身的特定参数进行了调优,保证各个模型能在相应的数据集上发挥较好的效果.具体参数设置如下:
1) Movielens1M及Jester.对于DeepFM、DCN、NFM的设置,dropout:0.3;优化器:adam;深度网络结构:隐藏层2层,每层4结点,全连接;激活函数:sigmoid;嵌入向量维度:8;损失函数:MSE.对于MUDEM的设置,优化器:adam;激活函数:sigmoid;嵌入向量维度:8;映射层系数数量:8*2;损失函数:MSE.
2) Movielens10M数据集.对于DeepFM、DCN、NFM的设置,dropout:0.3;优化器:adam;深度网络结构:隐藏层2层,每层16结点,全连接;激活函数:sigmoid;嵌入向量维度:16;损失函数:MSE.对于MUDE模型的设置,优化器:adam;激活函数:sigmoid;嵌入向量维度:16;映射层系数数量:16*2;损失函数:MSE.
2.5 实验结果及分析对不同模型达到收敛所需的时间进行评估,结果如表 1所示.不同模型的网络参数数量如表 2所示.表格中的最优成绩用粗体表现.
| 表 1 模型收敛时间 Tab. 1 Model convergence time |
| 表 2 模型参数数量 Tab. 2 Total parameters of model |
| 表 3 模型预测精度 Tab. 3 Prediction accuracy of model |
在嵌入向量维度相同的前提下,MUDEM相比其它模型拥有更少的网络参数,这是由于MUDEM在后续网络结构中参数需求很低.这种轻量的结构也使得MUDEM的运算量少于其它模型,具体表现在单轮Epoch耗时更低.在总耗时上,MUDEM优于DeepFM与DCN,但在MovieLens稀疏数据集上由于NFM收敛更快,MUDEM表现略差于NFM,其原因是NFM在经过最少的Epoch数后就快速收敛了,需要对其精确度进行评估,若NFM精确度接近所有模型平均水平,则认为其合理;若与平均水平差距较大,则认为其快速收敛表现是局限于模型的知识挖掘深度而非受益于模型的高效性,后续表 3的实验结果验证了NFM的表现属于后者.
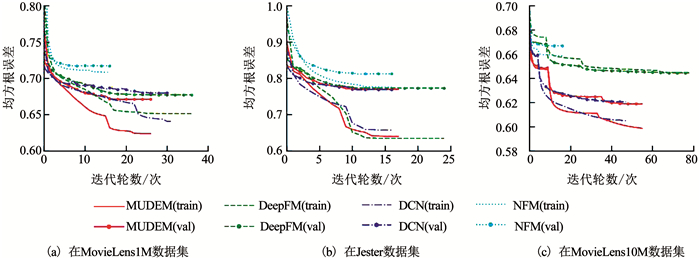
图 4是模型在3个训练集上的精确度表现,标注(train)/(val)用以区分训练集/验证集.
|
图 4 模型训练的RMSE曲线 Fig. 4 RMSE curves of model training |
在稀疏数据集MovieLens上,MUDEM表现明显优于其它模型;在较稠密数据集Jester上,其表现与DCN接近并优于DeepFM与NFM.收敛最快的NFM在预测精度上与其它模型差距较大.将模型收敛后的验证集RMSE结果展示在表 3中,数值越小结果越优,最优成绩用粗体表现.
MUDEM在相对稀疏的MovieLens数据集上效果优于其它3种模型,其中在最为稀疏的MovieLens10M数据集上,MUDEM的预测精度有0.2%~4%的提升;在稠密数据集Jester上,MUDEM表现与DCN类似,高于DeepFM与NFM.由此分析总结,面向数据标签类别稀少的预测任务,MUDEM能在保证较好精确度的同时较大减少训练耗时,在越稀疏数据集中其精度优势越明显;除去精度明显较差NFM(其它模型精确度的平均差距小于1%,而NFM的精确度差4%左右),MUDEM的收敛效率在各种数据集中均有30%以上提升.
接下来对MUDEM的统一域嵌入方法中核心的映射层所发挥的效果进行验证.设置有/无映射层的模型在MovieLens1M及Jester数据集上分别进行对比实验.在无映射层对比模型中,忽略映射层而将嵌入向量直接传递到输出层进行空间距离关系运算.实验结果如图 5,train与val区分训练集及验证集,实线与虚线区分有无映射层的模型.

|
图 5 映射层对比的RMSE曲线 Fig. 5 RMSE curves of comparison of mapping layers |
可见有映射层的模型在收敛效率及精确度上相比无映射层模型都有较大提升.在MovieLens1M上有映射层模型RMSE低5%;在Jester上有映射层模型RMSE低11%.这一结果表明了映射层的重要性,其可训练参数对整体领域知识的敏感性发挥了承接嵌入域与统一域的桥梁作用,是MUDEM统一域嵌入方法的核心组件.
3 结论本文提出了一种多标签统一域嵌入方法,并进一步设计实现了统一域嵌入的推荐模型,可以有效解决目标数据由于标签类别稀少及稀疏性带来的组合特征匮乏、关联知识学习能力差的问题.引入特征领域粒度的可训练映射方法与神经网络的嵌入层方法相结合,通过“嵌入层-映射层-输出层”架构,对原始特征进行嵌入编码、统一域映射、空间距离运算等处理,在统一域中构建多领域标签的嵌入表达,最终实现推荐预测,在精确度和网络收敛效率上都有较好的提升.
在未来的研究中,将进一步探讨模型内部规则,对理论方法和实现方式进行优化,希望模型能在更加通用的预测任务中取得较好的效果;同时,本文模型的中每个标签的嵌入与映射部分可以作为一个整体完成当前标签的处理任务,这为标签的快速迁移方法提供了较好基础,希望在后续的研究中以此为基础对标签迁移进行进一步研究.
| [1] |
EKSTRAND M D. Collaborative filtering recommender systems[J]. ACM Transactions on Information Systems, 2007, 22(1): 5. |
| [2] |
RENDLE S. Factorization machines[C]//Proceedings of 2010 IEEE International Conference on Data Mining. Sydney: IEEE, 2010: 995
|
| [3] |
RENDLE S. Factorization machines with libFM[J]. ACM Transactions on Intelligent Systems and Technology, 2012, 3(3): 1. |
| [4] |
RENDLE S, GANTNER Z, FREUDENTHALER C, et al. Fast context-aware recommendations with factorization machines[C]//Proceedings of the 34th International ACM SIGIR Conference on Research and Development in Information Retrieval. Beijing: ACM, 2011: 635
|
| [5] |
JUAN Yuchin, ZHUANG Yong, CHIN Weisheng, et al. Field-aware factorization machines for CTR prediction[C]//Proceedings of the 10th ACM Conference on Recommender Systems. Boston: ACM, 2016: 43
|
| [6] |
BLONDEL M, FUJINO A, UEDA N, et al. Higher-order factorization machines[C]//Proceedings of the 30th International Conference on Neural Information Processing Systems. Barcelona: Curran Associates Inc., 2016: 3359
|
| [7] |
LECUN Y, BENGIO Y, HINTON G. Deeplearning[J]. Nature, 2015, 521(7553): 436. DOI:10.1038/nature14539 |
| [8] |
SHAN Ying, HOENS T R, JIAO Jiao, et al. Deep crossing: Web-scale modeling without manually crafted combinatorial features[C]//Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. San Francisco: ACM, 2016: 255
|
| [9] |
CHENG Hengtze, KOC L, HARMSEN J, et al. Wide & deep learning for recommender systems[C]//Proceedings of the 1st workshop on deep learning for recommender systems. Boston: ACM, 2016: 7
|
| [10] |
WANG Ruoxi, FU Bin, FU Gang, et al. Deep & cross network for ad click predictions[C]//Proceedings of the ADKDD'17. Halifax: ACM, 2017: 12.
|
| [11] |
GUO Huifeng, TANG Ruiming, YE Yunming, et al. DeepFM: A factorization-machine based neural network for CTR prediction[C]//Proceedings of the 26th International Joint Conference on Artificial Intelligence. Melbourne: AAAI Press, 2017: 1725
|
| [12] |
HE Xiangnan, CHUA Tatseng. Neural factorization machines for sparse predictive analytics[C]//Proceedings of the 40th International ACM SIGIR Conference on Research and Development in Information Retrieval. Tokyo: ACM, 2017: 355
|
| [13] |
SARWAR B, KARYPIS G, KONSTAN J, et al. Item-based collaborative filtering recommendation algorithms[C]//Proceedings of WWW10, Conference. New York, NY: ACM, 2001, 1: 285
|
| [14] |
PAN S J, YANG Qiang. A survey on transfer learning[J]. IEEE Transactions on Knowledge and Data Engineering, 2010, 22(10): 1345. DOI:10.1109/TKDE.2009.191 |
| [15] |
MIKOLOV T, CHEN K, CORRADO G, et al. Efficient estimation of word representations in vector space[J]. arXiv preprint, 2013, 1301: 3781. |
| [16] |
HARPER F M, KONSTAN J A. The movielens datasets:History and context[J]. ACM Transactions on Interactive Intelligent Systems, 2016, 5(4): 19. |
| [17] |
CHAI T, DRAXLER R R. Root mean square error (RMSE) or mean absolute error (MAE)? Arguments against avoiding RMSE in the literature[J]. Geoscientific Model Development, 2014, 7(3): 1247. DOI:10.5194/gmd-7-1247-2014 |
 2020, Vol. 52
2020, Vol. 52


