2. 低维量子物理国家重点实验室(清华大学),北京 100084;
3. 北京量子信息科学研究院,北京 100193
2. State Key Laboratory of Low Dimensional Quantum Physics (Tsinghua University), Beijing 100084, China;
3. Beijing Academy of Quantum Information Sciences, Beijing 100193, China
19世纪初量子力学的发展拉开了近代物理学的序幕.微观世界的运行遵循量子力学规律,很多现象无法用经典物理理论解释,比如测不准原理和原子核外电子稳定的分立能级等.量子力学的发展促进了科学技术的发展,带来了如今日新月异的信息时代.当今物理学研究最大的分支领域——凝聚态物理领域研究的一个主要课题就是如何实现微观量子规律的宏观化,这样的量子材料有望实现与传统材料不同的性质并构建新奇量子器件[1].
一个著名的例子就是超导体.超导体中电子形成库珀对,在超导转变温度(TC)以下凝聚到一个量子态,表现为零电阻和完全抗磁性.超导体具有巨大的应用潜力,但TC低是主要障碍.在过去的几十年时间里,科学家们付出了大量努力并取得巨大进步:发现多种超导材料与体系,部分材料的TC远大于77 K,已应用到实际生活中.但高温超导的机理仍不清楚,材料体系也较复杂,实现更高温度甚至室温超导的路线仍不明朗[2].
构造量子材料的另一个方法是利用电子的拓扑性质[3-4].20世纪80年代开始,人们在多个二维电子气体系中发现了整数量子霍尔(quantum Hall,QH)现象[5-7]:在外加强磁场作用下,二维电子气中产生Landau能级,体内绝缘,边缘产生一维手性边缘态,具有量子化的霍尔电阻(ρyx=h/ne2,h是普朗克常数,e是基本电荷,n是非零整数)(图 1(c))和零纵向电阻(ρxx=0)[6-7].引入拓扑的概念后科学家们发现了一个新的量子数-陈(Chern)数,拓扑上不同于零Chern数的常规能带,它能够导致量子化的边缘态.一个很自然的问题是:零外加磁场情况下可否获得非零Chern数体系?1988年,美国Haldane教授[8]提出一个理论模型,可以在不需要外加强磁场的环境中获得QHE,即量子反常霍尔效应(quantum anomalous Hall effect,QAHE)(图 1(d)).但在后续20多年中,实验进展缓慢,直到拓扑绝缘体(topological insulator,TI)材料的发现[9-10].理论物理学家们提出:在时间反演对称性(time reversal symmetry,TRS)保护的TI材料中引入磁性,比如磁性掺杂或者磁性近邻效应,将会观测到QAHE[11-15].2012年底,本文作者所在团队与合作者[16]一起在Cr掺杂的(Bi, Sb)2Te3薄膜中首次观察到了QAHE的实验现象,为拓扑量子材料和新奇量子效应的研究提供了新的思路.

|
图 1 几种霍尔效应的霍尔电阻-磁场强度关系示意曲线 Fig. 1 Hall resistance-magnetic field curves of several Hall effects |
与超导体相似,低温是QAHE获得应用的主要阻碍.在磁性掺杂TI薄膜中,获得量子化反常霍尔电阻和零纵向电阻需要小于100 mK的极低温[16-23],远低于一般超导材料的TC.但从物理原理角度看,QAHE更为简单、清晰,目前为止,能带理论计算与实验结果符合的较好.从材料制备角度看,很多传统材料具有拓扑性,多种材料制备方法可以制备出高质量拓扑材料.在过去的七年间,QAHE在多个材料体系中获得了实验观测,且观测温度从30 mK提升到近2 K.本文将主要总结磁性TI中的QAHE研究,特别在提高其观测温度方面的研究进展.包括四个部分:前两个部分分别介绍磁性掺杂和磁性近邻TI体系中的QAHE研究,第三部分介绍最新发现的内禀磁性TI体系,最后一部分对设计和构造高温QAHE系统的原理和路线图给出一些建议和展望.
1 磁性掺杂拓扑绝缘体体系中的量子反常霍尔效应 1.1 量子反常霍尔效应的首次发现由于具有强自旋轨道耦合(spin-orbital coupling,SOC)和TRS的保护,TI的体能隙间存在无能隙拓扑表面态(topological surface state,TSS)(对于3D TI)或边缘态(对于2D TI)[9-10].理论预言,破坏TRS后可以实现多种新奇量子效应[13],比如QAHE.向3D TI中引入面外铁磁序,会在其表面态狄拉克点处打开能隙(图 2(a)),不同磁化方向的相邻磁畴间具有不同拓扑序,畴壁上产生手性边缘态(图 2(b)).向3D TI薄膜中引入面外铁磁序,如果上下表面磁化方向相同,由于拓扑序不同,在上下表面的边缘,即侧边会产生手性边缘态.如果薄膜足够薄,侧边态不导电,输运方法可以测量到量子化的霍尔电阻.如果上下表面磁化方向相反,由于拓扑序相同,不存在手性边缘态.材料在直流输运测量中表现为普通绝缘体(normal insulator,NI),但有理论预言其在交流输运测量中表现为轴子绝缘体(axion insulator),可以观测到拓扑磁电效应(topological magnetoelectric effect,TME)[13].进一步减薄3D TI薄膜的厚度,上下表面将会发生杂化,体系变为2D TI或者2D NI[24-27].如果杂化能隙小于铁磁交换能隙,仍可以观察到QAHE[14].

|
注:红色和蓝色代表具有不同拓扑序的区域,黑色箭头表明磁化矢量方向,黄色线代表手性边缘态. (a) Band structure of magnetic induced gapped TSS. (b) Different magnetic structures in magnetic TI thin films (Red and blue color represent topologically distinct regions. Black arrows indicate the direction of magnetization vector. Yellow lines with arrows indicate chiral edge states). 图 2 3D磁性TI示意图 Fig. 2 Schematic of 3D magnetic TI |
本文作者所在团队[26-30]从2009年开始使用分子束外延(molecular beam epitaxy,MBE)设备制备多种高质量TI薄膜;通过磁性掺杂获得均匀的面外铁磁序[31];使用化学元素掺杂和背栅极电压调控,调节费米能级和载流子浓度,对磁性掺杂TI进行了系统的研究[32].在半导体领域通常使用稀磁掺杂的方式引入磁性[33-34],一般通过载流子的RKKY机制传导磁性,而QAHE的观测需要实现体绝缘.理论发现,Bloembergen-Rowland(BR)或者van Vleck机制[14, 35]可以用来传导绝缘体铁磁性,实验上观察到Cr掺杂的(Bi, Sb)2Te3中铁磁性与与载流子类型和浓度无关[31].
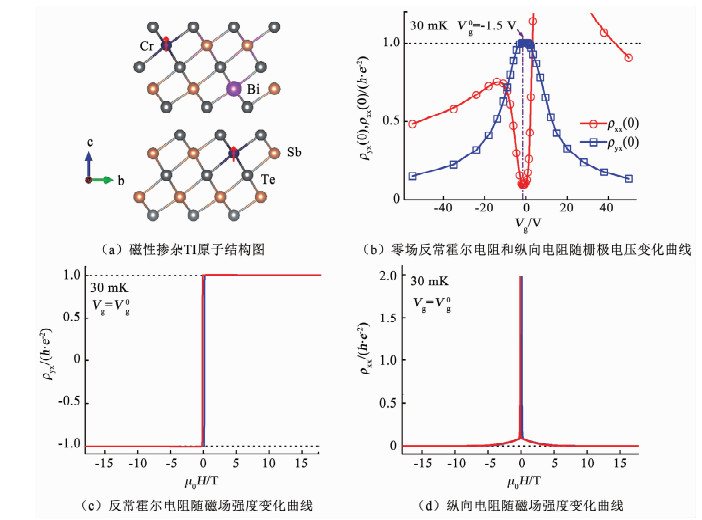
最终,本文作者所在团队[16]于2012年底在MBE生长的Cr掺杂的(Bi, Sb)2Te3薄膜中首次实验观测到QAHE.Bi2Te3和Sb2Te3是典型的二代3D TI材料[36-38],具有五层(quintuple layer,QL)结构.通过调节Bi/Sb比例可以获得一系列N型到P型的TI材料(Bi, Sb)2Te3[32].Cr的掺杂替代Bi/Sb位,引入具有面外易磁化轴的铁磁性[31],原子结构图见图 3(a).在5 QL的薄膜中,零场下观测到量子化反常霍尔电阻(ρyx=h/e2)和明显下降的纵向电阻(图 3(b)).在几个特斯拉的外加磁场下,可以实现完美的量子化(ρyx=h/e2,ρxx=0)[16](图 3(c)、(d)).由于Bi/Sb混合和Cr元素掺杂等引入无序,薄膜的迁移率小于100 cm2/Vs,但这种条件下获得完美的量子化平台正展现了材料的拓扑性.
|
(a) Atomic structure of Cr-doped (Bi, Sb)2Te3 material. (b) Gate dependence of zero-magnetic-field ρyx (0) and ρxx (0) at 30 mK. (c) Magnetic field dependence of ρyx. (d) Magnetic field dependence of ρxx. 图 3 QAHE首次在Cr掺杂(Bi, Sb)2Te3薄膜中实现[16] Fig. 3 The first observation of QAHE in Cr-doped (Bi, Sb)2Te3 thin films[16] |
理论上,QAHE的观测温度取决于磁能隙大小,即3D磁性TI表面态铁磁交换能隙的大小.在一般的磁性材料中,磁交换能隙与kBTCurie同数量级,kB是玻尔兹曼常数,TCurie是居里温度.但在Cr掺杂的(Bi, Sb)2Te3薄膜中,TCurie约为20 K,比QAHE的观测温度高2~3个数量级,引起了研究者的疑惑.后续研究发现,在Cr掺杂的(Bi, Sb)2Te3薄膜中,尽管Cr掺杂是随机分布且相对均匀的,但薄膜中铁磁性表现出强烈的无序现象[39-43].比如与常规铁磁材料不同,3D磁性TI中TCurie以下磁化强度-温度曲线(magnetization-temperature curve,M-T curve)表现为线性或者上凹(类似顺磁行为)[16, 31].顺磁类的M-T曲线表明材料的磁化强度波动性大,需要低温才能获得均匀的磁化强度,这与在远低于TCurie的材料中观察到完美QAHE的现象一致[16].扫描超导量子干涉装置(scanning superconducting quantum interference device,SQUID)的测量结果显示出超顺磁行为[39].输运和扫描隧道显微镜实验中也观察到磁性和电子结构的不均匀[40-43].由于随机分布的磁性杂质之间短程磁耦合[44-46],低载流子密度的稀磁掺杂半导体一般具有强烈的磁无序,存在很多磁能隙远低于kBTCurie的弱磁性耦合区域,可以通过极低温或强磁场来抑制这种磁无序,否则穿过磁无序区域的手性边缘态容易被散射.简而言之,QAHE的观测温度受铁磁性最弱的区域的限制.
1.2 其他磁性掺杂拓扑绝缘体体系中的量子反常霍尔效应提高磁性TI中QAHE的观测温度,不仅要增大材料的磁能隙,还应提高磁有序.一般选择不同的磁性掺杂元素即可改善材料的磁性.Chang等[22-23]发现,MBE制备的V掺杂(Bi, Sb)2Te3薄膜在25 mK下具有极大的矫顽场(>1 T),即极大的垂直方向磁各向异性,可能抑制2D磁性系统中的磁性波动,但仍需要100 mK以下的极低温才能观测到完美的QAHE.角分辨光电子能谱(angle-resolved photoemission spectroscopy,ARPES)结果显示,V掺杂(Bi, Sb)2Te3薄膜表面态狄拉克点低于价带顶(磁能隙由于太模糊而无法分辨)[47],因此,需要极低的温度使价带中载流子局域化,才能实现完全量子化.
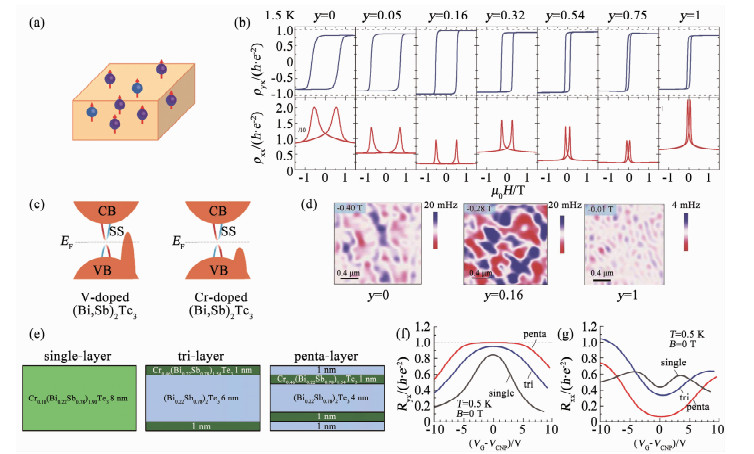
合金化和共掺杂也是改善材料磁性的有效方法.考虑前面的实验结果:在Cr掺杂TI中可以实现QAHE,但有强烈的磁无序;V掺杂TI有较强的磁各向异性,但狄拉克点低于价带顶(图 4(c)).如果结合这两种掺杂元素,是否可以获得更有效的磁性掺杂?Ou等[48]发现,在Cr-V共掺的(Bi, Sb)2Te3薄膜中可以获得QAHE(图 4(b)),完全量子化温度达到300 mK,1.5 K下零场反常霍尔电阻为97%量子化数值.磁力显微镜(magnetic force microscopy,MFM)测量发现,在矫顽场附近,共掺杂样品中的磁畴明显大于单纯Cr或者V掺杂样品中的磁畴(图 4(d)).
|
注:(a)磁性共掺杂体系示意图,不同颜色小球表示不同磁性元素;(b)1.5 K下Cr、V共掺TI中不同掺杂情况下反常霍尔电阻和纵向电阻随磁场强度变化曲线[48];(c)Cr、V共掺TI中能带结构示意图[48];(d)5层(CryV1-y)0.19(BixSb1-x)1.81Te3薄膜中矫顽场附近磁力显微镜的磁畴结构扫描图[48]; (e)调制掺杂体系的结构示意图[51];(f)0.5 K下反常霍尔电阻随栅极电压变化曲线[51];(g)0.5 K下纵向电阻随栅极电压变化曲线[51]. (a) Schematic of magnetically doped TI system (Balls with different color indicate different magnetic elements). (b) Magnetic field dependence of ρyx and ρxx in Cr- and V-doped TI thin films at 1.5 K[48]. (c) Schematic band structure of Cr- and V- doped TI[48]. (d) Magnetic domain structure in 5 QL (CryV1-y)0.19(BixSb1-x)1.81Te3 thin films near coercive field obtained from magnetic force microscope[48]. (e) Schematic structures of modulated Cr-doped (Bi, Sb)2Te3 thin films[51]. (f) Gate dependence of Ryx at 0.5 K[51]. (g) Gate dependence of Rxx at 0.5 K[51]. 图 4 其他磁性掺杂TI体系中的QAHE Fig. 4 QAHE in other magnetically doped TI systems |
提高磁能隙更直接的方法是增加磁性掺杂的掺杂浓度.由于3d元素的SOC强度比Bi/Sb和Te要弱的多,提高掺杂浓度将减小TI体能隙,材料可能会从TI转变为NI[49-50].通过在TI表面区域进行重磁性掺杂,在不改变体材料拓扑性质的同时,从某种程度上可以避免这个问题.Mogi等[51]发现通过对(Bi, Sb)2Te3薄膜的上下表面区域进行高达23%的Cr掺杂,可以显著提高QAHE的观测温度.有趣的是,将重型Cr掺杂层调节到亚表面将会进一步提高QAHE的温度到0.5 K(图 4(e)、(f)).这个温度高于He-3制冷机的基础温度,有利于更多研究团队和研究手段进行QAHE的研究.
这些结果说明磁性掺杂TI中的磁无序是低温QAHE的主要原因.然而,磁性掺杂TI永远无法完全消除磁无序.除了磁无序,磁性掺杂原子的随机分布带来的电子能带和化学势的空间波动、Bi/Sb比例的空间分布变化以及薄膜层厚的空间变化也会减小有效磁能隙,造成极低温下的QAHE.无序问题的最终解决方案可能在于寻找具有明确化学计量比的磁性TI材料或异质结构.在异质的磁性掺杂TI体系中,Mogi等[52-53]和Xiao等[54]还观测到了轴子绝缘体相,在直流输运测量中显示出清晰的零电导平台,未来有可能可以实现拓扑磁电效应,但实验观测仍是一个巨大的挑战.
2 近邻效应引起的量子反常霍尔效应引入磁性的另一种有效方式是近邻效应,且自然界中有很多具有有序磁结构的高温甚至超室温的铁磁绝缘体(ferromagnetic insulator,FMI)和反铁磁绝缘体(antiferromagnetic insulator,AFMI),如果能够制备出高质量的(A)FMI/TI/(A)FMI结构,则可能获得高温甚至超高温的QAHE.这个结构中的SOC和铁磁性来自不同空间层,因此可忽略它们的竞争关系.过去几年在这个方向上虽有大量研究,但进展依旧缓慢.理论工作表明在各种FMI/TI界面处,表面态波函数基本全部局域在TI层,在FMI层中的成分可以忽略不计,而铁磁矩也是一个短程作用力,导致铁磁性和表面态之间的相互作用较弱,磁能隙较小(几个meV)[55-57],因此很难获得高温QAHE.另外,在AFMI/TI/AFMI异质结构中如何控制上下两个反铁磁绝缘体层的磁化方向一致也是一个挑战.
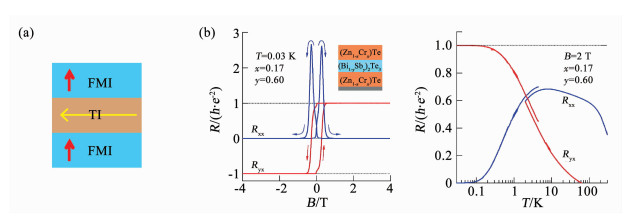
近期,Watanabe等[58]首次在磁性近邻结构(Zn, Cr)Te/(Bi, Sb)2Te3/(Zn, Cr)Te中观测到了QAHE.Cr和V掺杂TI中的QAHE说明3d轨道可能和Te的5p轨道有重叠,因此在(Zn, Cr)Te/(Bi, Sb)2Te3/(Zn, Cr)Te结构中,TI/FMI中Te的p轨道可能与FMI中的d轨道有近邻耦合,打开磁能隙获得QAHE,但QAHE观测温度仍低于100 mK(图 5(b)).
|
注:(a)FMI/TI/FMI结构示意图,红色箭头表示磁化方向,黄线表示边缘态;(b)30 mK下(Zn1-xCrx)Te/(Bi1-ySby)2Te3/(Zn1-xCrx)Te的输运测量结果[58],反常霍尔电阻和纵向电阻随磁感应强度(左)和温度(右)变化曲线. (a) Schematic of FMI/TI/FMI structure (Red arrows indicate magnetization orientation and yellow line indicates the chiral edge state). (b) Magnetic field (left) and temperature (right) dependence of Ryx and Rxx in (Zn1-xCrx)Te/(Bi1-ySby)2Te3/(Zn1-xCrx)Te at 30 mK[58]. 图 5 近邻效应引起的QAHE Fig. 5 QAHE in proximity-induced magnetic TI system |
2017年,Otrokov等[59]提出在典型的Bi2Te3薄膜表面近邻生长一层MnBi2Te4作为FMI层,可以获得最大77 meV的磁能隙.MnBi2Te4具有“七层”(septuple layer,SL)结构,每层包含Te/Bi/Te/Mn/Te/Bi/Te七个原子单层,可看作MnTe双原子层(bilayer,BL)插入到Bi2Te3五层结构中.与一般FMI/TI结构中局域化的磁矩和表面态不同的是,Bi2Te3的表面态可以“扩展”到单层MnBi2Te4中,使得表面态与磁矩有强烈的耦合,因此打开巨大的磁能隙.这个理论计算引起了人们极大的兴趣:为什么Bi2Te3的表面态可以“扩展”到MnBi2Te4中?
3 内禀磁性拓扑绝缘体体系结合前面介绍的重型Cr掺杂“五层结构”中的QAHE[51],本文作者团队敏锐地意识到MnBi2Te4可能是一种TI材料,于是从2017年开始使用MBE制备材料并进行原位电子结构表征和磁性测量.
2010年,Xu等[60]的理论计算指出,Bi2Se3家族TI中插层PbTe、GeTe等可形成复杂的原子结构,如AB2X4、A2B2X5以及AB4X7等,其中A为Pb或者Ge,B为Bi或者Sb,X为Te或者Se.如果A为磁性元素,则可能获得磁有序材料;2013年,Lee等[61]获得了多晶相MnBi2Te4;2017年,Hagmann等[62]和Hirahara等[63]分别在MBE共沉积生长的Mn、Bi、Se三元合金和MnSe/Bi2Se3异质结构中发现高质量MnBi2Se4结构.
MnTe和MnSe是反铁磁绝缘体,具有层内铁磁和层间反铁磁耦合,MBE可以制备出高质量的薄膜[63-66].MnTe的涅尔温度(TN)大于300 K,晶格常数与Bi2Te3和Bi2Se3近似.借鉴前面的研究经验,Gong等[67]使用MBE方法通过重复生长一个QL Bi2Te3和一个BL MnTe,获得了高质量的MnBi2Te4单晶薄膜.原位ARPES测量发现在厚度大于1 SL的薄膜中,体能隙中存在狄拉克型线性能带(图 6(d)).第一性原理计算表明,由于SOC与磁序之间的相互作用,该材料具有丰富的拓扑相[68-71].MnBi2Te4的基态是A型配型的3D AFM TI:SL层内铁磁耦合,相邻层间反铁磁耦合,具有面外指向的易磁化轴.该材料具有TRS和平移对称性保护相结合的拓扑非平庸特征.与受TRS保护的3D TI无能隙TSS不同,由于受到法线方向的净磁化作用,MnBi2-Te4的TSS在平行于(0001)的平面上有能隙,在垂直于(0001)的平面上无能隙.磁有序温度Tmo(由于MnBi2Te4可能有不同的磁性构型,表达上用Tmo来代替TCurie或者TN)以上,MnBi2Te4变成没有磁能隙的3D TI,所有表面为无能隙TSS;磁有序温度Tmo以下的奇数层MnBi2Te4薄膜中,上下表面磁化方向相同,类似前面磁性掺杂TI的磁矩情况,两个表面拓扑不同,将产生QAHE(图 6(c));而在偶数层MnBi2Te4薄膜中,上下表面磁化方向相反,两个表面拓扑相同,构成轴子绝缘体.MnBi2Te4层间的AFM耦合要比层内的FM耦合弱很多,通过施加几个特斯拉的外磁场可以转变为层间FM耦合[72](图 6(e)).至此,本文作者所在团队制备出第一个内禀磁性的TI材料,并预言其中存在丰富的拓扑相.

|
注:(a)原子结构示意图;(b)高分辨率透射电镜原子结构图;(c)第一性原理计算的能带结构图;(d)角分辨光电子能谱测量结果;(e)7 SL MnBi2Te4薄膜中阶梯状的霍尔电阻测量曲线,箭头表示每一层的磁构型. (a) Schematic of atomic structure. (b) Atomic structure obtained from high resolution transmission electron microscope. (c) Band structure obtained from first principle calculation. (d) Band structure obtained from ARPES measurement. (e) Step-like hysteresis loop of Hall resistance of 7 SL MnBi2Te4 thin films (Arrows indicate the magnetic configuration of each layer). 图 6 第一个内禀磁性TI体系MnBi2Te4[67] Fig. 6 MnBi2Te4 as the first intrinsic magnetic TI[67] |
因此,Bi2Te3表面态可以“扩展”到MnBi2Te4中:因为MnBi2Te4是3D TI.当两个3D TI堆叠起来,原本界面处的TSS变成体带,出现体能隙,在整个样品的表面将保持无能隙的TSS[73].
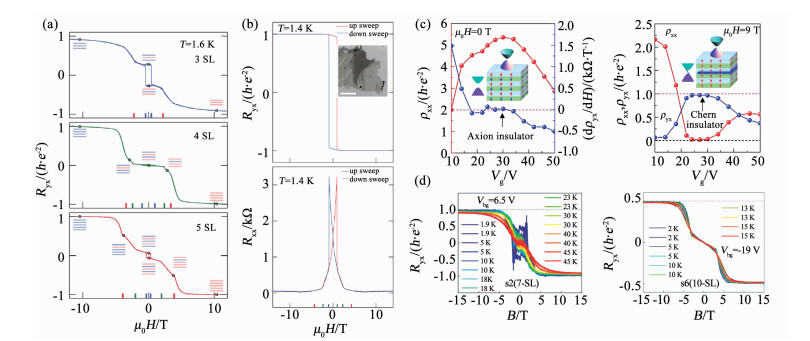
目前MnBi2Te4中很多理论预言的性质都已被实验证实[67, 74-81].M-T曲线显示了典型的具有面外易磁化轴的反铁磁性质[74-78].霍尔效应测量中的阶梯状磁滞回线说明在3~7 T外磁场作用下可以实现AFM到FM的磁相变[67, 74-81],阶梯数目与薄膜层厚有关(图 7(a)).在单晶剥离的3 SL到9 SL薄片中观测到量子化的反常霍尔电阻和纵向电阻消失现象[79-81].量子化霍尔电阻需要大于5 T的外加磁场,与AFM到FM的磁相变所需磁场强度相近,表明量子化霍尔电阻是由磁化引起的,因此不能完全排除QHE的影响,但仍应归因于反常霍尔效应.在偶数层样品中,Liu等[80]观测到强磁场下Chern绝缘体到轴子绝缘体的相变(图 7(c)).在奇数层样品中,多数样品的零场霍尔电阻远低于量子化数值[79, 81],但经过不断的样品优化和解理封装工艺的提升,近期Deng等[79]在一个高质量的5 SL剥离薄膜中获得了QAHE的实验观测.如图 7(b)所示,1.4 K零磁场下获得0.97h/e2的反常霍尔电阻和0.061h/e2的纵向电阻,且量子化与载流子类型和浓度无关,这是典型的QAH现象.在7.6 T的外磁场作用下,量子化霍尔电阻的观测温度高到6.5 K.通过栅极电压调节费米面,在外磁场下还观测到h/2e2的霍尔电阻平台,说明在表面态区域QHE与QAHE共存.Ge等[81]发现,当测量温度高于Tmo=25 K时,高场下的霍尔电阻仍非常接近h/e2(图 7(d)).理论计算的MnBi2Te4的磁能隙(~50 meV)比Tmo对应的能量尺度(25 K,~2 meV)大得多,这可以归因于MnBi2Te4的2D性质.2D磁性系统通常会受到磁波动的限制.磁能隙和交换能是系统基态(绝对零度)的性质,主要由层内磁耦合贡献,有可能比kBTmo大得多.外磁场会抑制磁波动,提高有效Tmo,使得霍尔电阻接近量子化数值.Ge等[81]在10 SL MnBi2Te4中还观察到Chern数为2的量子化平台,说明铁磁状态下的MnBi2Te4体相可能是磁性外尔半金属(Weyl semimetal, WSM).
|
注:(a)不同层厚薄膜中反常霍尔电阻随磁场强度变化曲线[79];(b)5 SL薄膜中的QAHE的输运测量结果[79],插图是解理薄膜的光学显微镜图像;(c)6 SL薄膜中轴子绝缘体相(左)与陈绝缘体相(右)的霍尔电阻/纵向电阻随栅极电压变化曲线[80];(d)7 SL(左)和10 SL(右)薄膜中反常霍尔电阻随磁感应强度变化曲线[81]. (a) Magnetic field dependence of Ryx in thin films with different thickness[79]. (b) Transport measurement of QAHE in 5 SL thin films[79] (Insert: optical image of few-layer flakes). (c) Gate dependence of ρyx and ρxx in axion insulator (left) and Chern insulator (right) at high magnetic field in 6 SL thin films[80]. (d) Magnetic field dependence of Ryx at different temperatures in 7 SL (left) and 10 SL (right) thin films[81]. 图 7 MnBi2Te4单晶解理薄膜中的QAHE Fig. 7 QAHE in single crystal cleaved MnBi2Te4 thin flakes |
除了增加外磁场,(MnTe)·a(Bi2Te3)超晶格结构可以减弱MnBi2Te4层间反铁磁耦合[76, 82-83],可能实现QAHE.a=1时是MnBi2Te4.在Mn掺杂的Bi2Te3单晶材料中,能够获得MnBi4Te7(a=2)、MnBi6Te10(a=3)和(MnTe)·a(Bi2Te3)多层结构,测量发现Tmo随着a的增加逐渐降低,层间反铁磁耦合也在降低,但由于单晶体材料有体导电通道,目前还没有观测到QAHE.通过制备(MnTe)·a(Bi2Te3)超晶格结构的薄膜也许可以解决这个问题.
迄今为止,尚未在MBE制备的MnBi2Te4薄膜中实现QAHE.与许多层状材料相似,由于层状材料与基底之间的弱相互作用导致薄膜中晶畴的存在,MBE制备的MnBi2Te4薄膜质量低于单晶样品.但单晶解理样品尺寸小,制备异质结构过程复杂,不利于大规模样品的制备.MBE样品在大尺寸均匀,适合制备各种异质及超晶格结构.进一步提高MBE制备的MnBi2Te4薄膜质量将有助于探索高温QAHE及多种量子效应.
4 设计高温量子反常霍尔效应系统尽管需要外磁场,MnBi2Te4中QAHE的观测温度高于磁性掺杂TI体系.有趣的是,具有类似结构的调制掺杂“五层结构”中也观测到了较高温度的QAHE.这两种系统可以看做是薄FMI层插入3D TI薄膜的插层结构.这种磁性插层TI(magnetically intercalated TI,MITI)在实现高温QAHE方面具有两个优势:1)由FMI贡献的铁磁性比随机分布的磁性掺杂贡献的铁磁性更强、更有序;2)与FMI/TI/FMI三明治结构相比,FMI插层足够薄,TSS波函数可以渗透并实现有效的磁化作用.同时有两点需要注意:首先FMI层间铁磁耦合优于反铁磁耦合,后者可能会降低有效磁能隙;其次FMI薄层需要克服2D磁波动.
更一般的情况,为了增强铁磁性和TSS的相互作用,应结合磁性原子和TI获得内禀磁性TI.但SOC和FM磁交换能存在竞争.通过在TI中增加更多的磁性原子可以增强FM,但可能会降低SOC,尤其是增加3d元素,弱化的SOC会减小磁能隙甚至材料的体能隙,发生TI到NI的相变.使用更重的4d、4f元素作为磁性掺杂将不会减小SOC,但通常会降低FM磁交换能和Tmo.
综上所述,要获得高温QAHE,需使MITI中磁性原子在TSS打开能隙的“效率”最大化.考虑到TSS是2D的,磁性原子与TSS之间相互作用最有效的方法是排列成紧凑的2D结构.
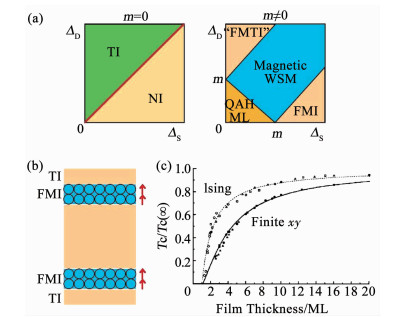
类似MnBi2Te4的MITI可以看做是FMI和TI的超晶格结构,Burkov等[84]对其拓扑相图进行了理论研究,引用并稍作修改的相图见图 8(a).在温度高于Tmo时MITI没有磁有序,是NI和TI的超晶格结构;横坐标ΔS表示TI中上下TSS的杂化能隙(跨越TI体能隙),纵坐标ΔD表示邻近TI层上下TSS的杂化能隙(跨越NI体能隙).显然,ΔS∝1/dTI,ΔD∝1/dNI,其中dTI和dNI表示TI和NI层的层厚.当NI层逐渐变薄,整个超晶格结构将变为TI,反之亦然.
|
注:(a)FMI/TI超晶格结构中磁有序温度以上(左)和磁有序温度以下(右)的相图(改编自参考文献[84]);(b)含有两个磁性原子单原子层的MITI结构示意图;(c)磁性薄膜中居里温度与薄膜厚度关系曲线[86]. (a) Phase diagram of FMI/TI superlattice structure above (left) and below (right) Tmo (revised from Ref. [84]). (b) Schematic of MITI structure with two monolayers of magnetic atoms with FM configuration. (c) Thickness dependence of TCurie in magnetic films[86]. 图 8 设计构造高温QAHE体系 Fig. 8 Design of high temperature QAHE system |
在Tmo以下,系统表现为FMI/TI的超晶格结构,相图变得复杂(FMI层间铁磁构型更可能获得高温QAHE,这里不考虑层间反铁磁构型的结构),图中m表示磁交换能隙.当ΔS很大而ΔD很小,系统是拓扑平庸的FMI;当ΔD很大而ΔS很小,系统可以整体看做“FMTI”(在FMI层比较厚时,可能会导致系统SOC减小,发生从TI到NI的相变,所以加一个引号),可以获得Chern数为1的QAHE;当ΔS和ΔD都很大的时候,系统变为磁性WSM,Chern数随膜厚的增加而增加,外加强磁场下10 SL MnBi2Te4就是这样的情况;当ΔS和ΔD都很小的时候,系统是FMI/TI/FMI三明治结构的堆叠,可看做QAH多层(multilayer,ML)结构,有效Chern数由TI的层数确定[85].
以MnBi2Te4为例设计构造高温QAHE材料体系.MnBi2Te4有两个劣势.首先MnBi2Te4的基态是反铁磁构型; 其次FMI层(MnTe层)只有一个单层的磁性原子,其2D性质会引起强烈的磁性波动导致Tmo偏低,且Tmo以下有磁无序.如果FMI层中包含两个单层磁原子层,将会大大抑制磁波动(图 8(b)).理论和实验表明,在用2D Ising模型描述的磁性薄膜中,因为交换相互作用是短程作用,Tmo主要由最近的近邻耦合贡献,两个单原子层的磁性原子可以贡献将近体材料一半的TCurie[86-87](图 8(c)).另外,仅包含两个单层磁性原子的FMI膜厚通常低于1 nm,TSS能够穿过并发生有效的磁化相互作用.因此,在包含两个(或三个)单层磁性原子的铁磁耦合FMI与TI的MITI中,有望实现高温QAHE.
M2Bi2Te5就是这样一种“九层”结构的材料[88] (M代表磁性元素),包括2 BL MTe.例如Mn2Bi2Te5. MnTe体材料Tmo~350 K,如果获得层间铁磁耦合的2 BL MnTe,则非常有可能获得高于77 K的QAHE.另外在范德瓦尔斯外延结构中,通过向TI中插入包含两层或者三层单原子层磁性原子的2D FMI材料,也可以制造人工MITI材料,获得高温QAHE.即使获得的材料是拓扑平庸的FMI,通过增加TI层的厚度,也可将其调整为磁性WSM或“FMTI”相.
5 结论提升QAHE的观测温度有几个方面的挑战.首先,SOC和FM交换能相互竞争,很难同时增强;其次,随机分布的磁性掺杂或者2D磁性插层中存在磁性波动,降低了Tmo和QAHE的观测温度;第三,在FMI/TI界面,TSS和FM之间的相互作用较弱,导致表面磁能隙小.这些问题可以在2或3个单层磁性原子插层的MITI中得到一定程度的解决,甚至可以在高于77 K的温度下观测到QAHE,比如复杂的内禀磁性TI(M2Bi2Te5族)或TI/FMI(包含2或3个单原子层磁性原子层)的人工范德瓦尔斯异质结构.
当然,上述方法不是实现高温QAHE的唯一方法,破坏2D TI中的TRS也可以实现QAHE[13].单原子层或者少数原子层的2D TI(锡烯[89-91],铋烯[92]和1T’-WTe2[93-94]等)与FMI可能具有更强的磁近邻效应,可以获得高温QAHE.最近在扭曲的双层石墨烯和ABC-三层石墨烯/六方氮化硼的莫尔超晶格结构中,由于TRS被电子相互作用产生的磁性破坏,观测到了QAHE[95-97].扭曲双层石墨烯中,1.6 K下实现了零磁场的量子化霍尔电阻和零纵向电阻[97],为寻找高温QAHE提供了一个新的方向.
在高于77 K的温度实现QAHE将使无耗散手性量子边缘态和许多拓扑量子效应的应用成为可能.同时,QAHE也是构建多种拓扑量子相的基础模块,高温QAHE的实现将会将拓扑量物质研究领域从基础物理学推向全新的未来.
| [1] |
TOKURA Y, KAWASAKI M, NAGAOSA N. Emergent functions of quantum materials[J]. Nature Physics, 2017, 13(11): 1056. DOI:10.1038/nphys4274 |
| [2] |
BOZOVIC I, AHN C. A new frontier for superconductivity[J]. Nature Physics, 2014, 10(12): 892. DOI:10.1038/nphys3177 |
| [3] |
HALDANE F D M. Nobel lecture: Topological quantum matter[J]. Reviews of Modern Physics, 2017, 89(4): 040502. DOI:10.1103/RevModPhys.89.040502 |
| [4] |
WEN Xiaogang. Colloquium: Zoo of quantum-topological phases of matter[J]. Reviews of Modern Physics, 2017, 89(4): 041004. DOI:10.1103/RevModPhys.89.041004 |
| [5] |
KLITZING K V, DORDA G, PEPPER M. New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance[J]. Physical Review Letters, 1980, 45(6): 494. DOI:10.1103/PhysRevLett.45.494 |
| [6] |
THOULESS D J, KOHMOTO M, NIGHTINGALE M P, et al. Quantized Hall conductance in a two-dimensional periodic potential[J]. Physical Review Letters, 1982, 49(6): 405. DOI:10.1103/PhysRevLett.49.405 |
| [7] |
AVRON J E, OSADCHY D, SELLER R. A topological look at the quantum Hall effect[J]. Physics Today, 2003, 56(8): 38. DOI:10.1063/1.1611351 |
| [8] |
HALDANE F D M. Model for a quantum Hall effect without Landau levels: condensed-matter realization of the "parity anomaly"[J]. Physical Review Letters, 1988, 61(18): 2015. DOI:10.1103/PhysRevLett.61.2015 |
| [9] |
HASAN M Z, KANE C L. Colloquium: Topological insulators[J]. Reviews of Modern Physics, 2010, 82(4): 3045. DOI:10.1103/RevModPhys.82.3045 |
| [10] |
QI Xiaoliang, ZHANG Shoucheng. Topological insulators and superconductors[J]. Reviews of Modern Physics, 2011, 83(4): 1057. DOI:10.1103/RevModPhys.83.1057 |
| [11] |
QI Xiaoliang, WU Yongshi, ZHANG Shoucheng. Topological quantization of the spin Hall effect in two-dimensional paramagnetic semiconductors[J]. Physical Review B, 2006, 74(8): 085308. DOI:10.1103/PhysRevB.74.085308 |
| [12] |
LIU Chaoxing, QI Xiaoliang, DAI Xi, et al. Quantum anomalous Hall effect in Hg1-yMnyTe quantum wells[J]. Physical Review Letters, 2008, 101(14): 146802. DOI:10.1103/PhysRevLett.101.146802 |
| [13] |
QI Xiaoliang, HUGHES T L, ZHANG Shoucheng. Topological field theory of time-reversal invariant insulators[J]. Physical Review B, 2008, 78(19): 195424. DOI:10.1103/PhysRevB.78.195424 |
| [14] |
YU Rui, ZHANG Wei, ZHANG Haijun, et al. Quantized anomalous Hall effect in magnetic topological insulators[J]. Science, 2010, 329(5987): 61. DOI:10.1126/science.1187485 |
| [15] |
NOMURA K, NAGAOSA N. Surface-quantized anomalous Hall current and the magnetoelectric effect in magnetically disordered topological insulators[J]. Physical Review Letters, 2011, 106(16): 166802. DOI:10.1103/PhysRevLett.106.166802 |
| [16] |
CHANG Cuizu, ZHANG Jinsong, FENG Xiao, et al. Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator[J]. Science, 2013, 340(6129): 167. DOI:10.1126/science.1234414 |
| [17] |
CHECKELSKY J G, YOSHIMI R, TSUKAZAKI A, et al. Trajectory of the anomalous Hall effect towards the quantized state in a ferromagnetic topological insulator[J]. Nature Physics, 2014, 10(10): 731. DOI:10.1038/nphys3053 |
| [18] |
KOU Xufeng, GUO Shih-ting, FAN Yabin, et al. Scale-invariant quantum anomalous Hall effect in magnetic topological insulators beyond the two-dimensional limit[J]. Physical Review Letters, 2014, 113(13): 137201. DOI:10.1103/PhysRevLett.113.137201 |
| [19] |
KANDALA A, RICHARDELLA A, KEMPINGER S, et al. Giant anisotropic magnetoresistance in a quantum anomalous Hall insulator[J]. Nature Communications, 2015, 6: 7434. DOI:10.1038/ncomms8434 |
| [20] |
CHECKELSKY J G, YE Jianting, ONOSE Y, et al. Dirac-fermion-mediated ferromagnetism in a topological insulator[J]. Nature Physics, 2012, 8(10): 729. DOI:10.1038/nphys2388 |
| [21] |
BESTWICK A J, FOX E J, KOU Xufeng, et al. Precise quantization of the anomalous Hall effect near zero magnetic field[J]. Physical Review Letters, 2015, 114(18): 187201. DOI:10.1103/PhysRevLett.114.187201 |
| [22] |
CHANG Cuizu, ZHAO Weiwei, KIM D Y, et al. High-precision realization of robust quantum anomalous Hall state in a hard ferromagnetic topological insulator[J]. Nature Materials, 2015, 14(5): 473. DOI:10.1038/nmat4204 |
| [23] |
CHANG Cuizu, ZHAO Weiwei, KIM D Y, et al. Zero-field dissipationless chiral edge transport and the nature of dissipation in the quantum anomalous Hall state[J]. Physical Review Letters, 2015, 115(5): 057206. DOI:10.1103/PhysRevLett.115.057206 |
| [24] |
LIU Chaoxing, ZHANG Haijun, YAN Binghai, et al. Oscillatory crossover from two-dimensional to three-dimensional topological insulators[J]. Physical Review B, 2010, 81(4): 041307. |
| [25] |
LU Haizhou, SHAN Wenyu, YAO Wang, et al. Massive Dirac fermions and spin physics in an ultrathin film of topological insulator[J]. Physical Review B, 2010, 81(11): 115407. DOI:10.1103/PhysRevB.81.115407 |
| [26] |
LI Yaoyi, WANG Guang, ZHU Xiegang, et al. Intrinsic topological insulator Bi2Te3 thin films on Si and their thickness limit[J]. Advanced Materials, 2010, 22(36): 4002. DOI:10.1002/adma.201000368 |
| [27] |
ZHANG Yi, HE Ke, CHANG Cuizu, et al. Crossover of the three-dimensional topological insulator Bi2Se3 to the two-dimensional limit[J]. Nature Physics, 2010, 6(8): 584. DOI:10.1038/nphys1689 |
| [28] |
SONG Canli, WANG Yilin, JIANG Yeping, et al. Topological insulator Bi2Se3 thin films grown on double-layer graphene by molecular beam epitaxy[J]. Applied Physics Letters, 2010, 97(14): 143118. DOI:10.1063/1.3494595 |
| [29] |
WANG Guang, ZHU Xiegang, SUN Yiyang, et al. Topological insulator thin films of Bi2Te3 with controlled electronic structure[J]. Advanced Materials, 2011, 23(26): 2929. DOI:10.1002/adma.201100678 |
| [30] |
WANG Guang, ZHU Xiegang, WEN Jing, et al. Atomically smooth ultrathin films of topological insulator Sb2Te3[J]. Nano Research, 2010, 3(12): 874. DOI:10.1007/s12274-010-0060-2 |
| [31] |
CHANG Cuizu, ZHANG Jinsong, LIU Minhao, et al. Thin films of magnetically doped topological insulator with carrier-independent long-range ferromagnetic order[J]. Advanced Materials, 2013, 25(7): 1065. DOI:10.1002/adma.201203493 |
| [32] |
ZHANG Jinsong, CHANG Cuizu, ZHANG Zuocheng, et al. Band structure engineering in (Bi1-xSbx)2Te3 ternary topological insulators[J]. Nature Communications, 2011, 2: 574. DOI:10.1038/ncomms1588 |
| [33] |
DIETL T, OHNO H, MATSUKURA F, et al. Zener model description of ferromagnetism in zinc-blende magnetic semiconductors[J]. Science, 2000, 287(5455): 1019. DOI:10.1126/science.287.5455.1019 |
| [34] |
OHNO H. Making nonmagnetic semiconductors ferromagnetic[J]. Science, 1998, 281(5379): 951. DOI:10.1126/science.281.5379.951 |
| [35] |
ZHU Jiaji, YAO Daoxin, ZHANG Shoucheng, et al. Electrically controllable surface magnetism on the surface of topological insulators[J]. Physical Review Letters, 2011, 106(9): 097201. DOI:10.1103/PhysRevLett.106.097201 |
| [36] |
ZHANG Haijun, LIU Chaoxing, QI Xiaoliang, et al. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface[J]. Nature Physics, 2009, 5(6): 438. DOI:10.1038/nphys1270 |
| [37] |
XIA Yiman, QIAN Dong, HSIEH D, et al. Observation of a large-gap topological-insulator class with a single Dirac cone on the surface[J]. Nature Physics, 2009, 5(6): 398. DOI:10.1038/nphys1274 |
| [38] |
CHEN Yulin, ANALYTIS J G, CHU J H, et al. Experimental realization of a three-dimensional topological insulator, Bi2Te3[J]. Science, 2009, 325(5937): 178. DOI:10.1126/science.1173034 |
| [39] |
LACHMAN E O, YOUNG A F, RICHARDELLA A, et al. Visualization of superparamagnetic dynamics in magnetic topological insulators[J]. Science Advances, 2015, 1(10): e1500740. DOI:10.1126/sciadv.1500740 |
| [40] |
FENG Xiao, FENG Yang, WANG Jing, et al. Thickness dependence of the quantum anomalous Hall effect in magnetic topological insulator films[J]. Advanced Materials, 2016, 28(30): 6386. DOI:10.1002/adma.201600919 |
| [41] |
LIU Minhao, WANG Wudi, RICHARDELLA A R, et al. Large discrete jumps observed in the transition between Chern states in a ferromagnetic topological insulator[J]. Science Advances, 2016, 2(7): e1600167. DOI:10.1126/sciadv.1600167 |
| [42] |
GRAUER S, SCHREYECK S, WINNERLEIN M, et al. Coincidence of superparamagnetism and perfect quantization in the quantum anomalous Hall state[J]. Physical Review B, 2015, 92(20): 201304. DOI:10.1103/PhysRevB.92.201304 |
| [43] |
LEE I, KIM C K, LEE J, et al. Imaging Dirac-mass disorder from magnetic dopant atoms in the ferromagnetic topological insulator Crx(Bi0.1Sb0.9)2-xTe3[J]. Proceedings of the National Academy of Sciences of the United States of America, 2015, 112(5): 1316. DOI:10.1073/pnas.1424322112 |
| [44] |
BHATT R N, BERCIU M, KENNETT M P, et al. Diluted magnetic semiconductors in the low carrier density regime[J]. Journal of Superconductivity, 2002, 15(1): 71. DOI:10.1023/A:1014031327996 |
| [45] |
TIMM C. Disorder effects in diluted magnetic semiconductors[J]. Journal of Physics-Condensed Matter, 2003, 15(50): R1865. DOI:10.1088/0953-8984/15/50/R03 |
| [46] |
DAS SARMA S, HWANG E H, KAMINSKI A. Temperature-dependent magnetization in diluted magnetic semiconductors[J]. Physical Review B, 2003, 67(15): 155201. DOI:10.1103/PhysRevB.67.155201 |
| [47] |
LI Wei, CLAASSEN M, CHANG Cuizu, et al. Origin of the low critical observing temperature of the quantum anomalous Hall effect in V-doped (Bi, Sb)2Te3 film[J]. Scientific Reports, 2016, 6: 32732. DOI:10.1038/srep32732 |
| [48] |
OU Yunbo, LIU Chang, JIANG Gaoyuan, et al. Enhancing the quantum anomalous Hall effect by magnetic codoping in a topological insulator[J]. Advanced Materials, 2018, 30(1): 1703062. DOI:10.1002/adma.201703062 |
| [49] |
ZHANG Jinsong, CHANG Cuizu, TANG Peizhe, et al. Topology-driven magnetic quantum phase transition in topological insulators[J]. Science, 2013, 339(6127): 1582. DOI:10.1126/science.1230905 |
| [50] |
OU Yunbo, LIU Chang, ZHANG Liguo, et al. Heavily Cr-doped (Bi, Sb)2Te3 as a ferromagnetic insulator with electrically tunable conductivity[J]. APL Materials, 2016, 4(8): 086101. DOI:10.1063/1.4960111 |
| [51] |
MOGI M, YOSHIMI R, TSUKAZAKI A, et al. Magnetic modulation doping in topological insulators toward higher-temperature quantum anomalous Hall effect[J]. Applied Physics Letters, 2015, 107(18): 182401. DOI:10.1063/1.4935075 |
| [52] |
MOGI M, KAWAMURA M, TSUKAZAKI A, et al. Tailoring tricolor structure of magnetic topological insulator for robust axion insulator[J]. Science Advances, 2017, 3(10): eaao1669. DOI:10.1126/sciadv.aao1669 |
| [53] |
MOGI M, KAWAMURA M, YOSHIMI R, et al. A magnetic heterostructure of topological insulators as a candidate for an axion insulator[J]. Nature Materials, 2017, 16(5): 516. DOI:10.1038/nmat4855 |
| [54] |
XIAO Di, JIANG Jue, SHIN J H, et al. Realization of the axion insulator state in quantum anomalous Hall sandwich heterostructures[J]. Physical Review Letters, 2018, 120(5): 056801. DOI:10.1103/PhysRevLett.120.056801 |
| [55] |
EREMEEV S V, MEN'SHOV V N, TUGUSHEV V V, et al. Magnetic proximity effect at the three-dimensional topological insulator/magnetic insulator interface[J]. Physical Review B, 2013, 88(14): 144430. DOI:10.1103/PhysRevB.88.144430 |
| [56] |
MEN'SHOV V N, TUGUSHEV V V, EREMEEV S V, et al. Magnetic proximity effect in the three-dimensional topological insulator/ferromagnetic insulator heterostructure[J]. Physical Review B, 2013, 88(22): 224401. DOI:10.1103/PhysRevB.88.224401 |
| [57] |
EREMEEV S V, MEN'SHOV V N, TUGUSHEV V V, et al. Interface induced states at the boundary between a 3D topological insulator Bi2Se3 and a ferromagnetic insulator EuS[J]. Journal of Magnetism and Magnetic Materials, 2015, 383: 30. DOI:10.1016/j.jmmm.2014.09.029 |
| [58] |
WATANABE R, YOSHIMI R, KAWAMURA M, et al. Quantum anomalous Hall effect driven by magnetic proximity coupling in all-telluride based heterostructure[J]. Applied Physics Letters, 2019, 115(10): 102403. DOI:10.1063/1.5111891 |
| [59] |
OTROKOV M M, MENSHCHIKOVA T V, VERGNIORY M G, et al. Highly-ordered wide bandgap materials for quantized anomalous Hall and magnetoelectric effects[J]. 2D Materials, 2017, 4(2): 025082. DOI:10.1088/2053-1583/aa6bec |
| [60] |
XU Suyang, WRAY L A, XIA Y, et al. Discovery of several large families of topological insulator classes with backscattering-suppressed spin-polarized single-Dirac-cone on the surface[Z]. arXiv: 1007.5111
|
| [61] |
LEE D S, KIM T H, PARK C H, et al. Crystal structure, properties and nanostructuring of a new layered chalcogenide semiconductor, Bi2MnTe4[J]. CrystEngComm, 2013, 15(27): 5532. DOI:10.1039/c3ce40643a |
| [62] |
HAGMANN J A, LI Xiang, CHOWDHURY S, et al. Molecular beam epitaxy growth and structure of self-assembled Bi2Se3/Bi2-MnSe4 multilayer heterostructures[J]. New Journal of Physics, 2017, 19: 085002. DOI:10.1088/1367-2630/aa759c |
| [63] |
HIRAHARA T, EREMEEV S V, SHIRASAWA T, et al. Large-gap magnetic topological heterostructure formed by subsurface incorporation of a ferromagnetic layer[J]. Nano Letters, 2017, 17(6): 3493. DOI:10.1021/acs.nanolett.7b00560 |
| [64] |
WATANABE R, YOSHIMI R, SHIRAI M, et al. Emergence of interfacial conduction and ferromagnetism in MnTe/InP[J]. Applied Physics Letters, 2018, 113(18): 181602. DOI:10.1063/1.5050446 |
| [65] |
KRIEGNER D, VÝBORNÝ K, OLEJNÍK K, et al. Multiple-stable anisotropic magnetoresistance memory in antiferromagnetic MnTe[J]. Nature Communications, 2016, 7: 11623. DOI:10.1038/ncomms11623 |
| [66] |
HE Qinglin, YIN Gen, GRUTTER A J, et al. Exchange-biasing topological charges by antiferromagnetism[J]. Nature Communications, 2018, 9(1): 2767. DOI:10.1038/s41467-018-05166-9 |
| [67] |
GONG Yan, GUO Jingwen, LI Jiaheng, et al. Experimental realization of an intrinsic magnetic topological insulator[J]. Chinese Physics Letters, 2019, 36(7): 076801. DOI:10.1088/0256-307X/36/7/076801 |
| [68] |
GONG Yan, ZHU Kejing, LI Zhe, et al. Experimental evidence of the thickness- and electric-field-dependent topological phase transitions in topological crystalline insulator SnTe(111) thin films[J]. Nano Research, 2018, 11(11): 6045. DOI:10.1007/s12274-018-2120-y |
| [69] |
LI Jiaheng, LI Yang, DU Shiqiao, et al. Intrinsic magnetic topological insulators in van der Waals layered MnBi2Te4-family materials[J]. Science Advances, 2019, 5(6): eaaw5685. DOI:10.1126/sciadv.aaw5685 |
| [70] |
ZHANG Dongqin, SHI Minji, ZHU Tongshuai, et al. Topological axion states in the magnetic insulator MnBi2Te4 with the quantized magnetoelectric effect[J]. Physical Review Letters, 2019, 122(20): 206401. DOI:10.1103/PhysRevLett.122.206401 |
| [71] |
OTROKOV M M, RUSINOV I P, BLANCO-REY M, et al. Unique thickness-dependent properties of the van der Waals interlayer antiferromagnet MnBi2Te4 films[J]. Physical Review Letters, 2019, 122(10): 107202. DOI:10.1103/PhysRevLett.122.107202 |
| [72] |
HUANG B, CLARK G, NAVARRO-MORATALLA E, et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit[J]. Nature, 2017, 546(7657): 270. DOI:10.1038/nature22391 |
| [73] |
CHANG Cuizu, TANG Peizhe, FENG Xiao, et al. Band engineering of Dirac surface states in topological-insulator-based van der Waals heterostructures[J]. Physical Review Letters, 2015, 115(3): 136801. |
| [74] |
OTROKOV M M, KLIMOVSKIKH I I, BENTMANN H, et al. Prediction and observation of an antiferromagnetic topological insulator[J]. Nature, 2019, 576(7787): 416. DOI:10.1038/s41586-019-1840-9 |
| [75] |
LEE S H, ZHU Yanglin, WANG Yu, et al. Spin scattering and noncollinear spin structure-induced intrinsic anomalous Hall effect in antiferromagnetic topological insulator MnBi2Te4[J]. Physical Review Research, 2019, 1(1): 012011. |
| [76] |
WU Jiazhen, LIU Fucai, SASASE M, et al. Natural van der Waals heterostructural single crystals with both magnetic and topological properties[J]. Science Advances, 2019, 5(11): eaax9989. DOI:10.1126/sciadv.aax9989 |
| [77] |
CUI Jianhua, SHI Mengzhu, WANG Honghui, et al. Transport properties of thin flakes of the antiferromagnetic topological insulator MnBi2Te4[J]. Physical Review B, 2019, 99(15): 155125. DOI:10.1103/PhysRevB.99.155125 |
| [78] |
CHEN Bo, FEI Fucong, ZHANG Dongqin, et al. Intrinsic magnetic topological insulator phases in the Sb doped MnBi2Te4 bulks and thin flakes[J]. Nature Communications, 2019, 10: 4469. DOI:10.1038/s41467-019-12485-y |
| [79] |
DENG Yujun, YU Yijun, SHI Mengzhu, et al. Quantum anomalous Hall effect in intrinsic magnetic topological insulator MnBi2Te4[J]. Science, 2020, 367(6480): 895. DOI:10.1126/science.aax8156 |
| [80] |
LIU Chang, WANG Yongchao, LI Hao, et al. Robust axion insulator and Chern insulator phases in a two-dimensional antiferromagnetic topological insulator[J]. Nature Materials, 2020. DOI:10.1038/s41563 |
| [81] |
GE Jun, LIU Yanzhao, LI Jiaheng, et al. High-Chern-number and high-temperature quantum Hall effect without Landau levels[Z]. arXiv: 1907.09947v3
|
| [82] |
HU Chaowei, GORDON K N, LIU Pengfei, et al. A van der Waals antiferromagnetic topological insulator with weak interlayer magnetic coupling[J]. Nature Communications, 2020, 11(1): 97. DOI:10.1038/s41467-019-13814-x |
| [83] |
DENG Haiming, CHEN Zhiyi, WOLOS A, et al. Observation of high-temperature quantum anomalous Hall regime in intrinsic MnBi2Te4/Bi2Te3 superlattice[Z]. arXiv: 2001.10579
|
| [84] |
BURKOV A A, BALENTS L. Weyl semimetal in a topological insulator multilayer[J]. Physical Review Letters, 2011, 107(12): 127205. DOI:10.1103/PhysRevLett.107.127205 |
| [85] |
JIANG Gaoyuan, FENG Yang, WU Weixiong, et al. Quantum anomalous Hall multilayers grown by molecular beam epitaxy[J]. Chinese Physics Letters, 2018, 35(7): 076802. DOI:10.1088/0256-307X/35/7/076802 |
| [86] |
HIMPSEL F J, ORTEGA J E, MANKEY G J, et al. Magnetic nanostructures[J]. Advances in Physics, 1998, 47(4): 511. DOI:10.1080/000187398243519 |
| [87] |
HUANG F, KIEF M T, MANKEY G J, et al. Magnetism in the few-monolayers limit: A surface magneto-optic Kerr-effect study of the magnetic behavior of ultrathin films of Co, Ni, and Co-Ni alloys on Cu(100) and Cu(111)[J]. Physical Review B, 1994, 49(6): 3962. DOI:10.1103/PhysRevB.49.3962 |
| [88] |
ZHANG Jinlong, WANG Dinghui, SHI Minji, et al. Dynamical magnetoelectric effect in antiferromagnetic insulator Mn2Bi2Te5[Z]. arXiv: 1906.07891
|
| [89] |
LIU Chengcheng, JIANG Hua, YAO Yugui. Low-energy effective Hamiltonian involving spin-orbit coupling in silicene and two-dimensional germanium and tin[J]. Physical Review B, 2011, 84(19): 195430. DOI:10.1103/PhysRevB.84.195430 |
| [90] |
LIU Chengcheng, FENG Wanxiang, YAO Yugui. Quantum spin Hall effect in silicene and two-dimensional germanium[J]. Physical Review Letters, 2011, 107(7): 076802. DOI:10.1103/PhysRevLett.107.076802 |
| [91] |
XU Yong, YAN Binghai, ZHANG Haijun, et al. Large-gap quantum spin Hall insulators in tin films[J]. Physical Review Letters, 2013, 111(13): 136804. DOI:10.1103/PhysRevLett.111.136804 |
| [92] |
REIS F, LI G, DUDY L, et al. Bismuthene on a SiC substrate: a candidate for a high-temperature quantum spin Hall material[J]. Science, 2017, 357(6348): 287. DOI:10.1126/science.aai8142 |
| [93] |
QIAN Xiaofeng, LIU Junwei, FU Liang, et al. Quantum spin Hall effect in two-dimensional transition metal dichalcogenides[J]. Science, 2014, 346(6215): 1344. DOI:10.1126/science.1256815 |
| [94] |
WU Sanfeng, FATEMI V, GIBSON Q D, et al. Observation of the quantum spin Hall effect up to 100 kelvin in a monolayer crystal[J]. Science, 2018, 359(6371): 76. DOI:10.1126/science.aan6003 |
| [95] |
SHARPE A L, FOX E J, BARNARD A W, et al. Emergent ferromagnetism near three-quarters filling in twisted bilayer graphene[J]. Science, 2019, 365(6453): 605. DOI:10.1126/science.aaw3780 |
| [96] |
SERLIN M, TSCHIRHART C L, POLSHYN H, et al. Intrinsic quantized anomalous Hall effect in a moiré heterostructure[J]. Science, 2020, 367(6480): 900. DOI:10.1126/science.aay5533 |
| [97] |
CHEN Guorui, SHARPE A L, FOX E J, et al. Tunable correlated Chern insulator and ferromagnetism in a moiré superlattice[J]. Nature, 2020, 579(7797): 56. DOI:10.1038/s41586-020-2049-7 |
 2020, Vol. 52
2020, Vol. 52


