2. 南京大学 现代工程与应用科学学院,南京 210093;
3. 南京大学 物理学院,南京 210093
2. College of Engineering and Applied Sciences, Nanjing University, Nanjing 210093, China;
3. School of Physics, Nanjing University, Nanjing 210093, China
光子是信息的重要载体,信息可以编码于频率、偏振、路径、空间模式等自由度上.近年来,光子轨道角动量作为一种全新的自由度,引起了人们的广泛关注.携带轨道角动量的光束也称为涡旋光束,其特征是具有形式为exp(ilθ)的螺旋相位,其中θ是方位角,l是任意整数,通常被称为拓扑荷数.螺旋型的相位分布使的此类光束携带轨道角动量(Orbital angular momentum, OAM),平均每个光子携带的轨道角动量为lħ[1].涡旋光存在不同的空间模式,包括拉盖尔-高斯光束、超几何-高斯光束,贝塞尔光束等.它们的共同特点是具有螺旋的波前,光束中心位置的相位奇点,以及相位奇点带来的中空强度分布.这些光束不同之处在于光场的振幅分布具有不同的数学形式.此外,光子轨道角动量具有无限多个本征值,且各个模式之间相互正交,因此可以构成一个无限维的Hilbert空间.携带轨道角动量光的上述新奇特性,使得它在诸多方面有重要的应用,包括微粒操控[2-3]、超分辨成像[4]、高容量光通信[5-6]、精密测量[7-8],以及量子信息技术[9]等.涡旋光的产生方式有很多,包括:通过螺旋相位片直接加载螺旋相位[10],基于计算全息技术及空间光调制器加载螺旋相位[11-12]、使用Q-plate实现自旋角动量至轨道角动量的转换[13]、全息光栅的衍射[14]、利用柱透镜进行模式转换[15],以及通过设计在激光腔内选择特定的模式[16]等.上述产生方法都是基于线性的光场调制,由于器件加工精度和响应波长的限制,能够产生的涡旋光拓扑荷数或波段有限.而在实际应用中,需要用到不同波段、不同拓扑荷数的涡旋光.非线性频率转换则为上述问题提供了解决方案.非线性相互作用过程中,为获得高效的非线性频率转换,需要同时满足以下的能量和动量守恒条件:
| $ \begin{gathered} \Delta E = {ħ}{\omega _3} - {ħ}{\omega _2} - {ħ}{\omega _1} = 0, \hfill \\ \;\;\;\;\Delta k = {k_3} - {k_2} - {k_1} = 0. \hfill \\ \end{gathered} $ | (1) |
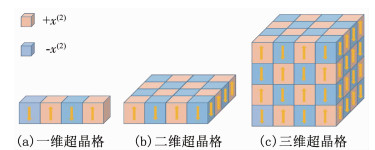
能量守恒在非线性频率转换过程中受Manley-Rowe关系的制约,一般被认为自动满足,也就是ħω3-ħω2-ħω1=0.在介质中,由于色散的存在,相互作用的光之间一般存在波矢失配,也就是式(1)中的Δk≠0.由此,能量会在基频光和谐波之间交替振荡,不能形成有效的转换.要满足动量守恒条件,或者说实现相位匹配,常用的方式有双折射相位匹配[17]和准相位匹配(Quasi-phase-matching, QPM)[18].双折射相位匹配是利用晶体的双折射特性,让相互作用的光处于不同的偏振态,从而实现相位匹配,这是一种完全相位匹配.双折射相位匹配受制于材料的双折射特性,只能使用二阶非线性系数的非对角元,并且存在空间走离效应,非线性频率转换的效率一般较低.在涡旋光非线性频率转换研究的早期工作中,人们就使用了LBO和KTP两种双折射晶体来研究拉盖尔-高斯光束的倍频特性[19-20].准相位匹配是通过对晶体材料二阶非线性系数的周期性调制,在倒格矢空间提供倒格矢G或者说是准动量,来补偿非线性频率转换过程中的动量差值,使得Δk=k3-k2-k1-G=0.这不是真正意义上的相位匹配,因为准动量的参与,所以被称为“准”相位匹配.与双折射相位匹配相比,准相位匹配有几点优势:首先,准相位匹配中相互作用的光可以处于相同的偏振态,利用晶体的最大非线性系数,且可以避免空间走离效应,从而提高非线性转换效率;其次,准相位匹配可以通过微结构的灵活设计,在晶体材料的透光波段范围内实现任意波长、任意非线性过程的相位匹配.基于准相位匹配原理的材料,因为其二阶非线性系数受到调制,因此又称为光学超晶格.光学超晶格可以是一维、二维或三维的,其结构也可以是周期、准周期、非周期或随机结构等,如图 1所示.究其本质,各种结构实际上对应于二阶非线性系数χ(2)在空间的不同分布函数.除了通过非线性频率转换搭建新波段的激光光源外[21],在光学超晶格中还可以实现光场的多维调控.例如,利用非线性惠更斯原理,可以构建同时具有倍频、聚焦和分束等多功能的集成光学超晶格器件[22].基于光学超晶格在非线性光场调控方面的优势,将光子轨道角动量这个重要维度引入到非线性频率转换过程中,一方面,可以拓展携带轨道角动量光的工作波段范围;另一方面,通过光学超晶格微结构的设计,可以实现光子轨道角动量的调控.
|
注:其中粉色代表自发极化向上的铁电畴,蓝色代表自发极化向下的铁电畴. (a) one dimensional, (b) two dimensional, and (c) three dimensional optical superlattice, where pink and blue represent the ferroelectric domain with up and down spontaneous polarization, respectively. 图 1 光学超晶格结构示意图 Fig. 1 Diagram of the domain structure for optical superlattice: |
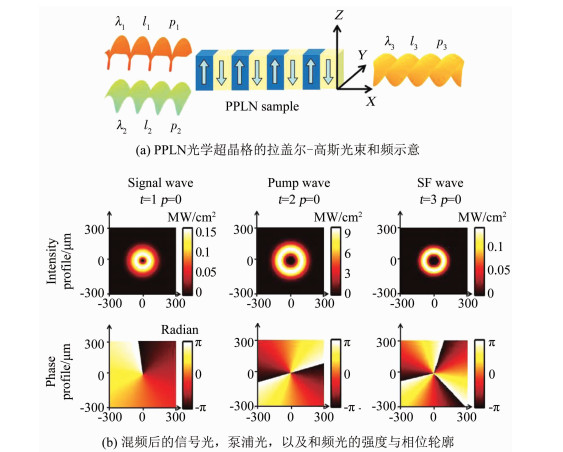
光学超晶格中轨道角动量的非线性频率转换,最早的研究始于2013年南京大学Guanghao Shao等[23]的一篇理论工作.他们考虑的是二阶非线性的和频过程,即两支入射的基频光波长λ不同,且光束是具有不同的角向指数l和径向指数p的拉盖尔高斯光束;非线性晶体选取的是周期极化铌酸锂(Periodically poled LiNbO3, PPLN),如图 2(a)所示.
|
(a) Diagram of sum frequency mixing of Laguerre-Gaussian beams in PPLN optical superlattice. (b) Intensity and phase profiles of the signal, pump, and generated sum frequency beams. 图 2 光学超晶格中轨道角动量的非线性频率转换[23] Fig. 2 Nonlinear frequency conversion of OAM in optical superlattice[23] |
通过求解非线性耦合波方程,他们研究了轨道角动量在准相位匹配相互作用中的规律.因此径向指数p不为零的情况比较复杂,在图 2(b)中给出了p=0时相互作用光场的强度和相位轮廓图.和平面波或高斯光入射时的情况不同,除了满足能量守恒和准动量守恒外,发现轨道角动量也是守恒的.比如,对于和频过程,谐波的拓扑荷数l3为两支基波拓扑荷数l1和l2的和,也就是:
| $ {l_3} = {l_1} + {l_2}. $ | (2) |
在此理论工作之后,中科大的Zhiyuan Zhou等[24]首次在实验上报道了准相位匹配的涡旋光倍频.他们使用周期性极化的KTP(PPKTP)晶体,实现了795 nm到397.5 nm的涡旋光倍频.实验结果表明,倍频光的拓扑荷数确实为基波的2倍.实验中产生的倍频光拓扑荷数最高达100,这么高的拓扑荷数在普通线性光学器件里面很难实现.可见通过非线性的倍频过程,不仅可以获得短波长,还可以利用拓扑荷数的守恒规律实现高拓扑荷数涡旋光的产生.涡旋光的倍频也可以在二维光学超晶格中实现[25].跟一维结构相比,二维超晶格拥有更丰富的倒格矢,可以同时发生共线与非共线的准相位匹配倍频过程.产生的多束倍频光拥有相同的拓扑荷数,但从不同的空间角度出射,由此可以实现轨道角动量态的批量复制.
中科大的课题组也在实验上研究了涡旋光准相位匹配的和频过程.他们发现,利用涡旋光与高斯光和频,可以在频率转换过程中保持涡旋光携带的轨道角动量信息[26-27].2016年,Zhiyuan Zhou等[27]报道了单光子轨道角动量态的频率上转换过程.他们以795 nm的高斯光作为泵浦,通过腔增强的PPKTP晶体中的和频过程,将1 560 nm的携带轨道角动量的光子上转换到525 nm.实验结果表明,和频光子与1 560 nm基频光子具有相同的轨道角动量态,并且单光子相干性也被继承,这在不同量子系统建立了光子轨道角动量态的非线性频率接口.
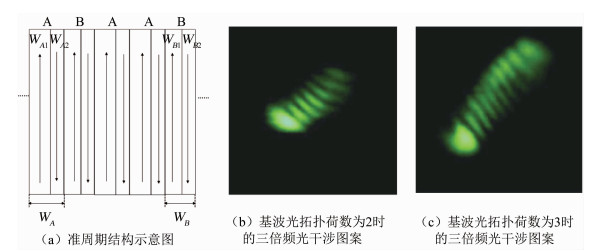
除了倍频与和频等简单的二阶非线性过程,光学超晶格中也可以高效产生涡旋光束的高次谐波.2016年,南京大学的Xinyuan Fang等[28]首次在准周期极化的钽酸锂超晶格中实现了涡旋光束的耦合三倍频.准周期光学超晶格的概念最早由南京大学研究团队提出,该团队在1997年利用准周期光学超晶格,实现了首个高效的耦合3倍频产生,在这项工作中相互作用的光是高斯光束[29].与普通周期结构不同,二组元的准周期光学超晶格由两个基本构造单元A和B组成,如图 3(a)所示.A和B均包括了一对正负畴,当它们按照一定的规律进行排列时,例如斐波那契序列,就构成了准周期的光学超晶格.准周期超晶格的倒格矢可以写为Gm, n=2πD-1(m+nτ),其中m, n为整数,D和τ是结构相关的参数.可见准周期结构可以提供两个以上独立的倒格矢,用于同时补偿多个非线性过程的波矢失配,从而实现高效的耦合非线性频率转换.如果入射到准周期超晶格的基频光携带轨道角动量,在发生耦合的三倍频过程时,基波携带的轨道角动量也会转移至倍频光和三倍频光,这两个过程所使用的倒格矢分别为G1, 1和G2, 3.从图 3(b)和(c)的三倍频光干涉图案可以看出,当基波光拓扑荷数为2和3时,三倍频光的拓扑荷数分别是6和9,是基波拓扑荷数的3倍,表明耦合三倍频过程满足轨道角动量守恒定律.此外,由于准周期超晶格的使用,实现了高效的涡旋光三倍频产生,这为获得蓝紫等空间光调制器工作波段之外的涡旋光源提供了新的途径.宽带的涡旋光非线性频率转换器件也有重要的应用价值.Yu Wu等[30]利用钽酸锂超晶格实现了可调谐的涡旋光级联三倍频.通过将啁啾引入到双周期结构中,使得超晶格的倒格矢呈现一定宽带的分布,从而可以完成宽带的准相位匹配.实验中产生的440 nm附近三倍频涡旋光的波长调谐带宽为3.3 nm.
|
(a) Diagram of the quasi-periodic structure. Interference patterns of the third harmonic wave when the topological charge of the fundamental wave is (b) 2 and (c) 3 respectively. 图 3 准周期光学超晶格中轨道角动量的耦合转换[28] Fig. 3 Coupled conversion of OAM in quasi-periodic optical superlattice[28] |
除了频率上转换获得短波长高拓扑荷数的涡旋光之外,光学超晶格也能实现涡旋光的频率下转换.利用涡旋光泵浦的光参量产生,光参量放大,以及光参量振荡(OPO)过程,可以将涡旋光束的产生波长拓展到近红外至中红外波段[31-35].Aadhi等[34]报道了基于连续光单共振OPO的中红外涡旋光源.通过对腔的设计,共振的信号光处于高斯模式,因此根据轨道角动量守恒,闲频光与泵浦光具有相同的拓扑荷数.实验中所用非线性晶体为掺杂MgO的周期极化铌酸锂(MgO:PPLN),拥有较高的光损伤阈值以及非线性系数,保证了OPO的高功率高效率运行.由于多通道极化周期的设计,闲频光波长覆盖从2 217 nm到3 574 nm,调谐范围高达1 357 nm.在拓扑荷数分别为1和2的1 064 nm涡旋光泵浦下,闲频光最大输出功率分别为5.23 W和2.3 W.之后他们又设计了双晶体单共振OPO[35],并用高斯光和涡旋光分别泵浦两块MgO:PPLN晶体,获得了更高功率以及更高拓扑荷数的中红外涡旋光输出.
在涡旋光的频率转换过程中,一般来说,n次谐波光的拓扑荷数lnth和基波光的拓扑荷数满足简单的代数关系,lnth=n·lFW,对于三倍频过程,三次谐波的拓扑荷数为基波的三倍.能否在频率转换的过程中,打破频率和拓扑荷数的依赖关系,是一个很有意思的课题.实际上,在受激发射损耗显微术中,确实同时需要短波长和小拓扑荷数的光源.南京大学的研究团队,利用准相位匹配的灵活设计特性,实现了拓扑荷数可控的涡旋光三倍频产生[36].他们用两支不同偏振、不同空间模式的1 342 nm近红外光作为基波光源.一支为z偏振的高斯光,其拓扑荷数为零;另一支偏振沿着y方向作为控制光,拓扑荷数不为零.非线性晶体为包括两段级联周期结构的钽酸锂光学超晶格.通过超晶格准相位匹配结构的精密设计,在第一段超晶格结构中,只发生z偏振光的零类倍频(ee-e)过程,产生z偏振的671 nm倍频红光,其拓扑荷数也为零.在第二段超晶格结构中,z偏振的671 nm高斯光和y偏振的基频控制光在第二段结构中发生第二类的和频(oe-o)过程获得447 nm的三次谐波.根据非线性频率转换中的轨道角动量守恒规律,以及相位匹配形式,三次谐波的拓扑荷数始终与y偏振的基频控制光相等,如图 4所示.这个工作充分体现了准相位匹配结构设计灵活性的特性,并且辅助使用光的偏振自由度,最终实现了轨道角动量可控的高次谐波产生.

|
(a) The fundamental waves and (c) the generated third harmonic waves. By using a tilted convex lens, the converted patterns indicate that (d) the harmonic waves carry the same OAM as that of the corresponding (b) fundamental waves. From left to right, the topological charges are l=1, 2 and 3 respectively. 图 4 轨道角动量可控的涡旋光三倍频[36] Fig. 4 Third-harmonic generation of vortex beam with controllable OAM[36] |
涡旋光非线性频率转换中的轨道角动量守恒规律,研究较多的是入射光携带的是整数阶的轨道角动量.如果入射光携带的是分数阶的轨道角动量,其倍频光的轨道角动量是否也等于基频光的两倍,这是一个有待探讨的有趣问题.近来的研究发现,因为分数阶轨道角动量不是光的本征态,所以对于分数阶的涡旋光的倍频过程研究不能沿用简单的算术关系,而必须以整数阶的涡旋光作为本征基矢,研究倍频光的轨道角动量谱分布.考虑到光学超晶格中涡旋光的共线倍频过程比较简洁,因此分数阶涡旋光的倍频过程也使用光学超晶格作为倍频晶体,Rui Ni等[37]设计了图 5的实验装置来研究分数阶轨道角动量的倍频规律.光源是一台声光调Q的1 064 nm纳秒激光器.利用空间光调制器(SLM1)加载如图 5所示的计算全息图案,可以让基波光携带的拓扑荷数分别为半整数分数4.5和非半整数分数4.7.分数阶的涡旋光入射到周期极化铌酸锂(PPLN)光学超晶格中,完成共线的准相位匹配倍频过程.倍频晶体后放置另外一台空间光调制器(SLM2),在SLM2上加载不同的整数阶螺旋相位,可用来分析基波光和倍频光的轨道角动量谱.

|
图 5 分数阶涡旋光倍频的实验装置示意图[37] Fig. 5 Schematic experimental setup for second harmonic generation of fractional OAM state[37] |
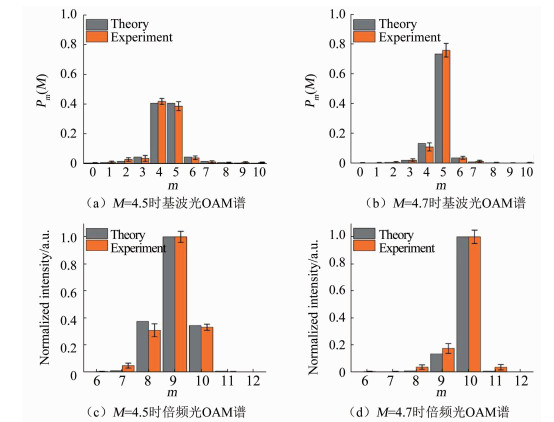
在倍频过程中,基频光的所有整数阶分量不仅发生了各自的倍频,不同的阶数之间还发生了类似和频(频率相同,拓扑荷数不同)过程.当基波光的拓扑荷数为半整数分数,例如M=4.5,基波光的拓扑荷数分量中4和5比例最大,且权重一样(图 6(a)).此时倍频光拓扑荷数的中心值为9,主要来源于基频光拓扑荷数主分量4和5的和频;两个边带8和10则主要来源于基波两个主分量分别的倍频,如图 6(c)所示.当基波的拓扑荷数为非半整数的分数时,例如M=4.7,因为基波光中M=5的分量最多(图 6(b)),因此倍频光的拓扑荷数中分量为10的占据主导地位,见图 6(d).
|
OAM spectra of the (a) fundamental wave and (c) second harmonic wave for M=4.5. OAM spectra of the (b) fundamental wave and (d) second harmonic wave for M=4.7. 图 6 分数阶涡旋光倍频的OAM谱[37] Fig. 6 OAM spectra for frequency doubling of frictional-order vortex beams[37] |
入射的基频光都携带轨道角动量.如果基频光是没有螺旋相位结构的平面波或者高斯光,也可以通过超晶格微结构设计来调制产生谐波波前相位,产生新频率涡旋光.早在2007年,以色列特拉维夫大学的Bahabad与Arie[38]在理论上提出了一种三维的非线性光子晶体,其非线性系数呈螺旋梯状分布.光子轨道角动量可以直接通过入射的高斯光在其中的倍频过程产生.2011年,上海交通大学的课题组也从理论上提出了将横向电光效应应用到三维螺旋极化的非线性光子晶体中,来实现涡旋光束的非线性产生与调控[39].然而,对铌酸锂等晶体的二阶非线性系数进行三维调制在技术上是一个巨大的挑战,因此当时并没有相关的实验报道.
2012年,Bloch等[40]提出,利用二维叉形极化或者螺旋极化的非线性光子晶体能扭曲光束,实现涡旋光的非线性产生.这类特殊非线性光子晶体的二阶非线性系数χ(2)的分布函数为
| ${\chi ^{(2)}}\left( {\mathit{\boldsymbol{r}}, \varphi } \right) = {d_{ij}}{\text{sign}}\{ {\text{cos}}[2\pi f\left( {\mathit{\boldsymbol{r}}, \varphi } \right) + {l_{\text{c}}}\varphi ]\} . $ | (3) |
其中:dij代表二阶非线性极化率的张量元,r和φ分别是极坐标下的径矢与方位角.lc是非线性晶体的拓扑荷数,反应了非线性光子晶体携带准轨道角动量的大小.f(r, φ)可以是一维或者二维的调制函数.将非线性系数进行傅立叶级数展开,其主分量为F1exp[i2πf(r, φ)+ilcφ],其中F1是展开系数.对于非线性叉形光栅,f(r, φ)=|r|cosφ/Λ=x/Λ,此时x方向具有周期性的非线性系数调制.当基波沿着z方向入射,倒格矢G1=2πx/Λ可以参与横向相位匹配,对应倍频的相位匹配形式是非线性拉曼-奈斯衍射.通过求解耦合波方程,可以给出一阶衍射倍频光场为
| $ {E_2} = {A_{2 \mathit{Č}}}\ {\text{exp}}(i2\pi x/\pi \mathit{\Lambda} + i{k_{2z}}z){\text{exp}}\left[ {i(2{l_1} + {l_{\text{c}}})\varphi } \right]. $ | (4) |
式中:A2Č和k2z分别是倍频光的振幅和z方向波矢,l1是基波的拓扑荷数.由于纵向相位失配的存在,晶体厚度应该合适选择以保证A2Č不为零.对于高阶衍射,倍频光拓扑荷数可以写为lm=2l1+mlc,m是衍射级次.由公式(4)可以知道,倍频光的拓扑荷数不是简单等于基波的两倍,还与非线性光子晶体的拓扑荷数有关,也就是说此时轨道角动量的守恒还需要考虑非线性光子晶体提供的准轨道角动量.
在线性光学中,叉形光栅是产生和检测涡旋光的常用器件.设计叉形光栅基于全息原理,通过高斯光与涡旋光倾斜干涉获得图案,当高斯光照射叉形光栅时,通过线性衍射还原出了涡旋光.类似地,叉形非线性光子晶体的设计则是基于非线性全息原理.高斯型非线性极化波与倍频涡旋光产生干涉,得到二阶非线性系数受到调制的图样,当高斯型的基频光入射时,则可通过非线性衍射产生倍频涡旋光,如图 7所示.基于非线性全息原理,Shapira等[41]提出了利用非线性光子晶体实现二维非线性光束整形的方法.应用到涡旋光的产生,除了可以控制倍频光的拓扑荷数,也能控制光束的径向强度分布.此方法可以用来产生一些涡旋光的本征模式,比如拉盖尔-高斯光束以及贝塞尔光束等.
|
图 7 非线性叉形光栅中涡旋光产生的示意图[40] Fig. 7 Schematic for generation of vortex beam from nonlinear fork grating[40] |
产生涡旋光的非线性光子晶体,其非线性系数分布可以是叉形结构或螺旋形状,具体取决于式(3)中调制函数f(r, φ)的形式.Bloch等[40]考虑过f(r, φ)=|r|/Λ的情况,此时非线性系数分布为螺旋形状.与非线性叉形光栅的情况不同,倍频光将发生径向衍射.由于每对正负级次倍频光衍射角大小相等,在空间中不能自然分立,因此总倍频场是成对带有相反拓扑荷数涡旋光的叠加.Dunzhao Wei等[42]研究了一种改进的螺旋极化非线性光子晶体,可以直接产生单一拓扑荷数的倍频涡旋光.极化图案设计为二值化的涡旋光与球面波的干涉图样,可以对倍频光产生聚焦功能,类似于菲涅尔波带片.非线性系数分布函数对应式(3)中f(r, φ)=-π|r|2/λζ的情况,其中λ是设计的工作波长,ζ为曲率半径.样品选取为30 um厚度的铌酸锂薄片,通过电场极化技术完成制备.当入射的基波为高斯光时,在焦平面处可以获得拓扑荷数为lc的倍频涡旋光,其中轨道角动量的转移规律与非线性叉形光栅中的倍频过程类似.不同点在于,螺旋极化的非线性光子晶体中倍频不需满足横向相位匹配,入射波长的改变只会引起焦距变化,因此可以作为一种宽工作波段的器件.
利用非线性全息进行涡旋光产生时,由于非线性系数不能连续变化,倍频场一般存在高阶衍射.而不同衍射级次具有不同的拓扑荷数,因此控制各衍射级次的能量分布也显得重要.Huijun Wang等[43]利用非线性超元胞光栅实现了倍频涡旋光的可控产生.将超元胞设计为达曼光栅结构或者利用遗传算法进行优化,可以使倍频衍射各级次能量均分,或者集中分布到特定级次.
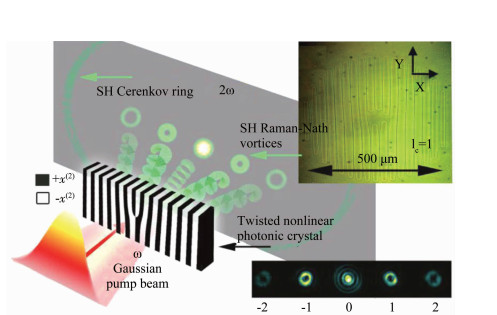
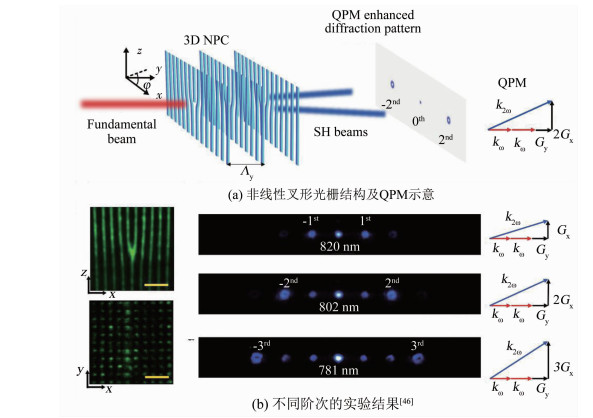
在二维的非线性光子晶体中利用全息的思想来进行光场的非线性调控,因为在传播方向存在相位失配,转换效率一般都较低.而三维非线性光子晶体的制备技术是一直以来困扰人们的难题之一.传统的基于半导体平面光刻工艺的高压电场极化技术,只能制备一维或者二维的光学超晶格.直到2018年,三维非线性光子晶体的制备技术取得了突破.南京大学和澳大利亚国立大学的研究组,分别独立提出了用飞秒激光在晶体的内部擦除非线性系数,以及实现铁电畴反转,首次在实验上制备出了铌酸锂以及Ca0.28Ba0.72Nb2O6三维非线性光子晶体,并展示了三维非共线的准相位匹配倍频[44-45].得益于技术的突破,在三维非线性光子晶体里面,全空间维度非线性系数调控使得高效非线性光束整形成为可能.南京大学的Dunzhao Wei等[46]利用飞秒激光定点擦除非线性系数,在铌酸锂晶体中成功制备了三维非线性叉形光栅.如图 8(a)所示,光栅平面选择垂直于铌酸锂晶体的y轴,当z偏振的基波沿着y方向入射时,倍频过程可以利用晶体最大非线性系数d33.实验倍频光斑如图 8(b)所示,在820 nm、802 nm以及781 nm基波输入下,±1、±2和±3衍射级次分别满足相位匹配,对应倍频光拓扑荷数分别为±1、±2和±3.由于y方向周期性结构提供的倒格矢,准相位匹配得以完全满足,倍频效率达到10-5,相比于二维非线性叉形光栅的倍频效率提高了一个数量级.
|
(a) Diagram of nonlinear fork grating structure and QPM configuration. (b) Experimental results for different orders. 图 8 三维非线性叉形光栅中涡旋光的倍频产生[46] Fig. 8 Nonlinear generation of vortex beam by frequency doubling in three dimensional nonlinear fork grating[46] |
本文中,我们简要综述了光学超晶格在涡旋光产生与调控方面的工作进展.使用光学超晶格作为非线性晶体,通过高效的倍频、和频、三倍频、光参量下转换等非线性光学过程,可以拓展涡旋光的工作波段,覆盖了蓝紫至中红外;通过超晶格倒格矢的设计,还可以产生拓扑荷数可控、宽调谐波段的蓝紫波段涡旋光.基于非线性全息的设计思想,在超晶格中可以调控非线性光场的波前相位、振幅等参量,从而产生轨道角动量可控的涡旋光束.涡旋光的产生和调控是近年来的一个热点研究领域,结合目前的研究进展,在以下几个方面仍有待探索:从基础物理研究层面来看,轨道角动量是能量、线性动量之外的一个重要守恒量,然而,这一守恒定律由什么来支配,以及其中的物理机制是什么,有待揭示;从应用层面来说,近年来,得益于三维光学超晶格制备技术的突破,高效的光束整形产生涡旋光已经取得了初步进展,在此基础上,有望充分利用三维空间的特点和优势,研发新型的非线性光子器件.
| [1] |
ALLEN L, BEIJERSBERGEN M W, SPREEUW R J C, et al. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes[J]. Physical Review A, 1992, 45(11): 8185. DOI:10.1103/PhysRevA.45.8185 |
| [2] |
PATERSON L, MACDONALD M P, ARLT J, et al. Controlled rotation of optically trapped microscopic particles[J]. Science, 2001, 292(5518): 912. DOI:10.1126/science.1058591 |
| [3] |
O'NEIL A T, MACVICAR I, ALLEN L, et al. Intrinsic and extrinsic nature of the orbital angular momentum of a light beam[J]. Physical Review Letters, 2002, 88(5): 3601. |
| [4] |
YU Wentao, JI Ziheng, DONG Dashan, et al. Super-resolution deep imaging with hollow Bessel beam STED microscopy[J]. Laser & Photonics Reviews, 2016, 10(1): 147. DOI:10.1002/lpor.201500151 |
| [5] |
GIBSON G, COURTIAL J, PADGETT M, et al. Free-space information transfer using light beams carrying orbital angular momentum[J]. Optics Express, 2004, 12(22): 5448. DOI:10.1364/OPEX.12.005448 |
| [6] |
WANG Jian, YANG Jengyuan, FAZAL I M, et al. Terabit free-space data transmission employing orbital angular momentum multiplexing[J]. Nature Photonics, 2012, 6(7): 488. DOI:10.1038/nphoton.2012.138 |
| [7] |
D'AMBROSIO V, SPAGNOLO N, REDEL L, et al. Photonic polarization gears for ultra-sensitive angular measurements[J]. Nature Communications, 2013, 4(9): 2432. |
| [8] |
LAVERY M P J, SPEIRITS F C, BARNETT S M, et al. Detection of a spinning object using light's orbital angular momentum[J]. Science, 2013, 341(6145): 537. DOI:10.1126/science.1239936 |
| [9] |
NAGALI E, SCIARRINO F, MARTINI F D, et al. Quantum information transfer from spin to orbital angular momentum of photons[J]. Physical Review Letters, 2009, 103(1): 013601. DOI:10.1103/PhysRevLett.103.013601 |
| [10] |
BEIJERSBERGEN M W, COERWINKEL R P C, KRISTENSEN M, et al. Helical-wavefront laser beams produced with a spiral phaseplate[J]. Optics Communications, 1994, 112(5/6): 321. DOI:10.1016/0030-4018(94)90638-6 |
| [11] |
HECKENBERG N R, MCDUFF R, SMITH C P, et al. Generation of optical phase singularities by computer-generated holograms[J]. Optics Letters, 1992, 17(3): 221. DOI:10.1364/OL.17.000221 |
| [12] |
FORBES A, DUDLEY A, MCLAREN M. Creation and detection of optical modes with spatial light modulators[J]. Advances in Optics and Photonics, 2016, 8(2): 200. DOI:10.1364/AOP.8.000200 |
| [13] |
MARRUCCI L, MANZO C, PAPARO D. Optical spin-to-orbital angular momentum conversion in inhomogeneous anisotropic media[J]. Physical Review Letters, 2006, 96(16): 163905. DOI:10.1103/PhysRevLett.96.163905 |
| [14] |
CHEN Shumei, CAI Yuan, LI Guixin, et al. Geometric metasurface fork gratings for vortex-beam generation and manipulation[J]. Laser & Photonics Reviews, 2016, 10(2): 322. DOI:10.1002/lpor.201500259 |
| [15] |
BEIJERSBERGEN M W, ALLEN L, VAN DER VEEN H, et al. Astigmatic laser mode converters and transfer of orbital angular momentum[J]. Optics Communications, 1993, 96(1/2/3): 123. DOI:10.1016/0030-4018(93)90535-D |
| [16] |
NAIDOO D, ROUX F S, DUDLEY A, et al. Controlled generation of higher-order Poincaré sphere beams from a laser[J]. Nature Photonics, 2016, 10(5): 327. DOI:10.1038/nphoton.2016.37 |
| [17] |
ANTHON D W, CROWDER C D. Wavelength dependent phase matching in KTP[J]. Applied Optics, 1988, 27(13): 2650. DOI:10.1364/AO.27.002650 |
| [18] |
MAGEL G A, FEJER M M, BYER R L. Quasi-phase-matched second-harmonic generation of blue light in periodically poled LiNbO3[J]. Applied Physics Letters, 1990, 56(2): 108. DOI:10.1063/1.103276 |
| [19] |
DHOLAKIA K, SIMPSON N B, PADGETT M J, et al. Second-harmonic generation and the orbital angular momentum of light[J]. Physical Review A, 1996, 54(5): R3742. |
| [20] |
COURTIAL J, DHOLAKIA K, ALLEN L, et al. Second-harmonic generation and the conservation of orbital angular momentum with high-order Laguerre-Gaussian modes[J]. Physical Review A, 1997, 56(5): 4193. DOI:10.1103/PhysRevA.56.4193 |
| [21] |
HU Xiaopeng, XU Ping, ZHU Shining. Engineered quasi-phase-matching for laser techniques[J]. Photonics Research, 2013, 1(4): 171. |
| [22] |
QIN Yiqiang, ZHANG Chao, ZHU Yongyuan, et al. Wave-front engineering by Huygens-Fresnel principle for nonlinear optical interactions in domain engineered structures[J]. Physical Review Letters, 2008, 100(6): 063902. DOI:10.1103/PhysRevLett.100.063902 |
| [23] |
SHAO Guanghao, WU Zijian, CHEN Jinhui, et al. Nonlinear frequency conversion of fields with orbital angular momentum using quasi-phase-matching[J]. Physical Review A, 2013, 88(6): 063827. DOI:10.1103/PhysRevA.88.063827 |
| [24] |
ZHOU Ziyuan, DING Dongsheng, JIANG Yunkun, et al. Orbital angular momentum light frequency conversion and interference with quasi-phase matching crystals[J]. Optics Express, 2014, 22(17): 20298. DOI:10.1364/OE.22.020298 |
| [25] |
FANG Xinyuan, WEI Dunzhao, LIU Dongmei, et al. Multiple copies of orbital angular momentum states through second-harmonic generation in a two-dimensional periodically poled LiTaO3 crystal[J]. Applied Physics Letters, 2015, 107(16): 161102. DOI:10.1063/1.4934488 |
| [26] |
ZHOU Ziyuan, LIU Shilong, LI Yan, et al. Orbital angular momentum-entanglement frequency transducer[J]. Physical Review Letters, 2016, 117(10): 103601. DOI:10.1103/PhysRevLett.117.103601 |
| [27] |
ZHOU Ziyuan, LI Yan, DING Dongsheng, et al. Orbital angular momentum photonic quantum interface[J]. Light: Science & Applications, 2016, 5(1): e16019. |
| [28] |
FANG Xinyuan, YANG Guang, WEI Dan, et al. Coupled orbital angular momentum conversions in a quasi-periodically poled LiTaO3 crystal[J]. Optics Letters, 2016, 41(6): 1169. DOI:10.1364/OL.41.001169 |
| [29] |
ZHU Shining, ZHU Yongyuan, MING Naiben. Quasi-phase-matched third-harmonic generation in a quasi-periodic optical superlattice[J]. Science, 1997, 278(5339): 843. DOI:10.1126/science.278.5339.843 |
| [30] |
WU Yu, NI Rui, XU Zhou, et al. Tunable third harmonic generation of vortex beams in an optical superlattice[J]. Optics Express, 2017, 25(25): 30820. DOI:10.1364/OE.25.030820 |
| [31] |
AADHI A, SAMANTA G K. High-power, high repetition rate, tunable, ultrafast vortex beam in the near-infrared[J]. Journal of Optics, 2017, 20(1): 01LT01. |
| [32] |
XIAO Na, FAN Jintao, ZHAO Jun, et al. Intrinsic conservation nature of orbital angular momentum in a vortex-pumped femtosecond optical parametric amplifier[J]. Journal of Physics D: Applied Physics, 2020, 53(11): 115104. DOI:10.1088/1361-6463/ab60eb |
| [33] |
AADHI A, SAMANTA G K, KUMAR S C, et al. Controlled switching of orbital angular momentum in an optical parametric oscillator[J]. Optica, 2017, 4(3): 349. |
| [34] |
AADHI A, SHARMA V, SINGH R P, et al. Continuous-wave, singly resonant parametric oscillator-based mid-infrared optical vortex source[J]. Optics Letters, 2017, 42(18): 3674. DOI:10.1364/OL.42.003674 |
| [35] |
AADHI A, SHARMA V, SAMANTA G K. High-power, continuous-wave, tunable mid-IR, higher-order vortex beam optical parametric oscillator[J]. Optics Letters, 2018, 43(10): 2312. DOI:10.1364/OL.43.002312 |
| [36] |
XU Zhou, LIN Zhongyu, YE Zhilin, et al. Control the orbital angular momentum in third-harmonic generation using quasi-phase-matching[J]. Optics Express, 2018, 26(13): 17563. DOI:10.1364/OE.26.017563 |
| [37] |
NI Rui, NIU Yunfei, DU Li, et al. Topological charge transfer in frequency doubling of fractional orbital angular momentum state[J]. Applied Physics Letters, 2016, 109(15): 151103. DOI:10.1063/1.4964712 |
| [38] |
BAHABAD A, ARIE A. Generation of optical vortex beams by nonlinear wave mixing[J]. Optics Express, 2007, 15(26): 17619. DOI:10.1364/OE.15.017619 |
| [39] |
IAN Linghao, YE Fangwei, CHEN Xianfeng. Optical vortex converter with helical-periodically poled ferroelectric crystal[J]. Optics Express, 2011, 19(12): 11591. DOI:10.1364/OE.19.011591 |
| [40] |
BLOCH N V, SHEMER K, SHAPIRA A, et al. Twisting light by nonlinear photonic crystals[J]. Physical Review Letters, 2012, 108(23): 233902. DOI:10.1103/PhysRevLett.108.233902 |
| [41] |
SHAPIRA A, SHILOH R, JUWILER I, et al. Two-dimensional nonlinear beam shaping[J]. Optics Letters, 2012, 37(11): 2136. DOI:10.1364/OL.37.002136 |
| [42] |
WEI Dunzhao, ZHU Yunzhi, ZHONG Weihao, et al. Directly generating orbital angular momentum in second-harmonic waves with a spirally poled nonlinear photonic crystal[J]. Applied Physics Letters, 2017, 110(26): 261104. DOI:10.1063/1.4990527 |
| [43] |
WANG Huijun, WEI Dunzhao, XU Xiaoyi, et al. Controllable generation of second-harmonic vortex beams through nonlinear supercell grating[J]. Applied Physics Letters, 2018, 113(22): 221101. DOI:10.1063/1.5050423 |
| [44] |
XU Tianxiang, SWITKOWSKI K, CHEN Xin, et al. Three-dimensional nonlinear photonic crystal in ferroelectric barium calcium titanate[J]. Nature Photonics, 2018, 12(10): 591. DOI:10.1038/s41566-018-0225-1 |
| [45] |
WEI Dunzhao, WANG Chaowei, WANG Huijun, et al. Experimental demonstration of a three-dimensional lithium niobate nonlinear photonic crystal[J]. Nature Photonics, 2018, 12(10): 596. DOI:10.1038/s41566-018-0240-2 |
| [46] |
WEI Dunzhao, WANG Chaowei, XU Xiaoyi, et al. Efficient nonlinear beam shaping in three-dimensional lithium niobate nonlinear photonic crystals[J]. Nature Communications, 2019, 10(1): 4193. DOI:10.1038/s41467-019-12251-0 |
 2020, Vol. 52
2020, Vol. 52


