2. 中国水利水电科学研究院, 北京 100048;
3. 同济大学 土木工程学院, 上海 200092
2. China Institute of Water Resources and Hydropower Research, Beijing 100048, China;
3. College of Civil Engineering, Tongji University, Shanghai 200092, China
重大水利工程作为国家重要的基础建设设施,其安全防护一直备受重视[1].各类爆炸对大坝的冲击作用都可能引起结构损伤,考虑到水下爆破具有较隐秘、威力大的特点,本文针对水下爆炸对大坝的影响展开研究,为坝体的防护提供依据.
水下爆炸是一个复杂的物理过程,由于现场试验成本较高,水下爆炸研究往往借助数值模拟开展.针对重力坝,学者利用数值模拟对比研究了水深[2]、炸药当量[2]、坝高[2]、近远场[3-4]以及气泡脉动[5]等因素对水下爆炸作用的影响.Zhang等[6]建立了大坝损伤评估模型,用于确定水下爆炸作用下坝体的安全防护距离.相比大规模加固已建坝体[7],降低蓄水位是最简单有效的坝体防护手段.Li等[8]保持炸药入水深度恒定,利用数值计算对比了正常蓄水位及死水位水下爆炸时坝体的损伤破坏特征,发现水位降低坝体毁伤明显减小.然而,目前数值模拟的结果还缺乏试验验证,蓄水高度对水下爆炸作用的影响机理还不清晰,尚无可靠理论确定安全蓄水位.
离心模型试验是目前研究水下爆炸最有效的工具之一[9-11],本文首先采用离心模型试验对数值模拟结果进行验证.在此基础上,通过数值模拟研究蓄水位变化对坝体动力响应的影响,揭示蓄水位对冲击波作用的影响机理.
1 研究思路及方法 1.1 研究思路为分析水下爆炸对结构的动力响应,分别采用离心模型试验及数值模拟进行研究.考虑试验能力,以重力坝为研究对象,坝高27.5 m,坝顶部宽2.5 m,底部宽18.75 m,坝体上游面垂直,下游坝坡为1: 0.75,模型下部坝基高5 m(如图 1所示).坝段之间分缝,每个坝段宽度为12 m,选择3个段坝进行试验.坝体和坝基均为混凝土材料,强度约15 MPa.有限元模型中,水与坝面接触面为流固接触面Sfs;水位上表面为自由液面Sfp;水体底部为天然沉积物,为无反射边界Sfr,水体各个侧面均为无限水域,同样为无反射边界Sfr.

|
图 1 研究对象 Fig. 1 Research object |
因无法直接开展原型试验对模拟结果进行验证,分别针对原型和离心缩比试验模型开展数值模拟.研究思路如下:首先,采用数值模拟,从理论上验证超重力场下缩比模型与原型的相似性;随后,开展离心模型试验,验证数值模型的可靠性;最后,基于验证后的数值模型,研究不同蓄水位条件下,水下爆炸对坝体作用的差异,并提出有效的指标评估蓄水位变化的差异.
1.2 数值模拟 1.2.1 模型简介数值模拟主要基于声固耦合方法开展,该方法假设流体为线性声学介质,水下爆炸冲击波满足波动方程:
| $ - \frac{{{\rho _{\rm{f}}}}}{{{K_{\rm{f}}}}}\frac{{{\partial ^2}p}}{{\partial {t^2}}} + {\nabla ^2}p = 0. $ | (1) |
式中:ρf为流体密度; p为流体压力; t为时间; Kf=ρ0c2为流体的体积模量; c为声速, 约1 465 m/s.当冲击波到达结构时,将形成一个散射波场,通常假定在流固交界面,流体与结构的法向速度相等,以此考虑流固耦合作用.
基于声学介质方法,模拟炸药在库前水域爆炸对背空结构的作用.水域采用线性声学单元,由于库区反射对坝体动力响应影响较小,为减小计算量,水域只截取坝前10 m的区域进行分析,可以模拟冲击波传播并作用于坝面的过程,这也是文献中常采用的简化方法[12].蓄水位高度根据工况设置进行灵活调整,其中水面设置为自由界面,保持压力恒定,其他边界为无反射边界,模拟无限水域和库底沉积物.水域最大网格尺寸为0.5 m,当蓄水位为25 m时,共包含77 688单元.
结构采用八节点实体单元,在爆炸冲击作用下,混凝土材料的应力应变关系及强度受应变率效应影响[13].本文采用Ren等(2015)[14]提出的损伤本构模型,其考虑了应变率效应,并引入损伤变量反映混凝土结构的动态损伤.数值模型结构底部为固定边界;各个坝体间采用摩擦接触,只承受压力和摩擦力,无法承受拉应力;最外侧表面约束法向位移,模拟周围坝段的约束作用.整个模型最大网格尺寸为0.25 m,最小网格尺寸0.15 m,含有1 103 040单元.
假定爆炸冲击波以球面波形式向四周传播,可采用Cole理论描述,其公式如下[15]:
| $ P\left( t \right) = {P_{\rm{m}}}{{\rm{e}}^{ - t/\theta }}, $ | (2) |
| $ {P_{\rm{m}}} = {K_1}{\left( {\frac{{{W^{1/3}}}}{R}} \right)^{{\alpha _1}}}, $ | (3) |
| $\theta = {K_2}{W^{1/3}}{\left( {\frac{{{W^{1/3}}}}{R}} \right)^{{\alpha _2}}}. $ | (4) |
式中:P(t)为冲击波压力时程,Pm为冲击波峰值压力,t为时间,θ为时间常数,W为炸药当量,R为与爆心距离,K1、K2、α1、α2为峰值压力、时间常数对应的经验系数.
1.2.2 基本参数由于离心机试验采用与原形一致的材料,在忽略尺寸效应的前提下,可以认为模型材料参数与原型一致.表 1列出数值模型所采用的材料参数,详细的本构模型介绍可参考文献[14].
| 表 1 材料参数 Tab. 1 Material parameters |
各坝段间的切向摩擦系数取0.6,法向为硬接触;对于水下爆炸冲击波,采用TNT对应的参数,α1=1.13,α2=0.89,K1=52.27,K2=5 768,由此可以计算各个工况入射波的时程曲线.
1.2.3 模拟工况采用数值模拟进行一系列研究,工况设置如表 2所示.其中,工况1~5在1g重力条件下模拟,其几何尺寸与图 1一致.工况6针对离心模型试验进行模拟,根据爆炸相似率(表 3)[10],其对应原型为工况3,几何比尺为1: 50,该工况用于检验离心试验相似性及数值模拟结果的有效性,离心模型试验详细工况将在1.3节介绍.
| 表 2 模拟工况 Tab. 2 Conditions of simulation |
研究表明,离心模型设备可以作为水下爆炸研究的有力工具.采用离心模型试验对工况6数值模拟结果进行验证.结构几何尺寸与原型满足几何相似,相似比尺为1: 50,试验在50g重力加速度下开展.
与图 1相似,模型坝高550 mm,坝顶部宽50 mm,底部宽375 mm,坝基高100 mm,坝体上游面为垂直面,下游坝坡为1: 0.75.模型坝分3个坝段浇筑,坝段采用水泥砂浆浇筑而成,水泥砂浆7 d抗压强度为10 MPa左右,28 d抗压强度为15.2 MPa,其单方砂浆用水255 kg、水泥235 kg、石粉157 kg、砂子1 647 kg.坝体浇筑完成后置于1 200 mm×720 mm×840 mm的铝合金容器内(如图 2),坝体背水面布置传感器测试动力响应,如图 3所示.对坝段之间及模型箱壁之间进行可靠的防水处理,水体底部放10 cm橡胶垫,模拟水底沉积物.模型蓄水高度50 cm,炸药当量为1.58 gTNT,爆距为30 cm,入水深度20 cm,根据离心模拟水下爆炸相似关系,模型可以模拟工况3的结果.

|
图 2 试验模型 Fig. 2 Test model |

|
图 3 传感器布置 Fig. 3 Layout of sensors |
由于难以开展原型试验,数值模拟结果可以通过离心模型试验进行验证.目前,超重力场条件下,水下爆炸对结构动力响应的相似性尚未验证.因而,首先采用有限元软件模拟了超重力场下缩比模型试验(工况6)及假想的原型(工况3),即分别在50g下采用缩尺模型并在1g下采用足尺模型进行模拟,并将缩尺模型预测结果按照相似关系换算至原型,与足尺模型结果进行对比.离心机虽然处于高速旋转状态,但是由于爆炸作用持续时间较短,模型相对运动产生的科式加速度并不会造成显著的误差(< 10%)[11],因而在模拟中,通常忽略离心机的旋转效应,将离心力作为重力施加至模型.对于缩尺模型和足尺模型,分别施加50gρc(工况6)和1gρc(工况3)的体力模拟重力效应.
图 4给出了原型尺度下工况3与工况6的加速度及应变对比.根据模拟结果,缩比试验的加速度、应变峰值、频率均与原型较为一致,整体的振动及变形响应也与原型相同,因而可以从理论上说明离心模型试验结果满足相似关系.

|
图 4 模型和原型数值计算结果对比 Fig. 4 Comparison of numerical simulation results between model and prototype |
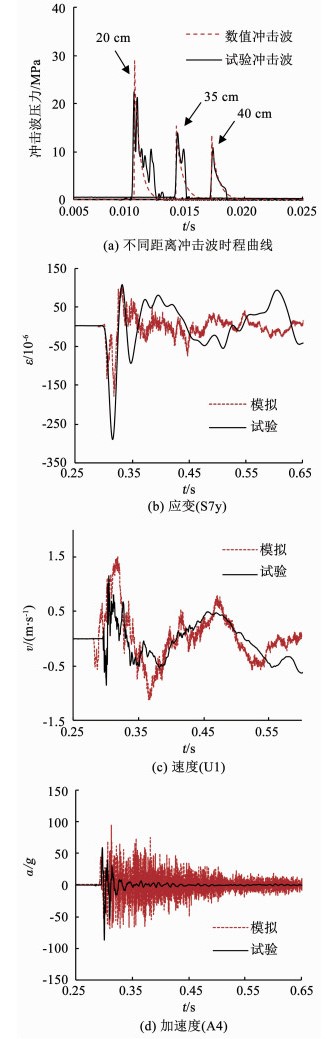
数值模拟的结果表明,离心模拟水下爆炸相似关系理论上成立.在此基础上,结合离心模型试验,对数值模拟结果的可靠性进行验证.图 5(a)给出不同距离处的冲击波压力波形,实测的冲击波压力与Cole公式基本一致,可以采用Cole公式作为数值模拟的载荷输入.图 5(b)~(d)在原型尺度下对比了工况3与离心模型试验的动力响应结果.
|
图 5 数值模拟和试验结果对比 Fig. 5 Comparison between simulated and test results |
总体上,数值模拟所得的应变、速度、加速度响应规律与试验基本一致,速度、加速度峰值也与试验相吻合.然而,数值所得的加速度衰减较慢,其原因可能是所用本构模型及阻尼参数与实际材料存在差异,导致结构能量衰减较慢;此外,为提高计算效率,数值模拟所设的水域范围较小,这也使冲击波能量在坝前无法快速消散,从而加速度衰减较慢.模拟所得的速度响应与试验基本一致,说明高频的加速度响应对结构运动影响较小,可以忽略.
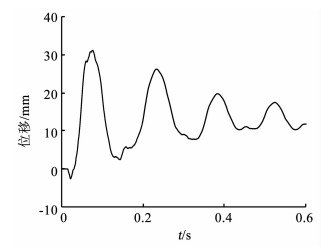
3 数值模拟结果及分析 3.1 坝体动力响应规律为了分析坝体在水下爆炸作用下的动力特征,以工况3为例给出数值模拟结果.图 6为坝顶位移时程曲线,在冲击波作用下,坝顶位移急剧增加,达到峰值后,坝体反向运动并逐渐振荡衰减,几个周期后趋于稳定.坝顶最大位移约为30 mm,最终塑性位移约13 mm.根据坝顶位移曲线,坝体自振周期约为0.1 s,坝体频率约10 Hz,与前人所得重力坝自振周期基本相符[16].
|
图 6 坝顶位移(工况3) Fig. 6 Displacement of dam crest (Condition 3) |
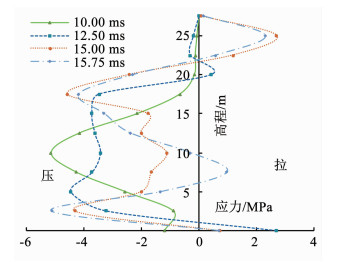
对于混凝土结构,拉应力是引起结构开裂、毁伤的重要参量,图 7给出典型时刻下坝体迎水面的竖直应力分布.当冲击波刚接触坝面时(10 ms),在冲击波压力作用下,正对爆源位置首先产生压应力,其压应力最大,迎水面几乎没有拉应力,如果压应力超过坝体的抗压强度,有可能使正对爆源位置产生局部的压碎破坏;随着冲击波峰值衰减并以球面向坝体四处传播,正对爆源位置压力逐渐衰减(12.5 ms),压应力向上下两端传播,在中上、中下部产生新的压应力峰值,而坝头及坝底逐渐产生拉应力,结构产生反弯点,随后在坝体变截面及坝底出现拉应力峰值(15 ms);随着时间发展,距离坝踵1/3处逐渐出现拉应力,而坝体变截面、坝体底部拉应力逐渐衰减(15.7 ms).根据模拟结果得出,正对爆源位置,压应力较大,易产生局部压缩破坏;坝体变截面、坝底以及坝体中下部是容易产生拉伸破坏的位置,容易产生水平拉裂缝.
|
图 7 不同时刻应力分布(工况3) Fig. 7 Distribution of stress at different time (Condition 3) |
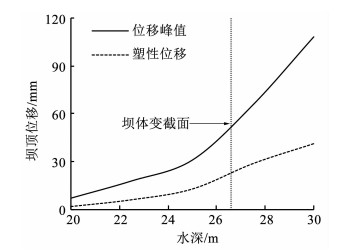
调控蓄水位是目前公认的坝体防御最行之有效的手段.为了研究蓄水位变化对坝体动力响应的影响,保持爆炸当量、爆距、结构尺寸、爆炸位置等因素不变,改变蓄水位高度进行了一系列模拟,蓄水位高度分别设置20,22.5,25,27.5,30 m.图 8给出不同蓄水位高度下,坝体顶部的位移峰值和塑性位移结果.随着蓄水位高度的增加,尽管炸药当量不变,坝顶的最大位移与残余塑性位移将明显增大.蓄水位高度超过变截面位置后,坝顶位移峰值及残余变形增长量明显增快.
|
图 8 不同蓄水位高度坝顶位移峰值 Fig. 8 Peak displacement of dam crest under different water storage levels |
质点振速是爆破工程中常用的毁伤判别指标.在冲击作用下,结构通常产生多个速度峰值,首个峰值由直接的冲击作用产生,频率及幅值均较高,其通常可能超过振速允许范围,但由于作用时间较短,并不会使结构产生显著破坏.冲击载荷作用后,结构将产生自由振动,而后形成的速度峰值通常可以作为结构是否产生毁伤的重要指标.图 9给出不同水深下速度峰值沿坝面的分布情况,总体上,当蓄水位较低时,坝体速度峰值位于坝顶和爆炸直接冲击部位.随着蓄水高度的增加,坝体中部速度峰值明显升高,而坝体底部与坝体顶部峰值速度变化并不明显.根据陈明等[17]的研究,28 d的混凝土容许峰度震动值为0.322~0.963 m/s,当蓄水深度在25 m以下时,坝体基本不会破坏;而当水位达到30 m时,坝体变截面及中下部速度峰值较大,均可能产生损伤.

|
图 9 不同蓄水位高度速度峰值分布 Fig. 9 Distribution of peak velocity under different water storage levels |
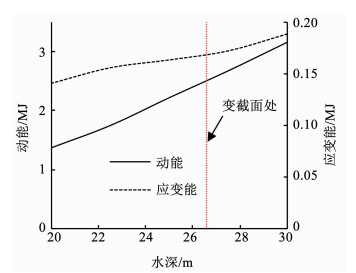
为了分析蓄水位对坝体动力响应影响的机理,整理了不同蓄水位高度下坝体的动能和应变能,如图 10所示,可以看出,随着水位的升高,结构所受能量明显升高,当水位超过坝体变截面位置,能量升高速度减缓,趋于稳定.这说明降低蓄水位可以有效地降低坝体所受的爆炸冲击波能量.
|
图 10 不同蓄水位高度应变能与动能 Fig. 10 Strain energy and kinetic energy of dam under different water storage levels |
胡晶等[18]基于球面波假定,采用结构遮挡的冲击波能量作为指标,得到如下形式的冲击因子:
| $ {F_{\rm{I}}} = \sqrt {{E_{\rm{s}}}\beta {L^2}} , $ | (5) |
式中:L为炸药距结构距离,β为炸药与结构边界组成的立体角,Es为炸药能流密度.
| $ {E_{\rm{s}}} = {K_{\rm{E}}}\cdot\sqrt[3]{W}\cdot{\left( {\sqrt[3]{W}/R} \right)^{{a_{\rm{E}}}}}. $ | (9) |
式中,对于TNT,KE=83,αE=2.05.在胡晶等[18]研究的基础上,考虑自由液面的截断效应,可得重力坝对应立体角的表达式:
| $ {\beta _{\rm{M}}} = 4f\left( {d, l} \right) + 2f({h_{\rm{w}}} - d, l) - 2f({h_{\rm{w}}} + d, l), $ | (7) |
| $ f\left( {x, y} \right) = {\rm{arcsin}}\left( {\frac{x}{{\sqrt {\left( {{L^2} + {x^2}} \right)} }}\frac{y}{{\sqrt {({L^2} + {y^2})} }}} \right). $ | (8) |
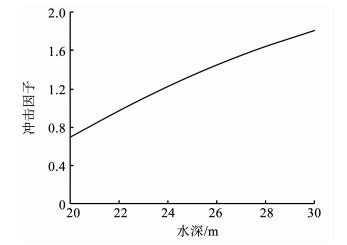
式中:d为炸药入水深度,l为坝体模型宽度的一半,hw为蓄水位高度.为了有效评估蓄水位变化对坝体动力响应的影响程度,将冲击因子作为指标,分析不同水位对应的冲击因子及冲击能量.计算各个工况对应的冲击因子,结果如图 11所示,可以看出,随着蓄水位升高,由于坝体迎水面积增加,冲击因子将逐渐增大.
|
图 11 不同蓄水位高度对应的冲击因子 Fig. 11 Shock factors under different water storage levels |
图 12给出了坝体应变能、动能与冲击因子的关系,可以看出,随着冲击因子的增加,坝体的应变能与动能均相应增加.坝体能量与冲击因子的关系可以采用幂函数拟合,冲击因子可以有效衡量蓄水位变化对坝体动力响应的影响.在此基础上深入研究,有望为安全蓄水位确定提供计算方法.

|
图 12 冲击因子与应变能及动能关系 Fig. 12 Relation between strain energy, kinetic energy, and shock factors |
1) 通过数值模拟证明,超重力场下,水下爆炸模型试验结果与原型满足相似关系,因而可以采用离心机试验对数值模拟的可靠性进行验证.
2) 在水下爆炸作用下,坝体变截面位置、坝底及坝体中下部易产生竖向拉应力峰值,从而产生水平裂缝并导致坝体毁伤.
3) 在坝体及炸药当量、相对位置不变的条件下,蓄水位增加引起坝顶峰值位移及永久位移增加,坝体振动速度峰值增加,导致坝体毁伤加剧;当蓄水位低于坝体变截面高度,坝体变形明显减小;且坝体中下部及靠近水面处的速度峰值较大,容易造成损伤.
4) 随着蓄水位高度增加,坝体湿表面面积增加,所接受的冲击波能量增加,坝体产生的动能及应变能也将明显增加,这是蓄水位变化引起坝体动力响应变化的主要原因.本文给出了考虑球面波效应的冲击因子,可以反映蓄水位高度变化引起的冲击波能量变化.其与坝体的动能、应变能存在幂函数关系.
| [1] |
LU Lu, LI Xin, ZHOU Jing. Study of damage to a high concrete dam subjected to underwater shock waves[J]. Earthquake Engineering and Engineering Vibration, 2014, 13(2): 337. DOI:10.1007/s11803-014-0235-z |
| [2] |
张社荣, 王高辉. 水下爆炸冲击荷载下混凝土重力坝的抗爆性能[J]. 爆炸与冲击, 2013, 33(3): 255. ZHANG Sherong, WANG Gaohui. Anti-explosion performance of concrete gravity dam under underwater explosion impact load[J]. Explosion & Shock, 2013, 33(3): 255. DOI:10.11883/1001-1455(2013)03-0255-08 |
| [3] |
LI Qi, WANG Gaohui, LU Wenbo, et al. Failure modes and effect analysis of concrete gravity dams subjected to underwater contact explosion considering the hydrostatic pressure[J]. Engineering Failure Analysis, 2018, 85: 62. DOI:10.1016/j.engfailanal.2017.12.008 |
| [4] |
CHEN Jianyun, LIU Xiaopeng, XU Qiang. Numerical simulation analysis of damage mode of concrete gravity dam under close-in explosion[J]. KSCE Journal of Civil Engineering, 2017, 21(1): 397. DOI:10.1007/s12205-016-1082-4 |
| [5] |
SAADATFAR S, ZAHMATKESH A. Evaluation of underwater blast on concrete gravity dams using three-dimensional finite-element model[J]. AUT Journal of Civil Engineering, 2018, 2(1): 69. |
| [6] |
ZHANG Sherong, WANG Gaohui, WANG Chao, et al. Numerical simulation of failure modes of concrete gravity dams subjected to underwater explosion[J]. Engineering Failure Analysis, 2014, 36: 49. DOI:10.1016/j.engfailanal.2013.10.001 |
| [7] |
XU Qiang, CHEN Jianyun, LI Jing, et al. Numerical study on antiknock measures of concrete gravity dam bearing underwater contact blast loading[J]. Journal of Renewable and Sustainable Energy, 2018, 10(1): 014101. DOI:10.1063/1.4986330 |
| [8] |
LI Qi, WANG Gaohui, LU Wenbo, et al. Influence of reservoir water levels on the protective performance of concrete gravity dams subjected to underwater explosions[J]. Journal of Structural Engineering, 2018, 144(9): 04018143. DOI:10.1061/(ASCE)ST.1943-541X.0002143 |
| [9] |
PRICE R S, ZUKE W G, INFOSINO C. A study of underwater explosions in a high gravity tank[R]. White Oak, MD: Naval Ordnance Lab, 1964
|
| [10] |
HU Jing, CHEN Zuyu, ZHANG Xuedong, et al. Underwater explosion in centrifuge part Ⅰ: Validation and calibration of scaling laws[J]. Science China Technological Sciences, 2017, 60(11): 1638. DOI:10.1007/s11431-017-9083-0 |
| [11] |
HU Jing, CHEN Zuyu, ZHANG Xuedong, et al. Modeling bubble motions by underwater explosion in a centrifuge[J]. Journal of Fluids Engineering, 2020, 142(4): 041401. DOI:10.1115/1.4045435 |
| [12] |
REN Xiaodan, SHAO Yu. Numerical investigation on damage of concrete gravity dam during noncontact underwater explosion[J]. Journal of Performance of Constructed Facilities, 2019, 33(6): 04019066. DOI:10.1061/(ASCE)CF.1943-5509.0001332 |
| [13] |
胡晶, 姚仰平, 张雪东, 等. 岩石类材料动态强度准则[J]. 岩土工程学报, 2020, 42(3): 495. HU Jing, YAO Yangping, ZHANG Xuedong, et al. Dynamic strength criterion for rock materials[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(3): 495. DOI:10.11779/CJGE202003011 |
| [14] |
REN Xiaodan, ZENG Shajie, LI Jie. A rate-dependent stochastic damage-plasticity model for quasi-brittle materials[J]. Computational Mechanics, 2015, 55(2): 267. DOI:10.1007/s00466-014-1100-7 |
| [15] |
COLE R H. Underwater explosions[M]. New York: Princeton University Press, 1948.
|
| [16] |
李正农, 齐月芹, 吴红华. 累积法在确定水工结构物自振周期中的应用[J]. 中国农村水利水电, 2001(2): 40. LI Zhengnong, QI Yueqin, WU Honghua. Application of cumulative method in determining natural vibration period of hydraulic structure[J]. China Academic Journal Electronic Publishing House, 2001(2): 40. DOI:10.3969/j.issn.1007-2284.2001.02.016 |
| [17] |
陈明, 卢文波. 新浇大坝基础混凝土爆破安全震动速度研究[J]. 武汉大学学报(工学版), 2004(1): 6. CHEN Ming, LU Wenbo. Research on safe vibration velocity of blasting concrete of newly cast dam[J]. Journal of Wuhan University (Engineering Science Edition), 2004(1): 6. |
| [18] |
胡晶, 陈祖煜, 魏迎奇, 等. 考虑球面波效应的水下爆炸冲击因子[J]. 水利学报, 2018, 49(10): 1227. HU Jing, CHEN Zuyu, WEI Yingqi, et al. The impact factor of underwater explosion considering spherical wave effect[J]. Journal of Fluids Engineering, 2018, 49(10): 1227. DOI:10.13243/j.cnki.slxb.20180663 |
 2020, Vol. 52
2020, Vol. 52


