近年来，随着空间技术和机械臂技术的发展，在空间探索任务中，空间机械臂的应用越来越广泛.利用空间机械臂辅助或代替航天员进行空间作业，不仅大大降低了航天员出舱活动的机率和风险，而且可以提高空间探索的效率^[1-3].2016年9月15日，天宫二号空间机械臂搭载发射升空，并成功完成了所有规划实验，这为后续空间站机械臂的设计和控制积累了宝贵的经验^[4].实验过程中，机械臂需完成一系列维护维修实例，如利用电动工具旋拧螺钉、拔插电连接器、拆除多层以及抓取漂浮小球等，这些操作实例基本覆盖了已知的在轨维护维修任务中将会面对的所有问题.如何控制机械臂完成以上任务且能克服环境变化的干扰，将是必须面对的挑战.

传统的预编程离线轨迹的方法虽然能够在结构化的空间中完成上述任务^[5]，但是环境适应性较差，一旦位置发生改变，则不能完成任务.虽然与视觉伺服^[6]、激光引导^[7]等方法相结合后，可提高一定的环境适应性，但是当与预知工况差别较大时，仍难以完成任务.同时，该方法需要对每一项任务单独编程，即使对同一类任务也需如此，大大增加了操作者的工作量.

针对上述问题，模仿学习策略是一种很好的解决方案^[8-10].该策略是一种技能学习策略，能够根据操作者提供的某类任务的运动学实例，构建该任务的运动模型，然后根据当前环境回归获得适合当前任务的轨迹.该策略能够有效地克服环境变化带来的干扰^[11-13]，且针对其他类别的任务，只需要输入对应的运动学实例即可，大大简化了操作.但该策略若直接应用在空间机械臂操作中仍存在一些问题.该策略主要关注的是机械臂能够克服环境变化的干扰，并方便快速地生成当前任务轨迹；但机械臂执行生成的轨迹时，没有考虑关节期望力矩产生的波动以及运动是否平滑等因素.而空间机械臂大的力矩波动很有可能造成控制不稳定，甚至导致任务失败^[1].

本文提出了一种基于动力学约束的模仿学习策略，相对于传统的模仿学习策略，该策略加入了基于机械臂动力学约束的优化，可使机械臂执行任务时的力矩波动和能量损耗均减小，提高控制器的稳定性.

1 方法概述

基于动力学约束的模仿学习策略是一种技能学习策略，相对以往的模仿学习策略，该策略重新设计了机械臂控制器，增加了针对自主生成轨迹的基于动力学约束的优化.基于动力学约束的模仿学习策略主要分为以下两个阶段，如图 1所示：

第一阶段为基于高斯过程的模仿学习.首先，该阶段需要对任务轨迹进行形式化；然后，应用高斯过程算法利用运动学实例对其进行训练，获得当前任务的运动模型；最后，利用训练好的模型以及全局相机和传感器采集到的当前环境状态信息, 回归出适合当前场景的笛卡尔期望轨迹的概率分布；

第二阶段为基于动力学约束的机械臂关节控制器设计.该阶段首先将第一阶段中获得的笛卡尔期望轨迹分布映射到关节空间，然后根据最优控制理论设计机械臂关节控制器，该控制器以机械臂动力学为约束条件，以关节期望力矩为输出.

2 基于高斯过程的模仿学习

与以往的模仿学习策略不同，基于高斯过程的模仿学习策略主要是利用高斯过程算法^[14]对运动模型进行训练，并利用高斯过程回归获得适合当前任务场景的笛卡尔轨迹分布，使所得结果为一个概率模型，而不仅仅是一条期望轨迹，这为后续的优化提供了条件.

在模仿学习阶段，首先需要对机械的任务轨迹进行建模.依据动态系统理论，将任务轨迹形式化成一阶自治常微分方程的形式，这种形式化方法可使模型在存在空间扰动时，表现出较强的鲁棒性^[15].具体表达形式为

$ \mathit{\boldsymbol{\dot \xi }} = f(\mathit{\boldsymbol{\xi}}) + \mathit{\boldsymbol{E}}. $

(1)

式中：f(·)：${\mathbb{R}^n} \to {\mathbb{R}^n}$为一个连续且可微的非线性微分方程，该方程具有唯一的平衡点${\mathit{\boldsymbol{\dot \xi }}^{\rm b}} = f({ \mathit{\boldsymbol{\xi}} ^{\rm b}}) = {\boldsymbol 0}$；$\mathit{\boldsymbol{E}} \in {\mathbb{R}^n}$表示动态系统的噪声，在本文中主要指来自传感器测量的噪声，并假设该噪声为高斯噪声，其形式为$\mathit{\boldsymbol{E}}\sim N({\boldsymbol 0},{\sigma ^2}\mathit{\boldsymbol{I}})$；$\mathit{\boldsymbol{\xi}} \in {\mathbb{R}^n}$为输入的状态变量，可根据实际情况选择(例如，ξ可以是机械臂的关节角度、末端位姿以及末端速度等)，不同的状态变量对应的微分方程的阶数也不同.根据实际情况，本文选择机械臂的末端位姿为输入的状态变量ξ =[x, y, z, R_x, R_y, R_z]，则可得$\mathit{\boldsymbol{\dot \xi }} = [\dot x,\dot y,\dot z,{\omega _x},{\omega _y},{\omega _z}]$.

为保证各个维度的独立性，需对式(1)进行改进，使其输出为一维.此时运动模型需要用6个表达式表示，以输出为沿X轴的速度${\dot x}$为例，其描述形式为

$ \dot x = {f_{\dot x}}(\mathit{\boldsymbol{\xi}}) + \varepsilon . $

(2)

式中:$\dot x = {f_{\dot x}}(\ \cdot \ ):{\mathbb{R}^n} \to {\mathbb{R}^n}$表示一个连续可微的非线性方程，其唯一的平衡点为${{\dot x}^*} = {f_{\dot x}}({{\mathit{\boldsymbol{\dot \xi }}}^{\rm b}}) = 0;\varepsilon \sim N(0,{\sigma ^2})$为噪声.状态变量ξ与式(1)中定义相同.

应用高斯过程算法，利用运动学实例$\{ {\mathit{\boldsymbol{\xi}} _i},{{\mathit{\boldsymbol{\dot \xi }} }_i}\} _{i = 1}^N$，对如式(2)形式的运动模型进行训练，获得当前任务的运动模型.在运动学实例中，N为采集的机械臂末端笛卡尔轨迹的位置点数目.ξ_i为第i个轨迹点的六维笛卡尔位姿，本文中由操作者利用CyberForce力反馈手柄^[16]操作机械臂获得，为训练的输入变量.${\mathit{\boldsymbol{\dot \xi }} }$为第i个轨迹点的六维末端速度，为训练的输出变量.${\mathit{\boldsymbol{\dot \xi }} }$由位置轨迹计算获得，已经包含了传感器噪声的影响，即已经包含了式(2)中的ε.同样以沿X方向的运动为例，所获得的运动学模型为

$ {\mathit{\boldsymbol{F}}_{\dot x}}(\mathit{\boldsymbol{\Xi}} ) = \left[ \begin{array}{l} {f_{\dot x}}({\mathit{\boldsymbol{\xi}} _1})\\ {f_{\dot x}}({\mathit{\boldsymbol{\xi}} _2})\\ \ \ \ \ \ \ \vdots \\ {f_{\dot x}}({\mathit{\boldsymbol{\xi}} _N}) \end{array} \right]\sim N({\mathit{\boldsymbol{m}}_{\dot x}}(\mathit{\boldsymbol{\Xi}} ),{\mathit{\boldsymbol{K}}_{\dot x}}(\mathit{\boldsymbol{\Xi}} ,\mathit{\boldsymbol{\Xi}} )). $

式中：Ξ =[ξ₁, ξ₂, …, ξ_N]为所有运动学实例中的输入变量矩阵${\mathit{\boldsymbol{m}}_{\dot x}}(\mathit{\boldsymbol{\Xi}} )$为均值矢量；${\mathit{\boldsymbol{K}}_{\dot x}}(\mathit{\boldsymbol{\Xi}} ,\mathit{\boldsymbol{\Xi}} )$为协方差矩阵；${\mathit{\boldsymbol{K}}_{\dot x}}(\mathit{\boldsymbol{\Xi}} ,\mathit{\boldsymbol{\Xi}} )$中的每个元素${\rm Ke}{{\rm r}_{\dot x}}({\mathit{\boldsymbol{\xi}} _i},{\mathit{\boldsymbol{\xi}} _j})$为ξ_i和ξ_j的协方差；Ker(·, ·)为高斯过程的核函数，本文中选择其为各向同性平方指数核函数：

$ \begin{array}{c} {\mathit{\boldsymbol{K}}_{\dot x(i,j)}}(\mathit{\boldsymbol{ \boldsymbol{\varXi} }},\mathit{\boldsymbol{ \boldsymbol{\varXi} }})) = Ke{r_{\dot x}}({\mathit{\boldsymbol{\xi }}_i},{\mathit{\boldsymbol{\xi }}_j}) = \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{1}{{\sigma _{\rm f}^2}} \cdot \exp \left( {\frac{{{{({\mathit{\boldsymbol{\xi }}_i} - {\mathit{\boldsymbol{\xi }}_j})}^{\rm T}}({\mathit{\boldsymbol{\xi }}_i} - {\mathit{\boldsymbol{\xi }}_j})}}{{ - 2 \cdot {l^2}}}} \right). \end{array} $

式中，σ_f和l均为该核函数的参数，可通过最小化负对数边界似然获得.

由式(2)可知，运动模型主要描述了当前任务中机械臂速度与位置之间的关系，即根据任务构建出一个速度场.在速度场中的任意位置，均可通过高斯过程回归获得该位置的期望速度：

$ {{\dot x}^*} = {f_{\dot x}}({\mathit{\boldsymbol{\xi}} ^*}) + {\varepsilon ^*}\sim N({m_{\dot x}}({\mathit{\boldsymbol{\xi}} ^*}),{{\mathit \Sigma} _{\dot x}}({\mathit{\boldsymbol{\xi}} ^*})). $

式中，ξ^*为输入的位置点，${{\dot x}^*}$为该位置点处回归得到的沿X轴方向的期望速度，其结果为一个高斯分布，${m_{\dot x}}({\mathit{\boldsymbol{\xi}} ^*})$和${{\mathit \Sigma} _{\dot x}}({\mathit{\boldsymbol{\xi}} ^*})$分别为该高斯分布的均值和方差，且

$ \left\{ {\begin{array}{*{20}{l}} {{{\bf{m}}_{\dot x}}({{\bf{\xi }}^*}) = {{\bf{K}}_{\dot x}}({{\bf{\xi }}^*},{\bf{\Xi }}) \cdot }\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{{({{\bf{K}}_{\dot x}}({\bf{\Xi }},{\bf{\Xi }}) + {\sigma ^2}{\bf{I}})}^{ - 1}} \cdot {f_{\dot x}}({\bf{\Xi }}),}\\ {{\Sigma _{\dot x}}({{\bf{\xi }}^*}) = {{\bf{K}}_{\dot x}}({{\bf{\xi }}^*},{{\bf{\xi }}^*}) + {\sigma ^2} - {{\bf{K}}_{\dot x}}({{\bf{\xi }}^*},{\bf{\Xi }}) \cdot }\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{{({{\bf{K}}_{\dot x}}({\bf{\Xi }},{\bf{\Xi }}) + {\sigma ^2}{\bf{I}})}^{ - 1}} \cdot {{\bf{K}}_{\dot x}}({\bf{\Xi }},{{\bf{\xi }}^*}).} \end{array}} \right. $

在实际应用中，利用t时刻的位置信息可回归出t时刻的期望速度，从而可以计算出t+1时刻期望的位置：

$ \left\{ \begin{array}{l} m_x^{t + 1} = m_x^t + m_{\dot x}^t \cdot \Delta t,\\ {\mathit \Sigma} _x^{t + 1} = {\mathit \Sigma} _{\dot x}^t \cdot {\left( {\Delta t} \right)^2}. \end{array} \right\} $

(3)

式中：Δt为机械臂的规划周期，$m_x^{t + 1}$和${\mathit \Sigma} _x^{t + 1}$分别为t+1时刻轨迹的均值和方差.从机械臂初始位置开始，迭代式(3)，直到到达机械臂的期望位置，即可获得机械臂的沿X方向的期望轨迹.可以按照相同的方法计算获得其他五维的期望轨迹分布, 为关节控制器设计提供了条件.

在实际应用中，由于该策略的运动学实例均是根据操作者控制机械臂运动的轨迹计算的，不可避免地带有操作者的一些操作特征.例如，在目标点附近时，操作者往往会反复来回移动操作手柄，以保证对准目标位置.这些操作将会造成生成的笛卡尔期望轨迹收敛时间过长，甚至引起发散.

因此，本文基于文献[17]改进了速度场方法，建立了一个线性速度场.在迭代式(3)的过程中，如果与目标点的距离＜δ，则轨迹生成不再继续迭代式(3)，而是根据线性速度场计算速度及其分布.同样以沿X轴方向为例，令x_g表示沿X轴方向的目标位置.一旦存在时刻t，使得|x_t-x_g|≤δ，则进入线性速度场范围，速度计算方法为

$ m_{\dot x}^{t + 1} = \frac{{m_x^t - {x_{\rm g}}}}{{m_x^{{\rm in}} - {x_{\rm g}}}} \cdot m_{\dot x}^{{\rm in}}. $

式中，$m_x^{{\rm in}}$和$m_{\dot x}^{{\rm in}}$为进入线性速度场时的位置和速度.而此时的速度方差为

$ {\mathit \Sigma} _{\dot x}^{t + 1} = {\left( {\frac{{m_x^t - {x_{\rm g}}}}{{m_x^{{\rm in}} - {x_{\rm g}}}}} \right)^2} \cdot {\mathit \Sigma} _{\dot x}^{{\rm in}}. $

3 基于动力学约束的机械臂关节控制器设计

基于高斯过程的模仿学习策略可根据机械臂及环境的状态，自主生成对应的笛卡尔任务分布，具有较强的环境适应性.但是，由于生成的轨迹分布均参考来自操作者的运动学实例，受人类生理特性影响，运动学实例本身就可能不够平滑，尤其经过较长时间工作后，操作者肌肉疲劳，这种现象更加明显；因此，直接将获得的期望轨迹分布均值用于机械臂控制，可能会造成关节控制力矩波动过大，甚至控制不稳定.

针对上述问题，提出了一种基于动力学约束的机械臂关节控制器.该控制器旨在保证成功完成任务的同时，减小关节输出力矩波动和能量消耗，使机械臂的运动更加平滑.

对于一项任务，一般均有多条不同轨迹能满足要求，即当轨迹位于一定的置信区间内，均可认为能够满足任务需求.而上节中的轨迹分布可用于计算该置信区间.因此，将控制器设计成线性二次跟踪型(LQT)的形式：

$ \begin{array}{l} {\rm min}\sum\limits_{t = 0}^{{t_f} = 1} {({{(\mathit{\boldsymbol{s}}(t) - {\mathit{\boldsymbol{s}}^*}(t))}^T}} \cdot \mathit{\boldsymbol{\hat Q}}(t) \cdot \\ \ \ \ \ \ \ \ \ \ (\mathit{\boldsymbol{s}}(t) - {\mathit{\boldsymbol{s}}^*}(t)) + {\mathit{\boldsymbol{u}}^T}(t) \cdot \mathit{\boldsymbol{R}} \cdot \mathit{\boldsymbol{u}}(t)) + \\ \ \ \ \ \ \ \ \ \ {(\mathit{\boldsymbol{s}}({t_f}) - {\mathit{\boldsymbol{s}}^*}({t_f}))^T} \cdot {\mathit{\boldsymbol{Q}}_f} \cdot (\mathit{\boldsymbol{s}}({t_f}) - {\mathit{\boldsymbol{s}}^*}({t_f})),\\ {\rm s.t.}\left\{ \begin{array}{l} \mathit{\boldsymbol{\dot s}}(t) = \mathit{\boldsymbol{A}}(t) \cdot \mathit{\boldsymbol{s}}(t) + \mathit{\boldsymbol{B}}(t) \cdot \mathit{\boldsymbol{u}}(t) + \mathit{\boldsymbol{Bia}}(t),\\ \mathit{\boldsymbol{s}}(t + 1) = \mathit{\boldsymbol{s}}(t) + \mathit{\boldsymbol{\dot s}}(t) \cdot \Delta T. \end{array} \right\} \end{array} $

(4)

式中：$\mathit{\boldsymbol{s}}(t) = {[\mathit{\boldsymbol{q}}(t),\mathit{\boldsymbol{\dot q}}(t)]^{\rm T}} \in {\mathbb{R}^{2n}}$为在t时刻实际轨迹的状态变量，s^*(t)为在t时刻期望轨迹的状态变量，两者均由关节位置和关节速度组成；n为空间机械臂的关节数；$\mathit{\boldsymbol{u}}(t) \in {\mathbb{R}^n}$为在t时刻的关节控制力矩，为控制器的输出；$\mathit{\boldsymbol{\hat Q}} \in {\mathbb{R}^{2n \times 2n}}$和$\mathit{\boldsymbol{R}} \in {\mathbb{R}^{n \times n}}$为该损失函数的参数，$\mathit{\boldsymbol{\hat Q}}(t)$为半正定矩阵，R为正定矩阵，两者用于权衡控制器位置跟踪精度与关节输出力矩；Q_f为$\mathit{\boldsymbol{\hat Q}}(t)$在终点时刻的值；ΔT为该控制器的控制周期；在约束条件中，$\mathit{\boldsymbol{\dot s}}(t) = \mathit{\boldsymbol{A}}(t) \cdot \mathit{\boldsymbol{s}}(t) + \mathit{\boldsymbol{B}}(t) \cdot \mathit{\boldsymbol{u}}(t) + \mathit{\boldsymbol{Bia}}(t)$为t时刻的机械臂线性动力学方程，由动力学方程在t时刻进行一阶泰勒展开获得，A(t)、B(t)和Bia(t)均为方程系数.

与传统的LQT问题不同，本文中的期望轨迹为高斯分布，具有不确定性.若使用传统的欧氏范数($\mathit{\boldsymbol{\hat Q}}(t)$为定值)计算，不能反应这种不确定性.因此，本文选择马氏范数，能够将期望轨迹分布的协方差纳入度量，即

$ \mathit{\boldsymbol{\hat Q}}(t) = {\mathit \Sigma} _t^{ - 0.5} \cdot \mathit{\boldsymbol{Q}} \cdot {\mathit \Sigma} _t^{ - 0.5}. $

式中：Σ_t为t时刻期望轨迹分布的协方差，Q为定值.引入马氏距离，可以理解为当Σ_t大时，期望轨迹的不确定性高，机械臂控制器可以有更大空间调整，优化将倾向于减少输出力矩，反之亦然.

本文采用微分动态规划方法^[18]对式(4)问题进行求解.带偏置的LQT问题的最优反馈控制律可写成如下形式：

$ {\mathit{\boldsymbol{u}}^*}(t) = - {\mathit{\boldsymbol{R}}^{ - 1}} \cdot {B^{\rm T}}(t) \cdot (\mathit{\boldsymbol{M}}(t) \cdot \mathit{\boldsymbol{s}}(t) + \mathit{\boldsymbol{p}}(t)). $

其中，M(t)和p(t)均可通过Ricatti递归进行求解,

$ \left\{ {\begin{array}{*{20}{c}} {{\bf{\dot M}}(t) = {\bf{M}}(t) \cdot {\bf{B}}(t) \cdot {{\bf{R}}^{ - 1}} \cdot {{\bf{B}}^{\rm{T}}}(t) \cdot }\\ {{\bf{M}}(t) \cdot {\bf{\hat Q}}(t) - 2 \cdot {\bf{M}}(t) \cdot {\bf{A}}(t)}\\ {{\bf{\dot p}}(t) = {{\bf{M}}^{\rm{T}}}(t) \cdot {\bf{B}}(t) \cdot {{\bf{R}}^{ - 1}} \cdot {{\bf{B}}^{\rm{T}}}(t) \cdot }\\ {{\bf{p}}(t) \cdot {{{\bf{\hat Q}}}^T}(t) \cdot {{\bf{s}}^*}(t) - {{\bf{A}}^{\rm{T}}}(t) \cdot }\\ {{\bf{p}}(t) - {\bf{M}}(t) \cdot {\bf{Bia}}(t)} \end{array}} \right. $

(5)

M(t)和p(t)可通过对式(5)进行数值积分获得.参数Q、R和Q _f需要人为调节，以使控制器达到更好的效果.

但是，该控制器工作在机械臂关节空间，而基于高斯过程的模仿学习策略的结果是笛卡尔空间的轨迹分布，因此需要对其进行映射.该分布的均值映射较为简单，直接利用逆运动学进行映射即可.而协方差映射需要从速度分布映射入手.由于笛卡尔空间的速度和关节空间的速度在瞬时为线性关系

$ \mathit{\boldsymbol{v}}(t) = \mathit{\boldsymbol{J}}(\mathit{\boldsymbol{q}}) \cdot \mathit{\boldsymbol{\dot q}}(t) $

其中v(t)、J(q)和$\mathit{\boldsymbol{\dot q}}(t)$分别为t时刻笛卡尔末端速度、雅可比矩阵和关节速度，且高斯分布的线性变换也为高斯分布^[19]，因此，关节速度协方差可以表示为

$ {\mathit \Sigma} _{\dot q}^t = {J^{ - 1}}(\mathit{\boldsymbol{q}}) \cdot {\mathit \Sigma} _v^t \cdot {J^{ - {\rm T}}}(\mathit{\boldsymbol{q}}) $

式中：${\mathit \Sigma} _{\dot q}^t$为期望关节速度协方差${\mathit \Sigma} _v^t$为期望笛卡尔速度协方差.根据${\mathit \Sigma} _{\dot q}^t$即可计算出关节位置的协方差.

4 实验验证

为验证策略的可行性，本文利用天宫二号空间机械臂进行实验验证.该机械臂为六自由度轻型机械臂，Denavit-Hartenberg(D-H)参数如表 1所示，惯量参数如表 2所示, 其坐标系如图 2所示.其中，惯量为相对于质心测量获得，质心位置为相对于D-H坐标系测量获得.为简化计算，在计算惯量参数时，将灵巧手和机械臂末端划分成一个整体.

本文利用空间机械臂定位螺钉的实验验证上述策略，如图 3所示.实验场所位于天宫二号空间实验室内，环境为空间微重力环境.该实验是天宫二号机械臂利用电动工具旋拧螺钉任务的重要组成部分.

实验开始时，空间机械臂已经完成了电动工具的抓取，需要通过基于动力学约束的模仿学习策略引导机械臂到达螺钉上方20 mm处的预旋拧位置，做好旋拧准备.具体执行步骤如下：

Step 1:操作者操作CyberForce力反馈手柄控制机械臂完成该任务，并记录末端轨迹.为兼顾结果的泛化能力和操作的便捷性，本实验中采集同一操作者的3组操作轨迹，并据此生成该任务的运动学实例.为验证算法的泛化能力，3组操作轨迹均为直接记录，未经过挑选.为方便后续计算，本文在螺钉上方20 mm处的目标位置处建立了目标坐标系，如图 3所示，并将运动学实例在该坐标系下表示，如图 4所示：

Step 2:利用全局相机以及机械臂自身传感器测量机械臂末端位姿与目标位姿，并在目标坐标系下表示，具体数值为[99.47 mm, -103.35 mm, -2.72 mm, 0°, 0°, 0°].然后，利用基于高斯过程的模仿学习策略生成期望的适合该任务的笛卡尔轨迹分布(目标坐标系下表示)，如图 5所示.其中虚线为期望的笛卡尔轨迹均值，灰色区域为置信区间，该区间根据置信度和分布的协方差计算得到，本文中设置置信度为68.27%(3σ原则).

由于机械臂和操作平台均为在轨重新组装，所以地面记录的位置并不准确.实际实验中发现，因为舱体膨胀以及操作台支架存在缝隙，实际偏差远远超出了电动工具的容差范围, 但是在利用基于动力学约束的模仿学习策略时仍能完成任务，体现了该策略具有较好的环境适应性.

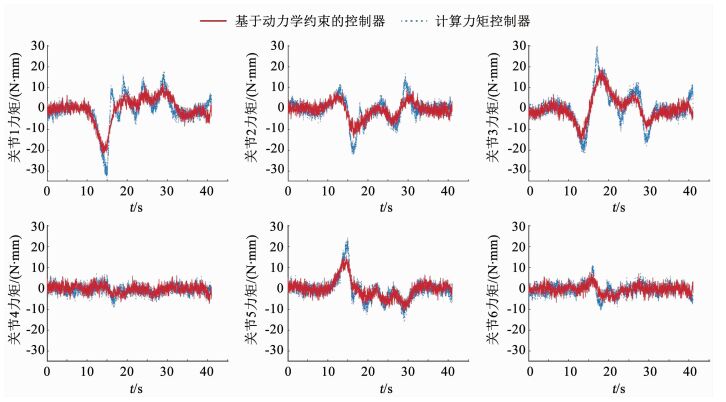
Step 3:设计基于动力学约束的机械臂关节控制器，生成期望的关节驱动力矩，并指导空间机械臂运行.初始状态下，机械臂实测关节角度为[79.85°, -9.44°, -76.48°, -83.47°, -81.54°, -10.46°].将该控制器与计算力矩控制器对比，关节控制力矩、关节角加速度和关节速度如图 6~8所示.

由图 6可以看出，与传统的计算力矩控制器相比，基于动力学约束的控制器能产生更加平滑的控制力矩.尤其是负载较大的前3个关节，效果更加明显.以第1关节为例，基于动力学约束的控制器产生的控制力矩的峰-峰值相对于计算力矩控制器减小了45%以上，波峰数也由原来的5个减小到了3个，减少了40%，并且有效平滑了尖峰.

由图 7可以看出，应用基于动力学约束的控制器可以产生更加平滑的关节角加速度.其变化趋势与关节力矩类似，各个关节角加速度的峰-峰值和波峰数均有明显减小，尤其是关节6，峰-峰值由1.077 8减小到0.405 2，减小了62%，波峰数由5个减小到3个，减小了40%.应用基于动力学约束的控制器时，关节角加速度没有尖峰，运动更加平滑.

如由8可以看出，应用基于动力学约束的控制器可使机械臂运动过程中速度的波峰数量减少，且波动的峰-峰值也会随之减小.

能耗是衡量空间机械臂性能的重要指标，本实验中的能耗对比如图 9所示.由图 9可知，应用基于动力学约束的控制器可使机械臂运行能耗明显降低，以该任务为例，相比于应用计算力矩控制器，基于动力学约束的控制器的能耗可减少31%.

图 10为应用基于动力学约束控制器时，机械臂末端轨迹在置信区间中的位置.

由图 10可以看出，末端轨迹均位于依据3σ原则建立的置信区间内，能够满足任务需求.

5 结论

1) 本文面向空间机械臂操作任务，提出了一种基于动力学约束的模仿学习策略.该策略主要分为两个阶段，第一阶段为基于高斯过程的模仿学习；第二阶段为基于动力学约束的机械臂控制器设计.与传统的模仿学习加计算力矩控制器的策略相比，该策略不仅具有操作便捷且克服空间扰动的优点，还可以有效降低关节力矩波动, 同时减小能量消耗.

2) 基于高斯过程的模仿学习阶段引入改进的速度场方法，克服了临近目标位置时笛卡尔期望轨迹收敛时间过长，甚至引起发散的问题.

3) 在基于动力学约束的机械臂控制器设计阶段引入马氏范数，充分考虑了期望轨迹分布的不确定性，使该控制器的调整优化更符合任务需求.

4) 为验证该方法的有效性，设计了机械臂定位螺钉的实验.实验结果表明，该策略与传统模仿学习加计算力矩控制的策略相比，大负载关节力矩波动的峰-峰值可减少45%，波峰数可减少40%，能耗可减少31%，且使得关节力矩、角加速度以及角速度更加平滑.未来该策略可以尝试应用于接触任务和自由漂浮基座空间机械臂.