2. 精密仪器技术及智能化工业和信息化部重点实验室(哈尔滨工业大学), 哈尔滨 150080
2. Key Lab of Ultra-precision Intelligent Instrumentation (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150080, China
外差激光干涉测量仪具有测量精度高、测量速度快、非接触、可直接溯源至长度基准等优点,是高精度位移测量的代表性精密仪器[1-4].随着超精密加工制造、精密计量、引力波探测等科学研究与工业技术领域的发展,对位移测量精度的需求逐渐由纳米量级过渡为亚纳米甚至皮米量级.在以光刻机为代表的超精密加工制造领域,为实现集成电路特征线宽达到5 nm甚至1 nm,外差激光干涉仪对硅片台和掩膜台位置的测量精度需要达到0.1 nm甚至数十皮米量级[5-6].在质量量子化基准装置中,外差激光干涉仪负责对能量/功率线圈的位移的精密测量,若要实现10-8量级以上的溯源精度,外差激光干涉仪的测量精度需要突破0.1 nm[7-11].在引力波探测装置LISA中,为了能够在数千至百万千米的等效臂长下实现不同频段引力波的探测,外差激光干涉仪需要精确识别出皮米量级的位移[12-15].
面临着上述亚纳米/皮米量级超精密位移测量精度需求的挑战,周期非线性误差的问题逐渐成为外差激光干涉仪测量精度进一步提升的障碍.周期非线性误差是外差激光干涉仪的一种原理性误差,其随着位移的变化表现为周期性的变化规律,当目标每运动半个波长时,该误差至少出现一次数纳米至数十纳米的峰值.外差激光干涉测量技术诞生后不久,Quenelle就发现了周期非线性误差的存在[16].随后,Sutton通过实验进一步验证了非线性误差随测量位移周期性变化的规律[17].此后,国内外研究人员对周期非线性误差的理论模型和抑制方法进行了广泛的理论与实验研究[18-24].针对外差激光干涉仪中的周期非线性误差问题,本文重点分析外差激光干涉仪中的两类周期非线性误差的形成机理,对具有代表性的周期非线性误差优化补偿方法进行了研究.本文旨在为抑制外差激光干涉测量技术中非线性误差,进一步提高外差激光干涉仪测量精度提供有益的参考.
1 外差激光干涉仪中的周期非线性误差形成机理在外差激光干涉仪中,根据误差来源不同,周期非线性误差可以分为两类:第1类周期非线性误差来源于共光路的测量光、参考光无法完全分离引起的“双频激光交叉混叠”,第2类周期非线性误差来源于主要测量光束引起的部分虚反射光束的“多阶多普勒频移虚反射光束自混叠”.下面详细分析两类周期非线性误差的形成机理.
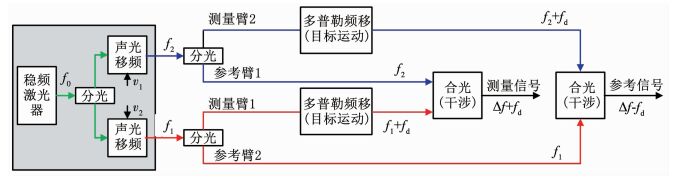
1.1 外差激光干涉仪中的第1类周期非线性误差在理想外差激光干涉仪中,偏振分光镜PBS将共轴传输的两个频率光f1、f2完全分离.但是实际中,如图 1所示,由于双频激光器存在椭偏化、安装误差、偏振分光镜不理想等原因[25-30],导致在测量光路或者参考光路中存在着另一频率的泄漏光,这种现象就是双频激光交叉混叠.
|
图 1 外差激光干涉仪中双频激光交叉混叠示意图 Fig. 1 Schematic of optical mixing in heterodyne laser interferometer |
由于双频激光交叉混叠,实际外差激光干涉仪中的测量与参考光束表示为
| $ \left\{ {\begin{array}{*{20}{l}} {{E_1} = A {\rm{cos}} ({\omega _1}t + \Delta \varphi ) + \beta {\rm{cos}} ({\omega _2}t + \Delta \varphi ),}\\ {{E_2} = B {\rm{cos}} ({\omega _2}t) + \alpha {\rm{cos}} ({\omega _1}t).} \end{array}} \right. $ | (1) |
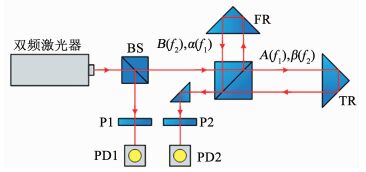
式中:A、B分别为主要测量和参考光束的幅值,α、β分别为参考和测量光路中泄漏光的幅值; Γ1=α/A, Γ2=β/B称为泄漏系数; Δφ=2πfd为测量位相,fd为目标运动所引入的多普勒频移; ω1=2πf1, ω2=2πf2.如图 2(a)所示,含有泄漏光的测量光束与参考光束干涉后形成测量信号为

|
图 2 双频激光交叉混叠误差形成机理和测量信号频谱分布 Fig. 2 Schematic of optical mixing errors and spectra of measurement signals |
| $ \begin{array}{*{20}{c}} {{I_{\rm{m}}} \propto AB {\rm{cos}} (\Delta \omega t + \Delta \varphi ) + (A\beta + B\alpha ) {\rm{cos}} (\Delta \omega t) + }\\ {\alpha \beta {\rm{cos}} (\Delta \omega t - \Delta \varphi ).} \end{array} $ | (2) |
式中:Δω=ω1-ω2;第1项为主要测量信号(main measurement signal, MMS),后两项分别为0阶和-1阶寄生干涉信号(parasite interference signal, PIS),对其进行仿真可以得到测量信号频谱如图 2(b)所示, 其中设置双频激光频差Δf=5 MHz,多普勒频移fd=1 MHz,泄漏系数Γ1=Γ2=0.1.可见受到双频激光交叉混叠影响的信号中,除了主要测量信号外,还包含有一阶和二阶寄生干涉信号.
对式(2)进行变形,可得
| $ {I_{\rm{m}}} \propto AB {\rm{cos}} (\Delta \omega t + \Delta \varphi + \Delta {\varphi _{{\rm{ nonlin }}}}). $ | (3) |
式中Δφnonlin1为非线性误差项,可以表示为
| $ \Delta {\varphi _{{\rm{ nonlin1 }}}} = {\rm{tan}}{ ^{ - 1}}\left[ {\frac{{ - (A\beta + B\alpha ) {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi - \alpha \beta {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} 2\varphi }}{{AB + (A\beta + B\alpha ) {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi + \alpha \beta {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} 2\varphi }}} \right]. $ | (4) |
对于一般的外差激光干涉仪,Γ1≪1,Γ2≪1,则式(4)可近似为
| $ \begin{array}{*{20}{l}} {\Delta {\varphi _{{\rm{ nonlin1 }}}} \approx \frac{{ - (A\beta + B\alpha ) {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \Delta \varphi - \alpha \beta {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} 2\Delta \varphi }}{{AB + (A\beta + B\alpha ) {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \Delta \varphi + \alpha \beta {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} 2\Delta \varphi }} = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \frac{{A\beta + B\alpha }}{{AB}} {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \Delta \varphi - \frac{{\alpha \beta }}{{AB}} {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} 2\Delta \varphi .} \end{array} $ | (5) |
根据外差激光干涉仪测量位移与位相的关系,可计算得外差激光干涉仪第1类周期非线性误差为
| $ \begin{array}{l} \Delta {L_{{\rm{ nonlin1 }}}} = \frac{\lambda }{{4\pi }}\Delta {\varphi _{{\rm{ nonlinl }}}} = \\ - \frac{\lambda }{{4\pi }}(\frac{{A\beta + B\alpha }}{{AB}} {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \Delta \varphi + \frac{{\alpha \beta }}{{AB}} {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} 2\Delta \varphi ). \end{array} $ | (6) |
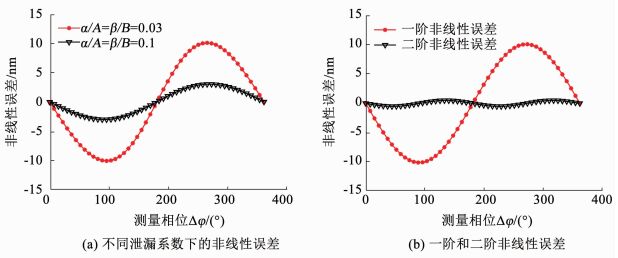
由式(6)可见,第1类周期非线性误差中包含有两项,其中第1项与第2项分别为一阶和二阶周期非线性误差.设定主要参考和测量光束幅值A=B=1,对式(6)进行仿真如图 3所示.图 3(a)为不同泄漏系数下的非线性误差曲线,从图中可以看出,随着泄漏系数的增大,非线性误差也随之增大.图 3(b)为泄漏系数为0.1的情况下,一阶和二阶非线性误差曲线,从图中可以看出,一阶非线性误差要远大于二阶非线性误差,这也说明了非线性误差大小主要取决于一阶非线性误差的大小,同时一阶和二阶寄生干涉信号引入的非线性误差都具有明显的周期性,且周期分别为2π和π.
|
图 3 双频激光交叉混叠导致的非线性误差曲线 Fig. 3 Curves of nonlinear errors caused by optical mixing |
伴随着位移测量精度要求逐渐过渡到亚纳米至皮米量级,哈尔滨工业大学胡鹏程等[23-24]发现外差激光干涉仪中存在着一种来源与表现形式都不同于第1类周期非线性误差的新型周期非线性误差——第2类周期非线性误差.研究表明第2类周期非线性误差来源于外差激光干涉仪中测量光束在光学界面处所产生的部分虚反射光引入的多阶多普勒频移虚反射光束自混叠.外差激光干涉仪的干涉光路由多个光学元件构成,存在着大量的光学界面.理论上主要测量光经过的每个光学界面上都会产生虚反射光束.图 4为多阶多普勒频移(Doppler frequency shift, DFS)光束形成的示意图.图 4(a)为主要测量光束的传播路径,光束在目标反射镜上反射1次,因此具有一阶多普勒频移;图 4(b)中,主要测量光束穿过PBS,在1/4波片(QWP)外表面发生反射,产生零阶多普勒频移虚反射光束;图 4(c)、4(d)分别表示具有二阶和三阶多普勒频移的虚反射光束产生过程.
在外差激光干涉仪中,主要测量光束表示为
| $ {E_{\rm{m}}} = A {\rm{cos}} ({\omega _1}t + \Delta \varphi ). $ | (7) |
根据图 4分析,包含多阶多普勒频移分量的虚反射光束可表示为
| $ \begin{array}{*{20}{l}} {{E_{{\rm{gh}}}} = {\gamma _0} {\rm{cos}} ({\omega _1}t) + {\gamma _1} {\rm{cos}} ({\omega _1}t + \Delta \varphi ) + }\\ {{\gamma _2} {\rm{cos}} ({\omega _1}t + 2\Delta \varphi ) + {\gamma _k} {\rm{cos}} ({\omega _1}t + k\Delta \varphi ).} \end{array} $ | (8) |
式中γk=AR|k-1|/2为各阶虚反射光束幅值,R为虚反射率.
参考镜固定不动,在参考光路中没有多阶多普勒频移产生,因此,参考光束可表示为
| $ {E_{\rm{r}}} = B {\rm{cos }}({\omega _2}t). $ | (9) |
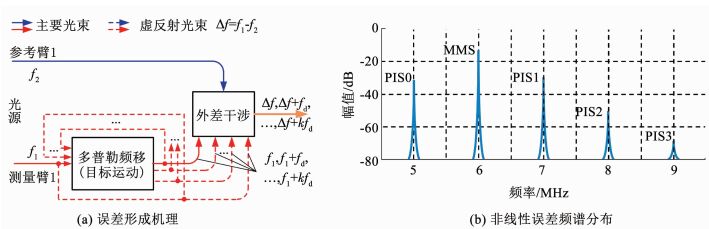
如图 5(a)所示,虚反射光束、测量光束与参考光束发生干涉后,得到测量信号为
| $ {I_{\rm{m}}} \propto ({E_{\rm{m}}} + {E_{\rm{r}}} + {E_{{\rm{gh}}}}) \cdot {({E_{\rm{m}}} + {E_{\rm{r}}} + {E_{{\rm{gh}}}})^ * }. $ | (10) |
|
图 5 多阶多普勒频移虚反射光束自混叠模型非线性误差形成机理与测量信号频谱分布 Fig. 5 Schematic of nonlinear errors caused by multi-order DFS ghost beam and spectra of measurement signals |
式(10)经过化简,得到
| $ \begin{array}{*{20}{l}} {{I_{\rm{m}}} \propto {\varGamma _0} {\rm{cos}} (\Delta \omega t) + {\varGamma _1} {\rm{cos}} (\Delta \omega t + \Delta \varphi ) + }\\ {{\varGamma _2} {\rm{cos}} (\Delta \omega t + 2\Delta \varphi ) + \cdots + {\varGamma _k} {\rm{cos}} (\Delta \omega t + k\Delta \varphi ).} \end{array} $ | (11) |
式中:Γ0-Γk为各干涉分量的幅值,Γk=Bγk=ABR|k-1|/2;Γ1cos(Δωt+Δφ)为主要测量信号;Γkcos(Δωt+kΔφ)为k阶寄生干涉信号.
设置双频激光频差Δf=5 MHz,多普勒频移fd=1 MHz,虚反射率R=1%,对式(11)进行仿真可以得到测量信号频谱如图 5(b)所示.相比于双频激光交叉混叠模型,在多阶多普勒频移虚反射光束自混叠模型中,没有-1阶寄生干涉信号,并且信号中含有大量高阶寄生干涉信号.
对各阶寄生干涉信号的影响进行独立分析,k阶寄生干涉信号引入的非线性误差可表示为
| $ \Delta {\varphi _{{\rm{ nonlin2 }}}} = {\rm{tan}}{ ^{ - 1}}\left[ {\frac{{{\varGamma _1} {\rm{sin}} (\Delta \varphi ) + {\varGamma _k} {\rm{sin}} (k\Delta \varphi )}}{{{\varGamma _1} {\rm{cos}} (\Delta \varphi ) + {\varGamma _k} {\rm{cos}} (k\Delta \varphi )}}} \right] - \Delta \varphi . $ | (12) |
由于Γk≪Γ1,对式(12)进行一阶泰勒展开后,可得由k阶寄生干涉信号引入的周期非线性误差为
| $ \Delta {\varphi _{{\rm{ nonlin 2}}}} = \frac{{{\varGamma _k}}}{{{\varGamma _1}}} {\rm{sin}} (k\Delta \varphi ) = {\varGamma _k} {\rm{sin}} (k\Delta \varphi ) = {R^{|k - 1|/2}} {\rm{sin}} (k\Delta \varphi ). $ | (13) |
根据外差激光干涉仪测量位移与位相的关系,可计算得外差激光干涉仪第2类周期非线性误差为
| $ \Delta {L_{{\rm{ nonlin2 }}}} = \frac{\lambda }{{4\pi }}\Delta {\varphi _{{\rm{ nonlin2 }}}} = \frac{\lambda }{{4\pi }}{R^{|k - 1|/2}} {\rm{sin}} (k\Delta \varphi ). $ | (14) |
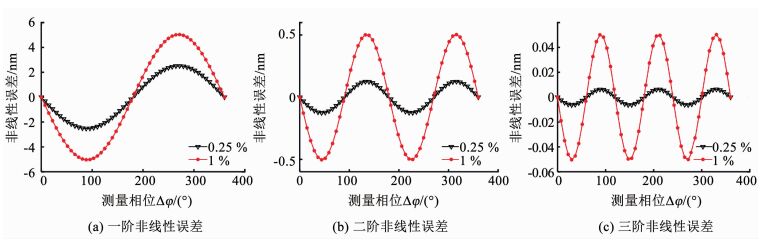
由式(14)可以看出,各阶非线性误差随虚反射率的增大而增大,且阶数越大,误差越小.对式(14)进行仿真得到不同阶次非线性误差曲线如图 6所示,可见多阶多普勒频移虚反射引入的非线性误差随着测量位相呈现周期性变化,且多普勒频移的阶次越高,变化周期越小;非线性误差的大小随着多普勒频移阶次的增大而减小,随着虚反射率的增大而增大.
|
图 6 多阶多普勒频移虚反射自混叠模型非线性误差曲线 Fig. 6 Corves of nonlinear errors caused by multi-order DFS phase mixing |
综上分析,第1类与第2类周期非线性误差形成机理和表现形式均有所不同.第1类周期非线性误差来源于双频激光交叉混叠,非线性误差中仅包含有一阶和二阶非线性误差,误差大小主要与外差激光干涉仪中的光学泄漏系数相关.第2类周期非线性误差来源于多阶多普勒频移虚反射光束自混叠,误差中包含有高阶非线性误差,误差大小主要与外差激光干涉仪中光学界面的虚反射率相关.一般来说,在外差激光干涉仪中,第1类周期非线性误差大于第2类周期非线性误差,并且二者同时存在.
2 周期非线性误差补偿方法非线性误差补偿方法是抑制周期非线性误差影响,提高外差激光干涉仪测量精度的重要措施.根据第1节的分析,第1类和第2类周期非线性误差的来源与形成原理互不相同,因此针对两者的非线性误差补偿措施也有所不同,下面分别介绍.
2.1 第1类周期非线性误差补偿方法针对第1类周期非线性误差的补偿,研究人员已经进行了广泛而深入的研究,并提出了多种补偿方法.这些非线性误差补偿方法大体上可以分为3种:第1种补偿方法主要通过调整光路来减小非线性误差[31-35],德国联邦物理技术研究院提出了基于正交测量的外差激光干涉仪周期非线性误差补偿方法[33],如图 7(a)所示,该方法利用PBS将测量信号分为两个偏振方向正交的信号同时进行探测,得到两个测量结果并相加,测量的周期非线性误差项由于符号相反相消而减小,从而达到补偿周期非线性误差的目的,这种方法能将外差激光干涉仪周期非线性误差补偿至几纳米.第2种补偿方法一般通过信号处理算法的改进来对包含有非线性误差的信号进行补偿[36-40].韩国标准与科学研究院提出了基于椭圆拟合的外差激光干涉仪周期非线性误差补偿方法[36],如图 7(b)所示,该方法通过椭圆拟合法提取椭圆参数对非线性误差进行补偿从而去除非线性误差,这种方法实际中可以将非线性误差补偿至亚纳米量级.可见现有的周期非线性误差补偿方法普遍比较复杂,而且难以将周期非线性误差抑制到0.1 nm以下.第3种非线性误差补偿方法为空间分离式外差激光干涉结构[41],如图 8所示,该方法采用独立产生的不共光路双频光源,其测量/参考光束在进行外差干涉之前从不共光路,避免了双频激光无法完全分离的问题.该方法可以从源头上消除双频激光交叉混叠引入的第1类周期非线性误差.为此,美国NIST[42-43]、美国Rochester大学[44]、德国PTB[45]、荷兰Delft理工大学[46]、我国清华大学[47]和哈尔滨工业大学[48]等设计了多种空间分离式外差激光干涉仪.这些空间分离式外差激光干涉仪原理上可完全消除第1类周期非线性误差,实验表明剩余非线性误差为数十皮米到一纳米,并且剩余非线性误差均为多阶多普勒频移虚反射光束自混叠引起的第2类周期非线性误差[23-24].

|
图 7 第1类周期非线性误差补偿方法 Fig. 7 First-type nonlinear error compensation method |
根据第2.1节的分析,空间分离式外差激光干涉结构可以从原理上去除第1类周期非线性误差.在此基础上,研究人员提出了多种第2类周期非线性误差的补偿方法.根据第1.2节的分析,第2类周期非线性误差与虚反射率的大小成正相关的关系.因此,镀增透膜以降低光学元件表面反射率来减弱虚反射光束的强度的方法被提出来[49].该方法基于薄膜干涉原理,在光学元件表面镀适当厚度的薄膜,使在薄膜两个面反射光的光程差恰好等于半个波长,从而相互抵消.在此基础上,为了进一步减低反射率,又提出了多层增透膜设计[50].普通宽带增透膜反射率为0.25%,而针对单一波长的窄带增透膜反射率可达0.1%.根据第1.2节中式(14)可以计算出不同反射率下周期非线性误差大小, 见表 1,可见仅仅通过降低反射率无法使周期非线性误差降至皮米量级.
| 表 1 不同反射率下各阶多普勒频移虚反射光束引入的周期非线性误差 Tab. 1 Nonlinear errors induced by DFS ghost beam of each order with different reflectivity |
此外,根据虚反射光束方向与产生该光束的光学界面角度相关的特点,可以通过调节虚反射面角度与空间滤波的方法来减小虚反射光束对外差激光干涉测量的影响[51-52].该方法通过调节虚反射面角度使虚反射光束与主要测量光束之间产生失配角,同时在接收器前加装透镜,利用透镜的聚焦作用滤除与主要测量光束失配角过大的虚反射光束,从而消除虚反射光束引起的第2类周期非线性误差.如图 9所示,空间滤波透镜焦距为100 mm,光纤接收器直径为10 μm,所有器件均镀有增透膜,反射率约为0.1%.当失配角大于200 μrad时,该虚反射面产生的虚反射光束引入的周期非线性误差基本被去除.德国联邦物理研究院的Weichert-type空间分离式外差激光干涉结构中采用了这些措施,该干涉结构的周期非线性误差能够达到±10 pm[45].然而,由于外差激光干涉仪中若干光学界面之间虚反射行为复杂,存在着单次、多次虚反射情况,简单调节部分虚反射面角度不能保证所有虚反射光束完全逸出主要测量光路.因此,亟需研发能够精确调整虚反射光束传输路径的优化和分析技术来消除虚反射光束引入的周期非线性误差.

|
图 9 调节虚反射角度与空间滤波去除第2类周期非线性误差原理与误差曲线 Fig. 9 Eliminating second-type nonlinear error by adjusting ghost reflection angle and spatial filter and corresponding error curve |
综上所述,第1类周期非线性误差与第2类周期非线性误差的补偿方法各不相同.针对第1类周期非线性误差,现有的补偿方法可将误差抑制至0.1 nm量级,近年来的空间分离式外差激光干涉结构可以从原理上消除第1类周期非线性误差.针对第2类周期非线性误差,通过降低虚反射率以及调节虚反射面角度和空间滤波的方法,可以将非线性误差减小至数十皮米.然而由于外差激光干涉仪中虚反射情况复杂,目前尚无针对性的优化和分析技术,不能完全满足皮米测量的需求.
3 结论1) 为提高外差激光干涉仪测量精度,对外差激光干涉仪中周期非线性误差的形成机理和补偿方法进行研究,对比分析了外差激光干涉仪中的两类周期非线性误差,即双频激光交叉混叠引起的第1类周期非线性误差和多阶多普勒频移虚反射光束自混叠引起的第2类周期非线性误差.前者周期非线性误差中只包含一阶和二阶非线性误差,后者除一阶和二阶非线性误差外,还包含有高阶非线性误差.此外,前者幅值可达数纳米到数十纳米,后者幅值为数纳米到数皮米.
2) 现有第1类周期非线性误差补偿方法,可将误差抑制至0.1 nm量级, 特别是空间分离式外差激光干涉仪, 从原理上完全消除了这一类误差;对于第2类周期非线性误差,现有方法可以将其减小到数十皮米.
3) 随着外差激光干涉测量精度需求逐渐由纳米量级到皮米量级,现有非线性误差补偿方法尚不能完全满足皮米测量的需求,亟需研发新的第2类周期非线性误差优化补偿技术.
| [1] |
DAN M. Displacement-measuring interferometers provide precise metrology[J]. Laser Focus World, 2003, 39(12): 80. |
| [2] |
ONDREI C, FRANTISEK P, ZDENEK B. Ultra-precise distance measurement for nanometrology[J]. Proc SPIE, 2004, 5457: 22. DOI:10.1117/12.545924 |
| [3] |
LAWALL J. Interferometry for accurate displacement metrology[J]. Optics and Photonics News, 2004, 15(10): 40. DOI:10.1364/OPN.15.10.000040 |
| [4] |
NOZATO H, KOKUYAMA W, OTA A. Improvement and validity of shock measurements using heterodyne laser interferometer[J]. Measurement Science and Technology, 2016, 77: 67. |
| [5] |
Semiconductor Industry Association. Internationaltechnology roadmap for semiconductors[EB/OL]. (2009-09-05)[2020-03-03].https://www.semiconductors.org/resources/2009-international-technology-roadmap-for-semiconductors-itrs/
|
| [6] |
MANSKE E, JAGER G, HAUSOTTE T, et al. Recent developments and challenges of nanopositioning and nanomeasuring technology[J]. Measurement Science and Technology, 2012, 23: 074001. DOI:10.1088/0957-0233/23/7/074001 |
| [7] |
ZHANG Zhonghua, HE Qing, LI Zhengkun, et al. The joule balance in NIM of China[J]. Metrologia, 2014, 51(2): 25. |
| [8] |
YANG Hongxing, LU Yunfeng, HU Pengcheng, et al. Measurement and control of movable coil position of joule balance with a system based on laser heterodyne interferometer[J]. Measurement Science and Technology, 2014, 25(6): 064003. DOI:10.1088/0957-0233/25/6/064003 |
| [9] |
LI Zhengkun, ZHANG Zhonghua, LU Yunfeng, et al. The first determination of the Planck constant with the joule balance NIM-2[J]. Metrologia, 2017, 54(5): 763. DOI:10.1088/1681-7575/aa7a65 |
| [10] |
BAI Yang, HU Pengcheng, LU Yunfeng, et al. A six-axis heterodyne interferometer system for the joule balance[J]. IEEE Transactions on Instrumentation and Measurement, 2017, 66(6): 1579. DOI:10.1109/TIM.2016.2634758 |
| [11] |
BAI Yang, LIU Yongmeng, LU Yunfeng, et al. Stability improvement for coil position locking of joule balance[J]. Metrologia, 2017, 54(4): 461. |
| [12] |
SCHULDT T, GOHLKE M, WEISE D, et al. Picometer and nanoradian optical heterodyne interferometry for translation and tilt metrology of the LISA gravitational reference sensor[J]. Classical & Quantum Gravity, 2009, 26: 085008. |
| [13] |
王运永, 朱兴江, 刘见, 等. 激光干涉仪引力波探测器[J]. 天文学进展, 2014, 32(3): 348. WANG Yunyong, ZHU Xingjiang, LIU Jian, et al. The laser interferometer gravitational wave detector[J]. Progress in Astronomy, 2014, 32(3): 348. DOI:10.3969/j.issn.1000-8349.2014.03.06 |
| [14] |
ABBOTT B P, ABBOTT R, ABBOTT T D, et al. Observation of gravitational waves from a binary black hole merger[J]. Physical Review Letters, 2016, 116(6): 061102. DOI:10.1103/PhysRevLett.116.061102 |
| [15] |
SCHULDT T, GOHLKE M, WEISE D, et al. Compact laser interferometer for translation and tilt metrology[J]. International Journal of Optomechatronics, 2017, 1(2): 168. |
| [16] |
QUENELLE R C. Nonlinearity in interferometer measurements[J]. Hewlett Packard Journal, 1983, 34: 10. |
| [17] |
SUTTON C M. Nonlinearity in length measurement using heterodyne laser Michelson interferometry[J]. Journal of Physics E: Scientific Instruments, 1987, 20(10): 1290. DOI:10.1088/0022-3735/20/10/034 |
| [18] |
ROSENBLUTH A E, BOBROFF N. Optical sources of nonlinearity in heterodyne interferometers[J]. Precision Engineering, 1990, 12(1): 7. DOI:10.1016/0141-6359(90)90003-H |
| [19] |
WU C, SU C. Nonlinearity in measurements of length by optical interferometry[J]. Measurement Science and Technology, 1996, 7(1): 62. DOI:10.1088/0957-0233/7/1/009 |
| [20] |
WU C, DESLATTES R. Analytical modeling of the periodic nonlinearity in heterodyne interferometry[J]. Applied Optics, 1998, 37(28): 6696. DOI:10.1364/AO.37.006696 |
| [21] |
COSIJNS S, HAITJEMA H, SCHELLEKENS P. Modeling and verifying non-linearities in heterodyne displacement interferometry[J]. Precision Engineering, 2002, 26(4): 448. DOI:10.1016/S0141-6359(02)00150-2 |
| [22] |
WU C. Periodic nonlinearity resulting from ghost reflections in heterodyne interferometry[J]. Optics Communications, 2003, 215(1): 17. |
| [23] |
HU Pengcheng, BAI Yang, ZHAO Jinlong, et al. Toward a nonlinearity model for a heterodyne interferometer: not based on double-frequency mixing[J]. Optics Express, 2015, 23(20): 25935. DOI:10.1364/OE.23.025935 |
| [24] |
FU Haijin, WANG Yue, HU Pengcheng, et al. Nonlinear errors resulting from ghost reflection and its coupling with optical mixing in heterodyne laser interferometers[J]. Sensors, 2018, 18(3): 758. DOI:10.3390/s18030758 |
| [25] |
钟志, 谭久彬, 陈洪芳, 等. 偏振分光镜传输系数不等对非线性误差的影响[J]. 光电工程, 2005, 32(9): 27. ZHONG Zhi, TAN Jiubin, CHEN Hongfang, et al. Nonlinearity from difference between transmission coefficients of PBS in laser heterodyne interferometer[J]. Opto-Electronic Engineering, 2005, 32(9): 27. DOI:10.3969/j.issn.1003-501X.2005.09.008 |
| [26] |
陈洪芳, 丁雪梅, 钟志. 偏振分光镜分光性能非理想对激光外差干涉非线性误差的影响[J]. 中国激光, 2006, 33(11): 562. CHEN Hongfang, DING Xuemei, ZHONG Zhi. Effect of nonlinearity by the nonideal splitting performance of polarization beam splitter in laser heterodyne interferometry[J]. Chinese Journal of Lasers, 2006, 33(11): 562. |
| [27] |
钟志, 杨刚, 陈洪芳, 等. 偏振分光镜旋转角度误差的确定[J]. 计量学报, 2006, 27(3A): 73. ZHONG Zhi, YANG Gang, CHEN Hongfang, et al. A method for confirmation of the rotation angel of PBS[J]. Acta Metrologica Sinica, 2006, 27(3A): 73. |
| [28] |
陈洪芳, 谭久彬, 钟志. 外差干涉仪中偏振分光镜对测量精度的影响[J]. 计量学报, 2008, 29(增刊1): 15. CHEN Hongfang, TAN Jiubin, ZHONG Zhi. Influence of polarized beam splitter on measurement precision in heterodyne interferometry[J]. Acta Metrologica Sinica, 2008, 29(Sup 1): 15. |
| [29] |
侯文玫, 张运波, 许琦欣. 分光镜对外差激光干涉仪非线性的影响[J]. 机械工程学报, 2008, 44(9): 163. HOU Wenmei, ZHANG Yunbo, XU Qixin. Effect of beam splitter on nonlinearity in heterodyne interferometers[J]. Chinese Journal of Mechanical Engineering, 2008, 44(9): 163. DOI:10.3321/j.issn:0577-6686.2008.09.027 |
| [30] |
孙志猛.双频激光干涉仪非线性误差测量技术研究[D].哈尔滨: 哈尔滨工业大学, 2012 SUN Zhimeng. Research of measurement technology of the nonlinearity error of dual-frequency laser interferometer[D]. Harbin: Harbin Institute of Technology, 2012 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D242262 |
| [31] |
HOU W, WILKENING G. Investigation and compensation of the nonlinearity of heterodyne interferometers[J]. Precision Engineering, 1992, 14: 91. DOI:10.1016/0141-6359(92)90054-Z |
| [32] |
WU C. Periodic nonlinearity resulting from ghost reflections in heterodyne interferometry[J]. Optical Communication, 2003, 215(1): 17. |
| [33] |
HOU Wenmei, ZHANG Yunbo, HU Haijiang. A simple technique for eliminating the nonlinearity of a heterodyne interferometer[J]. Measurement Science and Technology, 2009, 20(10): 105303. DOI:10.1088/0957-0233/20/10/105303 |
| [34] |
TAN Jiubin, FU Haijin, HU Pengcheng, et al. A laser polarization state measurement method based on the beat amplitude characteristic[J]. Measurement Science and Technology, 2011, 22(8): 085302. DOI:10.1088/0957-0233/22/8/085302 |
| [35] |
FU Haijin, HU Pengcheng, TAN Jiubin, et al. Simple method for reducing the first-order optical nonlinearity in a heterodyne laser interferometer[J]. Applied Optics, 2015, 54(20): 6321. DOI:10.1364/AO.54.006321 |
| [36] |
EOM T, CHOI T, LEE K, et al. A simple method for the compensation of the nonlinearity in the heterodyne interferometer[J]. Measurement Science and Technology, 2002, 13(2): 222. DOI:10.1088/0957-0233/13/2/313 |
| [37] |
SCHMITZ L, CHU D, HOUCK L. First-order periodic error correction: validation for constant and non-constant velocities with variable error magnitudes[J]. Measurement Science and Technology, 2006, 17(12): 3195. DOI:10.1088/0957-0233/17/12/001 |
| [38] |
LU C, TROUTMAN R, SCHMITZ T L, et al. Application of the continuous wavelet transform in periodic error compensation[J]. Precision Engineering, 2016, 44: 245. DOI:10.1016/j.precisioneng.2016.01.008 |
| [39] |
WANG C, BURNHAM-FAY E D, ELLIS J D. Real-time FPGA-based Kalman filter for constant and non-constantvelocity periodic error correction[J]. Precision Engineering—Journal of the International Societies for Precision Engineering and Nanotechnology, 2017, 48: 133. |
| [40] |
XIE Jiandong, YAN Linping, CHEN Benyong, et al. Iterative compensation of nonlinear error of heterodyne interferometer[J]. Optical Express, 2017, 25: 4470. DOI:10.1364/OE.25.004470 |
| [41] |
PISANI M, YACOOT A, BALLING P, et al. Comparison of the performance of the next generation of optical interferometers[J]. Metrologia, 2012, 49(4): 455. DOI:10.1088/0026-1394/49/4/455 |
| [42] |
LAWALL J, KESSLER E. Michelson interferometry with 10 pm accuracy[J]. Review of Scientific Instruments, 2000, 71(7): 2669. DOI:10.1063/1.1150715 |
| [43] |
WU C, LAWALL J, DESLATTES R D. Heterodyne interferometer with subatomic periodic nonlinearity[J]. Applied Optics, 1999, 38(19): 4089. DOI:10.1364/AO.38.004089 |
| [44] |
GILLMER S R, ELLIS J D. Design considerations in a novel fiber-coupled three degree-of-freedom displacement interferometer[J]. Optomechanical Engineering, 2013, 8836(21): 10660. DOI:10.1117/12.2023358 |
| [45] |
WEICHERT C, KÖCHERT P, KÖNING R, et al. A heterodyne interferometer with periodic nonlinearities smaller than ±10 pm[J]. Measurement Science and Technology, 2012, 23(9): 094005. DOI:10.1088/0957-0233/23/9/094005 |
| [46] |
JOO K N, ELLIS J D, SPRONCK J W, et al. Simple heterodyne laser interferometer with subnanometer periodic errors[J]. Optics Letters, 2009, 34(3): 386. DOI:10.1364/OL.34.000386 |
| [47] |
ZHAO Shijie, WEI Haoyun, ZHU Minhao, et al. Green laser interferometric metrology system with sub-nanometer periodic nonlinearity[J]. Applied Optics, 2016, 55: 3006. DOI:10.1364/AO.55.003006 |
| [48] |
HU Pengcheng, CHEN Peng, DIAO Xiaofei, et al. Highly stable heterodyne interferometer without periodic nonlinearity[J]. Technisches Messen, 2014, 81(5): 246. |
| [49] |
左德, 马超, 赵乐然, 等. 近红外增透薄膜的研究进展[J]. 冶金与材料, 2019, 39(1): 38. ZUO De, MA Chao, ZHAO Leran, et al. Research progress of near-infrared antireflection films[J]. Metallurgy and Materials, 2019, 39(1): 38. DOI:10.3969/j.issn.1674-5183.2019.01.018 |
| [50] |
OSENBACH K.光学镀膜[EB/OL]. (2014-03-07)[2020-03-03].https://www.thorlabs.com/newgrouppage9.cfm?objectgroup_id=5840 OSENBACH K. Optical coatings[EB/OL]. (2014-03-07)[2020-03-03]. https://www.thorlabs.com/newgrouppage9.cfm?objectgroup_id=5840 |
| [51] |
ISLEIF K, GERBERDING O, PENKERT D, et al. Suppressing ghost beams: backlink options for LISA[J]. IOP Conference Series: Journal of Physics, 2017, 840: 012016. DOI:10.1088/1742-6596/840/1/012016 |
| [52] |
SUHARA H. Interferometric measurement of the refractive-index distribution in plastic lenses by use of computed tomography[J]. Applied Optics, 2002, 41(25): 5317. DOI:10.1364/AO.41.005317 |
 2020, Vol. 52
2020, Vol. 52