钢管混凝土因具有良好的受力性能得到众多学者的关注[1-3].应用于超高层建筑的钢管混凝土柱通常为具有较大截面面积的巨型柱,为了减小钢管壁厚,增强钢管与混凝土共同工作性能,巨型钢管混凝土柱通常设计成分腔构造.为了适应建筑平面个性化的设计,超高层建筑采用异形截面钢管混凝土柱的案例已较多,大连国贸中心大厦、天津117大厦、北京中国尊大厦等均采用了异形截面多腔钢管混凝土巨型柱.
业内已有异形截面钢管混凝土柱受力性能的研究主要如下.蔡建等[4-5]对带约束拉杆的T型、L型钢管混凝土柱进行了偏压性能试验研究,并采用纤维模型法计算N-M相关曲线,研究结果表明,约束拉杆对混凝土约束作用明显,能够有效改善钢管的局部屈曲问题,提高试件轴压承载力以及延性;王丹等[6]对T型、L型钢管混凝土柱抗震性能进行了试验研究,分析了轴压比、钢管厚度以及混凝土强度对承载力及延性的影响;杜国锋等[7]对多腔T型钢管混凝土柱偏压性能进行了试验研究,参考国内外规范提出了偏压承载力计算公式;徐礼华等[8-9]对多边多腔钢管混凝土柱轴压及偏压性能进行了试验研究,分析了混凝土强度、钢管壁厚、是否设置钢筋笼、长细比以及偏心率等参数对受压性能的影响,建立了轴心和偏心受压承载力计算公式;Liu等[10]对L型截面以及T型截面钢管混凝土柱轴压性能进行了试验研究并提出了截面承载力计算公式;Tu等[11]对T型多腔钢管混凝土柱轴压性能进行了试验研究并采用不同规范对承载进行计算.本文课题组基于大连国贸中心大厦、天津117大厦、北京中国尊大厦等重大工程对不规则五边形、六边形、八边形截面多腔钢管混凝土柱进行了试验研究及理论分析[12-16],分析了不同构造对异形截面钢管混凝土柱轴压性能、偏压性能、抗震性能的影响,并建立有限元分析模型,提出了异形截面多腔钢管混凝土巨型柱的构造要求.
国内外针对钢管混凝土结构均发布了相关标准规范,给出了不同的计算分析方法,如中国标准GB 50936[17]将钢管及混凝土两种材料抗压强度统一为钢管混凝土抗压强度;美国规范AISC-LRFD[18]也将钢管与混凝土进行了统一,但与中国标准不同的是,美国规范中将混凝土材料统一到钢管当中,将钢管混凝土结构简化为钢结构进行计算;欧洲规范EC4[19]采用叠加钢管、混凝土及钢筋等各部件计算承载能力.但这些标准规范主要针对单腔矩(方)形及圆形截面钢管混凝土柱,对于异形截面多腔钢管混凝土巨型柱未给出具体的计算方法.
在超高层建筑中,异形截面多腔钢管混凝土柱因荷载(自重、风、地震等)的作用,通常处于反复的偏心受压状态.本文以中国尊大厦和天津117大厦结构巨型柱为原型,进行了4个大尺寸多腔钢管混凝土巨型柱模型试件在单向重复荷载下的偏压性能试验,包括1个中国尊八边十三腔巨型柱模型、1个中国尊八边十三腔巨型柱角部腔内设置圆钢管的模型、2个117大厦六边六腔巨型柱模型[20].试验研究各试件在单向重复偏心荷载下的受力性能,并探讨偏压荷载下的N-M相关曲线计算方法等问题.
1 试验设计 1.1 试件设计设计了4个异形截面多腔钢管混凝土巨型柱模型试件.试件截面设计图见图 1,截面具体参数见表 1.

|
图 1 截面设计图(mm) Fig. 1 Design of cross sections (mm) |
| 表 1 试件设计参数 Tab. 1 Design parameters of specimens |
以中国尊大厦多腔钢管混凝土柱为原型,模型按1/13缩尺,设计了试件SCFST-1和SCFST-2.试件SCFST-1:截面为不规则八边形,内部由分腔板分为13个腔体;长轴尺寸为1 060 mm,短轴尺寸为476 mm,截面面积为0.37 m2;异形截面多腔钢管由4 mm钢板焊接而成;横隔板采用4 mm厚钢板,宽度30 mm,沿柱高分布间距为300 mm,开直径10 mm圆孔穿过钢筋笼纵筋;纵向加劲肋采用3 mm钢板,宽度23 mm;内部钢筋笼纵筋及箍筋均采用2 mm钢丝,箍筋间距60 mm.试件SCFST-2:在SCFST-1角部腔体内置圆钢管,圆钢管壁厚4 mm、直径90 mm,其余构造二者相同.SCFST-1及SCFST-2偏心距相同,均为150 mm,偏心率为0.32.以天津117大厦多腔钢管混凝土柱为原型,模型按1/12缩尺,设计了SCFST-3及SCFST-4:截面为不规则六边形,用分腔钢板将截面分成6个腔体;长轴尺寸为936 mm,短轴尺寸为436 mm,截面面积为0.31 m2;异形截面多腔钢管由5 mm钢板焊接而成;纵向加劲肋采用3 mm钢板;内部钢筋笼纵筋采用12、10、8 mm钢筋,箍筋均采用6 mm钢筋;SCFST-3偏心距为200 mm(偏心率0.46),SCFST-4偏心距为100 mm(偏心率0.23).
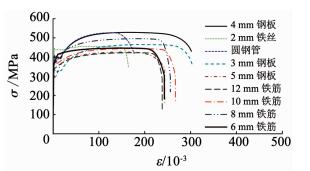
1.2 材料性能表 2为各材料实测性能.fcu, m为混凝土标准立方体抗压强度;fy为钢材屈服强度;fu为钢材极限强度;δ为钢材伸长率.混凝土坍落度为160 mm.图 2为钢材实测应力-应变曲线.
| 表 2 实测材料性能 Tab. 2 Measured mechanics properties of materials |
|
图 2 钢材应力-应变曲线 Fig. 2 σ-ε curves of steel |
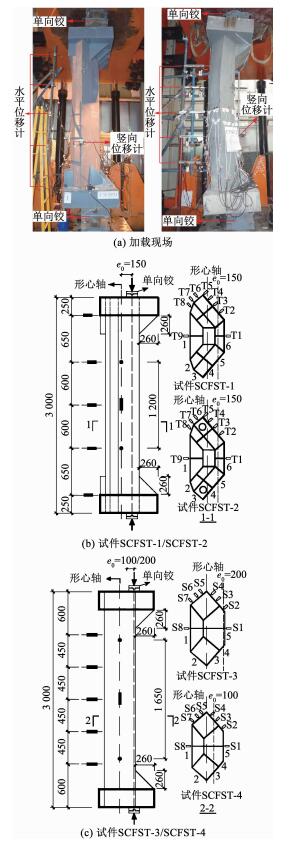
试验采用北京工业大学40 000 kN大型加载装置加载.试件加载端均设置单向铰支座.各试件设置5个测试水平挠度的位移计,用来监测试件的弯曲变形;设置2个轴线变形位移计,用来测试试件的轴向变形.在试件的中间位置布置系列轴线应变片,用来验证试件是否满足平截面假定.各试件的总高度均为3 000 mm,上、下均设置250 mm高的加载端头.试件加载装置、试件及测点布置见图 3.图 3中:巨型柱截面构造见1-1、2-2剖面,截面短轴为对称轴,应变片布置在对称轴一侧,应变测点编号示于截面图中;多腔钢管外侧钢板沿短轴两侧对称编号,其中一侧的钢板编号见数字“1~6”或“1~5”.荷载垂直截面作用于短轴.
|
图 3 加载装置、试件及测点布置(mm) Fig. 3 Test setup, specimens, and measurements (mm) |
采用单向重复加载方式,以测试试件弹塑性阶段不同挠度下的残余变形,试件明显屈服前采用荷载控制加载,试件出现明显屈服后每级加载采用位移控制.每级加载后卸载至2 000 kN,这样上下加载端头能够夹持柱试件,稳定荷载,观测损伤现象,之后施加下一级荷载.
2 试验结果及分析 2.1 损伤演化因为截面形状为多边形,描述巨型柱周边钢板损伤现象时,按照图 3所示钢板编号.试件损伤演化过程中的“水平挠度”为试件1 500 mm高度处挠度.
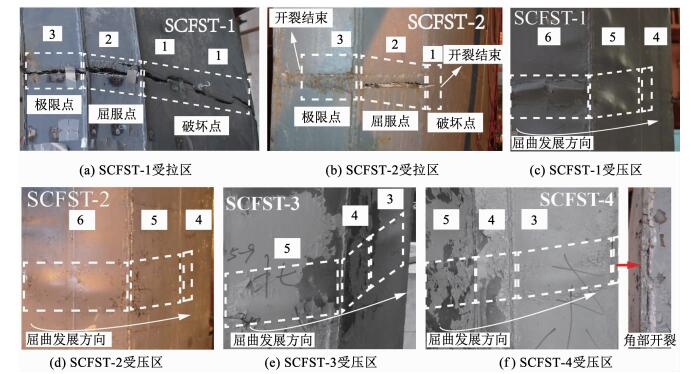
试件SCFST-1:加载至0.69Fu(水平挠度10.19 mm)时,受压区边缘钢管达到屈服应变,但未发生明显屈曲,受拉区边缘未达到屈服应变;当加载至屈服荷载(根据实测曲线,采用能量法求得[15])时,试件受压区钢板6首次发生明显屈曲,在达到峰值荷载之前屈曲范围主要沿试件纵向发展,此时受拉区无明显现象;加载至0.96Fu(水平挠度21.91 mm)时,受拉区边缘达到屈服应变;当达到峰值荷载时,钢板2和3交界处焊缝首先出现开裂;达到峰值荷载后,屈曲范围开始向钢板5和4发展;最终钢板4发生部分屈曲,而钢板6和5全部屈曲,受拉区焊缝开裂逐渐向钢板2和3延伸并在钢板2和3形成贯通裂缝退出工作,此时受拉区钢板1难以继续提供受拉区所需承载力,钢板1产生贯通裂缝.破坏特征见图 4(a)、(c).
|
图 4 试件破坏特征 Fig. 4 Failure modes of specimens |
试件SCFST-2:SCFST-1与SCFST-2比较,受压区损伤发展没有显著区别,达到峰值荷载前受拉区损伤无显著区别,达到峰值荷载后,受拉区损伤与SCFST-1产生明显区别:当加载至峰值荷载时,焊缝开裂首先发生在钢板2和3交界处,此时损伤发展与SCFST-1类似;随着加载的进行,焊缝开裂逐渐向钢板2和3延伸,但因为角部设置圆钢管,焊缝开裂在圆钢管处停止,钢板3未形成贯通的裂缝,仍然能够继续工作.因此,受拉区钢板1未形成贯通的裂缝.破坏特征见图 4(b)、(d).
试件SCFST-3:当加载至屈服点时,钢板5首先发生明显屈曲;当达到峰值荷载时,钢板4和钢板3漆皮出现褶皱但未发生明显屈曲;当达到破坏荷载时,屈曲由钢板5向钢板3延伸;最终钢板3发生部分屈曲.破坏特征见图 4(e).
试件SCFST-4:当加载至屈服点时,钢板5首先发生明显屈曲;当加载至峰值荷载时,钢板3和4漆皮出现褶皱,未发生明显屈曲,此时,损伤发展与SCFST-3类似;随着加载的继续进行,钢板4和钢板3在未达到破坏荷载时就发生了明显屈曲,当达到破坏荷载时,钢板3全部屈曲且钢板3与钢板2交界处焊缝开裂.破坏特征见图 4(f).
试件SCFST-3、SCFST-4:受拉区无焊缝,因此没有发生明显的损伤.
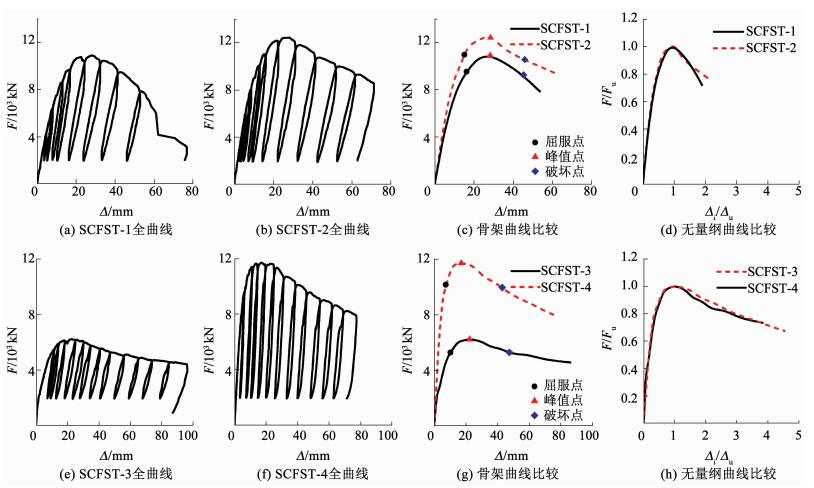
2.2 荷载-挠度实测各试件加载及卸载全曲线见图 5,横坐标为试件高度中部位置即1 500 mm高度处挠度Δ,纵坐标为竖向荷载F.Δi/Δu为全曲线第i级加载挠度Δi与全曲线峰值点挠度Δu的比值,为无量纲挠度;Fi/Fu为全曲线第i级荷载Fi与全曲线峰值点荷载Fu的比值,为无量纲荷载.
|
图 5 各试件荷载-变形曲线 Fig. 5 F-Δ curves of specimens |
由图 5可见:1)各循环卸载过程中,当混凝土受到钢管有效围压作用时,其卸载刚度和再加载刚度较稳定,表明多腔钢管对内部混凝土具有良好的约束作用;2)SCFST-1加载至受拉区钢板屈服后,骨架曲线下降段呈现加速下降的趋势,即承载力出现了突降;SCFST-2加载中,由于圆钢管制约了受拉区开裂的发展,下降段趋于平缓,承载力呈现减缓下降的趋势;从无量纲骨架曲线比较图中可以看出,设置圆钢管试件对骨架曲线上升段形状影响不明显,对下降段影响显著;3)SCFST-3、SCFST-4偏心距不同,偏心距较小的试件承载力显著高;无量纲骨架曲线图中,偏心距对骨架曲线影响不明显.
2.3 承载力及变形主要特征点实测数据见表 3.表中:Fy为屈服荷载,采用能量法求得[15];Δy为屈服挠度;Fu为峰值荷载;Δu为峰值点挠度;定义峰值荷载下降至85%的点为破坏点,Fd为破坏点荷载;Δd为破坏点挠度;μ=Δd/Δy为位移延性系数;η=Fy/Fu为屈强比.
| 表 3 特征点实测结果 Tab. 3 Measured results of feature points |
分析表 3可知:1)与SCFST-1相比,SCST-2屈服荷载提高16.3%,峰值荷载提高14.1%,说明试件角部腔体设置圆钢管后承载力明显提高;2)与SCFST-3相比,SCFST-4屈服荷载提高92.4%,峰值荷载提高88.3%,偏心距对试件承载力影响显著;3)SCFST-1与SCFST-2屈强比接近,SCFST-3与SCFST-4屈强比接近;4)SCFST-2与SCFST-1相比,屈服挠度略有下降,峰值点挠度接近,破坏点挠度略有提高,延性系数较大,说明试件角部腔体设置圆钢管后能够有效提高试件的延性;5)SCFST-3与SCFST-4相比,屈服挠度高40.8%,峰值点挠度高31.9%,破坏点挠度高10.7%;偏心距较大,试件的屈服挠度、峰值点挠度及破坏点挠度均较大,延性系数较小;偏心距较大时,荷载的二阶效应加大,挠度发展变快,峰值点挠度、破坏点挠度均较大.
恢复能力分析:加载、卸载过程中试件具有一定的恢复能力.采用水平挠度恢复系数λ1=Δi/Δj和轴向相对位移恢复系数λ2=Ui/Uj表达试件的复位能力,Δi、Ui分别为每级加载达到的最大挠度、轴向相对位移,Δj、Uj分别为每级加载后卸载至2 000 kN时的累积残余挠度、累积残余轴向相对位移,由实测数据所得λ1-Δ曲线、λ2-U曲线见图 6、7.SCFST-1、SCFST-2的横坐标U为1 200 mm标距段轴向相对位移,SCFST-3、SCFST-4的横坐标U为1 650 mm标距段轴向相对位移.λ越大,相对残余变形越小,复位能力越好.

|
图 6 λ1-Δ曲线 Fig. 6 λ1-Δ curves |

|
图 7 λ2-U曲线 Fig. 7 λ2-U curves |
分析图 6、7可知:1)SCFST-2与SCFST-1相比,相同Δ对应的λ1和相同U对应的λ2均较大,表明试件角部腔体设置圆钢管后试件的复位能力相对强;2)SCFST-3与SCFST-4相比,相同Δ对应的λ1和相同U对应的λ2均较大,表明偏心距较大试件的弯曲变形大,试件的复位能力相对好.
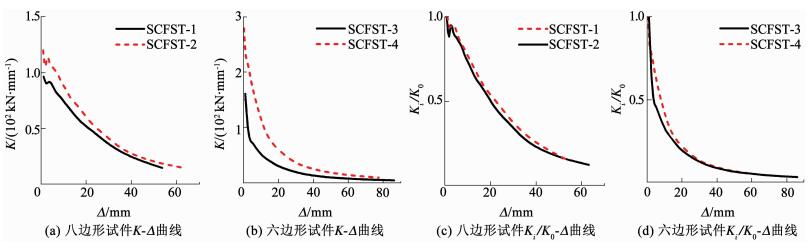
2.4 刚度及其退化采用割线刚度K-挠度Δ曲线分析刚度及其退化规律.割线刚度K=Fi/Δi,Fi为第i级加载的最大荷载,Δi为对应的挠度;Ki/K0为第i级加载的刚度退化系数,Ki为第i级加载的割线刚度,K0为初始割线刚度.由实测数据计算所得各试件的K-Δ曲线、Ki/K0-Δ曲线见图 8.
|
图 8 刚度-挠度曲线、刚度退化系数-挠度曲线 Fig. 8 K-Δ curves and Ki/K0-Δ curves |
由图 8可见:1)与SCFST-1相比,SCFST-2的刚度明显较大,说明内置圆钢管可有效提高试件的刚度;两个试件刚度退化系数曲线接近,表明二者刚度退化过程接近;2)SCFST-4的刚度显著大于SCFST-3,表明偏心距较小的试件刚度相对大;二者刚度退化过程相差不大.
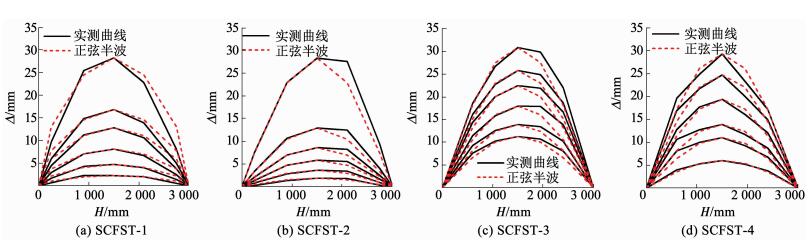
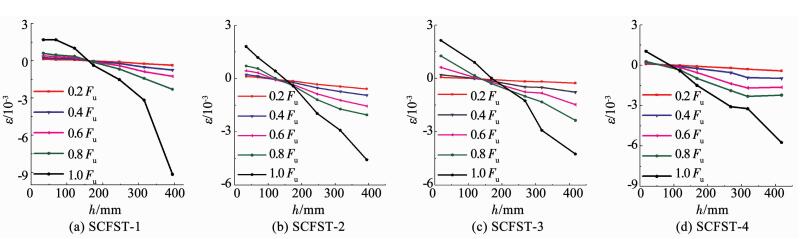
2.5 挠度曲线与截面应变实测所得各试件不同高度处水平挠度-试件高度(Δ-H)曲线与试件高度方向标准正弦半波曲线(sin H)的比较见图 9,不大于峰值荷载时,各试件实测挠度曲线基本符合正弦半波曲线的假定.实测所得各试件截面的各应变测点的应变-截面高度(ε-h)曲线见图 10,ε拉为正、压为负,h为试件截面短轴方向的高度,不大于峰值荷载时,各试件截面变形基本符合平截面假定.
|
图 9 挠度曲线 Fig. 9 Deflection curves |
|
图 10 截面应变 Fig. 10 Strain at different positions of section |
中国标准GB 50936[17]给出了钢管混凝土柱偏压荷载作用下N-M相关曲线计算方法,见式(1),该标准只给出了矩形(方形)、八边形以及圆形截面的参数计算方法,因此SCFST-1、SCFST-2轴压承载力Nu参数按照最为接近的八边形截面计算,SCFST-3、SCFST-4具体参数按照正方形截面计算,受弯承载力Mu计算时截面模量Wsc按照实际截面计算,系数N′E计算中试件长细比等于其计算高度除以回转半径;美国规范AISC-LRFD[18]给出了钢管混凝土柱偏压荷载作用下N-M相关曲线计算方法,见式(2);欧洲规范EC4[19]将N-M相关曲线简化成多段折线模型,见图 11.
中国标准GB 50936:
| $ \left\{ \begin{align} & \frac{N}{{{N}_{n}}}+\frac{{{\beta }_{m}}M}{1.5{{M}_{u}}(1-0.4N/N_{E}^{'})}\le 1, \frac{N}{{{N}_{u}}}\ge 0.255; \\ & \frac{-N}{2.17{{N}_{u}}}+\frac{{{\beta }_{m}}M}{{{M}_{u}}(1-0.4N/N_{E}^{'})}\le 1, \frac{N}{{{N}_{u}}}<0.255. \\ \end{align} \right. $ | (1) |
美国规范AISC-LRFD:
| $ \left\{ \begin{align} & \frac{N}{0.85{{N}_{u}}}+\frac{8M}{8.1{{M}_{u}}}\le 1, \frac{N}{0.85{{N}_{u}}}\ge 0.2; \\ & \frac{N}{1.7{{N}_{u}}}+\frac{M}{0.9{{M}_{u}}}\le 1, \frac{N}{0.85{{N}_{u}}}<0.2. \\ \end{align} \right. $ | (2) |
欧规EC4:
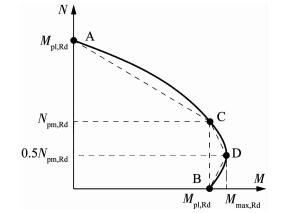
|
图 11 EC4 N-M相关曲线模型 Fig. 11 N-M interaction curves of EC4 |
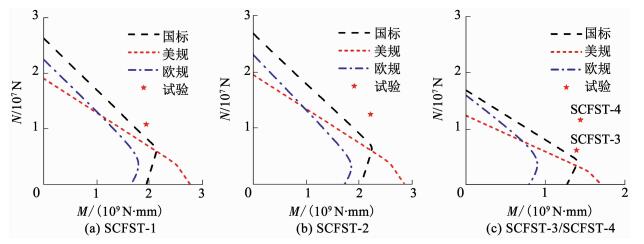
计算了各试件不同偏心距下的N-M相关曲线,计算中各材料强度均取实测值,并采用叠加法简化考虑了截面钢筋笼及纵向加劲肋的作用(这是目前规范未考虑的),计算所得各试件的N-M相关曲线及实测所得各试件给定偏心距对应的N-M关系点见图 12.试验结果与按照GB 50936计算的结果符合相对较好,按照GB 50936计算偏于安全.
|
图 12 计算N-M相关曲线 Fig. 12 Calculated N-M interaction curves |
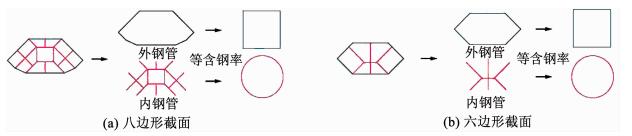
多腔钢管混凝土巨型柱对混凝土的约束效应明显高于普通的非圆形单腔钢管,本文考虑了多腔钢管对混凝土约束效应的提高,提出简化修正N-M相关曲线的计算方法.修正计算方法要点:将钢管周边钢板形成的钢管称为外钢管,外钢管与单腔钢管类似只有内侧受到混凝土的限制作用,在轴力作用下会发生向外侧的鼓曲变形;钢管的内部钢板与周边钢板围成多个腔体,尽管外钢管作用已分开考虑,但从腔体内外钢板共同形成强约束混凝土的角度,仍将两侧均有混凝土约束的钢管内部钢板称为内钢管,内钢管屈曲变形受到混凝土的限制,鼓曲变形明显轻于外部钢板;计算中假设,外钢管对混凝土的约束作用近似按照方钢管考虑,内钢管对混凝土的约束作用近似按照圆钢管考虑;笔者研究表明钢筋笼及横隔板对混凝土具有明显约束作用[21],按照等用钢量将横隔板及钢筋笼箍筋简化合并到钢管中.多腔钢管内外钢板承载及约束作用简化模型见图 13.
|
图 13 多腔钢管内外钢板作用简化模型 Fig. 13 Simplification models for inner and outer plates of multi-cell steel tube |
基于以上分析,在标准GB 50936中N-M相关曲线计算方法及韩林海钢管混凝土本构关系[22]基础上(主要针对单腔体钢管混凝土),考虑多腔钢管混凝土构造特点,提出一种修正的多腔钢管统一抗压强度fsc计算方法.计算外部方钢管和内部圆钢管的几何尺寸时,分别按照它们独立的、各自具有与试件截面面积相同的单腔体柱假设,简化后的方钢管混凝土截面总面积和圆钢管混凝土截面总面积都等于试件截面面积.内外钢管分别统一成单腔体钢管后,此时钢管已无内外之分,命名内外钢管只是便于区分型钢位置.该修正方法对材料强度的要求仍遵循原公式.
3.2.1 简化模型标准GB 50936中,截面含钢量是衡量钢管约束能力的重要参数.因此,按照等面积、等含钢率的原则进行简化:
| $ \frac{{{A}_{\text{sw}}}}{{{A}_{\text{c}}}}=\frac{{{A}_{\text{sf}}}}{{{A}_{\text{c}}}}, $ | (3) |
| $ \frac{{{A}_{\text{sn}}}}{{{A}_{\text{c}}}}=\frac{{{A}_{\text{sy}}}}{{{A}_{\text{c}}}}. $ | (4) |
式中:Ac为试件混凝土面积;Asw为试件外钢管面积,等效方钢管面积Asf=Asw,等效方钢管约束混凝土的面积等于Ac;Asn为试件内钢管面积,等效圆钢管面积Asy=Asn,等效圆钢管约束混凝土的面积等于Ac;试件截面面积Asc等于钢管面积与混凝土面积之和.
3.2.2 约束效应将多腔钢管分解简化为方钢管及圆钢管共同作用,需要分别考虑这两部分的约束效应.fscf、fscy分别为方钢管及圆钢管单独作用时的单腔体钢管混凝土统一抗压强度,按式(5)、(6)计算[17].本文采用先按照等效圆钢管计算fscy、再附加等效方钢管对混凝土约束贡献的增量Δfscf,Δfscf按式(7)计算,二者之和为多腔钢管混凝土统一抗压强度fsc,见式(8);也可采用先按照等效方钢管计算fscf、再附加等效圆钢管对混凝土约束贡献的增量Δfscy,二者之和为fsc;两种简化计算fsc的方法结果接近.
| $ {{f}_{\text{scf}}}=(1.212+{{B}_{\text{f}}}{{\theta }_{\text{f}}}+{{C}_{\text{f}}}\theta _{\text{f}}^{2}){{f}_{\text{c}}}, $ | (5) |
| $ {{f}_{\text{scy}}}=(1.212+{{B}_{\text{y}}}{{\theta }_{\text{y}}}+{{C}_{\text{y}}}\theta _{\text{y}}^{2}){{f}_{\text{c}}}, $ | (6) |
| $ \Delta {{f}_{\text{scf}}}=\frac{{{A}_{\text{sc}}}{{f}_{\text{scf}}}-{{A}_{\text{c}}}{{f}_{\text{c}}}-{{A}_{\text{sf}}}{{f}_{\text{s}}}}{{{A}_{\text{sc}}}}, $ | (7) |
| $ {{f}_{\text{sc}}}={{f}_{\text{scy}}}+\Delta {{f}_{\text{scf}}}, $ | (8) |
式中:θf为方钢管套箍系数;Cf、Bf为方钢管套箍效应影响系数;θy为圆钢管套箍系数;Cy、By为圆钢管套箍效应影响系数;fc为无约束混凝土棱柱体强度,本文取fc=0.76fcu, m.
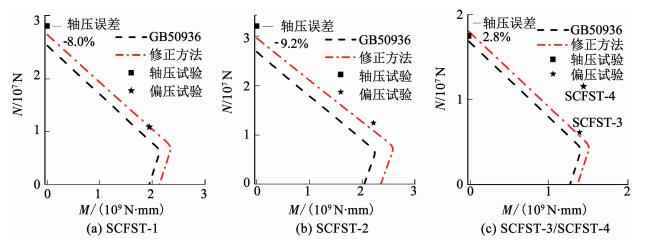
3.2.3 计算结果比较采用考虑多腔钢管提高混凝土约束效应修正的混凝土统一抗压强度,用GB 50936公式计算所得的N-M相关曲线,与不考虑附加混凝土约束效应计算所得的N-M相关曲线比较见图 14,4个试件偏压试验结果也示于图 14.本文考虑多腔钢管混凝土附加约束效应计算的N-M相关曲线与实测结果符合较好.笔者也进行了相同构造试件的轴压性能试验[20-21],将试验所得轴压承载力点示于图 14竖坐标轴上,采用本文修正后方法计算所得轴压承载力与实测符合较好,最大相对误差为9.2%.
|
图 14 修正方法计算N-M曲线 Fig. 14 N-M curves calculated by modified method |
试验表明巨型柱截面应变基本符合平截面假定,因此采用纤维模型法计算试件荷载-变形曲线.韩林海[22]给出了钢管混凝土纤维模型建模方法,并给出了方钢管混凝土本构关系及圆钢管混凝土本构关系,见式(9)、(10),纤维模型法的轴力及弯矩平衡方程见式(11),其中,σsi为各钢管微元的应力,hsi为各钢管微元到形心的距离,dAsi为各钢管微元的面积;σci为各混凝土微元的应力,hci为各混凝土微元到形心的距离,dAci为各混凝土微元的面积.在纤维模型法中,采用本文修正的混凝土本构关系计算F-Δ曲线.
上升段:
| $ \frac{\sigma }{{{\sigma }_{0}}}=2\frac{\varepsilon }{{{\varepsilon }_{0}}}-{{\left( \frac{\varepsilon }{{{\varepsilon }_{0}}} \right)}^{2}}, \left( \varepsilon /{{\varepsilon }_{0}}\le 1 \right). $ | (9) |
下降段:
| $ \left\{ \begin{align} & \frac{\sigma }{{{\sigma }_{0}}}=\frac{\varepsilon /{{\varepsilon }_{0}}}{\beta {{(\varepsilon /{{\varepsilon }_{0}}-1)}^{\eta }}+\varepsilon /{{\varepsilon }_{0}}},(\varepsilon /{{\varepsilon }_{0}}>1).矩(方)钢管 \\ & \frac{\sigma }{{{\sigma }_{0}}}=\frac{\varepsilon /{{\varepsilon }_{0}}}{\beta {{(\varepsilon /{{\varepsilon }_{0}}-1)}^{2}}+\varepsilon /{{\varepsilon }_{0}}},(\xi <1.12,\varepsilon /{{\varepsilon }_{0}}>1).圆钢管 \\ \end{align} \right. $ | (10) |
| $ \left\{ \begin{align} & N\left( {{e}_{0}}+\Delta \right)=\sum\limits_{1}^{n}{({{\sigma }_{si}}{{h}_{si}}\text{d}{{A}_{si}}+{{\sigma }_{ci}}{{h}_{ci}}\text{d}{{A}_{ci}});} \\ & N=\sum\limits_{1}^{n}{({{\sigma }_{si}}\text{d}{{A}_{si}}+{{\sigma }_{ci}}{{h}_{ci}}\text{d}{{A}_{ci}}).} \\ \end{align} \right. $ | (11) |
韩林海本构关系中,方钢管和圆钢管混凝土本构关系上升段公式形式相同,下降段曲线形式不同,见式(9)、(10).基于此,考虑本文多腔钢管混凝土统一抗压强度的计算方法,确定混凝土本构关系上升段强度;考虑塑性阶段混凝土性能退化加快,试件进入塑性阶段后,混凝土的本构关系除峰值点以外采用矩(方)形钢管混凝土本构关系曲线.
4.2 混凝土峰值应力混凝土峰值应力公式形式仍然采用韩林海建议公式.基于内外钢管叠加的思想:当方钢管单独作用时,混凝土峰值应力σf按照式(12)计算;当圆钢管单独作用时,混凝土峰值应力σy按式(13)计算;方钢管对混凝土峰值应力贡献的增量可按式(14)计算;综合考虑内部钢管和外部钢管作用的混凝土峰值应力σ0近似按式(15)计算.式中,ξf为方钢管单独作用时的约束效应系数, ξy为圆钢管单独作用时的约束效应系数, f′c为混凝土圆柱体强度.
| $ {{\sigma }_{\text{f}}}=[1+\left( -0.054\xi _{\text{f}}^{2}+0.4{{\xi }_{\text{f}}} \right){{\left( 24/f_{\text{c}}^{'} \right)}^{0.45}}]f_{\text{c}}^{'}, $ | (12) |
| $ {{\sigma }_{\text{y}}}=[1+\left( -0.0135\xi _{\text{y}}^{2}+0.1{{\xi }_{\text{y}}} \right){{\left( 24/f_{\text{c}}^{'} \right)}^{0.45}}]f_{\text{c}}^{'}, $ | (13) |
| $ \Delta \left( {{\sigma }_{\text{f}}} \right)={{\sigma }_{\text{f}}}-f_{\text{c}}^{'}, $ | (14) |
| $ {{\sigma }_{0}}={{\sigma }_{\text{y}}}+\Delta \left( {{\sigma }_{\text{f}}} \right). $ | (15) |
混凝土峰值应变公式形式仍然采用韩林海建议公式.基于内外钢管叠加的思想:对混凝土峰值应变ε0计算公式进行修正,见式(16),εcc为无约束混凝土峰值应变.
| $ {{\varepsilon }_{0}}\text{=}{{\varepsilon }_{\text{cc}}}+[1330+760\left( f_{\text{c}}^{'}/24-1 \right)]{{\left( {{\xi }_{\text{y}}}+{{\xi }_{\text{f}}} \right)}^{0.2}}. $ | (16) |
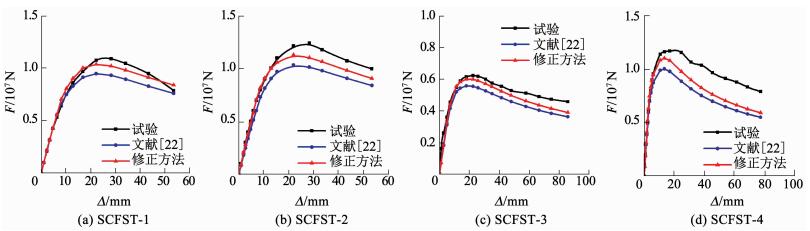
采用韩林海建议的本构关系计算所得“F-Δ”曲线、按照本文修正后的混凝土本构关系计算所得“F-Δ”曲线和实测“F-Δ”骨架曲线比较见图 15.由图 15可见:采用韩林海建议本构关系计算结果小于实测结果多些,更偏于安全;采用本文修正的混凝土本构关系计算结果也小于实测结果,符合程度好些.
|
图 15 修正方法计算F-Δ曲线 Fig. 15 F-Δ curves calculated by modified method |
将图 15相应的各试件计算所得极限承载力与实测极限承载力比较列于表 4.
| 表 4 实测与计算极限承载力比较 Tab. 4 Comparison of measured and calculated ultimate bearing capacity |
本文修正后的混凝土本构关系计算所得极限承载力最大相对误差为8.9%.综上,本文考虑多腔钢管特点,在标准GB 50936中N-M相关曲线计算方法及韩林海钢管混凝土本构关系基础上,提出的考虑混凝土约束效应提高的多腔钢管混凝土统一抗压强度fsc计算的简化修正方法与公式,计算所得试件的N-M相关曲线和承载力均与实测符合较好.
5 结论1) 试验研究表明:各多腔钢管混凝土巨型柱试件均具有良好的偏压受力性能;各试件在循环卸载过程中,混凝土受到钢管有效的围压作用时,其卸载刚度和再加载刚度较稳定,表明多腔钢管对内部混凝土有显著的约束作用;八边十三腔巨型柱角部腔内设置圆钢管后,试件承载力提高14.1%,试件损伤发展减缓,延性系数增大,变形能力增强,说明该类试件角部腔体设置圆钢管可有效提高试件的偏压受力性能;六边六腔巨型柱试件,偏心距较小的试件承载力高88.3%,偏心距较大的试件复位能力相对好;各试件截面应变基本符合平截面假定;各试件挠度曲线基本符合正弦半波曲线假定.
2) 基于多国规范及纤维模型法计算N-M相关曲线的方法(目前,钢管混凝土规范未涉及多腔钢管混凝土,没考虑钢筋笼及横隔板对混凝土的约束作用),考虑多腔钢管混凝土巨型柱对混凝土约束效应明显好于单腔钢管的特点,同时考虑钢筋笼及横隔板对混凝土的约束作用,提出考虑了混凝土约束效应提高的多腔钢管混凝土统一抗压强度fsc简化计算的修正方法,给出计算公式,计算所得试件的N-M相关曲线、偏压下试件的“F-Δ”曲线和承载力与实测符合较好,其中承载力误差在10%以内且偏于安全,可用于多腔钢管混凝土柱偏压简化计算.
| [1] |
赵立东, 曹万林, 阚文亮, 等. 不同构造复式钢管混凝土足尺柱抗震性能试验[J]. 哈尔滨工业大学学报, 2019, 51(12): 35. ZHAO Lidong, CAO Wanlin, KAN Wenliang, et al. Experimental study on the seismic behavior of large-scale double-skin concrete-filled steel tube columns with different constructions[J]. Journal of Harbin Institute of Technology, 2019, 51(12): 35. DOI:10.11918/j.issn.0367-6234.201811183 |
| [2] |
刘界鹏, 张素梅, 郭兰慧. 圆钢管约束高强混凝土短柱的轴压力学性能[J]. 哈尔滨工业大学学报, 2008, 40(4): 528. LIU Jiepeng, ZHANG Sumei, GUO Lanhui. Behavior of circular tube confined high strength concrete (HSC) short columns under axial compression[J]. Journal of Harbin Institute of Technology, 2008, 40(4): 528. DOI:10.3321/j.issn:0367-6234.2008.04.004 |
| [3] |
张素梅, 郭兰慧, 叶再利, 等. 方钢管高强混凝土轴压短柱的试验研究[J]. 哈尔滨工业大学学报, 2004, 36(12): 1610. ZHANG Sumei, GUO Lanhui, YE Zaili, et al. Experimental research on high strength concrete-filled SHS stub columns subjected to axial compressive load[J]. Journal of Harbin Institute of Technology, 2004, 36(12): 1610. DOI:10.3321/j.issn:0367-6234.2004.12.007 |
| [4] |
左志亮, 蔡健, 刘明峰, 等. 带约束拉杆T形钢管混凝土短柱偏压试验研究[J]. 建筑结构学报, 2011, 32(8): 79. ZUO Zhiliang, CAI Jian, LIU Mingfeng, et al. Experimental study of T-shaped CFT stub columns with binding bars subjected to eccentric load[J]. Journal of Building Structures, 2011, 32(8): 79. DOI:10.14006/j.jzjgxb.2011.08.010 |
| [5] |
蔡健, 左志亮, 赵小芹, 等. 带约束拉杆L形钢管混凝土短柱偏压试验研究[J]. 建筑结构学报, 2011, 32(2): 83. CAI Jian, ZUO Zhiliang, ZHAO Xiaoqin, et al. Experimental research on eccentrically loaded L-shaped concrete-filled steel tubular stub columns with binding bars[J]. Journal of Building Structures, 2011, 32(2): 83. DOI:10.14006/j.jzjgxb.2011.02.013 |
| [6] |
王丹, 吕西林. T形、L形钢管混凝土柱抗震性能试验研究[J]. 建筑结构学报, 2005, 26(4): 39. WANG Dan, LV Xilin. Experimental study on seismic behavior of concrete-filled steel T-section and L-section columns[J]. Journal of Building Structures, 2005, 26(4): 39. DOI:10.14006/j.jzjgxb.2005.04.006 |
| [7] |
杜国锋, 徐礼华, 徐浩然, 等. 组合T形截面钢管混凝土柱偏心受压试验研究[J]. 建筑结构学报, 2010, 31(7): 72. DU Guofeng, XU Lihua, XU Haoran, et al. Study on composite T-shaped concrete filled steel tubular columns under eccentric compression[J]. Journal of Building Structures, 2010, 31(7): 72. DOI:10.14006/j.jzjgxb.2010.07.009 |
| [8] |
徐礼华, 徐鹏, 侯玉杰, 等. 多边多腔钢管自密实高强混凝土短柱轴心受压性能试验研究[J]. 土木工程学报, 2017, 50(1): 37. XU Lihua, XU Peng, HOU Yujie, et al. Experimental study on axial compression behavior of short polygonal multi-cell and selfcompacting high-strength CFST columns[J]. China Civil Engineering Journal, 2017, 50(1): 37. DOI:10.15951/j.tmgcxb.2017.01.005 |
| [9] |
徐礼华, 宋杨, 刘素梅, 等. 多腔式多边形钢管混凝土柱偏心受压承载力研究[J]. 工程力学, 2019, 36(4): 135. XU Lihua, SONG Yang, LIU Sumei, et al. Study on the eccentric compressive bearing capacity of polygonal multi-cell concrete filled steel tubular columns[J]. Engineering Mechanics, 2019, 36(4): 135. DOI:10.6052/j.issn.1000-4750.2018.02.0090 |
| [10] |
LIU Xianggang, XU Chuangze, LIU Jiepeng, et al. Research on special-shaped concrete-filled steel tubular columns under axial compression[J]. Journal of Constructional Steel Research, 2018, 147: 203. DOI:10.1016/j.jcsr.2018.04.014 |
| [11] |
TU Y Q, SHEN Y F, LI P. Behaviour of multi-cell composite T-shaped concrete-filled steel tubular columns under axial compression[J]. Thin-Walled Structures, 2014, 85: 57. DOI:10.1016/j.tws.2014.08.003 |
| [12] |
乔崎云, 梁旭, 曹万林, 等. 多腔钢管混凝土分叉柱力学性能有限元分析[J]. 哈尔滨工业大学学报, 2017, 49(12): 75. QIAO Qiyun, LIANG Xu, CAO Wanlin, et al. FEM analysis on multi-cell CFST bifurcated columns[J]. Journal of Harbin Institute of Technology, 2017, 49(12): 75. DOI:10.11918/j.issn.0367-6234.201705141 |
| [13] |
王立长, 曹万林, 徐萌萌, 等. 五边形截面钢管混凝土巨型柱受压性能试验研究[J]. 建筑结构学报, 2014, 35(1): 77. WANG Lichang, CAO Wanlin, XU Mengmeng, et al. Experimental research on compression behavior of pentagonal cross-section CFST mega-columns[J]. Journal of Building Structures, 2014, 35(1): 77. DOI:10.14006/j.jzjgxb.2014.01.011 |
| [14] |
彭斌, 曹万林, 王智慧, 等. 不同方向水平力下多腔钢管混凝土巨型柱抗震性能研究[J]. 世界地震工程, 2012, 28(2): 90. PENG Bin, CAO Wanlin, WANG Zhihui, et al. Research on seismic behavior of multi-cell CFST mega-columns under horizontal forces in different directions[J]. World Earthquake Engineering, 2012, 28(2): 90. DOI:10.3969/j.issn.1007-6069.2012.02.015 |
| [15] |
YIN Fei, XUE Suduo, CAO Wanlin, et al. Experimental and analytical study of seismic behavior of special-shaped multicell composite concrete-filled steel tube columns[J]. Journal of Structural Engineering, 2020, 146(1): 04019170. DOI:10.1061/(ASCE)ST.1943-541X.0002442 |
| [16] |
曹万林, 武海鹏, 周建龙. 钢-混凝土组合巨型框架柱抗震研究进展[J]. 哈尔滨工业大学学报, 2019, 51(12): 6-7. CAO Wanlin, WU Haipeng, ZHOU Jianlong. Review on seismic technology progress of steel-concrete composite mega frame column[J]. Journal of Harbin Institute of Technology, 2019, 51(12): 6-7. DOI:10.11918/j.issn.0367-6234.201906155 |
| [17] |
钢管混凝土结构技术规范: GB 50936—2014[S].北京: 中国建筑工业出版社, 2014
|
| [18] |
American Institute of Steel Construction. Load and resistance factor design specification for structural steel buildings[S]. Chicago: American Institute of Steel Construction, 1999
|
| [19] |
European Committee for Standardization. Eurocode 4: Design of composite steel and concrete structures—Part 1-1. General rules and rules for buildings: EN1994-1-1[S]. Brussels: European Committee for Standardization, 2004
|
| [20] |
王智慧.多腔体钢管混凝土巨型柱及巨型框架工作性能试验研究[D].北京: 北京工业大学, 2012 http://cdmd.cnki.com.cn/Article/CDMD-10005-1012037151.htm
|
| [21] |
殷飞, 薛素铎, 曹万林, 等. 异形多腔钢管混凝土柱往复轴压性能试验[J]. 哈尔滨工业大学学报, 2019, 51(12): 94. YIN Fei, XUE Suduo, CAO Wanlin, et al. Hysteretic behavior of special-shaped multi-cell concrete-filled steel tube under axial compression[J]. Journal of Harbin Institute of Technology, 2019, 51(12): 94. DOI:10.11918/j.issn.0367-6234.201902094 |
| [22] |
韩林海. 钢管混凝土结构-理论与实践[M]. 第2版. 北京: 科学出版社, 2007: 72-86.
|
 2020, Vol. 52
2020, Vol. 52


