临近空间高超声速目标因具有飞行空域广、机动能力强和全球到达的特性,已成为国防安全的新型威胁.此类目标多采用乘波体、升力体、翼面融合体等气动构型,具有极强的机动能力,航迹设计具有较大的自由度,可进行多种类型的规避和突防策略穿越已知防区,甚至可通过大范围的侧向机动更换拟攻击目标,给航迹估计带来了新的挑战.
近年来,机动目标的航迹估计问题得到了广泛而深入的研究.研究者们根据不同的目标运动特性,设计相应的机动模型,并提出了各类估计方法[1-4].文献[1]给出了估计中常用的模型,包括恒速(constant velocity, CV)模型、恒加速度(constant acceleration, CA)模型、恒转弯速率(constant turn rate, CTR)模型、非对称法相加速度模型、Singer模型、当前统计模型等.当目标的动力学模型为线性且量测噪声为零均值高斯噪声时,卡尔曼滤波(Kalman filter, KF)可获得最优的航迹估计.但是在实际估计问题中,目标的动力学和机动模型往往是非线性的,因此研究者们提出了一系列基于非线性滤波的估计方法[3].针对机动目标航迹估计问题,文献[5]提出了一种基于改进Sage-Husa自适应卡尔曼滤波的机动目标跟踪方法,通过设计判断准则调整自适应滤波参数,抑制了目标跟踪误差的积累,提高了稳态滤波精度.文献[6]结合Singer机动模型与模糊推理,提出了一种多参数融合的Singer模型并将其用于目标机动估计,取得了较高的估计精度.文献[7]提出了一种带有加速度预测的非线性估计算法,通过最小二乘估计器对滑动窗口内目标机动的检测,以一定的策略调整目标机动方差的先验信息,提升了机动估计的精度.文献[8]提出了一种变速率粒子滤波算法,可递归的更新状态序列的后验分布,从而解决了变维状态推断问题,可用于机动模型不确定的目标跟踪问题.文献[9]将成本回溯自适应输入和状态估计(retrospective-cost-based adaptive input and state estimation, RCAISE)用于机动目标的跟踪,可通过优化回溯性能使得估计的机动加速度逼近目标真实的加速度.针对强机动目标跟踪时的滤波增益滞后和过程噪声不精确的问题,文献[10]提出了一种改进的自适应无迹卡尔曼滤波方法,通过在每步估计中加入自适应的比例因子更新过程噪声协方差阵提升了估计精度和动态性能.针对机动目标跟踪时的模型失配问题,文献[11]提出了一种自适应高阶无迹卡尔曼滤波方法,通过引入一种由预测残差估计协方差矩阵求取最优自适应因子减小了动态模型误差对估计的影响.这些方法均基于卡尔曼滤波或粒子滤波框架提出,使用单一的模型对目标航迹进行估计,并通过UT变换、自适应等技术应对机动模型的不确定性.对于临近空间高超声速目标的航迹估计问题,单一机动模型难以准确描述目标复杂的机动.在应用这些方法时,目标机动将带来大范围的模型不确定性,常见自适应机制难以应对,进而导致估计精度下降.但是,目标航迹是“设计-优化-控制”的结果,统计意义上存在一定的规律,可通过引入循环神经网络(recurrent neural networks, RNNs)对目标机动机动特性进行识别.
循环神经网络在20世纪80年代由Lipton等[12]提出.近年来在语音识别、文本生成、机器翻译等序列数据的处理领域得到了广泛的应用[13].目前,循环神经网络与非线性滤波的联合使用方面已有一些研究成果,提出了一系列循环神经网络与扩展卡尔曼滤波(extended Kalman filter, EKF)、无迹卡尔曼滤波(unscented Kalman filter, UKF)、粒子滤波(particle filter, PF)等结合的估计方法[14-16].文献[14]考虑视频有损压缩-解码中的伪影抑制问题,设计了一种深度卡尔曼滤波器,该方法使用两个卷积神经网络替代了卡尔曼滤波的状态和误差协方差阵预测步骤,提升了视频解码的质量.文献[15]提出了一种基于KF和循环神经网络的人体姿势估计算法,通过使用KF融合两个循环神经网络的跟踪结果,提升了跟踪的位置和速度精度.文献[16]提出了一种用于人体姿势估计的KF-LSTM网络结构,该方法将3个长短时记忆(long short-term memory, LSTM)网络嵌入KF中并通过训练学习运动和噪声模型,实现了优于现有结果的姿势估计精度.考虑机器人的视觉定位问题,文献[17]通过将系统模型和粒子滤波算法嵌入神经网络提出了PF-net网络结构,该方法由序列数据端对端的学习和优化粒子滤波中使用的模型.文献[18]考虑噪声条件下的手势识别问题,通过将UKF嵌入LSTM网络设计了NIUKF-LSTM网络,可有效抑制量测噪声提升识别精度.这些研究中所涉及的动力学模型均较为简单,滤波方法中的模型部分往往被循环神经网络完全的替代并通过训练学习.但是,临近空间高超声速目标的动力学模型存在较为复杂的非线性特性,难以直接通过训练学习.因此,需寻求新的RNN-EKF结合方式.
本文考虑临近空间高超声速目标的航迹估计问题,提出基于可学习扩展卡尔曼滤波(Learnable EKF, L-EKF)的航迹估计方法.通过将循环神经网络与扩展卡尔曼滤波方法深度嵌合,识别目标复杂的机动特征,提升滤波方法对复杂目标机动的应对能力,实现高精度的航迹估计.
1 临近空间高超声速目标机动特性分析与描述临近空间高超声速目标可在临近空间高度长时间滑翔飞行,具有非惯性的航迹形式和复杂的策略性机动,常见的CA、CV、Singer模型难以准确描述其机动特征.因此,本文对其机动特性进行分析和描述:首先,给出临近空间高超声速目标的动力学模型;然后,分析其机动特性,建立参数化的航迹估计模型,进而给出航迹估计问题的数学描述.
1.1 动力学模型忽略地球自转,高超声速目标的动力学模型可表示为[19]:
| $ {\dot r = v {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma , } $ | (1) |
| $ {\dot \theta = \frac{{v {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi }}{{r {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}, } $ | (2) |
| $ {\dot \varphi = \frac{{v {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi }}{r}, } $ | (3) |
| $ {\dot v = - \frac{{\rho {v^2}{S_{{\rm{ref}}}}{C_{\rm{D}}}}}{{2m}} - g {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma , } $ | (4) |
| $ {\dot \gamma = \frac{{\rho v{S_{{\rm{ref}}}}{C_{\rm{L}}} {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma }}{{2m}} + \left( {\frac{v}{r} - \frac{g}{v}} \right) {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma , } $ | (5) |
| $ {\dot \psi = \frac{{\rho v{S_{{\rm{ref}}}}{C_{\rm{L}}} {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma }}{{2m {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma }} - \frac{v}{r} {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi {\rm{tan}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi .} $ | (6) |
式中:r为目标到地心的距离;θ为经度;φ为纬度;v为速度;γ为航迹倾角; ψ为航迹偏角; σ为倾侧角;m为目标质量; Sref为参考面积; g为重力加速度;ρ=ρ0e-βh为大气密度; h=r-Re为目标高度,Re=6 378 135 m为地球半径; ρ0为海平面处大气密度; β为大气密度系数; CL、CD分别为升力、阻力系数.
由于本文所考虑的目标是非合作的,其精确的升力和阻力系数在实际的航迹估计中难以获得,因此使用马赫数无关模型[20]描述其升力和阻力,表示如下:
| $ {C_{\rm{D}}} = {C_{{\rm{D0}}}} + KC_{\rm{L}}^2, $ |
式中CD0、K分别为马赫数无关的气动参数.
目标的升阻比定义为
| $ E = \frac{{{C_{\rm{L}}}}}{{{C_{\rm{D}}}}} = \frac{{{C_{\rm{L}}}}}{{{C_{{\rm{D0}}}} + KC_{\rm{L}}^2}}. $ | (7) |
对式(7)求关于时间的导数,可得升阻比E的最大值,以及此时的CL、CD,记作E*, CD*, CL*分别为:
| $ \begin{array}{*{20}{c}} {C_{\rm{L}}^* = \sqrt {\frac{{{C_{{\rm{D0}}}}}}{K}} , }\\ {C_{\rm{D}}^* = 2{C_{{\rm{D0}}}}, }\\ {{E^*} = \frac{{C_{\rm{L}}^*}}{{C_{\rm{D}}^*}} = \frac{1}{{2\sqrt {{C_{{\rm{D0}}}}K} }}.} \end{array} $ |
归一化升力系数定义为
| $ {c_l} = \frac{{{C_{\rm{L}}}}}{{C_{\rm{L}}^*}}, $ |
则目标的升力系数CL和阻力系数CD可表示为:
| $ {{C_{\rm{L}}} = {c_l}C_{\rm{L}}^*, } $ | (8) |
| $ {{C_{\rm{D}}} = \frac{{c_l^2 + 1}}{2}C_{\rm{D}}^*.} $ | (9) |
联立式(1)~(6), 式(8)、(9)可得高超声速目标的动力学模型:
| $ \left\{ \begin{array}{l} \dot r = v {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma , \\ \dot \theta = \frac{{v {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi }}{{r {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}, \\ \dot \varphi = \frac{{v {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi }}{r}, \\ \dot v = - \frac{{\rho {v^2}{S_{{\rm{ref}}}}C_{\rm{D}}^ * \left( {c_l^2 - 1} \right)}}{{2m}} - {g_0} {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma , \\ \dot \gamma = \frac{{\rho v{S_{{\rm{ref}}}}C_{\rm{L}}^ * {c_l} {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma }}{{2m}} + \left( {\frac{v}{r} - \frac{{{g_0}}}{v}} \right) {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma , \\ \dot \psi = \frac{{\rho v{S_{{\rm{ref}}}}C_{\rm{L}}^ * {c_l} {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma }}{{2m {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma }} - \frac{v}{r} {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi {\rm{tan}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi . \end{array} \right.. $ | (10) |
在航迹估计过程中,归一化升力系数cl和倾侧角σ往往难以直接获得.同时,由于目标具有复杂且不确定的机动形式,cl和σ存在复杂时变特性,难以被直接识别.换而言之,动力学模型(10)无法在航迹估计中直接使用.因此,本文针对目标的机动特性机型分析,选择可识别的参数替代cl和σ,建立参数化的目标机动模型.
由现有的高超声速目标航迹规划文献可知,为满足热流、动压和过载约束,目标常常做准平衡滑翔(quasi-equilibrium gilding, QEG),即在飞行全程保持航迹倾角变化率ṙ≤0,使得目标航迹倾角γ和飞行高度h单调非增,从而抑制飞行过程中的跳跃现象.在实际的航迹设计中,为保持目标的高度以延长航程, 通常令航迹倾角变化率为0,即有
| $ \dot \gamma = 0. $ | (11) |
将式(8)、式(11)代入式(5)可得:
| $ \frac{{\rho v{S_{{\rm{ref}}}}C_{\rm{L}}^ * {c_l} {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma }}{{2m}} + \left( {\frac{v}{r} - \frac{g}{v}} \right) {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma = 0. $ | (12) |
考虑在目标实际飞行过程中航迹倾角γ为小量,即有cos γ≈1, sin γ≈γ.同时,由于目标高度h相对于地球半径Re为小量,在分析
| $ h = \frac{1}{\beta } {\rm{ln }}\frac{{{\rho _0}{v^2}{R_{\rm{e}}}{S_{{\rm{ref}}}}C_{\rm{L}}^ * }}{{2m({g_0}{R_{\rm{e}}} - {v^2})}} + \frac{1}{\beta } {\rm{ln}} {c_l} {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma . $ | (13) |
由式(13)可知, 准平衡滑翔目标h-v之间的关系由clcos σ决定.因此,选择clcos σ作为目标航迹的第1个特征参数,记作:
| $ {\lambda _1} = {c_l} {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma . $ | (14) |
对式(12)求关于时间的导数,可得
| $ \gamma = - \frac{{{g_0}}}{{\beta {E^*}{v^2}}} \cdot \frac{{c_l^2 + 1}}{{{c_l} {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma }}. $ | (15) |
将式(15)代入式(1),可得
| $ \dot h = - \frac{{{g_0}}}{{\beta {E^*}v}} \cdot \frac{{c_l^2 + 1}}{{{c_l} {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma }}. $ | (16) |
由式(16)可知,目标ḣ-v之间的关系由
| $ {\lambda _2} = \frac{{c_l^2 + 1}}{{{c_l} {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma }}. $ | (17) |
由于参数λ1, λ2仅与cos(σ)有关,无法表征目标侧向机动的方向,本文将倾侧角σ的符号选为目标航迹的第3个特征参数,即有
| $ {\lambda _3} = {\rm{sgn}} (\sigma ) = \left\{ {\begin{array}{*{20}{l}} {1, \sigma > 0;}\\ {0, \sigma = 0;}\\ { - 1, \sigma < 0.} \end{array}} \right. $ | (18) |
目标飞行过程中,其机动方向往往变化缓慢.为保证模型连续并描述其变化特性,将λ3近似为tanh函数,并使用一阶马尔科夫模型表述,即有:
| $ {{\lambda _3} \approx {\rm{tanh}} ({k_\chi }\chi ), } $ | (19) |
| $ {\dot \chi = - \frac{1}{{{T_\chi }}}\chi .} $ | (20) |
式中:kχ为侧向机动方向模型的增益系数,可将其设为一个很大的正数; Tχ为侧向机动方向模型的时间常数.
综合式(10)、(14)、(17)~(20)可得参数化的目标机动模型:
| $ \left\{ \begin{array}{l} \dot r = v {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma , \\ \dot \theta = \frac{{v {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi }}{{r {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}, \\ \dot \varphi = \frac{{v {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi }}{r}, \\ \dot v = - \frac{{\rho {v^2}C_{\rm{D}}^ * {\lambda _1}{\lambda _2}}}{{4m}} - g {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma , \\ \dot \gamma = \frac{{\rho vC_{\rm{L}}^ * {\lambda _2}}}{{2m}} + \left( {\frac{v}{r} - \frac{g}{v}} \right) {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma , \\ \dot \psi = \frac{{\rho vC_{\rm{L}}^ * {\rm{tanh}} ({k_\chi }\chi )\sqrt {{\lambda _1}{\lambda _2} - \lambda _2^2 - 1} }}{{2m {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma }} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{v}{r} {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi {\rm{tan}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi , \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \dot \chi = - \frac{1}{{{T_\chi }}}\chi . \end{array} \right.. $ | (21) |
由式(21)可知,通过参数λ1, λ2和参数λ3的时间常数Tχ即可描述目标的机动特性.这3个参数与目标的高度、速度、机动周期等特性具有较强的关联性,易于使用循环神经网络根据目标量测信息直接识别.
下面,给出航迹估计问题的标准形式.由于目标只有位置信息可被直接测量,因此选择状态为x=[r, θ, φ, v, γ, ψ, χ]T,量测为目标位置z=[r, θ, φ]T,输入为需识别的3个特征参数u=[λ1, λ2, Tχ]T,目标的航迹估计的标准形式为
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot x}} = f(\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{u}}) + \mathit{\boldsymbol{\omega , }}}\\ {\mathit{\boldsymbol{z}} = \mathit{\boldsymbol{Hx}} + \mathit{\boldsymbol{\nu , }}} \end{array}} \right. $ | (22) |
其中,ω为过程噪声,ν为量测噪声,f(x, u)为式(21)所示模型,
实现临近空间高超声速目标航迹估计的关键在于处理非惯性的航迹形式和复杂的策略性机动.临近空间高超声速目标机动特性分析与描述中,本文已经建立了可描述目标航迹特性的参数化机动模型(22),在航迹估计中需对这些特征参数进行识别.此外,受临近空间复杂气动环境的影响,目标很多的高阶动力学特性无法被模型描述,在航迹估计中也需对这些未建模的动力学特性进行处理.因此,本文考虑临近空间高超声速目标的航迹估计问题,提出可学习扩展卡尔曼滤波(Learnable extended Kalman filter, L-EKF)方法.首先,分析扩展卡尔曼滤波(EKF)方法在应对大范围模型和参数不确定性时存在的问题;然后,分别设计输入修饰网络(input modification network, IMN)和增益修饰网络(gain modification network, GMN), 并将其嵌入EKF中,用以识别和补偿估计中存在的各类不确定性;最后,给出完整的可学习扩展卡尔曼滤波算法.
2.1 扩展卡尔曼滤波考虑如下离散非线性系统:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{x}}_k} = f({\mathit{\boldsymbol{x}}_{k - 1}}, {\mathit{\boldsymbol{u}}_k}) + {\mathit{\boldsymbol{w}}_k}, }\\ {{\mathit{\boldsymbol{z}}_k} = h({\mathit{\boldsymbol{x}}_k}) + {\mathit{\boldsymbol{\nu }}_k}.} \end{array}} \right. $ |
式中:xk为状态; zk为量测; uk为输入; wk、vk分别为过程噪声和量测噪声,均为零均值的高斯噪声.

|
图 1 扩展卡尔曼滤波 Fig. 1 Diagram of EKF |
Step 1 预测状态和误差协方差阵:
| $ {{\mathit{\boldsymbol{\hat x}}}_{k|k - 1}} = f({{\mathit{\boldsymbol{\hat x}}}_{k - 1|k - 1}}, {\mathit{\boldsymbol{u}}_k}), $ | (23) |
| $ {\mathit{\boldsymbol{P}}_{k|k - 1}} = {\mathit{\boldsymbol{F}}_k}{\mathit{\boldsymbol{P}}_{k - 1|k - 1}}\mathit{\boldsymbol{F}}_k^{\rm{T}} + {\mathit{\boldsymbol{Q}}_k}. $ | (24) |
式中:
Step 2 计算次优卡尔曼增益:
| $ {{{\mathit{\boldsymbol{\tilde y}}}_k} = {\mathit{\boldsymbol{z}}_k} - h({{\mathit{\boldsymbol{\hat x}}}_{k|k - 1}}), } $ | (25) |
| $ {{\mathit{\boldsymbol{S}}_k} = {\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{P}}_{k|k - 1}}\mathit{\boldsymbol{H}}_k^{\rm{T}} + {\mathit{\boldsymbol{R}}_k}, } $ | (26) |
| $ {{\mathit{\boldsymbol{K}}_k} = {\mathit{\boldsymbol{P}}_{k|k - 1}}\mathit{\boldsymbol{H}}_k^{\rm{T}}\mathit{\boldsymbol{S}}_k^{ - 1}.} $ | (27) |
式中:zk为当前量测;
Step 3 更新状态和误差协方差矩阵:
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat x}}}_{k|k}} = {{\mathit{\boldsymbol{\hat x}}}_{k|k - 1}} + {\mathit{\boldsymbol{K}}_k}{{\mathit{\boldsymbol{\tilde y}}}_k}, }\\ {{\mathit{\boldsymbol{P}}_{k|k}} = (\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_k}{\mathit{\boldsymbol{H}}_k}){\mathit{\boldsymbol{P}}_{k|k - 1}}.} \end{array} $ |
在实际的航迹估计中,通常情况下EKF不是最优的估计器,其原因主要来源于模型的不确定性和线性化误差,具体体现在以下3个方面:
1) 模型的未建模不确定性.在实际的航迹估计中,目标很多的高价动力学特性无法被精确建模,即估计模型存在未建模不确定性.此类不确定性带来的过程噪声通常是非高斯的,难以被过程噪声协方差阵Qk精确的描述.
2) 模型的输入不确定性.如式(22)所述,在进行航迹估计时模型需要参数输入uk.由于所考虑的目标是非合作的,实际航迹估计中,这些参数难以被精确获得,即uk存在不确定性.
3) 模型的线性化误差.在EKF中,每一步估计均需对模型进行工作点处线性化,由此引入了模型线性化误差.
这些不确定性和误差在EKF框架下无法被准确的描述和处理,将影响航迹估计的性能.但从更为广义的角度,它们也是目标特性的一部分,对于某类具体目标而言存在一定的统计特性,可使用已有数据训练循环神经网络进行识别和补偿.因此,本文设计两个循环神经网络并将其嵌入EKF中:一个为输入修饰网络,用于应对模型的输入不确定性;另一个为增益修饰网络,用于应对模型的未建模不确定性和线性化误差.
2.2 输入修饰网络输入修饰网络(IMN)用于识别模型的特征参数并补偿由不精确输入造成的估计误差.如式(22)所示,模型的输入uk包含3个需识别的特征参数.由于这些参数与h, θ, φ, v和ḣ相关,因此选择量测zk和上一步状态估计
| $ ({\mathit{\boldsymbol{\kappa }}_k}, {{\mathit{\boldsymbol{\tilde u}}}_k}) = {\rm{RN}}{{\rm{N}}_{{\rm{im}}}}({\mathit{\boldsymbol{\kappa }}_{k - 1}}, {{\mathit{\boldsymbol{\hat x}}}_{k - 11k - 1}}, {\mathit{\boldsymbol{u}}_k}, {\mathit{\boldsymbol{z}}_k}), $ |
式中Kk为IMN的隐状态.
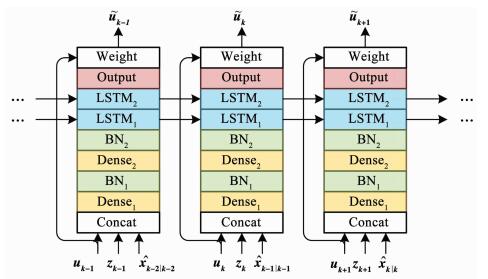
为了应对目标的周期性机动,IMN需要长时记忆能力.因此,本文将IMN设计为带有批规范化的LSTM编码网络结构.如图 2所示,网络由2个全连接层(Dense),2个LSTM[22]层,1个输出层(Output)和1个加权层(Weight)串联而成,并在每个全连接层后加入批规范化(batch normalization, BN)[23]层.全连接层用于在维度上丰富输入的特征信息,记作:
|
图 2 输入修饰网络 Fig. 2 Input modification network |
| $ {\mathit{\boldsymbol{\delta }}_{k, i}} = {\rm{Dense}}{ _i}({\mathit{\boldsymbol{\mu }}_{k, i}}) = {\rm{tanh}} (\mathit{\boldsymbol{\omega }}, {\mathit{\boldsymbol{\mu }}_{k, i}} + {\mathit{\boldsymbol{b}}_i}). $ |
式中:Densei为第i个全连接层;μk, i为Densei层的输入;δk, i为Densei层的隐状态,也是输出;ωi、bi分别为Densei层的可训练参数.
LSTM层用于在时间线上对特征信息进行“编码”, 以表征各时刻输入时间上的相关性,记作:
| $ \begin{array}{*{20}{l}} {[{\mathit{\boldsymbol{\delta }}_{k, i, {\rm{LSTM}}}}, {\mathit{\boldsymbol{C}}_{k, i, {\rm{LSTM}}}}] = }\\ {{\rm{LST}}{{\rm{M}}_i}({\mathit{\boldsymbol{\delta }}_{k - 1, i, {\rm{LSTM}}}}, {\mathit{\boldsymbol{C}}_{k - 1, i, {\rm{LSTM}}}}, {\mathit{\boldsymbol{\mu }}_{k, i, {\rm{LSTM}}}}).} \end{array} $ |
式中:LSTMi为第i个LSTM层;μk, i, LSTM为LSTMi的输入;δk, i, LSTM为LSTMi的隐状态,也是输出;Ck, i, LSTM为LSTMi的胞状态(cell states).
批规范化层则用于抑制过拟合,提升网络的泛化能力,其数学表述为
| $ {\mathit{\boldsymbol{\mu }}_{{\rm{bn}}}} = {\rm{BN}}(\mu ) = {\mathit{\boldsymbol{\omega }}_{{\rm{bn}}}}\frac{{\mathit{\boldsymbol{\mu }} - \mathit{\boldsymbol{\tilde \mu }}}}{{\sqrt {\mathit{\boldsymbol{\sigma }}_\mu ^2 + \mathit{\boldsymbol{\epsilon}}} }} + {\mathit{\boldsymbol{b}}_{{\rm{bn}}}}. $ |
式中:μ为批规范化层的输入;
输出层用于解算uk的加权系数,需根据模型输入uk的特性设计其值域.综上所述由模型(22)可知u=[λ1, λ2, Tχ]T,这3个参数均为正数且变化幅度不大,因此输出层使用带有偏置的tanh激活函数,表示为
| $ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{\kappa }}_{i, k}} = {\rm{Output}}{{\rm{ }}_{{\rm{imn}}}}({\mathit{\boldsymbol{\mu }}_k}) = }\\ { {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{tanh}} (\mathit{\boldsymbol{w}}_{\rm{o}}^{{\rm{imn}}}{\mathit{\boldsymbol{\mu }}_k} + \mathit{\boldsymbol{b}}_{\rm{o}}^{{\rm{imn}}}) + 1.} \end{array} $ |
加权层用于根据之前解算的加权系数计算修饰后的模型输入,使用乘性加权方式,设计为
| $ {{\mathit{\boldsymbol{\tilde u}}}_k} = {\mathit{\boldsymbol{\kappa }}_{i, k}} * {\mathit{\boldsymbol{u}}_k}, $ |
式中*为按元素乘法.
综上所述,输入修饰网络的数学表达如下:
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{\delta }}_{k, 1}} = {\rm{Dense}}{ _1}([{{\mathit{\boldsymbol{\hat x}}}_{k - 11k - 1}};{\mathit{\boldsymbol{u}}_k}]), }\\ {{{\mathit{\boldsymbol{\bar \delta }}}_{k, 1}} = {\rm{BN}}{ _1}({\mathit{\boldsymbol{\delta }}_{k, 1}}), }\\ {{\mathit{\boldsymbol{\delta }}_{k, 2}} = {\rm{Dense}}{ _2}({{\mathit{\boldsymbol{\bar \delta }}}_{k, 1}}), } \end{array}\\ {{\mathit{\boldsymbol{\bar \delta }}}_{k, 2}} = {\rm{B}}{{\rm{N}}_2}({\mathit{\boldsymbol{\delta }}_{k, 2}}), \\ \begin{array}{*{20}{l}} {[{\mathit{\boldsymbol{\delta }}_{k, 1, {\rm{LSTM}}}}, {\mathit{\boldsymbol{C}}_{k, 1, {\rm{LSTM}}}}] = {\rm{LST}}{{\rm{M}}_1}({\mathit{\boldsymbol{\delta }}_{k - 1, 1, {\rm{LSTM}}}}, {\mathit{\boldsymbol{C}}_{k - 1, 1, {\rm{LSTM}}}}, {{\mathit{\boldsymbol{\bar \delta }}}_{k, 2}}), }\\ {[{\mathit{\boldsymbol{\delta }}_{k, 2, {\rm{LSTM}}}}, {\mathit{\boldsymbol{C}}_{k, 2, {\rm{LSTM}}}}] = } \end{array}\\ \begin{array}{*{20}{l}} {{\rm{LST}}{{\rm{M}}_2}({\mathit{\boldsymbol{\delta }}_{k - 1, 2, {\rm{LSTM}}}}, {\mathit{\boldsymbol{C}}_{k - 1, 2, {\rm{LSTM}}}}, {\mathit{\boldsymbol{\delta }}_{k, 1, {\rm{LSTM}}}}), }\\ {{\mathit{\boldsymbol{\kappa }}_{i, k}} = {\rm{Output}}{{\rm{ }}_{{\rm{imn}}}}({\mathit{\boldsymbol{\delta }}_{k, {\rm{LSTM}}2}}), }\\ {{{\mathit{\boldsymbol{\tilde u}}}_k} = {\mathit{\boldsymbol{\kappa }}_{i, k}} * {\mathit{\boldsymbol{u}}_k}.} \end{array} \end{array} \right. $ |
增益修饰网络(GMN)用于识别和补偿模型的未建模不确定性和线性化误差造成的估计误差.如式(24)~(27)所示,这些误差产生于误差协方差矩阵Pk|k-1和次优卡尔曼增益Kk的计算过程中,并最终归结于次优卡尔曼增益Kk,所以本文直接对次优卡尔曼增益Kk进行修饰.因此,本文选择修饰后的模型输入ũk,上一步的状态估计
| $ ({\mathit{\boldsymbol{G}}_k}, {\mathit{\boldsymbol{K}}_k}) = {\rm{RN}}{{\rm{N}}_{{\rm{gm}}}}({\mathit{\boldsymbol{G}}_{k - 1}}, {\mathit{\boldsymbol{K}}_k}, {{\mathit{\boldsymbol{\hat x}}}_{k - 1|k - 1}}, {\mathit{\boldsymbol{P}}_{k - 1|k - 1}}, {{\mathit{\boldsymbol{\tilde u}}}_k}), $ |
式中Gk为GMN的隐状态.
类似于IMN,本文将GMN设计为带有批规范化的LSTM编码网络结构.如图 3所示,网络由2个全连接层(Dense),2个LSTM层,1个输出层(Output)和1个加权层(Weight)串联而成,并在每个全连接层后加入批规范化层(BN).全连接层用于在维度上丰富输入的特征信息;LSTM层用于在时间线上对特征信息进行“编码”,以表征每一时刻特征间的时间相关性;批规范化层用于应对过拟合,提升网络的泛化能力.

|
图 3 增益修饰网络 Fig. 3 Gain modification network |
输出层用于解算次优卡尔曼增益的加权系数,由于模型(22)中各状态量级差距较大,为保证加权系数具有足够的权重,使用指数函数作为输出层的激活函数,则有
| $ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{\kappa }}_{{\rm{g}}, k}} = {\rm{ Output}}{{\rm{ }}_{{\rm{gmn}}}}({\mathit{\boldsymbol{\mu }}_k}) = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{exp}} (\mathit{\boldsymbol{w}}_o^{{\rm{gmn}}}{\mathit{\boldsymbol{\mu }}_k} + \mathit{\boldsymbol{b}}_o^{{\rm{gmn}}}).} \end{array} $ |
式中:μk为GMN前序LSTM层的输出; κg, k为Kk的加权系数; w0gmn, b0gmn分别为输出层的可训练参数.
加权层用于根据之前解算的加权系数计算修饰后的次优卡尔曼增益,使用乘性加权方式,设计为
| $ {{\mathit{\boldsymbol{\tilde K}}}_k} = {\mathit{\boldsymbol{\kappa }}_{{\rm{g}}, k}} * {\mathit{\boldsymbol{K}}_k} $ |
综上所述,增益修饰网络的数学表达如下:
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{\delta }}_{k, 1}} = {\rm{Dense}}{ _1}([{{\mathit{\boldsymbol{\hat x}}}_{k - 11k - 1}};{\mathit{\boldsymbol{P}}_{k - 11k - 1}};{{\mathit{\boldsymbol{\tilde u}}}_k}]), }\\ {{{\mathit{\boldsymbol{\bar \delta }}}_{k, 1}} = {\rm{BN}}{ _1}({\mathit{\boldsymbol{\delta }}_{k, 1}}), }\\ {{\mathit{\boldsymbol{\delta }}_{k, 2}} = {\rm{Dense}}{ _2}({{\mathit{\boldsymbol{\bar \delta }}}_{k, 1}}), } \end{array}\\ {{\mathit{\boldsymbol{\bar \delta }}}_{k, 2}} = {\rm{B}}{{\rm{N}}_2}({\mathit{\boldsymbol{\delta }}_{k, 2}}), \\ \begin{array}{*{20}{l}} \begin{array}{l} [{\mathit{\boldsymbol{\delta }}_{k, 1, {\rm{LSTM}}}}, {\mathit{\boldsymbol{C}}_{k, 1, {\rm{LSTM}}}}] = \\ {\rm{LST}}{{\rm{M}}_1}({\mathit{\boldsymbol{\delta }}_{k - 1, 1, {\rm{LSTM}}}}, {\mathit{\boldsymbol{C}}_{k - 1, 1, {\rm{LSTM}}}}, {{\mathit{\boldsymbol{\bar \delta }}}_{k, 2}}), \end{array}\\ {[{\mathit{\boldsymbol{\delta }}_{k, 2, {\rm{LSTM}}}}, {\mathit{\boldsymbol{C}}_{k, 2, {\rm{LSTM}}}}] = } \end{array}\\ \begin{array}{*{20}{l}} {{\rm{LST}}{{\rm{M}}_2}({\mathit{\boldsymbol{\delta }}_{k - 1, 2, {\rm{LSTM}}}}, {\mathit{\boldsymbol{C}}_{k - 1, 2, {\rm{LSTM}}}}, {\mathit{\boldsymbol{\delta }}_{k, 1, {\rm{LSTM}}}}), }\\ {{\mathit{\boldsymbol{\kappa }}_{i, k}} = {\rm{Output}}{{\rm{ }}_{{\rm{imn}}}}({\mathit{\boldsymbol{\delta }}_{k, {\rm{LSTM}}2}}), }\\ {{{\mathit{\boldsymbol{\tilde K}}}_k} = {\mathit{\boldsymbol{\kappa }}_{{\rm{g}}, k}} * {\mathit{\boldsymbol{K}}_k}.} \end{array} \end{array} \right. $ |
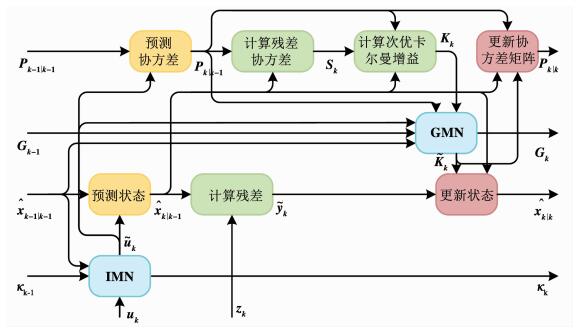
下面给出可学习扩展卡尔曼滤波(L-EKF)算法,如图 4所示,本文在EKF的状态和误差协方差预测之前嵌入了IMN,在EKF的状态和误差协方差更新之前嵌入了GMN.由于L-EKF对过程和量测噪声协方差阵Qk和Rk不敏感,本文在算法设计中用定常的噪声协方差阵Q, R代替了Qk, Rk,以简化参数设计.完整的L-EKF算法如下.
|
图 4 可学习扩展卡尔曼滤波 Fig. 4 Diagram of L-EKF |
Step 1 输入修饰:
| $ ({\mathit{\boldsymbol{\kappa }}_k}, {{\mathit{\boldsymbol{\tilde u}}}_k}) = {\rm{RN}}{{\rm{N}}_{{\rm{im}}}}({\mathit{\boldsymbol{\kappa }}_{k - 1}}, {{\mathit{\boldsymbol{\hat x}}}_{k - 1|k - 1}}, {\mathit{\boldsymbol{u}}_k}, {\mathit{\boldsymbol{z}}_k}). $ |
Step 2 预测状态和误差协方差阵:
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat x}}}_{k|k - 1}} = f({{\mathit{\boldsymbol{\hat x}}}_{k - 1|k - 1}}, {{\mathit{\boldsymbol{\tilde u}}}_k}), }\\ {{\mathit{\boldsymbol{P}}_{k|k - 1}} = {\mathit{\boldsymbol{F}}_k}{\mathit{\boldsymbol{P}}_{k - 1|k - 1}}\mathit{\boldsymbol{F}}_k^{\rm{T}} + \mathit{\boldsymbol{Q, }}} \end{array} $ |
式中,
Step 3 计算次优卡尔曼增益:
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\tilde y}}}_k} = {\mathit{\boldsymbol{z}}_k} - h({{\mathit{\boldsymbol{\hat x}}}_{k|k - 1}}), }\\ {{\mathit{\boldsymbol{S}}_k} = {\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{P}}_{k|k - 1}}\mathit{\boldsymbol{H}}_k^{\rm{T}} + \mathit{\boldsymbol{R, }}}\\ {{\mathit{\boldsymbol{K}}_k} = {\mathit{\boldsymbol{P}}_{k|k - 1}}\mathit{\boldsymbol{H}}_k^{\rm{T}}\mathit{\boldsymbol{S}}_k^{ - 1}, } \end{array} $ |
式中,
Step 4 增益修饰:
| $ ({{\mathrm{G}}_{k}},{{\mathrm{\tilde{K}}}_{k}})=RN{{N}_{\text{gm}}}\left( {{\mathrm{G}}_{k-1}},{{\mathrm{K}}_{k}},{{{\mathrm{\hat{x}}}}_{k-1\left| k-1 \right.}},{{\mathrm{P}}_{k-1\left| k-1 \right.}},{{{\mathrm{\tilde{u}}}}_{k}} \right). $ |
Step 5 更新状态和误差协方差矩阵:
| $ \begin{align} & {{{\mathrm{\hat{x}}}}_{k\left| k \right.}}={{{\mathrm{\hat{x}}}}_{k\left| k \right.-1}}+{{{\mathrm{\tilde{K}}}}_{k}}{{{\mathrm{\tilde{y}}}}_{k}}, \\ & {{\mathrm{P}}_{k\left| k \right.}}=(\mathrm{I}-{{{\mathrm{\tilde{K}}}}_{k}}{{c}_{k}}){{\mathrm{P}}_{k\left| k-1 \right.}}. \\ \end{align} $ |
注释 1 L-EKF方法给出了一种新的RNN-EKF联合使用方式.在各类不同的估计问题中,IMN和GMN可设计为任意结构的循环神经网络,包括但不限于Simple RNN, LSTM, GRU以及基于这些结构的自动编码网络.具体的网络结构需根据估计问题的特点和复杂程度设计.
3 仿真实验与分析本文将所提出的L-EKF方法应用于临近空间高超声速目标的航迹估计.首先,对L-EKF方法进行训练;然后,通过几个仿真案例将L-EKF方法与扩展卡尔曼滤波(EKF)、自适应扩展卡尔曼滤波(Adaptive EKF, AEKF)等航迹估计方法进行对比,分析其航迹估计性能.
3.1 L-EKF方法的训练L-EKF是一种“端对端”方法,训练中不需作为对数据进行标注,直接使用真实航迹的状态x和输入u作为标称值.本文将一台装有Intel Core i7-8700K CPU, Nvidia TITAN Xp显卡, 32 GB内存的计算机,并基于Python 3.7+Tensorflow+Keras平台对网络进行训练.训练的具体设置如下.
3.1.1 网络参数LSTM2层的神经元数分别为256-32-256-256;GMN的结构如图 3所示,Dense1, Dense2, LSTM1, LSTM2层的神经元数分别为128-16-128-128.
3.1.2 数据集使用一个由1 080条航迹构成的数据集进行训练.数据集使用CAV-H[24]的气动数据生成,包含不同cl的准平衡滑翔航迹,并考虑CV、CA、转弯、方波等多种类型的侧向机动.随机选择80%的航迹作为训练集,10%的航迹作为验证集,10%的航迹作为测试集.虽然可使用任意长度的航迹数据序列训练L-EKF,但受算力所限将训练中使用的航迹切割为长度100的定常片段.
3.1.3 损失函数损失函数为平衡各状态的量级,使用带加权的平均绝对误差损失函数(weighted mean absolute error, WMAE),设计如下:
| $ L=\frac{1}{N}\sum\limits_{i=1}^{N}{(c{{w}_{x}}\left| {{{\hat{x}}}_{i\left| i \right.}}-{{x}_{i}} \right|+(1-c){{w}_{u}}\left| {{{\tilde{u}}}_{i}}-{{u}_{i}} \right|).} $ |
式中:wx=[50, 1 000, 1 000, 0.5, 10 000, 5 000],wu=[1, 1, 0.01],c=0.5为加权系数; xi、ui分别为航迹状态和输入的标称值.
3.1.4 优化器使用RMSprop[25]优化器,训练20 epochs,学习率(learning rate)设置为0.001.
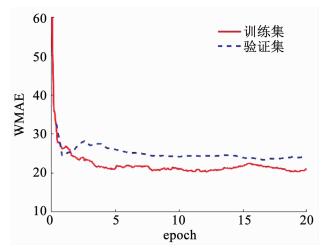
3.1.5 训练结果训练结果如图 5所示,可见经过充分的训练L-EKF的WMAE损失函数收敛.训练集和测试集上的损失函数基本相等,说明所提出的方法具有良好的泛化能力,可应对未知的目标机动.
|
图 5 训练结果 Fig. 5 Training results |
本文通过3个典型的目标机动场景,将所提出的L-EKF方法与传统的EKF、AEKF方法对比,分析其航迹估计性能.假设仅有目标的高度h、经度θ、纬度φ信息可通过预警系统量测获得,且量测信息带有均值为0,均方根误差分别为2 000 m, 0.01 rad, 0.01 rad的高斯白噪声.航迹仿真条件见表 1,场景设定如下.
| 表 1 仿真条件 Tab. 1 Simulation conditions |
场景1 纵向做变归一化升力系数的准平衡滑翔;侧向701~1 300 s做过载为3 g的CA机动,其余时间无机动.
场景2 纵向以恒定归一化升力系数做准平衡滑翔;侧向0~1 200 s做过载为1 g的方波机动,1 201~1 800 s做过载为5 g的大范围规避机动,其余时间无机动.
场景3 纵向做变归一化升力系数的准平衡滑翔;侧向401~800 s做过载为3 g的CA机动,1 501 s之后做过载为5 g的大范围规避机动,其余时间无机动.
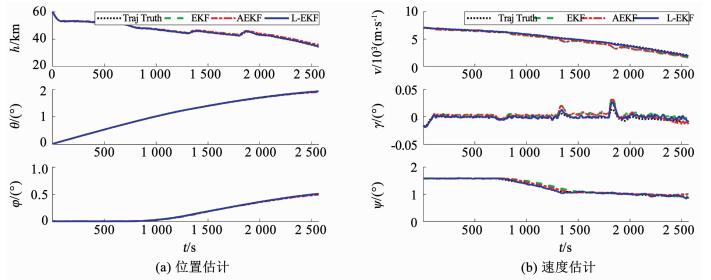
仿真结果见表 2和图 6~8所示.由表 2可知,在所有仿真场景中,L-EKF方法具有比EKF和AEKF更高的估计精度.由图 6~8可知,当目标不机动时,3种方法均有较高的估计精度.当目标机动时,受模型不确定性的影响,EKF的估计精度有着较大的下降,L-EKF和AEKF方法均可以一定程度上适应这种不确定性.由于IMN和GMN可准确的识别目标的机动特性并补偿由其引发的估计误差,L-EKF方法的估计精度和动态性能均优于AEKF方法.运算速度方面,由于嵌入了两个循环神经网络,L-EKF方法略慢于EKF和AEKF方法,但每步估计的计算耗时仍处于同一量级,说明L-EKF方法具有较好的实时性.综上所述,所提出的L-EKF方法可准确识别未知的模型参数并补偿由其带来的估计误差,有效应对临近空间高超声速目标复杂的机动,具有更高的估计精度和更好的估计动态性能.
| 表 2 估计结果 Tab. 2 Estimation results |
|
图 6 场景1仿真结果 Fig. 6 Simulation results of scenario 1 |

|
图 7 场景2仿真结果 Fig. 7 Simulation results of scenario 2 |

|
图 8 场景3仿真结果 Fig. 8 Simulation results of scenario 3 |
1) 分析了临近空间高超声速目标的机动特性,建立了参数化的目标机动模型,解决了经典机动模型难以描述高超声速目标运动特性的问题;
2) 针对目标复杂机动导致的参数和模型不确定性,提出了可学习扩展卡尔曼滤波(L-EKF)方法.通过设计和训练两个循环神经网络(IMN和GMN),并将其嵌入EKF中,实现了对目标复杂机动引起的参数和模型不确定性的在线识别与动态补偿;
3) 通过典型机动条件下的对比分析,可知所提出的L-EKF方法可有效应对目标复杂的机动,具有比传统方法更高的估计精度和更优的估计动态性能.
| [1] |
LI Xiaorong, JILKOV V P. Survey of maneuvering target tracking.Part I. Dynamic models[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1333. DOI:10.1109/TAES.2003.1261132 |
| [2] |
LI Xiaorong, JILKOV V P. Survey of maneuvering target tracking. Part II: Motion models of ballistic and space targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(1): 96. DOI:10.1109/TAES.2010.5417150 |
| [3] |
LI Xiaorong, JILKOV V P. A survey of maneuvering target tracking: Approximation techniques for nonlinear filtering[C]// Proceedings of the 2004 Signal and Data Processing of Small Targets. Bellingham, WA: SPIE, 2004, 5428: 537. DOI: 10.1117/12.553357
|
| [4] |
LI Xiaorong, JILKOV V P. Survey of maneuvering target tracking. Part V. Multiple-model methods[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(4): 1255. DOI:10.1109/TAES.2005.1561886 |
| [5] |
LUO Yuan, REN Lei. Target tracking based on amendatory Sage-Husa adaptive Kalman Filtering[C]//Proceedings of the 2015 International Conference on Electronic Science and Automation Control. Paris: Atlantis Press, 2015. DOI: |
| [6] |
JIA Shuyi, ZHANG Yun, WANG Guohong. Highly maneuvering target tracking using multi-parameter fusion Singer model[J]. Journal of Systems Engineering and Electronics, 2017, 28(5): 841. DOI:10.21629/JSEE.2017.05.03 |
| [7] |
CHEN Hongda, CHANG K C. Novel nonlinear filtering & prediction method for maneuvering target tracking[J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(1): 237. DOI:10.1109/TAES.2009.4805276 |
| [8] |
GODSILL S J, VERMAAK J, NG W, et al. Models and algorithms for tracking of maneuvering objects using variable rate particle filters[J]. Proceedings of the IEEE, 2007, 95(5): 925. DOI:10.1109/JPROC.2007.894708 |
| [9] |
HAN Liang, XIE Antai, REN Zhang, et al. Maneuvering target tracking with unknown acceleration using retrospective-cost-based adaptive input and state estimation[C]//Proceedings of the 34th Chinese Control Conference (CCC). Hangzhou: IEEE, 2015: 5029
|
| [10] |
LIU Changyun, SHUI Penglang, WEI Gang, et al. Modified unscented Kalman filter using modified filter gain and variance scale factor for highly maneuvering target tracking[J]. Journal of Systems Engineering and Electronics, 2014, 25(3): 380. DOI:10.1109/JSEE.2014.00043 |
| [11] |
ZHOU Weidong, HOU Jiaxin. A new adaptive high-order unscented Kalman filter for improving the accuracy and robustness of target tracking[J]. IEEE Access, 2019, 7: 118484. DOI:10.1109/ACCESS.2019.2936879 |
| [12] |
LIPTON Z C, BERKOWITZ J, ELKAN C. A critical review of recurrent neural networks for sequence learning[J]. arXiv preprint arXiv:1506.00019, 2015. |
| [13] |
SINGH S P, KUMAR A, DARBARI H, et al. Machine translation using deep learning: An overview[C]//Proceedings of the 2017 International Conference on Computer, Communications and Electronics (Comptelix). Jaipur, India: IEEE, 2017: 162. DOI: 10.1109/COMPTELIX.2017.8003957
|
| [14] |
LU G, OUYANG W, XU D, et al. Deep Kalman filtering network for video compression artifact reduction[C]//Proceedings of the15th European Conference on Computer Vision (ECCV). Cham: Springer, 2018: 568
|
| [15] |
KIM J B, PARK Y, SUH I H. Tracking human-like natural motion by combining two deep recurrent neural networks with Kalman filter[J]. Intelligent Service Robotics, 2018, 11(4): 313. DOI:10.1007/s11370-018-0255-z |
| [16] |
COSKUN H, ACHILLES F, DIPIETRO R, et al. Long short-term memory Kalman filters: Recurrent neural estimators for pose regularization[C]//Proceedings of the IEEE International Conference on Computer Vision.Washington, DC: IEEE, 2017: 5524
|
| [17] |
KARKUS P, HSU D, LEE W S. Particle filter networks with application to visual localization[C]//Proceedings of the 2nd Conference on Robot Learning. Zürich, Switzerland: [s.n.], 2018: 169
|
| [18] |
MA Chunyong, WANG Anni, CHEN Ge, et al. Hand joints-based gesture recognition for noisy dataset using nested interval unscented Kalman filter with LSTM network[J]. The Visual Computer, 2018, 34(6/7/8): 1053. DOI:10.1007/s00371-018-1556-0 |
| [19] |
VINH N X, BUSEMANN A, CULP R D. Hypersonic and planetary entry flight mechanics[M]. Ann Arbor, MI: University of Michigan Press, 1980.
|
| [20] |
VINH N X, MA D M. Optimal multiple-pass aeroassisted plane change[J]. Acta Astronautica, 1990, 21(11/12): 749. DOI:10.1016/0094-5765(90)90117-4 |
| [21] |
SUNAHARA Y. An approximate method of state estimation for nonlinear dynamical systems with state-dependent noise[J]. Journal International Journal of Control, 1970, 11(6): 957. DOI:10.1080/00207177008905976 |
| [22] |
HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735. DOI:10.1162/neco.1997.9.8.1735 |
| [23] |
IOFFE S, SZEGEDY C. Batch Normalization: Accelerating deep network training by reducing internal covariate shift[J]. arXiv:1502.03167,. |
| [24] |
JORRIS T R. Common aero vehicle autonomous reentry trajectory optimization satisfying waypoint and no-fly zone constraints[M]. Ohio: Air Force Institute of Technology, 2007.
|
| [25] |
TIELEMAN T, HINTON G. Lecture 6.5-rmsprop, coursera: Neural networks for machine learning[R]. COURSERA: Neural Networks for Machine Learning, 2012
|
 2020, Vol. 52
2020, Vol. 52


