在爱因斯坦的广义相对论中,引力波是由于带质量物体加速运动导致的时空涟漪,以光速从引力源向外传播.虽然引力波时时存在于整个宇宙,但是其引起的时空应变极其微弱,应变幅值约为10-21量级.为了验证引力波的存在,近一个世纪中大批物理学家前赴后继投入到这个领域.直到2015年, 美国地面激光干涉引力波天文台aLIGO成功探测到一例由双黑洞合并导致的引力波事件GW150914,证实了引力波的存在,也打开了引力波探测和引力波天文学的新纪元[1].由于引力波源的多样性,引力波频谱非常宽,频谱范围从小于微赫兹至千赫兹跨越十几个量级.不同的波谱段需要不同的探测方法.地面探测由于受到地表震动和引力梯度噪声的影响以及干涉臂长的限制,其可探测频段涵盖范围为10~1 000 Hz,无法覆盖由超大质量黑洞、致密双星、极端质量比双黑洞绕转系统等天体运动事件所产生的0.1 mHz~1.0 Hz中低频引力波,因此需要在太空中建立百万公里量级的长基线激光干涉引力波探测系统来探测毫赫兹波段更大特征质量和尺度的引力波源[2].
欧空局最早于1993年提出了LISA引力波空间探测计划[3],其后日本于2001年提出了DECIGO计划.近年来,国内也有学者提出了天琴、太极等引力波空间探测计划[4-5].其中LISA计划研究时间最久,技术积累及发展最为成熟,其技术验证星LISA Pathfinder已经于2015年12月成功发射[6-8],LISA也已被列为欧空局的L3大型空间任务,计划于2034年发射[9].目前,国内相关研究单位也正在加足马力推进相关关键技术的发展和探测计划的实施,空间引力波探测已经成为世界引力波研究热点和国际竞争的重点领域.
这些空间引力波探测计划虽然具体技术细节不同,但是基本测量原理是一致的,均由相距数十万或数百万km的3颗航天器组成等边三角形星座,由航天器中内置的激光器、自由悬浮测试质量及两航天器的星间链路组成激光干涉仪,当引力波经过航天器时,会引起一对测试质量之间的距离发生变化,根据激光往返干涉信号可获得测试质量间距变化值,进而可表征引力波引起的时空变化[9].作为整个探测系统传感器的测试质量,其运行稳定性会对测量分析结果产生巨大影响.按照任务需求,测试质量应只受引力作用,完全处于自由落体状态,但是太空中存在的太阳光压、宇宙辐射等非保守力会严重影响航天器的运行状态,进而导致航天器与测试质量之间发生相对位移;又由于测试质量周围残余气体、电荷涨落等因素的影响,测试质量与航天器腔体之间存在耦合效应,航天器的位移运动会耦合到测试质量,对测试质量运行稳定性形成干扰.所以目前所有的空间探测计划均采用无拖曳控制技术,使航天器能够实时跟踪内部自由飞行的测试质量,实现航天器与测试质量飞行的高度稳定性,满足高精度引力实验的需求,最终实现激光测距系统对引力波信号的有效探测[10].
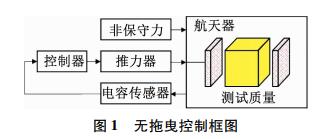
无拖曳控制的基本原理如图 1所示,当航天器受到非保守力的干扰,航天器与内部自由落体的测试质量会发生相对位移,此位移误差信号被电容传感器等高精度位移传感器件进行精确测量,并作为控制误差传递至控制器计算所需的推力指令,微推力器则依据推力指令精确快速输出相应推力,以抵消非保守力并消除航天器与测试质量之间的位移误差[11].由此可见,推力器作为无拖曳控制系统的执行机构,其推力输出性能的优劣严重制约着最终的无拖曳控制水平.
|
图 1 无拖曳控制框图 Fig. 1 Block diagram of drag-free control |
因为推力器的核心任务是实时精确补偿各项非保守扰动力,所以首先推力输出可调范围应完全覆盖扰动力变化范围;其次, 为保证补偿精度,推力输出分辨率应足够高;再次,推力同样作为航天器所受非保守力,其输出噪声应满足相应要求,若推力噪声过大,不仅不能达到消除太阳光压等非保守力的效果,反而引入新的噪声源,严重破坏系统稳定性;此外,由于空间引力波探测任务在轨测量时间多为数年,推力器应具备良好的长时间持续工作的稳定性和一致性.因此,鉴于推力器技术在整项探测任务中的必要性和重要性,所有空间引力波探测计划均对推力器提出了明确的指标需求.以LISA计划为例,推力调节范围需求为数微牛至百微牛,推力分辨率应<0.1 μN,工作期间推力噪声应低于0.1
在最初的无拖曳卫星中多采用冷气推力器作为执行机构,如1972年由美国海军发射的世界首颗无拖曳卫星TRIADI[13],2004年斯坦福大学等单位合作发射的GP-B(Gravity Probe B)卫星[14],均采用冷气推进系统补偿卫星扰动力.但是随着电推进技术发展的日趋成熟,电推进器比冲高、寿命长、推力分辨率高、有效载荷质量分数高等优势逐渐体现出来,目前已经广泛应用于位置保持等空间任务中[15-16].后期的无拖曳卫星也多采用电推进系统进行高精度轨控,重力梯度卫星GOCE是首颗采用电推进系统的无拖曳卫星,它采用T5离子推力器实现沿轨方向的无拖曳控制[17-18].其后, LISA Pathfinder卫星则采用胶体推力器执行非保守力干扰补偿[19-20].由此可见,电推进依赖于自身高比冲、高推力精度等性能优势,得到了各项空间精密测量任务的关注和认可,进而促成了无拖曳卫星推进系统由冷气推进向电推进的过渡和转变.
根据引力波探测任务特点,LISA 2017年最新发布的任务提议中列选了4种可能的推力器类型作为未来探测任务的候选者,分别是冷气微推力器、胶体推力器、射频离子推力器和会切型霍尔推力器[9].这4种推力器均可产生微牛量级推力,但是由于其各自特殊的工作原理和结构,均存在着暂时难以解决的技术问题.其中冷气推力器应用范围最广,技术成熟度最高,但是由于其比冲受限,难以满足引力波探测任务长时间、高总冲的需求.胶体推力器已经实现在轨验证,但是寿命、个体加工差异性、运行一致性等问题尚未解决[20].射频离子推力器的小型化研究尚在进行,其推力下限能否满足引力波探测需求仍不明确[21].会切型霍尔推力器由于其特殊的工作原理而具有推力大、范围可调、长寿命、输出稳定的特点[22],是一种理想的无拖曳所用推力器类型,但是作为一种新型推进方案,技术成熟度较低,尚处于实验室研究阶段.
国内关于会切型霍尔推力器的研究主要由哈尔滨工业大学等离子体推进技术实验室于达仁教授团队进行.该团队初期首先针对毫牛级推进任务进行了会切型霍尔推力器设计、模拟及实验研究.采用PIC(Particle in cell)模拟技术对推力器等离子体分布特性进行仿真计算,模拟获得了电子传导路径和电场形成过程[23-24].在实验研究方面,成功设计了通道内径为24 mm的毫牛级推力器,实验结果表明,该推力器可以实现0.37~19.20 mN的推力宽范围连续变化[25].此外,胡鹏博士对推力器的电离加速机制进行了深入的分析探讨,揭示了模式转变过程中的物理机制和推力大范围连续调节特性的形成原因[26-28].该团队已经基本掌握该型推力器的等离子体运动机理和工作机制,针对推力器在发射过程中可能受到的复杂力、热学环境进行了结构优化,研制出毫牛级会切型霍尔推力器工程样机.经过对毫牛级推力器的研究,已经确认了会切型霍尔推力器具备推力宽范围可调的能力,具备应用于无拖曳应用的可能.针对以空间引力波探测任务为代表的新型高精度微推进任务,团队基于前期的理论研究基础和工程设计经验,于2016年开始微牛级会切型霍尔电推进及无拖曳控制的相关研究.
本文介绍微牛级会切型霍尔推力器的设计理念、研究过程以及最终的性能实验结果;讨论分析推力的闭环控制方法,并通过数值仿真说明推力闭环控制对推力动态特性所带来的有益效果;通过无拖曳卫星仿真系统评估现有推力器在空间引力波探测任务中应用的可行性.
1 微牛级霍尔推力器设计及性能实验霍尔推力器由于具备结构简单、比冲高、推力密度大等优势,已经成为国际航天任务中广泛应用的一种空间电推进技术.由于应用场景需求,目前使用的霍尔推力器推力多在百毫牛量级,且为定工况工作,无需进行在线推力调节.但是引力波探测任务所需的推力器应是推力宽范围连续可调的微牛级推力器.因此,为研制出适用于探测任务的微牛级霍尔电推力器,现有的霍尔推力器应向微牛级发展,并且需要实现微牛级推力的宽范围可调稳定输出.
1.1 微牛级霍尔推力器设计实现微牛级推力最直接简便的方法就是减小工质供给流量,并且匹配等比缩小推力器各结构尺寸.但是,经过研究发现,依据此理念设计的小型霍尔推力器会遇到如下两点问题:
1) 推力下限难以满足要求.空间引力波探测任务所需的最小推力为1 μN,但是目前可查阅到的公开文献中推力最小的微型霍尔推力器(由斯坦福大学研制),在10 W功率下推力仍高达600 μN,效率已经低至10%[29], 且此推力器放电通道宽度仅为0.5 mm,难以通过进一步减小尺寸,降低推力下限.其中的物理机制是,由于推力器质量和尺寸的减小,在微尺度效应下,等离子体作用空间不足,磁约束不足导致电子损耗严重,电离不充分,小推力工况时电离率及效率低下,甚至会导致雪崩电离无法保证,电场难以建立,进而电子无法穿越磁力线,出现点火困难和极易熄火的现象.
2) 无法在宽范围变参数条件下稳定工作.同样以斯坦福大学研制的微型霍尔推力器为例,其推力调节范围为0.6~1.6 mN[29],推力调节比远小于引力波探测任务所需调节比,即推力调节范围无法满足要求.原因在于随着推力器尺寸的减小,面容比增大,等离子体约束困难,导致等离子体与壁面相互作用加剧,壁面损失严重,放电效率较低,特别在大推力工况时壁面热沉积严重,若壁面及磁路等组件热负荷过大,易出现推力器过热失稳现象.斯坦福大学研制的微型霍尔推力器使用水冷的方式对磁路进行冷却,以保证推力器稳定工作.因此受限于等离子体约束问题,推力可调节范围过窄.综上所述,仅仅通过降低流量、缩小推力器尺寸无法满足任务所需的推力要求.因此需要从物理角度重新思考、改进推力器的结构及工作方式.
霍尔推力器在小推力工况下,阳极电压设定必然较小,电子能量低,进而导致低能电子难以穿越磁力线实现放电.为保证小推力下稳定放电,需通过改进磁场设计,为电子提供一条低阻抗通道,使得电子可以顺利到达阳极维持放电.在大推力工况下,为避免推力器过热失稳,应引入磁屏蔽概念,并且适当增强磁场强度,以有效约束等离子体,降低与壁面的相互作用,同时减小壁面损失.基于以上分析,将采用会切型磁场来满足以上设计要求.
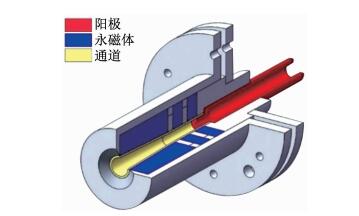
会切型霍尔推力器基本结构如图 2所示,其特点在于放电通道形状为圆柱形,磁场是由通道外极性相反的多级环形永磁体形成的会切型磁场.其余部件与传统霍尔推力器类似,在通道上游设置阳极和气体分配器,推力器外侧下游安装阴极.在推力器工作过程中,阴极释放的电子受到电场影响进入推力器内部被磁力线捕获,在磁镜效应的作用下电子于通道内部磁尖端处往复螺旋运动,在此过程中部分电子会与通道内的工质气体发生碰撞并电离形成新的离子和电子,发生雪崩电离.电子经过多次传导后到达阳极形成放电回路,离子则在电场作用下加速喷出形成推力.会切型霍尔推力器的构型特点和工作原理使其具有如下特点:

|
图 2 会切型霍尔推力器结构示意 Fig. 2 Structure of a cusped hall thruster |
1) 易实现微牛级放电.在小推力工况下,由于推力器中轴线处磁力线与壁面平行,为电子形成了一条弱磁场、低阻抗的传导路径,电子在羽流区借助于经典碰撞等传导过程,进入推力器内中轴线处,并沿着磁力线顺利前行到达阳极,所以该推力器可在低功率微小推力条件下顺利点火并可维持放电.其次, 该推力器无内磁极结构,采用圆柱形通道增大面容比,并且仅采用永磁铁构成磁路,无其余磁路组件,有助于大幅减小推力器尺寸实现小型化.其中,德累斯顿工业大学Hey所研制的NG-μHEMPT最小推力为6.257 5 μN[22],因此该类推力器非常有望满足引力波探测所提出的推力下限需求.
2) 推力宽范围连续可调,放电稳定性良好.推力器输入参数为阳极电压和供气流量,通过调节这两个参数可以实现推力的连续变化.对于传统霍尔推力器而言,其出口磁场强度最高值约为300 G,正梯度的典型值为90 G/mm,稳定工作电压约为300 V.当推力器放电电压过高时,电子约束能力不足,壁面热沉积严重,易失稳.而会切型霍尔推力器由于其特殊的会切磁场位形,在高放电电压条件下,电子主要沿着靠近壁面的外侧路径传导,此路径下电子的约束过程与霍尔推力器中的E×B运动过程较为相似.为了大幅提高推力器稳定放电电压,拓宽推力器工作范围及推力稳定输出范围,会切型霍尔推力器使用永磁铁形成出口强磁场,其强度设计值最高约为3 000 G,正梯度的典型值达到了500 G/mm,因此在达到与霍尔推力器同等的霍尔漂移速度条件下,会切型推力器的稳定工作电压最高可达3 000 V,实现高电压高功率工况下的有效电子约束和稳定放电.通道内部磁场位形为会切型,较强的磁场轴向分量可以有效地将电子约束在中轴线附近,电子趋向于轴线的传导过程也会使得通道内电离区无法形成大电势降,即离子主要在出口加速区获得加速能量,离子与壁面的相互作用程度不明显,因此该推力器通道内的等离子体均可得到有效的约束,增强大推力工况下的放电稳定性.同样以NG-μHEMPT为例,其推力稳定输出范围为6.257 5~4 800 μN[22],跨越3个数量级,因此该类推力器具备推力大范围连续可调的特性.
3) 壁面侵蚀弱,寿命长.会切型强磁场不仅使得推力可实现大范围连续可调,而且由于对等离子体的有效约束,通道壁面受到很好的保护,壁面侵蚀非常弱.德国泰勒斯公司利用工程样机HEMP-T 3050 EM进行寿命考核,实验结果表明:HEMP-T 3050 EM在额定工况(阳极电压为1 000 V,功率1 380 W)下工作1 200 h后,内尖端陶瓷被腐蚀形成凹槽的深度只有5 μm.由此可以预测其工作寿命能够达到数万小时以上[30].
根据以上物理过程分析及国外学者研究现状可知,会切型霍尔推力器因其独特的磁场位形和组件结构,具有推力大范围连续可调,微牛级推力稳定输出的能力,具备应用于空间引力波探测任务的可能.哈尔滨工业大学等离子体推进技术实验室基于前期毫牛级会切型推力器的研究基础和经验,于2016年开展了微牛级会切型霍尔推力器的研制工作.
为实现微牛级放电,首先进行推力器的小型化研究,基于毫牛级推力器的磁极比例、磁场强度,对推力器的特征尺寸及结构构型开展了一系列研究.在原有出口直径为24 mm的推力器基础上,维持通道长度不变,分别设计了出口直径6、12 mm的推力器,实验结果发现,不同出口直径显著地影响推力器的有效工作范围,当出口直径为6 mm时,推力器的最高功率为60 W以下,推力下限已经达到微牛量级.而且由于通道出口直径直接决定了相同流量下工质的通流密度,因此在低流量下,出口直径较小的推力器存有明显的推力性能优势.因此,为实现小推力下的较优性能,还应继续缩小推力器通道出口直径.
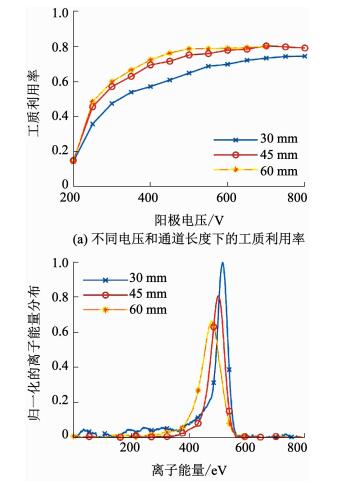
在出口直径为6 mm的推力器基础上,针对推力器的通道长度展开了一系列实验测试,采用通道总长度分别为30、45、60 mm的推力器进行实验测试.工质利用率及羽流离子能量的实验结果如图 3所示,由于通道较长推力器的电离区存在充分电离长度,通道较短的推力器不满足充分电离条件而导致工质利用率下降;由于过长的通道中的等离子体与壁面相互作用更剧烈,而造成了离子能量的损失以及离子的复合,总体效率下降.因此,会切场推力器存在较优通道长度,对出口直径为6 mm推力器,其较优长度应在30~45 mm.
|
图 3 不同通道长度推力器的工质利用率及羽流离子能量差异 Fig. 3 Propellant utilization and the normalized ion energy distribution of thrusters with different channel lengths |
为进一步减小推力,根据以上实验分析结果,设计了出口直径4 mm的推力器.为综合考虑推力器的充分电离长度和壁面作用,通道长度设定为30 mm.在永磁材料的选择上,采用磁性更强的钕铁硼来作为永磁体形成会切磁场,可进一步减小推力器外径,最终形成的推力器外壳直径仅为2 cm,其具体结构和样机如图 4和图 5所示.
|
图 4 微牛级会切型霍尔推力器结构 Fig. 4 Structure of a micro-Newton cusped hall thruster |

|
图 5 微牛级会切型霍尔推力器实验样机 Fig. 5 Experimental prototype of a micro-newton cusped hall thruster |
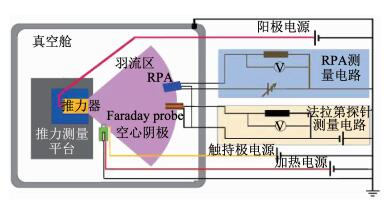
该推力器性能测试在哈尔滨工业大学等离子体推进技术实验室中完成.使用的真空系统为圆柱形腔室,长度4 m,内径1.2 m,极限真空可达1.0×10-3 Pa.由于实验室中的三丝扭摆推力测量平台测力量程未达微牛级,本次实验需采用其他方法间接测量推力.由于推力是单位时间羽流区各个离子动量的矢量和,可知推力的形成是羽流区离子电流分布及离子能量分布综合的结果.所以可通过在羽流区放置法拉第探针和RPA(retarding potential analyzer)探针来分别测量离子电流分布及离子能量分布,再联合两个探针的测量数据计算出推力变化.实验测试系统的布置示意图如图 6所示.
|
图 6 实验测试系统示意[32] Fig. 6 Schematic of experimental test system |
推力器和空心阴极放置在实验台上,两个探针被安装在步进电机控制的转台上,探针的扫描范围0°~90°,安装位置距离推力器出口中心13.5 cm,探针的离子接收面半径均为0.5 cm,用于排斥电子的法拉第探针外壳和RPA偏置栅电压均设为-24 V.具体的推力计算原理介绍如下[31].假设羽流中离子关于推力器中轴线轴对称,则推力T可利用空间某点推力元Tφ进行面积分获得
| $ T=2\pi {{R}^{2}}\int\limits_{0}^{\frac{\pi }{2}}{{{T}_{\varphi }}\cos \left( \varphi \right)}\sin \left( \varphi \right)\text{d}\varphi . $ | (1) |
式中:φ为推力元Tφ矢量方向与推力器中轴线的夹角, R为探针测量位置与推力器出口中心距离.根据推力形成原理可知,推力元
| $ {{T}_{\varphi }}={{\dot{m}}_{\varphi }}{{v}_{\varphi }}. $ | (2) |
式中:ṁφ为推力器在φ点的离子质量, vφ为φ点离子速度.根据能量守恒定律和质量守恒定律,
| $ {{v}_{\varphi }}=\sqrt{2{{U}_{\varphi }}e/{{m}_{i}}}, $ | (3) |
| $ {{\dot{m}}_{\varphi }}={{I}_{\varphi }}{{m}_{i}}/e. $ | (4) |
式中:Uφ为φ点离子加速电压, Iφ为φ点离子电流, mi、e为氙原子质量和电子电荷常数.将式(3)(4)带入式(2)可得
| $ {{T}_{\varphi }}={{I}_{\varphi }}\sqrt{2{{U}_{\varphi }}{{m}_{i}}/e}. $ |
其中Iφ可由法拉第探针测得,但是φ点的离子簇中不同离子受到的加速电压是有差异的,所以采用RPA探针进一步分析φ点的离子能量分布,最终Tφ计算公式如下:
| $ {{T}_{\varphi }}=\sum\limits_{i}{\Delta {{I}_{\varphi , i}}\sqrt{2{{U}_{\varphi , i}}{{m}_{i}}/e}}. $ |
式中:Uφ, i表示φ点部分离子的加速电压为i V, ΔIφ, i表示加速电压为Uφ, i的离子电流.尽管RPA能精确测出离子能量分布信息,但是由于RPA接收极前端设置了4层栅网,进入探针通道的离子电流会部分损耗在前级栅网上,使得接收极接收的有效电流信号的强度较低,离子数密度信息测量不准.所以需要使用法拉第探针得到的离子数密度信息作为权重加载于RPA探针得到的归一化离子能量分布函数上,这样便可获得准确的ΔIφ, i,计算得Tφ,最后基于式(1)可积分求得输出推力T.
基于上述方法搭建的双探针推力测试系统,该型推力器可在氙工质流量为0.15~0.25 mL/min,阳极电压为150~300 V的调节范围内实现推力0.2~112.7 μN的连续调节输出,在该推力范围内,实现了最高588.4 s的比冲,见图 7.

|
图 7 微牛级会切型霍尔推力器推力、比冲实验结果 Fig. 7 Thrust and specific impulse test results of the micro-Newton cusped hall thruster |
实验结果表明,该推力器的会切型磁场设计理念正确, 小型化思路及过程合理,达到预期设计效果,推力可调范围超过国外同类型推力器,满足空间引力波探测任务对推力器推力可调范围的需求.
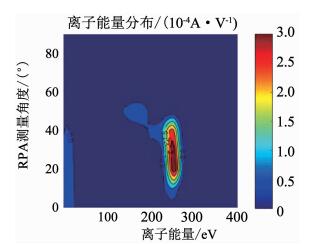
根据法拉第和RPA探针的测量数据,进一步分析了该推力器的羽流特性.由图 8可以看出,推力器羽流在工作范围内形貌稳定,显示出典型的空心羽流特征.图 9给出了羽流离子能量分布,可以看出该推力器的离子能量峰值集中在20°~40°的小角度范围内,波峰半高宽很小,离子加速效率很高,这说明该推力器有着良好的电离区、加速区分离特性,若进一步提升放电电压,将会优化比冲等工作性能参数.

|
图 8 0.2 mL/min流量下推力器羽流离子电流密度分布 Fig. 8 Ion current density distribution of the thruster at 0.2 mL/min |
|
图 9 0.2 mL/min流量下推力器羽流离子能量分布 Fig. 9 Ion energy distribution of the thruster at 0.2 mL/min |
在推力器设计阶段已经设计出满足引力波探测任务推力调节范围要求的微牛级会切型霍尔推力器,但是探测任务还对推力噪声、长期工作的一致性、推力精度等指标提出了严苛的要求.其中推力噪声是由输入装置如工质供给系统输出不确定性等因素导致的;长期工作一致性也会受到部件老化等因素的影响,推力输出性能会缓慢漂移,造成推力实现精度的降低.而这些指标参数是难以通过推力器结构设计改进就能达到的,所以需要从新的角度改进推力器及整个推进系统.闭环控制理论为解决这些问题提供了可能,为推力器增加闭环控制回路,进而通过控制手段改善推进系统工作稳定性、一致性,提高实现精度.
2.1 推力器闭环控制设计推力器闭环控制流程如图 10所示.由于工质流量供给系统属于大惯性环节,时间常数高达秒量级,远超推力闭环控制周期,所以工质流量采用基于推力指令的开环调节策略,其目的是实现推力的初步粗略调节;而阳极电压作为电参数可实现快速精确调节,所以阳极电压采用闭环控制结构精确微调推力器放电过程和输出推力,高精度实现推力指令.

|
图 10 推力器闭环控制示意 Fig. 10 Schematic diagram of thrust closed-loop control system |
为实现推力器闭环控制仿真,需要首先建立推力器的数学模型.以往关于电推进的研究多基于流体模拟方法或者PIC粒子模拟方法,根据中性原子、等离子体的物理运动过程建立推力器模型,此方法已经广泛应用于各种类型电推力器的研究中,并辅助发现了内部诸多的物理现象,解决了众多科学问题.但是此方法计算量异常巨大,不能进行实时计算,而且计算精度有限,无法满足该应用场景下对仿真模型定量计算精度的要求.因此本文采用系统辨识方法基于推力器实验数据建立推力器输入输出数学模型.推力器模型描述如式(1)所示,输入参数为工质供给流量ṁi和阳极电压Ua,输出参数为推力
| $ T=f\left( {{{\dot{m}}}_{i}}, {{U}_{a}} \right). $ | (5) |
推力器真实系统由式(5)数学模型所代替.由于在轨无法实时测量推力,所以需要使用电参数传感器实时测量推力器阳极电压Uam、放电电流Idm,并结合供给流量测量值ṁim在轨估计推力输出值Tm,形成反馈回路.推力估计模型同样采用输入输出描述:
| $ {{T}_{m}}=f\left( {{{\dot{m}}}_{im}}, {{U}_{am}}, {{I}_{dm}} \right). $ |
基于推力指令与推力估计值获得推力实现误差,将误差信号传递至控制器生成相应的电压指令,传递至电源系统并输出调节推力器状态,精确输出需求推力.需要注意, 由于实际电源系统和流量供给系统并非理想器件,其输出必然存在一定的噪声特性,并且会直接影响输出推力的稳定性,所以在仿真中应考虑电源系统和流量供给系统的输出噪声.
2.2 仿真算例及结果分析为了使得推进系统仿真结果尽可能贴近真实情况,在推力器实验过程中, 针对电源系统和流量供给系统的输出特性进行了时长10 000 s的精确测量,获取其输出噪声数据,同时根据流量系统特性设定其为一阶系统, 且时间常数为0.4 s,电源系统调节快速,忽略其响应延迟.并将这些数据代入推进系统模型中计算推力输出.
为清晰说明并分析出推力闭环控制对推力噪声、推力实现精度等参数的影响,针对推力长期定工况工作和推力小阶跃变化两种情景分别设置两个比较算例进行仿真.算例1为推进系统开环运行,算例2的推进系统采取闭环控制方法控制推力输出.
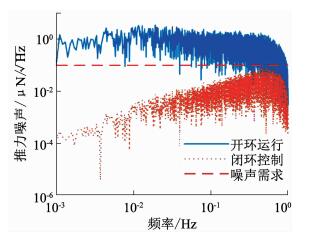
情景1:定推力长期工作.阳极电压设定为250 V,工质流量设定0.175 mL/min保持不变,仿真时长10 000 s.开、闭环运行下的推力数据频域幅值谱密度计算结果以及推力噪声需求指标见图 11.
|
图 11 定推力开闭环推力噪声幅值谱密度 Fig. 11 Amplitude spectral densities of thrust in open-loop and closed-loop control |
由图 11可知,推力器在开环工作下,由于工质供给流量等参数波动的影响,推力输出噪声幅值超过任务需求幅值一个数量级;而采用闭环方案,则可有效降低推力输出噪声幅值,并满足任务指标0.1
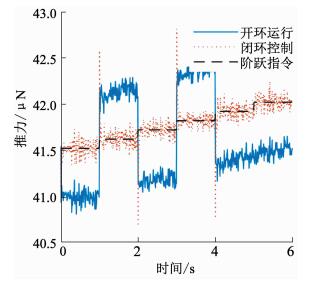
情景2:推力指令设定41.5~42.0 μN以0.1 μN阶跃变化.调节过程中推力输出结果如图 12所示,工质流量、阳极电压运行结果见图 13.开环运行算例中,当流量输出发生跳变时,推力会跟随出现大幅变化,推力实现误差约为0.5 μN;电压输出噪声同样会导致推力输出的小幅波动,综合流量波动和电压波动对推力输出的影响,推力最终输出值无法精确跟踪推力阶跃指令;而在采用推力闭环控制后,可明显看出推力输出可以较好地跟踪指令值.尽管由于流量供给系统输出的突跳,推力仍存在大幅变化现象,但是电源可以实时根据推力误差反馈值高频闭环调节推力器阳极电压,修正推力器工作状态.从图 13(b)阳极电压的变化曲线可知,当供给流量突增时,反馈回路可以迅速感知推力增大,并调小阳极电压以弥补流量的影响,维持推力实现精度.
|
图 12 推力小阶跃指令下推力输出结果 Fig. 12 Thrust results under thrust step command |

|
图 13 推力小阶跃指令下工质流量、阳极电压运行结果 Fig. 13 Flow rate and anode voltage under thrust step command |
由以上计算及分析可知,推力反馈通道的引入对降低推力噪声和提高输出精度至关重要,可以保证推力器在轨工作时推力输出的稳定性和非保守力的补偿精度.
当然,由于阳极电压波动幅值仍然较大,推力输出虽能跟踪指令,但仍然存在明显波动.所以仍需研究阳极电源输出波动的抑制方法,后期将在阳极电源与推力器之间加入RLC滤波回路,利用RLC回路有效降低推力器工作对电源的影响,以进一步优化电源电压输出稳定性,进而提高推力稳定性和精度.此外,目前实验中所使用的工质流量供给系统是工业级用的流量系统,流量输出范围远高于目前微牛级推力器所需的流量供给范围,所以针对引力波探测任务的微推进、微流量特殊需求,计划后期自主设计微流量系统,重点关注流量可调范围和输出稳定性、快速性,具体的系统设计方法还有待进一步的商讨和研究.若采用降低量程、流量输出更稳定的微流量供给系统,必然会对推力输出稳定产生有益效果.
3 推力器实现无拖曳应用的可行性分析推力器作为无拖曳控制系统的执行机构,其输出性能严重影响无拖曳控制精度.为精确分析推力器闭环控制的有效性,建立了无拖曳卫星仿真系统,通过仿真手段准确评估微牛级会切型霍尔推力器在空间引力波探测任务中应用的可行性.
3.1 无拖曳卫星仿真系统建模由无拖曳控制框图可知,控制系统仿真程序主要包含4个部分:航天器与测试质量的轨道运动计算, 非保守力计算, 控制律设计以及推进系统模型计算.推进系统模型在上节中已经介绍,此节重点讨论其余3个部分的建模方法.
3.1.1 轨道运动状态方程航天器的轨道运动状态由地球引力、环境非保守扰动力、测试质量的耦合力和推力器输出推力共同决定,根据牛顿运动定律,其运动方程为
| $ {{\dot{r}}_{s}}={{v}_{s}}, {{\dot{v}}_{s}}=g\left( {{r}_{s}} \right)+{{a}_{d}}+{{a}_{k}}+{{a}_{T}}. $ |
式中:rs、vs∈R3分别为航天器位置和速度;g为地球引力函数,包含地球非球形摄动力,由航天器位置决定;ad、ak、aT∈R3分别为由环境非保守扰动力、耦合力和推力导致的加速度.测试质量由于处于航天器内部密闭空间内,仅会受到地球引力和耦合力的影响,所以测试质量运动的状态方程为
| $ {{\dot{r}}_{t}}={{v}_{t}}, {{\dot{v}}_{t}}=g\left( {{r}_{t}} \right)-{{a}_{k}}. $ |
式中rt、vt∈R3为测试质量位置和速度.
3.1.2 非保守力计算仿真考虑了两类非保守力,一类是由于磁场、残余气体、电荷涨落等因素导致的航天器腔体与测试质量之间的耦合力,根据弗罗里达大学Nguyen等[33]的分析结果,该耦合力可以视为弹簧作用,所以耦合加速度可表示为耦合系数k乘以两者的相对位移r.另一类则是由于航天器所处太空环境导致的环境扰动力,由于空间引力波探测任务所采用的飞行轨道的轨道高度多为数十万km,甚至处于拉格朗日点等更远的星际空间,所以非保守扰动力主要成分为太阳辐射光压,光压计算公式如下[34]:
| $ {{a}_{\text{d}}}=-\frac{v}{m}\cdot \frac{S}{c}\cdot {{C}_{\text{R}}}\cdot {{S}_{\text{S}}}\cdot \widehat{u}. $ |
式中:m为卫星质量;ν为阴影函数,ν=0时表明航天器被星体遮挡,无光照影响,ν=1表明航天器直接受到太阳照射,光压需要考虑;S为航天器所在位置的太阳辐射强度;c为光速常数;CR=1~2为航天器光辐射系数,CR=1表明航天器外壳材料会吸收表面入射的所有光子动量,CR=2表明入射光子被完全反射,对航天器作用力加倍;Ss∈R3表征航天器受照面积;
基于比例-微分反馈控制理论,根据航天器与测试质量之间的相对位移误差和速度误差的测量反馈信号消除两者之间的运动误差.所以,控制律表达式为
| $ {{a}_{\text{T}}}=-{{a}_{\text{d}}}-2k\Delta r+g\left( {{r}_{1}} \right)-g\left( {{r}_{\text{s}}} \right)-{{k}_{\text{p}}}\Delta r-{{k}_{\text{d}}}\Delta \dot{r}. $ |
式中:kp、kD∈R3为比例增益和微分增益.
仿真程序设定航天器轨道高度为10×104 km,偏心率为0,轨道倾角为74.39°.航天器轨道控制频率为10 Hz,推进系统内部控制频率为100 Hz.根据以上建模办法及设定参数, 便可编写代码计算航天器与测试质量各个时刻的运动状态,获取两者之间的状态误差,观察无拖曳控制实现水平.
3.2 仿真结果分析为了进一步说明推力器闭环控制对航天器无拖曳控制精度的影响,基于无拖曳卫星仿真系统对推力器开环运行和闭环控制运行两种工作模式分别进行了无拖曳仿真计算.图 14为两种工作模式下推力输出与光压的运行数据,其中推力器开环运行时,光压补偿误差平均值为0.387 μN;采用闭环控制模式,推力与光压之间的平均差值减小至0.017 μN,体现了非保守力补偿精度的大幅提升.

|
图 14 推力器开闭环运行下的推力输出与光压 Fig. 14 Thrust and solar radiation force under open-loop and closed-loop thrust control |
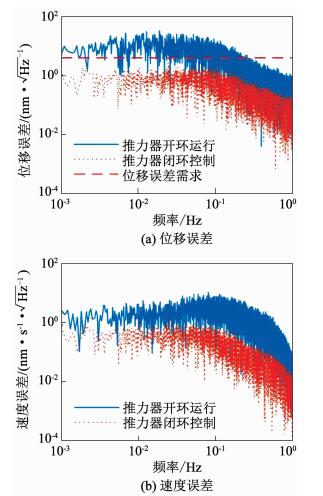
另外,作为无拖曳控制系统的性能指标,航天器与测试质量之间的位移误差和速度误差的仿真结果如图 15所示.
|
图 15 航天器与测试质量之间位移误差、速度误差的幅值谱密度 |
图 15(a)中红色线为中国空间引力波探测计划对航天器与测试质量之间的位移误差需求指标.由此可见,采用闭环控制,确实有效降低了位移误差和速度误差,位移误差平均值从2.876 nm降至0.086 nm,速度误差平均值也从1.364 nm/s减小至0.058 nm/s,其中,位移误差已经满足探测计划的控制精度需求.推力闭环控制不仅可提高推力实现精度,还可大幅改善卫星无拖曳控制水平,因此,推力器闭环控制研究是实现其引力波探测任务应用的必经之路.
4 结论1) 针对霍尔推力器小型化过程中遇到的物理限制问题,从推力器设计角度出发,经过对推力器磁场位形和结构的多次迭代优化,最终研制出符合空间引力波探测任务所需的会切型霍尔推力器, 其推力在1~100 μN连续可调.
2) 针对推力噪声、输出精度等指标需求,基于反馈控制理论设计了推力器的推力闭环控制系统,仿真结果验证了闭环控制的有效性,可以降低推力噪声,使其满足任务需求,同时可确保推力指令的精确快速实现.无拖曳控制仿真结果表明,推力闭环控制引入可大幅降低非保守力补偿误差, 提高无拖曳控制精度.
3) 空间引力波探测任务所采用的超稳超静航天器平台对推力器的推力输出性能提出了极为苛刻的指标要求,这对推力器研究人员而言既是机遇也是挑战.我国如果在这一领域能够取得突破性进展,不仅对推动我国电推进技术的发展具有重要的意义,而且对我国航天器无拖曳控制技术以及空间引力波探测计划都具有非凡的推动作用.
| [1] |
ABBOTT B P, ABBOTT R, ABBOTT T D, et al. Observation of gravitational waves from a binary black hole merger[J]. Physical Review Letters, 2016, 116(6): 61102. DOI:10.1103/PhysRevLett.116.061102 |
| [2] |
罗子人, 白姗, 边星, 等. 空间激光干涉引力波探测[J]. 力学进展, 2013, 43(4): 415. LUO Ziren, BAI Shan, BIAN Xing, et al. Space laser interferometry gravitational wave detection[J]. Advances in Mechanics, 2013, 43(4): 415. DOI:10.6052/1000-0992-13-044 |
| [3] |
DANZMANN K. LISA-An ESA cornerstone mission for the detection and observation of gravitational waves[J]. Advances in Space Research, 2003, 32(7): 1233. DOI:10.1016/S02-73-1177(03)90323-1 |
| [4] |
LUO J, CHEN L S, DUAN H Z, et al. TianQin: a space-borne gravitational wave detector[J]. Classical & Quantum Gravity, 2015, 33(3): 35. DOI:10.1088/0264-9381/33/3/035010 |
| [5] |
黄双林, 龚雪飞, 徐鹏, 等. 空间引力波探测:天文学的一个新窗口[J]. 中国科学:物理学力学天文学, 2017(1): 38. HUANG Shuanglin, GONG Xuefei, XU Peng, et al. Gravitational wave detection in space: a new window in astronomy[J]. Sci Sin-Phys Mech Astron, 2017(1): 38. DOI:10.1360/SSPMA2016-00438 |
| [6] |
ARMANO M, AUDLEY H, BAIRD J, et al. LISA pathfinder platform stability and drag-free performance[J]. Physical Review D, 2019, 99(8): 82001. DOI:10.1103/PhysRevD.99.082001 |
| [7] |
AUDLEY H, BAIRD J, BINETRUY P, et al. Beyond the required lisa free-fall performance: new LISA pathfinder results down to 20 μHz[J]. Physical Review Letters, 2018, 120(6): 61101. DOI:10.1103/PhysRevLett.120.061101 |
| [8] |
ARMANO M, BENEDETTI M, BOGENSTAHL J, et al. LISA Pathfinder: the experiment and the route to LISA[J]. Classical & Quantum Gravity, 2009, 26(9): 1159. DOI:10.1088/0264-9381/26/9/094001 |
| [9] |
DANZMANN K. LISA-A proposal in response to the ESA call for L3 mission concepts[EB/OL]. [2020-02-18]. https://www.cosmos.-esa.int/documents/678316/1700384/LISA_L3-_20170120Submitted.pdf/5b036a72-ed33-dbad-871d-f16ed282723d.
|
| [10] |
邓剑峰, 蔡志鸣, 陈琨, 等. 无拖曳控制技术研究及在我国空间引力波探测中的应用[J]. 中国光学, 2019, 12(3): 503. DENG Jianfeng, CAI Zhiming, CHEN Kun, et al. Drag-free control and its application in China's space gravitational wave detection[J]. Chinese Optics, 2019, 12(3): 503. DOI:10.3788/-CO.20191203.0503 |
| [11] |
胡明, 李洪银, 周泽兵. 无拖曳控制技术及其应用[J]. 载人航天, 2013, 19(2): 61. HU Ming, LI Hongyin, ZHOU Zebing. Drag-free control technology and its application[J]. Manned Spaceflight, 2013, 19(2): 61. DOI:10.3969/j.issn.1674-5825.2013.02.010 |
| [12] |
ZIEMER J K, MARRESE-READING C M, ARESTIE S M, et al. LISA colloid microthruster technology development plan and progress[C]//36th International Electric Propulsion Conference. Vienna: IEPC, 2019
|
| [13] |
SNYDER N J, WILLIAMS W M, DENTON D L, et al. A Satellite freed of all but gravitational forces: "TRIAD I"[J]. Journal of Spacecraft & Rockets, 1974, 11(9): 637. DOI:10.2514/3.62146 |
| [14] |
BENCZE W J, DEBRA D B, HERMAN L, et al. On-orbit performance of the Gravity Probe B drag-free translation control system[C]//Advances in the Astronautical Sciences. Breckenridge: Univelt Inc, 2006
|
| [15] |
张天平, 张雪儿. 空间电推进技术及应用新进展[J]. 真空与低温, 2013(4): 187. ZHANG Tianping, ZHANG Xueer. Electric propulsion progress in technologies and applications[J]. Vacuum & Cryogenics, 2013(4): 187. DOI:10.3969/j.issn.1006-7086.2013.040.-01 |
| [16] |
MAZOUFFRE S. Electric propulsion for satellites and spacecraft: established technologies and novel approaches[J]. Plasma Sources Science & Technology, 2016, 25(3): 33. DOI:10.1088/0963-0252/25-/3/033002 |
| [17] |
EDWARDS C H, WALLACE N C, TATO C, et al. The T5 ion propulsion assembly for drag compensation on GOCE[C]//Proc. Second International GOCE User Workshop "GOCE, The Geoid and Oceanography". Frascati: ESA, 2004
|
| [18] |
CORBETT M H. Thrust control algorithms for the GOCE ion propulsion assembly[C]//30th International Electric Propulsion Conference. Florence: IEPC, 2007
|
| [19] |
ANDERSON J, ANDERSON M, AVENI G, et al. Experimental results from the ST7 mission on LISA Pathfinder[J]. Physical Review D, 2018, 98(10): 102005. DOI:10.1103/PhysRevD.-98.102005 |
| [20] |
ZIEMER J, MARRESE-READING C, DUNN C, et al. Colloid microthruster flight performance results from space technology 7 disturbance reduction system[C]//35th International Electric Propulsion Conference. Atlanta: IEPC, 2017
|
| [21] |
LEITER H, LOTZ B, FEILI D, et al. Design development and test of the RIT-μX mini ion engine system[C]//31st International Electric Propulsion Conference. Michigan: IEPC, 2009
|
| [22] |
HEY F G. Micro Newton thruster development[M]. Berlin: Springer Vieweg, 2018: 117. DOI:10.1007/978-3-658-21209-4
|
| [23] |
LIU Hui, YU Daren, WU Huan, et al. Study of the electric field formation in a multi-cusped magnetic field[J]. Physics of Plasmas, 2014, 21(9): 90706. DOI:10.1063/1.4896250 |
| [24] |
ZHAO Y J, LIU H, YU D R, et al. Particle-in-cell simulations for the effect of magnetic field strength on a cusped field thruster[J]. Journal of Physics D Applied Physics, 2014, 47(4): 45201. DOI:10.1088/0022-3727/47/4/045201 |
| [25] |
HU P, HU Y L, MAO W, et al. Study on the large-range thrust throttling ability in a multi-cusped field thruster[J]. Vacuum, 2019, 168: 108807. DOI:10.1016/j.vacuum.2019.108807 |
| [26] |
HU P, LIU H, CAO Y Y, et al. Study on the structure and transition of the hollow plume in a multi-cusped field thruster[J]. Physics of Plasmas, 2016, 23(10): 103517. DOI:10.1063/1.4965910 |
| [27] |
HU P, MAO W, HU Y, et al. Experimental study on two kinds of electron conduction routes in a multi-cusped field thruster[J]. Plasma Research Express, 2019, 1(2): 25006. DOI:10.1-088/2516-1067/ab172f |
| [28] |
YU D R, HU P, LIU H, et al. Experimental study on the ionization regions in a multi-cusped field thruster[J]. Plasma Sources Science and Technology, 2018, 27(7): 75012. DOI:10.1088/-1361-6595/aac961 |
| [29] |
ITO T, GASCON N, CRAWFORD W S, et al. Experimental characterization of a micro-Hall thruster[J]. Journal of Propulsion & Power, 2007, 23(5): 1068. DOI:10.2514/1.27140 |
| [30] |
KOCH N, SCHIRRA M, WEIS S, et al. The HEMPT concept : A survey on theoretical considerations and experimental evidences[C]//32nd International Electric Propulsion Conference. Wiesbaden: IEPC, 2011
|
| [31] |
KELLER A. Feasibility of a down-scaled HEMP-thruster[D]. Giessen: Justus Liebig University Giessen, 2013: 89
|
| [32] |
胡鹏.多级会切磁场等离子体推力器的电离和加速机制研究[D].哈尔滨: 哈尔滨工业大学, 2017 HU Peng. Study on the ionization and acceleration mechanisms of the multi-cusped field thruster[D]. Harbin: Harbin Institute of Technology, 2017 |
| [33] |
NGUYEN A N, CONKLIN J W. Three-axis drag-free control and drag force recovery of a single-thruster small satellite[J]. Journal of Spacecraft & Rockets, 2015, 52(6): 1. DOI:10.-2514/1.A33190 |
| [34] |
CURTIS H D. Orbital mechanics for engineering students[M]. Third Edition. Oxford: Elsevier, 2014: 709.
|
 2020, Vol. 52
2020, Vol. 52


