2. 哈尔滨工业大学 机电工程学院, 哈尔滨 150001;
3. 哈尔滨工业大学 空间环境与物质科学研究院, 哈尔滨 150001
2. School of Mechatronics Engineering, Harbin Institute of Technology, Harbin 150001, China;
3. School of Space Enviroment and Physical Science, Harbin Institute of Technology, Harbin 150001, China;
近年来,声子晶体因其在结构减振降噪领域巨大的潜在应用价值而得到了科研人员的广泛关注,其带隙特性研究已成为工程振动控制领域的前沿基础性问题之一[1].声子晶体是由两种或两种以上介质组成的具有弹性波带隙特性的周期性复合材料或结构[2].某些频率范围内的弹性波无法在其中传播,相应的频率范围称为带隙,其他频率范围称为通带[3].带隙的形成机理有两种,即Bragg散射机理和局域共振机理,相应的带隙称为Bragg带隙和局域共振带隙[4].
Bragg带隙具有宽度大、衰减能力强的优点.但受到Bragg条件的限制,只有当该型声子晶体晶格尺寸与弹性波半波长相当时才会出现[5].若想获得低频带隙,需要将晶格尺寸设计的很大.这限制了Bragg型声子晶体在工程振动控制领域的应用,因为工程中往往对结构尺寸设计有严格要求.
2000年,Liu等首次发现并制备了局域共振型声子晶体,该型声子晶体表现出负等效质量、负等效刚度和负等效弹性模量等性质,这些与自然界中物质的物理性质迥然相异[6].类比于电磁学超材料的概念,科研人员将这种声子晶体称为声学超材料[7].声学超材料带隙频率对应的波长远远大于晶格尺寸,这一发现突破了Bragg条件的限制,为低频减振降噪提供了新思路.但声学超材料低频带隙较窄,若要将其应用于工程结构的振动控制,有待深入研究.
综上所述,为了突破局域共振带隙宽度窄的瓶颈,本文尝试将剪切模式的磁流变弹性体(magnetorheological elastomer, MRE)引入局域共振单元,设计一种以单胞负等效质量为带隙主要成因的新型声学超材料梁并对其带隙特性进行分析[6].相应研究成果将为声学超材料的低频宽频带隙设计提供理论支撑和有益参考.
1 问题描述局域共振带隙与声学超材料局域共振单元的固有频率息息相关,一般条件下,固有频率决定了局域共振带隙的位置.以往的相关研究中,超材料结构一经设计,局域共振单元的刚度也随之确定,使得相应带隙局限在这一确定的固有频率附近,造成局域共振带隙宽度远小于Bragg带隙宽度.本文便以此为突破口,研究变刚度局域共振单元对局域共振带隙的影响,以求有效增大带隙的宽度.
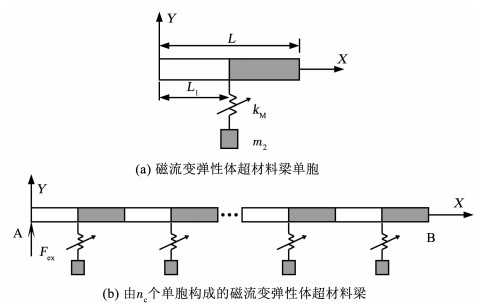
本文主要以图 1所示的超材料梁为研究对象.其中,L和L1分别为单胞总长与局域共振单元吊点左侧梁段的长度,kM和m2分别为磁流变弹性体局域共振单元刚度和附加质量块质量,Fex为外激励.初始模型参数见表 1,其中,m1为不计局域共振单元时单胞内梁段总质量,kM将在后文中给出.文中涉及到的材料参数见表 2.
|
(a) A cell of MRE metamaterial beam; (b) MRE metamaterial beam composed by nc cells 图 1 磁流变弹性体超材料梁 Fig. 1 MRE metamaterial beam |
| 表 1 初始模型参数 Tab. 1 Parameters of the initial model |
| 表 2 文中涉及的材料参数 Tab. 2 Material parameters used in the paper |
谱元法是基于波动方程精确解并结合有限元法和动力学刚度法的思想发展而来的一种精确频域方法.鉴于本文将要进行超材料梁的带隙特性分析,频域内计算结果的准确性至关重要,因此,本文将采用谱元法进行建模,下面构建谱单元.
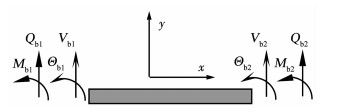
2.1 谱梁单元在谱梁单元的构建过程中,不考虑剪切变形的影响,即采用如图 2所示欧拉梁模型.图中,Vb1,Θb1,Vb2和Θb2为谱梁单元的节点位移分量,Qb1,Mb1,Qb2和Mb2为其节点力分量.时域内梁的自由弯曲振动运动方程为
| $ E I \frac{\partial^{4} v(x, t)}{\partial x^{4}}+\rho A \frac{\partial^{2} v(x, t)}{\partial t^{2}}=0. $ | (1) |
|
图 2 谱梁单元的节点力和节点位移 Fig. 2 Nodal forces and displacements of the spectral beam element |
式中:I为抗弯截面惯性矩;A为梁的横截面积;v(x, t)为时域内的横向位移.
依据离散傅里叶变换理论和奈奎斯特定理,v(x, t)可以写为谱表达形式
| $ v(x, t)=\frac{1}{N} \sum\limits_{n=0}^{N-1} V(x, \omega) \mathrm{e}^{\mathrm{i} \omega t}. $ | (2) |
式中:V(x, ω)为时域内横向位移的谱分量;ω为第n阶谐波频率.
将式(2)代入式(1)可得
| $ E I \frac{\partial^{4} V(x, \omega)}{\partial x^{4}}-\rho A \omega^{2} V(x, \omega)=0. $ | (3) |
求解方程(3),并结合位移连续边界条件可得
| $ \boldsymbol{V}(x, \omega)=\boldsymbol{N}_{\mathrm{b}} \boldsymbol{V}_{\mathrm{b}}. $ | (4) |
式中:Vb为频域内的节点位移向量;Nb是谱梁单元的动力学形函数,其具体表达式可参见参考文献[8].
对式(3)应用加权积分法和分部积分可得
| $ \boldsymbol{S}_{\mathrm{b}}(\omega) \boldsymbol{V}_{\mathrm{b}}=\boldsymbol{f}_{\mathrm{b}}. $ | (5) |
式中:fb为谱梁单元的节点力向量;Sb(ω)为谱梁单元的单元刚度矩阵,具体表达式为
| $ \boldsymbol{S}_{\mathrm{b}}(\omega)=\int_{0}^{L} E I N_{\mathrm{b}}^{\prime \prime \mathrm{T}} N_{\mathrm{b}}^{\prime \prime} \mathrm{d} x-\int_{0}^{L} \rho A \omega^{2} N_{\mathrm{b}}^{\mathrm{T}} N_{\mathrm{b}} \mathrm{d} x. $ | (6) |
将Nb的表达式代入式(6)可得
| $ \boldsymbol{S}_{\mathrm{b}}(\omega)=\frac{E I}{L_{\mathrm{b}}^{3}}\left[\begin{array}{cccc} R_{\mathrm{b1}} & R_{\mathrm{b} 2} L_{\mathrm{b}} & R_{\mathrm{b} 3} & R_{\mathrm{b} 4} L_{\mathrm{b}} \\ & R_{\mathrm{b5}} L_{\mathrm{b}}^{2} & -R_{\mathrm{b} 4} L_{\mathrm{b}} & R_{\mathrm{b} 6} L_{\mathrm{b}}^{2} \\ & & R_{\mathrm{b} 1} & -R_{\mathrm{b} 2} L_{\mathrm{b}} \\ Sy m.& & R_{\mathrm{b} 5} L_{\mathrm{b}}^{2} \end{array}\right]. $ | (7) |
式中
| $ R_{\mathrm{b1}}=\frac{\left(\cos k_{\mathrm{b}} L_{\mathrm{b}} \sinh k_{\mathrm{b}} L_{\mathrm{b}}+\sin k_{\mathrm{b}} L_{\mathrm{b}} \cosh k_{\mathrm{b}} L_{\mathrm{b}}\right) k_{\mathrm{b}}^{3} L_{\mathrm{b}}^{3}}{1-\cos k_{\mathrm{b}} L_{\mathrm{b}} \cosh k_{\mathrm{b}} L_{\mathrm{b}}} $ | (8) |
| $ R_{\mathrm{b} 2}=\frac{\left(\sin k_{\mathrm{b}} L_{\mathrm{b}} \sinh k_{\mathrm{b}} L_{\mathrm{b}}\right) k_{\mathrm{b}}^{2} L_{\mathrm{b}}^{2}}{1-\cos k_{\mathrm{b}} L_{\mathrm{b}} \cosh k_{\mathrm{b}} L_{\mathrm{b}}}, $ | (9) |
| $ R_{\mathrm{b} 3}=-\frac{\left(\sin k_{\mathrm{b}} L_{\mathrm{b}}+\sinh k_{\mathrm{b}} L_{\mathrm{b}}\right) k_{\mathrm{b}}^{3} L_{\mathrm{b}}^{3}}{1-\cos k_{\mathrm{b}} L_{\mathrm{b}} \cosh k_{\mathrm{b}} L_{\mathrm{b}}}. $ | (10) |
| $ R_{\mathrm{b} 4}=\frac{\left(-\cos k_{\mathrm{b}} L_{\mathrm{b}}+\cosh k_{\mathrm{b}} L_{\mathrm{b}}\right) k_{\mathrm{b}}^{2} L_{\mathrm{b}}^{2}}{1-\cos k_{\mathrm{b}} L_{\mathrm{b}} \cosh k_{\mathrm{b}} L_{\mathrm{b}}}, $ | (11) |
| $ R_{\mathrm{b} 5}=\frac{\left(-\cos k_{\mathrm{b}} L_{\mathrm{b}} \sinh k_{\mathrm{b}} L_{\mathrm{b}}+\sin k_{\mathrm{b}} L_{\mathrm{b}} \cosh k_{\mathrm{b}} L_{\mathrm{b}}\right) k_{\mathrm{b}} L_{\mathrm{b}}}{1-\cos k_{\mathrm{b}} L_{\mathrm{b}} \cosh k_{\mathrm{b}} L_{\mathrm{b}}}, $ | (12) |
| $ R_{\mathrm{b} 6}=\frac{\left(-\sin k_{\mathrm{b}} L_{\mathrm{b}}+\sinh k_{\mathrm{b}} L_{\mathrm{b}}\right) k_{\mathrm{b}} L_{\mathrm{b}}}{1-\cos k_{\mathrm{b}} L_{\mathrm{b}} \cosh k_{\mathrm{b}} L_{\mathrm{b}}}. $ | (13) |
式中:Lb为谱梁单元长度;kb为弯曲波数,具体表达式为
| $ k_{\mathrm{b}}=\sqrt{\omega}\left(\frac{\rho A}{E I}\right)^{1 / 4}. $ | (14) |
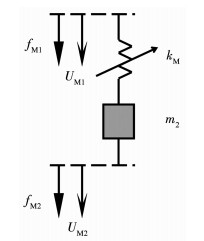
图 3所示为磁流变弹性体局域共振谱单元,其中,UM1,UM2,fM1和fM2表示该单元的节点位移和节点力分量.磁流变弹性体在剪切模式下的刚度可写为[9]
| $ \boldsymbol{k}_{\mathrm{M}}=\frac{2 A_{\mathrm{M}}}{\boldsymbol{h}}\left[\frac{G_{0}^{2}+2 G_{0} \boldsymbol{\eta}(\mathrm{i} \omega)^{\alpha}+\left(G_{0}+\boldsymbol{\eta}(\mathrm{i} \omega)^{\alpha}\right) \Delta G}{G_{0}+\boldsymbol{\eta}(\mathrm{i} \omega)^{\alpha}}\right]. $ | (15) |
|
图 3 磁流变弹性体局域共振谱单元 Fig. 3 Spectral MRE local resonator element |
式中:AM为磁流变弹性体剪切面的面积;h为垂直于剪切面的磁流变弹性体厚度;G0为磁流变弹性体固化后未施加外磁场条件下的剪切模量;η为动力粘度;α为不同铁粒子体积分数的磁流变弹性体对应的微分阶数;G为外磁场作用下磁流变弹性体剪切模量的变化量,其具体表达式为
| $ \Delta G=\frac{18 \mu_{0} \mu_{1} \chi^{2} H_{0}^{2} \varphi A_{\mathrm{c}} k_{0}^{3}\left(1-\varepsilon_{\text {matrix }}\right)^{3}\left(4-\gamma^{2}\right)}{\left(1+\gamma^{2}\right)^{3.5}\left[3 k_{0}^{3}\left(1-\varepsilon_{\text {matrix }}\right)^{3}-4 \chi A_{\mathrm{c}}\right]^{2}}. $ | (16) |
式中:μ0和μ1分别为磁流变弹性体基体的真空磁导率和相对磁导率;χ为粒子的磁化率;H0为外加磁场强度;ϕ为铁粒子的体积分数;Ac为由粒子极化数量决定的系数,当极化的粒子足够多时,该系数为定值;k0为无纵向压力条件下铁粒子间距与半径的比值;εmatrix为磁流变弹性体基体的正压应变;γ为振荡剪切应变的振幅.
利用力-位移关系,由文献[10]的推导可得磁流变弹性体局域共振谱单元的运动方程为
| $ \boldsymbol{S}_{\mathrm{M}}(\omega) \boldsymbol{U}_{\mathrm{M}}=\boldsymbol{f}_{\mathrm{M}}. $ | (17) |
式中:UM和fM分别为磁流变弹性体局域共振谱单元的节点位移和节点力向量;SM(ω)为该谱单元的单元刚度矩阵,具体表达式为
| $ \boldsymbol{S}_{\mathrm{M}}(\omega)=\left[\begin{array}{cc} k_{\mathrm{M}} & -k_{\mathrm{M}} \\ -k_{\mathrm{M}} & k_{\mathrm{M}}-m_{2} \omega^{2} \end{array}\right]. $ | (18) |
基于上述谱梁单元与磁流变弹性体局域共振谱单元,采用相应节点位移叠加的方式进行组装即可完成对磁流变弹性体超材料梁的动力学建模,具体组装过程可参见文献[11].
制备磁流变弹性体一般选用粒径为3~6 μm的铁粒子,当铁粒子的体积分数达到30%左右时,磁流变弹性体在外磁场作用下的刚度可调控性最佳[12-13].因此,本文选择将铁粒子体积分数为34%的磁流变弹性体应用于局域共振单元的设计,基于已有研究数据,初始参数见表 3[9, 14-15].
| 表 3 初始模型磁流变弹性体局域共振单元参数 Tab. 3 Parameters of MRE local resonator element in the initial model |
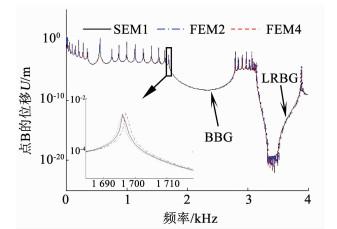
基于初始模型,梁的材料选用铝.当局域共振单元刚度kM为固定值7×105 N/m时,在图 1(b)A点沿Y方向施加外激励Fex=10eiωt,边界条件为两端自由,分别采用谱元法和有限元法计算B点沿Y方向的频响曲线,如图 4所示.图中SEM1为采用谱元法建模过程中,单胞内吊点两侧的梁段仅用1个谱梁单元建模计算的结果;FEM2和FEM4表示有限元法分别用2个和4个单元进行建模的计算结果.由图 4可见,随着网格的细化,有限元法的频响曲线计算结果趋近于谱元法的结果,证明了本文方法的正确性.图中1 710~2 800 Hz和3 180~3 880 Hz 2个频段分别对应于Bragg带隙(BBG)和局域共振带隙(LRBG).
|
图 4 谱元法与有限元法计算的频响曲线 Fig. 4 Frequency response calculated by spectral element method and finite element method |
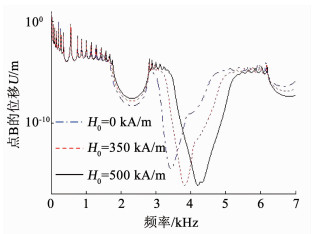
基于初始模型,改变外加磁场强度的大小,计算得到的频响曲线如图 5所示,相应的磁流变弹性体局域共振单元刚度分别为0 kN/m、726.3 kN/m和1 028 kN/m.由图可见,随着外加磁场强度的增大,Bragg带隙的衰减能力有所减弱,下界频率增大,上界频率不变,带宽略有减小;局域共振带隙向高频移动,带宽增大.
|
图 5 外加磁场强度对超材料梁带隙特性的影响 Fig. 5 Influence of intensity of applied magnetic field on the band-gap property of metamaterial beam |
值得注意的是,图 5中的局域共振带隙宽度已经超越了相邻Bragg带隙的宽度,这与已有局域共振带隙的研究结论形成鲜明对比,突破了该型带隙带宽小的传统印象和瓶颈.这一发现源于图 5计算结果所对应的局域共振单元刚度不同于正确性检验,它不是固定值,而是通过式(15)计算而来.该磁流变弹性体局域共振单元刚度是谐波频率ω和外加磁场强度H0的函数,并且与两者呈非线性关系[9].换言之,本文设计的磁流变弹性体局域共振单元可以有效增加相应超材料梁的局域共振带隙宽度,从而提升该超材料梁的减隔振能力.
为获得低频带隙,本文进一步增加磁流变弹性体局域共振单元的附加质量,相应频响曲线如图 6所示.从图中可以发现,随着附加质量的增加,本文所设计超材料梁的Bragg带隙下界频率减小,上界频率几乎不变,导致其带隙宽度增加.同时,局域共振带隙受到相邻Bragg带隙上界频率的限制,仅能在一定范围内整体向低频移动,带宽减小.

|
图 6 局域共振单元质量对超材料梁带隙特性的影响 Fig. 6 Influence of local resonator mass on the band-gap property of metamaterial beam |
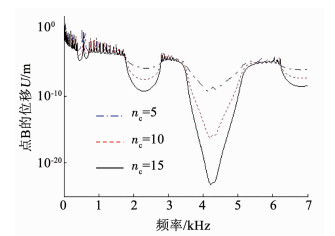
在初始模型基础上,将外加磁场强度调整为50 kA/m,改变图 1超材料梁的单胞数nc,计算得到的频响曲线如图 7所示.随着单胞数的增加,Bragg带隙和局域共振带隙的位置和宽度均保持不变,衰减能力明显增强.
|
图 7 单胞数对超材料梁带隙特性的影响 Fig. 7 Influence of cell number on the band-gap property of metamaterial beam |
上述改进方式对获得低频宽频带隙而言作用有限,为此,本文在nc=10的图 7计算模型基础上,依据表 2给出的材料参数改变单胞中局域共振单元吊点左右两侧梁段的材料组合,计算结果如图 8所示.

|
图 8 单胞材料组合对超材料梁带隙特性影响 Fig. 8 Influence of cell-material combination on the band-gap property of metamaterial beam |
总体上,材料组合差异越大,低频带隙越多,总带宽越大.具体而言,随着材料组合中两种材料差异的增大,所有带隙衰减能力均明显提高.Bragg带隙数量明显增多,带宽增大;局域共振带隙向低频移动,带宽有所减小.
4 结论1) 采用基于磁流变弹性体的局域共振单元设计超材料梁,使局域共振带隙宽度达到与Bragg带隙相当的水平,是突破局域共振带隙宽度窄这一传统瓶颈的有效方式.
2) 增大磁流变弹性体局域共振单元附加质量,将减小超材料梁Bragg带隙的下界频率(本文50 Hz以上)并拓展其带隙宽度,与此同时,局域共振带隙向低频移动,提高了相应超材料梁的低频减振能力.
3) 增加磁流变弹性体超材料梁单胞数是提高其Bragg带隙和局域共振带隙衰减能力的有效手段(本文每增加5个单胞,带隙内的位移减小约2个量级),并且这两类带隙的位置和带宽不随之发生改变.
4) 通过对磁流变弹性体超材料梁进行材料周期性设计可大幅提升其低频减振性能.材料组合中两种材料的性质差异越大,低频带隙越多,总带宽越大,衰减能力越强.
| [1] |
俞孟萨, 林立. 船舶水下噪声研究三十年的基本进展及若干前沿基础问题[J]. 船舶力学, 2017, 21(2): 244. YU Mengsa, LIN Li. Some progresses of underwater noise of ships in recent thirty years and several new basic problems[J]. Journal of Ship Mechanics, 2017, 21(2): 244. DOI:10.3969/j.issn.1007-7294.2017.02.015 |
| [2] |
温激鸿, 郁殿龙, 赵宏刚, 等. 人工周期结构中弹性波的传播[M]. 北京: 科学出版社, 2015. WEN Jihong, YU Dianlong, ZHAO Honggang, et al. Propagation of elastic waves in artificial periodic structures[M]. Beijing: Science Press, 2015. |
| [3] |
WU Zhijing, LI Fengming, ZHANG Chuanzeng. Band-gap analysis of a novel lattice with a hierarchical periodicity using the spectral element method[J]. Journal of Sound and Vibration, 2018, 421: 246. DOI:10.1016/j.jsv.2018.02.009 |
| [4] |
JIANG Shan, CHEN Hao, DAI Longxiang, et al. Multiple low-frequency broad band gaps generated by a phononic crystal of periodic circular cavity sandwich plates[J]. Composite Structures, 2017, 176: 294. DOI:10.1016/j.compstruct.2017.05.048 |
| [5] |
DEYMIER P A. Acoustic metamaterials and phononic crystals[M]. Berlin: Springer, 2013.
|
| [6] |
PAI P F, PENG Hao, JIANG Shuyi. Acoustic metamaterial beams based on multi-frequency vibration absorbers[J]. International Journal of Mechanical Sciences, 2014, 79: 195. DOI:10.1016/j.ijmecsci.2013.12.013 |
| [7] |
HUSSEIN M I, LEAMY M J, RUZZENE M. Dynamics of phononic materials and structures: historical origins, recent progress, and future outlook[J]. Applied Mechanics Reviews, 2014, 66(4): 040802. DOI:10.1115/1.4026911 |
| [8] |
WEN Shurui, LU Nianli, WU Zhijing. Dynamic property analysis of the space-frame structure using the spectral element method[J]. Waves in Random and Complex Media, 2014, 24(4): 404. DOI:10.1080/17455030.2014.930758 |
| [9] |
KUMBHAR S B, CHAVAN S P, GAWADE S S. Adaptive tuned vibration absorber based on magnetorheological elastomer-shape memory alloy composite[J]. Mechanical Systems and Signal Processing, 2018, 100: 208. DOI:10.1016/j.ymssp.2017.07.027 |
| [10] |
李凤明, 刘荣强, 吴志静. 铰接桁架结构动力学问题研究[J]. 宇航学报, 2012, 33(5): 556. LI Fengming, LIU Rongqiang, WU Zhijing. Study on the dynamics problems of truss structures with joints[J]. Journal of Astronautics, 2012, 33(5): 556. DOI:10.3873/j.issn.1000-1328.2012.05.005 |
| [11] |
WU Zhijing, LI Fengming. Spectral element method and its application in analysing the vibration band gap properties of two-dimensional square lattices[J]. Journal of Vibration and Control, 2016, 22: 710. DOI:10.1177/1077546314531805 |
| [12] |
KALLIO M, LINDROOS T, AALTO S, et al. Dynamic compression testing of a tunable spring element consisting of a magnetorheological elastomer[J]. Smart Materials & Structures, 2007, 16(2): 506. |
| [13] |
LERNER A A, Cunefare K A. Performance of MRE-based vibration absorbers[J]. Journal of Intelligent Material Systems and Structures, 2007, 19(5): 551. DOI:10.1177/1045389X07077850 |
| [14] |
DENG Huaxia, GONG Xinglong. Adaptive tuned vibration absorber based on magnetorheological elastomer[J]. Journal of Intelligent Material Systems and Structures, 2007, 18(12): 1205. DOI:10.1177/1045389X07083128 |
| [15] |
GUO Fei, DU Chengbin, LI Runpu. Viscoelastic parameter model of magnetorheological elastomers based on Abel dashpot[J]. Advances in Mechanical Engineering, 2014, 6: 629386. DOI:10.1155/2014/629386 |
 2020, Vol. 52
2020, Vol. 52


