离合器作为车辆传动系统的重要部件,在各类型的变速器上得到了广泛的应用[1-4].对离合器接合过程进行品质控制可降低车辆冲击度,减少接合滑磨功,减轻对传动零部件冲击,使车辆使用寿命和驾乘舒适性得到提高[5-7].国内外对离合器接合过程品质有不同的评价参数,研究多集中在接合过程轨迹最优和执行机构跟踪效果两个方面[8-9]. Haj-Fraj、彭建鑫、胡宏伟等[10-12]分别利用动态规划法、遗传算法和接合曲线修正算法等多种方法实现离合器接合过程最优控制;陈清洪等[13]以滑磨功最小为目标、冲击度为约束进行接合过程的最优控制;Wang、单外平等[14-15]通过试验与数学模型相结合方法模拟离合器接合轨迹对接合过程品质的影响;离合器接合轨迹研究过程中,从动盘端多加载定值信号,较难反映实际载荷的非平稳性.因离合器执行机构及离合器自身具有较强非线性特性,多采用具有鲁棒性的控制器实现执行机构跟踪[16-18].滑模控制方法算法简单,能克服系统的不确定性, 对外界噪声干扰和未建模动态参数摄动具有鲁棒性,对非线性系统具有良好的控制效果[19-22]. Li Junqiu、赵韩、孙承顺等[23-25]采用滑模控制方法实现离合器接合过程中车速、油压及其位移的鲁棒跟踪;Li、赵治国等[26-27]采用滑模控制和不确定观测器相结合的方法实现离合器接合过程扭矩估计和油压轨迹跟踪.考虑系统内外部扰动等因素,以冲击度和滑磨功为约束条件的离合器接合轨迹及跟踪相结合控制的研究较少.
本文在变速器换挡规律确定的前提下,以装载机V型重载后退换挡中离合器接合过程为研究对象,通过建立冲击度和滑磨功相结合的二次型性能指标泛函和依据Pontryagin极大值原理等方法,实现其时变控制律下的可变扭矩最优轨迹,并采用滑模方法进行跟踪控制设计.通过对离合器冲击度、滑磨功和跟踪精度等数据分析,验证了设计方法的有效性,改善了离合器接合过程品质.
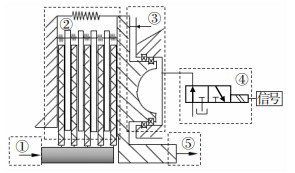
1 离合器接合过程数学模型在换挡规律确定前提下,离合器接合过程的研究主要集中在主从动摩擦片开始接触直至两者转速差为零的滑磨时间段,该过程是车辆冲击度和滑磨功产生的阶段[7].离合器接合过程系统结构原理如图 1所示.
|
①离合器主动端(动力端)模型;②接合过程动力学模型;③执行机构模型;④压力控制模型;⑤离合器从动端(载荷端) 图 1 接合过程系统结构原理简图 Fig. 1 Schematic diagram of structural principle of engagement process system |
以装载机V型重载后退换挡中变速箱输入输出端实测载荷和转速数据为基础进行参数化模型构建,有利于后续台架或车辆试验前的仿真和加载.部分元器件安装和测试采集的数据曲线如图 2所示.

|
图 2 部分元器件安装图和测试曲线 Fig. 2 Part component installation diagram and test curves |
对0.8~1.5 s内多组变速器输出端扭矩随机试验样本数据的平稳性进行轮次数检验,可知该时间段信号非平稳,其重构数学模型为[28]
| $ {x_t} = {d_t} + {s_t}. $ | (1) |
式中:xt为某一时间历程非平稳随机载荷,dt为xt中的确定性分量,st为xt中平稳随机分量.
利用变速器输出扭矩所构建的参数化数学模型均值数据与文献[6, 10]等所得数据误差在1%以内,说明该模型在一定程度上可用于系统仿真和试验加载.变速器输入端扭矩和转速数据去除确定性分量后,两者符合均值为零正态分布,亦可用式(1)进行参数化模型表达.
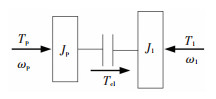
1.2 接合过程动力学模型为更好地研究离合器接合过程的动态特性,对模型进行简化并作如下假设:1)离合器接合滑磨过程采用冷却油冷却,忽略摩擦片热变形;2)忽略零部件间隙和轴横向振动的影响;3)忽略轴承、轴承座和齿轮啮合的弹性变形;4)忽略系统中弹性元件的惯性和惯性元件的弹性.根据上述假设,离合器接合过程滑磨阶段模型如图 3所示.
|
图 3 接合过程模型 Fig. 3 Engagement process model |
动力学方程为
| $ \left\{ {\begin{array}{*{20}{l}} {{J_{\rm{p}}}{{\dot \omega }_{\rm{p}}} = {T_{\rm{p}}} - {c_{\rm{p}}}{\omega _{\rm{p}}} - {T_{{\rm{cl}}}},}\\ {{J_1}{{\dot \omega }_1} = {T_{{\rm{cl}}}} - {c_1}{\omega _1} - {T_1}.} \end{array}} \right. $ | (2) |
式中:Jp为离合器主动盘之前(包括主动盘)的动力系折算到主动盘的等效转动惯量,Tp为动力系折算到离合器主动盘的等效动力矩,ωp为离合器主动盘转速,Tcl为离合器主从动盘传递的扭矩,Jl为离合器从动盘之后(包括从动盘)的传动系折算到从动盘的等效转动惯量,Tl为负载端扭矩折算到从动盘的等效阻力矩,ωl为离合器从动盘转速,cp和cl为等效的旋转黏性阻尼系数.
1.3 执行机构模型此阶段离合器活塞停止运动,钢片与摩擦片间隙消除,作如下假设:1)离合器腔压力油温度和黏度不变;2)离合器腔无泄漏;3)忽略摩擦片的弹性变形.离合器执行机构模型如图 4所示.

|
图 4 离合器执行机构模型 Fig. 4 Clutch actuator model |
离合器受力平衡方程为
| $ {F_{\rm{s}}} = {F_{\rm{p}}} + {F_{\rm{d}}} - {F_{{\rm{cl}}}} - {F_{\rm{g}}} - {F_{{\rm{seal}}}}. $ | (3) |
式中:Fs为离合器复位力;Fp和Fd分别为液压油作用于离合器活塞的静压力和动压力,Fd=ρAp2(αωp)2/(4π);Fcl为离合器摩擦片对活塞反作用力,Fcl=Tcl/(μ(t)ZR);Fg为齿圈花键摩擦力;Fseal为离合器活塞密封阻力;ρ为液压油密度;α为液压油旋转速度滞后系数;Ap为离合器活塞面积;μ(t)为摩擦副动摩擦因数;Z为摩擦副数量;R为摩擦力作用等效半径.
离合器腔流量压力动态方程为
| $ {Q_{\rm{c}}} = ({A_{\rm{p}}}{x_{{\rm{max}}}} + {V_0}){\dot p_{\rm{c}}}/E. $ | (4) |
式中:Qc为流入离合器腔流量,xmax为活塞运动最大位移,V0为离合器腔和油道初始总体积,E为流体体积弹性模量,pc为离合器腔控制压力.
1.4 压力控制模型压力控制通过PWM控制的高速电磁开关阀来实现,在忽略油道液阻力、管路和阀自身泄漏基础上,进入离合器腔控制流量方程为
| $ \left\{ {\begin{array}{*{20}{l}} {{Q_{\rm{c}}} = {{\bar Q}_{{\rm{in}}}} - {{\bar Q}_{{\rm{out}}}},}\\ {{{\bar Q}_{{\rm{in}}}} = \tau {C_{\rm{v}}}{A_{\rm{v}}}\sqrt {\frac{{2({p_{\rm{s}}} - {p_{\rm{c}}})}}{\rho }} ,}\\ {{{\bar Q}_{{\rm{out}}}} = (1 - \tau ){C_{\rm{v}}}{A_{\rm{v}}}\sqrt {\frac{{2({p_{\rm{c}}} - {p_0})}}{\rho }} .} \end{array}} \right. $ | (5) |
式中:Qin为流入离合器腔的平均流量,Qout为流出离合器腔的平均流量,τ为占空比,Cv为阀流量系数,Av为阀进出油口面积,ps为系统供油压力,p0为变速箱内压力.
由以上数学模型知,离合器接合过程的系统之间有较强的非线性时变特性,可采用鲁棒性较强的非线性控制理论来实现其控制.选取的典型工况下离合器接合过程控制设计方法见图 5.

|
图 5 接合过程控制设计流程 Fig. 5 Engagement process control design |
将滑磨功和冲击度作为离合器接合过程品质的评价指标[7],其数学模型为
| $ \left\{ {\begin{array}{*{20}{l}} {W = \int_{{t_0}}^{{t_{\rm{f}}}} {{T_{{\rm{cl}}}}} ({\omega _{\rm{p}}} - {\omega _1}){\rm{d}}t,}\\ {j = \frac{{{r_{\rm{w}}}}}{{{i_0}{J_1}}}\frac{{{\rm{d}}{T_{{\rm{cl}}}}}}{{{\rm{d}}t}}.} \end{array}} \right. $ | (6) |
式中:W为离合器接合过程滑磨功,t0为接合开始时刻,tf为主从动盘转速差为零时刻,j为冲击度,i0为变速器至驱动轮传动比,rw为车轮半径.
考虑滑磨功和冲击度式(6)并结合式(2),取状态向量x=(ωp, ωp-ωl, Tcl)T,控制变量为u,建立的状态方程为
| $ \mathit{\boldsymbol{\dot x}} = {({\dot x_1},{\dot x_2},u)^{\rm{T}}} = \mathit{\boldsymbol{Ax}}(t) + \mathit{\boldsymbol{B}}u(t) + \mathit{\boldsymbol{D}}(t). $ | (7) |
式中:
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} { - \frac{{{c_{\rm{p}}}}}{{{J_{\rm{p}}}}}}&0&{ - \frac{1}{{{J_{\rm{p}}}}}}\\ { - \frac{{{c_{\rm{p}}}}}{{{J_{\rm{p}}}}} + \frac{{{c_1}}}{{{J_1}}}}&{ - \frac{{{c_1}}}{{{J_1}}}}&{ - \frac{1}{{{J_{\rm{p}}}}} - \frac{1}{{{J_1}}}}\\ 0&0&0 \end{array}} \right], $ |
| $ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{l}} 0\\ 0\\ 1 \end{array}} \right],\quad \mathit{\boldsymbol{D}}(t) = \left[ {\begin{array}{*{20}{c}} {\frac{{{T_{\rm{p}}}}}{{{J_{\rm{p}}}}}}\\ {\frac{{{T_{\rm{p}}}}}{{{J_{\rm{p}}}}} + \frac{{{T_1}}}{{{J_1}}}}\\ 0 \end{array}} \right]. $ |
根据离合器接合过程的特点,本文最优控制问题可归结为终端时刻tf有限,终端状态x2(tf)有约束的最优控制问题[29].
二次型性能指标泛函如式(8)所示,其中对冲击度的评价定义为接合过程冲击度平方总和.
| $ J = 0.5\int_{{t_0}}^{{t_{\rm{f}}}} {({x_2}u + \beta {u^2})} {\rm{d}}t = 0.5(W + \gamma \beta \int_{{t_0}}^{{t_{\rm{f}}}} {{j^2}} {\rm{d}}t). $ | (8) |
式中:
| $ \mathit{\boldsymbol{Q}} = \left[ {\begin{array}{*{20}{c}} 0&0&0\\ 0&0&{0.5}\\ 0&{0.5}&0 \end{array}} \right], $ |
R为控制加权矩阵,β为权重系数,γ为系数(i0Jl/rw)2.
构造的Hamiltonian函数为
| $ \begin{array}{*{20}{c}} {H(\mathit{\boldsymbol{x}},u,\lambda ) = 0.5({\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{Qx}} + \beta {u^2}) + \mathit{\boldsymbol{\lambda }}{{(t)}^{\rm{T}}}(\mathit{\boldsymbol{Ax}}(t) + }\\ {\mathit{\boldsymbol{B}}u(t) + \mathit{\boldsymbol{D}}(t)).} \end{array} $ |
式中λ(t)为待定的拉格朗日乘子向量函数.
初始条件和终端约束条件:
| $ \begin{array}{l} \mathit{\boldsymbol{x}}({t_0}) = {[{\omega _{{\rm{p0}}}},{\omega _{{\rm{p0}}}} - {\omega _{10}},{T_{{\rm{clo}}}}]^{\rm{T}}},\\ N[\mathit{\boldsymbol{x}}({t_{\rm{f}}}),{t_{\rm{f}}}] = {x_2}({t_{\rm{f}}}) = 0. \end{array} $ |
由极值条件,得
| $ \left\{ {\begin{array}{*{20}{l}} {\partial H/\partial u = \beta u + {\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{\lambda }}(t) = 0,}\\ {{u^*}(t) = - {\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{\lambda }}(t)/\beta .} \end{array}} \right. $ | (9) |
同时由于
| $ {\partial ^2}H/\partial {u^2} = \beta > 0, $ |
根据Pontryagin极大值原理,可知式(9)中确定的u*(t)是泛函取得极小值的最优控制.
同时,规范方程为
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot x}} = \partial H/\partial \mathit{\boldsymbol{\lambda }} = \mathit{\boldsymbol{Ax}}(t) + \mathit{\boldsymbol{B}}u(t) + \mathit{\boldsymbol{D}}(t),}\\ {\mathit{\boldsymbol{\dot \lambda }} = - \partial H/\partial \mathit{\boldsymbol{x}} = - \mathit{\boldsymbol{Qx}} - {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{\lambda }}(t).} \end{array}} \right. $ |
横截条件为
| $ \mathit{\boldsymbol{\lambda }}({t_{\rm{f}}}) = {[0,\nu ,0]^{\rm{T}}}. $ | (10) |
式中ν为待求值λ2(tf).
干扰矩阵D(t)的存在,使最优控制u*(t)无法通过求解Riccati方程中P(t)来获得λ(t)[29]. λ(t)通过如下方程组构建
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\lambda }}(t) = \mathit{\boldsymbol{P}}(t)\mathit{\boldsymbol{x}}(t) + \mathit{\boldsymbol{G}}(t)\nu + \mathit{\boldsymbol{H}}(t),}\\ {\psi = {x_2}({t_{\rm{f}}}) = F(t)\mathit{\boldsymbol{x}}(t) + m(t)\nu + n(t).} \end{array}} \right. $ | (11) |
式中:P(tf)为3阶零矩阵,G(tf)=[0, 1, 0]T用于求解v,H(tf)=[0, 0, 0]T用于补偿向量D(t),F(tf)=[0, 1, 0],m(tf)=0,n(tf)=0.
联立方程(9)、(10)和(11)及相关方程的微分,在通过Riccati微分方程求解P(t)基础上得G(t)、H(t)、F(t)、m(t)和n(t),待定值v求解后得最优控制:
| $ {u^*}(t) = - \frac{{{\mathit{\boldsymbol{B}}^{\rm{T}}}}}{\beta }[\mathit{\boldsymbol{P}}(t)\mathit{\boldsymbol{x}}(t) + \mathit{\boldsymbol{G}}(t)\nu + \mathit{\boldsymbol{H}}(t)]. $ |
在2.2节分析基础上,确定tf为1.1 s和权重系数β为1~100范围后,根据表 1中参数对离合器接合过程进行仿真及分析. 在式(7)对u与Tcl的定义和Tcl≤ Tclmax约束下,得离合器接合过程可变扭矩最优轨迹Tcl*(t).
| 表 1 离合器接合过程相关参数 Tab. 1 Parameters of clutch engagement process |
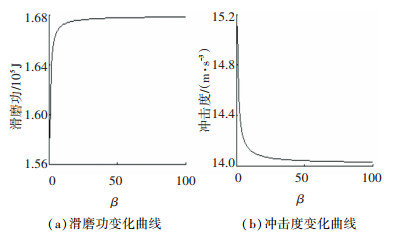
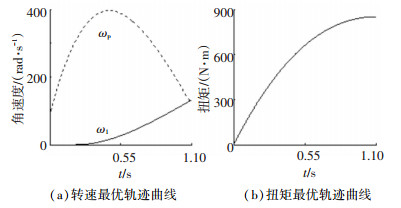
在冲击度小于我国标准17.64 m/s3下使J极小以确定β,图 6为不同权重系数β下滑磨功和冲击度曲线. 图 7为离合器主从动盘接合过程转速和可变扭矩最优轨迹曲线,得tf为1.09 s,β为1,冲击度最大值为15.05 m/s3,比标准低14.68%.
|
图 6 权重系数β对评价指标的影响 Fig. 6 Influence of weighting coefficients β on evaluation index |
|
图 7 最优轨迹曲线 Fig. 7 Optimal trajectory curves |
在离合器摩擦片从动盘阻力矩幅值±5%Tl的变化集合下进一步分析最优轨迹的特性,由图 8和表 2可知,最优轨迹在数学模型增加误差幅度状态下的关键参数变化程度对其性能影响较小.

|
图 8 ±5% Tl变化下最优轨迹曲线 Fig. 8 Optimal trajectory curves under ±5%Tl |
| 表 2 ±5% Tl下关键参数变化百分比 Tab. 2 Percentage changes of key parameters under ±5%Tl |
考虑变速器较多挡位数量和摩擦片用扭矩传感器可靠性(实际车辆中难以将其安装使用[5]),无法通过检测该扭矩信号实现闭环控制.为实现离合器接合过程中最优轨迹的精准跟踪,采用对系统参数摄动和外干扰具有完全不变性的滑模控制方法.
3 基于接合轨迹的滑模控制针对非线性特性执行机构参数摄动下最优轨迹的跟踪精度影响接合过程品质的问题,将难检测的可变扭矩转化为可通过压力传感器检测的离合器压力跟踪问题.与采用车速反馈跟踪相比,该方法能实现离合器换挡过程中充油阶段的检测,有利于整个换挡过程品质的控制设计[30-32].通过式(3)中离合器受力平衡,可实现可变扭矩最优轨迹向压力最优轨迹的转化.
| $ p_{\rm{c}}^*(t) = \frac{{{F_{\rm{s}}}}}{{{A_{\rm{p}}}}} + \frac{{T_{{\rm{cl}}}^*(t)}}{{\mu (t){A_{\rm{p}}}ZR}} - \frac{{\rho {A_{\rm{p}}}{\alpha ^2}\omega _{\rm{p}}^{*2}(t)}}{{4\pi }}. $ | (12) |
选取的切换面为
| $ s = ce + \dot e. $ | (13) |
式中c为滑模面系数.
当切换面s=0时,其滑动模态方程为
| $ ce + \dot e = 0. $ |
在c>0保证系统在切换面稳定前提下,通过Hurwitz确定c范围[22].
选取的指数趋近律为
| $ \dot s = - \varepsilon {\rm{sign}} (s) - ks,\quad \varepsilon > 0,k > 0. $ | (14) |
式中:ε为增益系数,k为趋近律,-εsign(s)项有在一定时间内全局到达切换面的作用,k项保证了趋近时间不过长.
3.2 滑模控制器设计定义状态变量y2=pc(t),控制输入为τ,联立式(4)和(5),建立的跟踪系统状态方程为
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot y}_1} = {y_2},}\\ {{{\dot y}_2} = {K_1}({p_{\rm{c}}})\tau - {K_2}({p_{\rm{c}}}).} \end{array}} \right. $ |
式中y1为状态变量y2的积分值,
| $ \begin{array}{*{20}{c}} {{K_1}({p_{\rm{c}}}) = \frac{{E{C_{\rm{v}}}{A_{\rm{v}}}}}{{{A_{\rm{p}}}{x_{{\rm{max}}}} + {V_0}}}\sqrt {\frac{2}{\rho }} (\sqrt {{p_{\rm{s}}} - {p_{\rm{c}}}} + \sqrt {{p_{\rm{c}}} - {p_0}} ),}\\ {{K_2}({p_{\rm{c}}}) = \frac{{E{C_{\rm{v}}}{A_{\rm{v}}}}}{{{A_{\rm{p}}}{x_{{\rm{max}}}} + {V_0}}}\sqrt {\frac{{2({p_{\rm{c}}} - {p_0})}}{\rho }} .} \end{array} $ |
选择离合器压力最优轨迹pc*(t)作为参考输入r2,引入偏差变量跟踪误差e,建立微分方程为
| $ \left\{ {\begin{array}{*{20}{l}} {\dot e = {{\dot r}_1} - {{\dot y}_1} = {r_2} - {y_2},}\\ {\ddot e = {{\dot r}_2} - {{\dot y}_2} = {{\dot r}_2} - {K_1}({p_{\rm{c}}})\tau + {K_2}({p_{\rm{c}}}).} \end{array}} \right. $ | (15) |
联立式(13)和(14),并将式(15)带入,得
| $ \tau = \frac{1}{{{K_1}({p_{\rm{c}}})}}[\varepsilon {\rm{sign}} (s) + ks + c\dot e + {\dot r_2} + {K_2}({p_{\rm{c}}})]. $ |
基于Lyapunov稳定性理论,选取函数V=0.5 s2,进行稳定性分析.在切换面s≠0时,所设计的控制τ能使控制系统状态在有限时间内收敛至切换面s=0,之后进入滑动模态后
| $ \dot V = s\dot s = s[ - \varepsilon {\rm{sign}} (s) - ks] = - \varepsilon |s| - k{s^2} < 0, $ |
为避免或削弱滑动模态中的抖振,采用饱和函数sat(s)代替符号函数sign(s).
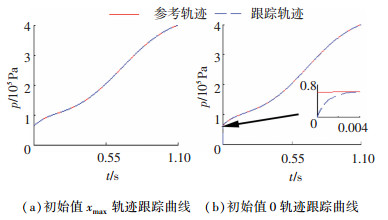
3.3 仿真验证及分析根据前述离合器接合过程动力学模型及滑模控制器,利用Matlab/Simulink建立离合器压力最优轨迹跟踪仿真模型.取c=30, ε=2,k=2 000, 边界层厚度为0.001,设置不同初始点,仿真结果见图 9.其中(a)初始值为离合器位移xmax时压力跟踪曲线,(b)初始值为0,初始值的不同使得图(b)收敛时间延迟0.004 s,两者最大跟踪偏差分别在0.001%和0.280%以内,设计的控制器使离合器接合压力在t0~tf内有效地实现了对参考输入r2的精准跟踪.
|
图 9 初始值对轨迹跟踪影响 Fig. 9 Influence of initial values on trajectory tracking |
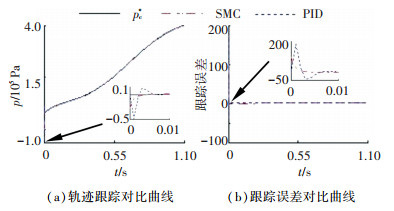
图 10为传统PID控制方法与滑模控制方法在图 9(b)基础上的跟踪效果对比图.由图 10可知:所采用的滑膜控制方法在开始0.01 s内跟踪偏差比传统PID控制方法小40%~130%,该方法在0.01 s后跟踪偏差小于0.1%,总体跟踪效果相对更好.
|
图 10 PID和SMC跟踪效果对比 Fig. 10 Comparison of tracking effects between PID and SMC |
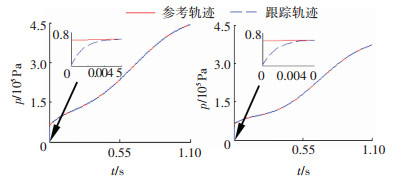
为进一步分析具有非线性特性离合器执行机构的参数摄动对所设计控制器性能的影响,对式(12)中摩擦因数μ(t)±10%摄动变化,由图 11可知,所设计的控制器能实现精准跟踪,最大跟踪偏差和收敛延迟时间分别在0.3%和0.05 s以内.
|
图 11 ±10% μ(t)下轨迹跟踪曲线 Fig. 11 Trajectory tracking curves under ±10% μ(t) |
1) 基于最优化理论的非平稳随机循环工况下,离合器接合轨迹在一定程度上能有效地降低冲击度和滑磨功,利于提高车辆换挡接合品质和驾乘舒适性.
2) 采用指数趋近律滑模控制方法实现离合器腔压力偏差0.3%内精准鲁棒跟踪,并克服了系统不确定性及外界摄动影响.
3) 非平稳随机循环工况下离合器接合轨迹优化及跟踪控制的方法为解决某土方机械变速器离合器接合压力跟踪偏差过大导致的摩擦片烧结故障问题提供了理论性的工程借鉴.
| [1] |
DELLA G A, IANNELLI L, PISATURO M, et al. A survey on modeling and engagement control for automotive dry clutch[J]. Mechatronics, 2018, 55: 63. DOI:10.1016/j.mechatronics.2018.08.002 |
| [2] |
HARIA H, PIETRON G M, MEYER J, et al. In-vehicle characterization of wet clutch engagement behaviors in automatic transmission systems[J]. SAE International Journal of Passenger Cars-Mechanical Systems, 2018, 11: 369. DOI:10.4271/2018-01-0395 |
| [3] |
SENATORE A. Advances in the automotive systems: An overview of dual-clutch transmissions[J]. Recent Patents on Mechanical Engineering, 2009, 2(2): 93. DOI:10.2174/1874477X10902020093 |
| [4] |
LUCENTE G, MONTANARI M, ROSSI C. Modelling of an automated manual transmission system[J]. Mechatronics, 2007, 17: 73. DOI:10.1016/j.mechatronics.2006.11.002 |
| [5] |
MISHRA K, SRINIVASAN K. Robust control and estimation of clutch-to-clutch shifts[J]. Control Engineering Practice, 2017, 65: 100. DOI:10.1016/j.conengprac.2017.05.007 |
| [6] |
WAN Guoqiang, LI Keqiang, PEI Ling, et al. Optimal tracking control for automatic transmission shift process[J]. Journal of Beijing Institute of Technology, 2015, 24(4): 458. DOI:10.15918/j.jbit1004-0579.201524.0405 |
| [7] |
葛安林, 吴锦秋, 郭万富. 自动控制离合器接合特性的研究[J]. 吉林大学学报(工学版), 1988(2): 75. GE Anlin, WU Jinqiu, GUO Wanfu. Engaging characteristics of clutch under automatic control[J]. Journal of Jilin University(Engineering and Technology Edition), 1988(2): 75. DOI:10.13229/j.cnki.jdxbgxb1988.02.010 |
| [8] |
REIF K. Automotive mechatronics[J]. Control Engineering Practice, 2015, 12(11): 1343. DOI:10.1007/978-3-658-03975-2 |
| [9] |
LUCENTE G, MONTANARI M, ROSSSI C. Modelling of a car driveline for servo-actuated gear-shift control[C]// IEEE International Symposium on Industrial Electronics. Dubrovnik: IEEE, 2005: 279.DOI: 10.1109/ISIE.2005.1528925
|
| [10] |
HAJ-FRAJ A, PFEIFFER F. Optimal control of gear shift operations in automatic transmissions[J]. Journal of the Franklin Institute, 2001, 338(2): 371. DOI:10.1016/s0016-0032(00)00091-0 |
| [11] |
彭建鑫, 金辉, 陈慧岩. 基于最优化理论的离合器接合曲线研究[J]. 北京理工大学学报, 2009, 29(11): 964. PENG Jianxin, JIN Hui, CHEN Huiyan. Engagement curve of clutch based on optimization theory[J]. Transactions of Beijing Institute of Technology, 2009, 29(11): 964. DOI:10.15918/j.tbit101-0645.2009.11.012 |
| [12] |
胡宏伟, 王向红, 武和全. 基于遗传算法的双离合器式变速器换挡过程离合器摩擦力矩优化控制[J]. 机械科学与技术, 2011, 30(3): 489. HU Hongwei, WANG Xianghong, WU Hequan. Anoptimal control method for the friction torque of clutches during the shifting of a dual clutch transmission[J]. Mechanical Science and Technology for Aerospace Engineering, 2011, 30(3): 489. DOI:10.13433/j.cnki.1003-8728.2011.03.037 |
| [13] |
陈清洪, 秦大同, 叶心. AMT重型汽车起步离合器最优控制[J]. 中国公路学报, 2010, 23(1): 116. CHEN Qinghong, QIN Datong, YE Xin. Optimal control about AMT heavy-duty truck starting clutch[J]. China Journal of Highway and Transport, 2010, 23(1): 116. DOI:10.1972/j.cnki.1001-7372.2010.01.019 |
| [14] |
WANG Y, LI Y, LIU Y, et al. Modeling and experimental research on engaging characteristics of wet clutch[J]. Industrial Lubrication and Tribology, 2019, 71(1): 94. DOI:10.1108/ilt-12-2017-0383 |
| [15] |
单外平, 李翔晟, 叶文. 基于可变力轨迹AMT离合器结合品质的研究[J]. 机械传动, 2018, 42(11): 46. SHAN Waiping, LI Xiangsheng, YE Wen. Research of the engagement quality for AMT clutch based on variable force trajectory[J]. Journal of Mechanical Transmission, 2018, 42(11): 46. DOI:10.16578/j.issn.1004.2539.2018.11.007 |
| [16] |
HAGGAG S A. Sliding mode adaptive PID control of an automotive clutch-by-wire actuator[J]. SAE International Journal of Passenger Cars-Mechanical Systems, 2016, 9(1): 424. DOI:10.4271/2016-01-9106 |
| [17] |
陈权瑞, 万里翔, 刘雪莱, 等. 离合器设计参数对汽车起步振动的影响研究[J]. 噪声与振动控制, 2017(5): 109. CHEN Quanrui, WAN Lixiang, LIU Xuelai, et al. Study on the influence of clutch design parameters on vehicle starting vibration[J]. Noise And Vibration Control, 2017(5): 109. DOI:10.3969/j.issn.1006-1355.2017.05.023 |
| [18] |
李宏玲, 金建, 孙文芳. 干式双离合器低速起步时非线性动力学研究[J]. 九江学院学报(自然科学版), 2017, 32(4): 29. LI Hongling, JIN Jian, SUN Wenfang. Nonlinear dynamic study on dry double clutch at low speed starting[J]. Journal of Jiujiang University(Natural Sciences), 2017, 32(4): 29. DOI:10.19717/j.cnki.jjun.2017.04.009 |
| [19] |
UTKIN V. Variable structure systems with sliding modes[J]. IEEE Transactions on Automatic Control, 1977, 22(2): 212. DOI:10.1109/TAC.1977.1101446 |
| [20] |
YOUNG K D, UTKIN V I, OZGUNER U. A control engineer's guide to sliding mode control[J]. IEEE Transactions on Control Systems Technology, 2002, 7(3): 328. DOI:10.1109/87.761053 |
| [21] |
高为炳, 程勉. 变结构控制系统的品质控制[J]. 控制与决策, 1989(4): 1. GAO Weibing, CHENG Mian. Quality control of variable structure control systems[J]. Control and Decision, 1989(4): 1. DOI:10.13195/j.cd.1989.04.3.gaowb.001 |
| [22] |
高为炳. 非线性系统的变结构控制[J]. 自动化学报, 1989, 15(5): 408. GAO Weibing. Variable structure control to nonlinear systems[J]. Acta Automatica Sinica, 1989, 15(5): 408. DOI:10.16383/j.aas.1989.05.004 |
| [23] |
LI Junqiu, WANG Yihe, CHEN Jianwen, et al. Study on oil pressure characteristics and trajectory tracking control in shift process of wet-clutch for electric vehicles[J]. Mathematical Problems in Engineering, 2016, 2016: 1. DOI:10.1155/2016/4869891 |
| [24] |
赵韩, 邱明明, 黄康. 基于微分几何的离合器接合过程速度跟踪滑模控制[J]. 中国机械工程, 2015, 26(17): 2302. ZHAO Han, QIU Mingming, HUANG Kang. Sliding mode control for speed tracking based on differential geometry during clutch engaging process[J]. China Mechanical Engineering, 2015, 26(17): 2302. DOI:10.3969/j.issn.1004132X.2015.17.005 |
| [25] |
孙承顺, 张建武, 程东升. 反馈线性化与滑模控制方法在汽车AMT中的应用[J]. 系统仿真学报, 2004, 16(4): 630. SUN Chengsun, ZHANG Jianwu, CHENG Dongsheng. Application of feedback linearization and sliding mode control to AMT of vehicles[J]. Journal of System Simulation, 2004, 16(4): 630. DOI:10.3969/j.issn.1004-731X.2004.04.006 |
| [26] |
LI Shihua, WU Chienshin, SUN Zongxuan. Design and implementation of clutch control for automotive transmissions using terminal sliding mode control and uncertainty observer[J]. IEEE Transactions on Vehicular Technology, 2016, 65(4): 1890. DOI:10.1109/TVT.2015.2433178 |
| [27] |
赵治国, 何露, 杨云云, 等. 干式DCT起步离合器传递转矩滑模观测估计[J]. 汽车技术, 2015(11): 23. ZHAO Zhiguo, HE Lu, YANG Yunyun, et al. Sliding mode observation and estimation of clutch transmitted torque for dry dual clutch transmission during starting[J]. Automobile Technology, 2015(11): 23. DOI:10.3969/j.issn.1000-3703.2015.11.006 |
| [28] |
李晓祥, 王安麟, 付志翼. 面向典型换挡工况重构的参数化试验载荷模型[J]. 哈尔滨工业大学学报, 2020, 52(1): 43. LI Xiaoxiang, WANG Anlin, FU Zhiyi. Parameterized test load model for typical shifting condition reconstruction[J]. Journal of Harbin Institute of Technology, 2020, 52(1): 43. DOI:10.11918/201811064 |
| [29] |
GLIELMO L, VASCA F. Optimal control of dry clutch engagement[R]. Warrendale: SAE technical paper, 2000.DOI: 10.4271/2000-01-0837
|
| [30] |
SONG Xingyong, ZULKEFLI M A M, SUN Zongxuan, et al. Automotive transmission clutch fill control using a customized dynamic programming method[J]. Journal of Dynamic Systems Measurement & Control, 2011, 133(5): 054503. DOI:10.1115/1.4003797 |
| [31] |
SONG Xingyong, SUN Zongxuan. Pressure-based clutch control for automotive transmissions using a sliding-mode controller[J]. IEEE/ASME Transactions on Mechatronics, 2012, 17(3): 534. DOI:10.1109/tmech.2011.2106507 |
| [32] |
GAO Bingzhao, CHEN Hong, ZHAO Haiyan, et al. A reduced-order nonlinear clutch pressure observer for automatic transmission[J]. IEEE Transactions on Control Systems Technology, 2010, 18(2): 446. DOI:10.1109/TCST.2009.2024758 |
 2020, Vol. 52
2020, Vol. 52


