随着载人探月工程的逐步深入,对于月球探测车的可靠性、稳定性、精准性等性能提出了更高的要求.太阳翼作为能源系统的关键部件,为航天器提供能量[1],亦是月球探测车的重要组成.太空的极端环境易引起铰链变形、铰链间隙减小,从而增大展开阻力,导致太阳翼无法展开.如:1987年,因一侧太阳翼无法展开,德国TVSAT卫星任务失败,其根本原因是铰链的装配异常[2].显然,研究铰链间隙的影响[3],避免机构卡死,是保证太阳翼可展机构可靠展开、重复精准展开的关键.
学者们针对可展太阳翼进行了大量研究工作,但关注点多侧重于帆板展开功能的实现及展开结构的动力学性能,研究方法以仿真分析为主,实验研究相对较少.如Rong等[4]完成了太阳帆板在航天器上的展开动力学仿真,指出在对支撑管施加适当约束控制的前提下,太阳帆板能够顺利有效地展开.王晛等[5]建立了可展太阳翼仿真模型,分析了地面展开及锁定过程中空气阻力、吊挂装置摩擦阻力等因素对太阳翼冲击载荷的影响. Yakovlev等[6]根据机构运动学的形式化描述原理,提出了一种求解太阳能帆板展开机构运动学模型的原始方法. Taherbaneh等[7]针对可展开太阳能帆板,设计并实现了同时基于模糊的最大功率点跟踪器(MPPT)和太阳跟踪器. Starinova等[8]在有限元仿真系统中对框架式太阳帆板进行了非线性静力分析. Septanto等[9]提出了一种基于仿真的确定固定安装可展开太阳能帆板系统位置的方法,该方法能提供最大的功率.基于速度变分原理和单向递推组集方法,段柳成等[10]建立了太阳阵刚柔耦合多体系统动力学模型,预测了太阳阵展开历程及航天器本体姿态扰动情况.在ADMAS中建模,谷勇霞[11]等分析了含柔性和间隙的二级太阳翼展开过程的动力学行为.史加贝等[12]建立了大型太阳电池阵展开过程的动力学模型.丁建中等[13]在板式卫星天线展开机构中考虑了铰链间隙对指向精度的影响.
进行月球车太阳翼展开实验研究,不能忽略低重力因素,需建立低重力补偿系统.目前,常用的低重力补偿的方法有气浮法、配重法、悬吊法等[14],其中悬吊法应用最为广泛.侯鹏等[15]采用多自由度配重悬挂法,过质心线吊点吊挂太阳翼,抵消太阳翼水平展开试验过程中的重力. Xiang等[16]提出了一种新颖的主动悬架重力补偿系统的设计方案和初步实验,该系统可以施加一个期望的恒定垂直力.蒋银飞[17]设计了恒拉力系统,将绳索离散成若干个质量-弹簧-阻尼单元,简化了低重力模拟系统的模型.乔国勇[18]采用悬吊法设计了两级可展帆板同步主动控制低重力模拟系统.
综合现有可展太阳翼研究成果、方法及不足,本文研制了绳系内错式重复可展太阳翼原理样机.在样机的结构设计、理论分析及实验研究过程中,充分考虑了铰链间隙对太阳翼展开运动的影响.对太阳翼末端位姿进行仿真分析和实验测试,分析太阳翼末端重复展开精度,为设计重复可展太阳翼,分析并提高重复折展可靠性提供依据.
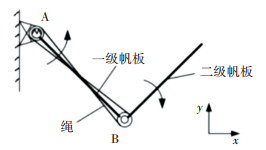
1 含间隙铰重复可展太阳翼系统 1.1 重复可展太阳翼展开传动考虑月球车太阳翼在极端工作环境下实现往复同步折展的功能需求,采用绳系内错式传动实现太阳翼折展.太阳翼展开运动示意图参见图 1.
绳系内错式传动由伺服电机驱动一级帆板转动,传动绳内错布置系于铰链A与铰链B处,借助摩擦带动二级帆板随之同步转动,完成同步折展.太阳翼展开机构设有锁定机构,保证太阳翼展开至工作位置后,具有确定位姿.
绳系预紧力会产生附加载荷于铰链传动轴处,导致传动轴弯曲变形,影响太阳翼的折展,结构设计中通过卸载结构解决了预紧力引起的变形问题.
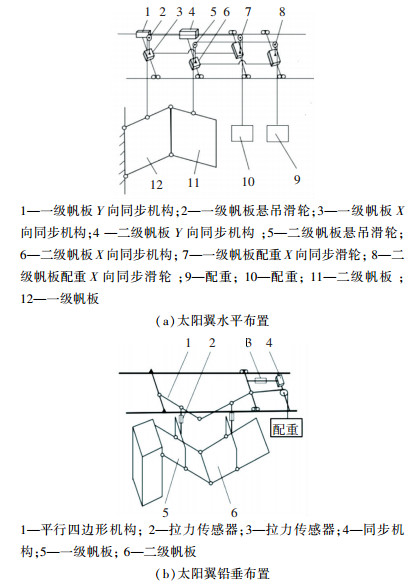
1.2 重复可展太阳翼低重力模拟为进行有效实验,用悬吊法进行可展太阳翼的低重力模拟.采用水平和铅垂两种布置方式,见图 2(a)、图 2(b).
|
图 2 低重力模拟示意 Fig. 2 Low gravity simulation |
水平布置低重力模拟.利用平行四边形原理,保证悬吊点与两级太阳翼质心同步运动,使两组悬吊拉力分别与内外侧太阳翼5/6重力相平衡.同步运动通过配重及同步伺服机构实现.
铅垂布置低重力模拟.分别悬吊过两级太阳翼质心的吊点,通过配重及滑轮组补偿相应太阳翼的重力.吊点同步机构具有X, Y两方向自由度,可通过速度伺服实现帆板上下吊点的同步运动.
2 太阳翼重复展开末端位姿精度分析 2.1 含隙铰误差模型重复定位精度直接影响重复可展太阳翼展开性能,太阳翼多次展开外侧翼板末端标记点的标准差越小,重复精度越高.太阳翼为串联机构,铰间隙是影响其末端位姿精度的主要因素,其随机性导致了末端精度的不确定性.
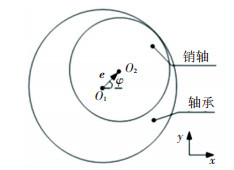
采用间隙矢量来描述间隙[18],如图 3所示,定义轴承孔中心指向销轴中心为矢量方向.
|
图 3 关节间隙矢量表示 Fig. 3 Joint space vector representation |
建立铰间隙变量概率密度函数用以描述关节间隙的随机性.设密度函数为fi(xi, yi),铰间隙矢量为e,其中i取为1和2,分别代表一级和二级帆板.设铰间隙密度函数服从二维正态分布[18],则
| $ {f_i}\left( {{x_i},{y_i}} \right) = \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{K}}{\mathit{\boldsymbol{e}}^{l\left( {{x_i},{y_i}} \right)}},\;\;\;0 \le x_i^2 + y_i^2 \le 1};&{}\\ {0,\quad x_i^2 + y_i^2 < 0,x_i^2 + y_i^2 > 1}.&{} \end{array}} \right. $ |
式中:
| $ \begin{array}{*{20}{c}} {K = 1/\left( {2{\rm{ \mathsf{ π} }}{\sigma _1}{\sigma _2}\sqrt {1 - {\rho ^2}} } \right),}\\ {l\left( {{x_i},\;{y_i}} \right) = - \frac{1}{{2\left( {1 - {\rho ^2}} \right)}}\left[ {\frac{{{{\left( {x - {\mu _1}} \right)}^2}}}{{\sigma _1^2}} - } \right.}\\ {\left. {2\rho \frac{{\left( {x - {\mu _1}} \right)\left( {y - {\mu _2}} \right)}}{{2{\sigma _1}{\sigma _2}}} + \frac{{{{\left( {y - {\mu _2}} \right)}^2}}}{{\sigma _2^2}}} \right].} \end{array} $ |
其中:μ1、μ2、σ1、σ2和ρ均为常数,且σ1>0, σ2>0, |ρ| < 1.即(xi, yi)服从参数为μ1、μ2、σ1、σ2和ρ的二维正态分布.
间隙矢量分布区间为[0, 1],得到μ=0,σ=1/3,由概率分布的性质可得ρ=0,K=9/2π,铰间隙密度函数为:
| $ {f_i}\left( {{x_i},{y_i}} \right) = \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{K}}{\mathit{\boldsymbol{e}}^{ - \frac{9}{2}\left( {x_i^2 + y_i^2} \right)}},0 \le x_i^2 + y_i^2 \le 1;}\\ {0,\quad x_i^2 + y_i^2 < 0,\;x_i^2 + y_i^2 > 1.} \end{array}} \right. $ |
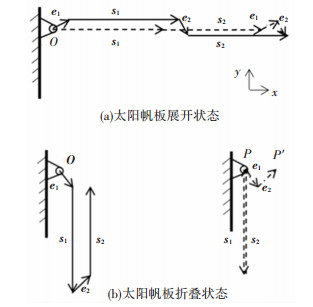
两级铰链的间隙矢量分别为e1和e2,两级太阳帆板的宽度矢量分别记为s1和s2,二级帆板理想末端位置记为P,考虑铰链间隙条件下二级帆板末端位置为记P′. 图 4(a)、(b)分别为太阳帆板展开与折叠两种状态的末端位姿误差[18].
|
图 4 太阳帆板展开末端位姿 Fig. 4 Terminal poses of solar panel |
由图 4可知,
| $ {l_{O{P^\prime }}} = {\mathit{\boldsymbol{e}}_1} + {\mathit{\boldsymbol{s}}_1} + {\mathit{\boldsymbol{e}}_2} + {\mathit{\boldsymbol{s}}_2} = {l_{OP}} + {l_{P{P^\prime }}}. $ |
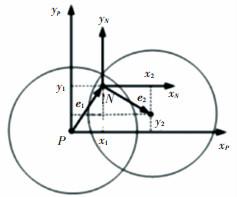
分别建立坐标系PxPyP和NxNyN,如图 5所示,坐标原点分别为间隙矢量e1和e2的起点.在坐标系PxPyP中,e1的末端点N的坐标为(x1, y1),e2的末端点P′的坐标为(x, y).在坐标系NxNyN中,e2的末端点P′的坐标为(x2, y2),铰链间隙满足如下条件:
|
图 5 铰链间隙矢量坐标系 Fig. 5 Hinge clearance vector coordinate system |
| $ x_1^2 + y_1^2 \le 1,\;x_2^2 + y_2^2 \le 1; $ |
两级太阳帆板的铰链间隙不相关,可得
| $ {f^*}\left( {{x_1},{y_1},{x_2},{y_2}} \right) = f\left( {{x_1},{y_1}} \right)f\left( {{x_2},{y_2}} \right). $ |
则末端点P′的密度函数为
| $ f(x,y) = \left\{ {\begin{array}{*{20}{c}} {\iint\limits_S {{K^2}{e^{ - \frac{9}{2}l\left( {{x_1},{y_1}} \right)}}{\rm{d}}{x_1}{\rm{d}}{y_1},} }&{{x^2} + {y^2} \le 4;}\\ {0,}&{其他.} \end{array}} \right. $ |
式中:l(x1, y1)=x12+y12+(x-x1)2+(y-y1)2.
假设铰链间隙引起的二级帆板末端位置的误差服从圆域分布,得太阳翼末端位置误差分布函数为
| $ F = \iint_{\sqrt {{x^2} + {y^2}} \le t} {f(x,y){\rm{d}}x{\rm{d}}y,\quad 0 \le t \le n.} $ | (1) |
式中:t为误差分布圆的半径(比例误差),n为串联关节数目.
将比例关节间隙值设为1,则有
| $ r{\rm{ }}/{\rm{ }}R = t{\rm{ }}/{\rm{ }}T. $ | (2) |
式中:r为比例关节间隙,R为实际关节间隙,t为比例误差,T为关节间隙引起的末端位姿误差.对应不同间隙值,误差分布参见表 1.
| 表 1 铰链间隙误差及分布 Tab. 1 Hinge clearance errors and distribution |
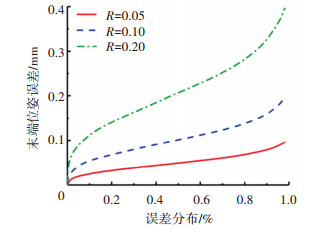
当铰链间隙R分别为0.05、0.10、0.20 mm时,由式(1)、式(2)和表 1数据得到铰链间隙与太阳翼末端位姿误差分布关系曲线,参见图 6.
|
图 6 铰链间隙与太阳翼末端误差分布关系曲线 Fig. 6 Distribution curves of hinge clearance and solar wing end error |
取误差分布为80%的数据进行分析,间隙值R分别为0.20、0.10、0.05 mm时,末端位姿误差分别近似为0.140、0.070、0.035 mm,显然3组误差与铰链间隙近似成比例关系.从曲线图可知,间隙越小误差分布范围越小.
综合数值分析结果,可知铰链间隙值的合理设计,可使末端位姿误差分布稳定,从而便于位置反馈补偿误差,提高重复位姿精度.
3 太阳翼重复展开末端位姿仿真 3.1 建立仿真模型利用CREO建立可展太阳翼三维模型,以6061铝板为材料制作帆板,每级帆板质量约5.33 kg.导入ADAMS进行约束,建立可展太阳翼刚性仿真模型.将三维模型导入ANSYS对模型进行柔性化处理,再导入ADAMS中,替换其中刚性太阳翼,重新驱动被约束的模型,完成动力学仿真模型的建立.
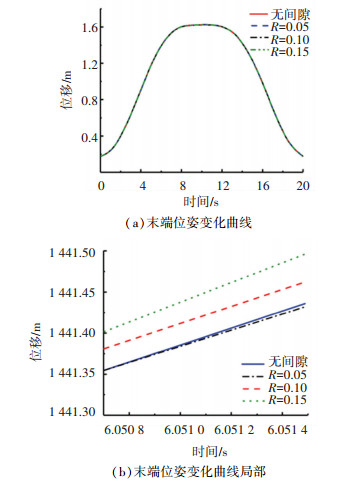
3.2 仿真分析针对不同间隙值进行太阳翼重复展开仿真分析.展开过程中,太阳翼末端位姿随展开时间的变化见图 7.
|
图 7 间隙大小与帆板末端位姿关系 Fig. 7 Relation between clearance size and terminal pose of panel |
低重力环境下太阳翼展开至工作位置时其末端位置参数见表 2.当太阳翼折叠收拢至待机位置时其末端位置参数见表 3.
| 表 2 太阳翼展开至工作位置时的末端位置参数 Tab. 2 Terminal position parameters of solar wing when it expands to operating position |
| 表 3 太阳翼折叠收拢至待机位置时的末端位置参数 Tab. 3 Terminal position parameters of solar wing when it is folded to standby position |
仿真结果表明,太阳翼末端位姿精度会随铰链间隙的增大而降低.考虑实际工程中太阳翼具有柔度,分别对刚性模型与柔性模型进行仿真.仿真结果表明,柔性会直接导致太阳翼展开时产生误差.但相同的间隙变化范围,柔性帆板的末端位置误差变化幅度小于刚性帆板,即帆板柔性能够补偿间隙对帆板重复展开末端位姿的影响,在许可误差范围内,铰链间隙值具有较大的可取范围.
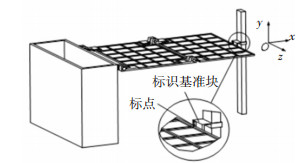
4 太阳翼重复展开性能测试 4.1 测试准备首先,在太阳翼二级帆板末端制作一个标记点;然后,建立标识基准,该基准为太阳翼二级帆板展开后帆板末端标记点的理论位置.基于标识基准,建立测试坐标系,如图 8所示.展开太阳帆板,分别测量帆板标记点与标识基准在x、y、z方向上的相对位置,进行数据比较,分析太阳翼的重复展开位姿精度.
|
图 8 标识基准坐标系 Fig. 8 Identification reference coordinate system |
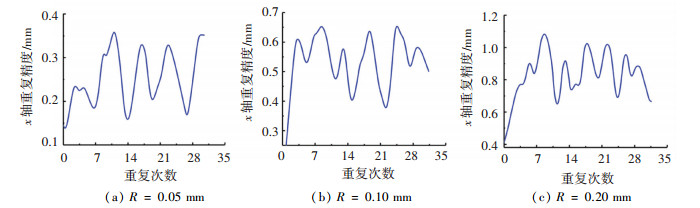
太阳帆板重复展开性能实验工况:分别采用铰链间隙0.05、0.10、0.20 mm进行太阳翼重复展开精度测试,重复实验频次为30.重复展开太阳帆板,测量帆板标点位置,与理想基准位置进行比较. x、y、z方向太阳翼末端位置精度分别见图 9~11和表 4.
|
图 9 太阳翼重复展开x向位置精度 Fig. 9 Position accuracy solar of repeated expansion of wing in x direction |
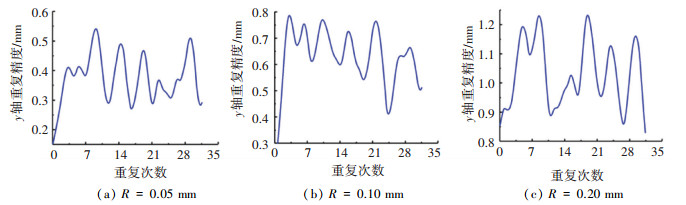
|
图 10 太阳翼重复展开y向位置精度 Fig. 10 Position accuracy of repeated expansion of solar wing in y direction |
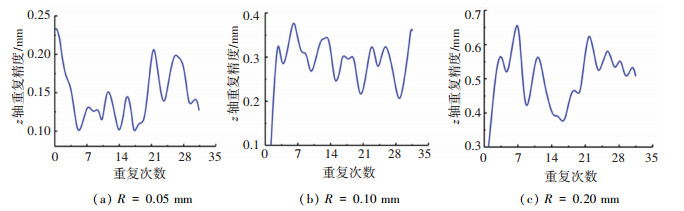
|
图 11 太阳翼重复展开z向位置精度 Fig. 11 Position accuracy of repeated expansion of solar wing in z direction |
| 表 4 太阳翼重复展开位置参数 Tab. 4 Position parameters of repeated expansion of solar wing |
分析表 4可知,随着铰链间隙的增大,太阳翼重复展开末端位置误差随之增大.因此,合理设计铰链关节间隙,对于提高机构的定位精度是有益的.
4.3 重复展开运动参数测定太阳翼展开角度直接反映太阳翼展开位姿是否准确,太阳翼展开角加速度则直接体现太阳翼展开运动是否平稳,二者是影响太阳翼性能的主要参数,因此针对上述两个参数进行测试实验.
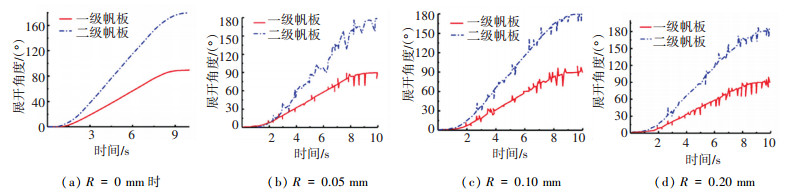
4.3.1 太阳翼展开角度测定在完全展开状态下,太阳翼二级帆板展开的测试角度分别为θa、θb;平均值记为θa、θb;二级帆板理论展开角度分别为θA、θB;试验值与理论值的误差记为Δθ=|(θ-θ)/θ|.记太阳帆板展开的同步误差为ΔT=[(θb-2θa)/100]×100%,太阳帆板展开角度测试曲线参见图 12,末端角度及误差见表 5.
|
图 12 间隙大小与帆板展开角度关系 Fig. 12 Relation between clearance size and panel angle |
| 表 5 太阳帆板展开角度 Tab. 5 Solar panel expansion angle |
分析图 12及表 5数据可知,展开过程中铰链间隙可导致帆板抖动,并引起二级帆板展开角度误差.展开角度误差及二级帆板展开的同步度误差亦随间隙增大而增大,末端角度误差由二级帆板展开角度误差累加形成.
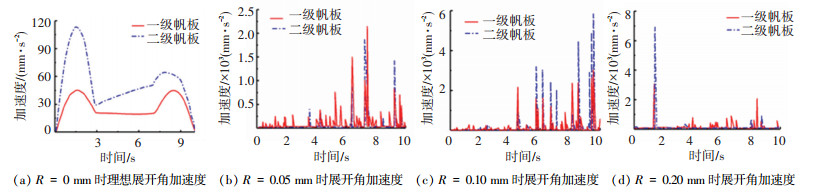
4.3.2 太阳翼展开加速度测定太阳翼展开加速度运动曲线见图 13.由图 13可知,在匀加速和匀速运动阶段,太阳翼展开的加速度波动相对平缓;在匀减速运动阶段则波动加剧;当铰链间隙变大,二级帆板的加速度波动幅度随之变大,但加速度波动频率随之降低.因此,在展开锁定时,铰链关节间隙对机构稳定性和精准性影响显著.
|
图 13 间隙值与帆板展开加速度关系曲线 Fig. 13 Relation between clearance size and acceleration of panel |
1) 绳系内错式传动方案可实现太阳翼同步重复可展功能.
2) 铰链间隙与太阳翼重复展开末端位姿误差间近似成比例关系,间隙越小误差分布范围越小.铰链间隙值的合理设计,可使末端位姿误差分布稳定,从而便于位置反馈补偿误差,提高重复位姿精度.
3) 柔性可直接导致太阳翼重复展开的末端位置误差.但帆板柔性与铰链间隙的耦合作用能够补偿间隙对帆板重复展开末端位姿的影响.合理匹配两因素,在许可误差范围内,可使铰链间隙值具有较大的可取范围.
4) 在展开锁定时,铰链间隙对机构稳定性和精准性影响显著.
| [1] |
GUO Tao, LIU Guangtong, FAN Youguang, et al. Automatic posture alignment method of spacecraft in docking process of solar wing[C]//2017 10th International Symposium on Computational Intelligence and Design(ISCID).Hangzhou: IEEE, 2017: 53.DOI: 10.1109/ISCID.2017.122
|
| [2] |
杨维垣. 空间机构分类及可靠性研究[J]. 航天器工程, 1994(1): 31. YANG Weiyuan. Classification and reliability of space agencies[J]. Spacecraft Engineering, 1994(1): 31. |
| [3] |
叶培建, 黄江川, 孙泽洲, 等. 中国月球探测器发展历程和经验初探[J]. 中国科学(技术科学), 2014, 44(6): 543. YE Peijian, HUANG Jiangchuan, SUN Zezhou, et al. Exploration of the development history and experience of China's lunar probe[J]. Science in China:Technical Science, 2014, 44(6): 543. |
| [4] |
RONG Siyuan, LIU Jiafu, ZHAO Biao, et al.Inflatable deployment dynamics simulation of solar sail spacecraft support tube[C]//2019 International Conference on Mechatronics and Automation.Changchun: IEEE, 2009: 2239. DOI: 10.1109/ICMA.2009.5246679
|
| [5] |
王晛, 陈天智, 柴洪友. 太阳翼地面展开锁定的动力学仿真分析[J]. 航天器工程, 2011, 20(3): 86. WANG Xian, CHEN Tianzhi, CHAI Hongyou. Dynamics simulation analysis of solar array ground deployment and locking[J]. Journal of Spacecraft Engineering, 2011, 20(3): 86. DOI:10.3969/j.issn.1673-8748.2011.03.014 |
| [6] |
YAKOVLEV A, MALYSHENKO A.Automatic derivation of kine-matic equations of deployable solar panel arrays[C]//2016 International Siberian Conference on Control and Communications(SIBCON). Moscow: IEEE, 2016.DOI: 10.1109/SIBCON.2016.7491692
|
| [7] |
TAHERBANEH M, FARD H G, REZAIE A H, et al.Combination of fuzzy-based maximum power point tracker and sun tracker for de-ployable solar panels in photovoltaic systems[C]//2007 IEEE Interna tional Fuzzy Systems Conference.London: IEEE, 2007: 4295553. DOI: 10.1109/FUZZY.2007.4295553
|
| [8] |
STARINOVA O L, KHABIBULLIN R M, GORBUNOVA I V. The project of the small frame-type solar sail spacecraft[C]//Procee-dings of 7th International Conference on Recent Advances in Space Technologies. Istanbul: IEEE, 2015: 643.DOI: 10.1109/RAST.2015.7208422
|
| [9] |
SEPTANTO H, SUDJANA O.Simulation approach to determine position of the fixed installed deployable solar panel[C]//2018 IEEE International Conference on Aerospace Electronics and Remote Sensing Technology (ICAERS).Bali: IEEE, 2018: 159.DOI: 10.1109/ICARES.2018.8547098
|
| [10] |
段柳成, 李海泉, 刘晓峰, 等. 航天器太阳阵的刚柔耦合动力学与控制研究[J]. 振动工程学报, 2015, 28(5): 770. DUAN Liucheng, LI Haiquan, LIU Xiaofeng, et al. Study on rigid-flexible coupling dynamics and control of spacecraft solar array[J]. Chinese Journal of Vibration Engineering, 2015, 28(5): 770. DOI:10.16385/J.CNKI.ISSN.1004-4523.2015.05.012 |
| [11] |
谷勇霞, 杨天夫, 郭峰. 考虑多间隙的帆板式展开机构动力学分析[J]. 振动.测试与诊断, 2015, 1(36). GU Yongxia, YANG Tianfu, GUO Feng. Dynamic analysis of a windsurf-type deployment mechanism considering multiple gaps[J]. Vibration, 2015, 1(1): 36. |
| [12] |
史加贝, 刘铸永, 洪嘉振. 大变形太阳电池阵展开的多体动力学分析[J]. 宇航学报, 2017, 38(8): 789. SHI Jiabei, LIU Zhuyong, HONG Jiazhen. Multi-body dynamics analysis of deployment of solar arrays with large deformation[J]. Acta Astronautica Sinica, 2017, 38(8): 789. |
| [13] |
丁建中, 王春洁. 含铰链间隙板式卫星天线展开精度分析[J]. 北京航空航天大学学报, 2016, 42(12): 2625. DING Jianzhong, WANG Chunjie. Deployment accuracy analysis of planar satellite antenna with joint clearances[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(12): 2625. DOI:10.13700/j.bh.1001-5965.2015.0808 |
| [14] |
杨巧龙, 闫泽红, 任守志, 等. 套筒驱动的大型可展收柔性太阳翼地面展开重力卸载研究[J]. 载人航天, 2017, 23(4): 536. YANG Qiaolong, YAN Zehong, REN Shouzhi, et al. Study on gravity compensation in ground deployment tests of large retractable flexible solar array driven by telescopic boom[J]. Manned Spaceflight, 2017, 23(4): 536. DOI:10.16329/j.cnki.zrht.2017.04.016 |
| [15] |
侯鹏, 李志慧, 宋涛, 等. 卫星太阳翼板面水平展开试验方法[J]. 哈尔滨工业大学学报, 2016, 48(10): 176. HOU Peng, LI Zhihui, SONG Tao, et al. A novel method for horizontal deployable experiment of satellite solar array[J]. Journal of Harbin Institute of Technology, 2016, 48(10): 176. DOI:10.11918/j.issn.0367-6234.2016.10.026 |
| [16] |
XIANG Sheng, GAO Haibo, LIU Zheng, et al.A novel active sus-pension gravity compensation system for physically simulating human walking in microgravity[C]//IEEE International Conference on Robotics and Biomimetics(ROBIO). Qingdao: IEEE, 2016: 1052. DOI: 10.1109/ROBI-O.2016.7866464
|
| [17] |
蒋银飞.悬吊式低重力模拟系统研究[D].成都: 电子科技大学, 2017 JIANG Yinfei. Research on suspended low gravity simulation system[D].Chengdu: University of Electronic Science and Technology, 2017 http://cdmd.cnki.com.cn/Article/CDMD-10614-1017069776.htm |
| [18] |
乔国勇.月球车含隙铰可展帆板原理样机研制[D].秦皇岛: 燕山大学, 2017 QIAO Guoyong. Prototype development of lunar rover developable panel mechanism with joint clearance[D]. Qinhuangdao: Yanshan University, 2017 http://cdmd.cnki.com.cn/Article/CDMD-10216-1017726041.htm |
 2020, Vol. 52
2020, Vol. 52