2. 北京理工大学 宇航学院, 北京 100081
2. School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China
计算成本及计算能力的限制使得我们在做计算时常常要将计算对象假定为不可压缩无粘流体.这一物理假设虽然可以在一定程度上减小计算成本,但同时也会在结果中引入一定程度的误差.为解决上述问题,本文提出了一种适用于求解弱可压缩粘性流动问题的数值解法.该方法的数学推导基于边界数据浸入法(Boundary Data Immersion Method, BDIM),并且该方法充分考虑了运动固体对流场计算结果的影响.
对于计算域内含有动边界的问题,浸入边界法(Immersed Boundary Method, IBM)是一种准确有效的求解方法.该法由Peskin[1]于1972年首次提出,用于对人类心脏中血液流动的模拟.其主要思想是将流场的复杂边界等效为一个体积力并施加于N-S动量方程中.此后的几十年中,该法得到了不断发展且被广泛使用.为改善体积不守恒问题,Peskin[2]引入新的投影算子替代原有方程中的哈密顿算子;自适应加密算法与IBM的结合[3-5]使得计算效率得到了提高; 针对流体与运动刚体之间相互作用的研究,这些年来逐渐发展出了离散直接力法[6-8]、虚拟边界法[9-10]、反馈力法[11-13]等不同方法.此外,如何提高边界浸入法的计算精度也引起了不少研究学者的关注. Yusof[14]将B样条(B-spline)与浸入边界法结合以获得高阶精度,且消除了时间步长的限制;Tseng[10]通过在边界上靠近固体一侧的区域进行虚拟网格重建的方法来提高计算精度;Yang[15]通过对离散delta函数的光滑处理,有效抑制了体积力中的非物理振荡;宫兆新等[16]通过虚拟解法验证了正则化δ函数的改变对于计算精度的提高没有任何帮助;李秋实等[17]通过改变力源的构造以及边界速度插值的方式获得二阶精度结果;及春宁等[18-20]将力源项的求解内嵌到压力泊松方程的迭代过程,得到了一种高精度的嵌入式迭代浸入边界法.
然而与原始浸入边界法相同,上述研究对象大多为不可压缩无粘流体,并未成功地将边界浸入法推广到可压缩流动中来.对于不可压缩流动来说,使用边界浸入法只需要给出速度边界条件(即无滑移速度边界)即可;但是对于可压缩流动来说,因流体的一些变量,如密度、温度等都会在运动中发生较大的变化,所以需要除了速度边界条件以外的其他边界条件才可以顺利完成流场的求解.为了将浸入边界法应用到可压缩流动中来,研究人员进行了大量工作[21-24]. Palma等[21-22]将IBM与求解预置可压缩N-S方程的解法相结合用于求解流场中复杂几何结构的问题;Qiu等[23]依次使用无滑移速度边界条件对流体的密度、速度、温度以及压力依次进行修正,推导出了一种边界条件浸入法(Boundary condition-enforced);Schlanderer[25]提出一种适用于求解可压缩流动的浸入边界法——边界数据浸入法(Boundary Data Immersion Method).该方法使用广义积分核公式将计算域内不同子域的控制方程进行重组,得到具有统一形式的方程,并且使得重组后的方程不仅在各子域内有效,且在边界处也可以实现光滑过渡.此外,现在对于弱可压缩粘性流动问题的求解方法主要是predictor-corrector方法[26-27]或者人工可压缩的方法[28].在这里我们将借鉴Caltagirone[29]对流体弱可压缩粘性的处理方式,并结合Schlanderer[25]的边界数据浸入法推导出一种可以求解水下弱可压缩粘性流动问题的简单算法.
1 算法推导对于单相弱可压缩粘性的流体,从连续性方程与流体状态方程出发,经过推导可以得到如下关于压力项的方程[29]:
| $ \frac{{\partial p}}{{\partial t}} = - (\overrightarrow u \cdot \nabla p + \rho c_T^2\nabla \cdot \overrightarrow u ). $ | (1) |
式中,p为流体压强,
| $ \rho c_T^2 = (p + \gamma B). $ |
式中:γ为比热容比系数,这里取6.1;B为水的刚度系数,其具有与压力相同的量纲,取值345 MPa.将上式代入式(1),并对其进行离散化处理,有
| $ {p^{n + 1}} = {p^n} - \Delta t \cdot [\nabla {p^n} + ({p^n} + \gamma B\nabla \cdot {\overrightarrow u ^n})], $ | (2) |
式中,上标n表示物理量的当前时刻,n+1表示下一时刻.
对动量方程进行离散可以得到速度项的离散方程[25]如下:
| $ {\overrightarrow u ^{n + 1}} = {\overrightarrow u ^n} - \Delta t \cdot {\overrightarrow u ^n}\nabla \cdot {\overrightarrow u ^n} + \frac{{\Delta t}}{{{\rho ^n}}}[\mu {\nabla ^2}{\overrightarrow u ^n} - \nabla {p^{n + 1}}]. $ | (3) |
式中:ρn为n时刻的流体密度;μ为流体的动力黏度系数,且上述物理量单位均采用国际单位制.
在得到流体的压力与速度的离散方程之后,可以对流场进行求解.但在实际的流场计算中,常常会遇到整个计算域中存在多个不同物理性质的子域,因此需要得到求解整个流场的计算方法.为解决上述问题,Schlanderer等[25]提出了基于广义积分核公式的边界数据浸入法.这种方法通过积分核公式,将不同子域物理变量的控制方程和界面条件结合起来,实现了对整个计算域的模拟.使用这种方法得到的具有统一形式的控制方程不仅保留了原系统中的物理变量特性,还做到了不同子域间的光滑过渡,使得我们可以对包含运动物体的可压缩粘性流动进行计算.本文在这里直接使用可将各子域控制方程连结起来的控制方程[25]:
| $ {\varphi _\varepsilon } = {b_f}(\varphi , \overrightarrow x , t)\mu _0^{_\varepsilon } + {b_s}(\varphi , \overrightarrow x , t)(1 - \mu _0^{_\varepsilon }). $ | (4) |
式中:
相较于流体速度,固体速度
| $ \overrightarrow U (\overrightarrow x , t) = {\overrightarrow u ^{n + 1}}(\overrightarrow x , t)\mu _0^{_\varepsilon } + {\overrightarrow V ^{n + 1}}(\overrightarrow x , t)(1 - \mu _0^{_\varepsilon }). $ | (5) |
对于刚体内部,其压力方程具有如下形式:
| $ \frac{{Dp}}{{Dt}} = 0, $ |
将该式改写后可得
| $ \frac{{\partial p}}{{\partial t}} = - \overrightarrow V \frac{{\partial p}}{{\partial x}}. $ | (6) |
为满足刚体与流体边界处上压力连续变化的条件,刚体边界上压力方程修正后有如下形式:
| $ \frac{{\partial p}}{{\partial t}} = - \overrightarrow V \frac{{\partial p}}{{\partial x}} + (p + \gamma B)\nabla \cdot \overrightarrow V . $ | (7) |
其中式(7)中右边第二项恒为0.流体的压力方程有以下形式:
| $ \frac{{\partial p}}{{\partial t}} = - \overrightarrow u \frac{{\partial p}}{{\partial x}} + (p + \gamma B)\nabla \cdot \overrightarrow u . $ | (8) |
将式(7)和式(8)进行离散化处理,并且结合式(4)整理可得适用于整个计算域中压强p′的方程为
| $ p' = {p^n} - \Delta t \cdot [{\overrightarrow U ^m} \cdot \nabla {p^n} + ({p^n} + \gamma B)\nabla \cdot {\overrightarrow u ^m}]. $ | (9) |
至此,我们在弱可压缩粘性流动与BDIM的基础上,得到了可用于求解包含运动固体的可压缩粘性流动的完整算法.
2 算法验证为对算法的有效性及准确性进行充分说明,我们在本章计算了3个二维圆柱的经典算例,并将计算结果与前人在相同工况下的计算结果进行了对比.
2.1 静止圆柱绕流在本节,我们首先计算了静止圆柱绕流问题,验证了算法在计算包含静止固体的可压缩粘性流动问题时的有效性及准确性.
基于入流速度
数值计算结果整理在表 1中,并且给出了使用其他数值算法所得结果以供对比.通过表 1中的对比,可以看出:总体而言,使用新算法得到的时均阻力系数CD、升力系数振荡的幅值C′L以及斯特劳哈尔数(
| 表 1 Re= 100时静止圆柱绕流的阻力、升力系数与斯特劳哈尔数 Tab. 1 Drag and lift coefficients and Strouhal number for flow around a stationary cylinder at Re= 100 |
图 1中给出了当流动稳定时,圆柱表面的时均压力系数

|
图 1 Re= 100时,流动稳定后静止圆柱时均表面压力系数CP分布图 Fig. 1 Distribution of time-averaged surface pressure coefficient on stationary cylinder when flow is stable at Re= 100 |
|
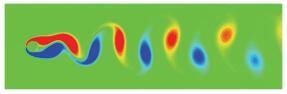
图 2 Re = 100时静止圆柱扰流稳定时涡量图 Fig. 2 Vortex diagram for flow past a stationary cylinder when the flow is stable at Re = 100 |
上节使用算法计算了包含静止固体的可压缩粘性流动的算例,本节更进一步,验证当物体发生运动时算法的有效性及准确性.本节考虑另一个二维算例——横向振动圆柱绕流的算例.
基于入流速度
| $ y(t) = Asin(2\pi {f_0}t). $ |
表 2对比了采用不同数值方法计算得到时均阻力系数以及阻力系数和升力系数的均方根.通过对比,可以发现:使用我们的算法计算得到的3个数值在量级上与其他算法所得结果相同,具有较好的一致性;具体而言,计算得到的时均阻力系数值比其他算法得到的数值小1.1%~7.8%,阻力系数的均方根同文献[30, 37]中结果几乎相同,而升力系数的均方根则略大于文献[30, 36-37]中的计算结果.产生这一差异化现象的原因是参考文献中采用数值计算方法均为不可压缩流体,其计算域的压力出口边界条件与本文采用的弱可压缩流体的压力边界条件不同.
| 表 2 Re= 185时振动圆柱绕流的时均阻力系数、阻力及升力系数的均方根 Tab. 2 Time-averaged drag coefficient and root mean square of drag and lift coefficient for flow around an oscillating cylinder at Re= 185 |
此外,本文引入不同的圆柱振动特性进行计算,探究其变化对计算结果的影响.文中采用改变单一变量的方法,计算了振动频率为0.156时,圆柱振动幅度A分别为0.2d、0.3d、0.4d、0.5d的4种情况以及振动幅度A为0.2d时,圆柱振动频率分别为0.156、0.3、0.45的3种情况.对比结果见表 3及表 4.从表 3可以看出,振动幅度的增大,使得3种系数均呈现不断增大的趋势;而从表 4可以看出,随着圆柱振动频率的增大,3个系数均有不同程度的增幅,其中,升力系数均方根的增幅远大于时均阻力系数与阻力系数均方根,达到了十倍以上.
| 表 3 圆柱振动频率为0.156时,不同振幅对应的时均阻力系数、阻力及升力系数的均方根 Tab. 3 Time-averaged drag coefficient and root mean square of drag and lift coefficient associated with different oscillating amplitudes when the oscillating frequency is 0.156 |
| 表 4 圆柱振动幅度为0.2d时,不同振动频率对应的时均阻力系数、阻力及升力系数的均方根 Tab. 4 Time-averageddrag coefficient and root mean square of drag and lift coefficient associated with different oscillating frequencies when the oscillating amplitude is 0.2d |
图 3和图 4给出了阻力系数及升力系数随圆柱位移变化的图像.从图中可以看出,无论是阻力还是升力,其数值大小均为对称分布,其中,前者是以静止位置(yc=0)轴对称,而后者则以(0, 0)点呈中心对称.此外,在图 5中也给出了流动稳定时的涡量图.

|
图 3 Re= 185时振动圆柱扰流的阻力系数随位移变化图 Fig. 3 Variation of drag coefficient with displacement for flow past an oscillating cylinder at Re= 185 |

|
图 4 Re= 185时振动圆柱扰流的升力系数随位移变化图 Fig. 4 Variation of lift coefficient with displacement for flow past an oscillating cylinder at Re= 185 |

|
图 5 Re= 185时振荡圆柱流动稳定时涡量图 Fig. 5 Vortex diagram for flow past an oscillating cylinder when flow is stable at Re= 185 |
上述2个算例对算法的有效性及准确性做了验证,本节通过验证横向振动圆柱,对算法在声学层面的应用进行验证.
计算域的大小为30d×30d,整个计算域的网格尺寸为0.05d,时间步长为0.01.圆柱在横向上的振动规律同2.2节,即圆柱位移与时间的函数关系式为
| $ y(t) = A{\rm sin}(2\pi {f_0}t). $ |
图 6给出了圆柱在振动稳定时,计算域内压力云图变化的整个周期.通过图 6可以看出,圆柱在发生振动时所产生的压力脉动在声学上等同于一个偶极子,这与理论分析相一致.此外,从图 7中可以看出,对方向谱而言,计算结果同偶极子振动的理论解有很好的一致性.从而验证了算法在计算包含运动物体的可压缩粘性流动时声学层面的有效性.

|
图 6 圆柱振动压力云图 Fig. 6 Pressure contour of oscillating cylinder |

|
图 7 声压辐射方向谱 Fig. 7 Directional spectrum of sound pressure |
相比于传统的浸入边界法,本文所采用的边界数据浸入法不仅可对包含运动物体的流域进行求解,更可与弱可压缩粘性流结合起来以考虑流体的可压缩性及粘性对计算结果的影响.本文从可压缩粘性流的连续性方程及水的状态方程出发,使用边界数据浸入法将运动物体的固体子域与流体子域的变量方程进行重组,严格推导了适用于整个流场的压力与速度方程.该方程不仅有效保留了在各子域内的所有物理性质,而且成功地在各子域之间交界面上实现了光滑过渡.
此外,通过3个二维经典算例,在力学与声学层面上验证了算法在计算包含静止物体及运动物体的流场时的有效性.通过将计算所得结果与其他算法所得结果进行对比,对算法的准确性进行了验证说明.相较于目前已有的可压缩粘性流动问题的求解方法,本算法推导简单,无需过多假设,且计算结果与实验数据具有良好的吻合程度.
| [1] |
PESKIN C S. Flow patterns around heart valves: a numerical method[J]. Journal of Computational Physics, 1972, 10: 252. DOI:10.1016/0021-9991(72)90065-4 |
| [2] |
PESKIN C S, PRINTZ A B F. Improved volume conservation in the computation of flows with immersed elastic boundaries[J]. Journal of Computational Physics, 1993. DOI:10.1006/jcph.1993.1051 |
| [3] |
ROMA A M, PESKTH C S, BERGER M J. An adaptive version of the immersed boundary method[J]. Journal of Computational Physics, 2000, 153: 509. DOI:10.1006/jcph.1999.6293 |
| [4] |
MTHION M L. Two methods for the study of vortex patch evolution on locally refined grids[D]. Berkeley: Lawrence Berkeley Laboratory University of California, 1994
|
| [5] |
ROMA A M. A multilevel self-adaptive version of the immersed boundary method[D]. New York: Courant Institute of Mathematical Science, New York University, 1996
|
| [6] |
FADLUN E A, VERZICCO R, ORLANDI P, et al. Combined immersed-boundary finite-difference methods for three-dimensional complex flow simulations[J]. Journal of Computational Physics, 2000, 161(1): 35. DOI:10.1006/jcph.2000.6484 |
| [7] |
XU Sheng. A boundary condition capturing immersed interface method for 3D rigid objects in a flow[J]. Journal of Computational Physics, 2011, 230(19): 7176. DOI:10.1016/j.jcp.2011.05.019 |
| [8] |
王文全, 张国威, 闫妍. 模拟复杂流动的一种隐式直接力浸入边界方法[J]. 工程力学, 2017, 34(2): 28. WANG Wenquan, ZHANG Guowei, YAN Yan. An implicit direct force immersed boundary method for simulating complex flow[J]. Engineering Mechanics, 2017, 34(2): 28. |
| [9] |
GOLDSTEIN D, HANDLER R, SIROVICH L. Modeling a no-slip flow boundary with an external force field[J]. Journal of Computational Physics, 1993, 105(2): 354. DOI:10.1006/jcph.1993.1081 |
| [10] |
TSENG Y H, FERZIGER J H. A ghost-cell immersed boundary method for flow in complex geometry[J]. Journal of Computational Physics, 2003, 192(2): 593. DOI:10.1016/j.jcp.2003.07.024 |
| [11] |
LAI M C, PESKIN C S. An immersed boundary method with formal second-order accuracy and reduced numerical viscosity[J]. Journal of Computational Physics, 2000, 160(2): 705. DOI:10.1006/jcph.2000.6483 |
| [12] |
LE D V, WHITE J, PERAIRE J, et al. An implicit immersed boundary method for three-dimensional fluid-membrane interactions[J]. Journal of Computational Physics, 2009, 228(22): 8427. DOI:10.1016/j.jcp.2009.08.018 |
| [13] |
王文全, 苏仕琪, 闫妍. 基于反馈力浸入边界法模拟复杂动边界流动[J]. 计算力学学报, 2015, 32(4): 560. WANG Wenquan, SU Shiqi, YAN Yan. Numerical simulation on complex moving boundary flow using feedback immersed boundary method[J]. Chinese Journal of Computational Mechanics, 2015, 32(4): 560. DOI:10.7511/jslx201504019 |
| [14] |
MOHD-YUSOF J. Combined immersed boundary/b-spline methods for simulation of flow in complex geometries[C]//Center for Turbulence Research, Annual Research Briefs. 1997: 317
|
| [15] |
YANG Xiaolei. A smoothing technique for discrete delta functions with application to immersed boundary method in moving boundary simulations[J]. Journal of Computational Physics, 2009, 228: 7821. DOI:10.1016/j.jcp.2009.07.023 |
| [16] |
宫兆新, 鲁传敬, 黄华雄. 正则化δ函数对浸入边界法精度的影响[J]. 应用数学和力学, 2012, 33(11): 1352. GONG Zhaoxin, LU Chuanjing, HUANG Huaxiong. Effect of the regularized Delta function on the accuracy of the immersed boundary method[J]. Applied Mathematics and Mechanics, 2012, 33(11): 1352. DOI:10.3879/j.issn.1000-0887.2012.11.010 |
| [17] |
李秋实, 徐飞, 李志平. 一种包含运动边界的高精度流场数值计算方法[J]. 航空学报, 2013, 35(7): 1815. LI Qiushi, XU Fei, LI Zhiping. A numerical method for simulating flow involving moving boundaries with high order accuracy[J]. Acta Aeronautica et Astronautica Sinica, 2013, 35(7): 1815. DOI:10.7527/S1000-6893.201300456 |
| [18] |
及春宁, 刘爽, 杨立红, 等. 基于嵌入式迭代的高精度浸入边界法[J]. 天津大学学报, 2014, 47(5): 377. JI Chunning, LIU Shuang, YANG Lihong, et al. An accurate immersed boundary method based on built-in iterations[J]. Journal of Tianjin University, 2014, 47(5): 377. DOI:10.11784/tdxbz201207069 |
| [19] |
杨枭枭, 及春宁, 陈威霖, 等. 三角形排列圆柱绕流尾流模式及其流体力特性[J]. 水动力学研究与进展(A辑), 2019, 34(1): 69. YANG Xiaoxiao, JI Chunning, CHEN Weilin, et al. Wake patterns and hydrodynamics force of flow around circular cylinders in an equilateral triangular arrangement[J]. Chinese Journal of Hydrodynamics, 2019, 34(1): 69. |
| [20] |
陈威霖, 及春宁, 许栋. 不同控制角下附加圆柱对圆柱涡激振动影响[J]. 力学学报, 2019, 51(2): 432. CHEN Weilin, JI Chunning, XU Dong. Effects of the added cylinders with different control angles on the vortex-induced vibrations of a circular cylinder[J]. Chinese Journal of Teheoretical and Applied Mechanics, 2019, 51(2): 432. DOI:10.6052/0459-1879-18-208 |
| [21] |
PALMA P D, TULLIO D, PASCAZIO G, et al. An immersed-boundary method for compressible viscous flows[J]. Computers & Fluids, 2006, 35(7): 693. DOI:10.1016/j.compfluid.2006.01.004 |
| [22] |
TULLIO D, PALMA P D, IACCARINO G, et al. An immersed boundary method for compressible flows using local grid refinement[J]. Journal of Computational Physics, 2007, 225(2): 2098. DOI:10.1016/j.jcp.2007.03.008 |
| [23] |
QIU Y L, SHU C, WU J, et al. A boundary condition-enforced immersed boundary method for compressible viscous flows[J]. Computers & Fluids, 2016, 136: 104. DOI:10.1016/j.compfluid.2016.06.004 |
| [24] |
BAILOOR S, ANNANGI A, SEO J H, et al. A fluid-structure interaction solver for compressible flows with applications in blast loading on thin elastic structures[J]. Applied Mathematical Modelling, 2017, 52: 470. DOI:10.1016/j.apm.2017.05.038 |
| [25] |
SCHLANDERER S C, WEYMOUTH G D, SANDBERG R D. The boundary data immersion method for compressible flows with application to aero-acoustics[J]. Journal of Computational Physics, 2016, 333: 440. DOI:10.1016/j.jcp.2016.12.050 |
| [26] |
YABE T, YUAN P. Unified numerical procedure for compressible and incompressible flow[J]. The Physical Society of Japan, 1991, 60(7): 2105. |
| [27] |
CAIDEN R, FEDKIW R P, ANDERSON C. A numerical method for two phase flow consisting of separate compressible and incompressible regions[J]. Journal of Computational Physics, 2001, 166: 1. DOI:10.1006/jcph.2000.6624 |
| [28] |
NOURGALIEV R, DINH T, THEOFANOUS T. Adaptive characteristics-based matching for compressible multifluid dynamics[J]. Journal of Computational Physics, 2006, 213: 500. DOI:10.1016/j.jcp.2005.08.028 |
| [29] |
CALTAGIRONE C P, VINCENT S, CARUYER C. A multiphase compressible model for the simulation of multiphase flows[J]. Computers and Fluids, 2011, 50: 24. DOI:10.1016/j.compfluid.2011.06.011 |
| [30] |
UHLMANN M. An immersed boundary method with direct forcing for the simulation of particulate flows[J]. Journal of Computational Physics, 2005, 209: 448. DOI:10.1016/j.jcp.2005.03.017 |
| [31] |
LIU C, ZHENG X, SUNG C. Preconditioned multigrid methods for unsteady incompressible flows[J]. Journal of Computational Physics, 1998, 139: 35. DOI:10.1006/jcph.1997.5859 |
| [32] |
PARK J, KWON K, CHOI H. Numerical solutions of flow past a circular cylinder at Reynolds numbers up to 160[J]. Journal of Mechanical Science and Technology, 1998, 12(6): 1200. DOI:10.1007/bf02942594 |
| [33] |
RAJANI B N, LANKA H G, MAJUMDAR S. Laminar flow past a circular cylinder at Reynolds number varying from 50 to 5000: NALPDCF0501[R]. Bangalore: National Aerospace Laboratories, 2005
|
| [34] |
HOMANN F. Influence of higher viscosity on flow around cylinder[J]. Forschung im Ingenieurwesen-engineering Research (German), 1936, 17: 1. |
| [35] |
NORBERG C. Pressure forces on a circular cylinder in cross flow[C]// Bluff-Body Wakes, Dynamics and Instabilities. Berlin Heidelberg: Springer, 1993: 275
|
| [36] |
LU X Y, DALTON C. Calculation of the timing of vortex formation from an oscillating cylinder[J]. Journal of Fluids and Structures, 1996, 10(5): 527. DOI:10.1006/jfls.1996.0035 |
| [37] |
KAJISHIMA T, TAKIGUCHI S. Interaction between particle clusters and particle-induced turbulence[J]. International Journal of Heat and Fluid Flow, 2002, 23: 639. DOI:10.1016/S0142-727X(02)00159-5 |
 2020, Vol. 52
2020, Vol. 52


